Умножение и: Умножение и деление целых чисел

Умножение и деление целых чисел

При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.

При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

---

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

---

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

---

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

---

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

---

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. В таких случаях применяется следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают короче:  −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

2 × 3 = 6

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить множимое 2. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

---

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно решение записывают покороче:

12 × (−5) = −60

---

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Запишем решение покороче:

10 × (−4) × 2 = −40 × 2 = −80

---

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях применяется следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Запишем решение покороче (−4) × (−2) = 8

---

Пример 5. Найти значение выражения  −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число  −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = −2 × 6 + (−2) × 4

Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

Первое действие:

−2 × 6 = −12

Второе действие:

−2 × 4 = −8

Третье действие:

−12 + (−8) = −20

Значит значение выражения −2 × (6 + 4) равно −20

Запишем решение покороче:

−2 × (6 + 4) = (−12) + (−8) = −20

---

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

(−2) × (−3) = 6

Второе действие:

6 × (−4) = −(6 × 4) = −24

Значит значение выражения (−2) × (−3) × (−4) равно −24

Запишем решение покороче:

(−2) × (−3) × (−4) = 6 × (−4) = −24

---

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4,  8 – это делимое, 2 – делитель, 4 – частное.

Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

---

На ноль делить нельзя

Любое число запрещено делить на ноль.

Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2

Точно так же можно поступать и с другими выражениями. Если к примеру 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6

12 : 6 = 2

Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

5 × 0 = 0

Если записать это выражение в обратном порядке, то получим:

0 : 0 = 5

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

0 : 0 = 2

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8

… × 2 = 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

8 : 2 = 4

Получили число 4. Запишем его вместо многоточия:

4 × 2 = 8

Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

… × 0 = 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

,  при b ≠ 0

Это выражение можно прочитать так:

Число a можно разделить на число b, при условии, что b не равно нулю.

---

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

(12 × 4) : (4 × 4) = 48 : 16 = 3

Получили ответ 3.

Теперь попробуем не умножить, а разделить делимое и делитель на число 4

(12 : 4) : (4 : 4) = 3 : 1 = 3

Снова получили ответ 3.

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

---

Деление целых чисел

Пример 1. Найти значение выражения 12 : (−2)

Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.

12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6

Обычно записывают покороче:

12 : (−2) = −6

---

Пример 2. Найти значение выражения −24 : 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.

−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4

Запишем решение покороче:

−24 : 6 = −4

---

Пример 3. Найти значение выражения −45 : (−5)

Это деление отрицательных чисел. Чтобы решить этот пример, нужно

модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

−45 : (−5) = |−45| : |−5| = 45 : 5 = 9

Запишем решение покороче:

−45 : (−5) = 9

---

Пример 4. Найти значение выражения −36 : (−4) : (−3)

Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим −36 на (−4), и полученное число разделим на −3

Первое действие:

−36 : (−4) = |−36| : |−4| = 36 : 4 = 9

Второе действие:

9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3

Запишем решение покороче:

−36 : (−4) : (−3) = 9 : (−3) = −3

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Свойства умножения и деления. Распределительное и переместительное свойство

Поможем понять и полюбить математику

Начать учиться

На уроках математики в 5 классе мы тренируемся умножать, делить, складывать и вычитать. Самое интересное — это хитрить и упрощать выражения. В этом помогают свойства умножения и деления, про которые мы сейчас расскажем.

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b

верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

Примеры:

• 6 * 5 = 5 * 6 = 30;
• 4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

Пример:

• 3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

или

• 3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

С учетом переместительного свойства умножения можно переформулировать правило так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

С учетом переместительного свойства умножения можно переформулировать правило так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел Деление на нуль невозможно. Деление нуля на число: 0 : a = 0. Деление равных чисел: a : a = 1. Деление на единицу: a : 1 = a. Для деления переместительное свойства не выполняется: a : b ≠ b : a. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c). Деление произведения на число: (a * b) : c = (a : c) * b , если a делится на c; (a * b) : c = a * (b : с), если b делится на c; (a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c. Деление числа на произведение: a : (b * c) = (a : b) : c = (a : c) : b.

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 2

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Ответ: 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Сравнение десятичных дробей

К следующей статье

Свойства сложения и вычитания

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Все умножение на умножении.

Учителя и дети любят наши:

• Стратегии построения памяти
• Автобирные викторины
• премиум-членство
• .

  Умножение, сложение, вычитание, деление, классная комната

  Премиум-членство

  Supercharged LEARNING

  Тесты с автооценкой

  Умножение, сложение, вычитание, деление

  Успех для ВСЕХ детей

  От второго класса до старшей школы, с особыми потребностями для одаренных, это работает и работает быстро!

  3 наиболее часто задаваемых вопроса

  • Сколько времени потребуется, чтобы узнать факты?

    Это действительно зависит от усилий и времени ребенка. Большинство учителей планируют от одного до трех месяцев на освоение умножения. Используя наш метод картинок/рассказов, многие ученики выучили их менее чем за неделю. Запланируйте три недели, если ваш ребенок плохо знаком с фактами умножения. После того, как ребенок узнал факты, важно, чтобы они продолжали практиковаться в течение от 6 месяцев до года, чтобы закрепить их в долговременной памяти.

  • В каком возрасте следует начинать ребенку?

    Обычно диапазон составляет от семи до десяти лет, но дети намного младше узнают факты умножения. Наша система очень успешно использовалась во многих средних и старших школах

  • У меня сработала механическая память. Почему это не сработает для моего ребенка?

    Многие взрослые, кажется, забыли, как сложно и долго было изучать факты умножения. Механическая память, похоже, плохо работает для большинства детей. Запоминание фактов умножения не должно быть трудным и разочаровывающим. Исследования говорят, что лучший способ запомнить — это использовать визуальные образы и истории. Это именно то, что делает наша система. Это действительно может быть ИНТЕРЕСНО!

  Автоматически адаптируется, чтобы дети быстрее учились.

  Автоматически отслеживает и адаптируется к индивидуальным потребностям учащихся (При наличии Премиум-членства вся реклама удаляется — Игры и занятия отображаются на весь экран)

• Дети действительно ХОТЯТ практиковать факты умножения (Дети любят игры и занятия.)

• Работает! (Хотя многие родители и учителя настроены скептически, когда они попробуют, они будут в восторге от результатов.)

• Облегчает рабочую нагрузку (система исправляет и записывает викторины и отслеживает прогресс во время игр, занятий и викторин .)

• Успех для ВСЕХ детей (От второго класса до старшей школы, особые потребности для одаренных, это работает и работает быстро!)

Отзывы

Что мне больше всего нравится в Премиум-системе обучения, так это то, что она позволяет мне отслеживать успеваемость учащихся в режиме реального времени. Студентам это нравится, потому что с Zippy в качестве руководства и играми, чтобы развлечь их, программа больше похожа на игру, чем на работу.

Скотт, учитель третьего класса

Каждый учащийся получает пользу от этого уникального подхода к изучению фактов умножения. Настоящая сила этой программы заключается в спасении, которое она предлагает учащимся с ограниченными академическими возможностями и учащимся из групп риска.

Кароль, учитель третьего класса

У моего сына в прошлом году были проблемы с математикой, постепенно он терял уверенность в себе. Я знал, что это потому, что он просто не знал этих фактов. Он почти завершил программу и тесты со 100% точностью

Дайан, родитель

Предыдущие следующие

Увлекательные

• Смешные анимационные фильмы
• . Увлекательные мероприятия
• Multi-Player Соревнования

.0002 Самостоятельно

• Автоматические вмеряния к способности
• игр приспосабливаются к ученику
• Veizzes Monitor Возможность
• Ежедневная автоматическая настройка

Insight

• Инструменты отчетности
• Интуитивная графическая графика
• .
• Беглость, точность, время

Умножение и деление: Введение в умножение

Урок 1: Введение в умножение

Что такое умножение?

Когда вы умножаете , вы фактически добавляете определенное число более одного раза. Например, если вы съели 4 конфеты, затем съели еще 4, затем еще 4, вы можете сказать, что вы умножили на количество съеденных конфет.

В реальной жизни умножение происходит постоянно. Например, рассмотрим ситуацию ниже.

• Представьте, что вы покупаете 6 банок газировки. У вас есть 1 набор из 6 банок.

• В терминах умножения мы бы сказали, что у вас есть 1 x 6 банок. Вы можете прочитать это как один раз шесть .

• Что, если вы купите 2 упаковки по 6 штук?

• Теперь у вас есть 2 комплекта по 6 банок или 2 x 6 банок. Это 2 умножить на столько банок, сколько у вас было раньше!

• Это может продолжаться вечно. Как насчет 3 x 6 банок или в 3 раза больше банок?

• Теперь у вас есть 8 x 6 банок. Это 8 раз столько банок, сколько у вас было в начале.

• Важно знать, что числа в выражении умножения можно записывать в любом порядке.

• Таким образом, 8 x 6 также можно записать как 6 x 8.

• Другими словами, 6 x 8 = 8 x 6.

• Итак, если вы купили 6 наборов по 8 банок в каждом. .

• Итак, если вы купили 6 комплектов по 8 банок в каждом… это будет тот же , что и 8 комплектов по 6 банок в каждом. У вас будет точно такое же количество банок.

Запись выражения умножения

Как вы только что видели, выражение умножения записывается следующим образом:

2 x 6

два раза 9 Символ умножения (x) также можно назвать символом умножения на . Помните, вы всегда ставите между числами, которые хотите умножить.

Многие жизненные ситуации можно выразить с помощью умножения. Например, представьте, что вы хотите испечь три торта. В рецепте сказано, что на каждую лепешку понадобится два яйца. Другими словами, вам нужно 3 х 2 яйца.

Попробуйте!

Запишите следующие ситуации в виде выражений умножения. Пока не пытайтесь их решить.

У вас есть шесть пар носков по два в каждой.

Вам необходимо принимать по две таблетки по четыре раза в день.

Каждый пакет содержит девять пончиков. Вы покупаете три пакета .

Решение задач на умножение

Счет и сложение можно использовать для решения небольших простых задач на умножение. Например, на последней странице мы пытались вычислить, сколько яиц нам понадобится, чтобы испечь три торта. Для каждого торта требовалось два яйца, поэтому мы записали задачу так:

3 x 2

Как вы уже знаете, это выражение означает три раза по два , или 3 лепешки с 2 яйцами в каждой. Это простая проблема. Чтобы решить ее, вы можете либо подсчитать яиц, либо добавить их : 2 + 2 + 2. В любом случае ответ будет 6. Мы знаем, что 3 x 2 = 6.

Хотя это работает для небольших задач, подсчет больших чисел может занять много времени — и это тоже довольно скучно.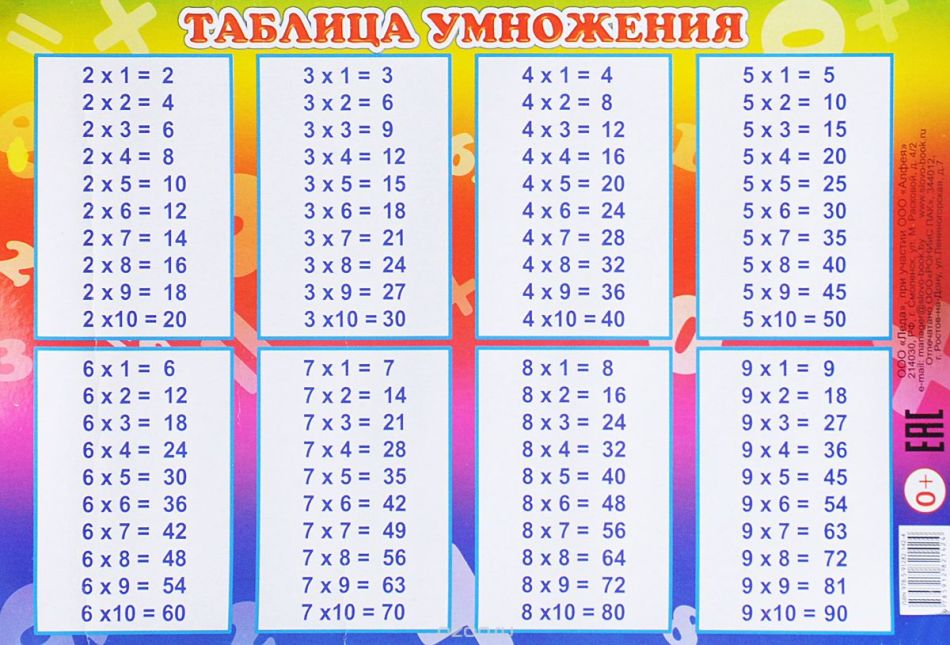 По этой причине большинство людей запоминают общих задач на умножение, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. Чем больше ты потренируйтесь , тем легче будет запомнить ответы на задачи.

До тех пор вы можете решать задачи на умножение с помощью таблицы умножения . Ее также называют таблицей умножения на . Таблица умножения — это таблица с ответами на все задачи на умножение, в которых используются числа от 1 до 12. Она проста в использовании. Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.

• Это таблица умножения на .

• В верхней части таблицы умножения вы можете найти числа от 1 до 12. Они идут по порядку от слева направо.

• Каждое из чисел сверху находится в начале столбца . Например, это столбец, который идет с 5. Все числа в этом столбце кратны из 5. Это означает, что все эти числа можно получить, умножив 5.

• Вы также можете найти числа от 1 до 12 в левой части таблицы умножения. Здесь числа идут по порядку от сверху вниз .

• Каждое из этих чисел является началом строки . Эта строка содержит числа, кратные 4.

• Давайте попробуем решить задачу с таблицей умножения. Начнем с 7 x 3.

• В 7 x 3 найдите первое число, на которое мы умножаем, слева от знака времени. Это 7.

• Найдите 7 вверху таблицы.

• Далее, посмотрите на второе число, на которое мы умножаем, справа от знака времени. В 7 х 3 это 3,

• Найдите цифру 3 сбоку от таблицы.

• Ответ будет в квадрате, где столбец 7 и ряд 3 встречаются и перекрываются.

• Это квадрат, 21. Итак, 7 x 3 равно 21.

• Попробуем еще раз. На этот раз мы решим 5 x 9.

• Во-первых, для 5 x 9 мы находим столбец 5.

• Далее, для 5 x 9, мы найдем 9-й ряд.

  No related posts.