Пускаем корни — Popmath
Скажите, какого это — ощущать себя обманутым, покинутым, преданным теми, кому больше всего доверял? Как справиться с этой пожирающей изнутри экзистенциальной бездной? Только не надо говорить, что вам такое не известно, так как до сих пор личная жизнь была образцовой — дело вовсе не в этом. Предателя нужно искать не в воспоминаниях и выцветших телефонных книгах, а в наших статьях. И этот предатель — мы. В прошлый раз, говоря о степенях, мы сознательно, с циничным и холодным расчётом умолчали о целом типе степеней, без которого разобраться в полном курсе математики вряд ли получится.
В принципе, это можно было заметить сразу. Говоря о том, как возводить в степень различные дроби, мы не упомянули обратную ситуацию — а что если сама степень является дробной? В таком случае привычная логика (это в которой можно использовать кубики) даёт нехилый сбой — умножить число само на себя неполное число раз едва ли получится, тем более представить всё это через сложение. Наверное, пора тянуться к справочникам, наизусть заучивать определения и десяток-другой не самых симпатичных формул? Не стоит отчаиваться, давайте разрешим эту задачу так же, как и все другие — последовательно, мудро и с неизменным юмором.
Наверное, пора тянуться к справочникам, наизусть заучивать определения и десяток-другой не самых симпатичных формул? Не стоит отчаиваться, давайте разрешим эту задачу так же, как и все другие — последовательно, мудро и с неизменным юмором.
Начнём с простого. Вот, допустим, перед нами возникло что-то вроде , как с этим быть? Сходу, как уже сказали, сделать ничего не получится, а направления, в котором следует мыслить, нам никто ещё не подсказал. Выхода не остаётся, кроме как исходить из уже известного. А что известно-то? Вроде как это бессмыслица. Но нами было установлено, что при умножении элементов с одинаковыми основаниями показатели степеней складываются. Так же было замечено, что любое число в первой степени это оно само и есть. Значит, можно сказать, что . Что из этого следует?
А следует, что это такое число, которое при умножении само на себя (т.е. возведении в квадрат) даёт двойку. Опираясь на прошлые рисунки, сразу скажем, что тут мы выполняем обратную задачу. Если раньше у нас были какие-то числа и мы строили на их основе квадраты, то теперь наоборот, у нас уже есть некий квадрат с заданный площадью, а нам нужно найти его сторону. Число в центре здесь указывает на общую площадь фигуры, а числа около сторон — на их длины:
Число в центре здесь указывает на общую площадь фигуры, а числа около сторон — на их длины:
Записывается это следующим образом: и читается как «квадратный корень из двух». Нелепый знак называется «радикал», а операция, которую он обозначает — «извлечением арифметического корня».
Эм…Шеф, не гони лошадей. Почему корень квадратный-то, да и только? Ведь указанная нами выше логика работает и для всех остальных показателей. В том смысле, что можно определить степень , по которой и так далее, вплоть до степени .
Подмечено верно, корни могут быть не только квадратными, также они могут быть и кубическими (то есть, когда степень корня это тройка), и хоть пятой, хоть любой другой степени. Записывается это всё путём указания верхнего индекса для корня, к примеру это «корень третьей степени из двойки», ну а это «корень степени из «.
А как так вообще вдруг получилось, что степень это квадрат, а — это куб? Ой, да мы же это проходили уже! Квадрат это значит, что мы такой квадратик нарисовать можем. А в третьей степени, это значит, что кубик с похожими сторонами можно найти везде, хоть бы и в магазине игрушек. А вот со всем, что больше, ну или меньше, такого ясного-понятного не представить и с реальными предметами не проделать. Печаль-тоска-огорчение…
А в третьей степени, это значит, что кубик с похожими сторонами можно найти везде, хоть бы и в магазине игрушек. А вот со всем, что больше, ну или меньше, такого ясного-понятного не представить и с реальными предметами не проделать. Печаль-тоска-огорчение…
Надо признать, что сама по себе запись может оказаться достаточно путаной. В частности, тут есть место извечной людской неаккуратности — знак корня постоянно забывают ясно закрыть, по итогам чего совершенно невозможно понять, что является реальным подкоренным выражением, а что стоит совершенно независимо. Подкоренное выражение — это то, что и заносится под знак корня, между прочим. Вообще, если что-то когда-то кажется недостаточно понятным и удобным (например, какое-то объяснение в учебнике), то скорее всего оно так и есть, первое впечатление не обманывает.
Если уж говорить о путаности, то надо заметить, что нами был упущен ещё один важный момент, всё ещё касающийся дробных степеней. Как видите, эта тема — просто-таки непаханое поле для всяких затруднений и неприятностей. Со свойственным нашему изложению изяществу мы показали, что , но что делать, если наша степень такова, что у неё в числителе стоит не единица? Например, как понимать запись вида ? Для ответа на этот вопрос следует прибегнуть к уже знакомой нам логике — будем отталкиваться от единицы.
Со свойственным нашему изложению изяществу мы показали, что , но что делать, если наша степень такова, что у неё в числителе стоит не единица? Например, как понимать запись вида ? Для ответа на этот вопрос следует прибегнуть к уже знакомой нам логике — будем отталкиваться от единицы.
Мы знаем, что , этого должно быть достаточно. Помня о сложении степеней при умножении, имеем . Следовательно, для нахождения искомого значения нам надо разделить на , иначе говоря, получить дробь вида . Собственно, это верно не только для , а вообще для любого случая:
Отлично, с задачей мы справились, можно идти дальше!.. Как это не справились? Вот же формула, всё выведено, измерено, что не так? А… Вам интуитивность какая-то ещё нужна, наглядность… Ну хорошо, давайте попробуем. Для этого воспользуемся подходящим примером, например, взяв в качестве опытного материала восьмёрку. Чему равна ? Согласно нашей инструкции, нужно разделить на , что мы и сделаем, попутно обнаружив, что кубический корень восьмёрки равен , т. к. . Итак, считаем:
к. . Итак, считаем:
Обратим внимание, что , то есть, мы извлекли корень в той степени, на которую указывал в выражении знаменатель, а полученный результат возвели в степень, на которую указывал числитель. Совпадение? Не думаем!
Смотрите, давайте рассмотрим это явление подробнее, только подберём пример посложнее, например, . Как понимать вот это всё? Да очень просто, мы всего лишь представляем это слабо понятное месиво в более привычном для нас виде .
Видите? В этом нет ничего сложного, ведь если разложим любую дробную степень на сумму степеней с числителем равным единице (то есть, на корни в степени знаменателя), то смысл этого числителя станет понятным — он указывает нам на то, сколько раз была перемножена сама на себя исходная степень. Идея это достаточно простая, но давайте ещё раз проговорим. Вот у нас , что это? Это корень степени , возведённый в -ю степень. Почему? Потому что выше мы показали, что данное выражение раскладывается на множителей, где у каждого в числителе степени стоит единица. А сколько будет, если пять единиц сложить друг с другом? То-то же!
А сколько будет, если пять единиц сложить друг с другом? То-то же!
Давайте наконец жирно подчеркнём то, что с таким трудом узнали:
Знаменатель — это корень. Числитель — это степень. Если забыли, просто вспомните, что квадратный корень это степень , а уж у него-то понятно, что обозначает знаменатель. И да — в степень возводится весь корень, а не подкоренное выражение. Это надо запомнить лучше, чем пароль от платного аккаунта на pornhub. Хотя минуточку… вдруг запоминание подобной ерунды как-то помешает по памяти воспроизвести сам пароль? Давайте-ка убедимся, что это действительно необходимо.
Допустим, что у нас есть всё то же , которое, как только что установлено, равно . А чему тогда будет равно ? Давайте посмотрим. У нас есть , из которого извлекается корень степени , то есть наше возводится в степень , при возведении одной степени в другую показатели перемножаются, значит, получаем:
Чудны дела твои, Господи!
А-ха-ха, это опять шутка, ведь никакого бога нет. Тем не менее, результат примечателен — в силу специфики указанной операции нет разницы, имеем мы дело со степенью выражения с корнем в своём составе, или со степенью подкоренного выражения как такового. А знаете, как это легко запомнить? Вообще не приплетая корни, ведь без этих обозначений никакой неразберихи нет вообще, так как мы точно знаем какие переменные в каких отношениях друг с другом находятся, ну и где у них там все степени стоят.
Тем не менее, результат примечателен — в силу специфики указанной операции нет разницы, имеем мы дело со степенью выражения с корнем в своём составе, или со степенью подкоренного выражения как такового. А знаете, как это легко запомнить? Вообще не приплетая корни, ведь без этих обозначений никакой неразберихи нет вообще, так как мы точно знаем какие переменные в каких отношениях друг с другом находятся, ну и где у них там все степени стоят.
При кажущейся простоте всего упомянутого следует помнить, что большой проблемой здесь выступает отсутствие внятной иллюстрации происходящего. Конечно, в случае с уже разобранным примером вы сначала можете найти площадь квадрата , затем использовать эти данные для нахождения площади квадрата со сторонами в , ну а потом уже найти финальную площадь прямоугольника , однако согласитесь, что это скорее усложняет дело, чем его упрощает.
Во всём этом проявляется одно интересное, даже удивительное свойство математического мышления — оторванность от «реальных примеров». Уяснив на конкретной иллюстрации в чём смысл той или иной операции, мы можем бесконечно её усложнять, в том числе и до таких случаев, когда обычное, ничем не расширенное человеческое мышление представить каких-то визуальных воплощений оказывается не в силах. Собственно, если бы не эта особенность, то весь изучаемый материал ограничивался бы… ну… примерно тем, чем он и ограничивается в школе и вузах…
Уяснив на конкретной иллюстрации в чём смысл той или иной операции, мы можем бесконечно её усложнять, в том числе и до таких случаев, когда обычное, ничем не расширенное человеческое мышление представить каких-то визуальных воплощений оказывается не в силах. Собственно, если бы не эта особенность, то весь изучаемый материал ограничивался бы… ну… примерно тем, чем он и ограничивается в школе и вузах…
Да нет, опять шутим, конечно, даже в базовом школьном материале содержится куда больше идей, чем те, которые можно получить, чертя многоугольники на песке.
Теперь, когда мы не только раскрыли секрет непонятных степеней, но и снабдили всё это небольшим философским комментарием, перейдём к свойствам операций с арифметическим корнем. Именно к тем свойствам, которые по несколько вечеров в неделю заучивают и повторяют девочки-отличницы, и которых почти не помнят их ровесники-мальчики, больше увлечённые вопросами собственного полового созревания. Именно к тем свойствам, без знания которых у вас не получится нормально написать почти ни одну контрольную, не говоря уже о сдаче итоговых экзаменов. Короче говоря, именно к важным, обязательным для успешного понимания всего, что только можно, свойствам.
Короче говоря, именно к важным, обязательным для успешного понимания всего, что только можно, свойствам.
Свойства эти… как бы вам помягче сказать… они отсутствуют. Их нет. Серьёзно, на этот раз без шуток. Нет никаких особенных свойств операций с корнями, которые надо было бы запоминать, записывать на бедре под колготками, проносить на шпаргалках в рукаве. Почему? Да потому что абсолютно все «свойства операций с арифметическим корнем» это уже до боли (приятной) знакомые свойства операций со степенями! Несмотря на простоту этого факта, он почему-то часто ускользает от внимания не столько учеников и студентов, сколько уважаемых педагогов с многолетним опытом и общественным признанием.
Повторяем, это не шутка, всё очень серьёзно. Покажем свою правоту, пройдясь по каждому из этих «уникальных свойств» в отдельности.
Начнём с того, что часто называют «правилом вынесения и внесения под корень» и с чем гарантированно хоть раз путался любой, кто с этим сталкивался. Как выносить и вносить, да и причём тут степени? Внимание на экран:
Таким образом, «вынесение из под корня» это обычная формула для степени произведения, которую мы детально препарировали в предыдущем материале. Для большей очевидности поясним всё это на примере. Вот у нас есть и от нас требуется «вынести множитель из под знака корня», как нам поступить?
Для большей очевидности поясним всё это на примере. Вот у нас есть и от нас требуется «вынести множитель из под знака корня», как нам поступить?
А так, что мы вообще забываем про какие-то корни и имеем дело только со степенями. . Иными словами, мы делим подкоренное выражение на две (или больше) части, извлекаем корень оттуда, откуда можно, и записываем итоговое произведение.
Аналогично решается и задача с «внесением под корень»: . То есть, мы просто ищем изначально заданное число, от которого и была вычислена степень . Запись имеет ровно такой смысл, ведь степени при такой операции перемножаются, т.е. взаимно сокращаются, оставляя .
Э-э-э!! Не выношу вообще тех, которые мутят что-то, если на деле ситуация и так ясная совершенно. Зачем вилять, ерунду городить, когда напрямую сказать можно? Не надо ни про какие «корни» думать, есть просто дробные степени — вот это всё, закрыли ситуацию. Попадись такие умники моему дяде Агабеку…
Чего там ещё осталось? Например, нахождение корней от дроби. Типа, стоит такая запись , и что с ней делать? Эх, сложно это всё, придётся ручку доставать, заучивать, повторять. Хотя нет, нам ничего этого делать никогда не придётся. Почему? Ответ такой же, как и в случае последних вопросов — мы знаем про операции со степенями. Не станем скрывать свои знания:
Типа, стоит такая запись , и что с ней делать? Эх, сложно это всё, придётся ручку доставать, заучивать, повторять. Хотя нет, нам ничего этого делать никогда не придётся. Почему? Ответ такой же, как и в случае последних вопросов — мы знаем про операции со степенями. Не станем скрывать свои знания:
Да-да, посмотрите на это хорошенько, не отводите взгляд. Тут ровно то, что мы пристально разглядели раньше — возведение дроби в степень. Кто бы мог подумать, что благодаря этому мы больше никогда не запутаемся во всех этих корнях? Повторяйте за нами: «больше никогда не запутаемся».
Остаётся совсем немного. Например, как не указать на такой необычный факт, что при умножении чисел на дробь возможны сокращения? Правда-правда, вы только не пугайтесь, но всё именно так и есть. Вот как эта истина выглядит на величественном языке арифметических корней:
Не впечатляет? Это всё потому, что вы слишком испорчены пониманием того, что корни это сокращённый вариант записи степеней (это мы не устанем повторять, совсем как ваша мама, умоляющая надеть шапку при температуре на улице меньше градусов). Не знай вы этого обстоятельства, то перед очередным зачётом могли бы не одну ночь развлекали себя мыслью «разве это всё кто-нибудь может запомнить?».
Не знай вы этого обстоятельства, то перед очередным зачётом могли бы не одну ночь развлекали себя мыслью «разве это всё кто-нибудь может запомнить?».
Совсем уж напоследок упомянем и особый случай. Особый случай это когда люди, составляющие задания для школьных и студенческих учебников, по какой-то причине не очень довольны своей жизнью. Печально, зато у них в руках есть какая-никакая, а власть. Что надо с властью делать? Правильно, использовать её, чтобы отомстить тем, чья жизнь ещё полна радостей и перспектив — проклятым молодым поколениям. Как этого добиться? Путём составления излишне сложных и неприятных задач, решение которых ничуть не приближает к пониманию сути производимых операций, да и вообще едва ли когда либо ещё пригодится.
Почётное место в списке таких упражнений занимают всевозможные «лесенки». Когда одно нагромождается на другое, тем более с учётом низкого качества типографии, достигается главная цель — морально унизить и потрясти читателя, создать ощущение вала информации, тотальной неразберихи и обречённости на поражение.
Есть лесенки и применительно к корням. Давайте их сейчас уничтожим (раз добраться до авторов-составителей всё равно не получится):
По мере просмотра этого упрощения у вас может возникнуть закономерный вопрос — если итоговое выражение достаточно простое, то зачем в самом начале записывать его таким чудовищным образом? А затем, читатель, чтобы ты подольше мучался, пытаясь привести его в удобоваримый вид.
Вообще, по итогам прочтения статьи у вас могло сложиться мнение, что сама манера обозначения арифметических корней нам не нравится. Что они неуинтуитивны, в них легко запутаться, а при записи от руки они требуют идеальной точности, либо велик риск по мере вычисления возвращаться на действий назад снова и снова. Что ж… это всё так и есть. В случае небольшого количества элементов использование корней и правда придаёт некоторую узнаваемость происходящему. А вот во всех остальных случаях от них стоит воздержаться. Если воздержание оказалось неудачным, то следует помнить главную максиму нашего изложения: корни — это степени.
Думаете, про степени уже знаете всё? Как бы ни так, ведь совсем по-близости уже рыскает в темноте очередная статья…
| |||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||
Степень, корни и радикалы: определение и примеры
Степени предлагают очень полезный способ упростить математическую запись, когда нам нужно многократно умножить число само на себя .
Если вам нужно отменить процесс , чтобы узнать, какое число было возведено в заданную степень, вы можете использовать корни , также известные как радикалы . В этой статье мы определим, что такое силы и корни, и более подробно объясним, как они связаны друг с другом, их правила и свойства, а также некоторые практические примеры их решения.
Определение степени
Степень — это степень, в которую возводится переменная. Например, выражение x² читается как «x в степени 2» или « x в квадрате» , что означает, что значение x умножается само на себя столько раз, сколько значение степени или степени . В этом случае x умножается сам на себя два раза. LOLA
Примеры мощностей
Если значение x равно 5, то мы можем вычислить следующим образом,
.
Точно так же мы можем вычислить и :
.
Обратите внимание: если вы уже знаете значение 5², равное 25, вы можете умножить его на 5 еще раз, чтобы получить значение 5³.
.
Важно помнить
Если переменная не имеет степени или степени, то предполагается, что она равна 1. Например,.
Кроме того, любая переменная в степени 0 (ноль) равна 1. По соглашению имеем .
По соглашению имеем .
Правила и свойства полномочий
Вы можете обратиться к Powers and Exponents за более подробным объяснением правил, которые необходимо использовать при работе с полномочиями.
Вот правила и свойства степеней, также известные как экспоненциальные свойства или законы, о которых вам нужно помнить.
| Совет: Легко запоминающееся имя свойства | Выражение свойства |
| Произведение на той же основе | |
| Same-exponent product | |
| Same-exponent division | |
| Double exponent | |
| Zero exponent | |
| Negative exponent | |
| Fractional exponent |
Свойства смарт-экспоненты — StudySmarter
Корни и радикалы Определение
Корни , также известные как радикалы , являются обратными степенями. Чтобы вычислить корень числа , нам нужно найти, какое число, умноженное само на себя n раз, дает нам число внутри подкоренного символа (x), которое называется подкоренным числом.
Чтобы вычислить корень числа , нам нужно найти, какое число, умноженное само на себя n раз, дает нам число внутри подкоренного символа (x), которое называется подкоренным числом.
Корень числа x
Примеры корней и радикалов
Индекс n корня может быть любым положительным целым числом, и он дает имя радикалу. Давайте рассмотрим примера наиболее распространенных корней и радикалов 9.0004, который вы найдете в Math.
Квадратные корни
Если , относится к квадратному корню числа x. В этом случае мы обычно опускаем 2 и пишем просто .
Если вы хотите найти квадратный корень из числа , вам нужно выяснить, какое число само по себе даст нам число внутри квадратного корня.
Если вы хотите найти квадратный корень из 25, вам нужно найти, какое число, умноженное само на себя, равно 25.
Но почему результат ± 5?
Это потому, что и 5, и -5 при возведении в степень 2 дают 25:
Следовательно, всегда есть два ответа , когда мы извлекаем квадратный корень из положительного числа.
Квадратный корень из отрицательного числа не имеет действительного решения; в этом случае требуются мнимые числа. Таким образом можно извлечь квадратный корень только из положительных чисел, потому что мы не можем найти ни одного числа, возведенного в степень 2, которое дало бы нам отрицательное число.
Типы квадратных корней
Квадратные корни можно классифицировать в соответствии с типом числа внутри корня следующим образом.
Квадратный корень из полных квадратов дает в результате целое число. Его очень легко вычислить, и его полезно помнить при работе с выражениями, содержащими степени и корни. Это помогает оценить и упростить эти типы выражений. Напоминаю, вот первая десятка.
Квадратный корень из чисел, не являющихся полными квадратами, не является целым числом. Они производят иррациональные числа с бесконечными десятичными знаками. Чтобы представить этот тип числа более точно, они оставлены в своей корневой форме.
.
Если число внутри корня имеет в качестве множителя квадратное число, то его можно упростить.
шаги, которые следует выполнить для упрощения радикалов :
Упростить термины
Cube COORTS
IAR, IAR. число х.
Если вы хотите найти кубический корень числа, нужно узнать какое число умножив само на себя трижды даст нам число внутри кубического корня. Это противоположно возведению числа в степень.
Если вы хотите найти кубический корень из 8, вам нужно найти, какое число, умноженное само на себя трижды, равно 8.
, на самом деле
Обратите внимание, что в этом случае у нас только один ответ , а не два . Это потому, что когда вы трижды умножаете отрицательное число само на себя, результат также будет отрицательным.
.
Следовательно, единственный возможный ответ — 2.
Кубические корни МОГУТ извлекать кубический корень из отрицательного числа.
Примеры корней и радикалов: Другие корни
4 й Корень: Правила аналогичны правилам для квадратных корней.
5 й Корень: Правила аналогичны кубическим корням.
Вообще говоря, нечетные корни имеют одно решение, а четные корни имеют два решения.
Правила и свойства корней и радикалов
При работе с корнями и радикалами необходимо помнить следующие правила и свойства:
Умножение корня на индекс
2 то же самое, вы можете
умножать подкоренные числа с разными числами внутри корня, просто объединяя их в один корень и перемножая числа внутри корня. Точно так же вы можете разделить корень на отдельные корни, используя множители.
.
.
Разделение радикалов
Точно так же, пока индексы корней одинаковы, вы можете разделить радикалы с разными числами внутри корня, объединив их в один корень и разделив числа внутри корня.
.
.
Умножение квадратного корня на самого себя
Если умножить квадратный корень из числа на самого себя , вы должны получить исходное значение.
.
.
Умножение числа на радикал
При умножении числа на радикал порядок множителей не имеет значения, и результатом должно быть число, за которым следует радикал.
.
.
Добавление или вычитание радикалов
Чтобы добавить или вычесть радикалы , число внутри корней должно быть одинаковым. Вы добавляете или вычитаете числа вне корня.
Чтобы добавить или вычесть радикалы, вам может понадобиться сначала упростить их, чтобы найти похожие термины.
Добавить нельзя, но можно сначала упростить,
.
Тогда вы можете решить .
Умножение скобок, содержащих радикалы
Чтобы умножить скобки , содержащие радикалы , каждый член в первой скобке должен быть умножен на каждый член во второй скобке. Затем вы можете комбинировать похожие термины.
Как записать силы как корни и корни как силы?
Чтобы записать степени в виде корней и корни в виде степеней, нам нужно понять, как работают дробные показатели.
Дробные экспоненты
Дробные экспоненты эквивалентны корням, как показано в следующем законе экспонент.
.
Используя это выражение, вы можете записать любой дробный показатель степени как корень .
Вы можете использовать то же выражение для записи любого корня в виде дробной степени .
Прочтите объяснение Rational Exponents, чтобы узнать больше об этой теме.
Разрешающие степени, корни и радикалы
Теперь, когда вы знаете, как работать с дробными показателями, и, учитывая законы показателей, у вас есть все необходимое для вычисления или упрощения выражений, содержащих степени, корни и радикалы. Вот некоторые примеры.
а) Вычислите или упростите
Вспоминая правильные квадраты, можно заменить на
не может быть далее упрощено, поэтому он оставлен в форме квадратного корня.
b) Вычислите или упростите
Преобразование корней в дробные показатели степени.
Использование закона показателей.
Использование закона показателей.
c) Оценить или упростить
Используя закон экспонент и упрощая .
Использование закона показателей.
D) Оценить или упростить
с использованием закона экспонентов переворачивает фракцию ,
Распределение показателя в числитель и знаменатель,
Использование Закона Экспонентов,
w3.org/1998/Math/MathML¨»«mo»=«/mo»«mfrac»«msup»«mi»x«/mi»«mn»9«/mn»«/msup»«mrow»«msup»«mi»x«/mi»«mn»3«/mn»«/msup»«msup»«mi»y«/mi»«mn»6«/mn»«/msup»«/mrow»«/mfrac»«/math»» role=»math» src=»data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHhtbG5zOndycz0iaHR0cDovL3d3dy53aXJpcy5jb20veG1sL21hdGhtbC1leHRlbnNpb24iIGhlaWdodD0iNDciIHdpZHRoPSI1OCIgd3JzOmJhc2VsaW5lPSIyOSI+PCEtLU1hdGhNTDogPG1hdGggeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzE5OTgvTWF0aC9NYXRoTUwiPjxtbz49PC9tbz48bWZyYWM+PG1zdXA+PG1pPng8L21pPjxtbj45PC9tbj48L21zdXA+PG1yb3c+PG1zdXA+PG1pPng8L21pPjxtbj4zPC9tbj48L21zdXA+PG1zdXA+PG1pPnk8L21pPjxtbj42PC9tbj48L21zdXA+PC9tcm93PjwvbWZyYWM+PC9tYXRoPi0tPjxkZWZzPjxzdHlsZSB0eXBlPSJ0ZXh0L2NzcyI+QGZvbnQtZmFjZXtmb250LWZhbWlseTonbWF0aDE3ZjM5ZjgzMTdmYmRiMTk4OGVmNGM2MjhlYic7c3JjOnVybChkYXRhOmZvbnQvdHJ1ZXR5cGU7Y2hhcnNldD11dGYtODtiYXNlNjQsQUFFQUFBQU1BSUFBQXdCQVQxTXZNaTdpQkJNQUFBRE1BQUFBVG1OdFlYREV2bUtVQUFBQkhBQUFBRFJqZG5RZ0RWVU5Cd0FBQVZBQUFBQTZaMng1Wm9QaTJWc0FBQUdNQUFBQXNtaGxZV1FRQzJxeEFBQUNRQUFBQURab2FHVmhDR3NYU0FBQUFuZ0FBQUFrYUcxMGVFMnJSa2NBQUFLY0FBQUFDR3h3WTJFQUhUd1lBQUFDcEFBQUFBeHRZWGh4QlQwRlBnQUFBckFBQUFBZ2JtRnRaYUJ4bFk0QUFBTFFBQUFCbjNCdmMzUUI5d0Q2QUFBRWNBQUFBQ0J3Y21Wd2ExdXJhZ0FBQkpBQUFBQVVBQUFEU3dHUUFBVUFBQVFBQkFBQUFBQUFCQUFFQUFBQUFBQUFBUUVBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUNBZ0lDQUFBQUFnMVVBRGV2OTZBQUFENkFDV0FBQUFBQUFDQUFFQUFRQUFBQlFBQXdBQkFBQUFGQUFFQUNBQUFBQUVBQVFBQVFBQUFEMy8vd0FBQUQzLy8vL0VBQUVBQUFBQUFBQUJWQU1zQUlBQkFBQldBQ29DV0FJZUFRNEJMQUlzQUZvQmdBS0FBS0FBMUFDQUFBQUFBQUFBQUNzQVZRQ0FBS3NBMVFFQUFTc0FCd0FBQUFJQVZRQUFBd0FEcXdBREFBY0FBRE1SSVJFbElSRWhWUUtyL2FzQ0FQNEFBNnY4VlZVREFBQUNBSUFBNndMVkFoVUFBd0FIQUdVWUFiQUlFTEFHMUxBR0VMQUYxTEFJRUxBQjFMQUJFTEFBMUxBR0VMQUhQTEFGRUxBRVBMQUJFTEFDUExBQUVMQURQQUN3Q0JDd0J0U3dCaEN3QjlTd0J4Q3dBZFN3QVJDd0F0U3dCaEN3QlR5d0J4Q3dCRHl3QVJDd0FEeXdBaEN3QXp3eE1CTWhOU0VkQVNFMWdBSlYvYXNDVlFIQVZkVlZWUUFBQUFFQUFBQUJBQURWZU01Qlh4ODg5UUFEQkFELy8vLy8xam9UYy8vLy8vL1dPaE56QUFEL0lBU0FBNnNBQUFBS0FBSUFBUUFBQUFBQUFRQUFBK2ovYWdBQUYzQUFBUCsyQklBQUFRQUFBQUFBQUFBQUFBQUFBQUFBQUFJRFVnQlZBMVlBZ0FBQUFBQUFBQUFvQUFBQXNnQUJBQUFBQWdCZUFBVUFBQUFBQUFJQWdBUUFBQUFBQUFRQUFONEFBQUFBQUFBQUZRRUNBQUFBQUFBQUFBRUFFZ0FBQUFBQUFBQUFBQUlBRGdBU0FBQUFBQUFBQUFNQU1BQWdBQUFBQUFBQUFBUUFFZ0JRQUFBQUFBQUFBQVVBRmdCaUFBQUFBQUFBQUFZQUNRQjRBQUFBQUFBQUFBZ0FIQUNCQUFFQUFBQUFBQUVBRWdBQUFBRUFBQUFBQUFJQURnQVNBQUVBQUFBQUFBTUFNQUFnQUFFQUFBQUFBQVFBRWdCUUFBRUFBQUFBQUFVQUZnQmlBQUVBQUFBQUFBWUFDUUI0QUFFQUFBQUFBQWdBSEFDQkFBTUFBUVFKQUFFQUVnQUFBQU1BQVFRSkFBSUFEZ0FTQUFNQUFRUUpBQU1BTUFBZ0FBTUFBUVFKQUFRQUVnQlFBQU1BQVFRSkFBVUFGZ0JpQUFNQUFRUUpBQVlBQ1FCNEFBTUFBUVFKQUFnQUhBQ0JBRTBBWVFCMEFHZ0FJQUJHQUc4QWJnQjBBRklBWlFCbkFIVUFiQUJoQUhJQVRRQmhBSFFBYUFCekFDQUFSZ0J2QUhJQUlBQk5BRzhBY2dCbEFDQUFUUUJoQUhRQWFBQWdBRVlBYndCdUFIUUFUUUJoQUhRQWFBQWdBRVlBYndCdUFIUUFWZ0JsQUhJQWN3QnBBRzhBYmdBZ0FERUFMZ0F3VFdGMGFGOUdiMjUwQUUwQVlRQjBBR2dBY3dBZ0FFWUFid0J5QUNBQVRRQnZBSElBWlFBQUF3QUFBQUFBQUFIMEFQb0FBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBTGtIRVFBQWpZVVlBTElBQUFBVkZCT3hBQUUvKWZvcm1hdCgndHJ1ZXR5cGUnKTtmb250LXdlaWdodDpub3JtYWw7Zm9udC1zdHlsZTpub3JtYWw7fTwvc3R5bGU+PC9kZWZzPjx0ZXh0IGZvbnQtZmFtaWx5PSJtYXRoMTdmMzlmODMxN2ZiZGIxOTg4ZWY0YzYyOGViIiBmb250LXNpemU9IjE2IiB0ZXh0LWFuY2hvcj0ibWlkZGxlIiB4PSI4LjUiIHk9IjI5Ij49PC90ZXh0PjxsaW5lIHN0cm9rZT0iIzAwMDAwMCIgc3Ryb2tlLWxpbmVjYXA9InNxdWFyZSIgc3Ryb2tlLXdpZHRoPSIxIiB4MT0iMTkuNSIgeDI9IjU0LjUiIHkxPSIyMy41IiB5Mj0iMjMuNSIvPjx0ZXh0IGZvbnQtZmFtaWx5PSJBcmlhbCIgZm9udC1zaXplPSIxNiIgZm9udC1zdHlsZT0iaXRhbGljIiB0ZXh0LWFuY2hvcj0ibWlkZGxlIiB4PSIzMy41IiB5PSIxOCI+eDwvdGV4dD48dGV4dCBmb250LWZhbWlseT0iQXJpYWwiIGZvbnQtc2l6ZT0iMTIiIHRleHQtYW5jaG9yPSJtaWRkbGUiIHg9IjQxLjUiIHk9IjExIj45PC90ZXh0Pjx0ZXh0IGZvbnQtZmFtaWx5PSJBcmlhbCIgZm9udC1zaXplPSIxNiIgZm9udC1zdHlsZT0iaXRhbGljIiB0ZXh0LWFuY2hvcj0ibWlkZGxlIiB4PSIyNS41IiB5PSI0MyI+eDwvdGV4dD48dGV4dCBmb250LWZhbWlseT0iQXJpYWwiIGZvbnQtc2l6ZT0iMTIiIHRleHQtYW5jaG9yPSJtaWRkbGUiIHg9IjMzLjUiIHk9IjM2Ij4zPC90ZXh0Pjx0ZXh0IGZvbnQtZmFtaWx5PSJBcmlhbCIgZm9udC1zaXplPSIxNiIgZm9udC1zdHlsZT0iaXRhbGljIiB0ZXh0LWFuY2hvcj0ibWlkZGxlIiB4PSI0MS41IiB5PSI0MyI+eTwvdGV4dD48dGV4dCBmb250LWZhbWlseT0iQXJpYWwiIGZvbnQtc2l6ZT0iMTIiIHRleHQtYW5jaG9yPSJtaWRkbGUiIHg9IjQ5LjUiIHk9IjM2Ij42PC90ZXh0Pjwvc3ZnPg==»> 9005. , Корни и радикалы — ключевые выводы
, Корни и радикалы — ключевые выводы
 , Корни и радикалы — ключевые выводы
, Корни и радикалы — ключевые выводы Степень — это показатель степени, до которого возводится переменная или число.
Корни или радикалы обратны степеням.
Нечетные корни будут иметь одно решение, а четные — два.
Только положительные числа могут извлекать квадратные корни без использования мнимых чисел.
Отрицательные числа могут иметь кубический корень.
Знание квадратных корней из полных квадратов и законов показателей очень полезно при вычислении или упрощении алгебраических выражений, содержащих степени и корни.
Степени, степени и корни чисел
В этой статье мы обсудим корни и степени или степени чисел.
Содержание
- 1 Powers and Expunents
- 1,1 Экспоненциальный рост
- 1.1.1 Положительная основа больше, чем 1
- 1,1,2 Положительная база, менее 1
- 1,1,3 Отрицательная база меньше -1
- 1111111010101,3 Отрицательная база меньше -1
- 1,1.
 4 Отрицательное основание от -1 до 0
4 Отрицательное основание от -1 до 0
- 1.2 Законы экспонент
- 1.2.1 Единицы измерения Цифра
- 1.2.1.1 Strategy for finding units digit
- 1.2.1 Единицы измерения Цифра
- 1,1 Экспоненциальный рост
- 2 Roots
- 2.1 Square Root
- 2.1.0.1 Idea 1
- 2.1.0.2 Idea 2
- 2.1.0.3 Idea 3
- 2.1.0.4 Idea 4
- 2.1.0.5 Idea 5
- 2.2 Cube Root and Other Roots
- 2.2.0.1 Idea 1
- 2.2.0.2 Idea 2
- 2.2.0.3 Idea 3
- 2.2 .0.4 Идея 4
- 2.3 Собственные свойства корней
- 2.3.0.1 Распределительное свойство корней
- 2.3.0.2 Добавление и вычитание корней
- 2.3.0.3 Разрушение и подразделение
- 02012010401040404040404040404040.40404040404040402040404040404040404.402020404040404040404040404040404.402020202. 2.4 Уравнения с квадратными корнями0014 Степени и экспоненты
Экспоненты — это способ одновременного выполнения большого количества умножений.

По сути, A n означает, что мы умножаем n множителей числа A вместе. 1 в любой степени равно единице. 0 в любой степени равно 0. Отрицательное в четной степени положительно. Отрицательное в нечетной степени отрицательно.
Любой квадрат уравнения, равный положительному числу, имеет два решения, например, x 2 = 4 имеет два решения x = 2 и x = -2.
Уравнение, в котором выражение в четной степени равно отрицательному, не имеет решения, но в нечетной степени может равняться отрицательному, например.
(x-1) 2 = -4 не имеет решения, но уравнение вида (x-4) 3 = -1 имеет решение x-4 = -1 -> x = 3.
Экспоненциальный рост
В этой подтеме мы рассмотрим некоторые важные закономерности со степенями различных видов чисел. Для разных случаев мы посмотрим, что происходит со степенями, когда показатели степени возрастают через целые числа.
Положительное основание больше 1
При положительном основании больше единицы значения постоянно увеличиваются с большой скоростью.

7 1 = 1 ……… 7 3 = 343 …….. 7 6 = 117649.
Положительное основание меньше 1
При положительном основании меньше единицы значения постоянно уменьшаются .
(1/2) 1 =1/2 ….. (1/2) 4 =1/16 …… (1/2) 8 = 1/256
Отрицательное основание меньше — 1
Абсолютные значения здесь увеличиваются, но знаки +/- чередуются.
(-3) 1 =-3
(-3) 2 =9
(-3) 3 = -27
(-3) 4 = 81
(-3) 5 = -243
. между -1 и 0
Абсолютные значения становятся меньше по мере приближения к нулю, но знаки +/- чередуются.
(-1/2) 1 = -1/2
(-1/2) 2 = 1/4
(-1/2) 3 90 0 0 8
(-1/2) 4 = 1/16
Рассмотрим пример:
Если x < 1 и x != 0, является ли x 7 > x 6 ?
Если x — любое отрицательное число, то x 7 — отрицательное, а x 6 — положительное, поэтому x 7 < x 6 , поэтому ответ — нет.

Также, если o < x < 1, значения уменьшаются по мере увеличения мощности, поэтому x 7 < x 6 , ответ — нет.
Так что во всех случаях ответ — нет.
Подводя итог, мы обсудили закономерности экспоненциального роста, то есть то, как увеличение показателя степени меняет величину степени различных видов оснований.
Laws of Exponents
- a m * a n = a m+n
- a m /a n = a m-n
- a 0 = 1 (prove A M /A M = 1 = A M-M = A 0 = 1) Для всех A! = 0
- (A M ) N = A M*3333353 3 33333353 3 333333333353 33333333. 33 3 3 3 3 3 3 3 3 3 3 3 3 ) N . a -n = 1/a n (докажите a 0-n )
- (a/b) -n = (b/a) n
- (ab) n = (a n )(b n )
- (a/b) n = a n /b n
Let’s look at пример:
Ранжируйте от меньшего к большему.

(а) (1/3) -8 (б) 3 -3 (в) (1/3) 5
(1/3) 5 0 9025 3 = 1/3 9 < 3 -3 = 1/3 3 < (1/3) -8 = 3 8
Цифра единиц
На цифру единиц любого продукта влияют только цифры единиц факторов. Поэтому нам нужно учитывать только однозначных продукта при попытке определить единицу измерения продукта.
Например, какова цифра единиц 57 123 ?
Идея состоит в том, чтобы найти закономерность для последней цифры значения каждой степени следующим образом.
7 1 = …7
7 2 =… 9
7 3 =… 3
7 4 =… 1
7 5 =… 7
7 6 =… 9 0005
7
7 = 3 .
7 8 = …1
В этой точке мы начинаем видеть шаблон, 7,9,3,1 повторяются как последние цифры.
И мы также замечаем, что для каждой степени, кратной 4, значение заканчивается на 1, мы можем перейти к 120, и шаблон продолжится до 123.

7 120 = …1
7 121 = …7
7 122 = …9
7 123 = …3
And so the units digit of 57 123 is 3.
Strategy for finding units digit
- Focus только при однозначном умножении.
- Найдите повторяющийся паттерн и определите период паттерна, как в 4 (7,9,3,1) в приведенном выше примере.
- Расширьте шаблон, используя кратные точки.
Корни
Корнем числа A является другое число X, которое при умножении на себя заданное количество раз равно A, например, квадратный корень из A равен X в X*X = A. Используются следующие символы :
√ для квадратного корня, 3 √ для кубического корня и вообще n √ для всех остальных корней.
Квадратный корень
Во многих случаях в математике мы знаем квадрат числа и должны найти исходное число, которое было возведено в квадрат. Если квадрат искомого числа является полным квадратом, то легко найти число по его квадрату.

Ниже приведены некоторые основные понятия о квадратном корне.
Идея 1
Невозможно извлечь квадратный корень из отрицательного числа, например √-1, потому что положительные числа, возведенные в квадрат, положительны, а отрицательные числа, возведенные в квадрат, положительны, поэтому невозможно найти квадратный корень из отрицательного числа. Для А ≥ 0, √А ≥ 0,
Идея 2
Для положительных чисел квадратный корень сохраняет порядок неравенства.
Другими словами, если A < B < C, то √A < √B < √C
Мы знаем, что 36 < 41 <49, поэтому √36 < √41 < √49 → 6 < √41 < 7. Отсюда, не зная точного значения √41, мы можем узнать, что оно находится между 6 и 7.
Идея 3
Есть несколько простых квадратных корней, для которых мы можем запомнить грубые приближения:
√2 ∼ = 1,4
√3 ∼= 1,7
√5 ∼= 2,2
Если мы знаем только эти три с точностью до десятых, мы можем сделать очень много приближений.
Идея 4
Знак √ является оператором, таким же, как +,-,×,÷, и, подобно им, может работать с числами или переменными.

Этот оператор отменяет возведение в квадрат, но не обязательно прямо противоположное. Например, предположим, что x отрицательно, тогда y 2 будет положительным и √y 2 также будет положительным. Мы не возвращаемся к тому, с чего начали, то есть к отрицательному y.
Технически, поскольку результат √ всегда положителен независимо от того, положителен y или отрицателен, мы можем сказать √y 2 = |y| (абсолютное значение y).
Когда мы видим операцию √, результат всегда положительный. Это отличается от того, когда мы возводим переменную в квадрат и приравниваем к чему-то, и мы должны решить для переменной, например x 2 = A.
В этом случае решение состоит из 2 частей, как мы уже обсуждали выше в разделе показателей, х = ±√A
Идея 5
При обсуждении экспоненциального роста выше мы обсуждали, что если A > 1, то положительные степени A становятся больше, т.е. A 2 > A.
корень должен сделать их меньше
√A < A
Но, как мы видели также в уроке экспоненциального роста, все наоборот для положительных чисел меньше 1.

Если 0 < A < 1, то положительные степени A уменьшаются то есть А 2 < A.
Если возведение в квадрат этих чисел уменьшает их, то извлечение квадратного корня должно увеличивать их.
√A > A
√(4/9) = 2/3 > 4/9
Рассмотрим следующий пример:
Если 7K — натуральное число, и если √K > K, то является ли K целым числом?
Если √K > K, десять K должно быть числом от 0 до 1. Таким образом, оно не может быть целым числом. Нет, это ответ.
Кубический корень и другие корни
Точно так же, как квадратный корень отменяет действие возведения в квадрат, существуют корни более высокого порядка, которые также отменяют другие силы.
Например, кубических корня отменяют действие возведения числа в куб.
Точно так же, как мы используем обозначение √ для квадратного корня, обозначения для всех других корней аналогичны. Мы используем тот же подкоренной знак √, но для всех остальных корней мы ставим небольшое число перед подкоренным, чтобы обозначить порядок корня.

Таким образом, кубический корень из x записывается как 3 √x.
Ниже приведены некоторые основные идеи.
Идея 1
Правила ± для кубов другие.
Помните, что (положительное) 3 = положительное и (отрицательное) 3 = отрицательное.
Следовательно, x 3 = положительное число имеет только одно положительное решение , а x 3 = отрицательное число имеет только одно отрицательное решение .
С квадратными корнями мы можем найти квадратные корни только из положительных чисел и не можем извлечь квадратный корень из отрицательных.
Напротив, мы можем извлечь кубический корень из любого числа на числовой прямой, положительного, нулевого или отрицательного.
3 √8 = 2
3 √0 = 0
3 √ -8 = -2
Идея 2
для быстрых вычислений, это хорошо, чтобы запомнить Куби до 10.

1 3 = 1
2 3 = 8
3 3 = 27
4 3 = 64
5 3 = 125
6 3 = 216
7 3 = 343
8 3 = 512
9 3 = 729
10 3 = 1000
Then, we automatically have some cube roots memorized as well
3 √1 = 1
3 √8 = 2
3 √ 27 = 3
3 √64 = 4
3 √125 = 5
3 √216 = 6
3 √343 = 7
3 √512 = 8
3 √729 = 9
3 √1000 = 10
Идея 3
Квадратный корень √a, корень четвертой степени 4 √a, корень шестой степени 6 √a и т. д. называются четными корнями.
Кубический корень 3 √a, корень пятой степени 5 √a, корень седьмой степени 7 √a и т.
 д. называются нечетными корнями.
д. называются нечетными корнями.Как и в случае с квадратными корнями, мы можем извлечь четный корень из положительных чисел, что приведет к положительному результату, но мы не можем извлечь четный корень из отрицательного числа.
Как и в случае с кубическими корнями, любой нечетный корень из положительного числа является положительным, а любой нечетный корень из отрицательного числа отрицательным.
Идея 4
Для всех n,
n √0 = 0 и n √1 = 1
Все корни сохраняют порядок неравенства,
0 < c, < a0 < b n √a < n √b < n √c.
Предположим, нам нужно оценить 4 √50.
Поскольку 16 < 50 < 81, мы 4 √16 < 4 √50 < 4 √81 → 2 < 4 √50 < 3. Мы также можем сравнить разные размеры корней.
Если x > 1 и n > m, то 1 < n √x < m √x < x.
Если 0 < x < 1 и если n > m, то 0 < x < m √x < n √x < 1.

Таким образом, чем выше порядок корня, тем ближе результат до 1.
Свойства корней
По сути, корни являются частным случаем показателей, поэтому некоторые свойства показателей совпадают со свойствами корней.
В этой подтеме мы обсудим связь между корнями и показателями.
Мы собираемся использовать квадратные корни, чтобы обсудить свойства корней, и предположим, что числа A и B положительны.
Несмотря на то, что мы используем квадратные корни, все эти свойства также работают для всех корней более высокого порядка, а для нечетных корней задействованные числа не обязательно должны быть положительными.
Распределяющее свойство корней
Распределение корней при умножении и делении √AB = √A * √B, √(A/B) = √A / √B.
Предположим, у нас есть √N.
Если N имеет в качестве одного из своих множителей полный квадрат A, то мы можем заменить N на A*B для некоторого B и взять квадратные корни из множителей по отдельности.

Квадратный корень из идеального квадрата А выйдет поровну.
например √63 = √(9*7) = 3√7
Для больших чисел мы можем найти простую факторизацию, и тогда будет легко найти упрощенный квадратный корень.
Каждая пара простых множителей и каждая четная степень простого множителя являются полным квадратом и могут быть упрощены.
Например, предположим, что у нас есть (2 6 )(3 5 )(5 2 )(7) как простая факторизация числа, мы можем выразить √N в упрощенной форме.
√N = √2 6 * √3 5 * 5 2 * 7
= √(2 3 * 2 3 ) * √(3 2 * 3 2 * 3 1 ) * √5 2 * √7
= 2 3 * 3 2 √3 * 5 * √7
= 360 (√3) (√7)
= 360 √21
Сложение и вычитание корней
Мы можем комбинировать два термина, только если они имеют один и тот же радикал.
Например, √72 – √32 = √(36*2) – √(16*2) = 6√2 – 4√2 = 2√2
Но выражение 6√2 – 4√3 нельзя упростить дальше .

Умножение и деление корней
Мы можем использовать свойство распределения для упрощения произведений или делений корней
Например, (2√42) * (4√63) = 8√(42*63) = 8√(2* 3*7*3*3*7) = 8√(3*3) * √(7*7) * √(2*3) = 8*3*7*√6 = 168√6.
Степени корней
Подкоренные выражения, возведенные в степени, можно упростить. Имейте в виду, что любую четную степень квадратного корня можно записать как степень целого числа.
Например, (√2) 48 = ((√2) 2 ) 24 = 2 24.
Мы не можем навскидку вычислить это числовое значение, но все же можем сравнить размер с что-то другое. Например, мы можем увидеть (√2) 48 > 2 20 .
Когда мы возводим подкоренное выражение в степень, мы распределяем показатель степени по каждому множителю. Любая четная степень радикала является степенью целого числа.
Уравнения с квадратными корнями
У нас может быть уравнение, включающее квадратный корень, например, √(x+2) = 3.

Поскольку мы можем отменить квадратный корень, возведя его в квадрат, все, что нам нужно сделать, это возвести обе стороны в квадрат и решить .
√(x+2) = 3 → x+3 = 9 → x = 7.
Поскольку мы знаем, что √x 2 = x не всегда верно. Это верно для положительных чисел и нуля, но не для отрицательных чисел.
Это говорит о том, что мы можем столкнуться с какой-то проблемой, когда возникают отрицательные значения.
Получается, что в радикальных уравнениях нужно остерегаться посторонних корней.
Когда мы правильно выполняем всю нашу алгебру, включая возведение в квадрат обеих частей уравнения, алгебра может привести к ответам, которые на самом деле не работают в исходном уравнении. Это посторонние корни.
Рассмотрим пример:
√(x+3) = x-3 → x+3 = (x-3) 2 → x+3 = x 2 -6x+9
→ 0 = х 2 -7х+6 = (х-6)(х-1)
x = 1 или 6.
Теперь нам нужно проверить, работают ли эти значения в исходном уравнении.

Проверка х = 1;
√(x+3) = √(1+3) = √4 = 2
x-3 = 1-3 = -2
x = 1 не работает, так как 2 != -2.
Проверка х = 6;
√(x+3) = √9 = 3
x-3 = 6-3 = 3
x = 6 работает, поэтому это единственное правильное значение x.
Если мы получим квадратное число после возведения в квадрат обеих частей уравнения с радикальной частью, алгебра приведет к 2 корням.
Иногда работают оба корня.
Иногда работает один корень и один посторонний.
Иногда оба являются посторонними и уравнение не имеет решений.
Например, √(2x-4) = √(x-4)
2x – 2 = x -4 → x-2 = -4 → x = -2
Когда мы подставляем это в исходное уравнение, это получается квадратный корень из минуса с обеих сторон. Следовательно, уравнение не имеет решения.
Наконец, имейте в виду, что мы должны возводить в квадрат обе стороны только тогда, когда радикал сам по себе находится на одной стороне уравнения.
Если радикал появляется с другими элементами на стороне, нам придется изолировать радикал на одной стороне, прежде чем будет иметь смысл квадратировать обе стороны.

Например, 2+√(4-3x) = x
√(4-3x) = x-2 → 4-3x = (x-2) 2 → 0 = x 2 – x = x( x-1)
Алгебра приводит к двум корням x = 0 и x = 1.
Когда мы проверяем оба корня в исходном уравнении, ни один из них не работает, поэтому уравнение НЕ имеет решения.
Рационализация
Рационализация — это процесс изменения формы уравнения или выражения, содержащего радикал в знаменателе, таким образом, чтобы знаменатель больше не содержал радикала. Этот процесс называется рационализацией знаменателя.
Другими словами, устранение корней из знаменателя дроби называется рационализацией.
Если дробь имеет единственный корень в знаменателе, мы рационализируем, умножая на этот корень саму себя.
Например:
Упрощение (4-√6) / 2√3
( (4-√6) / 2√3 ) * √3/√3
( 4√3 – √6 * √3 ) / (2*3)
(4√3 – 3√2) / 6
Если знаменатель дроби содержит сложение или вычитание, включающее подкоренное выражение, то для рационализации нам нужно умножить на сопряженную часть знаменателя над собой.

Используя разность двух квадратов, то есть (x-y)(x+y) = x 2 – y 2 , мы можем удалить корни из таких знаменателей.
Например, Упростить 2/(√5 – 1)
Мы просто умножаем и делим на сопряженное число √5 – 1
(2/(√5 – 1)) * ( (√5 + 1)/(√ 5 + 1) )
2(√5 + 1) / ((√5) 2 – 1 2 )
(√5 + 1)/2
- 2.1 Square Root
Дробные показатели делают явной связь между корнями и показателями.
Например, 2 1/2 = A, если возвести в квадрат A, мы получим (2 1/2 ) 2 = A 2 → A 2 = 2 → A = √2.
Следовательно, 2 1/2 = √2.
Обычно X 1/2 = √X.
То же самое применимо к X 1/3 = 3 √X.
Таким образом, обычно X 1/м = м √X.
Также X н/м = ( м √X) н.
Например, 8 4/3 = ( 3 √8) 4
Показательные уравнения
Показательное уравнение – это уравнение, в котором переменные находятся в показателях степени.
Если две степени с одинаковым основанием равны, то и степени должны быть равны.
A x = A y → x = y
Это правило работает для всех оснований, кроме 0 или ±1.
Чтобы решить показательные уравнения, мы должны получить равные основания с обеих сторон. Это может включать выражение заданных оснований в виде степеней меньших оснований.
Когда основания с обеих сторон равны, мы можем приравнять степени и решить.
Давайте рассмотрим несколько примеров.
- Если ( 5 √3) 3x+7 = 3 2x , найти x?
(3 1/5 ) 3x+7 = 3 2x → (3x+7)/5 = 2x → x = 1.


 Нахождение дробной степени числа
Нахождение дробной степени числа Рiвнiсть векторiв
Рiвнiсть векторiв Квадратный корень из произведения двух неотрицательных множителей равен произведению корней из этих множителей:
Квадратный корень из произведения двух неотрицательных множителей равен произведению корней из этих множителей:


 Для цього множать чисельник і знаменник дробу на такий вираз (поєднане зі знаменником), щоб корінь в знаменнику видалявся.
Для цього множать чисельник і знаменник дробу на такий вираз (поєднане зі знаменником), щоб корінь в знаменнику видалявся.

 Запишемо двочлен як добуток числа і двочлена суми.
Запишемо двочлен як добуток числа і двочлена суми. Наводимо подібні члени (складаємо коефіцієнти однакових коренів).
Наводимо подібні члени (складаємо коефіцієнти однакових коренів).
 У квадратного кореня чим більше підкореневий вираз, тим більше значення кореня.
У квадратного кореня чим більше підкореневий вираз, тим більше значення кореня. Розкладемо 91 на прості множники і виносимо корінь за дужки із загальними підкореневими множниками (13*5).
Розкладемо 91 на прості множники і виносимо корінь за дужки із загальними підкореневими множниками (13*5). Винесемо квадратні корені із ступенів і поставимо числа коефіцієнтами квадратних коренів.
Винесемо квадратні корені із ступенів і поставимо числа коефіцієнтами квадратних коренів.
 4 Отрицательное основание от -1 до 0
4 Отрицательное основание от -1 до 0

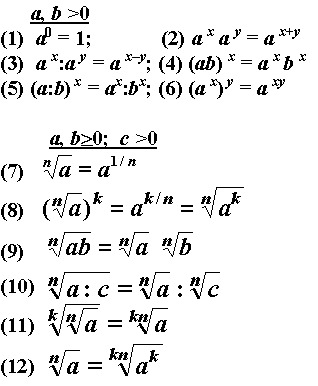







 д. называются нечетными корнями.
д. называются нечетными корнями.


