Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а12 |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
0 | 1 | а21 | а22 | а21 | а22, | ||
т.е. АЕ = ЕА = А (11)
Произведение
квадратной матрицы любого порядка на
соответствующую единичную матрицу
равняется первоначальной матрице. Таким
образом, при умножении матриц единичная
матрица играет роль единицы, поэтому и
называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А-1, запишем
А-1А = АА-1 = Е (12)
Если обратная матрица А-1 существует, то матрица А
Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
а11 | а12 | а13 | ||
А= | а21 | а22 | а23 | |
а31 | а 32 | а33 |
а11 | а12 | а13 | |||
DА = | а21 | а22 | а23 | ≠ 0 | |
а31 | а32 | а33 | |||
Обратной матрицей А-1 будет матрица
A11/DА | A21/DА | A31/DА | ||||
A-1 = | A12/DА | A22/DА | A32 /DА | , | ( 13 ) | |
A13/DА | A23/DА | A33/DА |
где Аij – алгебраическое дополнение элемента аij определителя DA.
Убедиться в этом можно, умножая матрицу А на матрицу А-1. Например, элементы с11 и с23 определяются так:
c23=a21···=
== 0
В итоге
а11 | а12 | а13 | A11/DА | A21/DА | A31/DА | 1 | 0 | 0 | |||
С=AA-1= | а21 | а22 | а23 | A12/DА | A22/DА | A32/DА | = | 0 | 1 | 0 | =E |
а31 | а32 | а33 | A13/DА | A23/DА | A | 0 | 0 | 1 |
Матрица
A11 | A21 | A31 | ||||
= | A12 | A22 | A32 | ( 14 ) | ||
A13 | A23 | A33 |
называется матрицей, присоединённой к А. (Используется также обозначение ).
Обратная матрица А-1 через присоединённую выражается так:
(Используется также обозначение ).
Обратная матрица А-1 через присоединённую выражается так:
= | 1 | ( 15 ) | |
DA |
Обратную матрицу будем находить по следующей схеме:
1. Находим определитель матрицы А.
3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).
4. Умножаем полученную
матрицу на 1/DA.
Пример 6. (Лена Иванова, КШ-061).
Дана матрица
2 | 5 | 7 | |
A = | 6 | 3 | 4 |
5 | -2 | -3 |
Найти обратную матрицу.
1. Вычисляем определитель матрицы А:
2 | 5 | 7 | 2 | 5 | 7 | ||||
DA = | 6 | 3 | 4 | = | 0 | -12 | -17 | = | (492 — 493) = -1 |
5 | -2 | -3 | 0 | -29/2 | -41/2 |
Так как DA ≠ 0, то матрица А является невырожденной, и, значит, можно
найти матрицу А-1.
2. Находим алгебраические дополнения элементов этого определителя:
A11 = | 3 | 4 | = -1, | A21= — | 5 | 7 | = 1, | A31= | 5 | 7 | = -1, |
-2 | -3 | -2 | -3 | 3 | 4 |
A12= — | 6 | 4 | = 38, | A22= | 2 | 7 | = -41, | A32= — | 2 | 7 | = 34, |
5 | -3 | 5 | -3 | 6 | 4 |
A13 = | 6 | 3 | = -27, | A23=- | 2 | 5 | = 29, | A33= | 2 | 5 | =
-24. |
5 | -2 | 5 | -2 | 6 | 3 |
Следовательно,
-1 | 1 | -1 | 1 | -1 | 1 | ||
A-1 = -1 | 38 | -41 | 34 | = | -38 | 41 | -34 |
-27 | 29 | -24 | 27 | -29 | 24 |
Лекция 4.
Линейная алгебра
Линейная алгебраЛинейная алгебра |
1.3. Матрицы. Операции над матрицами | назад | оглавление | вперёд |
Две матрицы A и B называются равными ,если они имеют
один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся :
Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент
матрицы умножить на это число:
Сложение матриц.
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой.
Произведение матриц .
Пример:
.==
.=
.
Если для матриц А и В выполняется равенство А* В=В*А ,то
матрицы называются перестановочными.
Если для матриц А , В , С имеет смысл операция произведения,
то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
Транспонирование матриц
Рассмотрим матрицы
AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
назавают главной диагональю
Очевидно:
Если А является квадратной матрицей(n*n), то элементы матрицы
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
Понятие обратной матрицы.
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят
единицы, а вне главной диагонали — нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную ,то ее определитель отличен от
нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том ,что определитель произведения
равен произведению определителей.
что и требовалось доказать.
Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
*=
Отсюда, в частности, следует:
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля , то эту систему можно решить методом Крамера причем решение (3) — единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
Алгоритм нахождения обратной матрицы методом Крамера.
Первоначально находим определитель матрицы А и если он
равен нулю , то обратной матрицы не существует.
Если определитель отличен от нуля , то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
Элементарные преобразования матриц.
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
- умножение любой строки матрицы на число , отличное от нуля;
- к любой строке можно добавить любую другую строку , умноженую на любое число;
- перестановка двух строк.
пример
=
Матрицы, полученные с помощью элементарных преобразований
называются эквивалентными
А~ В , В~ С , А~ С
Вычисление обратной матрицы с помощью элементарных преобразований.
Расмотрим квадратную матрицу А и предположим , что
тогда используя элементарные преобразования эту матрицу
можно привести к единичной матрице .Таким образом единичная
матрица эквивалентна любой невырожденой матрице того же
порядка.
Теорема
Если элементарные преобразования:
переводят невырожденую матрицу А в единичную , то
те же самые преобразования, взятые в том же порядке, переводят
единичную матрицу в обратную для A.
Доказательство:
отсюда
назад | оглавление | вперёд
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.
Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits. Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1.
Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2.
Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.
L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1. 2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.
2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1. 2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1.
2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.
Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1. 3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1).
3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1.
Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.
Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2. 1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейЗадачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1.
1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейЗадачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1.
Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2.
Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1.
Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1.
2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.
Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3. 5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1).
5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Матрицы, определители, системы линейных уравнений (Лекция №12)
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.
Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если и , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно
сопоставить такую матрицу B из
n строк и m столбцов, у которой каждая
строка является столбцом матрицы A с
тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером).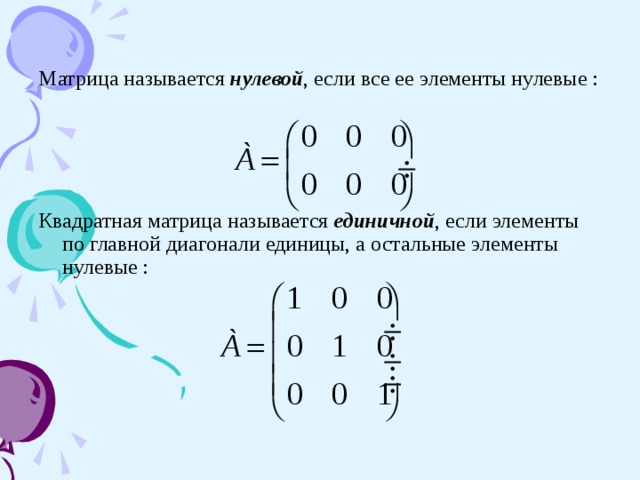 Итак,
если , то .
Итак,
если , то .
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
или
Примеры. Найти сумму матриц:
Найти сумму матриц:
- .
- — нельзя, т.к. размеры матриц различны.
- .
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
- .
Примеры.
- .
- Найти 2A-B, если , .
.
- Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:
Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (aij) размера m×n на
матрицу B = (bij) размера n×p, то получим матрицу C
размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате
произведения элементов i-ой строки матрицы A на соответствующие элементы j-го
столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
.
Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
- .
- — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов .
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
- .
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.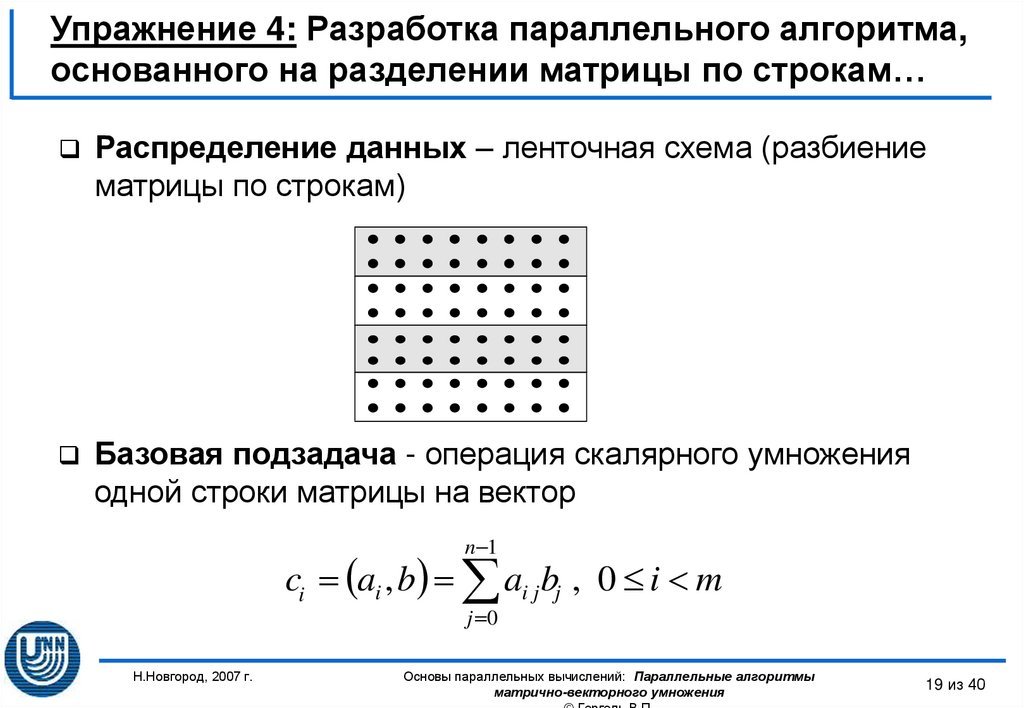
Примеры. Вычислить определитель третьего порядка.
- .
- .
- Решите уравнение..
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
как найти произведение двух или трех разных размеров, условия и формулы
Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.
Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.
Умножение матриц — определение
Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.
При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:
Но для начала разберёмся, что такое согласованные матрицы.
Согласованные матрицы
Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.
Индексы показывают координаты равных элементов.
Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.
com/embed/d2NUqXRVdq0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Основные свойства матричного произведения
Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).
Умножение квадратных матриц
Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.
В математическом виде это выглядит так: ЕА = АЕ = А
Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.
Следовательно, формула такова: АА(-1) = Е
Умножение прямоугольных матриц
Существуют четыре основных свойства умножения:
- Сочетательное свойство, или ассоциативность: (AB)C = A(BC)
- Распределительное свойство, или дистрибутивность: А(В+С) = АВ + АС / (А+В)С = АС + ВС
- Умножение на единичную матрицу: ЕА = А
- Умножение на нулевую матрицу: 0А = 0
Напомним, что у нулевой матрицы все элементы равны нулю.
Произведение трех матриц
Произведение АВС можно получить двумя альтернативными способами:
- Найти АВ и умножить на С
- Найти ВС и умножить на А
(АВ) С = А (ВС)
Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.
Умножение матрицы на число
Для умножения на число необходимо умножить каждый матричный элемент на это число:
Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.
Умножение матрицы на вектор
Здесь работает правило «строка на столбец».
При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.
При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.
Примеры задач на умножение матриц
Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.
Решение:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 — 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Ответ:
Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.
Решение:
c11 = a11·b11 + a12·b21 = 2·1 + (-1)·2 + 3·(-1) = -3
c21 = a11·b12 + a12·b22 = 4⋅1 + 2⋅2 + 0⋅2 = 8
c31 = a21·b11 + a22·b21 = −1⋅1 + 1⋅2 + 1⋅(−1) = 0
Ответ:
Изучение матричных операций очень увлекательное, но сложное занятие. Если у вас нет времени на учёбу, ФениксХэлп может помочь в решении контрольных и самостоятельных работ, написании статей и диссертаций.
Алгебра матриц и линейные пространства
Главная / Математика / Алгебра матриц и линейные пространства / Тест 5
Упражнение 1:
Номер 1
Возведение матрицы в нулевую степень дает в результате
Ответ:
 (1) единицу 
 (2) единичную матрицу 
 (3) нулевую матрицу 
Номер 2
Что получится в результате возведения матрицы в нулевую степень?
Ответ:
 (1) нуль 
 (2) нулевая матрица 
 (3) единичная матрица 
Номер 3
Получится ли нулевая матрица в результате возведения другой матрицы в нулевую степень?
Ответ:
 (1) нет, не получится 
 (2) да, получится 
 (3) не во всех случаях 
Упражнение 2:
Номер 1
Матрица считается обратной исходной в том случае, если
Ответ:
 (1) произведение двух этих матриц равно 0 
 (2) произведение двух этих матриц равно 1 
 (3) произведение двух этих матриц равно единичной матрице 
Номер 2
Если умножение матрицы на другую дает в результате единичную матрицу, то
Ответ:
 (1) эта матрица нулевая 
 (2) эта матрица обратная данной 
 (3) эта матрица треугольная 
Номер 3
Как называется матрица, которая при умножении на другую матрицу дает единичную матрицу?
Ответ:
 (1) обратимая 
 (2) обратная 
 (3) транспонированная 
Упражнение 3:
Номер 1
Если обратная матрица B к матрице A существует, то
Ответ:
 (1) ее определитель равен нулю 
 (2) она однозначно определена 
 (3) она неопределена 
Номер 2
Обратная к другой матрице матрица определяется
Ответ:
 (1) множественным образом 
 (2) однозначно 
 (3) порядком матрицы 
Номер 3
Верно ли утверждение, что обратная матрица определяется множественным образом?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это верно только в некоторых частных случаях 
Упражнение 4:
Номер 1
Для любого элемента моноида обратный элемент является
Ответ:
 (1) неоднозначным 
 (2) единственным 
 (3) неопределенным 
Номер 2
Для любого элемента моноида обратный элемент является единственным.Верно ли это?
Ответ:
 (1) да, утверждение верно 
 (2) нет, это не так, но только в некоторых случаях 
 (3) нет, обратных элементов существует бесконечное множество 
Номер 3
Можно ли считать верным утверждение о том, что для любого элемента моноида существует не менее двух обратных элементов?
Ответ:
 (1) да, так и есть 
 (2) утверждение верно только в некоторых частных случаях 
 (3) нет, это неверно 
Упражнение 5:
Номер 1
Если определитель матрицы равен нулю, то
Ответ:
 (1) обратная матрица будет единичной 
 (2) обратная матрица будет нулевой 
 (3) обратная матрица не существует 
Номер 2
Может ли существовать обратная матрица, если определитель исходной равен нулю?
Ответ:
 (1) нет, не может 
 (2) может, но такие случаи встречаются редко 
 (3) да, может всегда 
Номер 3
Определитель матрицы равен нулю.Верно ли, что матрица, обратная данной тоже будет нулевой?
Ответ:
 (1) нет, это неверно 
 (2) да, так и есть, согласно определению 
 (3) это верно только в частных случаях 
Упражнение 6:
Номер 1
Элемент обратной матрицы получается в результате
Ответ:
 (1) перемножения элементов исходной матрицы на величину определителя 
 (2) сложения определителя с элементами главной диагонали 
 (3) деления соответствующих элементов присоединенной матрицы на определитель 
Упражнение 7:
Номер 1
Верно ли, что определитель обратной матрицы обратно пропорционален определителю исходной матрицы?
Ответ:
 (1) нет, утверждение противоречит определению обратной матрицы 
 (2) да, это верно 
 (3) это верно только в частных случаях 
Номер 2
Произведение определителя обратной матрицы на определитель исходной дает в результате
Ответ:
 (1) 1 
 (2) 0 
 (3) -1 
Номер 3
Что является результатом произведения определителя обратной матрицы на определитель исходной?
Ответ:
 (1) нулевая матрица 
 (2) единица 
 (3) двойка в степени размерности матрицы по строкам 
Упражнение 8:
Номер 1
Матрица, имеющая правую обратную
Ответ:
 (1) необратима 
 (2) обратима 
 (3) неопределена 
Номер 2
Если матрица обратима, то она имеет
Ответ:
 (1) левую обратную 
 (2) правую обратную 
 (3) как левую обратную, так и правую 
Номер 3
Верно ли утверждение, что матрица, имеющая правую обратную, обратима?
Ответ:
 (1) нет, это противоречит определению 
 (2) да, это верно 
 (3) это может быть верно только в очень редких случаях 
Упражнение 9:
Номер 1
Для существования матрицы, обратной произведению двух матриц необходимо, чтобы
Ответ:
 (1) существовала матрица, обратная левой матрице 
 (2) существовала матрица, обратная правой матрице 
 (3) существовали обе обратные матрицы 
Номер 2
Верно ли то, что матрица, обратная к произведению двух матриц, равна произведению матриц, обратных к данным?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это может быть очень редко, а в основном утверждение неверно 
Упражнение 10:
Номер 1
Дает ли матрица, обратная обратной в результате исходную?
Ответ:
 (1) да, это верно 
 (2) нет, утверждение неверно 
 (3) это может быть правильно только в очень редких случаях, а в остальном неверно 
Номер 2
От обратной матрицы взяли обратную, и в результате получили
Ответ:
 (1) нулевую матрицу 
 (2) единичную матрицу 
 (3) исходную матрицу 
Номер 3
Множество обратимых матриц с операцией умножения является
Ответ:
 (1) детерминированной группой 
 (2) линейной группой 
 (3) интерпретационной группой 
Упражнение 11:
Номер 1
Множество матриц с единичным определителем с операцией умножения является
Ответ:
 (1) линейной группой 
 (2) специальной линейной группой 
 (3) обратимой линейной группой 
Номер 2
Специальная линейная группа - это
Ответ:
 (1) множество обратимых матриц с операцией умножения 
 (2) множество необратимых матриц с операцией конъюнкции 
 (3) множество матриц с единичным определителем с операцией умножения 
Упражнение 12:
Номер 1
Если обратная матрица равна транспонированной, то исходная матрица называется
Ответ:
 (1) ортогональной 
 (2) деструктивной 
 (3) интерпретационной 
Номер 2
Матрица называется ортогональной тогда, когда
Ответ:
 (1) все элементы ниже побочной диагонали равны нулю 
 (2) транспонированная матрица равна обратной 
 (3) элементы побочной диагонали противоположны по знаку элементам главной 
Номер 3
Верно ли то, что матрица является ортогональной тогда, когда ее транспонированная матрица равна обратной?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это может быть верно только в частных случаях 
Главная / Математика / Алгебра матриц и линейные пространства / Тест 5
Свойства матричных операций
Свойства матричных операций
Свойства дополнения
Основные свойства сложения действительных чисел справедливы и для
матрицы.
Пусть А, Б и С быть m x n матриц
- А + В = В + А коммутативный
- А + (В + С) = (А + В) + С ассоциативный
- Существует уникальный м
xn матрица O
с
A + O = A добавка личность
- Для любого m
xn матрица A
существует матрица m x n
Б (называемый -А)
с
A + B = O добавка обратный
Все доказательства одинаковы. Докажем первое свойство.
Доказательство собственности 1
У нас есть
(А + В) ij = A ij + B ij определение сложения матриц
= B ij + A ij коммутативный свойство сложения действительных чисел
= (B + A) ij определение добавления матрицы
Обратите внимание, что нулевая матрица отличается для разных m
и н. Например
Например
Свойства умножения матриц
В отличие от сложения матриц, свойства умножения действительных чисел не не все обобщаются на матрицы. Матрицы редко коммутируют, даже если AB и бакалавр оба определены. Часто не существует мультипликативной обратной матрицы, даже если матрица квадратная. Есть несколько свойств умножение действительных чисел, которые обобщаются на матрицы. Мы излагаем их в настоящее время.
Пусть А, Б и С — матрицы размерностей такие, что следующие определения определены. Затем
- А(ВС) = (АВ)С ассоциативный
- А(В + С) = АВ + АС дистрибутив
- (А + В)С = АС + ВС
распределительный
- Существуют уникальные матрицы I m и I n с
I m А = А I n = А мультипликативное тождество
Мы часто опускаем нижний индекс и пишем I вместо
тождественная матрица. Единичная матрица представляет собой квадратную скалярную матрицу с единицами.
по диагонали. Например
Единичная матрица представляет собой квадратную скалярную матрицу с единицами.
по диагонали. Например
Мы докажем второе свойство, а остальное оставим вам.
Доказательство Имущества 2
Снова покажем, что общий элемент левой части такой же, как и правой сторона руки. У нас есть
(А(В + С)) ij = С(А ик (Б + C) kj ) определение умножения матриц
знак равно S(A ik (B kj + C kj )) определение сложения матрицы
знак равно S(A ik B kj + A ik C kj ) распределительное свойство действительных чисел
знак равно С А ик Б кдж + С A ik C kj коммутативный свойство действительных чисел
= (AB) ij + (AC) ij определение умножения матриц
где
сумма берется от 1 до k.
Пример
Мы продемонстрирует свойство 1 с
Мы есть
так что
Мы есть
так что
Свойства скалярного умножения
Поскольку мы можем умножить матрицу на скаляр, мы можем исследовать свойства что имеет это умножение. Все свойства умножения действительные числа обобщают. В частности, у нас есть
Пусть г и s — действительные числа и А и Б быть матрицами. Затем
- r(sA) = (rs)A
- (r + s)A = rA + sA
- r(A + B) = rA + rB
- А(rB) = r(AB) = (rA)B
Мы докажем свойство 3, а остальное оставим вам. У нас есть
(r(A + B)) ij = (r)(A + B) ij определение скалярного умножения
= (r)(A ij + B ij ) определение сложения матриц
= rA ij + rB ij распределительный свойство действительных чисел
= (rA) ij + (rB) ij определение скалярного умножения
= (rA + rB) ij определение добавление матриц
Свойства транспонирования матрицы
Напомним, что транспонирование матрицы — это операция переключения строк и
столбцы. Укажем следующие свойства. Мы доказали первое
имущество в последнем разделе.
Укажем следующие свойства. Мы доказали первое
имущество в последнем разделе.
Пусть г быть действительным числом и A и В быть матрицы. Затем
- (А Т ) Т = А
- (А + В) Т = А Т + В Т
- (AB) T = B T A T
- (rA) T = rA T
Назад на главную страницу матриц и приложений
Назад на домашнюю страницу линейной алгебры
Назад к математике Домашняя страница отдела
электронная почта Вопросы и предложения
Умножение матриц, матрицы идентичности, больше транспозиций
Умножение матриц, Матрицы тождества, Больше транспозицийУмножение матриц, единичные матрицы, другие транспозиции
 На странице рассматриваются различные формы матрицы идентичности.
Он также кратко описывает создание и поведение обратной матрицы.
Несколько рисунков используются для демонстрации того, что две ненулевые матрицы могут иметь произведение, равное нулю.
Наконец, мы рассмотрим некоторые свойства транспонирования на нескольких примерах. В этих примерах используются 9 матриц.0079
На странице рассматриваются различные формы матрицы идентичности.
Он также кратко описывает создание и поведение обратной матрицы.
Несколько рисунков используются для демонстрации того, что две ненулевые матрицы могут иметь произведение, равное нулю.
Наконец, мы рассмотрим некоторые свойства транспонирования на нескольких примерах. В этих примерах используются 9 матриц.0079 ВАЖНОЕ ПРИМЕЧАНИЕ: TI-83 использует ключ, чтобы добраться до МАТРИЦА экран. Калькуляторы TI-83 Plus и TI-84 Plus используют последовательность двух клавиш
добраться до МАТРИЦА экран. На этой странице будет последовательно использоваться последовательность двух клавиш
продемонстрировать переход к Экран МАТРИЦА . Пользователям TI-83 придется заменить две клавиши, представленные здесь, одной клавишей.
Пользователям TI-83 придется заменить две клавиши, представленные здесь, одной клавишей.
| Во-первых, мы переходим к MATRIX , чтобы увидеть, что матрицы находятся в калькулятор, по крайней мере, в отношении строк и столбцов. [См. примечание выше для методов ввода желаемых матриц, если это необходимо.] | |
| На рис. 2 показано содержимое [A] и [b] . | |
| Выберите [A] из MATRIX окно, затем , выберите [B] в окне MATRIX , а затем нажмите для выполнения команды. Полученная матрица показана на рисунке 3. |
Здесь нам нужно остановиться и изучить результат умножения двух матриц.
Полученный ответ не так ясен, как для матричного сложения,
вычитание, скалярное умножение или их комбинация. Для выполнения матричного умножения каждый элемент ответа равен
образованный путем получения суммы произведений элементов
соответствующую строку левой матрицы с элементами
соответствующий столбец правой матрицы.
На рисунке 3 5 в ответе находится в строке 1 столбце 2.
Следовательно, число 5 получено путем сложения произведений
умножая каждый элемент строки 1 левой матрицы, [A] ,
с каждым элементом столбца 2 правой матрицы, [B] .
Первая строка [A] была 1 2 .
Второй столбец [B] был -1 3 .
Мы умножаем 1*(-1) и 2*3, , чтобы получить -1 и 9.0003 6 ,
который мы добавляем, чтобы получить 5 , элемент в строке 1, столбце 2 ответа.
Этот процесс изображен для всех 4 позиций ответа на следующих рисунках.
Для выполнения матричного умножения каждый элемент ответа равен
образованный путем получения суммы произведений элементов
соответствующую строку левой матрицы с элементами
соответствующий столбец правой матрицы.
На рисунке 3 5 в ответе находится в строке 1 столбце 2.
Следовательно, число 5 получено путем сложения произведений
умножая каждый элемент строки 1 левой матрицы, [A] ,
с каждым элементом столбца 2 правой матрицы, [B] .
Первая строка [A] была 1 2 .
Второй столбец [B] был -1 3 .
Мы умножаем 1*(-1) и 2*3, , чтобы получить -1 и 9.0003 6 ,
который мы добавляем, чтобы получить 5 , элемент в строке 1, столбце 2 ответа.
Этот процесс изображен для всех 4 позиций ответа на следующих рисунках.
Умножить ряд 1 из [A] умножить на столбец 1 из [B] чтобы получить строки 1 столбца 1 ответа. | |
| Умножить ряд 1 из [A] умножить на столбец 2 из [B] чтобы получить строки 1 столбца 2 ответа. | |
| Умножить ряд 2 из [A] умножить на столбец 1 из [B] чтобы получить строки 2 столбца 1 ответа. | |
| Умножить ряд 2 из [A] умножить на столбец 2 из [B] чтобы получить строки 2 столбца 2 ответа. |
Умножение матриц полно сюрпризов. Во-первых, обратите внимание, что умножение матриц не является коммутативным.
если у нас есть два числа, a и b , мы знаем, что а * б = б * а . Это называется коммутативным свойством умножения действительных чисел.
На рис. 7 показаны результаты для [A] * [B] , а затем для [B] * [A] , и эти два ответа явно не совпадают.
Следовательно, умножение матриц НЕ коммутативное. Это называется коммутативным свойством умножения действительных чисел.
На рис. 7 показаны результаты для [A] * [B] , а затем для [B] * [A] , и эти два ответа явно не совпадают.
Следовательно, умножение матриц НЕ коммутативное.Помните, что для сложения двух матриц они должны имеют одинаковые размеры. Нижняя часть рисунка 7 указывает калькулятору умножать [А] , a 2 х 2 матрица, раз [C] , a 2 х 3 матрица. | |
Интересно, что калькулятор выполняет умножение и выдает 2 x 3 результат. Метод умножения для
матрицы привязывает элементы ответа к соответствующим строкам левой матрицы и
соответствующие столбцы
правильная матрица. Каждая из 6 записей в результатах, показанных на
Рисунок 8 имеет соответствующую строку в [A] и соответствующий столбец в [C] . Кроме того, длина каждой строки в [A] (которая определяется количеством столбцов в [A] , точно равна длине каждого столбца в [C] (что равно
определяется количеством строк [C] ). Кроме того, длина каждой строки в [A] (которая определяется количеством столбцов в [A] , точно равна длине каждого столбца в [C] (что равно
определяется количеством строк [C] ).Рисунок 8 заканчивается формулировкой команды умножения [С] * [А] . Эта команда приводит к ошибке, как показано на рис. 9. | |
Сообщение об ошибке короткое: DIM MISMATCH . В данном случае, поскольку мы хотели сделать
умножение, калькулятор настаивает на том, чтобы число записей в каждой строке
левая матрица, [C] должна соответствовать количеству записей в каждом столбце
правой матрицы, [A] . Однако [C] имеет 3 записи в каждой строке (потому что [C] имеет 3 столбца), тогда как [A] имеет только 2 записи в каждом столбце (потому что [A] имеет всего 2 ряда). Схема этого следующая: Мы можем сказать это Выйти или Перейти к . Мы продемонстрируем первый позже, но чтобы
перейти к рисунку 10 мы будем нажимать
до G или . Мы можем сказать это Выйти или Перейти к . Мы продемонстрируем первый позже, но чтобы
перейти к рисунку 10 мы будем нажимать
до G или . | |
| После выбора Goto на рисунке 9, калькулятор отображает оскорбительную команду так что мы можем редактировать его. В этом случае мы заменим [A] на [E] . Для этого нажмите чтобы перейти к рисунку 11. | |
| Несмотря на то, что мы нажали курсор влево только один раз, выделение перемещено в начало символа [A] . Помните, что это один символ даже если он занимает место в три символа. | |
Возвращаемся на экран MATRIX и выбираем пункт 5, [E]. Калькулятор вставляет это
новый символ поверх старого. Затем нажмите для выполнения команды.
Результат умножения [C] * [E] , a 2 x 3 матрица, умноженная на 3 x 2 это 2 x 2 матрица.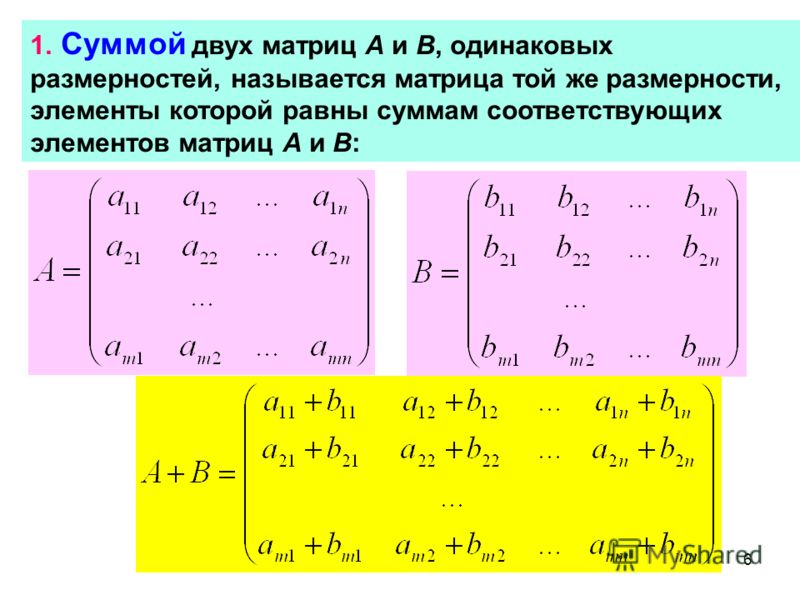 | |
| С другой стороны, [B] * [C] , a 3 x 2 матрица, умноженная на 2 x 3 представляет собой матрицу 3 x 3 . Именно таких результатов мы и ожидали, особенно после изучения рисунок выше (рядом с рисунком 9) где мы видим, что умножение работает, если «внутреннее» размеры совпадают, и в результате получается матрица с «внешними» размерами. | |
| Учитывая [C] * [G] , внутренние размеры совпадают ( [C] имеет 3 столбца и [G] имеет три ряда. Поэтому умножение должно работать, и результат должен
иметь 2 строки (количество строк в [C] и 3 столбца, количество столбцов в [Г] . Однако мы ожидаем, что команда [G] * [C] завершится ошибкой, поскольку внутренние размеры не совпадают. | |
| Действительно, команда на рис. 14 не сработала. На этот раз мы выберем Выйдите из опции , нажав клавишу . | |
| Поскольку мы выходим на РИС. 15, калькулятор оставляет вызывающую ошибку команду на экран, не выполняя его. Теперь калькулятор готов новая команда. | |
| Просто чтобы добавить сюда последний рабочий пример, мы формируем команду [G] * [E] , команда, которая, как мы ожидаем, будет работать с [G] . имеет 3 столбца и [E] имеет 3 строки. Мы ожидаем, что результат будет иметь 3 строки и 2 столбца. Оно делает. | |
Мультипликативная единичная матрица представляет собой квадратную матрицу с
значение 1 в каждой записи на главной диагонали и нулевое значение во всех остальных местах. Конечно, мы могли бы ввести или использовать редактор для создания мультипликативной идентичности.
матрица. Тем не менее, калькулятор предоставляет хороший способ генерировать такие
матрица. Мы возвращаемся к Окно MATRIX , затем переместите выделение
вправо, чтобы увидеть подокно MATH , показанное на рисунке 18.
Оказавшись там, мы находим начало идентификатора (оператор функции как
вариант 5, выделенный на рисунке 18.
ЕСЛИ мы нажмем, чтобы выбрать эту опцию, калькулятор
вставьте начало команды на наш экран. Конечно, мы могли бы ввести или использовать редактор для создания мультипликативной идентичности.
матрица. Тем не менее, калькулятор предоставляет хороший способ генерировать такие
матрица. Мы возвращаемся к Окно MATRIX , затем переместите выделение
вправо, чтобы увидеть подокно MATH , показанное на рисунке 18.
Оказавшись там, мы находим начало идентификатора (оператор функции как
вариант 5, выделенный на рисунке 18.
ЕСЛИ мы нажмем, чтобы выбрать эту опцию, калькулятор
вставьте начало команды на наш экран. | |
| На рис. 19 показано начало команды. Теперь нам нужно закончить его. Все мы need — размерность искомой матрицы. Это будет квадратная матрица, как и все тождества. матрица, но для каждого измерения существует своя единичная матрица. Чтобы выполнить команду, нам нужно указать размерность желаемая единичная матрица. | |
На рис.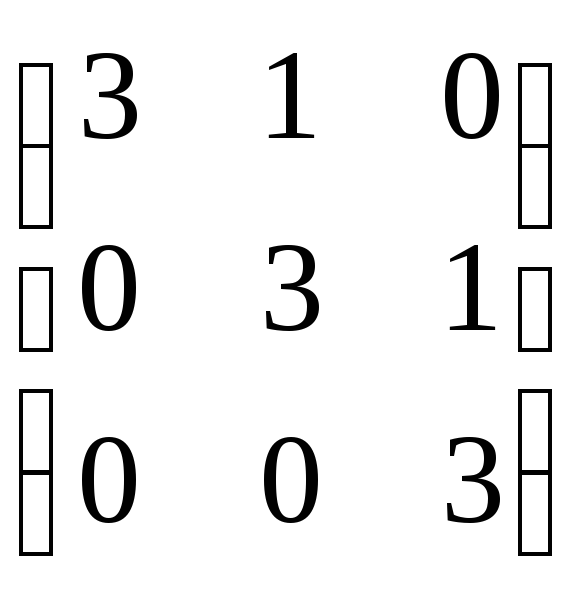 20 мы выполнили команду, и калькулятор
выполнить это. Мы запросили 3 x 3 тождественная матрица, и калькулятор создал ее. 20 мы выполнили команду, и калькулятор
выполнить это. Мы запросили 3 x 3 тождественная матрица, и калькулятор создал ее. | |
| Мы можем продемонстрировать нашу матрицу идентичности, используя ее слева с помощью любая из матриц, состоящая из трех строк. Мы будем использовать [G] . И, как и ожидалось, продукт идентичен [G]. | |
| Поскольку [G] — это квадратная матрица, мы могли бы умножить ее справа на 3 x 3 единичная матрица. Для рисунка 22 мы вспоминаем команду identity(3) и выполняем ее, затем строим команду [G] * Ans . | |
Выполнив команду, завершившую рис. 22, мы увидим результаты на рис. 23. Опять же,
ответ идентичен [G] . Точно так же мы конструируем и выполняем команду
умножить [C] справа от 3 x 3 единичная матрица. Результат идентичен [C] . Точно так же мы конструируем и выполняем команду
умножить [C] справа от 3 x 3 единичная матрица. Результат идентичен [C] . | |
| Однако, поскольку [C] имеет 2 строки, тождественная матрица, которая нам нужно использовать, чтобы умножить слева от [C] должно быть 2 x 2 единичная матрица, как показано на рисунке 24. | |
| Рисунок 25 – это возврат к окну MATRIX и подокну MATH . В этом случае мы хотим использовать дополнение (опция . | |
Здесь мы вставили на экран начало аугмента (функция ).
Теперь нам нужно предоставить функцию
с двумя матрицами, а именно twop, которые имеют одинаковое количество
ряды. Augment объединит две матрицы в одну матрицу. Augment объединит две матрицы в одну матрицу. | |
| Завершаем функцию augment( с матрицей [G] а затем Ответ , который содержал 3 x 3 матрица идентичности с начала рисунка 26. В результате получается новая матрица с 3 строками, а теперь с 6. столбцы. | |
| Часть матрицы на рис. 27 была обрезана. Мы можем использовать ключ, чтобы переместить окно вправо. | |
Возврат в окно MATRIX , подокно MATH ,
чтобы найти a, выберите команду rref(.
Помните, что rref выполнит серию
элементарные операции со строками, которые превратят первый м столбцов в м x n матрицу в
имея 1 вниз по главной диагонали и 0 выше и ниже этой диагонали. | |
| На рис. 30 мы попросили калькулятор выполнить функцию rref( ). на расширенной матрице, которую мы создали ранее. Функция rref( имеет целью получить главную диагональ для первых 3 столбцов (поскольку здесь 3 строки) быть все 1. Элементарные операции со строками, которые выполняются для этого и получения 0 выше и ниже этой диагонали, также измените значения в оставшихся 3 столбцах, те, которые начинались как расширенная матрица идентичности. На рис. 30 можно показать только часть этих новых значений, так как их недостаточно. комната на экране. | |
| Используйте ключ для перемещения окно справа, показывающее больше расширенных значений. | |
Другой подход заключается в использовании команды в меню MATH .
чтобы калькулятор отображал результаты в дробной форме. На рисунке 32 мы
перейдите в меню MATH, нажав клавишу .
Затем мы можем выбрать команду, нажав
ключ. На рисунке 32 мы
перейдите в меню MATH, нажав клавишу .
Затем мы можем выбрать команду, нажав
ключ. | |
| На рис. 33 показана команда после того, как она была вставлена и выполнена (калькулятор автоматически предоставил Ans в команде). Матрица снова отображается с десятичные значения теперь отображаются как дроби. В виде дробей легче увидеть большую часть матрицы на экран. Нам все еще нужно переместить окно в право увидеть остальные результаты. | |
| На рис. 34 показана большая часть матрицы. | |
Команда на рис. 35 запрашивает значение, обратное [G] , но выраженное в дробной форме.
Мы сравниваем эти значения с теми, которые мы нашли в правой части таблицы.
расширенную матрицу, показанную на рисунках 33 и 34.
Что касается значений, отображаемых на экране, это одни и те же записи. | |
| Здесь мы видим остальную часть ответа с рис. 35. Опять же, эти значения точно совпадают со значением в предыдущем расширенная матрица. | |
| Хотя жаль тратить впустую наши прежние усилия по внедрению матрицы в [H] , так как у нас есть небольшое количество доступных матриц нам придется уничтожить старое содержание [H] , если мы хотим сохранить только что вычисленную матрицу, а именно значение [G] -1 . Как только мы сохранили значение в [H] , мы можем проверить [Г] * [Ч] . | |
Этот продукт представляет собой единичную матрицу. Следовательно, [H] — правая мультипликативная обратная.
для [G] (потому что мы видели, что умножение двух матриц на [H] справа дает единичную матрицу). Затем формулируем команду для [H] * [G] . | |
| Это также дает единичную матрицу. Следовательно, [H] также является левым мультипликативом. инверсия [G] . Увидев, что оба продукта с [H] на слева и справа дают единичную матрицу, мы можем замкнуть обозначение и просто сказать, что [H] является мультипликативной инверсией [Г] . И, конечно же, получается [G] . мультипликативные инверторы [Ч] . |
Работа с рис. 26 по рис. 39 может показаться немного разрозненной. Зачем проходить это дополненное матричная работа с последующим применением rref( команда, если мы можем просто получить нужные значения, используя ключ, как мы сделали на рисунке 35?
Ответ на этот вопрос скорее исторический, чем математический.
В какой-то степени это та же причина, что
учим и изучаем элементарные операции с рядами
хотя rref( нам доступен. Было время, когда для того, чтобы найти обратную матрицу для
заданной матрицы, можно было бы дополнить исходную матрицу единичной матрицей, затем
выполнить все необходимые
элементарные операции со строками над расширенной матрицей с
цель
достижение единичной матрицы в левой половине расширенной матрицы, что дает
обратная матрица в правой половине расширенной матрицы.
Это болезненный и подверженный ошибкам процесс, который в настоящее время устарел благодаря использованию
ключа после имени или значения матрицы.
Было время, когда для того, чтобы найти обратную матрицу для
заданной матрицы, можно было бы дополнить исходную матрицу единичной матрицей, затем
выполнить все необходимые
элементарные операции со строками над расширенной матрицей с
цель
достижение единичной матрицы в левой половине расширенной матрицы, что дает
обратная матрица в правой половине расширенной матрицы.
Это болезненный и подверженный ошибкам процесс, который в настоящее время устарел благодаря использованию
ключа после имени или значения матрицы.
| Ранее мы видели, что умножение матриц, вообще говоря, не является коммутативным. Теперь рассмотрим еще одно, казалось бы, странное поведение матриц. Начнем с определения двух новых матриц и сохраняя их в [A] и [B] . Следует отметить, что ни в одной из матриц нет ни одной записи, равной 0. | |
Затем мы умножаем две матрицы, [A] * [B] ,
только чтобы обнаружить, что произведение этих двух ненулевых матриц равно
нулевая матрица. Это поведение, которое сильно отличается от поведения чисел.
где мы знаем, что если произведение двух чисел равно нулю, то хотя бы одно
из двух чисел должен быть равен нулю. Это поведение, которое сильно отличается от поведения чисел.
где мы знаем, что если произведение двух чисел равно нулю, то хотя бы одно
из двух чисел должен быть равен нулю. | |
| Чтобы добавить немного интереса к этому повороту событий, на рис. 42 мы смотрим на [B] * [A] только для того, чтобы узнать, что это не нулевая матрица! | |
| Рисунок 43 возвращается к обсуждению транспонирования матриц из более раннего веб-страница. Здесь мы сначала отмечаем матричное произведение [D] * [F] , а затем значение этого транспонированного, а именно, ( [D] * [F] T . Вторая матрица именно то, что мы ожидаем для транспозиция. | |
На рис. 44 впервые представлены ( [F] T ) * ( [D] T ) который дает то же значение, что и ( [D] * [F] T . Таким образом, мы замечаем, что когда
мы делаем транспонирование
произведение матриц равно обратному произведению перестановки двух матриц. Таким образом, мы замечаем, что когда
мы делаем транспонирование
произведение матриц равно обратному произведению перестановки двух матриц.Чтобы еще раз убедиться в этом, взгляните на Рисунок 44, чтобы увидеть результат отсутствия обратного порядка. из двух матриц. Мы видим, что ( [D] T ) * ( [F] T ) не только не дает одинаковых значений, он даже не производит матрицу того же размера! |
© Роджер М. Палай
Салин, Мичиган 48176
Сентябрь 2010 г.
6.2 — Операции с матрицами
6.2 — Операции с матрицамиРавенство
Две матрицы равны тогда и только тогда, когда
- Порядок матриц одинаковый
- Соответствующие элементы матриц совпадают
Дополнение
- Порядок матриц должен быть одинаковым
- Сложить соответствующие элементы вместе
- Сложение матриц коммутативно
- Сложение матриц ассоциативно
Вычитание
- Порядок матриц должен быть одинаковым
- Вычесть соответствующие элементы
- Вычитание матриц не является коммутативным (как и вычитание действительных чисел)
- Вычитание матриц не является ассоциативным (как и вычитание действительных чисел)
Скалярное умножение
Скаляр — это число, а не матрица.
- Матрица может быть любого порядка
- Умножить все элементы матрицы на скаляр
- Скалярное умножение коммутативно
- Скалярное умножение ассоциативно
Нулевая матрица
- Матрица любого порядка
- Состоит из всех нулей
- Обозначается заглавной буквой O
- Аддитивная идентичность для матриц
- Любая матрица плюс нулевая матрица является исходной матрицей
Умножение матриц
A m×n × B n×p = C m×p
- Количество столбцов в первой матрице должно быть равно количество строк во второй матрице. То есть внутренние размеры должны быть одинаковыми.
- Порядок произведения равен количеству строк в первой матрице на количество столбцов в вторая матрица. То есть размеры изделия – это наружные габариты.
- Так как количество столбцов в первой матрице равно количеству строк во второй
матрица, вы можете спаривать записи.

- Каждый элемент в строке i из первой матрицы соединяется с элементом в столбце j из вторая матрица.
- Элемент в строке i , столбце j произведения образован путем умножения этих парных элементов и их суммирование.
- Каждый элемент произведения представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
- Будет n произведений, которые суммируются для каждого элемента произведения.
См. полный пример умножения матриц.
Умножение матриц не является коммутативным
- Умножение действительных чисел.
- Внутренние размеры могут не совпадать при изменении порядка матриц.
Не перемножайте соответствующие элементы
- Поскольку порядок (размеры) матриц может не совпадать, соответствующие элементы, чтобы умножить вместе.
- Умножить строки первого на столбцы второго и сложить.

Нет деления матрицы
- Не существует определенного процесса деления матрицы на другую матрицу.
- Матрица может быть разделена на скаляр.
Идентификационная матрица
- Квадратная матрица
- Единицы на главной диагонали
- Нули везде
- Обозначается I. Если индекс включен, это порядок единичной матрицы.
- I — мультипликативная идентичность для матриц
- Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
- Умножение на единичную матрицу является коммутативным, хотя порядок изменить
Идентификационная матрица размера 2
| I 2 = | 1 | 0 | ||
| 0 | 1 |
Идентификационная матрица размера 3
| I 3 = | 1 | 0 | 0 | ||
| 0 | 1 | 0 | |||
| 0 | 0 | 1 |
Свойства матриц
| Собственность | Пример |
|---|---|
| Коммутативность сложения | А + В = В + А |
| Ассоциативность сложения | А + (В + С) = (А + В) + С |
| Ассоциативность скалярного умножения | (кд) А = с (дА) |
| Скалярная идентичность | 1А = А(1) = А |
| Распределительный | с (А + В) = сА + сВ |
| Распределительный | (с + г) А = сА + дА |
| Аддитивный идентификатор | А + О = О + А = А |
| Ассоциативность умножения | А (ВС) = (АВ) С |
| Левая распределительная | А (В + С) = АВ + АС |
| Правый распределитель | ( А + В ) С = АС + ВС |
| Скалярная ассоциативность/коммутативность | с (АВ) = (сА) В = А (сВ) = (АВ) с |
| Мультипликативная идентичность | ИА = АИ = А |
Свойства действительных чисел, которые не являются свойствами матриц
Коммутативность умножения
- Вы не можете изменить порядок задачи на умножение и ожидать
чтобы получить то же самое
товар.
 АБ≠БА
АБ≠БА - Вы должны быть осторожны при факторизации общих факторов, чтобы убедиться, что они находятся на такой же сторона. AX+BX = (A+B)X и XA+XB = X(A+B), но AX+XB не учитывается.
Свойство нулевого продукта
- Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.
Мультипликативное свойство равенства
- Если A=B, то AC = BC. Это свойство остается верным, но обратное не обязательно верно. Тот факт, что AC = BC, не означает, что A = B.
- Поскольку умножение матриц не является коммутативным, вы должны предварительно умножить или постумножить на обеих сторонах уравнения. То есть, если A=B, тогда AC = BC или CA = CB, но AC≠CB.
Нет деления матрицы
- Вы должны умножить на обратную матрицу
Вычисление функции с использованием матрицы
Рассмотрим функцию f(x) = x 2 — 4x + 3 и матрицу A
| А = | 1 | 2 | ||
| 3 | 4 |
Первоначальная попытка вычислить f(A) состояла бы в замене каждого x
с A, чтобы получить f(A) = A 2 — 4А+3. Есть одно небольшое
проблема однако. Константа 3
не матрица, и сложить нельзя
матрицы и скаляры вместе. Итак, мы умножаем
постоянная по матрице идентичности.
Есть одно небольшое
проблема однако. Константа 3
не матрица, и сложить нельзя
матрицы и скаляры вместе. Итак, мы умножаем
постоянная по матрице идентичности.
f(A) = A 2 — 4A + 3I.
Вычислите каждый член функции, а затем сложите их вместе.
| А 2 = | 1 | 2 | * | 1 | 2 | = | 7 | 10 | ||||||
| 3 | 4 | 3 | 4 | 15 | 22 |
| -4 А = -4 | 1 | 2 | = | -4 | -8 | ||||
| 3 | 4 | -12 | -16 |
| 3И = 3 | 1 | 0 | = | 3 | 0 | ||||
| 0 | 1 | 0 | 3 |
| ф(А) = | 7 | 10 | + | -4 | -8 | + | 3 | 0 | = | 6 | 2 | ||||||||
| 15 | 22 | -12 | -16 | 0 | 3 | 3 | 9 |
Факторные выражения
Показаны некоторые примеры факторинга.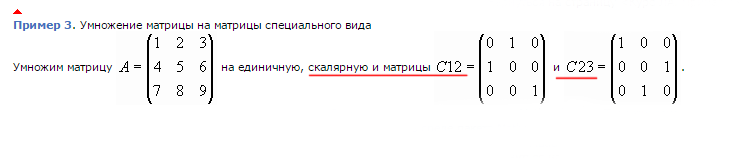 Упрощайте и решайте как обычно, но помните
эта матрица
умножение не коммутативно
и нет матричного деления.
Упрощайте и решайте как обычно, но помните
эта матрица
умножение не коммутативно
и нет матричного деления.
2Х + 3Х = 5Х
АХ + ВХ = (А+В)Х
ХА + ХВ = Х(А+В)
АХ + 5Х = (А+5I)Х
AX+XB не учитывает
Решение уравнений
Систему линейных уравнений можно записать в виде AX=B, где A — коэффициент матрица, X — вектор-столбец, содержащий переменные, а B — правая часть сторона. В следующем разделе мы научимся решать это уравнение.
Если существует более одной системы линейных уравнений с одинаковым коэффициентом матрицу, то вы можете расширить матрицу B, чтобы иметь более одного столбца. Помещать каждую правую часть в свой столбец.
Умножение матриц
Умножение матриц включает суммирование произведения. Уместно там, где вы нужно умножить вещи вместе, а затем добавлять. Например, умножение количества единиц на стоимость единицы будет дать общее Стоимость.
Найдены единицы товара
путем проведения модульного анализа на
матрицы. Этикетки для товара – это этикетки строк первого
матрица и метки столбцов
вторая матрица.
Этикетки для товара – это этикетки строк первого
матрица и метки столбцов
вторая матрица.
Identity Matrix — Что такое Identity Matrix? Примеры
Единичная матрица называется мультипликативной идентичностью матриц. Прежде чем перейти к изучению того, что такое единичная матрица, давайте вспомним значение тождества в математике. Тождество — это математическая величина, которая при оперировании с некоторой величиной оставляет ту же самую величину. Рассмотрим следующие примеры.
- Аддитивная идентичность равна 0, так как добавление любого числа к 0 дает то же число, что и сумма.
Например, 3 + 0 = 3, 0 + (-1) = -1 и т. д. - Мультипликативное тождество равно 1, так как умножение любого числа на 1 дает то же число, что и произведение.
Например, 3 × 1 = 3, 1 × (-1) = -1 и т. д.
Точно так же, конечно, мы знаем, что, добавляя нулевую матрицу \(\left[\begin{array}{rr}0 & 0 \\ \\ 0 & 0 \end{array}\right]\ ) для любой матрицы 2 × 2 дает нам одну и ту же матрицу, и, следовательно, нулевая матрица называется аддитивной единичной матрицей. Но что такое мультипликативное тождество по отношению к матрицам? Ответом является единичная матрица, и давайте подробно изучим ее здесь.
Но что такое мультипликативное тождество по отношению к матрицам? Ответом является единичная матрица, и давайте подробно изучим ее здесь.
| 1. | Что такое матрица идентичности? |
| 2. | Идентификационная матрица разных порядков |
| 3. | Проверка идентификационной матрицы |
| 4. | Свойства матрицы идентичности |
| 5. | Нахождение обратной матрицы с использованием единичной матрицы |
| 6. | Применение матрицы идентичности |
| 7. | Часто задаваемые вопросы о Identity Matrix |
Что такое матрица идентичности?
Единичная матрица представляет собой квадратную матрицу, в которой каждый из элементов ее главной диагонали равен 1, а каждый из других элементов равен 0. Она также известна как единичная матрица.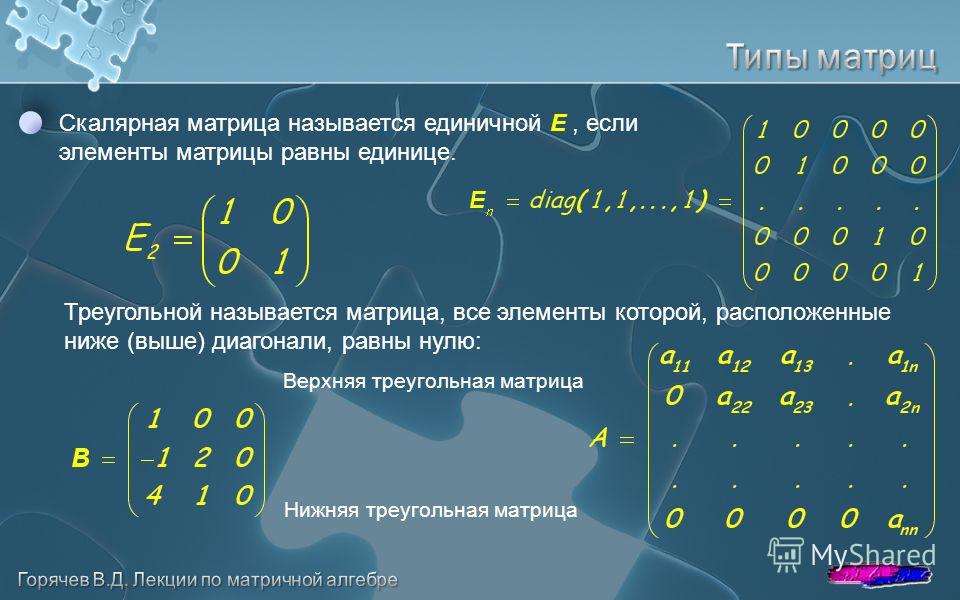 Представим единичную матрицу порядка n × n (или n) в виде I и . Иногда мы обозначаем это просто как I. Математическое определение единичной матрицы:
Представим единичную матрицу порядка n × n (или n) в виде I и . Иногда мы обозначаем это просто как I. Математическое определение единичной матрицы:
- I n (или) I = [a ij ] n × n , где a ij = 1, когда i = j, и a ij = 0, когда i ≠ j.
Единичная матрица в целом является идентичной относительно умножения. Таким образом, для любой матрицы A
AI = IA = A
, т. е. умножая любую матрицу A на единичную матрицу того же порядка, мы получаем ту же матрицу, что и произведение, отсюда и название «единичная» для Это.
Идентификационная матрица разных порядков
Вот несколько примеров единичных матриц разного порядка. Обратите внимание, что единичная матрица всегда является квадратной матрицей.
- Единичная матрица 2×2: I 2 = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{массив}\right]\).
- 3×3 единичная матрица: I 3 = \(\left[\begin{array}{rr}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{массив}\right] \).

- Единичная матрица 4×4: I 4 = \(\left[\begin{array}{rr}1 & 0 & 0&0\\ 0 & 1 & 0&0\\ 0 & 0 & 1&0\\0&0&0&1\end{массив} \Правильно]\).
Проверка идентификационной матрицы
Если I — единичная матрица, а A — любая матрица того же порядка, то по определению AI = IA = A. Проверим это, взяв матрицы порядка 2 × 2.
A = \(\left [\begin{array}{rr}1 и 5 \\ \\-3 & 2 \end{массив}\right]\) и I = \(\left[\begin{array}{rr}1 & 0 \ \ \\ 0 & 1 \end{array}\right]\) (что является тождеством относительно умножения).
Проверка AI = A
AI = \(\left[\begin{array}{rr} 1 & 5 \\ \\-3 & 2 \end{array}\right]\) \(\left[\ begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\)
= \(\left[\begin{array}{rr}1(1)+5( 0) & 1(0)+5(1) \\ \\ -3(1)+2(0) & -3(0)+2(1) \end{массив}\right]\)
= \(\left[\begin{array}{rr}1 & 5 \\ -3 & 2 \end{array}\right]\)
= A
Поскольку матрицы не обязательно должны быть коммутативными относительно умножение, мы также должны убедиться, что IA = A.
Проверка IA = A
IA = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\) \(\left[\begin {массив}{rr}1 и 5 \\ -3 и 2 \end{массив}\right]\)
= \(\left[\begin{массив}{rr}1(1)+0(-3 ) & 1(5)+0(2) \\ \\ 0(1)+1(-3) & 0(5)+1(2) \end{массив}\right]\)
= \( \left[\begin{array}{rr}1 & 5 \\ \\ -3 & 2 \end{array}\right]\)
= A
Таким образом, мы убедились, что AI = IA = A.
Аналогично можно попробовать проверить единичную матрицу порядков 3 × 3, 4 × 4 и т. д.
Свойства матрицы идентичности
Вот свойства матрицы идентичности , основанные на ее определении.
- Единичная матрица всегда является квадратной матрицей.
- При умножении единичной матрицы на любую другую матрицу получается та же самая матрица.
- Каждая единичная матрица является диагональной матрицей, поскольку только элементы ее главной диагонали не равны нулю.
- Единичная матрица симметрична как I Т = И.

- Каждая единичная матрица является скалярной матрицей, так как все элементы ее главной диагонали равны, а остальные элементы равны нулю.
- Определитель каждой единичной матрицы равен 1.
- Обратная единичная матрица сама по себе имеет вид I · I -1 = I -1 · I = I.
- I n = I для любого целого числа n. т. е. квадрат единичной матрицы равен самому себе, куб единичной матрицы равен самому себе и т. д.
- При умножении матрицы на обратную получается единичная матрица
- Мы можем найти обратную матрицу, используя единичную матрицу (давайте посмотрим на это в следующем разделе).
Нахождение обратной матрицы с использованием единичной матрицы
Обратная матрица A (которая записывается как A -1 ) является матрицей B (и наоборот) тогда и только тогда, когда AB = BA = I, где A, B и I — квадратные матрицы тот же порядок. Имея A и B, легко проверить, являются ли они обратными друг другу, просто проверив, что AB = BA = I. Но если дана матрица A, то как мы можем найти ее обратную B? Мы можем найти обратную матрицу матрицы, используя следующие шаги:
Но если дана матрица A, то как мы можем найти ее обратную B? Мы можем найти обратную матрицу матрицы, используя следующие шаги:
- Шаг 1: Запишем расширенную матрицу, к которой примыкаем заданную матрицу с единичной матрицей того же порядка и разделяем эти две матрицы линией.
- Шаг 2: Мы применяем операции со строками, чтобы преобразовать левостороннюю матрицу (то есть A) в единичную матрицу.
- Шаг 3: Матрица, которая осталась в правой части, сама является нашей обратной матрицей.
Мы можем увидеть пример нахождения обратной матрицы с использованием этих шагов в разделе «Примеры матрицы идентичности» ниже.
Применение матрицы идентичности
Единичная матрица используется для различных целей в линейной алгебре. Вот приложения единичной матрицы.
- Единичная матрица используется для нахождения обратной матрицы.
- Кроме того, единичная матрица используется для проверки того, являются ли любые две заданные матрицы обратными друг другу.

- Для нахождения собственных значений и собственных векторов используется единичная матрица.
- При решении системы уравнений с помощью элементарных операций над строками используется единичная матрица.
Важные примечания к матрице идентичности:
Ниже приведены некоторые важные моменты, которые следует отметить, связанные с матрицей идентичности.
- Если вы видите единичную матрицу без указания операции, то по умолчанию следует понимать, что это единичная матрица относительно умножения.
- Чтобы написать единичную матрицу некоторого порядка, сначала напишите пустую матрицу заданного порядка, запишите единицы вместо элементов главной диагонали и, наконец, запишите 0 вместо всех остальных элементов.
- Если AB = BA = I, то A и B обратны друг другу.
- Чтобы найти обратную матрицу, запишите ее, присоединив к ней единичную матрицу того же порядка с правой стороны. Примените операции со строками ко всей расширенной матрице, стремясь сделать левостороннюю матрицу единичной матрицей.
 Тогда матрица правой части будет обратной заданной матрице.
Тогда матрица правой части будет обратной заданной матрице.
☛ Связанные темы:
Вот некоторые темы, которые могут вас заинтересовать при чтении о единичной матрице.
- Добавление матриц
- Вычитание матриц
- Калькулятор матрицы идентичности
- Калькулятор сложения матриц
Часто задаваемые вопросы о Identity Matrix
Что такое определение матрицы идентичности в линейной алгебре?
Единичная матрица , обозначаемая I, представляет собой квадратную матрицу, в которой все элементы главной диагонали равны единицам, а все остальные элементы равны нулям. Для любой матрицы A AI = IA = A. Она также известна как единичная матрица.
Как определить матрицу идентичности?
Если в квадратной матрице
- каждый элемент главной диагонали равен 1 и
- все остальные элементы нули
, то мы говорим, что это единичная матрица.
Что такое матрица идентичности в квадрате?
Квадрат любой единичной матрицы равен самому себе. Например, \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\)\(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{массив}\right]\) = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{массив}\right ]\).
Что такое формула матрицы идентичности?
Единичная матрица — это матрица с единицами на главной диагонали и нулями на всех остальных местах. Таким образом, его формула I n (или) I = [a ij ] n × n , где a ij = 1, когда i = j, и a ij = 0, когда i ≠ j.
Что такое Матрица идентичности 3-го порядка?
В единичной матрице порядка 3 × 3 все элементы главной диагонали равны 1, а остальные элементы равны 0. Он задается как \(\left[\begin{array}{rr}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right]\).
Как найти обратную матрицу, используя единичную матрицу?
Чтобы найти обратную матрицу A, запишите A вместе с единичной матрицей (I) того же порядка в матрице, разделив их линией (такой, что A слева, а I справа). Примените операции со строками, чтобы преобразовать левую матрицу в I. Тогда правая матрица будет не чем иным, как A -1 .
Примените операции со строками, чтобы преобразовать левую матрицу в I. Тогда правая матрица будет не чем иным, как A -1 .
Почему это называется матрицей идентичности?
Если единичную матрицу (I) умножить на матрицу (A) того же порядка, получится та же самая матрица (A). т. е. AI = IA = A. Так же и имя (относительно умножения).
Что такое обратная матрица идентичности?
Обратная единичная матрица сама по себе. Потому что для любой единичной матрицы I имеем I · I = I · I = I.
Что такое транспонирование идентификационной матрицы?
Транспонирование матрицы получается путем записи ее строк в виде столбцов (или столбцов в виде строк). Транспонированием единичной матрицы является она сама. Например, если I = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\), то его транспонирование равно I T = \( \left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{массив}\right]\) = I.
Identitymatrix — обзор | ScienceDirect Topics
ScienceDirectRegisterSign in
Команда IdentityMatrix[n] возвращает идентификационную матрицу размера n×n.
Из: Mathematica by Example (Sixth Edition), 2022 г.
PlusAdd to Mendeley Александр С. Позняк, в Advanced Mathematical Tools for Automatic Control Engineers: Definitive Techniques, Volume 1, 2008
Definition 2.6 2.6 Для матрицы
A∈ℝm×n размерrundefined(1≤r≤min(m,n))
единичной матрицы в канонической форме для A называется рангом A, записанным r = ранг A , Если A = O m×n , то ранга A = 0, иначе ранга A ≥ 1.
Для каждых четырех канонических форм в (2.18) имеем для m=nrank [Im×mOm×(n−m)]=m для m
Предложение 2.10
Для квадратной матрицы A∈ℝn×n ранг A = n тогда и только тогда, когда она неособая.
Доказательство
Оно непосредственно следует из предложения (2. 9).
9).
Следствие 2.4
Ранг матрицы A∈ℝm×n равен порядку ее наибольшего ненулевого минора.
Несколько важных свойств ранга перечислены ниже.
- 1.
( Неравенство Фробениуса ) Если A, B и C являются прямоугольными матрицами и произведение ABC корректно определено, то
(2.19)ранг (AB)+ранг (BC)≤ранг (A)+ранг (ABC)
(2.20)rank (AB)≤min{rank (A), rank (B)}
Действительно, принимая в (2.19) первые A и C подходящего размера, получаем (2.20).
- 2.
Для любой комплексной матрицы A
ранг (A)=ранг (AA*)=ранг (A*A)не определено
- 3.
Если P и Q неособые, а A квадратное, то
(2.21)rank (PAQ)=rank (A)
0 Действительно, из него следует
0
ранг (PAQ) ≤ мин {ранг (P), ранг (AQ)} = мин {n, ранг (AQ)} = ранг (AQ) undefined ≤ мин {ранг (A), ранг (Q)} = ранг ( A)=ранг (P-1[PAQ]Q-1)undefined≤min{ранг (P-1), ранг ([PAQ]Q-1)}=ранг ([PAQ]Q-1)undefined≤min{ ранг (PAQ), ранг (Q−1)}=ранг (PAQ)
- 4.

(2.22)ранг (A)=ранг (AT)=ранг (A*)не определено
- 5.
Для любого A∈ℝm×n
(2.23)ранг (A+B)≤ранг (A)+ранг (B)undefined
- 6.
- 6 правило Сильвестра Для любых A∈ℝm×n и B∈ℝn×p
(2.24)ранг (A)+ранг (B)−n≤ранг (AB)≤min{ранг (A), ранг (B)}
- 7.
Для любых A∈ℝm×m и B∈ℝn×m
(2.25)rank (A⊗B)=(rank A)undefined(rank B)
Это следует из (2.11).
Просмотр главыКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780080446745500055
In Applied Dimension Analysis and Modeling (Second Edition), 2007 5 020 Теорема 920 -9. Если D единичная матрица, и если j-й столбец C содержит все нули, кроме одного «1» в 2-й строке, то1213-й столбец матрицы B и столбец j-й матрицы A можно поменять местами без изменения матрицы C . Если D является единичной матрицей, то ее i-я строка содержит все нули, кроме одной «1», которая находится в ее i -м (= j -м) столбце. Поэтому i-й столбец D идентичен j -му столбцу C , и, таким образом, их замена по теореме 9-9 не повлияет на C. Это доказывает следствие. Просмотреть главуКнига покупок Прочитать главу полностью URL: https://www.sciencedirect.com/science/article/pii/B9780123706201500150 Robert G. Mortimer, по физике (Robert G. Mortimer, по физике) 2013 Теперь определим матрицу идентичности E так, что Тот факт, что мы требуем, чтобы E было единичной матрицей при умножении с обеих сторон A , требует, чтобы и A , и E были квадратными матрицами. (13,44)E=100⋯0010⋯0001⋯0⋮⋮⋮⋱⋮000⋯1. диагональных элементов любой квадратной матрицы — это те, у которых оба индекса равны. Все диагональные элементы E равны 1, а остальные элементы ( недиагональных элементов ( ) исчезают. Это может быть представлено уравнением Eij=δij=1ifi=j,0ifi≠j, , где δij называется дельтой Кронекера . Exercise 13.19 Show by explicit matrix multiplication that 1000010000100001a11a12a13a14a21a22a31a41a31a31a31a41a41a41a31a41=a11a12a13a14a21a21a31a41a31a31a31a41a41a41a31a41.
Доказательство.
13.4.5 Матрица идентичности
 С квадратными матрицами мы получим полное сходство между операторной алгеброй и матричной алгеброй. В единичной матрице может быть любое количество строк и столбцов. Он имеет вид
С квадратными матрицами мы получим полное сходство между операторной алгеброй и матричной алгеброй. В единичной матрице может быть любое количество строк и столбцов. Он имеет вид
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B97801241580136
William Ford, в численной линейной алгебре с приложениями, 2015
1,3 Powers of Matrices
Определение 1. 10
10
. N × N Матрица I = [ Δ IJ ], определено Δ IJ = 1 IF I IJ = 1 IF I IJ = 1 IF I IJ = 1 IF I IJ = 1 IF I IJ = 1 IF I IJ = 1 IF Δ IJ = 1 IF Δ IJ ) если я ≠ j , называется n × n тождественной матрицей порядка n . Другими словами, столбцы единичной матрицы порядка n представляют собой векторы
e1=10⋮00,e2=01⋮00,…,en=00⋮01.
Например, I=1001 и I=100010001. Единичная матрица играет решающую роль в линейной алгебре. Когда любая n × n матрица A умножается на единичную матрицу слева или справа, результат равен А . Таким образом, единичная матрица действует как 1 в действительной системе счисления. Например,
Например,
261729-15-4100010001=21+60+1020+61+1020+60+11729-15-4=261729-15-4.
Определение 1.11
( k -я степень матрицы). Если A является матрицей n × n , мы определяем A k следующим образом: Aoccursktimes для k ≥ 1,9относится к матрицам.
>>A=11;10A=1110
>>A∧8ans=34212113
Число известно как матрица Фибоначчи , так как оно генерирует элементы знаменитой последовательности Фибоначчи
- 0,10,5 900 ,2,3,5,8,13,21,34,…
- ■
Единичная матрица 3 на 3
MatrixForm [IdentityMatrix[3]]
100010001
Единичные матрицы являются тождествами относительно умножения векторов в матричных пространствах.
MatrixForm [A = {{9, 1, 6}, {9, 4, 1}, {3, 4, 0}}]
1340 MatrixForm [A.IdentityMatrix[3] == A]
True
Матрицы идентичности также могут быть сформированы с помощью функции SparseArray путем указания значений ненулевых элементов.
- ■
Единичная матрица 2 на 2
MatrixForm [Normal [s = SparseArray [{{1, 1} → 1, {2,2} → 1, {3,3} → 1} ]]]
100010001
View chapterPurchase book
Read full chapter
URL: https://www.sciencedirect.
 com/science/article/pii/B9780124095205500163
com/science/article/pii/B9780124095205500163Scott L. Miller, Donald Childers , в книге «Вероятность и случайные процессы» (второе издание), 2012 г.
7.1.1 Оценка среднего значения случайных величин IID
Предположим, что X i имеют некоторую общую PDF, f x ( x ), которая имеет некоторое среднее значение, μ X . Учитывая набор наблюдений IID, мы хотим сформировать некоторую функцию,
(7.3)µˆ=g(X1,X2,…,Xn),
, которая будет служить оценкой среднего. Но какую функцию выбрать? Что еще более важно, какой критерий мы должны использовать для выбора функции?
Существует много широко используемых критериев. Для начала мы хотели бы, чтобы среднее значение оценки среднего было равно истинному среднему. То есть мы хотим, чтобы E[µˆ]=µX. Если этот критерий выполняется, мы говорим, что µˆ является несмещенная оценка μ X .
 Учитывая, что оценка несмещена, мы также хотели бы, чтобы ошибка в оценке была как можно меньше. Определите ошибку оценки как ɛ=μˆ-μX. Общим критерием является выбор оценки, которая минимизирует второй момент ошибки (среднеквадратическую ошибку), E[ɛ2]=E[(µˆ-µX)2]. Если этот критерий выполняется, мы говорим, что µ является эффективной оценкой µ X . Чтобы начать с относительно простого подхода, предположим, что мы хотим найти линейную оценку. То есть ограничимся оценками вида
Учитывая, что оценка несмещена, мы также хотели бы, чтобы ошибка в оценке была как можно меньше. Определите ошибку оценки как ɛ=μˆ-μX. Общим критерием является выбор оценки, которая минимизирует второй момент ошибки (среднеквадратическую ошибку), E[ɛ2]=E[(µˆ-µX)2]. Если этот критерий выполняется, мы говорим, что µ является эффективной оценкой µ X . Чтобы начать с относительно простого подхода, предположим, что мы хотим найти линейную оценку. То есть ограничимся оценками вида(7.4)μˆ=a1X1+a2X2+…+anXn=∑i=1naiXi.
Затем мы пытаемся найти константы a 1 , a 2 , …, a n , такие, что оценка (1) минимизирует — квадратная ошибка. Такой оценщик называется лучшим линейным несмещенным оценщиком (СИНИЙ).
Для упрощения записи в этой задаче будем писать X = [ X l, X 2 ,…, x N ] T и A = [ A x , A 2 , 121212121212.
 Линейная оценка µ тогда может быть записана как µ = aTX. Во-первых, чтобы оценка была несмещенной, нам нужно
Линейная оценка µ тогда может быть записана как µ = aTX. Во-первых, чтобы оценка была несмещенной, нам нужно(7,5)µX=E[µˆ]=E[aTX]=aTE[X].
Поскольку все X i являются IID, все они имеют средние значения, равные μ X . Следовательно, средний вектор для x составляет всего μ x 1 N , где 1 N 4441212121212121212121212121212121212121212121212121212121212121212121212121212121212. Тогда линейная оценка будет несмещенной, если
(7.6)∑i-1nai=aT1n=1.
Среднеквадратическая ошибка определяется как
(7.7)E[ɛ2]=E[(aTX-µX)2]=aTE[XXT]a-2µXaTE[X]+µX2=aTRa-2µX2aT1n+µX2
In это выражение, R = E [ XX T ] — корреляционная матрица для вектора X . Используя ограничение (7.
 6), среднеквадратическая ошибка упрощается до с учетом ограничения a T 1 n = 1.
6), среднеквадратическая ошибка упрощается до с учетом ограничения a T 1 n = 1.Для решения этой задачи многомерной оптимизации мы используем стандартные методы множителей Лагранжа. Сформируйте вспомогательную функцию
(7.9)h(λ)=aTRa+λaT1n.
Затем решите уравнение ∇ h = 0. Нетрудно показать, что градиент функции h получается равным ∇ h = 2 Ra + λ 9113 1 номер . Следовательно, оптимальный вектор a будет удовлетворять
(7.10)Ra=(-λ2)1n
Решение для a в этом уравнении и последующее применение ограничения a T l n = 1 дает решение
(7.11)a=R-11n1nTR-11n.
Из-за того, что X i являются IID, форму корреляционной матрицы можно легко показать как
(7.
 12)R=µX21n1nT+σX2I,
12)R=µX21n1nT+σX2I,, где единичная матрица, σ 2 X — дисперсия случайных величин IID. Это можно показать с помощью леммы об обращении матрицы 1 , обратной этой корреляционной матрице является
(7.13)R-1=+σX-2[I-µX2/σX21+nµX2/σX21n1nT].
Отсюда легко показать, что R −1 1 n пропорционально 1 n , и, следовательно, результирующий вектор оптимальных коэффициентов равен
07 (
5 9.0044). н11н.
С точки зрения оценки µ наилучшей линейной несмещенной оценкой среднего значения последовательности IID является
(7.15)µˆ=n11nTX=n1∑i=1nXi.
Этот оценщик обычно называют средним значением выборки . Предыдущий вывод доказывает следующую теорему 7.1.
. Теорема 7.1.
Другой возможный подход к оценке различных параметров распределения заключается в использовании подхода максимального правдоподобия (ML), представленного в главе 6 (раздел 6.
 5.2). В подходе ML параметры распределения выбираются так, чтобы максимизировать вероятность появления наблюдаемых значений выборки. Предположим, как и в предыдущем обсуждении, нас интересует оценка среднего значения распределения. Учитывая набор наблюдений, X 1 = x 1 , X 2 = x 2 , …, X n = x n , the ML estimate of μ X будет значением μ X , которое максимизирует f X ( x ). Несколько примеров пояснят эту концепцию.
5.2). В подходе ML параметры распределения выбираются так, чтобы максимизировать вероятность появления наблюдаемых значений выборки. Предположим, как и в предыдущем обсуждении, нас интересует оценка среднего значения распределения. Учитывая набор наблюдений, X 1 = x 1 , X 2 = x 2 , …, X n = x n , the ML estimate of μ X будет значением μ X , которое максимизирует f X ( x ). Несколько примеров пояснят эту концепцию.Пример 7.1
Предположим, что X i совместно являются гауссовыми, так что
fX(x)=1(2πσ2)n/2exp(-12σ2∑i=1n(xi-μ)2).
Значение μ, которое максимизирует это выражение, минимизирует
∑i=1n(xi-μ)2.
Дифференцирование и приравнивание к нулю дает уравнение
-2∑i=1n(xi-μ)=0 .
Решением этого уравнения является
µˆML=n1∑i=1nxi.

Следовательно, выборочное среднее также является оценкой ML среднего значения, когда случайные величины следуют распределению Гаусса.
Пример 7.2
Теперь предположим, что случайные величины имеют экспоненциальное распределение,
fX(x)=∏i=1n1µexp(-xiµ)µ(xi)=µn1exp(-µ1∑i=1nxi)∏i=1nµ(xi) .
Дифференцирование по μ и приравнивание к нулю приводит к
-nμn+1exp(-1μ∑i=1nxi)+1μ2(∑i=1nxi)1μnexp(-1μ∑i=1nxi)=0 .
Решение для µ дает
µˆML=1n∑i=1nxi.
Опять же, выборочное среднее является оценкой максимального правдоподобия среднего распределения.
Поскольку выборочное среднее встречается так часто, полезно изучить эту оценку более подробно. Во-первых, отметим, что выборочное среднее само по себе является случайной величиной, поскольку оно является функцией n Случайные величины IID. Мы уже видели, что выборочное среднее является несмещенной оценкой истинного среднего; то есть E[µˆ]=µX. Полезно также взглянуть на дисперсию этой случайной величины.

(7.16)Var(µˆ)=E[((1n∑i=1nXi)-µX)2]=E[(1n∑i=1n(Xi-µX))2]=1n2∑i=1n∑j =1nE[(Xi-µX)(Xj-µX)]=1n2∑i=1n∑j=1nCov(Xi,Xj).
Все члены двойного ряда в предыдущем уравнении равны нулю, за исключением тех, где i = j , так как X i и X j не коррелированы для всех i ≠ j . Таким образом, дисперсия выборочного среднего составляет
(7.17)Var(µˆ)=1n2∑i=1nVar(Xi)=1n2∑i=1nσX2=σX2n.
Это означает, что если мы используем n выборок для оценки среднего, дисперсия полученной оценки уменьшится в n раз по сравнению с тем, какой была бы дисперсия, если бы мы использовали только одну выборку.
Рассмотрим, что происходит в пределе, когда n → ∞. Пока дисперсия каждой из выборок конечна, дисперсия среднего значения выборки приближается к нулю. Конечно, на практике у нас никогда не бывает бесконечного числа выборок, но это означает, что выборочное среднее может достигать любого уровня точности (т.
 е. сколь угодно малой дисперсии), если взято достаточное количество выборок. Мы изучим это ограничивающее поведение более подробно в следующем разделе. А пока обратим внимание на оценку других параметров распределения.
е. сколь угодно малой дисперсии), если взято достаточное количество выборок. Мы изучим это ограничивающее поведение более подробно в следующем разделе. А пока обратим внимание на оценку других параметров распределения.Просмотреть книгу Глава покупки
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/b9780123869814500102
BISWA Nath Datta Datta, в цифровой цифре.
Норма Фробениуса и все подчиненные нормы непротиворечивы.
Примечания
- 1.
Для единичной матрицы I , ||I||F=n, тогда как || I || 1 = || I || 2 = || I || ∞ = 1.
- 2.
||A||F2=trace(A*A), где trace ( A ) определяется как сумма диагональных элементов A , что IS, если A = ( A IJ ), затем трасса ( A ) = A 11 + A 22 29444 + + A 22 2
+ + + + 2 A 22 29444 + + + A 22 29444 + + + A + A .  След А иногда будет обозначаться как Tr ( A ) или tr ( A ).
След А иногда будет обозначаться как Tr ( A ) или tr ( A ).Просмотреть главуКнига покупок
Прочитать всю главу
URL-адрес: https://www.sciencedirect.com/science/article/pii/B97801220350069
Elementary Edition (Davilliller ), 2016
Степени квадратных матриц
Любую квадратную матрицу можно умножить саму на себя, поскольку количество строк равно количеству столбцов. На самом деле квадратные матрицы — единственные матрицы, которые можно умножать сами на себя (почему?). Различные неотрицательные степени квадратной матрицы определяются естественным образом.
Определение
Пусть A будет любой матрицей n × n . Тогда (неотрицательные) способности A даны A 0 = I N , A 1 = A A 1 = 918 — A 1 = A A8 1
= A 1 = A 1 = A 1 = A 1 . 1(А).
1(А).Пример 5
Предположим, что A=21−43. Тогда
A2=(A)(A)=21−4321−43=05−205 и A3=(A2)(A)=05−20521−43=−2015−60−5.
Пример 6
Единичная матрица I n является квадратной, поэтому Ink существует для всех k ≥0. However, since I n A = A , for any n × n matrix A , we have I n I n = I n . Таким образом, Ink=In, для всех к ≥0.
Следующая теорема утверждает, что два известных закона показателей в алгебре по-прежнему справедливы для степеней квадратной матрицы. Доказательство остается в виде упражнения 20.
Теорема 1.17
Если A — квадратная матрица и если s и t — неотрицательные целые числа, то
(11212 t ) = () As)(At)(2)(As)t=Ast=(At)s.

В качестве примера части (1) этой теоремы имеем A 4+6 = ( А 4 )( А 6 ) = А 10 . В качестве примера части (2), мы имеем ( A 3 ) 2 = A (3) (2) = ( A 2 ) 3 =
= = = = = = = = = = = = = = = = = = = = = = ) 6 .Один закон показателей в элементарной алгебре, который не переносится на матричную алгебру, имеет вид ( xy ) q = x q г д . In fact, if A and B are square matrices of the same size, usually ( AB ) q ≠ A q B q , if q — целое число ≥ 2.
 Даже в простейшем случае q = 2, обычно ( AB )( AB )≠( AA )( BB ), потому что умножение является матрицей 91-го порядка важный.
Даже в простейшем случае q = 2, обычно ( AB )( AB )≠( AA )( BB ), потому что умножение является матрицей 91-го порядка важный.Пример 7
Пусть
A=2−413 и B=32−15.
ТогдаAB2=10−160172=100−4320289.
ОднакоA2B2=0−2055716−823=160−460−5195.
Следовательно, в данном конкретном случае ( AB ) 2 ≠ A 2 B 2 .Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B978012800853
13
BISWA NATH DATTA, in Numerical Methods for Linear Control Systems, 2004
Теорема 13.2.1
геометрическая и алгебраическая кратность как λ ) .
Доказательство.
 Определить матрицу 2 n × 2 n :
Определить матрицу 2 n × 2 n :(13.2.2)J=(0I−I0),
, где I — это n × n единичная матрица. Тогда легко увидеть, что J −1 HJ = − JHJ = − H T , что показывает, что H и − H
- 3
3 подобны. Следовательно, λ также является собственным значением — H T . Поскольку собственные значения — H T являются минусами собственных значений H , а комплексные собственные значения встречаются в сопряженных парах, теорема доказана. ▪
Следующие теоремы показывают, что решение X CARE определяется соответствующей гамильтоновой матрицей.
Теорема 13.2.2
Матрица × является решением CARE тогда и только тогда, когда столбцы (IX) охватывают n-мерное инвариантное подпространство гамильтоновой матрицы H, определяемой формулой (13.2.1) .

Доказательство. Сначала докажем, что если столбцы (IX) порождают n -мерное инвариантное подпространство H , то X это решение CARE.
Итак, предположим, что существует матрица n × n L такая, что
(13.2.3)H(IX)=(IX)L.
Умножая обе части (13.2.3) на J −1 , где J определяется формулой (13.2.2), получаем
(13.2.4)J−1H(IX)=J −1(IX)л.
Учитывая, что J−1=(0−II0), из (13.2.4) получаем
(13.2.5)(QATA−S)(IX)=(−XI)L.
Предварительное умножение обеих частей (13.2.5) на ( I, X ), мы получаем
XA+ATX+Q−XSX=0,
, показывая, что X удовлетворяет CARE.
Чтобы доказать обратное, заметим, что если X является решением CARE, то
(13.2.6)H(IX)=(A−SX−Q−ATX)=(A−SXX(A −SX))=(IX)(A−SX),
, то есть столбцы (IX) охватывают инвариантное подпространство H .
 ▪
▪Следствие 13.2.1.
Если столбцы (X1X2) охватывают n-мерное инвариантное подпространство гамильтоновой матрицы H, связанное с CARE и X 1 является обратимым, то X=X2X1−1 является решением CARE .
Доказательство.
Пролет колонн (x1x2) = промежуток колонн (x1x2) x1 — 1 = промежуток колонн (IX2x1 — 1).
Следовательно, по теореме 13.2.2 мы видим, что X=X2X1−1 является решением CARE. ▪
Следующая теорема показывает, как собственные значения матрицы Гамильтона H связаны с собственными значениями оптимальной замкнутой матрицы.
Теорема 13.2.3
Пусть × — симметричное решение CARE. Тогда собственные значения гамильтоновой матрицы H являются собственными значениями A – BK вместе с собственными значениями − ( A – BK ) T , , где K = R −1 3 Т Х .
Доказательство.
 Определите T=(I0XI), где I и X равны n × n . Затем
Определите T=(I0XI), где I и X равны n × n . Затем(13.2.7)T-1HT=(I0-XI)(A-S-Q-AT)(I0XI),=(A-SX-S-(ATX+XA+Q-XSX)-(A-SX )T),=(A−SX−S0−(A−SX)T).
Таким образом, собственные значения H являются собственными значениями A – SX вместе с собственными значениями -( A – SX ) T .
Результат теперь следует, отметив, что:
A-SX=A-BR-1BTX=A-BK.
(Напоминаем, что S = BR −1 B T .) ▪
Смотреть главуКнига покупок
Read full chapter
URL: https://www.sciencedirect.com/science/article/pii/B97801220350173
Roberto S. Mariano, Suleyman Ozmucur, in Handbook of Statistics, 2020
4.11 Dynamic факторные модели — небольшое количество индикаторов
Если количество индикаторов невелико, можно использовать структуру пространства состояний со всеми квартальными и месячными индикаторами (Mariano and Murasawa, 2003).
 Здесь приведен аналогичный пример. Существует несколько пакетов с моделями пространства состояний, в том числе Stats (R Statistical Functions, R Core Team (2018)), Astsa (Applied Statistical Time Series Analysis, Stoffer (2017)), DLM (Байесовский и вероятностный анализ динамических линейных моделей). , by Petris (2018)), KFAS (фильтр Калмана и сглаживатель для экспоненциальных моделей пространства семейных состояний, Helske (2018)), FKF (быстрый фильтр Калмана, Luethi et al. (2018)) и MARSS (многомерное авторегрессивное состояние). -Космическое моделирование) Холмса и др. (2018)). Здесь используется MARSS. В этом примере с одним состоянием процесса. В системе 2 квартальных и 17 месячных переменных. Есть 234 ежемесячных наблюдения (19 января99–июнь 2018 г.). Как и в Мариано и Мурасава (2003), квартальные переменные появляются в последний месяц квартала. Фильтр Калмана позволяет оценить недостающие значения.
Здесь приведен аналогичный пример. Существует несколько пакетов с моделями пространства состояний, в том числе Stats (R Statistical Functions, R Core Team (2018)), Astsa (Applied Statistical Time Series Analysis, Stoffer (2017)), DLM (Байесовский и вероятностный анализ динамических линейных моделей). , by Petris (2018)), KFAS (фильтр Калмана и сглаживатель для экспоненциальных моделей пространства семейных состояний, Helske (2018)), FKF (быстрый фильтр Калмана, Luethi et al. (2018)) и MARSS (многомерное авторегрессивное состояние). -Космическое моделирование) Холмса и др. (2018)). Здесь используется MARSS. В этом примере с одним состоянием процесса. В системе 2 квартальных и 17 месячных переменных. Есть 234 ежемесячных наблюдения (19 января99–июнь 2018 г.). Как и в Мариано и Мурасава (2003), квартальные переменные появляются в последний месяц квартала. Фильтр Калмана позволяет оценить недостающие значения.Полная модель MARSS с гауссовыми ошибками имеет вид: Dtdt+Htvt, где vt~MVN0Rt
Исходные условия:
X1~MVNpAorX0~MVNpA
В структуре динамической факторной модели матрица B является матрицей идентичности.
 Алгоритм EM используется в оценке.
Алгоритм EM используется в оценке.> print(dfa4,what =»model»)
Форма модели: dfa. Структура модели:
m: 1 состояние процесса(ов) с именем X1
n: 19 временных рядов наблюдений с именем GDP DEF X01 X02 X03 X04 X05 X06 X07 X08 X09 X10 X11 X12 X13 X14 X15 X907 X19
Z : неограниченный (19 x 1)
A : фиксированный и нулевой (19 x 1)
R : диагональный и равный (19 x 19)
B : фиксированный и все один (1 x 1)
U : фиксированный и ноль (1 x 1)
Q : фиксированный и все один (1 x 1)
V0 : фиксированный и все 5 (1 x 1)
D : фиксированный и ноль (19 x 1)
C : фиксированный и ноль (1 x 1)
d : фиксированный и нулевой (1 x 1)
c : фиксированный и нулевой (1 x 1)
G : фиксированный и все один (1 x 1)
H : идентификационный (19 x 19)
L : фиксированный и все один (1 x 1)
(y,model = list(),form =»dfa»)
Успех! abstol и log-log тесты прошли за 64 итерации.

Предупреждение: упр.тест.наклон.допуск равен 0,5.
Протестируйте с меньшими значениями (< 0,1), чтобы обеспечить сходимость.
Размер MARSS
Метод оценки: kem
Проверка сходимости: conv.test.slope.tol = 0,5, abstol = 0,001
Оценка сходилась за 64 итерации.
Log-likelihood: -5327.154
AIC: 10694.31 AICc: 10694.51
Estimate
Z.11 -0.12001
Z.21 0.25067
Z.31 -0,06314
Z.41 -0,03190
Z.51 -0.00603
Z.61 -0.04349
Z.71 -0.20350
Z.81 0.08894
Z.91 -0.12532
Z .101 0.01145
Z.111 -0.08487
Z.121 0.17015
Z.131 0.24958
Z.
 141 0.22233
141 0.22233Z.151 0.21469
Z. 161 0,22380
Z.171 0,04736
Z.181 -0,14378
Z.191 0,15794
R.DIAG 0,74024
R.DIAG 0,74024
1168.
Стандартные ошибки не рассчитаны.
Используйте MARSSparamCIs для вычисления CI и оценок смещения.
> MARSSparamCIs(dfa4)
Подходит для MARSS
Метод оценки: kem
Проверка сходимости: conv.test.slope.tol = 0,5, abstol = 0,001
Оценка сходилась за 64 итерации.
Log -Likelihood: -5327.154
AIC: 10694.31 AICC: 10694.51
мл.est Std. 0,061275
Z.21 0,25067 0,0380 0,1763 0,325056
Z.31 -0.06314 0.0170 -0.0965 -0.029791
Z.41 -0.03190 0.0158 -0.0630 -0.000851
Z.
 51 -0.00603 0.0155 -0.0363 0.024258
51 -0.00603 0.0155 -0.0363 0.024258Z.61 -0.04349 0.0159 -0.0747 -0.012243
Z.71 -0.20350 0.0262 -0.2548 -0.152145
Z.81 0.08894 0.0173 0.0550 0.122922
Z.91 -0.12532 0.0202 -0.1649 -0.085781
Z.101 0.01145 0.0152 -0,0184 0,041301
Z.111 -0.08487 0.0176 -0.1194 -0.050370
Z.121 0.17015 0.0236 0.1239 0.216415
Z.131 0.24958 0.0305 0.1898 0.309401
Z.141 0.22233 0.0282 0.1670 0.277616
Z.151 0.21469 0.0268 0.1622 0.267228
Z.161 0.22380 0.0278 0.1694 0.278245
Z.171 0.04736 0.0161 0.0158 0.078882
Z.181 -0.14378 0.0213 -0.1856 -0.102003
Z.191 0.15794 0.0222 0.1144 0.201466
R.diag 0.74024 0.0166 0.7078 0.772733
Initial states (x0) defined at t = 0
CIs calculated at alpha = 0.
 05 via method = гессиан
05 via method = гессианПросмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/S01697161143
Матрица Умножение матриц
61
1
умножение: умножение матрицы на число и умножение матрица на другую матрицу.
Как умножить матрицу на число
Когда вы умножаете матрицу на число, вы умножаете каждый элемент матрицы по тому же номеру. Эта операция создает новую матрицу, которая называется скалярное число , кратное .
Например, если x составляет 5, а матрица A —
A = 813444993 1813444993 1813444 .0303 400
Then, x A = 5 A and
5 A = 5 100 200 300 400 5 A = 5 * 100 5 * 200 5 * 300 5 * 400 5 A = 500 1000 1500 2000 = B В приведенном выше примере каждый элемент A умножается на 5, чтобы получить скалярное число, Б .

Примечание. В некоторых текстах эта операция упоминается как умножение матрицы на скаляр. (Скаляр — это действительное число или символ, представляющий действительное число.)
Реклама
Как умножить матрицу на матрицу
Произведение матриц A B определено только когда количество столбцов в A равно количество строк в B . Сходным образом, матричное произведение B A определено только когда количество столбцов в B равно количество строк в A .
Предположим, что A является матрицей i x j , и B — это матрица j x k . Затем матрица продукт A B приводит к матрице C , который имеет i строк и k столбцов; а также каждый элемент в C может быть вычислен в соответствии с следующую формулу.

С я к = Σ j A I J B J K
, где
C I
. столбец k из матрицы C
A i j = элемент в строке i и столбец j из матрицы A
B j k = элемент в строке j и столбец k из матрицы B
Σ j = знак суммы, что указывает на то, что a i j b j k термины должны быть суммируется по jДавайте рассмотрим пример, чтобы показать, как работает приведенная выше формула. Предположим, мы хотим вычислить A B , учитывая приведенные ниже матрицы.
А = 0 1 2 3 4 5 B = 6 7 8 9 10 11 Пусть А В = 9.
 Поскольку A имеет 2 строки, мы знаем, что C будет
иметь два ряда; и поскольку B имеет 2 столбца, мы знаем, что C будет иметь 2 столбца.
Чтобы вычислить значение каждого элемента в матрице 2 x 2 C ,
мы используем формулу С я к =
Σ j A i j B j k ,
как показано ниже.
Поскольку A имеет 2 строки, мы знаем, что C будет
иметь два ряда; и поскольку B имеет 2 столбца, мы знаем, что C будет иметь 2 столбца.
Чтобы вычислить значение каждого элемента в матрице 2 x 2 C ,
мы используем формулу С я к =
Σ j A i j B j k ,
как показано ниже.- C 1 1 = Σ A 1 j В к 1 = 0*6 + 1*8 + 2*10 = 0 + 8 + 20 = 28
- C 1 2 = σ A 1 J B J 2 2 2 B 2 B 2 B 2 B B
 = 0*7 + 1*9 +2*11 = 0 + 9 + 22 = 31
= 0*7 + 1*9 +2*11 = 0 + 9 + 22 = 31- C 2 1 = Σ A 2 j B j 1 = 3*6 + 4*8 +5*10 = = 18 + 32 + 50 = 100
- С 2 2 = Σ A 2 j B j 2 = 3*7 + 4*9 +5*11 = 21 + 36 +55 = 112
Based on the above calculations, we can say
A B = C = 28 31 100 112 . Что было на MATRIX
.1817 С не было сложный. Все, что мы сделали, это умножили элементы строки в Матрица A соответствующими элементами столбца в Матрица Б .

Порядок умножения
Как мы уже упоминали, в некоторых случаях умножение матриц определено для A B , но не для Б А ; наоборот. Однако, даже если умножение матриц возможно в обоих направлениях, результаты могут быть разными. То есть, А B не всегда равно Б А .
Поскольку порядок важен, жаргон матричной алгебры превратился в четко указать порядок умножения матриц.
- Для описания матричного произведения A B , мы можем сказать, что A равно , умноженному на . по В ; или мы можем сказать, что B есть предварительно умножить на A .
- Аналогично, для описания матричного произведения Б А ,
мы можем сказать, что B равно , умноженному на .
 по А ; или мы можем сказать, что A есть предварительно умножить на B .
по А ; или мы можем сказать, что A есть предварительно умножить на B .
Суть: когда вы перемножаете две матрицы, порядок имеет значение.
Идентификационная матрица
Идентификационная матрица является н х н диагональная матрица с единицами по диагонали и нулями везде. Матрица идентичности обозначается I или I n . Ниже показаны две матрицы идентичности.
I 3 = 1 0 0 0 1 0 0 0 1 Матрица идентичности обладает уникальным талантом.
 Любая матрица, которая может быть
предварительно умноженное или постумноженное на I остается
такой же; то есть:
Любая матрица, которая может быть
предварительно умноженное или постумноженное на I остается
такой же; то есть:А I = I А = A
Проверьте свое понимание
Задача 1
Рассмотрим приведенные ниже матрицы — A , B , и C
Предположим, что A B = C . Какие из следующих утверждений верны?
(A) w = a*e + b*h
(B) x = a*f + b*h
(C) y = c*g + d*h
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленногоРешение
Правильный ответ (B). Чтобы вычислить значение любого элемента в матрицы C используем формулу C i k = Σ j A i j B j 9.

- 3
Пример 1.10
Пусть A=74−9−5. Давайте исследуем степени A и посмотрим, сможем ли мы найти формулу для A n .
А2=74-9-574-9-5=138-18-11,А3=138-18-1174-9-5=1912-27-17,А4=1912−27−1774−9−5=2516−36−23, A5=2516−36−2374−9−5=3120−45−29.
Элементы в позициях (1, 2) и (2, 1) следуют шаблону. Элемент в позиции (1, 2) всегда равен 4 n , а элемент в позиции (2, 1) всегда равен − 9 n . Элемент в (1, 1) равен 6 n + 1, поэтому нам нужен только шаблон для записи в (2, 2). Это всегда на один (1) больше, чем − 6 n , поэтому оно имеет значение 1 − 6 n . Вот формула для A n .
Элемент в (1, 1) равен 6 n + 1, поэтому нам нужен только шаблон для записи в (2, 2). Это всегда на один (1) больше, чем − 6 n , поэтому оно имеет значение 1 − 6 n . Вот формула для A n .
An=1+6n4n−9n1−6nifn≥1.
Это не математическое доказательство, а просто пример распознавания образов. Результат можно формально доказать с помощью математической индукции (см. Приложение Б).
Наш последний пример матричных степеней является результатом теории графов . Граф представляет собой набор из вершин и соединений между ними, называемых ребрами . Вы видели много графиков; например, карта системы автомагистралей между штатами — это график, как и карта маршрутов авиакомпаний в конце скучных журналов, которые вы найдете на рейсах авиакомпаний. Рассмотрим простой график на рис. 1.8. А путь из одной вершины v в другую вершину w представляет собой последовательность ребер, соединяющих v и w . For instance, here are three paths from A to F : A — B — F , A — B — D — F , and A — Б — С — Е — Б — Ф . Длина пути между v и w — это количество ребер, которые необходимо пересечь при переходе от одного к другому. Например, в наших трех путях первый имеет длину 2, второй — 3, а третий — 5.
For instance, here are three paths from A to F : A — B — F , A — B — D — F , and A — Б — С — Е — Б — Ф . Длина пути между v и w — это количество ребер, которые необходимо пересечь при переходе от одного к другому. Например, в наших трех путях первый имеет длину 2, второй — 3, а третий — 5.
Рисунок 1.8. Неориентированный граф.
Если граф имеет n вершин, матрица смежности графа представляет собой матрицу n × n , которая указывает расположение ребер. Эту концепцию лучше всего иллюстрирует отображение матрицы смежности для нашего шестивершинного графа, а не математическое определение.
ABCDEFAdj=ABCDEF010000101111010010010001011000010100
Единица (1) встречается в строке A , столбце B , поэтому существует ребро, соединяющее B и . Точно так же единица находится в строке E , столбце C , поэтому есть ребро, соединяющее E и C . Между A и D нет ребра, поэтому строка A столбца D содержит ноль (0).
Точно так же единица находится в строке E , столбце C , поэтому есть ребро, соединяющее E и C . Между A и D нет ребра, поэтому строка A столбца D содержит ноль (0).
Существует связь между матрицей смежности графа и количеством возможных путей между двумя вершинами. Ясно, Прил 1 определяет все пути длины 1 из одной вершины в другую (ребро).
Если Adj является матрицей смежности для графа, то Adj k определяет количество возможных путей длины k между любыми двумя вершинами. Мы не будем пытаться это доказать, а возьмем в качестве примера наш график.
Adj2=101111051111112111111211111121111112, Adj3=051111546666162232162223163222162322.
Глядя на Adj 2 , мы видим, что существует один путь длины 2 между C and E , C — B — E , and two paths of length 2 connecting E to E ( E — C — E , E — В — Е ). There are five (5) paths of length 3 between B and A ( B — A — B — A , B — D — B — A , Б — С — B — A , B — E — B — A , B — F — A ). Обратите внимание, что если мы реверсируем каждый путь длины три из B в A , мы получим путь, который начинается в A и заканчивается в B . Посмотрите внимательно на Adj, Adj 2 и Adj 3 и обратите внимание, что запись в позиции ( i , j ) всегда совпадает с записью в ( и , и ). Такая матрица называется симметричной . Если поменять местами строки и столбцы, матрица останется прежней. Есть много применений симметричных матриц в науке и технике.
There are five (5) paths of length 3 between B and A ( B — A — B — A , B — D — B — A , Б — С — B — A , B — E — B — A , B — F — A ). Обратите внимание, что если мы реверсируем каждый путь длины три из B в A , мы получим путь, который начинается в A и заканчивается в B . Посмотрите внимательно на Adj, Adj 2 и Adj 3 и обратите внимание, что запись в позиции ( i , j ) всегда совпадает с записью в ( и , и ). Такая матрица называется симметричной . Если поменять местами строки и столбцы, матрица останется прежней. Есть много применений симметричных матриц в науке и технике.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www. sciencedirect.com/science/article/pii/B9780123
sciencedirect.com/science/article/pii/B9780123
Fred E. Szabo PhD, 5 0 1 0 Albra



 Верно ли это?
Верно ли это? Верно ли, что матрица, обратная данной тоже будет нулевой?
Верно ли, что матрица, обратная данной тоже будет нулевой? ( [G] имеет 3 столбца, но [C] имеет только 2 строки.
( [G] имеет 3 столбца, но [C] имеет только 2 строки.

 АБ≠БА
АБ≠БА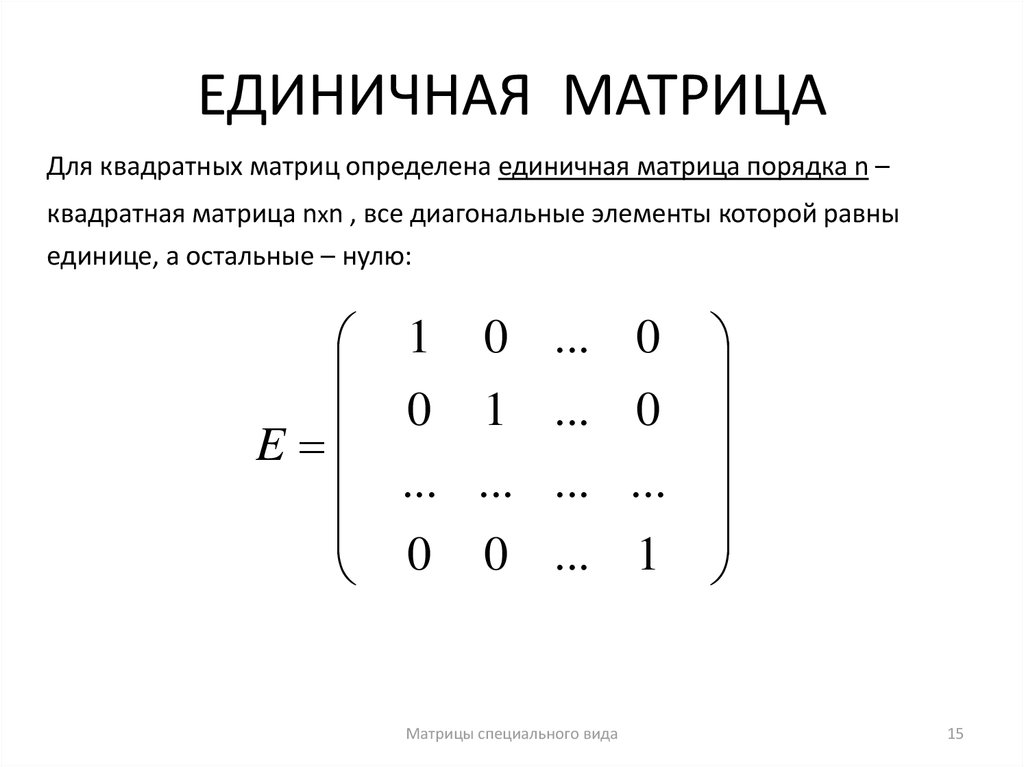


 Тогда матрица правой части будет обратной заданной матрице.
Тогда матрица правой части будет обратной заданной матрице.