Плюс минус
Плюс минусПлюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.
Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.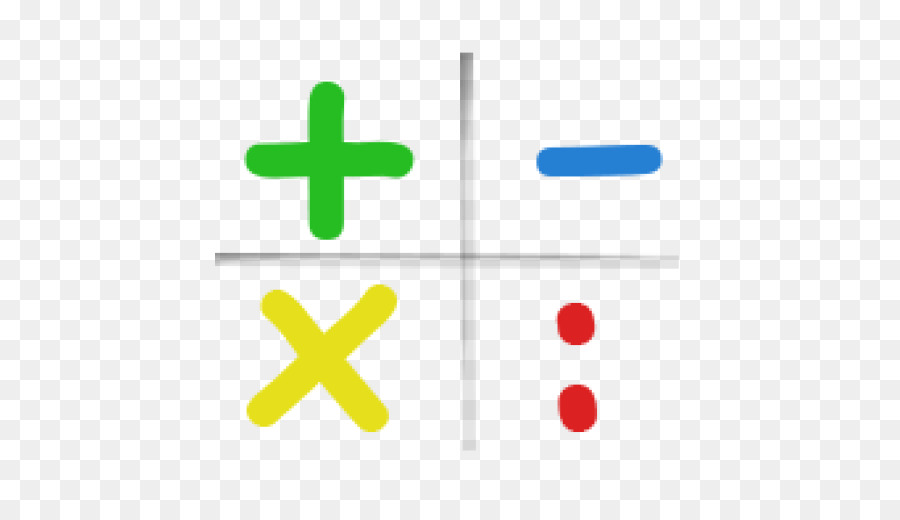
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС — ОТВЕТ
«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m».
Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс.
Теперь прилепливаем полученный плюс к ранее полученной двойке
(-6) : (-3) = +2
Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:
(-6) : (-3) = 2
«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.
© 2006 — 2021 Николай Хижняк. Все права защищены.
§ Умножение отрицательных чисел. Умножение рациональных чисел
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с
одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).
Примеры умножения отрицательных и положительных чисел.
- (−3) · (−6) = +18 = 18
- 2 · 3 = 6
Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак «−».
Примеры умножения отрицательных и положительных чисел.
- (−0,3) · 0,5 = −0,15
- 1,2 · (−7) = −8,4
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.
Запомните!
Минус на минус даёт плюс,
Плюс на минус даёт минус.
| + · (+) = + | + · (−) = − |
| − · (−) = + | − · (+) = − |
В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
Пример.
(−6) · (−3) · (−4) · (−2) · 12 · (−1) =
В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 · 3 · 4 · 2 · 12 · 1 = 1728
Конечный результат умножения исходных чисел будет:
(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728
Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
- 0 · a = 0
- a · 0 = 0
- a · 1 = a
Примеры:
- 0 · (−3) = 0
- 0,4 · 1 = 0,4
Особую роль при умножении рациональных чисел играет
отрицательная единица «−1».
Запомните!
При умножении на «−1» число меняется на противоположное.
В буквенном выражении это свойство можно записать:
a · (−1) = (−1) · a = −a
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.
Пример умножения отрицательных и положительных чисел.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
базовых математических символов | Словарь
математика (BrE) | математика (AmE) является сокращенной формой математика
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.
+плюс/дополнение
Знак плюс
а.
понятие положительное Любое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — одно и то же число.
б. операция сложения
3 + 5 = 8
три плюс пять равно восьми
пять прибавить к трем, получится восемь
три прибавить к пяти, получится восемь
Сложение дает нам сумму . В 3 + 5 = 8 сумма равна восьми.
—
знак минус/знак вычитания
Знак минус означает:
а. понятие отрицательного
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3
минус три
б. операция вычитания
8 — 5 = 3
восемь минус пять равно трем
пять вычесть из восьми равно трем
если из восьми вычесть пять, то получится три
если из восьми вычесть пять, то получится три
Вычитание дает нам разницы .
×
знак умножения / знак умножения
Знак умножения на означает:
умножение 5 x 6 = 30
пять раз шесть равно тридцати
пять умножить на шесть равно тридцати
пять шестерок равно тридцати
если умножить 5 на 6 получится тридцать
Умножение дает нам произведение . В 5 х 6 = 30 произведение равно 30.
÷ ИЛИ /
знак деления
Знак деления представляет:
подразделение
15 ÷ 3 = 5
15 / 3 = 5
пятнадцать разделить на три равно пяти
пять получится пятнадцать трижды
если пятнадцать разделить на три получится пять
если три разделить на пятнадцать получится пять
дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.
Подытожим вышеописанные четыре операции следующим образом:
| операция | результат | ||
|---|---|---|---|
| дополнение | «плюс» | 2 + 2 = 4 | сумма |
| вычитание | «минус» | 5 — 3 = 2 | разница |
| умножение | «раз» | 3 х 5 = 15 | товар |
| отделение | «делится на» | 21/7 = 3 | частное |
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7
три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно НЕ равно:
- два плюс два равно четыре
-
два плюс два равно четырем
меньше
3 < 4
три меньше четырех
>
больше
4 > 3
четыре больше трех
≠
НЕ равно
x ≠ z
x не равно z
≥
больше или равно
x ≥ z
x больше или равно z
≤
меньше или равно
z ≤ x
z меньше или равно x
¾
дробь
см.
дроби
.
десятичный разделитель | точка
Десятичный разделитель отделяет целое число от его дробной части справа:
1,23
В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).
см. десятичные дроби
,
разделитель тысяч
В английском языке разделитель тысяч разделяет целые числа на группы по три справа.
10 987 654 321
В английском языке разделителем тысяч обычно является запятая (,). Обратите внимание, что в некоторых языках разделителем тысяч является точка (.), а иногда и пробел ( ).
см. тыс.
%
знак процента
Знак процентов указывает число или отношение в виде доли от 100 ( процентов ).
40%
сорок процентов
Только сорок процентов людей проголосовали за нее.
Какой процент проголосовал за нее? Сорок процентов.
√
квадратный корень
√16 = 4
квадратный корень из шестнадцати равен четырем
квадратный корень из шестнадцати равен четырем
Порядок действий – элементарная математика
Уменьшение двусмысленности по договоренности
В общем, никто не хочет, чтобы его неправильно поняли. В математике так важно, чтобы читатели понимали выражения именно так, как задумал автор, что математика устанавливает соглашения, согласованные правила для интерпретации математических выражений.
Означает ли 10 − 5 − 3, что мы начинаем с 10, вычитаем 5, а затем вычитаем еще 3, оставляя 2? Или это означает, что мы вычитаем 5 − 3 из 10?
Является ли 2 + 3 × 10 равным 50, потому что 2 + 3 равно 5, а затем мы умножаем на 10, или автор имеет в виду, что мы добавляем 2 к результату 3 × 10?
Чтобы избежать этих и других возможных неясностей, математика установила соглашения (соглашения) о том, как мы интерпретируем математические выражения. Одно из этих соглашений гласит, что когда все операции одинаковы, мы действуем слева направо, поэтому 10 — 5 — 3 = 2, поэтому автору, который хотел бы другую интерпретацию, пришлось бы писать выражение по-другому: 10 — (5).
− 2). Когда операции не такие, как в 2 + 3 × 10, некоторым может быть отдано предпочтение перед другими. В частности, умножение выполняется перед сложением независимо от того, какое из чисел появляется первым при чтении слева направо. Например, в 2 + 3 × 10 умножение должно быть выполнено первым, даже несмотря на то, что оно стоит справа от сложения, а выражение означает 2 + 30.
Полные правила порядка операций см. ниже.
Условные обозначения для чтения и записи математических выражений
Основной принцип: «более мощные» операции имеют приоритет над «менее мощными».
Использование числа в качестве показателя степени (например, 58 = 390625) имеет, как правило, «самый сильный» эффект; использование того же числа в качестве множителя (например, 5 × 8 = 40) дает более слабый эффект; сложение имеет, как правило, самый «слабый» эффект (например, 5 + 8 = 13). Хотя эти термины (мощный, слабый) в математике не употребляются, смысл сохраняется в языке «возведение 5 в 8-ю степень».
Возведение в степень «мощно», поэтому оно на первом месте! Сложение/вычитание «слабые», поэтому они идут последними. Умножение/деление находится между ними.
Возведение в степень «мощно», поэтому оно на первом месте! Сложение/вычитание «слабые», поэтому они идут последними. Умножение/деление находится между ними.Когда важно указать другой порядок , как это иногда бывает, мы используем круглые скобки для упаковки чисел и более слабую операцию, как если бы они представляли одно число.
Например, хотя 2 + 3 × 8 означает то же, что и 2 + 24 (поскольку умножение имеет приоритет и выполняется первым), (2 + 3) × 8 означает 5 × 8, поскольку (2 + 3) пакетное предложение, количество, которое необходимо выяснить перед его использованием. На самом деле (2 + 3) × 8 часто произносится как «два плюс три, количество, умноженное на восемь» (или «количество два плюс три, умноженное на восемь»).
Краткое изложение правил:
- Сначала скобки. Обращение к ним как к «пакетам» часто помогает детям вспомнить их цель и роль.
- Экспоненты рядом.
- Далее умножение и деление. (Ни один из них не имеет приоритета, и когда они идут последовательно, они выполняются слева направо.
