3.3. Умножение в двоичной системе счисления
Для того, чтобы умножить двоичное число на 2 (десятичная двойка это 10 в двоичной системе) достаточно к умножаемому числу справа приписать один ноль.
Пример 3.3. Выполнить операцию умножения 10101 * 10 = 101010.
Проверка.
10101 = 1*24 + 0*23 + 1*22 + 0*21 +1*20 = 16 + 4 + 1 = 21
101010 =1*25 + 0*24 + 1*23 + 0*22 +1*21 +0*20 = 32 + 8 + 2 = 42
21 * 2 = 42.
Если вспомнить,
что любое двоичное число разлагается
по степеням двойки, то становится ясно,
что умножение в двоичной системе
счисления сводится к умножению на 10 (то
есть на десятичную 2), а стало быть,
умножение это ряд последовательных
сдвигов. Общее правило таково: как и для
десятичных чисел, умножение двоичных
выполняется поразрядно.
Пример 3.4. Выполнить операцию умножения 1011 * 101.
Умножение можно свести к сумме трёх поразрядных умножений:
1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111.
В столбик это же самое можно записать так:
1 | 0 | 1 | 1 | ||
* | 1 | 0 | 1 | ||
1 | 0 | 1 | 1 | ||
0 | 0 | 0 | 0 | ||
1 | 0 | 1 | 1 | ||
1 | 1 | 0 | 1 | 1 | 1 |
Проверка:
101 = 5 (десятичное)
1011 = 11 (десятичное)
110111 = 55 (десятичное)
5*11 = 55 верное равенство
Умножение
двоичных многоразрядных чисел производится путём образования частичных
произведений и последующего их
суммирования. В соответствии с таблицей
двоичного умножения каждое частичное
произведение равно нулю, если в
соответствующем разряде множителя
стоит 0, или равно множимому, сдвинутому
на соответствующее число разрядов
влево, если в соответствующем разряде
множителя стоит 1. Таким образом, операция
умножения сводится к операциям сдвига
и сложения. Положение точки определяется
так же, как и при умножении десятичных
чисел.
В соответствии с таблицей
двоичного умножения каждое частичное
произведение равно нулю, если в
соответствующем разряде множителя
стоит 0, или равно множимому, сдвинутому
на соответствующее число разрядов
влево, если в соответствующем разряде
множителя стоит 1. Таким образом, операция
умножения сводится к операциям сдвига
и сложения. Положение точки определяется
так же, как и при умножении десятичных
чисел.
Пример 3.5. Выполнить операцию умножения 1010.1 на 101.01.
При делении двоичных чисел используются таблицы двоичного умножения и вычитания.
Пример 3.6. Выполнить деление двоичного числа 1010.101 на двоичное число 10.1:
Деление выполняется по тем же правилам, что и деление в десятичной системе счисления.
Выше были рассмотрены
три действия и уже понятно, что, в
общем-то, действия над двоичными числами
мало отличаются от действий над
десятичными числами.
2 | 3 | 4 | 7 | |
Выделяем справа
(от старшего разряда) такое количество
цифр, чтобы получившееся число было как
можно меньше и в то же время больше
делителя. 2 – меньше делителя, следовательно,
необходимое нам число 23.
2 | 3 | 4 | 7 | ||
– | 2 | 1 | 3 | ||
2 |
Описанную операцию
повторяем до тех пор, пока полученный
остаток не окажется меньше делителя. Когда это случится, число, полученное
под чертой, это частное, а последний
остаток – это остаток операции. Операция
деления двоичного числа выполняется
точно также.
Когда это случится, число, полученное
под чертой, это частное, а последний
остаток – это остаток операции. Операция
деления двоичного числа выполняется
точно также.
Пример 3.7. Разделить 10010111(2) на 101(2).
1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
Ищем число, от
старшего разряда которое первое было
бы больше чем делитель. Это четырехразрядное
число 1001. Оно выделено жирным шрифтом.
Теперь необходимо подобрать делитель
выделенному числу. И здесь мы опять
выигрываем в сравнении в десятичной
системой. Дело в том, что подбираемый
делитель это обязательно цифра, а цифры
у нас только две. Так как 1001 явно больше
101, то с делителем всё понятно это 1.
Выполним
Это четырехразрядное
число 1001. Оно выделено жирным шрифтом.
Теперь необходимо подобрать делитель
выделенному числу. И здесь мы опять
выигрываем в сравнении в десятичной
системой. Дело в том, что подбираемый
делитель это обязательно цифра, а цифры
у нас только две. Так как 1001 явно больше
101, то с делителем всё понятно это 1.
Выполним
1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
– | 1 | 0 | 1 | 1 | |||||||
1 | 0 | 0 |
Остаток от
выполненной операции 100. Это меньше чем
101, поэтому чтобы выполнить второй
шаг деления,
необходимо добавить к 100 следующую
цифру, это цифра 0. Теперь имеем следующее
число:
Это меньше чем
101, поэтому чтобы выполнить второй
шаг деления,
необходимо добавить к 100 следующую
цифру, это цифра 0. Теперь имеем следующее
число:
1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
– | 1 | 0 | 1 | 1 | |||||||
1 | 0 | 0 | 0 |
1000 больше 101 поэтому
на втором шаге мы опять допишем в частное
цифру 1 и получим следующий результат
(для экономии места сразу опустим
следующую цифру).
1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
– | 1 | 0 | 1 | 1 | 1 | ||||||
1 | 0 | 0 | 0 | ||||||||
– | 1 | 0 | 1 | ||||||||
1 | 1 | 0 |
Третий шаг. Полученное число 110 больше 101, поэтому
и на этом шаге мы запишем в частное 1.
Получиться так:
Полученное число 110 больше 101, поэтому
и на этом шаге мы запишем в частное 1.
Получиться так:
1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
– | 1 | 0 | 1 | 1 | 1 | 1 | |||||
1 | 0 | 0 | 0 | ||||||||
– | 1 | 0 | 1 | ||||||||
1 | 1 | 0 | |||||||||
– | 1 | 0 | 1 | ||||||||
1 | 1 |
Полученное число
11 меньше 101, поэтому записываем в частное
цифру 0 и опускаем вниз следующую цифру. Получается так:
Получается так:
1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | ||||
– | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |||||||
1 | 0 | 0 | 0 | |||||||||||
– | 1 | 0 | 1 | |||||||||||
1 | 1 | 0 | ||||||||||||
– | 1 | 0 | 1 | |||||||||||
1 | 1 | 1 |
Полученное число
больше 101, поэтому в частное записываем
цифру 1 и опять выполняем действия. Получается такая картина:
Получается такая картина:
1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||
– | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | ||||||
1 | 0 | 0 | 0 | |||||||||||
– | 1 | 0 | 1 | |||||||||||
1 | 1 | 0 | ||||||||||||
– | 1 | 0 | 1 | |||||||||||
1 | 1 | 1 | ||||||||||||
– | 1 | 0 | 1 | |||||||||||
1 | 0 |
Полученный остаток
10 меньше 101, но у нас закончились цифры
в делимом, поэтому 10 это остаток, а 1110
это искомое частное.
Проверим в десятичных числах
10010011 = 147
101 = 5
10 = 2
11101 = 29
1 | 4 | 7 | 5 | ||
– | 1 | 0 | 2 | 9 | |
4 | 7 | ||||
– | 4 | 5 | |||
2 |
Запись числа в
двоичной системе существенно упрощает
арифметические операции, но в то же
время сама запись становится значительно
длиннее, что уменьшает ценность
полученного упрощения, поэтому необходимо
найти такие задачи, решение которых
существенно проще в двоичных числах.
11 умножить на 11 в двоичной системе счисления
Вы искали 11 умножить на 11 в двоичной системе счисления? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выполните умножение в двоичной системе счисления, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «11 умножить на 11 в двоичной системе счисления».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 11 умножить на 11 в двоичной системе счисления,выполните умножение в двоичной системе счисления,выполните умножение в двоичной системе счисления 10010 10001,выполните умножение в двоичной системе счисления 10011 11000,выполните умножение в двоичной системе счисления 1101 1110,выполнить умножение в двоичной системе счисления,двоичная система счисления умножение,двоичное умножение,деление в двоичной системе калькулятор,деление двоичных чисел онлайн,деление двоичных чисел онлайн калькулятор,деление двоичных чисел онлайн калькулятор с решением,деление двоичных чисел онлайн калькулятор с решением столбиком,деление чисел в двоичной системе счисления онлайн,как умножать в двоичной системе,как умножать в двоичной системе счисления,как умножать двоичную систему счисления,как умножать двоичные числа,как умножать двоичные числа столбиком,как умножать числа в двоичной системе счисления,калькулятор двоичной системы счисления онлайн умножение,калькулятор двоичных чисел умножение,калькулятор систем счисления онлайн с решением умножение,калькулятор систем счисления онлайн умножение,калькулятор систем счисления с решением онлайн умножение,калькулятор систем счисления умножение,калькулятор систем счисления умножение онлайн,калькулятор умножение в двоичной системе,калькулятор умножение в двоичной системе счисления онлайн,калькулятор умножение двоичных чисел,калькулятор умножение систем счисления,калькулятор умножение систем счисления онлайн,калькулятор умножения двоичных чисел,онлайн деление в двоичной системе,онлайн калькулятор деление двоичных чисел,онлайн калькулятор деление двоичных чисел с решением,онлайн калькулятор систем счисления с решением умножение,онлайн калькулятор систем счисления умножение,онлайн калькулятор умножение в двоичной системе счисления,онлайн калькулятор умножение двоичных чисел с решением,онлайн калькулятор умножение систем счисления,онлайн калькулятор умножение систем счисления с решением,онлайн умножение в двоичной системе счисления,онлайн умножение восьмеричных чисел,онлайн умножение двоичных чисел,онлайн умножение чисел в двоичной системе счисления,онлайн умножить двоичные числа,примеры умножение двоичных чисел,система счисления онлайн умножение,система счисления умножение онлайн,умножение в 2 системе счисления,умножение в двоичной,умножение в двоичной системе,умножение в двоичной системе калькулятор,умножение в двоичной системе счисления,умножение в двоичной системе счисления онлайн,умножение в двоичной системе счисления онлайн калькулятор,умножение в системах счисления онлайн,умножение двоичная система счисления,умножение двоичной системы,умножение двоичной системы счисления,умножение двоичной системы счисления онлайн калькулятор,умножение двоичных чисел,умножение двоичных чисел калькулятор,умножение двоичных чисел калькулятор онлайн,умножение двоичных чисел онлайн,умножение двоичных чисел онлайн калькулятор,умножение двоичных чисел онлайн калькулятор с решением,умножение двоичных чисел примеры,умножение над двоичными числами,умножение онлайн в двоичной системе счисления,умножение систем счисления калькулятор,умножение систем счисления онлайн калькулятор,умножение систем счисления онлайн калькулятор с решением,умножение системы счисления,умножение чисел в двоичной системе,умножение чисел в двоичной системе счисления,умножение чисел в двоичной системе счисления онлайн,умножения двоичных чисел калькулятор,умножить двоичные числа онлайн,умножьте два числа в двоичной системе счисления 110112 1012. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 11 умножить на 11 в двоичной системе счисления. Просто введите задачу в окошко и нажмите
«решить» здесь (например, выполните умножение в двоичной системе счисления 10010 10001).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 11 умножить на 11 в двоичной системе счисления. Просто введите задачу в окошко и нажмите
«решить» здесь (например, выполните умножение в двоичной системе счисления 10010 10001).
Где можно решить любую задачу по математике, а так же 11 умножить на 11 в двоичной системе счисления Онлайн?
Решить задачу 11 умножить на 11 в двоичной системе счисления вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Двоичное сложение, умножение, вычитание и деление | by Malay Biswas
Основные математические операции с двоичными числами аналогичны десятичной системе. 0). Таким образом, мы сохраняем 0 в столбце 1 и сдвигаем (переносим) 1 в столбец 2.
0). Таким образом, мы сохраняем 0 в столбце 1 и сдвигаем (переносим) 1 в столбец 2.
Другие правила такие же, как и в десятичной системе, т. е. мы добавляем справа налево, а результат переноса добавляется к цифрам в следующем столбце.
Теперь давайте попробуем добавить 11 к 13. Двоичный код для 11 равен 1011, а для 13 — 1101. 1 к 2 цв.
Умножение
Умножение в двоичном формате точно такое же, как и в десятичном, т. е. умножение чисел справа налево и умножение каждой цифры одного числа на каждую цифру другого числа, они суммируют их. 3 основных правила двоичного умножения также аналогичны десятичному.
- 1 * 1 = 1
- 1 * 0 = 0 * 1 = 0
- 0 * 0 = 0
Кроме того, помните, что к каждому сдвигу влево цифры множителя необходимо добавлять дополнительный ноль к продукту. Это также похоже на десятичную систему.
Это также похоже на десятичную систему.
1011
x 1101
- 1011 * 1 (COL Multipier 1) = 1011
- 1011 * 0 (Multiplier 2 Col) = 00000 (один нулевой добавлен на конце)
- 1011 * 1 (Multipier 4) Col) Col) Col) Col). = 101100 (два нуля в конце)
- 1011 * 1 (множитель 8) = 1011000 (три нуля в конце)
- Суммируем. 1011 + 00000 + 101100 + 1011000 = ((1011 + 00000) + 101100) + 1011000 = (01011 + 101100) + 1011000 = 110111 + 1011000 = 10001111 90 = 128 + 8 + 4 + 2 + 1 = 143 = 11 * 13.
- Мы проверяем часть дивиденда слева от него, которая >= делителя.
- Затем мы вычитаем кратное делителю, которое равно <= части делимого.
 Множитель (1) прибавляется к частному, а результатом вычитания является остаток.
Множитель (1) прибавляется к частному, а результатом вычитания является остаток. - Мы опускаем по 1 биту за раз (слева направо) для оставшейся части делимого и проверяем, является ли выражение (остаток + пониженный бит) >= делителем. Если нет, мы добавляем 0 к частному или снова повторяем шаг 2.
- Is 1 (крайний левый бит 110) >= 11. Нет (здесь нам не нужно добавлять 0 к частному, так как 0 слева равны незначительно).
- Является 11 (осталось 2 крайних бита из 110) >= 11. Да. Мы добавляем 1 (множитель) к частному и вычитаем 11 из 11. Это дает нам остаток 0. Обратите внимание, мы вычитаем «один-один из одного-один НЕ одиннадцать из одиннадцати».
- Теперь мы уменьшаем оставшийся бит (0) из 110. 0 >= 11. Нет. Итак, мы добавляем 0 к частному.
Вычитание
Прежде чем приступать к вычитанию, нам нужно понять, как отрицательные числа представлены в двоичном виде. Какая бы система ни использовалась (например, 4-битная, 8-битная, 16-битная и т. д.), все числа со знаком должны иметь одинаковое количество битов. 0 используются для заполнения пустых битов. Мы будем использовать 8-бит для этого урока. Существует 3 основных стандарта записи отрицательных чисел.
Величина со знаком
В этой записи дополнительный бит добавляется слева от числа для обозначения его знака. 0 указывает +ve, а 1 указывает -ve. Используя 8 бит, +13 соответствует 00001101, а +11 соответствует 00001011. -13 соответствует 10001101 и -11 соответствует 10001011.
0 указывает +ve, а 1 указывает -ve. Используя 8 бит, +13 соответствует 00001101, а +11 соответствует 00001011. -13 соответствует 10001101 и -11 соответствует 10001011.
Дополнение до единиц
В этой записи положительные числа представляются точно так же, как обычные двоичные числа. Таким образом, 13 будет 00001101, а 11 будет 00001011. Отрицательные числа представляются простым переворачиванием бита, т. е. 0 становится 1, а 1 становится 0. Таким образом, -13 будет 11110010, а -11 будет 11110100.
Вычитание с использованием дополнения 1
В этом методе вычитаемое число должно быть инвертировано с использованием дополнения до 1, а затем добавлено (не вычтено) к другому числу. Поскольку все числа со знаком должны иметь одинаковое количество битов, любой бит «переполнения» должен быть добавлен обратно к остальной части результата.
Если мы хотим сделать 13–11, это по существу 13 + (-11) или 00001101 + 11110100. Сложение их даст 100000001. Обратите внимание, что это не 9 бит, поэтому мы сохраняем самые правые 8 бит 00000001 и добавляем ‘ переносим в него 9-й бит (в данном случае 1), что дает нам 00000010 = 2 = 13–11.
Теперь давайте попробуем 11–13 или 11 + (-13) = 00001011 + 11110010 = 11111101. Слева от него стоит 1, что указывает на его отрицательное значение. Используя дополнение до 1, мы можем вычислить абсолютное (положительное) число, которое равно 00000010 или 2. Таким образом, результат равен -2. 9n или проще говоря, результат вычитания числа из 2n. В этом методе отрицательное число обозначается сначала определением дополнения до 1 положительного числа, а затем добавлением к нему 1. Таким образом, 8-битное -13 будет 11110010 (дополнение до 1) + 1 = 11110011; -11 будет 11110101.
При добавлении или вычитании двоичных чисел в дополнении до 2 все лишние (переносные) биты отбрасываются.
Теперь давайте попробуем те же примеры, что и в дополнении 1.
13–11 = 13 + (-11) = 00001101 + 11110101 = 100000010. Отбрасывание остатка 9й бит слева мы получаем результат как 00000010 = 2.
11–13 = 11 + (-13) = 00001011 + 11110011 = 11111110. 1 в крайнем левом бите означает отрицательное число. Так как это в дополнении до 2, мы вычитаем из него 1, чтобы получить нотацию дополнения до 1 11111101. Переворачивая биты, мы получаем 00000010 или 2, что означает, что наш результат равен -2 в нотации дополнения до 2.
Так как это в дополнении до 2, мы вычитаем из него 1, чтобы получить нотацию дополнения до 1 11111101. Переворачивая биты, мы получаем 00000010 или 2, что означает, что наш результат равен -2 в нотации дополнения до 2.
При выполнении двоичных операций важно знать используемое соглашение, чтобы выполнять операцию в соответствии с применимыми правилами.
Деление
Двоичное деление аналогично десятичному. Единственное отличие состоит в том, что в десятичной системе, поскольку мы делим традиционные числа, делимое (или его часть) может быть 0, 1 или более чем в 1 раз больше делителя. Однако в двоичном формате это может быть только 0 или 1 раз, то есть делимое (или его часть) >= или < делителя.
Давайте попробуем разделить 6 на 3. Двоичное число 6 равно 110, а это или 3 равно 11. Следуя соглашению о десятичном делении
Таким образом, шаги для 6/3 или 110/11 равны
Поскольку в делимом больше не осталось битов, мы останавливаемся здесь и проверяем. Наш остаток равен 0, а частное 10 (двоичное) = 2.
Деление может быть более сложным для чисел со знаком и двоичных чисел с плавающей запятой (не рассматриваются в этом руководстве).
Правила, таблица и примеры решений
Двоичное умножение аналогично любому другому арифметическому умножению десятичных чисел. Единственная разница заключается в представлении чисел. Там, где двоичные числа записываются как 0 и 1, в десятичных числах используются цифры от 0 до 9..
Двоичное умножение — это еще одна двоичная операция, представляющая собой способ умножения двух или более двоичных чисел, чисел, которые записываются в форме 0 и 1.
Что такое двоичное умножение?Двоичное умножение — это одна из четырех основных операций, выполняемых над двоичными числами: сложение, вычитание, умножение и деление. Это умножение похоже на десятичное умножение, но использует только две цифры 0 и 1, в отличие от 0 до 9.в десятичных числах.
Двоичная таблица умножения Поскольку в двоичных числах используются только две цифры, то есть 0 и 1, при выполнении умножения мы можем умножать только эти двоичные числа. Таблица умножения для двоичных чисел выглядит следующим образом:
Таблица умножения для двоичных чисел выглядит следующим образом:
| Бинарные номера | . 0\) | 0 |
| \(0\times 1\) | 0 | |
| \(1\times 1\) | 1 |
In binary multiplication, у нас есть множитель и множимое. Основные правила умножения двоичных чисел:
| Множимое | Множитель | Произведение | |||
| 0 | 0 | \ (0 \ Times 0 \) = 0 | |||
| 0 | 1 | \ (0 \ Times 1 \) = 0 | 9161 | \ (0 \) = 0 | 61916161699161616161616161616169\. (1 \ times 0 \) = 0 |
| 1 | 1 | \ (1 \ Times 1 \) = 1 |
 значений, то есть 0 и 1, процесс умножения этих чисел становится проще по сравнению с десятичными числами. Шаги, связанные с умножением двоичных чисел, приведены ниже:
значений, то есть 0 и 1, процесс умножения этих чисел становится проще по сравнению с десятичными числами. Шаги, связанные с умножением двоичных чисел, приведены ниже:Пример: Умножьте 11101 на 1001.
Шаг 1: Запишите множимое 11101 и множитель 1001 один под другим в соответствующих столбцах.
Шаг 2: Начните процесс умножения с крайней правой цифры множителя, которая в данном случае равна 1, со всеми цифрами множимого.
Шаг 3: Добавьте заполнитель «X» перед началом умножения со следующей цифрой множителя в следующей строке.
Шаг 4: Повторяйте ту же процедуру до тех пор, пока крайняя левая цифра множителя не будет умножена на все цифры множимого.
Шаг 5: Произведение, полученное в каждой строке, называется частичным произведением. Наконец, все частичные произведения складываются по правилам двоичного сложения.
(Правила двоичного сложения: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0, 1 перенос).
Давайте посмотрим на фактическое умножение:
| 1 | 1 | 1 | 0 | 1 | ||||
|---|---|---|---|---|---|---|---|---|
| x | 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 1 | 0 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | x | |||
| 0 | 0 | 0 | 0 | 0 | x | x | ||
| + | 1 | 1 | 1 | 0 | 1 | x | x | x |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Следовательно, мы можем сказать, что произведение 11101 и 1001 равно 100000101. Мы также можем проверить наш результат, заменив двоичные числа десятичными. Десятичный эквивалент числа 11101 равен 29, а числа 1001 — 9. Произведение 29 и 9 равно 261, что в двоичной системе счисления записывается как 100000101.
Мы также можем проверить наш результат, заменив двоичные числа десятичными. Десятичный эквивалент числа 11101 равен 29, а числа 1001 — 9. Произведение 29 и 9 равно 261, что в двоичной системе счисления записывается как 100000101.
Умножение двоичных чисел с десятичными точками — простая процедура. Это похоже на умножение двух двоичных чисел без десятичных знаков. Единственная разница в том, что после выполнения всего умножения нам нужно поставить десятичную точку, подсчитав десятичные разряды в множителе и множимом.
Let us understand this with an example:
Example: Multiply: 1011.01 and 110.1
Solution: We will perform simple binary multiplication and insert a decimal point in the final answer:
| 1 | 0 | 1 | 1 | 0 | 1 | ||||
| x | 1 | 1 | 0 | 1 | |||||
| 1 | 0 | 1 | 1 | 0 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | x | |||
| 1 | 0 | 1 | 1 | 0 | 1 | x | x | ||
| + | 1 | 0 | 1 | 1 | 0 | 1 | x | x | x |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
The answer obtained by multiplying 101101 and 1101 is 1001001001. Now as we have to multiply 1011.01 and 110.1, the final answer is 1001001.001.
Now as we have to multiply 1011.01 and 110.1, the final answer is 1001001.001.
Двоичное умножение со знаком также известно как умножение с дополнением до 2. Мы можем выполнить это умножение, просто умножив величины двух чисел, а затем расширив его до исходного бита знака числа.
Следует отметить, что в отличие от сложения, когда мы умножаем n-битное число на m-битное число, получается n+m-битное число.
Давайте разберем это знаковое умножение на примере:
Пример: Умножение -5 и 7 в двоичном умножении со знаком.
Решение: Мы знаем, что в двоичных числах -5 записывается как 1011, а 7 записывается как 0111. \times0\ =\ 0\), \(0\times0\ =\ 0\) и \(1\times1\ =\ 1\).
После окончательного умножения мы должны расширить каждую строку до количества знаковых битов, в данном случае до 8 бит. Как только все строки расширены, мы можем сложить строки вместе, используя правила сложения, и получить результат в 8-битном представлении.
| 1 | 0 | 1 | 1 | ||||||
| x | 0 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | x | ||
| 1 | 1 | 1 | 0 | 1 | 1 | x | x | ||
| + | 0 | 0 | 0 | 0 | 0 | x | x | x | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
The final result is represented in 8-bit ignoring the extra two digits in the front.
Таким образом, результат умножения со знаком для 1011 и 0111 равен 11011101.
Двоичное умножение без знакаРешение двоичного умножения без знака — простой процесс. Это умножение можно решить так же, как и любое другое десятичное умножение.
Давайте проверим решенный пример для лучшего понимания:
Пример: Умножьте 13 и 9 в двоичном формате.
Solution: 13 in binary can be written as 1101 and 9 in binary is denoted as 1001.
Performing unsigned multiplication:
| 1 | 1 | 0 | 1 | |||
| x | 1 | 0 | 0 | 1 | ||
| 1 | 1 | 0 | 1 | |||
| 0 | 0 | 0 | 0 | x | ||
| 0 | 0 | 0 | 0 | x | x | |
| 1 | 1 | 0 | 1 | x | x | x |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
So, unsigned multiplication for 1101 and 1001 is 1110101. That is 13 multiplied by 9 gives 117.
That is 13 multiplied by 9 gives 117.
Пример 1: Используя правила двоичного умножения, решите 11011 и 101.
Решение: Умножая 11011 и 101, мы получаем:
| 1 | 1 | 0 | 1 | 1 | |||
| x | 1 | 0 | 1 | ||||
| 1 | 1 | 0 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | x | ||
| 1 | 1 | 0 | 1 | 1 | x | x | |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Таким образом, результатом умножения 11011 и 101 будет 10000111.
Solution: On multiplying 1011.1 and 10.1, we get
| 1 | 0 | 1 | 1 | 1 | ||
| x | 1 | 0 | 1 | |||
| 1 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | x | |
| 1 | 0 | 1 | 1 | 1 | x | x |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Умножив 10111 на 101, мы получим 1110011. Сложив десятичные точки, мы получим ответ как 11100,11.
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
В.1 Что такое двоичное умножение?
Ответ 1 Двоичное умножение похоже на десятичное умножение, но использует только две цифры, т.е. 0 и 1, в отличие от 0-9 в десятичных числах.
В.2 Как умножить двоичное число на 3?
Ответ 2 3 в двоичных числах записывается как 11. Таким образом, чтобы умножить любое число на 3, мы должны умножить число на 11, следуя простым правилам двоичного умножения.
Q.3 Каковы правила двоичного умножения?
Ответ 3 Двоичное умножение можно выполнить, следуя 4 простым правилам, аналогичным десятичному умножению.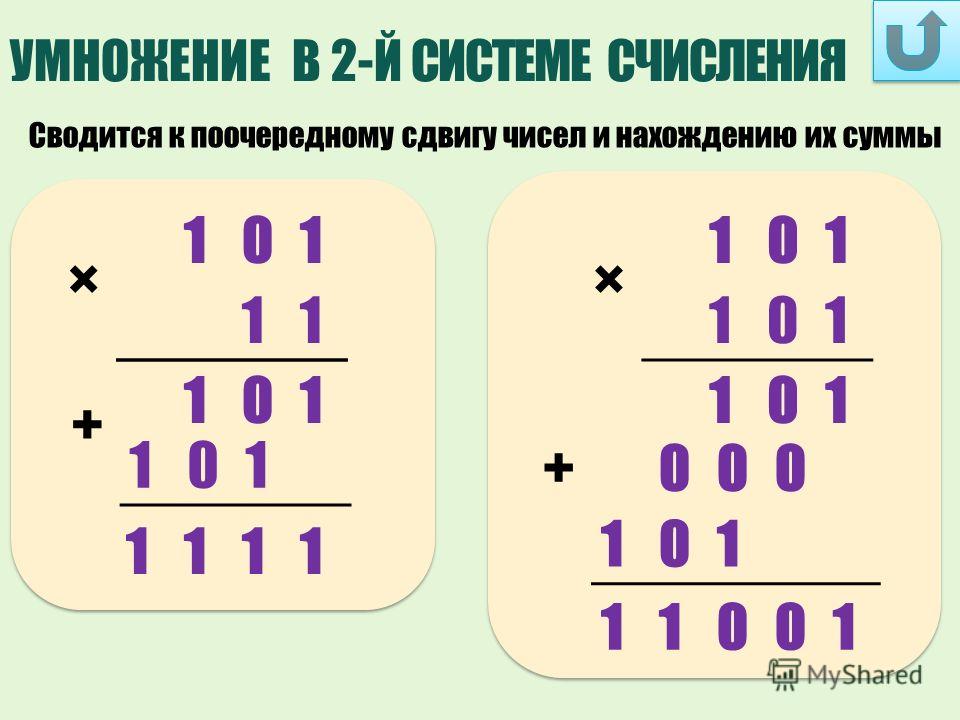

 Множитель (1) прибавляется к частному, а результатом вычитания является остаток.
Множитель (1) прибавляется к частному, а результатом вычитания является остаток.