Линейная функция метод наименьших квадратов: Репозиторий Самарского национального исследовательского университета имени академика С.П. Королёва: Недопустимый идентификатор

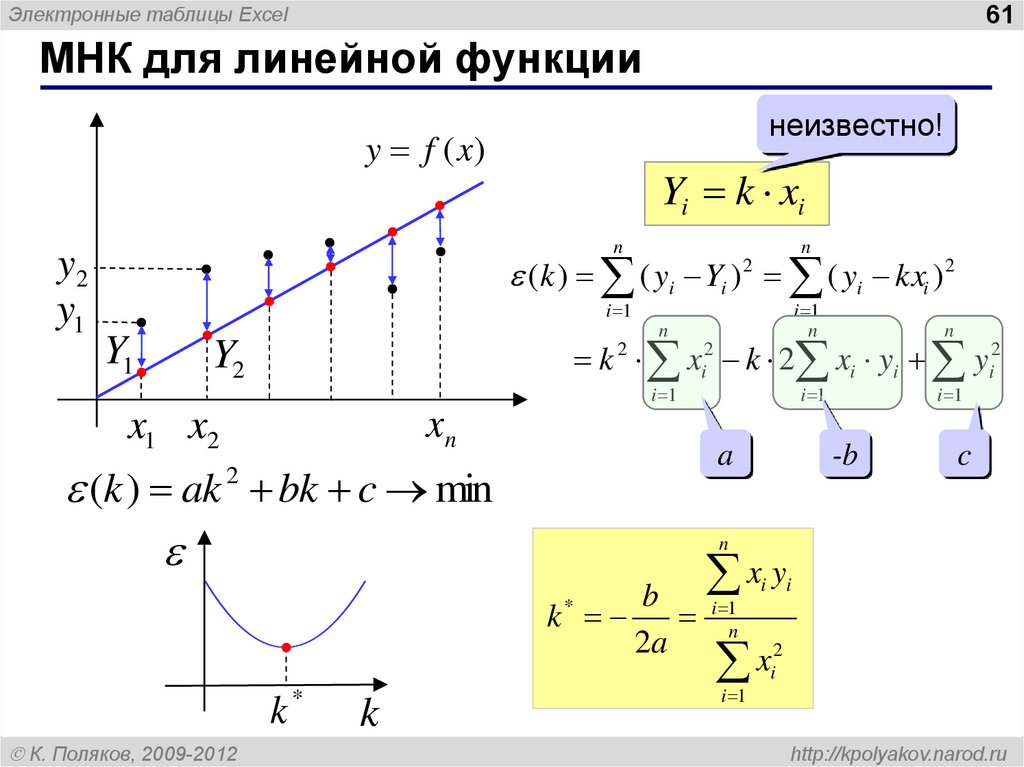
Метод наименьших квадратов

Получение регрессионной модели происходит в два этапа:

Первая задача не имеет строгого решения. Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.

Чаще всего выбор производится среди следующих функций:

у = ах + b — линейная функция;

у = ах² + bх + с — квадратичная функция;

у = а ln(х) + b — логарифмическая функция;

у = а е^bx — экспоненциальная функция;

у = а х^b ~ степенная функция.

Квадратичная функция называется также полиномом второй степени. Иногда используются полиномы и бо­лее высоких степеней, например, полином третьей степени имеет вид: у == ах³ + bх² + cx + d.

Если вы выбрали (сознательно или наугад) одну из предлагаемых функций, то следующим шагом нужно подобрать параметры (а, b, с и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам.

Что значит «располагалась как можно ближе»? Ответить на этот вопрос — значит предложить метод вычисления параметров. Такой метод был предложен в XVIII веке немецким математиком К. Гауссом. Он называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений у-координат всех экспериментальных точек от у-координат графика функции была бы минимальной.

Мы не будем здесь производить подробное математиче­ское описание метода наименьших квадратов. Достаточно того, что вы теперь знаете о существовании такого метода. Он очень широко используется в статистической обработке данных и встроен во многие математические пакеты про­грамм. Важно понимать следующее: методом наименьших квадратов по данному набору экспериментальных точек можно построить любую (в том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлетворять, это уже другой вопрос — вопрос критерия соответствия. На рис. 2.14 изображены три функции, построенные методом наименьших квадратов по данным, представленным в пре­дыдущем параграфе.

Данные рисунки получены с помощью MS Excel. График регрессионной модели называется трендом. Английское слово trend можно перевести как общее направление, или тенденция.

Уже с первого взгляда хочется отбраковать вариант ли­нейного тренда. График линейной функции — это прямая. Полученная по МНК прямая отражает факт роста заболевае­мости от концентрации угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квад­ратичный и экспоненциальный тренды ведут себя очень правдоподобно. Теперь пора обратить внимание на надписи, присутствующие на графиках. Во-первых, это записанные в явном виде искомые функции — регрессионные модели:

линейная функция: у = 46,361x — 99,881; экспоненциальная функция: у = 3,4302 е0’7555; квадратичная функция: у = 21,845×2 — 106,97x: + 150,21.

На графиках присутствует еще одна величина, получен­ная в результате построения трендов. Она обозначена как R². В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной является полученная регрессионная модель. Коэф­фициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессион­ной модели предельно неудачен. Чем R2 ближе к 1, тем удачнее регрессионная модель.

Из трех выбранных моделей значение R² наименьшее у линейной. Значит она самая неудачная (нам и так это было понятно). Значения же R² у двух других моделей до­статочно близки (разница меньше одной 0,01). Если опреде­лить погрешность решения данной задачи как 0,01, по кри­терию R

2 эти модели нельзя разделить. Они одинаково удачны. Здесь могут вступить в силу качественные сообра­жения. Например, если считать, что наиболее существенно влияние концентрации угарного газа проявляется при боль­ших величинах, то, глядя на графики, предпочтение следу­ет отдать квадратичной модели. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.

Аппроксимация функций (метод наименьших квадратов)

Похожие презентации:

Численное моделирование. Метод наименьших квадратов. (Лекция 7)

Парная линейная регрессия и метод наименьших квадратов

Линейная модель парной регрессии. Метод наименьших квадратов

Метод наименьших квадратов

Метод наименьших квадратов

Эконометрика. Обобщенный метод наименьших квадратов

Метод наименьших квадратов

Регрессионный анализ. Метод наименьших квадратов

Метод наименьших квадратов. Лекция 6

Метод наименьших квадратов

1. Аппроксимация функций (метод наименьших квадратов)

Задача:
статистически обработать данные, и составить
эмпирические формулы для нахождения
зависимости одной величины от другой, когда
известна таблица их значений, полученных в
результате некоторой серии экспериментов.
Важнейшее отличие постановки данной задачи от
задачи интерполирования состоит в том, что не
требуется обязательное совпадение данных,
полученных в результате измерений со значениями
искомой функции в выделенных точках.

3. Анализ задачи:

• результаты измерений не могут быть
точными,
• выделенные точки (узлы), как правило,
ничем не отличаются от всех остальных
и непонятно, почему именно в них мы
должны требовать точного совпадения
данных.

4. Меры приближения:

• Максимальное по модулю отклонение
искомой функции в узлах от данных
значений.
• Сумма модулей отклонений искомой
функции в узлах от данных значений.
• Сумма квадратов отклонений искомой
функции в узлах от данных значений.

5. ПОСТАНОВКА ЗАДАЧИ.

Дана таблица зависимости функции Y от
аргумента X:
Х
Х1 Х2 ………
Хn
У
У1 У2 ………
Уn
Надо среди функций основных видов
определить такую (найти значения
соответствующих параметров), чтобы сумма
квадратов разностей значений этой функции в
узлах и величин Yi была минимальна.

6. Обычно ограничиваются функциями одного из следующих видов:

Y=ax+b
Y=ax2+bx+c
Y=сxn
Y=a eх
Y=1/(ax+b)
Y=a ln(x)+b
Y=a/(x+b)

7.

Нахождение наилучшей линейной приближающей функции.Разберем решение задачи, когда решение ищется в виде
линейной функции: Y=ax+b.
Цель — определить коэффициенты a и b таким образом, чтобы
величина
n
F (a, b) (axi b y i ) 2
i 1
приняла наименьшее значение
Функция F(a,b) представляет из себя
многочлен второй степени относительно
величин a и b с неотрицательными
значениями, поэтому решение всегда
существует.
n
F ‘b (a, b) 2(axi b yi ) 0
i 1
n
F ‘ (a, b) 2(ax b y ) * x 0
i
i
i
a
i 1
n
n
n 2
a x i b x i y i x i
i 1
i 1
i 1
n
n
a x bn
yi
i
i 1
i 1
Пусть зависимость задана таблицей
X
-3
-1 1 3 5
Y
3
4
6 8 10
Для вычисления искомых моментов построим таблицу:
Сумма
Среднее значение
(М)
X
-3
-1
1
3
5
5
1
Y
3
4
6
8
10
31
6.2
X2
9
1
1
9
25
45
9
XY
-9
-4
6
24
50
67
13. 4
Отсюда получаем систему
9a+b=13.4
a+b=6.2
или
a=0.9
b=5.3
Проделайте аналогичные выкладки и
получите систему уравнений для поиска
коэффициентов a, b, c при подборе
эмпирической квадратичной зависимости
X
-3
-1
1
3
5
Y
3
4
6
8
10

13. Сведение поиска функций другого вида к поиску линейной функции

При поиске функций другого вида задача
сводится к рассмотренной задаче нахождения
наилучшей линейной функции. Для этого
производится некоторая замена переменных,
которая подбирается таким образом, чтобы
вновь полученная задача свелась к
нахождению линейной зависимости, а после
применения описанной конструкции
происходит обратная замена.

14. Функция вида y=1/(ax+b)

При поиске такой функции, для сведения задачи к линейной мы
произведем замену t =1/y, после которой задача сводится к
нахождению наилучшей линейной функции t=ax+b. А
коэффициенты, найденные при ее решении и будут искомыми в
первоначальной задаче.
Алгоритм вычислений:
• заменяем в исходной таблице переменную Y на t, а все
числа, записанные в нижней строке — на обратные
• для получившейся таблицы находим линейную зависимость
• получившиеся значения a и b берем без изменения.

15. Функция вида Y=a ln(x)+b

Аналогичные действия производятся при поиске
наилучшей приближающей функции вида Y=a ln(x)+b.
Но замена, которую необходимо произвести для
сведения к линейной задаче, в этом случае имеет вид
u=ln(x).
Алгоритм вычислений:
• заменяем в исходной таблице переменную X на u, а
все числа, записанные в верхней строке — на их
логарифмы
• для получившейся таблицы находим линейную
зависимость
• получившиеся значения a и b берем без изменения.

English     Русский Правила

Линейная регрессия с использованием метода наименьших квадратов | Адарш Менон

Линейная регрессия — это простейшая форма машинного обучения. В этом посте мы увидим, как работает линейная регрессия, и реализуем ее в Python с нуля.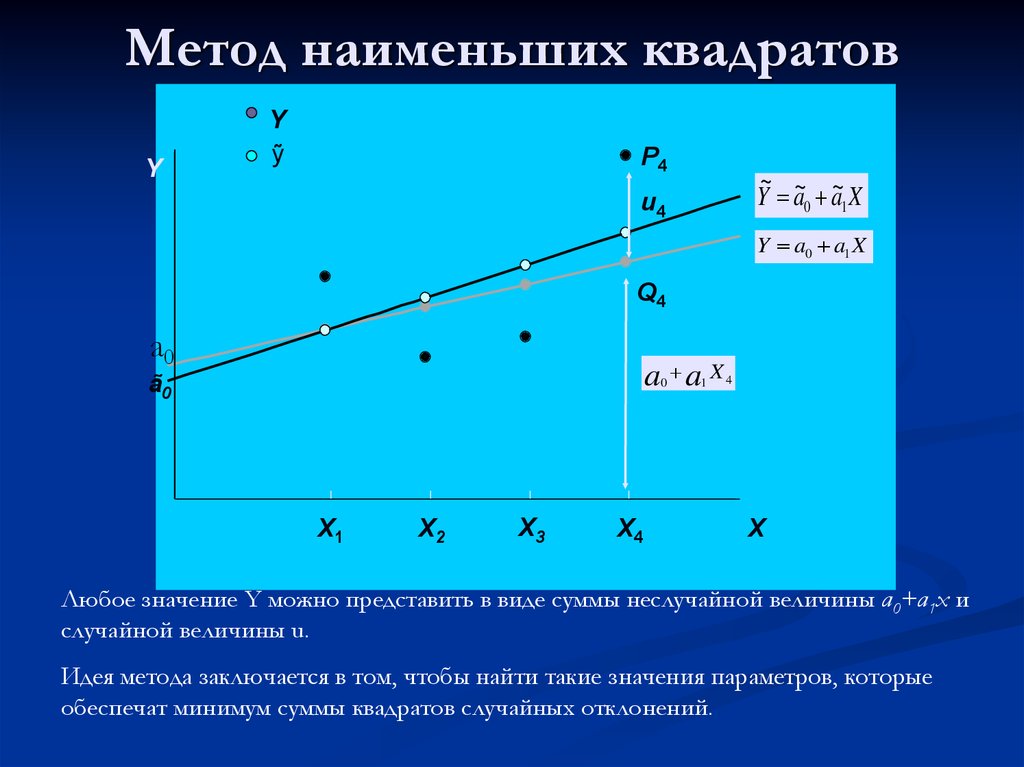 Это письменная версия вышеуказанного видео. Смотрите, если вам так больше нравится.

В статистике линейная регрессия — это линейный подход к моделированию связи между зависимой переменной и одной или несколькими независимыми переменными. В случае одной независимой переменной это называется простой линейной регрессией. Для более чем одной независимой переменной процесс называется множественной линейной регрессией. В этом уроке мы будем иметь дело с простой линейной регрессией.
Пусть X будет независимой переменной, а Y будет зависимой переменной. Мы определим линейную зависимость между этими двумя переменными следующим образом:

Это уравнение для прямой, которую вы изучали в старшей школе. м — это наклон линии, а c — точка пересечения у. Сегодня мы будем использовать это уравнение для обучения нашей модели с заданным набором данных и прогнозирования значения Y для любого заданного значения X .

Наша задача сегодня состоит в том, чтобы определить значение m и c , что дает минимальную ошибку для данного набора данных. Мы будем делать это, используя метод наименьших квадратов .

Итак, чтобы свести к минимуму ошибку, в первую очередь нам нужен способ вычисления ошибки. Функция потерь в машинном обучении — это просто мера того, насколько прогнозируемое значение отличается от фактического значения.
Сегодня мы будем использовать квадратичную функцию потерь для расчета потерь или ошибок в нашей модели. Его можно определить как:

Мы возводим его в квадрат, потому что для точек ниже линии регрессии y — p будет отрицательным, а мы не хотим отрицательных значений в нашей общей ошибке.

Теперь, когда мы определили функцию потерь, осталось только минимизировать ее. Это делается путем нахождения частной производной L , приравнивания ее к 0, а затем нахождения выражения для m и c . После того, как мы проведем математику, у нас останутся следующие уравнения:

Здесь x̅ — среднее значение всех значений во входных данных X и ȳ является средним значением всех значений в желаемом выходе Y . Это метод наименьших квадратов. Теперь реализуем это на питоне и будем делать прогнозы.

 1.287357370010931 9.908606190326509 

Точности не будет, потому что мы просто берем прямую линию и заставляем ее наилучшим образом соответствовать данным. Но вы можете использовать это, чтобы делать простые прогнозы или получать представление о величине/диапазоне реального значения. Также это хороший первый шаг для новичков в машинном обучении.

Найдите набор данных и код здесь: https://github.com/chasinginfinity/ml-from-scratch/tree/master/01%20Linear%20Regression%20using%20Least%20Squares

Есть вопросы ? Нужна помощь ? Свяжитесь со мной!

Электронная почта: adarsh2021@gmail. com

.com/adarsh_menon_

Instagram: https://www.instagram.com/adarsh_menon_/

Метод наименьших квадратов. Математика линейной регрессии | by Maarten De Baecke

Математика линейной регрессии

Фото Fakurian Design на Unsplash

Возможно, вы слышали о Пизанской башне. В ходе строительства башня стала постепенно наклоняться набок.

Допустим, Джино, один из инженеров, хотел предсказать будущий наклон башни. Он хочет знать, увеличится ли наклон и насколько до следующего года. Единственная информация Джино — это следующая таблица, содержащая наклон в десятых долях миллиметра в год.

Чтобы лучше понять эти данные, Джино построил следующую диаграмму рассеяния.

Рисунок 1: диаграмма рассеяния | автор

Точечная диаграмма графически визуализирует взаимосвязь между двумя количественными переменными. Иногда одна переменная зависит от другой переменной. В этом случае независимая переменная размещается на горизонтальной оси, а зависимая переменная — на вертикальной.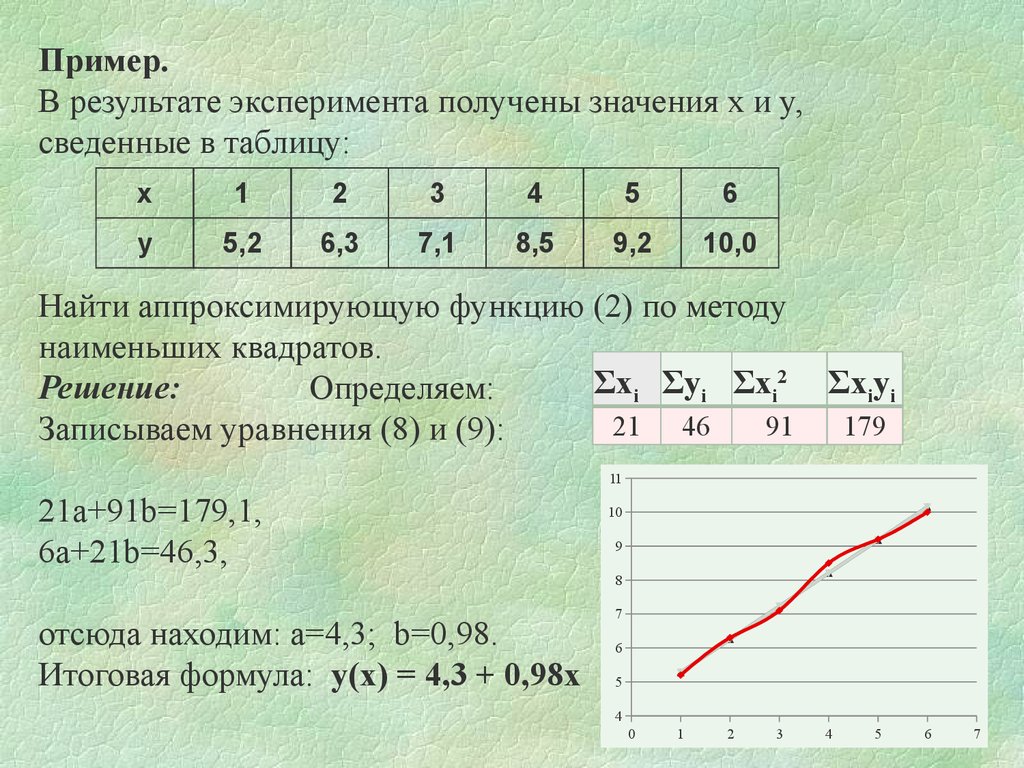 Если это не так, мы можем выбрать, куда поместить каждую переменную. Для нашей башни наклон зависит от года. Поэтому год откладывается по горизонтальной оси, а наклон по вертикальной.

Джино замечает, что точки данных описывают прямую линию с положительным наклоном, если смотреть на график.

Когда набор точек данных возрастает, мы говорим о положительной связи между нашими переменными. Когда набор нисходящий, мы говорим об отрицательном отношении. Кроме того, если наши точки данных действительно хорошо описывают прямую линию или определенную кривую, мы говорим о сильной корреляции. Если наши точки просто описывают линию или кривую, мы говорим о слабой корреляции (см. рис. 2.а). Также возможно вообще не иметь никакой корреляции (см. рис. 2.b).

Рисунок 2: слабая корреляция и отсутствие корреляции | by author

Целью Джино было использовать свой график (см. рис. 1), чтобы предсказать будущий наклон башни. Он мог сделать это, вычислив правило функции прямой линии, которая лучше всего соответствует заданным точкам данных. Другими словами, он мог провести линейную регрессию.

Коэффициент корреляции

Прежде чем мы поговорим о линейных регрессиях, я сначала хочу поговорить о коэффициенте корреляции r. Он не только может сказать нам, стоит ли вообще проводить линейную регрессию. Он также играет очень важную роль в самой регрессии.

Коэффициент r отображает силу и направление (положительное или отрицательное) линейной корреляции. Когда существует положительная связь между обеими переменными, r положителен. Когда связь между переменными отрицательна, r также отрицательна. Если точки данных точно описывают прямую линию, r равно 1 или −1. При отсутствии корреляции r будет равно нулю (или действительно близко к нулю). Если определенный набор точек данных имеет довольно низкий коэффициент корреляции (0,5 > r > -0,5), мы знаем, что линейная регрессия, вероятно, не даст нам очень надежных результатов. Регрессию целесообразно проводить только тогда, когда r выше 0,5 или ниже -0,5.

Для расчета r мы можем использовать формулу Пирсона :

В этой формуле n — количество точек данных, xᵢ координата x точки данных i, x̄ среднее значение всех координат x, yᵢ y -координата точки данных i, ȳ среднее значение всех координат y, sₓ стандартное отклонение всех координат x и sᵧ стандартное отклонение всех координат y. Если вы никогда не слышали о термине «стандартное отклонение». Это квадратный корень из среднего квадратичного отклонения.

По сути, чем больше разбросаны наши точки данных по оси x/y, тем больше sₓ/sᵧ.

Кстати, формула Пирсона существует во многих формах, но вывод формулы для заданного набора точек всегда должен быть одним и тем же.

Логика формулы Пирсона

Хотя поначалу формула Пирсона может показаться немного сложной, логика, стоящая за ней, на самом деле не так уж сложна. Предположим, что для набора точек данных мы выполняем определенный расчет, в результате чего получается положительное значение, если наши точки описывают положительный наклон, и отрицательное значение для отрицательного наклона. Для этого мы могли бы разделить наш набор точек на четыре области или квадранта со средним значением всех значений x (x = x̄) и средним значением всех значений y (y = ȳ), разделяющих квадранты.

Рисунок 3: точечная диаграмма с квадрантами | автор

При наличии положительной связи между нашими точками (набор точек восходящий) большинство точек будет лежать в квадрантах I и III.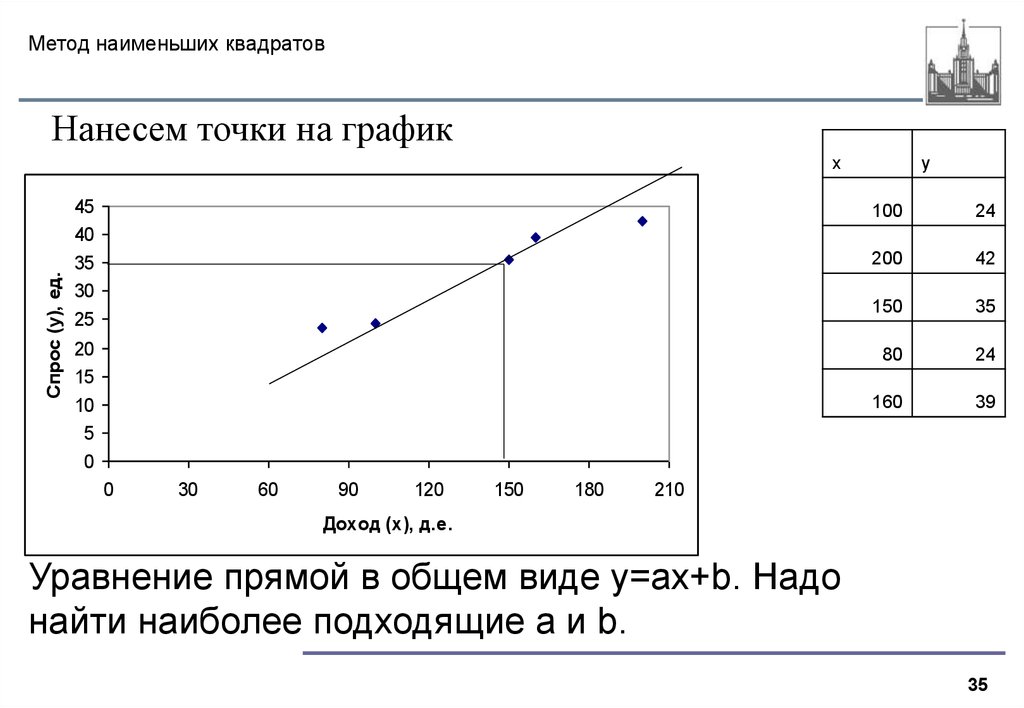 В случае отрицательной связи большинство точек будет лежать в квадрантах II и IV. Зная это, мы могли бы присвоить положительное значение (+1) каждой точке в квадранте I или III и отрицательное значение (-1) каждой точке в квадранте II или IV. Сумма всех этих положительных и отрицательных значений даст нам положительный результат, когда есть положительная связь, и отрицательный результат, когда есть отрицательная связь.

Хотя этот метод может дать нам информацию о знаке нашего наклона, он не дает нам никакой информации о самой корреляции. Например, результат суммы всех присвоенных значений на рисунке 4.a такой же, как и на рисунке 4.b (оба +6). Тем не менее, существует значительная разница в корреляции между двумя графиками.

Рисунок 4: слабая корреляция и сильная корреляция | автор

Если вы изучите разницу между рис. 4.а и рис. 4.б, то поймете, что, хотя точки расположены очень похожим образом, расстояние от каждой точки до осей различается. Если много точек близко (только) к одной из осей, корреляция будет очень слабой. Итак, в нашем методе мы хотим дать более высокую оценку точкам, которые находятся дальше от обеих осей, и более низкую оценку точкам, которые находятся близко к одной из осей.

Мы можем рассчитать расстояние от точки до оси x, вычитая среднее значение всех координат x из координаты x нашей точки (xᵢ − x̄). Тот же ход мыслей применим и к оси Y (yᵢ−ȳ). Поскольку расстояние не может быть отрицательным, мы обычно берем абсолютное значение этой разницы. Но знак «расстояния» до осей x и y может сказать нам, находится ли точка в четном или нечетном квадранте.

Например, когда точка находится в первом квадранте, оба (xᵢ − x̄) и (yᵢ−ȳ) положительны. Если бы точка находилась во втором квадранте, (xᵢ − x̄) было бы отрицательным, а (yᵢ−ȳ) положительным. Точка, расположенная в третьем квадранте, будет иметь как отрицательное значение (xᵢ — x̄), так и (yᵢ-ȳ). И так далее… (см. рис. 5)

Рисунок 5: точечная диаграмма с расстояниями | автор

Теперь кое-что очень полезное получается, когда мы берём произведение расстояний по осям x и y от каждой точки до осей.

Это произведение является положительным, когда точка находится в нечетном квадранте (оба члена имеют одинаковый знак), и отрицательным, когда точка находится в четном квадранте (оба члена имеют разные знаки). Если затем мы возьмем сумму всех этих положительных и отрицательных значений, наш результат будет отрицательным, если большинство точек расположены в четном квадранте, и положительным, если большинство точек находится в нечетном квадранте.

Поскольку большинство точек расположены в квадрантах I и III в случае положительной связи и квадрантах II и IV в случае отрицательной связи, мы также можем использовать этот метод для вычисления знака связи между точками данных. Но помните, целью этой новой формулы было не только вычисление знака. Мы уже нашли для этого менее сложный метод. Наша цель состояла в том, чтобы расширить наш метод, чтобы также описать силу корреляции.

Ранее мы обнаружили, что если много точек расположены близко к одной из осей, корреляция будет очень слабой. Следовательно, вывод нашей формулы должен быть очень маленьким, когда точка находится близко к одной из осей, и больше, если точка находится дальше от обеих осей. Посмотрим, соответствует ли наша новая формула этому требованию.

Когда точка находится близко к одной из осей, либо (xᵢ − x̄), либо (yᵢ−ȳ) очень малы. Поэтому и результат от этого продукта будет меньше. Но когда точка находится дальше от обеих осей, и (xᵢ — x̄), и (yᵢ-ȳ) будут большими. Соответственно и изделие будет большим.

В качестве примера мы можем рассчитать коэффициент корреляции для рисунков 6.a и 6.b.

Рисунок 6: слабая корреляция и сильная корреляция | автор

Для рисунка 6.а мы находим следующее:

Объяснение символов:

• ⇔ : тогда и только тогда, когда
• ∧ : и

Для рисунка 6.b мы находим это:

Наша новая формула, кажется, работает. В обоих случаях знак коэффициента положителен, как и должно быть (связь между переменными в обоих случаях положительна), а выход выше (85,11 > 82,875), когда точки расположены ближе друг к другу (что также должно быть случай). Но мы еще не там.

Предположим, что мы использовали метр в качестве единицы измерения на наших осях на рисунках 6.a и 6.b. Если бы мы затем изменили эту единицу измерения, например, по оси X на рис. 6.а, с метров на миллиметры, наш коэффициент корреляции внезапно стал бы намного выше. Это потому, что x-координаты наших точек теперь будут в тысячу раз больше. Но этого не должно было случиться, так как соотношение между точками фактически не изменилось.

Здесь на помощь приходит стандартное отклонение. Если вы забыли, стандартное отклонение показывает, насколько разбросаны/близки друг к другу наши точки. Когда мы делим (xᵢ − x̄) на стандартное отклонение всех координат x, sₓ, мы получаем так называемый z-показатель этой точки. Эта оценка показывает, на сколько стандартных отклонений наша точка отличается от среднего, x̄. Например, если бы наше среднее значение было x = 5, стандартное отклонение sₓ = 3 и координата x нашей точки xᵢ = 11, z-оценка была бы равна 2. Поскольку наша точка находится на расстоянии двух стандартных отклонений от нашего среднего.

Поскольку знак стандартного отклонения всегда положительный, знак нашего z-показателя зависит только от знака xᵢ − x̄. Это означает, что мы также можем использовать произведение z-оценки от xᵢ и yᵢ для вычисления знака взаимосвязи между переменными.

Теперь реальный вопрос: не зависит ли z-показатель от единицы измерения осей? Что ж, z-оценка показывает не то, насколько далеко точка от центра, а то, на сколько стандартных отклонений она удалена.

Если мы умножим координаты наших точек на тысячу, стандартное отклонение также будет в тысячу раз больше. Например:

Поскольку наше стандартное отклонение имеет ту же «единицу», что и наши оси, количество стандартных отклонений точки, удаленной от центра, всегда будет оставаться одним и тем же. Следовательно, z-оценка не зависит от единицы наших осей.

Использование z-оценки делает нашу формулу независимой от используемой единицы измерения. Наша новая формула теперь выглядит так:

Используя эту формулу, мы находим коэффициент корреляции, равный 10,413 для рисунка 6. a и коэффициент 13,93 для рисунка 6.b.

С этой формулой все еще есть одна проблема. Результат формулы зависит от количества точек данных. Например, предположим, что мы добавили к рисунку 6.a точку с координатой x 13 и координатой y 8. Эта точка ослабит нашу корреляцию, поскольку она далеко не является возможной прямой линией. Но с нашей текущей формулой наш коэффициент корреляции даже немного увеличился бы.

Чтобы решить эту проблему, мы можем взять среднее значение всех членов суммы. Поскольку мы уже подсчитываем все члены, нам нужно только разделить наше уравнение на количество точек, n. Ну, n-1, если быть точным. Причина этого выходит за рамки этой статьи, просто знайте, что в этом случае мы берем среднее значение всех условий путем деления на n-1. Наша окончательная формула — это формула Пирсона:

Теперь для рисунка 6.a мы находим r = 0,69, а для рисунка 6.b мы находим r = 0,93.

Метод наименьших квадратов

В начале этой статьи я представил вам Джино. Джино хотел вычислить правило функции прямой линии, которое лучше всего соответствовало бы заданным точкам данных из его графика рассеяния. Как я упоминал ранее, вычисление этого правила функции называется линейной регрессией.

Метод, лежащий в основе этой регрессии, называется методом наименьших квадратов.

Взгляните на следующий график:

Рисунок 7: линейная регрессия| автор

На этом графике мы называем координату y каждой точки yᵢ и координату y нашей линии с той же координатой x, что и наша точка ŷᵢ. yᵢ называется наблюдаемым значением y, а ŷᵢ — прогнозируемым значением y.

Когда мы рисуем линию, мы хотим, чтобы расстояние по оси Y от каждой точки до нашей линии было как можно меньше. Это расстояние равно разнице между наблюдаемым значением и прогнозируемым значением.

Проблема с этим уравнением в том, что d отрицательно, когда ŷᵢ больше, чем yᵢ. В этом случае мы хотим работать только с положительными значениями. Чтобы решить эту проблему, мы можем просто возвести нашу разницу в квадрат.

Отсюда и пошло название «метод наименьших квадратов».

Рисунок 8: метод наименьших квадратов | автор

Наша линия регрессии теперь представляет собой прямую линию, на которой сумма всех dᵢ является наименьшей.

Функциональное правило этой строки следующее:

Это можно доказать математически или с помощью компьютерного моделирования.

Регрессия Джино

Теперь, когда мы знаем, как вычислить линейную регрессию. Попробуем рассчитать ожидаемый наклон Пизанской башни в 1888 году.

Это данные Джино:

Для коэффициента корреляции находим r = 0,995 . Очень высокий коэффициент. Таким образом, определенно полезно использовать линейную регрессию. Для правила функции мы находим следующее:

Чтобы убедиться, что мы не допустили ошибок, мы можем нарисовать линию на нашей диаграмме рассеяния.

Выглядит неплохо, правда?

Теперь мы можем использовать эту линию для предсказания будущего наклона.

Для 1988 года мы прогнозируем наклон 767,8.