Умножить число на вектор онлайн: Онлайн калькулятор. Умножение вектора на число

Умножение вектора на число.

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Онлайн калькулятор. Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число

— это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; … ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение:

(-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Умножение вектора на число

Произведением вектора x на число β (x≠0, β≠0) называется вектор, модуль которого равен |

x||β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β<0. Если x=0 и (или) β=0, то βx=0.

Рис. 1

На рисунке Рис. 1 вектор x умножен на число 1.5. Полученный вектор y’ имеет то же направление, что и x т.к 1.5>0, и имеет длину 1.5 раз превысшающее длину x.

Вектор q имеет противополжное к p направление, т.к. вектор p умножено на отрицательное число -0.5, и имеет длину 2 раза меньше длины p.

Рассмотрим процесс умножения вектора на число.

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Пусть имеется вектор

где координаты вектора x, и пусть β некоторое число. Тогда

То есть для умножения вектора на число достаточно умножить каждый координат данного вектора на это число.

На рисунке Рис. 1 вектор x имеет координаты x=(6,4). Для умножения вектора x на число 1.5, умножим каждый координат вектора x на число 1.5:

Вариант 2. Начальные точки векторов произвольные.

Пусть имеется вектор x, с начальной точкой и конечной точкой . Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A.

Переместим вектор x на начало координат. Получим новый вектор x’ с начальными и конечными точками:

Умножим x’ на β:

Параллельно переместив начальную точку вектора

x’ на точку A, получим вектор x» с начальными и конечными точками:

На рисунке Рис. 1 вектор p=AB имеет координаты A(2,3) и B(8,1). Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p’=A’B’ с координатами A’(0,0) и B’(8-2, 1-3)=B’(6,-2). Умножим вектор p’ с числом -0.5:

Перемесив начальную точку вектора q’ на точку A, получим вектор q=AE, где точка E имеет координаты:

Операция умножения вектора на число обладает следующими свойствами:

1.β(x+y)=βx+βy (дистрибутивность относительно сложения векторов).

2. (α+β)a=αa+βa (дистрибутивность относительно сложения чисел).

3. α(βa)=(αβ)a (ассоциативность).

4. 1·a=a (умножение на единицу).

Пример 1. Умножить вектор y=(3,5,-6) на число 2.5.

Для умножения вектора y на число 2.5, просто умножаем каждый координат вектора y на данное число:

Пример 2. Умножить вектор x=AB на число 3, где A(2,2), B(7,6).

Переместим вектор AB на начало координат. Начальное и конечное точки перемещенного вектора будут:

Умножив полученный вектор на число 3, изменяется расположение конечной точки B’:

.

Переместив вектор на точку A, получим вектор 3·x, со следующими начальной и конечной точками:

 

Умножение векторов – типы, процесс и примеры

Умножение векторов помогает нам понять, как ведут себя два вектора при объединении. Эта векторная операция имеет широкое применение в физике, инженерии и астрономии, поэтому нам необходимо изучить эти методы, особенно если мы изучаем высшую математику. Умножение векторов охватывает два важных метода векторных операций: скалярное произведение и векторное произведение. Изучение умножения векторов также может помочь нам освежить наши знания о векторах и темах их применения. В этой статье мы обсудим два типа векторного умножения и узнаем разницу между ними. Обязательно держите свои заметки по следующим понятиям под рукой, так как нам, возможно, придется освежить их, изучая векторное умножение.

• Понимание различных компонентов, составляющих вектор.
• Посмотрите, как мы складываем и вычитаем векторы.
• Понять, как скалярный фактор влияет на заданный вектор.

А пока давайте продолжим и изучим два важных метода векторного умножения.

Когда мы умножаем два или более векторов, важно определить, хотим ли мы получить произведение, имеющее скалярную величину или векторную величину. Техника, которую нам нужно будет применить, зависит от нашего ответа на этот вопрос. На самом деле существует три возможных продукта векторного умножения: вектор, умноженный на скалярный множитель, точечный (или скалярный) продукт и перекрестный (или векторный) продукт.

• К этому моменту мы должны были узнать о распределении скалярных коэффициентов по вектору, и это первая процедура. Обязательно проверьте ссылки, которые мы включили в первый раздел.
• Скалярное произведение, известное как скалярное произведение, как вы уже догадались, возвращает скалярную величину.
• Аналогично, векторное произведение возвращает векторную величину.

Наше обсуждение сосредоточится на двух последних методах: точечных произведениях и перекрестных произведениях. Эти имена помогут вам определить операцию, которую необходимо выполнить, поскольку их операторы представляют собой точку ($\cdot$) и крестик ($\times$) соответственно.

Каковы правила умножения векторов?

Два продукта будут иметь разные результаты и процессы. Вот почему нам нужно понять, что представляют собой точечные и перекрестные произведения. Скалярный продукт и его правила Скалярное произведение представляет собой проекцию одного вектора на другой вектор. Допустим, у нас есть $\overrightarrow{A}$ и $\overrightarrow{B}$, скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ — это просто проекция $\overrightarrow{A} $ на вектор $\overrightarrow{B}$.

Вот визуализация того, что происходит, когда мы находим скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$. Что происходит, так это то, что мы используем векторную составляющую $\overrightarrow{A}$ вдоль направления $\overrightarrow{B}$ и умножаем эту составляющую на величину $\overrightarrow{B}$. \begin{align}\overrightarrow{A} \cdot \overrightarrow{B} &= (A \cos\theta)(B)\\&= AB\cos\theta\end{align} Это означает, что скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ ($\overrightarrow{A} \cdot \overrightarrow{B})$ – это просто произведение двух векторов’ величин и косинус угла между ними . Полученное произведение является скалярным, поэтому -точечное произведение также известно как скалярное произведение. Вот некоторые важные свойства скалярного произведения, о которых следует помнить:

• Скалярное произведение коммутативно: $\overrightarrow{A} \cdot \overrightarrow{B} = \overrightarrow{B} \cdot \overrightarrow{A}$. 9{\circ}$ равно $0$).

Есть еще один способ вычислить скалярное произведение двух векторов: мы умножаем их соответствующие декартовы компоненты на . Допустим, $\mathbf{i}$, $\mathbf{j}$ и $\mathbf{k}$ — единичные векторы вдоль осей $x$, $y$ и $z$ соответственно, мы можем найдите произведение $\overrightarrow{A}$ и $\overrightarrow{B}$, как показано ниже. \begin{align}\overrightarrow{A} &= A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}\\\overrightarrow{B} &= B_1\mathbf{i} + B_2\ mathbf{j} + B_3\mathbf{k}\\\\\overrightarrow{A} \cdot \overrightarrow{B}&=A_1B_1 + A_2B_2 +A_3B_3 \end{выровнено} Мы можем вычислить эти два способа скалярного произведения (или скалярного произведения) двух векторов. Теперь давайте перейдем ко второму важному результату векторного умножения: перекрестному или векторному произведению. Перекрестное произведение и его правила Возможно, вы уже видели здесь шаблон — для векторных произведений мы используем оператор $\times$, и результирующее произведение является вектором. Из-за этого перекрестное или векторное произведение предполагает, что мы будем учитывать направление. Отличный способ визуализировать векторное произведение двух векторов — определить площадь параллелограмма по векторам. Отсюда мы видим, что перекрестное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно произведению $A\sin\theta$ и $\overrightarrow{B}$. \begin{align}\overrightarrow{A} \times \overrightarrow{B} &= (A \sin \theta)(B)\\&= AB \sin \theta \mathbf{n} \end{align} Имейте в виду, что $\mathbf{n}$ — это просто единичный вектор, перпендикулярный и $\overrightarrow{A}$, и $\overrightarrow{B}$. Это означает, что мы можем найти перекрестное произведение на умножение величин двух векторов при наличии двух векторов и угла между ними . Затем мы можем умножить результат на синус угла между двумя векторами . Вот некоторые важные свойства векторных или кросс-произведений, которые могут пригодиться:

• Векторные или перекрестные произведения антикоммутативны: $\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}$.
• Векторное произведение является дистрибутивным относительно сложения: $\overrightarrow{A} \times (\overrightarrow{B}\times \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \ раз \overrightarrow{C}$.
• Перемножение двух параллельных векторов всегда будет равно $0$.

Как и в случае со скалярными произведениями, мы также можем найти векторное произведение двух векторов, учитывая их декартовы формы. Используя те же единичные векторы, мы имеем $\overrightarrow{A} = A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}$ и $\overrightarrow{B} = B_1\mathbf{i} + B_2\mathbf{j}+ B_3\mathbf{k}$. Важным свойством для наблюдения являются векторные произведения векторов с тремя единицами. Мы собрали для вас продукты: Мы можем разработать формулу векторного произведения, распределив два вектора на сложение и используя векторные произведения единичных векторов. Однако, чтобы упростить обсуждение, вот как мы можем вычислить векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$. \begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено} Если вы уже изучали детерминанты в прошлом, есть еще один способ понять векторное произведение, и вы также можете помочь себе запомнить операцию.

• Мы можем записать единичные векторы в первый массив.
• Компоненты двух векторов в следующих двух массивах.
• Чтобы найти коэффициент перед $\mathbf{i}$, мы находим определитель оставшейся матрицы $2\times2$ после того, как покроем строку и столбец, содержащие $\mathbf{i}$.
• Примените аналогичный процесс, чтобы найти компоненты для $\mathbf{j}$ и $\mathbf{k}$ .

\begin{align}\overrightarrow{A} \times \overrightarrow{B}&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ A_1 & A_2 & A_3\\ B_1 & B_2 & B_3\end{vmatrix}\\&=\begin{vmatrix}  A_2 & A_3\\B_2 & B_3\end{vmatrix}\mathbf{i}- \begin{vmatrix}  A_1 & A_3\\B_1 & B_3\end{vmatrix}\mathbf{j}+\begin{vmatrix}  A_1 & A_2\\B_1 & B_2\end{vmatrix}\mathbf{k}\\&=(A_2B_3 – A_3B_2)\mathbf{i} — (A_1B_3 – A_3B_1)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{выровнено} Независимо от подхода, он все равно должен возвращать одни и те же результаты. Это все, что нам нужно узнать о векторном умножении, так почему бы нам не попробовать решить приведенные ниже задачи, чтобы лучше понять векторные произведения и скалярные произведения? 9{\ circ} $

Раствор

Эта задача требует, чтобы мы умножили величины $\overrightarrow{F}$ и $\overrightarrow{s}$ и косинус образовавшегося угла $\theta$. Короче говоря, нам нужно скалярное произведение $|\overrightarrow{F}| $ и $|\overrightarrow{s}| . \begin{align}\overrightarrow{F} \cdot \overrightarrow{s} &= |\overrightarrow{F}||\overrightarrow{s}|\cos \theta \end{align} Мы будем использовать одну и ту же формулу для всех трех значений, поэтому продолжим и суммируем расчеты в одной таблице. 9{\circ}\\&= 600 \cdot \dfrac{1}{2}\\&=300 \end{выровнено} \begin{выровнено}\overrightarrow{F} \cdot \overrightarrow{s} &=300 \text{N}\cdot\text{m}\end{выровнено}

Это отличный способ применить нашу формулу скалярного произведения, а также получить представление об одном из многих приложений векторного умножения.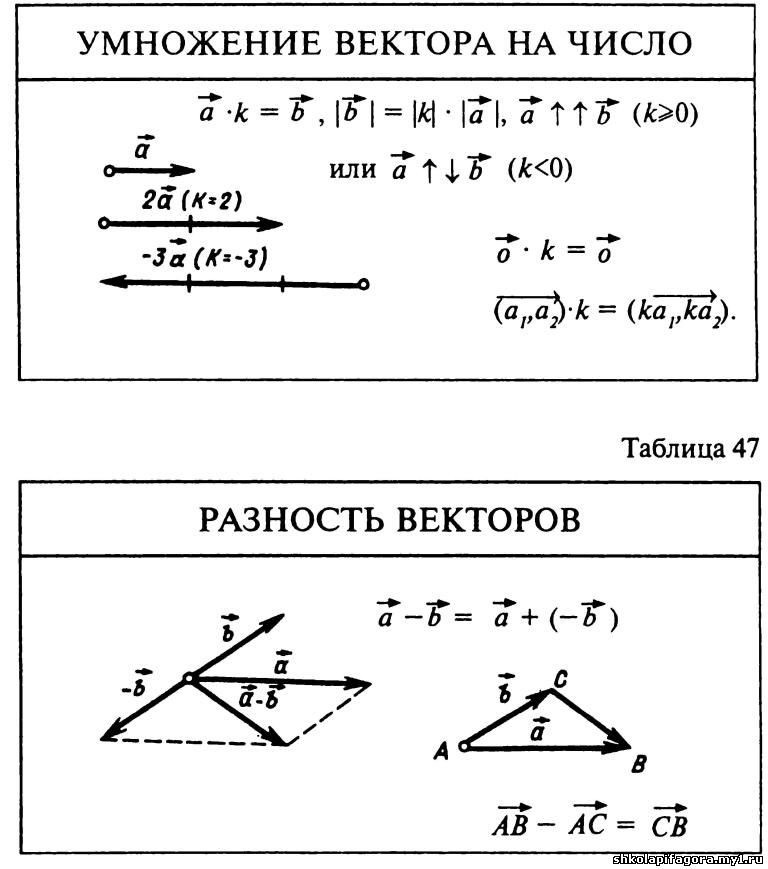 Пример 2 Найдите выражения для $\overrightarrow{A} \cdot \overrightarrow{B}$ и $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов: \begin{align} \overrightarrow{A} &= 2\mathbf{i} – 3\mathbf{j}\\\overrightarrow{B} &=3\mathbf{i}+ 2\mathbf{j}\end{ выровнено}

Решение

Зная декартовы формы векторов, мы все еще можем найти их точечные и перекрестные произведения.

• Мы можем перемножить коэффициенты соответствующих компонентов, а затем сложить произведения, чтобы найти скалярный продукт.
• Для перекрестного произведения вида $a\mathbf{i} + b\mathbf{j}$ члены распределяются алгебраически и исключаются перекрестные произведения одинаковых единичных векторов.

Почему мы не работаем с $\overrightarrow{A} = 2\mathbf{i} – 3\mathbf{j}$ и $\overrightarrow{B} =3\mathbf{i} + 2\mathbf{j}$ сначала лучше понять процесс? Скалярное произведение будет простым — мы умножаем коэффициенты перед $\mathbf{i}$ и $\mathbf{j}$. \begin{align}\overrightarrow{A} \cdot\overrightarrow{B}&= ({\color{blue}2}\mathbf{i} – {\color{red}3}\mathbf{j}) \cdot ({\ color{blue}3}\mathbf{i} + {\color{red}2}\mathbf{j})\\&= ({\color{blue}2})({\color{blue} 3}) + ({\color{red}-3})({\color{red}2})\\&= 6 – 6\\&= 0\end{выровнено} Это означает, что скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно $0$. Поскольку векторное произведение является дистрибутивным относительно сложения, мы можем распределить члены алгебраически и сократить $\mathbf{i}\times\mathbf{i}$ или $\mathbf{j}\times\mathbf{j}$ . \begin{align}\overrightarrow{A} \times\overrightarrow{B}&= (2\mathbf{i} – 3\mathbf{j}) \times (3\mathbf{i} + 2\mathbf{j} )\\&= (2\mathbf{i})\times (3\mathbf{i} + 2\mathbf{j}) – 3\mathbf{j}\times (3\mathbf{i} + 2\mathbf {j})\\&= [(2)(3) \mathbf{i}\times\mathbf{i} +(2)(2) \mathbf{i}\times\mathbf{j}]+[( -3)(3) \mathbf{j}\times\mathbf{i} + (-3)(2)\mathbf{j}\times\mathbf{j}]\end{выровнено} Напомним, что перекрестное произведение идентичных векторов будет равно нулю, поэтому давайте воспользуемся этим, чтобы сократить члены.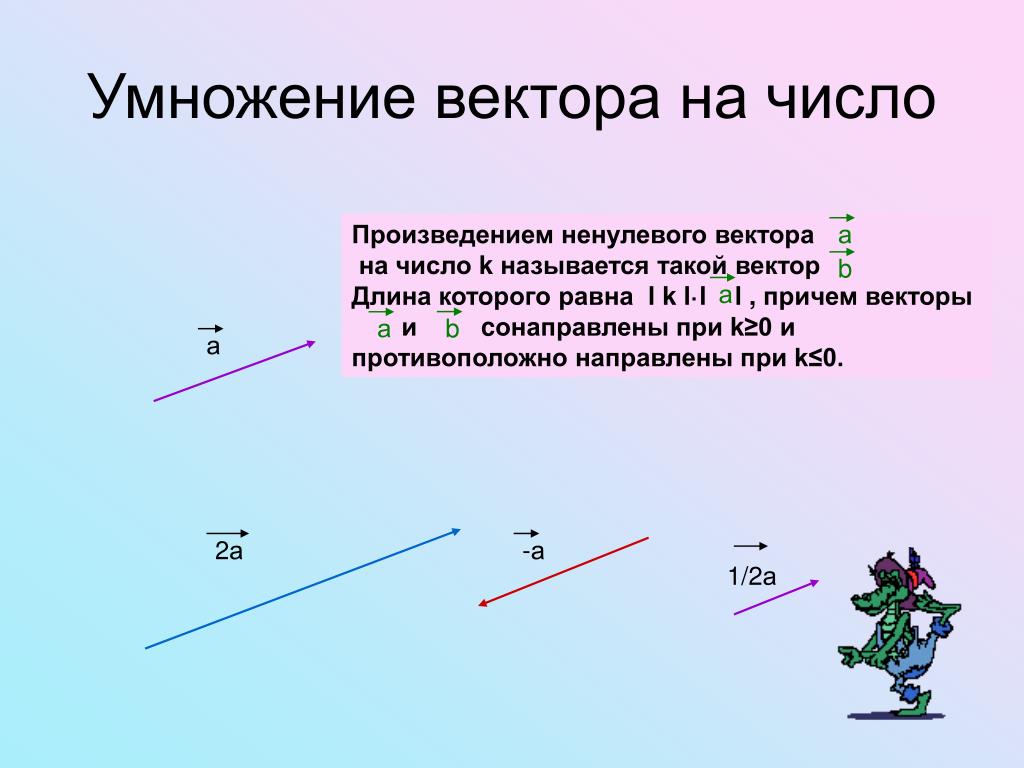 Кроме того, просмотрите руководство, которое мы предоставили для векторных произведений других единичных векторов. \begin{выровнено}\overrightarrow{A} \times\overrightarrow{B}&= (0 + 4\mathbf{k})+(-9(\mathbf{-k} )+ 0)  \\&= (4 + 9)\mathbf{k}\\&= 13\mathbf{k}\end{align} Таким образом, мы показали, как можно найти перекрестное и скалярное произведения двух векторов вида $a\mathbf{i} + b\mathbf{j}$. Пример 3 Оцените следующие выражения, учитывая декартовы формы трех векторов, показанных ниже. \begin{align} \overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{C} &=3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k}\end{align} а. $\overrightarrow{A} \times\overrightarrow{B}$ б.$\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{B})$ в. $(\overrightarrow{A} \times \overrightarrow{B})\times \overrightarrow{C}$

Решение

У нас есть два способа найти векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$: используя формулу, полученную из распределения двух векторов, или используя наши знания об определителях. Мы пока будем использовать первый вариант: \begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено} Следовательно, мы имеем векторное произведение двух векторов: \begin{align}\overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{A} \times \overrightarrow{B}&=(-5\cdot -3 – 6\cdot 4)\mathbf{i} +(-3 \cdot 4 – 4\cdot -3)\mathbf{j}+(4\cdot 4 – -5\cdot -2)\mathbf{k}\\&=-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}\\&=-9\mathbf{i} +6\mathbf{k}\end{выровнено} Мы будем использовать этот результат для следующих двух задач, поэтому давайте назначим $\overrightarrow{M}$ для представления $-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}$ или $ -9\mathbf{i} +6\mathbf{k}$. Чтобы найти $\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B})$, мы просто умножаем коэффициенты соответствующих единичных векторов как $\overrightarrow{A}$, так и полученного вектор, $\overrightarrow{M}$. \begin{align}\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B}) &=\overrightarrow{B}\cdot\overrightarrow{M}\\&=(-2\mathbf{ i}+ 4\mathbf{j}- 3\mathbf{k})\cdot(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\\&= (-2)(-9)+ (4)(0) +(-3)(6)\\& =18-18\\&=0\конец{выровнено} Для третьей задачи найдем перекрестное произведение $(\overrightarrow{A} \times \overrightarrow{B}) = \overrightarrow{M}$ и $\overrightarrow{C}$, взяв определители коэффициентов. \begin{align}(\overrightarrow{A}\times\overrightarrow{B}) \times\overrightarrow{C} &=\overrightarrow{M}\times\overrightarrow{C}\\&=(-9\mathbf{ i}+0\mathbf{j}+6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})\end{выровнено} Давайте перепишем их в матричной форме и начнем вычислять определители полученных матриц $2\times2$, как показано ниже. \begin{выровнено}(-9\mathbf{i}+ 0\mathbf{j} +6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})&=\begin{vmatrix }\mathbf{i} & \mathbf{j} & \mathbf{k}\\ -9 & 0 & 6\\3 & 2 & -6\end{vmatrix}\\&=\begin{vmatrix}  0 & 6\\2 & -6\end{vmatrix}\mathbf{i}-\begin{vmatrix}  -9 & 6\\3 & -6\end{vmatrix}\mathbf{j}+\begin{vmatrix}  — 9 & 0\\3 & 2\end{vmatrix}\mathbf{k}\\&=(0 — 12)\mathbf{i} -(54 — 18)\mathbf{j}+(-18- 0) \mathbf{k}\\&=-12\mathbf{i} -36\mathbf{j}-18\mathbf{k}\end{выровнено} 9{\circ}$?

$37,5$ N$\cdot$m

$37,5\sqrt{2}$ N$\cdot$m

$75$ N$\cdot$m

$75\sqrt{3}$ N$\cdot$m

4. Что из следующего показывает выражение для $\overrightarrow{A} \cdot \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ конец {выровнен}

$-17$

$-34$

$17$

$34$

5. Что из следующего показывает выражение для $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ end{align}

$-4 \mathbf{j}$

$-4 \mathbf{k}$

$-8 \mathbf{j}$

$-8 \mathbf{k}$

6. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $\overrightarrow{A} \cdot \overrightarrow{C}$?

18$

27$

36$

54$

7. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{C})$?

18$

27$

36$

54$

8. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $(\overrightarrow{A} \times \overrightarrow{C})\times \overrightarrow{B}$?

$ ​​-99\mathbf{i} -60\mathbf{j} +12\mathbf{k}$

$ ​​-33\mathbf{i} -20\mathbf{j} +6\mathbf{k}$

$ ​​33\mathbf{i} +20\mathbf{j} -6\mathbf{k}$

$99\mathbf{i} +60\mathbf{j} +12\mathbf{k}$

 

Изображения/математические чертежи создаются с помощью GeoGebra.

Предыдущий урок | Главная страница | Следующий урок

Скалярное произведение матрицы Объяснение

Данные собираются в различных форматах: от чисел до изображений, категорий и звуковых волн. Однако нам нужны числовые данные, чтобы анализировать их на компьютерах. Модели машинного обучения и глубокого обучения требуют больших объемов данных. Их производительность сильно зависит от объема данных. Таким образом, мы стремимся собрать как можно больше данных, чтобы построить надежную и точную модель. По мере увеличения объема данных операции, выполняемые со скалярами, становятся неэффективными. Нам нужны векторизованные или матричные операции для эффективного выполнения вычислений. Вот где на помощь приходит линейная алгебра.

Что такое скалярное произведение матрицы?

Скалярное произведение матрицы — это базовое вычисление линейной алгебры, используемое в моделях глубокого обучения для более эффективного выполнения операций с большими объемами данных. Это результат умножения двух матриц с совпадающими строками и столбцами, таких как матрица 3×2 и матрица 2×3. Его также можно рассчитать в NumPy с помощью операции np.dot.

Линейная алгебра — одна из самых важных тем в области науки о данных. В этом посте мы рассмотрим две основные, но очень важные операции линейной алгебры: скалярное произведение и умножение матриц. Эти базовые операции являются строительными блоками сложных моделей машинного обучения и глубокого обучения, поэтому важно понимать их.

 

Как найти скалярное произведение

Скалярное произведение двух векторов представляет собой сумму произведений элементов относительно положения. Первый элемент первого вектора умножается на первый элемент второго вектора и так далее. Сумма этих продуктов представляет собой точечный продукт, который можно сделать с помощью функции np.dot().

Давайте сначала создадим два простых вектора в виде массивов NumPy и посчитаем скалярное произведение.

Два пустых массива. | Изображение: Soner Yildirim

Скалярное произведение этих двух векторов представляет собой сумму произведений элементов в каждой позиции. В этом случае скалярное произведение равно (1*2)+(2*4)+(3*6) .

Скалярный продукт для двух массивов NumPy. | Изображение: Soner Yildirim

Поскольку мы умножаем элементы в одних и тех же позициях, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение.

Учебное пособие по основам скалярного произведения. | Видео 3Blue1Brown.

Подробнее о науке о данных: пошаговое объяснение анализа главных компонентов

 

Как рассчитать матрицу скалярного произведения

В науке о данных мы в основном имеем дело с матрицами. Матрица — это набор векторов строк и столбцов, объединенных структурированным образом. Таким образом, умножение двух матриц включает множество операций скалярного произведения векторов. Будет понятнее, когда мы рассмотрим несколько примеров. Давайте сначала создадим две матрицы 2×2 с помощью NumPy.

Два массива 2×2 Num{y. | Изображение: Soner YildirimДва массива 2×2. | Изображение: Soner Yildirim

Матрица 2×2 состоит из двух строк и двух столбцов. Индекс строк и столбцов начинается с нуля. Например, первая строка A (строка с нулевым индексом) — это массив [4,2]. Первый столбец A — это массив [4,0]. Элемент первой строки и первого столбца равен четырем. Мы можем получить доступ к отдельным строкам, столбцам или элементам с помощью следующего синтаксиса NumPy.

Синтаксис NumPy для доступа к первому столбцу и строке массивов. | Изображение: Сонер Йилдирим

Это важные понятия, которые необходимо понять, чтобы понять умножение матриц.

Умножение двух матриц включает скалярное произведение между первой строкой матрицы и столбцами второй матрицы. Первым шагом является скалярное произведение между первой строкой A и первым столбцом B. Результатом этого скалярного произведения является элемент результирующей матрицы в позиции [0,0] (т. е. первая строка, первый столбец).

Нахождение скалярного произведения двух матриц. | Изображение: Сонер Йилдирим

Таким образом, результирующая матрица C будет иметь (4*4) + (2*1) в первой строке и первом столбце. С[0,0] = 18 .

Следующим шагом является скалярное произведение первой строки A и второго столбца B.

Нахождение скалярного произведения первой строки A и второго столбца B. | Изображение: Soner Yildirim

C будет иметь (4*0) + (2*4) в первой строке и втором столбце. С[0,1] = 8 .

Первый ряд A готов, поэтому мы начинаем со второго ряда A и выполняем те же действия.

Продолжение процесса скалярного произведения, умножение второй строки A и первого столбца B. | Изображение: Soner Yildirim

C будет иметь (0*4) + (3*1) во второй строке и первом столбце. С[1,0] = 3 .

Последним шагом является скалярное произведение между второй строкой A и вторым столбцом B.

Заключительный шаг в процессе скалярного произведения, умножение второй строки A и второй строки B. | Изображение: Soner Yildirim

C будет иметь (0*0) + (3*4) во второй строке и втором столбце. С[1,1] = 12 .

Теперь мы видели, как это делается шаг за шагом. Все эти операции также можно выполнить с помощью операции np.dot :

Нахождение матрицы скалярного произведения с помощью операции np.dot. | Изображение: Soner Yildirim

Как вы помните из векторного скалярного произведения, два вектора должны иметь одинаковую длину, чтобы получить скалярное произведение. Каждая операция скалярного произведения в матричном умножении должна следовать этому правилу. Скалярные произведения выполняются между строками первой матрицы и столбцами второй матрицы. Таким образом, строки первой матрицы и столбцы второй матрицы должны иметь одинаковую длину.

Здесь я хочу подчеркнуть важный момент: длина строки равна количеству столбцов. Точно так же длина столбца равна количеству строк.

Рассмотрим следующую матрицу D:

Пример матрицы 3×2. | Изображение: Soner Yildirim

D имеет три строки и два столбца, поэтому это матрица 3×2. Длина строки равна двум, что является количеством столбцов, а длина столбца равно трем, что является количеством строк.

Длина строки и столбца для матрицы D. | Изображение: Сонер Йилдирим

Это длинное объяснение, но суть в том, что для выполнения матричного умножения количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.

Подробнее о науке о данных: 4 способа добавить столбец в Pandas

Например, мы можем умножить матрицу 3×2 на матрицу 2×3.

Умножение матриц 3×2 и 2×3 для получения матрицы скалярного произведения 3×3. | Изображение: Soner Yildirim

Форма результирующей матрицы будет 3×3, потому что мы выполняем три операции скалярного произведения для каждой строки A, а A имеет три строки.