«Комплексные числа и координатная плоскость»
Урок по алгебре в 10 классе
по учебнику А.Г. Мордковича, П.В. Семенова «Алгебра и начала анализа. Профильный уровень».
Цели урока:
— Помочь учащимся овладеть умением выполнять геометрическую интерпретацию комплексного числа, выполнять действия сложения и вычитания над комплексными числами в алгебраической и векторной форме;
— Развивать умения наблюдать, анализировать, обобщать;
— Прививать навыки самостоятельной работы.
Ход урока:
I. Организационный момент.
II. Повторение теоретического материала
1) Что называют комплексным числом?
(Комплексным числом называют сумму действительного числа и чисто мнимого числа z=- мнимая единица)
2) В каком случае выражения и считаются равными?
(Выражения и считаются равными тогда и только тогда, когда а=с и b=d)
3) При каком условии комплексное число отождествляется с действительным числом а?
(Каждое выражение вида а+0i отождествляется с действительным числом а)
4) Какое комплексное число называют мнимым числом?
(Комплексное число вида bi называют мнимым числом)
5) Какое комплексное число называют мнимой единицей?
(Комплексное число i называют мнимой единицей)
6)
Что
называют действительной частью, мнимой частью числа z=.
Как обозначают действительную часть, мнимую часть числа z=?
(Число а называют действительной частью числа
z= и обозначают , число b называют мнимой частью числа и обозначают Im z=b)
7) Что называют суммой комплексных чисел и ?
(Cуммой выражений и называют выражение (a+c)+(b+d)i)
8) Что называют разностью комплексных чисел и ?
(Разностью комплексных чисел и называют выражение )
III. Объяснение нового материала
1. Алгебраический способ изображения комплексных чисел.
1) Как известно,
действительные числа можно изображать точками числовой прямой. При этом,
каждому действительному числу соответствует единственная точка числовой прямой.
расстоянии в единиц длины (рис.1) Обратно, каждой рис.1
точке числовой прямой соответствует вполне определенное действительное число.
Например, точкам А и В соответствуют рациональные числа и -2, а точке С – иррациональное число.
Таким образом, множество всех действительных чисел находится во взаимно однозначном соответствии с множеством всех точек числовой прямой.
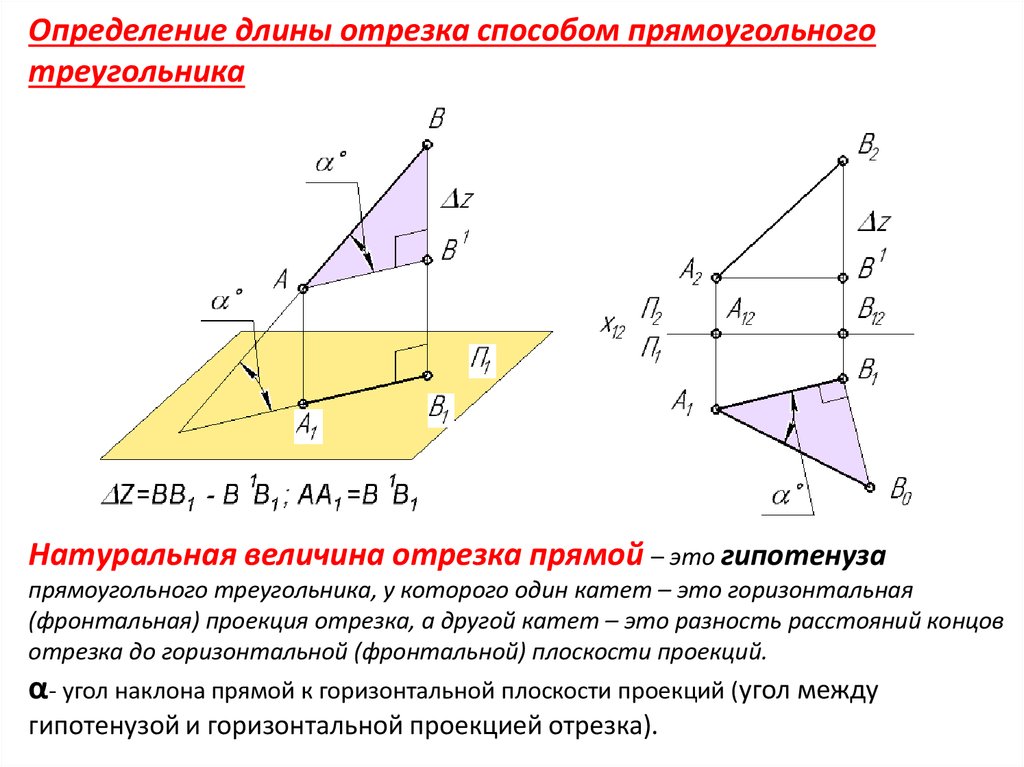
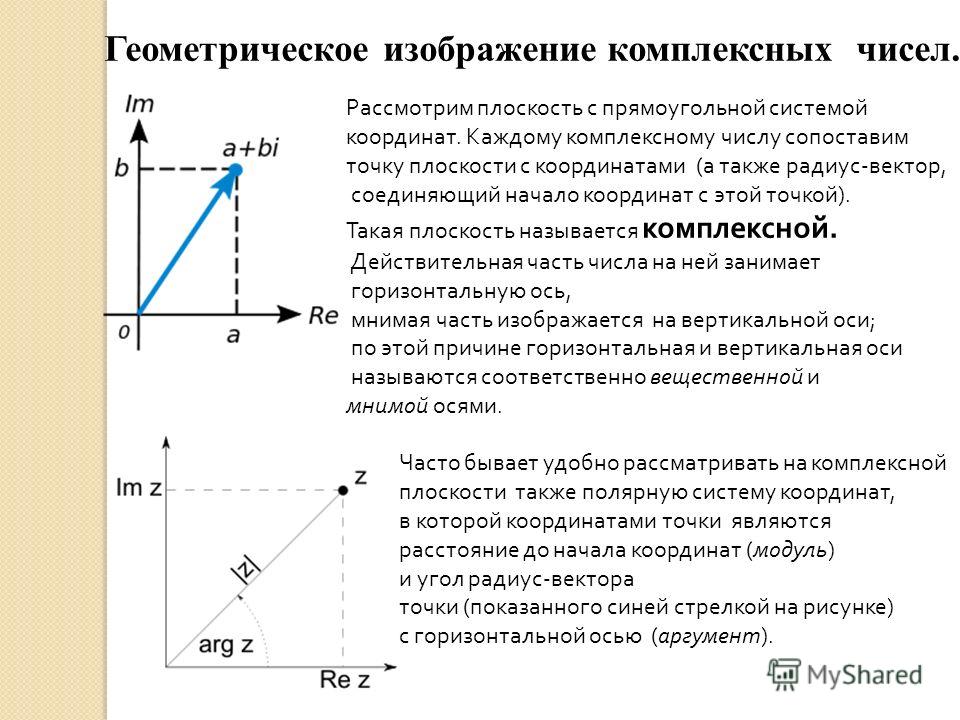
2) Подобно тому, как действительные числа можно изображать точками числовой прямой, комплексные числа можно геометрически представлять точками плоскости.
Пусть на плоскости задана
прямоугольная система координат.
Комплексное число изображается
точкой плоскости с координатами (рис.2).
Каждая точка плоскости имеет определенные координаты. Поэтому при выбранном соответствии каждой точке плоскости будет соответствовать некоторое комплексное число.
Например, точке А с координатами (2;3) соответствует число 2 +3i, точке В с координатами (-1;1) — число -1 + i, точке С с координатами (4;0) — число 4 +0i, а
точке D с координатами (0;-2) – число 0-2i (рис.3).
рис.3
3) Но не может ли случиться
так, что одной и той же точке плоскости, например, точке , будут соответствовать различные
комплексные числа. Например, и ? Если бы было так, то мы имели бы ; .
Отсюда . Но в таком случае, числа и были
бы равны между собой. Итак, каждому комплексному числу соответствует единственная точка
плоскости с координатами и, наоборот, каждой
точке плоскости с координатами соответствует единственное
комплексное число .
Таким образом, множество всех комплексных чисел находится во взаимно однозначном соответствии с множеством всех точек плоскости.
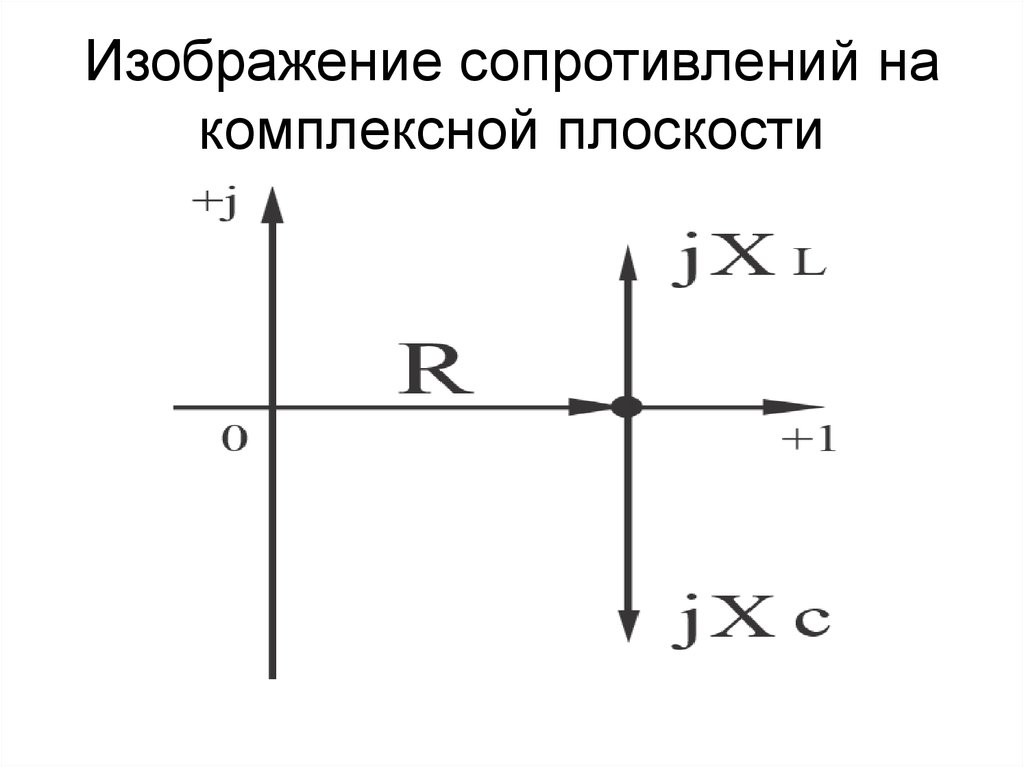
4) При такой интерпретации действительные числа а, т.е. комплексные числа вида а + 0i, изображаются точками с координатами (а;0), т.е. точками оси абсцисс. Поэтому ось абсцисс называют действительной осью. Чисто мнимые числа bi=0 + bi изображаются точками с координатами (0;b), т.е. точками оси ординат, поэтому ось ординат называют мнимой осью. При этом точка с координатами (0;b) обозначается bi. Например, точка (0;1) обозначается i, точка (0;-1) – это точка – i, точка (0;2) – это точка 2i. Начало координат — это точка О
( рис4).
рис.4 рис.5
Плоскость, на которой
изображаются комплексные числа, называется комплексной плоскостью.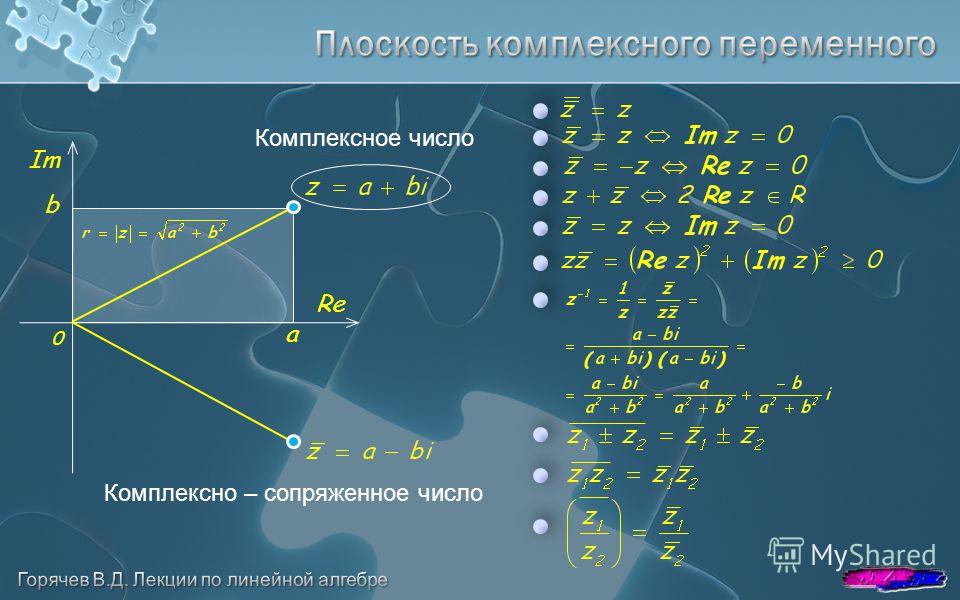
5) Пример. Изобразите на координатной плоскости множество всех комплексных чисел, у которых:
а) действительная часть равна -4;
б) мнимая часть является четным однозначным натуральным числом;
в) отношение мнимой части и действительной части равно 2;
г) сумма квадратов мнимой и действительной частей равна 9.
Решение.
а) нас интересуют комплексные числа , у которых х = — 4. Это уравнение прямой, параллельной оси ординат.
б) Нас интересуют комплексные числа , у которых у = 2,4,6,8. Геометрический образ состоит из четырех прямых, параллельных оси абсцисс.
в) Нас интересуют комплексные числа , у которых , или у=2х, х≠0. Это прямая, проходящая через начала координат.
Вывод:
— В чем же состоит алгебраический способ изображения комплексных чисел?
(Любую точку на координатной плоскости можно воспринимать как упорядоченную пару (а;b) действительных чисел).
2.
Векторный
способ изображения комплексных чисел.
Взаимно однозначное соответствие приводит к следующей геометрической интерпретации комплексных чисел: каждое комплексное число геометрически изображается на плоскости как А(а;b) или как вектор с началом в начале координат и с концом в точке А с координатами (а;b) (рис.6).
Рис.6
3. Действия над комплексными числами.
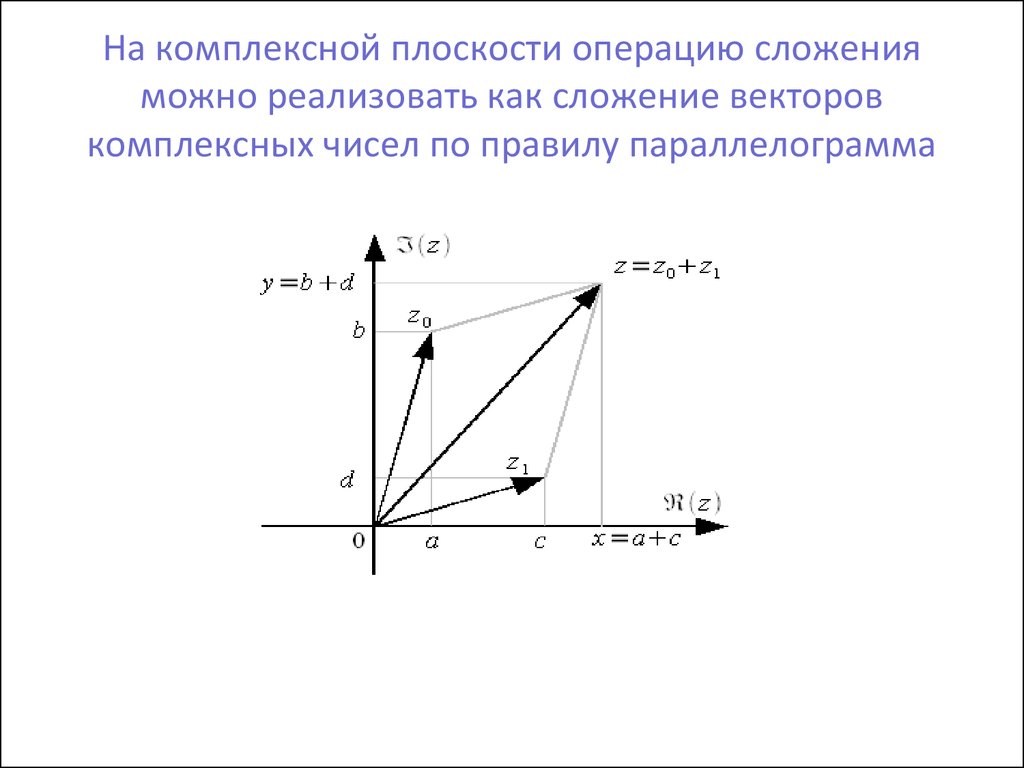
Пользуясь геометрическим изображением комплексных чисел с помощью векторов легко дать геометрическую интерпретацию сложения и вычитания комплексных чисел.
а) Геометрическое изображение суммы комплексных чисел.
Рассмотрим геометрическую
интерпретацию сложения двух комплексных чисел и . Сумма чисел и есть число Рассмотрим
векторы , конец которого находится в точке , , конец
которого находится в точке , и , конец которого находится в точке .
Вектор является
диагональю параллелограмма (рис.7).
Рис.7
Таким образом, сложение комплексных чисел и можно интерпретировать как правило сложение по правилу параллелограмма соответствующих им векторов и .
— С каким геометрическим преобразованием связана операция сложения комплексных чисел?
( Сложению комплексных чисел отвечает сложение векторов точек, изображающих эти числа на комплексной плоскости; отсюда следует, что отображение , сопоставляющее каждой точке z точку z+a, имеет простой геометрический смысл- оно является параллельным переносом на вектор, равный радиус-вектору точки А(а)).
б) Геометрическое изображение разности комплексных чисел.
Векторы, изображающие
противоположные комплексные числа и , симметричны относительно начала
координат, поскольку концы этих векторов – точки M(a;b) и N(-a;-b) – симметричны относительно начала
координат)(рис.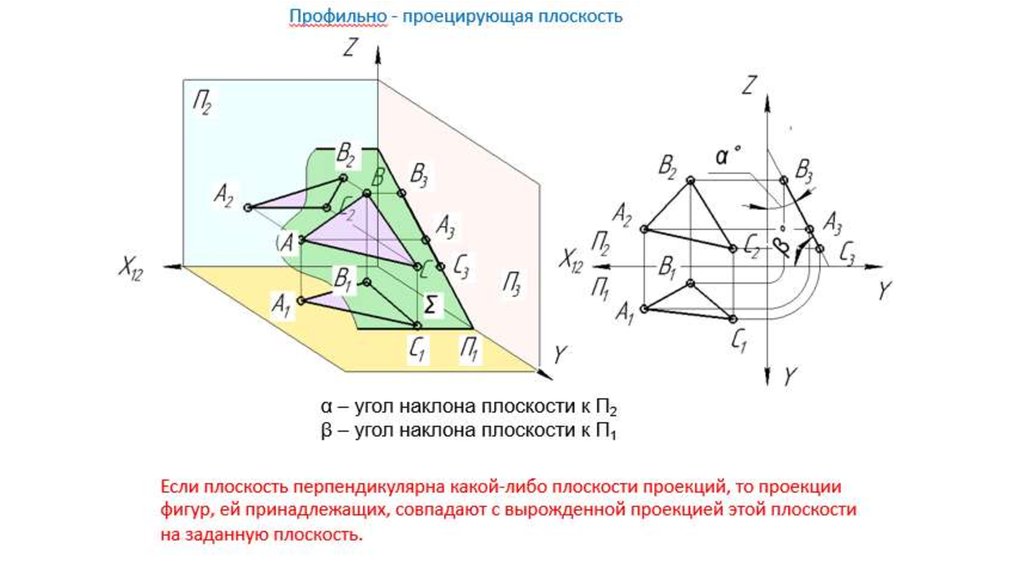
8).
Рис.8 рис.9
Пусть даны числа и . Так как , то вычитание из числа числа можно заменить прибавлением к числу числа, противоположного числу .
Рассмотрим векторы , конец которого находится в точке ; вектор , конец которого находится в точке , и , конец которого находится в точке (рис.9).
Построим параллелограмм . Тогда , т.е. вектор изображает разность комплексных чисел — . Так как также является параллелограммом, то . Это означает, что длина отрезка , соединяющего точки, соответствующие комплексным числам и , равна и модуль разности двух комплексных чисел и представляет собой расстояние между точками и , изображающими эти числа.
в) Геометрическое изображение сопряженных комплексных чисел.
В координатной плоскости ясный
геометрический смысл имеет операция сопряжения (перехода к сопряженному числу).
Значит, геометрическая операция сопряжения есть осевая симметрия относительно оси абсцисс. Сопряженные друг другу комплексные числа равноудалены от начала координат, а вектора, изображающие их, наклонены к оси абсцисс под одинаковыми углами, но расположены по разные стороны от этой прямой. Сложим, например, «по правилу параллелограмма» комплексные числа и , а затем отразим их, и весь параллелограмм симметрично относительно оси абсцисс. Получим: .
IV. Упражнения для закрепления
33.2 а) Отметьте на координатной плоскости точки, соответствующие комплексным числам = — 5 – 4i, = 1 + 8i, = -2-4i, =8 +I, = -1-8i.
б) Соедините заданные точки
последовательно отрезками. Сколько получилось точек пересечения с осями
координат? Запишите комплексные числа, которым соответствуют эти точки.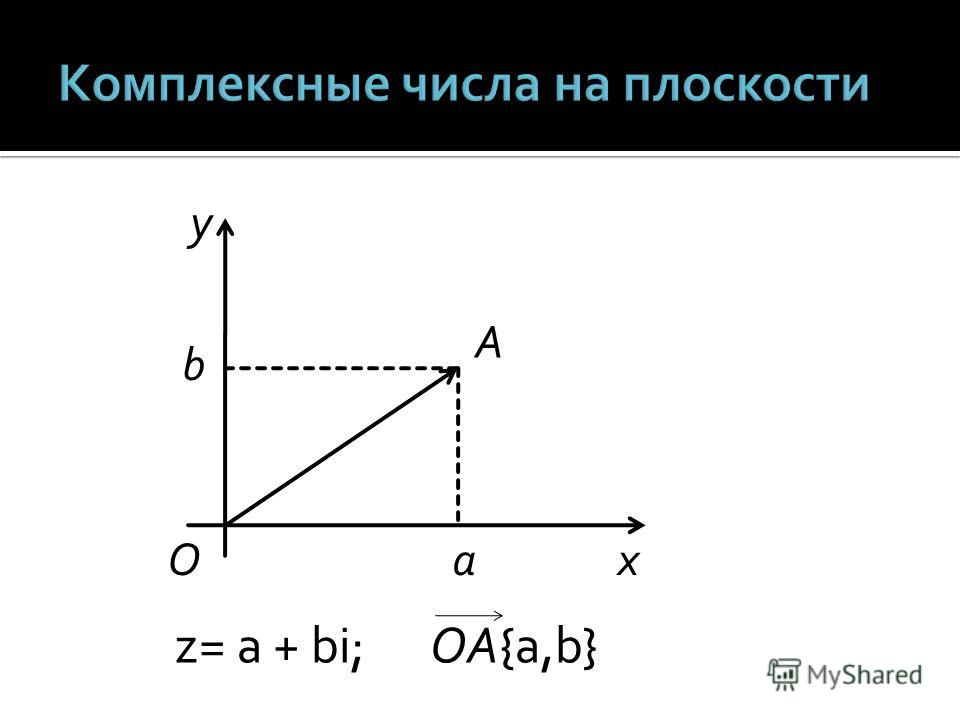
Решение.
-2; -1; 7; 2i; 4i; -3i; -6i.
33.6 Изобразите на координатной плоскости множество всех комплексных чисел z, удовлетворяющих условию:
а) действительная часть на 4 больше мнимой части;
б) сумма действительной и мнимой части равна 4;
в) сумма квадратов действительной и мнимой частей равна 4;
г) действительная часть равна квадрату мнимой части или квадрат действительной части равен мнимой части.
Решение.
а) Нас интересуют комплексные числа , у которых у=х-4-это уравнение прямой, проходящей через точки с координатами (0;-4) и (4;0).
33.15.
а) Изобразите на координатной плоскости числа =-3+i и =5+2i .
б) Найдите действительный коэффициент а, при котором — чисто мнимое число.
в) По правилу параллелограмма постройте сумму чисел и а из пункта б).
г) Найдите действительный коэффициент а, при котором — действительное число. По
правилу параллелограмма найдите сумму этих чисел.
Решение.
б) =-3+i и =5+2i; = 0+ уi; -3+5a=0; 5a=3; a=0,6.
в) 0,6=3+1,2i.
г) =-3+i и =5+2i; =х+0i; 1+2a=0; 2a=-1; a=-0,5.
-0,5=-2,5-i.
V. Самостоятельная работа
Вариант 1 1) Постройте точки, соответствующие комплексным числам: -1; 3+4i, 2-3i, -5+2i 2) Найти сумму и разность комплексных чисел и : а) = — 2 + i, = 3 +(-1) i, б) = 2 + 3i, = 2 + (-3) i, в) = 1 + (-2) i, = (-1) + (-2) i, г) = 3 i; = 2 + 0i, 3) Что представляет геометрическое множество всех комплексных чисел : а) х=2 б) Imz=2Rez в) -2≤x≤0 и 1≤у≤3.
| Вариант 2 1) Постройте точки, соответствующие комплексным числам: -8-7i, 2i, -3i, 1, 2) Найти сумму и разность комплексных чисел и : а) = 2 + (-1) i, = 0 + 2i, б) = -3, = 4i в) = 1 + (-2) i, = -1 + 2i, г) = 2 + (-2) i, = -1 + i. 3) Что представляет геометрическое множество всех комплексных чисел : а) 1 ≤ х ≤3; б) 0 ≤ у ≤ 2; в) Rez=Imz.
|
VI. Подведение итогов урока
— В чем состоит геометрическое изображение комплексных чисел?
— Какому геометрическому преобразованию плоскости соответствует сумма двух комплексных чисел?
— Как расположены точки комплексной плоскости, соответствующие числам a+bi и a-bi?
— Как расположены на комплексной плоскости точки, соответствующие противоположным числам z и -z?
— Во что переходит круг единичного радиуса с центром в начале координат при преобразовании ?
VII. Домашнее задание
§33 № 33.1: Отметьте на координатной плоскости точки, соответствующие комплексным числам.
№ 33.4: Изобразите на
координатной плоскости множество всех комплексных чисел z, удовлетворяющих заданным условиям.
Читать онлайн «Квантовый ум. Грань между физикой и психологией» — Минделл Арнольд — RuLit
5. Дальнейшее обсуждение можно найти в книге Карла Б. Бойера «История математики» (Carl. B. Boyer, A History of Mathematics), С. 611 и следующие.
6. Физик Дэвид Дарлинг приводит это утверждение о Галилее, которое вначале меня потрясло, в книге «Дзен физики» (David Darling. Zen Physics, Р. 123). Я был поражен потому, что процессуально-ориентированная психология, развитием которой я с увлечением занимался на протяжении многих лет, основывается на первичных и вторичных процессах, то есть процессах, с которыми отождествляемся и разотождествляемся. Для понимания людей необходимы и те, и другие.
7. Альберт Эйнштейн, «Смысл относительности», С. 1.
8. Все числа являются комплексными числами, и потому комплексные числа находятся на вершине иерархии.
Комплексные числа представляют собой сумму действительных и мнимых чисел. Мнимые числа – это действительные числа, умноженные на V-1. А действительные числа бывают рациональными или иррациональными.
8. Конъюгация означает осознанное сновидение
Если вы сохраняете свой ум достаточно активным, в то время как склонность к вхождению в БДГ-сон сильна, то вы чувствуете, что ваше тело засыпает, но вы, то есть ваше сознание, остается бодрствующим. В следующим момент вы понимаете, что находитесь в мире сновидения, полностью осознавая этот факт.
Стивен Лаберж, исследователь сновидений, в книге «Осознанное сновидение».
Продолжая наше путешествие, мы увидели, что математика комплексных чисел может помочь нам обдумывать то, как сознание входит в процесс наблюдения. Кроме того, математика может помогать нам наблюдать, как наше осознание влияет на субатомный мир и на все окружающее. Математика подобна тайному коду для взаимодействий между наблюдателем и наблюдаемым, и изучение того, как расшифровывать тайну, – это волнующее приключение.
В нем мы будем находить не только повседневную реальность, но и принцип осознанного сновидения, то есть сохранения осознания в сновидениях.
Помните идею комплексного поля? Это своего рода карта. Подобно тому, как, зная местоположение своего дома, вы можете найти его на карте к востоку, западу, северу или югу от центра вашего города, комплексные числа могут находиться на поле комплексных чисел, одна ось которого является действительной, а другая – мнимой. Например, на рис. 7.2 в главе 7 комплексное число 2 + 3i находится на расстоянии двух единиц вправо по оси действительных чисел и трех единиц вверх по оси мнимых чисел.
Конъюгаты и зеркальные отражения
В общем, любое комплексное число a + ib может быть представлено на поле комплексных чисел.
Рис. 8.1. Число a + ib на комплексной плоскости Теперь давайте пойдем дальше. Я хочу показать, как точка a + ib может отражаться на этой карте, то есть на комплексной плоскости.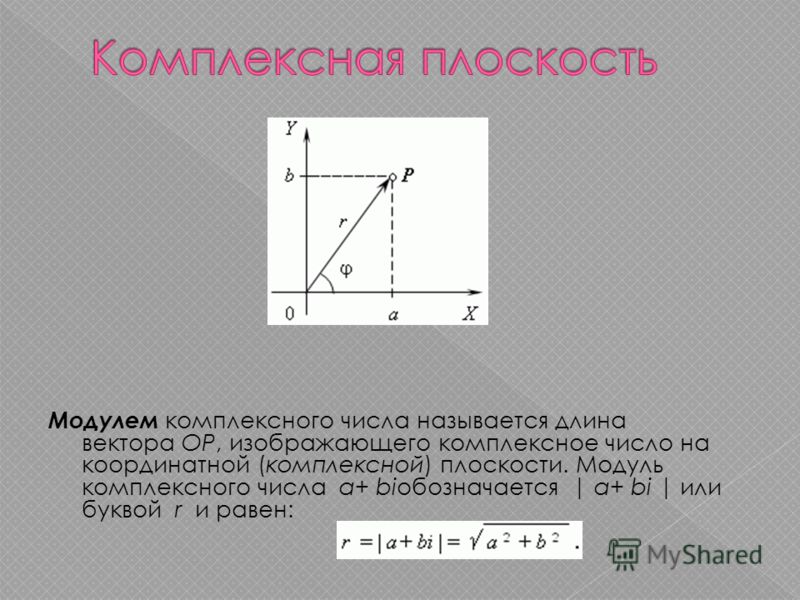
Представьте себе, что комплексная плоскость – это комната, на которую мы смотрим сверху. При взгляде сверху действительная ось выглядит как линия, соответствующая зеркальной стене.
Когда вы смотрите на себя сверху, кажется, что ваше отражение смотрит на вас снизу, то есть с другой стороны зеркала)
Рис. 8.2. Ваше отражение
Если бы вы стояли в точке a + ib, глядя в зеркало на стене, то видели бы собственное отражение в зеркале. Ваше отражение выглядело бы так, будто вы стоите в точке a – ib, на другой стороне зеркала, за стеной. Если бы вы стояли на расстоянии 3 метра от зеркала, то b было бы равно 3 м, а -b, где находится ваше отражение, соответственно, -3, то есть за зеркалом. Ваше зеркальное отражение – это более или менее то же самое, что и вы, за исключением того, что оно находится в точке —b, а не +b’.
Теперь вернемся к комплексной плоскости.
Точно так же, если бы вы стояли в точке a + ib, то видели бы свое зеркальное отражение стоящим в точке a – ib. Точка a – ib – это, так сказать, зеркальное отражение a + ib.
Математики называют это зеркальное отражение комплексного числа конъюгатом (или сопряженным комплексным числом. – примеч. пер.). Иными словами, если мы меняем знак перед i в комплексном числе a + ib на противоположный, то получаем его конъюгат a – ib. Если два комплексных числа различаются только знаком своих мнимых частей, то они представляют собой конъюгаты. Например 4 + 3i и 4 – 3i – это конъюгаты.
Средство просмотра графиков сложных функций
Средство просмотра сложных функций
Этот инструмент визуализирует любые комплексные функции.
функционировать как конформная карта, назначая цвет каждой точке в
комплексную плоскость в соответствии со значением функции в этой точке.
Введите любое выражение в z.
Функция идентификации z показывает, как назначаются цвета: серое кольцо на |z| = 1 и черный и белый кружок вокруг любого нуля и цветные круги вокруг 1, я, -1, и я. Шашки покрывают самолет в масштабе 1/16. единичная сетка. Цвета бирюзовые в положительное направление, красный в негативе, золотисто-зеленый к +i, пурпурный к -я, и темнее к бесконечности. Существует также цветной круг, направленный в бесконечность на |г| > 16 которое можно увидеть на любом полюсе в направлении бесконечности, например в 1/з. 92,з,12)
Конформные карты земного шара
Конформные карты берут свое начало в картографировании 18-го века,
когда новые математические разработки позволили картографам понять
как точно устранить локальные искажения формы на картах.
Нажмите кнопку ⊕ в нижней
правый угол, чтобы переключиться на конформное отображение поверхности
земли. Конформные карты сохраняют локальные углы везде,
хотя они могут искажать размеры для этого.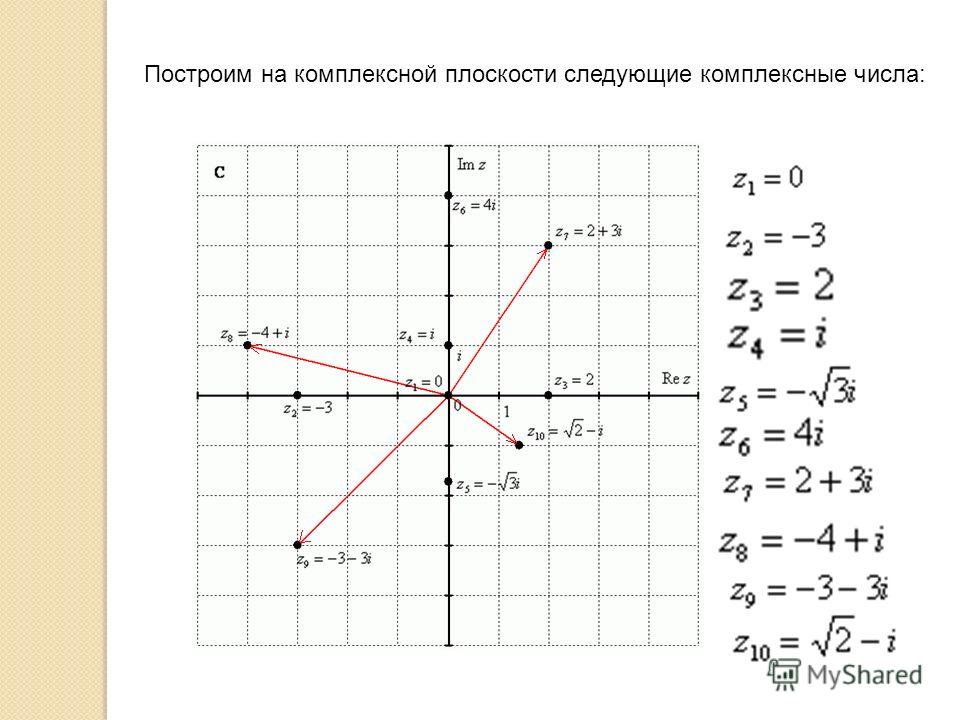
Проекция Меркатора является примером. Попробуйте: 92
Подробнее о конформных проекциях в картографии на
Красиво иллюстрированный Карлос А. Фурути
картографический сайт
Анимация конформных карт
Чтобы визуализировать отношения внутри семейств сложных функций, параметризуйте их переменными t, u, s, r или n. Инструмент будет отображать ряд сложных функций для значений параметра, настраиваемых с помощью ползунок или показано в прицеливании. Параметр t будет изменяться линейно от 0 до 1; u будет кружить по сложным единицам; s следует за синусоидой между -1 и 1; r следует по синусоиде от 0 до 1 и обратно; и n считает целые числа от 1 до 60. 93+t
На земном шаре, умножая на степени единства, мир вращается по кругу. оси:
u(z-i)/(z+i)
Поскольку вычисляется более 300 кадров, параметризованные выражения могут
нужно много времени, чтобы полностью отобразить.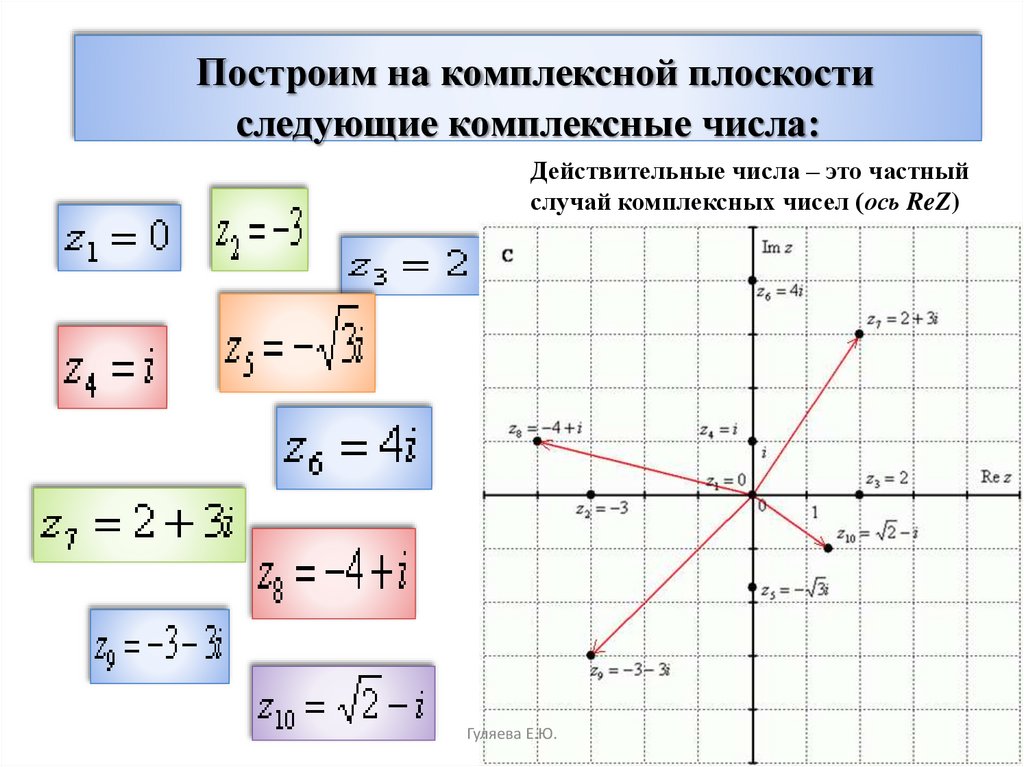
Грубый, размытый набросок рисуется быстро,
и более мелкозернистый рендеринг будет следовать в течение нескольких минут. Когда закончите,
кадры будут сглажены и анимированы со скоростью 24 кадра в секунду.
Простые семейства рациональных функций производят завораживающую анимацию:
9(n+1)/(n+1))Хорошо видны радиусы сходимости в последних двух примерах
инструмент по David BauГрафический калькулятор от MathLab: Руководство пользователя
Поиск ВВЕДЕНИЕ
Pro Features против бесплатной версии
Часто задаваемые вопросы, FAQS
1.1 Navigation
1,2 UI Элементы
1.3 Клавиля
1.4 Navigation
1,2 UI Элементы
1.3. Кнопки «Удалить», «Очистить» и «ОТМЕНА»
1.5 Рабочая область
1.6 Редактирование выражений/уравнений
1.7 Использование последнего ответа
1.8. Запись комментариев
1.9 CLEAR, Комиссии Копии и Вставки
1.10 РАБОТА
4.
1 2D-графика
4.2 3D-графика
4.3 Увеличение области графика
4.4 Изменение фона на белый
4.5 Скрытие клавиатуры
4.6 Градусная или радианная шкала
4.7 Фиксированная шкала
4.8 Шкала по оси R
4.9 Логарифмическая шкала
4.10 Отслеживание значений и наклонов графиков
4.11 Специальные точки: корни и критические точки
4.12 Пересечения графиков
4.13 Задать домен
4.15 Показать все — корни и критические точки
4.15 Показать все — корни и критические точки
5.1 Совместное использование функций
5.2 2D-таблица
5.3 3D-таблица
5.4 Функции редактирования
5.5 Прокрутка результатов
5.6 Результаты Precision
5.7 Элементы управления масштабированием
5.8 Сохранить и загрузить таблицу
5.9 Таблица тригонометрических функций в градусах
6.1 Десятиц
6.2 Фракции
6,3 Пресцены
6,4 Научная нотация
6,5 Инженерная нотация
6,6 Закругление
6.
7 Интехнологические и фракционные детали
6.8 Заказ Операции
6,9 6,7 Постоянные и фракционные детали
6.8. Делитель
6.11 Модуль
6.12 Двоичные, восьмеричные, десятичные, шестнадцатеричные числа
6.13 Комплексные числа
6.14 Полярная форма комплексных чисел
6.15 Полярно-прямоугольные координаты
7.1 Arithmetic Operations
7.2 Exponents
7.3 Absolute Values
7.4 Variables
7.5 Evaluating Expressions
7.6 Polynomials
7.7 Roots
7.8 Logarithms
8.1 Linear Equation
8.2 Absolute Value Equation
8.3 Quadratic Equation
8.4 Cubic Equation
8.5 Polynomial Уравнение
8.6 Рациональное уравнение
8.7 Радикальное уравнение
8.8 Показательное уравнение
8.9 Логарифмическое уравнение
9.1 Символы неравенства
9,2 Линейное неравенство
9,3 Абсолютное неравенство в значении
9,4 Квадратичное неравенство
9,5 Полиномиальное неравенство
9,6 рациональное неравенство
9,7 Составные неравенства
9.
8 Неравенства
Неравенства
Неравенства
Неравенства
Неравенства
Неравенства
Неравенства
Неравенства
Уравнения
Уравнения
. неравенств
10.5 Графики систем неравенств
10.6 Решение неявных уравнений
11.1 Построение точек
11.2 Как графически отображать функции?
11,3 Установка прикладного домена
11,4 Линейная функция
11,5 Функция абсолютного значения
11,6 Квадратичная функция
11,7 Полиномиальная функция
11,8 Рациональная функция
11,9 Радикальная функция
11.10 Логариритмическая функция
11.11 Экспонентальная функция
11.10 11.10. Функция -wise
12.1 Операции с матрицами
12.2 Редактирование записей матрицы
12.3 Переменные матрицы
12.4 Матричные и векторные формы
12.5 Преобразование матрицы переменных в систему линейных уравнений
12.
6 Решение систем линейных уравнений с использованием матричных уравнений
13.1 Градусы и радианы
13.2 Тригонометрические функции и ее кратные
13.6 График тригонометрической функции
13.7 График гиперболической функции
13.8 График обратной функции
14.1 Конические сечения
14,2 Параметрические уравнения
14,3 Полярные графики
14,4 3D График
15.1 Право предел
15,2 Левый предел
15,3 Предел функции
15.4 Предел полинома
15.5 Предел предела реля
15.6 15.6.6.6.6.6. a Радикальная функция
15.7 Предел функции абсолютного значения
15.8 Предел тригонометрической функции
15.9 Предел экспоненциальной и логарифмической функций
15.10 Предел кусочной функции
15.11 Предел на бесконечности
15.12 Неопределенные формы
15.13 Предел гиперболической функции
16.1 Ключ первого производного
16.2 Второй производной ключ
16,3 Третий и более высокий производный ключи
16,4 Правила дифференцировки
16,5 Производители.
Тригонометрические, логарифмические и экспоненциальные функции
16.8 Дополнительные сведения о производных
17.1 Приращения
17.2 Производная функции df (или dy)
17.3 Производная функция df (f не в терминах x)
17,4 Частичные производные
17,5 Частичные производные более высокого порядка
17,6 Общая производные
18,1 Неопределенные интегралы
18,2 Определенные интегралы
19.1 Суммирование Новация
19.2. и Максимум
19,4 Факториал, nCr и nPr
19,5 Показатели центральной тенденции
19,6 Показатели изменчивости
19,7 Показатели положения
19,8 Двумерный анализ данных
20.1 Gamma Function
20.2 Logarithmic Gamma Function
20.3 Digamma Function
21.1 Arithmetics
21.2 Algebra
21.3 Trigonometry
21.4 Statistics
21.5 Calculus
Руководство пользователя, PDF для загрузки | ДАЛЕЕ: Введение> |
© 2011–2022, Mathlab Apps, LLC | calc@mathlab.