Онлайн комплексное число: Комплексные числа онлайн

Комплексные числа и квадратные уравнения

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Комплексные числа и
квадратные уравнения.
-решение квадратных уравнений на
множестве комплексных чисел;
-алгоритм извлечения квадратного
корня из комплексного числа;
-полезные следствия для формулы
корней квадратного уравнения
Квадратное уравнение с
действительными коэффициентами
?
На множестве С можно находить
корни любых квадратных уравнений!

• Как извлечь квадратный корень из
отрицательных действительных чисел?
• Решение квадратных уравнений с
действительными коэффициентами и D<0.
• Как извлечь квадратный корень из любого
комплексного числа? (в алгебраической и
тригонометрической форме записи).
• Решение квадратных уравнений с комплексными
коэффициентами.
Как извлечь квадратный корень из
отрицательных действительных чисел?
• Определение: квадратным корнем(корнем
второй степени) из комплексного числа z
называют комплексное число, квадрат
которого равен z.
Формула извлечения квадратного
корня из отрицательных
действительных чисел
Решение квадратных уравнений с
действительными коэффициентами и D<0.
• Важно знать!
Если у уравнения есть комплексный корень, то и
сопряжённое ему число – тоже является корнем
этого уравнения!
Сопряжённые числа
Как извлечь квадратный корень из любого
комплексного числа? (в алгебраической и
тригонометрической форме записи).
• Теорема: Если b≠0, то
Что равносильно системе условий:
Например:
Избежать громоздких вычислений
позволяет тригонометрическая форма
записи комплексного числа.
• Теорема:
Доказательство:
Всегда 2 корня!
=
=
=
Аналогично:
Важно запомнить!
При возведении комплексного числа в
квадрат – его аргумент удваивается!!!
Алгоритм извлечения квадратного
корня из комплексного числа:
1) Найти модуль ρ и аргумент α этого числа;
2) Провести окружность радиусом √ρ с центром
в начале координат;
3) Провести через начало координат прямую
под углом к положительному направлению
оси абсцисс;
4) Две точки пересечения проведённых
окружности и прямой – дают ответ.
1).
=
=
z
-2
2)-4).
-1
1
2
Решение квадратных уравнений с
комплексными коэффициентами.
• Так как множества
и
совпадают между
собой , то для решения квадратных уравнений
с комплексными коэффициентами можно
сохранить привычную формулу корней
квадратного уравнения:
Полезные следствия для формулы
корней квадратного уравнения:
• (теорема Виета)
Если Z1 и Z –корни квадратного уравнения
2
то
• (формула разложения квадратного трёхчлена
на линейные множители)
Если Z1 и Z –корни квадратного уравнения
2
то
Домашнее задание:
• §35 изучить
• № 35. 7
• № 35.12
• № 35.13

English     Русский Правила

Деление комплексных чисел в тригонометрической форме онлайн. Деление комплексных чисел в алгебраической форме

Определение:

Комплексное число =x – yi называется сопряженным числом по отношению кw =

x + yi .

Примеры сопряженных комплексных чисел:

–1 + 5i и –1 – 5i , 2 – 3i и 2 + 3i .

Для деления двух комплексных чисел в алгебраической форме, как правило, удобно числитель и знаменатель дроби домножать на число, сопряженное знаменателю .

Пример 4 Выполнить деление:= [домножаем числитель и знаменатель дроби на число, сопряженное знаменателю] =

Заметим, что
есть выражение, а не число, поэтому его нельзя рассматривать как ответ.

Пример 5 Выполнить действия:
=

=


=
.

Пример 6 Выполнить действия:
= [домножаем числитель и знаменатель дроби на числа, сопряженные обоим числам знаменателя] =

1. Извлечение квадратного корня из комплексного числа в алгебраической форме

Определение. Комплексное число

называется квадратным корнем из комплексного числаz , если
.

Пример 7 Вычислить
.

Решение. Пусть
= x + yi , тогда

Решим отдельно биквадратное уравнение:

Ответ:{‑3 + 4i ; 3 ‑ 4i }.

Другой способ решения возможен после введения тригонометрической формы записи комплексного числа (см. с. 14).

1. Решение линейных и квадратных уравнений для комплексных чисел

В области комплексных чисел верны те же формулы для решения линейных и квадратных уравнений, что и в области действительных чисел.

Пример 8 Решить уравнение: (‑2 ‑i )z = 3 +i .

Пример 9 Решить уравнение:
.

Решение. Воспользуемся формулой для нахождения корней квадратного уравнения:

Ответ:{‑2 +i ; ‑2 –i }.

Пример 10 Решить уравнение:
.

Решение:

Ответ:{1 ‑ 2i ; 1 –i }.

Пример 11 Решить уравнение:
.

Решение:

Вычислим
:

Составляем систему, приравнивая вещественные и мнимые части левой и правой частей равенства:

Ответ:{2;i }.

Пример 12 Решить систему уравнений:

Решение. Выражаем из первого уравнения системы переменнуюx через переменнуюy :

Домножаем числитель и знаменатель дроби на число, сопряженное знаменателю:

В числителе дроби раскрываем скобки и приводим подобные слагаемые:

Подставляем полученное значение переменной x во второе уравнение системы:

;

Ответ: {1 +i ; i }.

1. Тригонометрическая форма записи комплексных чисел

   1. Геометрическое изображение комплексных чисел

При изучении свойств комплексных чисел весьма удобной является их геометрическая интерпретация .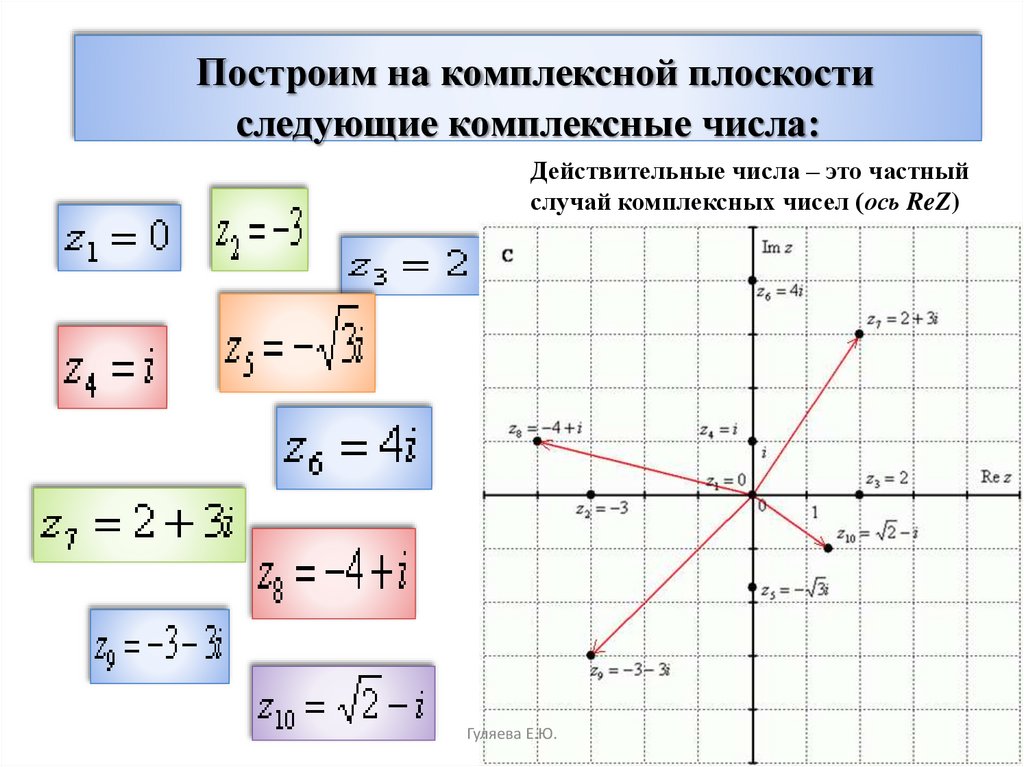

Поскольку комплексное число определяется как пара действительных чисел, то каждое комплексное число z = a + bi изображается точкой плоскости (x , y ) с координатамиx = a и y = b . Такая плоскость называется комплексной плоскостью , ось абсцисс ‑ действительной (Rez ), а ось ординат ‑ мнимой осью (Imz ).

Пример 13 Изобразить на плоскости точки, соответствующие числам:

Решение . У числаz 1 действительная часть равна ‑2, а мнимая ‑ 0. Следовательно, изображением числаz 1 служит точка (‑2, 0) (рис. 1.1).

У числа z 2 действительная часть равна 0, а мнимая равна 3. Следовательно, изображением числа

z 2 служит точка (0, 3). У числаz 3 действительная часть равна 1, а мнимая ‑4. Следовательно, изображением числаz 3 служит точка (1, ‑4).

У числа z 4 действительная часть равна 1 и мнимая 1. Следовательно, изображением числаz 4 служит точка (1, 1).

У числа z 5 действительная часть равна ‑3, а мнимая ‑2. Следовательно, изображением числаz 5 служит точка (‑3, ‑2).

Сопряженные числа изображаются точками на комплексной плоскости, симметричными относительно действительной оси Rez .

В соответствии с определением деления действительных чисел устанавливается следующее определение.

Определение. Разделить комплексное число a + bi на комплексное число a» + b»i — значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.

Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di)=

Пример 1. Найти частное (7 — 4i):(3 + 2i).

Записав дробь (7 — 4i)/(3 + 2i), расширяем её на число 3 — 2i, сопряженное с 3 + 2i. Получим:

((7 — 4i)(3 — 2i))/((3 + 2i)(3 — 2i)) = (13 — 26i)/13 = 1 — 2i.

Пример 1 предыдущего пункта даёт проверку.

Пример 2. (-2 +5i)/(-3 -4i) = ((-2 + 5i)(-3 — 4i))/((-3 — 4i)(-3 + 4i)) = (-14 -23i)/25 = -0,56 — 0.92i.

Чтобы доказать, что правая часть действительно является частным, достаточно помножить её на a» + b». Получим a + bi.

Решение уравнений с комплексными переменными

комплексный число сложение переменная

Рассмотрим сначала простейшее квадратное уравнение z2 = a, где а — заданное число, z — неизвестное. На множестве действительных чисел это уравнение:

• 1) имеет один корень z = 0, если а = 0;
• 2) имеет два действительных корня z1,2 = , если а>0;
• 3) не имеет действительных корней, если а

На множестве комплексных чисел это уравнение всегда имеет корень.

Задача 1. Найти комплексные корни уравнения z2 = a, если:

• 1) а = -1; 2) а = -25; 3) а = -3.
• 1) z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2 — i2 = 0. Отсюда, раскладывая левую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i. Ответ. z1,2 = i.
• 2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение:

z2 = i2 52, z2 — 52 i2= 0, (z-5i)(z+5i) = 0, откуда z1 = 5i, z2 = -5i.Ответ:

3) z2 = -3, z2 = i2()2, z2 — ()2i2 = 0, (z — i)(z + i) = 0

Ответ: z1,2 = i.

Вообще уравнение z2 = a, где а

Используя равенство i2 = -1, квадратные корни из отрицательных чисел принято записывать так: = i, = 2i, = i .

Итак, определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с — действительные числа, а 0, имеет корни. Эти корни находятся по известной формуле:

Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 = = = 2 3i.

Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.

Число 4 — это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13- свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 — корни уравнения az2+bz+c = 0, z1+z2 = , z1z2 = .

Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i.

Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим

P=-(z1+z2)=2, q=z1z2=5. Ответ z2-2z+5=0.

i и наоборот путем вычисления значений модуля и главного аргумента комплексного числа.

Результаты

Экспоненциальная форма комплексного числа — dCode

Теги: Арифметика, Геометрия

Поделиться

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным помощником в играх, головоломках и геокэшинге задачи решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Преобразователь комплексных чисел

Из комплексного числа a+ib

Комплексный номер z (формат a+ib)

Из декартовых координат (значения a и b в a+ib)

Значение а=
Значение б=

Из полярных координат (модуль и аргумент)

Значение r (модуль)
Значение θ (аргумент/угол)

См. {i \theta} $$ 9{i\theta } = \cos {\theta} + i \sin {\theta} $$ with $ \theta \in \mathbb{R} $

Как преобразовать декартовы координаты в полярные координаты?

Преобразование комплексных декартовых координат в комплексные полярные координаты для комплексных чисел $z = ai + b$ (с $(a,b)$ декартовыми координатами) как раз и состоит в том, чтобы записать это число в комплексно-показательной форме, чтобы получить модуль $r$ и аргумент $\theta$ (с $(r,\theta)$ полярными координатами). 9{i(-\pi/2)} = \cos{-\pi/2} + i\sin{-\pi/2} = -i $

Исходный код

Исходный код формы». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Экспоненциальная форма сложного числа», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Комплексного Числовая экспоненциальная форма» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Экспоненциальной формы комплексного числа» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Экспоненциальная форма комплексного числа» или любых ее результатов разрешена, если вы цитируете dCode!
Цитировать как источник (библиографию):
Экспоненциальная форма комплексного числа на dCode.fr [онлайн-сайт], получено 27 ноября 2022 г., https://www.dcode.fr/complex-number-exponential-form

Сводка

• Преобразователь комплексных чисел
• Что такое экспоненциальная форма комплексного числа? (Определение)
• Что такое формула Эйлера?
• Как преобразовать декартовы координаты в полярные координаты?
• Каковы свойства комплексного возведения в степень?

Similar pages

• Complex Number Modulus/Magnitude
• Complex Number Argument
• Pythagore Triple
• Complex Number Affix
• Product ∏
• Base N Convert
• Closest Prime Number
• DCODE’S TOOLS LIST

Support

• PayPal
• Patreon
• Подробнее

Форум/Справка

Ключевые слова

Экспоненциал, нотация, аргумент, модуль, комплекс, номер

.

Комплексные и мнимые числа | Бесплатный онлайн-курс

Это увлекательный курс, специально разработанный для обучения вас чисто мнимым числам. При работе с мнимыми числами следует узнать о сложении, вычитании и других операциях над мнимыми числами. Этот курс также анализирует концепции поля комплексных чисел. Если вас спросят о комбинировании чисто мнимых чисел с действительными числами, вы должны знать, что для этого необходимо поле комплексных чисел. Например, для выполнения алгебраических операций с мнимым числом «i» необходимо понимать, как возводить «i» в любую степень. Знаете ли вы, что комплексная плоскость состоит из действительной числовой прямой и числовой прямой для всех чисто мнимых чисел? Приготовьтесь узнать о сопряжениях и делении комплексного числа, рационализации знаменателей, домене и диапазоне отношения, а также тесте вертикальной и горизонтальной линии для функции. Точно так же вы должны узнать об алгебраических правилах умножения двух двучленов, множественных способах представления функции, а также о поведении и характеристиках функций.

Если вы хотите узнать о различных типах специальных функций и их свойствах, вам следует пройти этот курс. Вы сможете идентифицировать другие специальные функции по их уравнениям и построить их графики. Мы рассмотрим различия между константными и тождественными функциями, поможем вам понять алгебраические определения функций абсолютного значения и научим вас свойствам линейной функции и функции наибольшего целого числа. Знаете ли вы, что при построении графика квадратичной функции полученная фигура называется «параболой»? Чтобы лучше понять параболу, вам также необходимо понять вершину и ее координаты. Также крайне важно, чтобы вы узнали об особенностях и различиях между полиномиальными и рациональными функциями. Уравнение и график экспоненциальной функции также будут широко освещены, наряду с различиями, областью, свойствами и правилами кусочных и сигнум-функций.

Изучение того, как выполнять различные арифметические операции и вычислять обратную функцию, бросит вызов вашему мышлению и завершит курс.