Умножить матрицы: Онлайн калькулятор. Умножение матриц

Содержание

Лекции по алгебре

ПРЕДИСЛОВИЕ
ГЛАВА I. ЦЕЛЫЕ ЧИСЛА
§ 1. Теория делимости целых чисел
2. Деление с остатком.
3. Наибольший общий делитель.
4. Алгоритм Евклида.
5. Взаимно простые числа.
6. Простые числа.
§ 2. Теория сравнений
2. Действия над классами.
3. Приведенная система вычетов и примитивные классы.
§ 3. Некоторые общие понятия алгебры
2. Кольца и поля.
3. Изоморфизм.
ГЛАВА II. КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Обоснование комплексных чисел
3. Свойства действий.
4. Возвращение к обычной форме записи.
5. Вычитание и деление комплексных чисел.
§ 2. Тригонометрическая форма комплексного числа
2. Модуль и аргумент комплексного числа.
3. Тригонометрическая запись комплексного числа.
4. Неравенства для модуля суммы и модуля разности двух комплексных чисел.

5. Умножение комплексных чисел в тригонометрической записи.
6. Возведение комплексного числа в степень с целым показателем и формула Муавра.
7. Применения формулы Муавра к преобразованиям тригонометрических выражений.
§ 3. Извлечение корня из комплексного числа
2. Исследование формулы извлечения корня.
3. Извлечение квадратного корня.
§ 4. Корни из единицы
§ 5. Показательная и логарифмическая функции комплексной переменной
ГЛАВА III. ПРОСТЕЙШИЕ СВЕДЕНИЯ ОБ АЛГЕБРЕ ПОЛИНОМОВ
§ 1. Полиномы от одной буквы
2. Высший член и степень полинома.
3. Степени элемента в ассоциативном кольце.
4. Значение полинома.
5. Схема Хорнера и теорема Безу.
6. Число корней полинома в коммутативной области целостности.
7. Теорема о тождестве.
§ 2. Алгебраическое решение уравнений третьей и четвертой степени
2. Исследование формулы Кардано.
3. Решение уравнений четвертой степени.
§ 3. Полиномы от нескольких букв

3. Теорема о тождестве.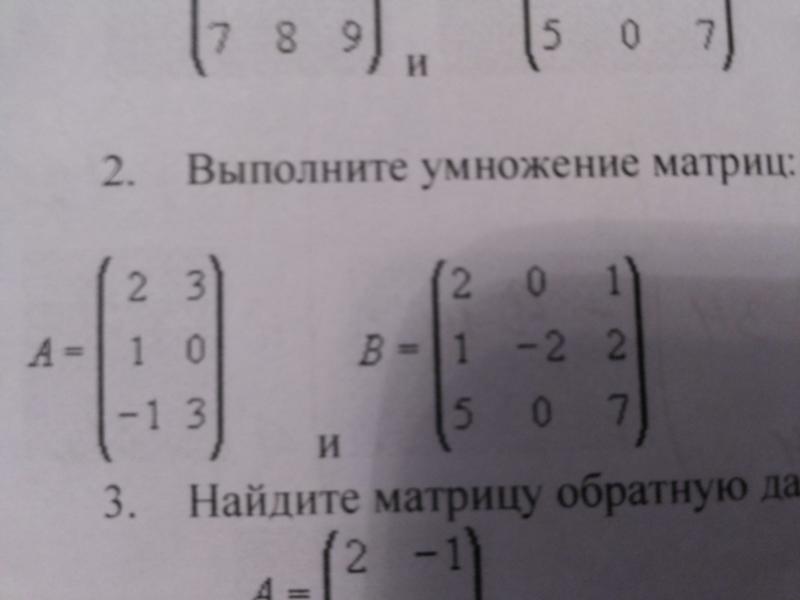

4. Теорема о несущественности алгебраических неравенств.
ГЛАВА IV. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
§ 1. Матрицы и действия над ними
2. Сложение матриц и умножение матрицы на число.
3. Умножение матриц.
4. Транспонирование матриц.
5. Обзор действий над матрицами.
§ 2. Теория определителей
2. Элементарные сведения теории перестановок.
3. Определитель порядка n. Определение.
4. Свойства определителя.
5. Алгебраические дополнения и миноры.
6. Вычисление определителей.
7. Определитель Вандермонда.
9. Некоторые следствия из теоремы Крамера.
§ 3. Линейная зависимость и линейная независимость строк (столбцов)
2. Линейные зависимости столбцов матрицы с линейно зависимыми строками.
3. Теорема о линейной зависимости линейных комбинаций.
4. Базис и ранг совокупности строк.
5. Линейно эквивалентные совокупности строк.
6. Ранг матрицы.
7. Условие линейной зависимости множества строк квадратной матрицы.
8. Ранг матрицы в терминах определителей.

9. Определение ранга матрицы при помощи элементарных преобразований.
§ 4. Системы линейных уравнений общего вида
§ 5. Дальнейшие свойства определителей
2. Умножение матриц, разбитых на клетки.
3. Умножение матрицы на вспомогательную матрицу как линейное преобразование строк (столбцов).
4. Определитель произведения двух квадратных матриц.
5. Примеры применения теоремы об определителе произведения квадратных матриц к вычислению определителей.
6. Теорема Бине — Коши.
§ 6. Обращение квадратных матриц
§ 7. Характеристический полином матрицы
2. Теорема Кэли—Гамильтона.
ГЛАВА V. КВАДРАТИЧНЫЕ ФОРМЫ
§ 1. Преобразование квадратичной формы к каноническому виду линейной подстановкой букв

§ 2. Закон инерции квадратичных форм
2. Критерий Сильвестра положительности квадратичной формы.
3. Закон инерции квадратичных форм.
§ 3. Ортогональное преобразование квадратичной формы к каноническому виду
2. Собственные значения вещественной симметричной матрицы.

3. Построение ортогональных матриц.
4. Ортогональное преобразование квадратичной формы к каноническому виду.
5. Коэффициенты канонического вида квадратичной формы и столбцы преобразующей ортогональной матрицы.
6. Одновременные преобразования двух квадратичных форм к каноническому виду.
§ 4. Эрмитовы формы
2. Свойства эрмитовых форм.
ГЛАВА VI. ПОЛИНОМЫ И ДРОБИ
§ 1. Теория делимости для полиномов от Одной буквы
§ 2. Производная
2. Разложение полинома по степеням линейного двучлена.
3. Разделение множителей различной кратности.
§ 3. Рациональные дроби
2. Поле частных.
3. Правильные рациональные дроби.
4. Разложение рациональной дроби на простейшие.
5. Разложение рациональной дроби на простейшие над полем С комплексных чисел.
6. Разложение рациональной дроби на простейшие над полем R вещественных чисел.
7. Разложение на простейшие правильной рациональной дроби, знаменатель которой разложен на попарно простые линейные множители.

§ 4. Интерполяция
2. Интерполяционная формула Лагранжа.
3. Способ интерполяции Ньютона.
4. Приближенная интерполяция.
ГЛАВА VII. СРАВНЕНИЯ В КОЛЬЦЕ ПОЛИНОМОВ И РАСШИРЕНИЯ ПОЛЕЙ
§ 1. Сравнения в кольце полиномов над полем
§ 2. Расширение полей
2. Конструирование простых расширений.
ГЛАВА VIII. ПОЛИНОМЫ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ПОЛИНОМЫ НАД ФАКТОРИАЛЬНЫМИ КОЛЬЦАМИ
§ 1. Полиномы с целыми коэффициентами
§ 2. Полиномы от одной буквы над факториальным кольцом

ГЛАВА IX. РАСПРЕДЕЛЕНИЕ КОРНЕЙ ПОЛИНОМА
§ 1. Существование корней в С
§ 2. Распределение корней на плоскости комплексной переменной
2. Принцип аргумента.
3. Теорема Руше.
4. Непрерывность корней полинома.
§ 3. Распределение вещественных корней полинома с вещественными коэффициентами
2. Теорема Штурма.
3. Построение ряда Штурма.
§ 4. Обобщенная теорема Штурма
§ 5. Приближенное вычисление корней полинома
2. Метод непрерывных дробей.
ГЛАВА X. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
§ 2.

Нормальные подгруппы и факторгруппы
§ 3. Гомоморфизм
§ 4. Прямое произведение групп
§ 5. Группы преобразований
2. Классы сопряженных элементов.
3. Строение однородных пространств.
4. К теории подстановок.
5. Примеры из геометрии.
6. Централизатор элемента и нормализатор подгруппы.

7. Центр p-группы.
8. Преобразования.
9. Автоморфизмы группы.
§ 6. Свободная группа
§ 7. Свободные произведения групп
§ 8. Конечные абелевы группы
§ 9. Конечно порожденные абелевы группы
ГЛАВА XI. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ
§ 1. Выражение симметрических пэлииов через основные
§ 2. Значения симметрических полиномов от корней полинома
2. Степенные суммы.
3. Дискриминант полинома.
4. Алгебраическое решение уравнений третьей и четвертой степени в свете теории симметрических полиномов.
§ 3. Результант
2. Другой способ построения результанта.
3. Линейное представление результанта.
4. Применение результанта к исключению неизвестного из системы двух алгебраических уравнений с двумя неизвестными.

5. Связь дискриминанта полинома с результантом полинома и его производной.
ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА
2. Линейные комбинации, линейная зависимость и линейная независимость.

3. Координаты вектора.
4. Замена базиса и преобразование координат.
§ 2. Подпространства
3. Прямая сумма подпространств.
4. Относительная линейная независимость и относительный базис.
5. Факторпространство.
§ 3. Линейные функции
§ 4. Линейные отображения векторных пространств
§ 5. Линейные операторы в векторном пространстве
2. Действия над операторами.
3. Инвариантные подпространства.
4. Циклическое подпространство и минимальный аннулятор вектора.
5. Матрица оператора на циклическом подпространстве и ее характеристический полином.
6. Минимальный полином оператора.
7. Разложение пространства с оператором в прямую сумму примарных подпространств.
8. Разложение примарного пространства в прямую сумму циклических примарных подпространств.
9.

Модули над кольцом главных идеалов.
10. Некоторые следствия.
11. Каноническая форма матрицы оператора.
12. Оператор проектирования.
13. Полуобратные линейные отображения.
§ 6. Операторы в векторных пространствах над полем С комплексных чисел
2. Корневые векторы.
3. Нильпотентный оператор.
4. Каноническая форма Жордана матрицы оператора.
5. Пример.
§ 7. Операторы в векторных пространствах над полем R вещественных чисел
ГЛАВА XIII. ЕВКЛИДОВО И УНИТАРНОЕ ПРОСТРАНСТВА
1. Скалярное произведение.
§ 2. Подпространства унитарного (или евклидова) пространства
§ 3. Пространства, сопряженные с евклидовым и унитарным пространствами
§ 4. Операторы в унитарном пространстве
§ 5. Операторы в евклидовом пространстве
§ 6. Преобразование уравнения гиперповерхности второго порядка к каноническому виду
§ 7. Линейные отображения унитарного пространства в унитарное
§ 8. Объем параллелепипеда в евклидовом пространстве
ГЛАВА XIV. ЭЛЕМЕНТЫ АЛГЕБРЫ ТЕНЗОРОВ

§ 2.

Действия над тензорами
§ 3. Симметричные и антисимметричные тензоры
§ 4. Тензорные произведения векторных пространств
ГЛАВА XV. АЛГЕБРЫ
1. Определение и простейшие свойства алгебр.
2. Структурные константы алгебры.
3. Некоторые классы алгебр.
4. Идеалы алгебры.
5. Присоединение единицы.
6. Вложение ассоциативной алгебры в алгебру матриц.
§ 2. Алгебра кватернионов
§ 3. Внешняя алгебра
СПИСОК ЛИТЕРАТУРЫ

Умножение матрицы на скаляр. Сложение и вычитание матриц. Умножение матриц. Транспонирование матриц

Другие предметы \ Радиотехника

Страницы работы

18 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Содержание

Задание к курсовой работе . …………………………2

Теоретическая часть :

1. Умножение матрицы на скаляр ……………………3

2. Сложение и вычитание матриц ……………………3

3. Умножение матриц ……………………………..4

4. Транспонирование матриц ……………………….5

5.Поиск максимального (минимального) элемента матрицы .6

6. Формирование вектора из элементов матрицы ……….7

Блок-схема алгоритма решения задачи …………………9

Программа решения задачи ………………………….13

Результаты вычисления по программе …………………16

Краткие выводы по решению задачи …………………..17

Список используемой литературы …………………….18

Задание к курсовой работе

Составить программу вычисления и преобразования матрицы D=F(A,B,C), где F(A,B,C) -матричное выражение А,В,С-исходные матрицы размер и значение элемнтов которых выбираются произвально.

Выражение для расчёта матрицы D и действия по её преобразованию выбираются из таблицы № 1 и №2 в соответствии с номером варианта задания.

В программе предусмотреть вывод на печать всех исходных, промежуточных и разультирующих матриц, а также результатов преобразования

Таблица №1

D= (2*A*B^T-С)^T

Таблица №2

Определить количество элементов, удовлетворяющих условиям:

1) Pij>Q1 2)Pij<Q2 3)Q2<=Pij<=Q1.

Значения Q1 и Q2 выбрать произвольно

1. Умножение матрицы на скаляр

Чтобы умножить матрицу на скаляр, необходимо каждый элемент этой матрицы умножить на скаляр. Например, если требуется вычислить А=d*В, где А и В матрицы, d — скаляр, то каждый элемент матрицы А определяется по формуле а_ij = в*в_ij; i = 1, 2,…, n; j = 1, 2,…, m, (1)

где n, m — размеры матриц.

Алгоритмы умножения матрицы на скаляр представлен на рис.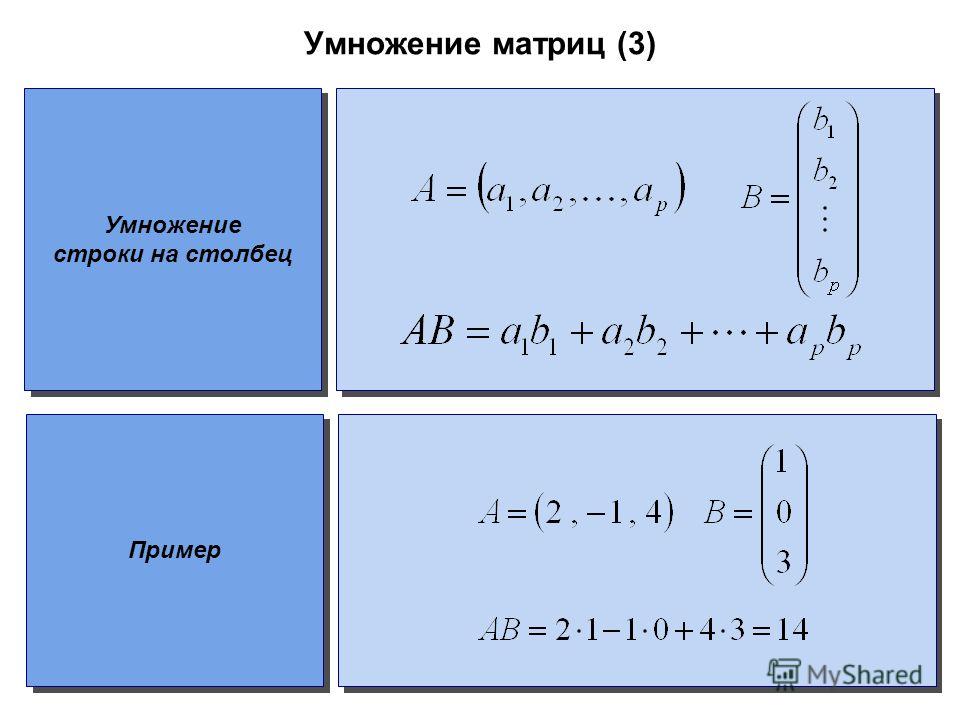 1. Здесь центральный оператор вычисления очередного элемента матрицы-произведения (блок 4) является телом двойного цикла по строкам (i) и столбцам (j).

Рис. 1

Входные параметры матрица В(n,m) скаляр d

ВХОД

i=I,(1),n

j=I,(1),m

A_ij =d*B_ij

ВЫХОД

2. Сложение и вычитание матриц

Чтобы сложить (вычесть) две матрицы, необходимо сложить (вычесть) соответствующие элементы этих матриц. Например, если требуется вычислить С = А⁺В, где А и В — матрицы, то каждый элемент матрицы С определяется по формуле с_ij= a_ij⁼b_ij ; i = 1, 2,…, n ; j = 1, 2,…, m, (2)

где n, m — размеры матриц.

Из выражения (2) следует, что складывать (вычитать) можно только матрицы одинакового размера. Алгоритм сложения (вычитания) матриц будет таким же, как на рис. 1, если в блоке 4 вместо формулы (1) записать формулу (2). при этом соответственно изменятся и выходные параметры.

3. Умножение матриц

При перемножении матриц каждый элемент матрицы-произведения определяется как сумма произведений элементов строки матрицы-множителя [1]. Например, если требуется вычислить C = A*B, где A и B — матрицы, то каждый элемент матрицы С определяется по формуле

С_ij = a_ik * b_kj , i = 1, 2,. .., n ; j = 1, 2,…, m, (3)

k=1 где n — число строк матрицы А;

i — число столбцов матрицы B;

m — число столбцов матрицы А или число строк матрицы В. Из (3) следует, что перемножать можно только такие матрицы, у которых число столбцов матрицы-множимого равно числу строк матрицы-множителя, т.е.

a_{ij nm} * b_{ij nl} = c_{ij nl}.

Блок-схема алгоритма перемножения матриц представлена на рис. 2. Здесь каждый элемент матрицы-произведения вычисляется в блоках 4-7 как сумма произведений. В блоке 4 сумма сбрасывается в ноль, в блоке 6 производится непосредственное суммирование произведений, в блоке 7 накопленная сумма записывается в выходной массив.

Рис. 2

Входные параметры матрица А(n,m), В(n,l)

ВХОД

i=I,(1),n

j=I,(1),m

S=0

Информация о работе

Скачать файл

Объяснение урока: Скалярное умножение матриц

В этом объяснении, мы научимся умножать скаляр на матрицу и определять свойства их размножения.

Матрица содержит массив чисел, упорядоченных по строкам и столбцам. До мы можем научиться использовать матрицы для практических приложений, мы должны сначала знать, как выполнять операции с матрицами. В этом объяснении мы сосредоточимся на скалярное умножение.

Скаляр относится к одному числу, например, −2 или 13. Как умножить матрицу, массив числа, на масштаб -2 или на 13? Давайте начнем с определение этой алгебраической операции для общих матриц.

Определение: скалярное умножение

Для матрицы порядка 𝑚×𝑛, определенной как 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ 𝑎𝑎𝑎 ⋯ ⋮⋮ ⋱ ⋮ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠,  Мы можем завершить «скаляр умножение» на число 𝑘. Это требует умножения каждой записи 𝐴 по 𝑘: 𝑘𝐴 = ⎛⎜⎜⎜⎝𝑘 × 𝑎𝑘 × 𝑎 ⋯ 𝑘 × 𝑎𝑘 × 𝑎𝑘 × 𝑎… 𝑘 × 𝑎 ⋮⋮ ⋱ ⋮ 𝑘 × 𝑎𝑘 × 𝑎 ⋯ × 𝑎⎞⎟⎟⎟⎠.  Эта операция часто называют «масштабированием» матрицы константой 𝑘.

Другими словами, мы можем умножить число (скаляр) на матрицу путем умножения номер каждой записи в матрице.

Например, рассмотрим матрицу 𝐴=⎛⎜⎜⎝53−1−311061754−27−26−26−38⎞⎟⎟⎠.

Теперь предположим, что мы хотим масштабировать матрицу на константу −2. Затем мы умножаем каждую запись 𝐴 на −2, следовательно, находя, что )×1(−2)×0(−2)×6(−2)×1(−2)×7(−2)×5(−2)×4(−2)×(−2)(− 2)×7(−2)×(−2)(−2)×6(−2)×(−2)(−2)×6(−2)×(−3)(−2)×8⎞ ⎟⎟⎟⎠.

Завершение операции для каждой записи дает −2𝐴=⎛⎜⎜⎝−10−626−2−20−12−2−14−10−84−144−124−126−16⎞⎟⎟⎠.

Это не тот случай, когда мы ограничены масштабированием матрицы целым числом, и мы могли бы в равной степени выбрать масштабирование дробью, иррациональным числом, или даже комплексное число, если мы чувствуем себя авантюрно. Хотя это не является строго необходимым, при масштабировании матрицы дробью обычно считается хорошая практика для упрощения любых результирующих фракций до их простейшей формы. Например, мы определяем матрицу 𝐵=5−36488306−11−1 и решим масштабироваться на константу 13. Мы обнаружим, что 13𝐵=⎛⎜⎜⎜⎜⎝13×513×(−3)13×613×413×813×813×313×013×613×(−1)13×113×(−1)⎞⎟⎟⎟⎟⎠ .

Приведение как можно большего числа дробей к их низшей форме дает 13𝐵=⎛⎜⎜⎜⎜⎝53−12438383102−1313−13⎞⎟⎟⎟⎟⎠.

Скалярное умножение матрицы умножает константу на каждый элемент матрицы матрица, как мы видели. Исходя из этого определения, мы видим, что скалярное умножение на 1 сохраняет любую матрицу, а скалярное умножение на 0 превращает любую матрицу в нулевую матрицу.

Свойство: мультипликативное тождество и умножение на ноль в Скалярное умножение

Для любой матрицы 𝐴, 1𝐴=𝐴 и 0𝐴=𝑂, где 𝑂 — нулевая матрица в том же порядке, что и 𝐴.

Прежде чем обсуждать некоторые сложные проблемы, возникающие в связи с определением скалярного умножения, мы сначала попрактикуемся в одном вопросе.

Пример 1. Умножение матрицы на скаляр

Учитывая, что 𝐴=(−1−8), найти 3𝐴.

Ответ

Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице.

Чтобы умножить 𝐴 на 3, мы умножаем каждую запись на это число, и поэтому мы имеем 3𝐴=(3×(−1)3×(−8))=(−3−24).

Один из ключевых принципов скалярного умножения заключается в том, что к каждой отдельной записи применяется один и тот же процесс, а именно, что каждая запись умножить на то же число. Скалярное умножение никогда не умножает разные записи на разные числа. Следующий вопрос дает пример того, как этот принцип может быть применен с точки зрения решения задач линейной алгебры.

Пример 2. Нахождение скалярного множителя матрицы

Учитывая, что 𝑥×−20−3−5=1402135, найдите значение 𝑥.

Ответ

Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице.

Умножая каждую запись на 𝑥 в левой матрице, мы ищем 𝑥, которая решает следующее уравнение: 𝑥×(−2)𝑥×0𝑥×(−3)𝑥×(−5)=1402135, что эквивалентно можно записать как −2𝑥0−3𝑥−5𝑥=1402135.

Напомним, что две матрицы равны, если они имеют одинаковый порядок и каждая пары записей из одной строки и столбца равны. Мы видим, что матрицы имеют одинаковый порядок, так как они обе имеют 2 строки и 2 столбцы. Поэтому мы должны соответствовать пары записей в одной и той же строке и столбце из двух матриц.

Получается система линейных уравнений −2𝑥=14,0=0,−3𝑥=21,−5𝑥=35.

Помимо тривиального второго уравнения, которое явно верно, мы видим, что каждое уравнение решается, полагая 𝑥=−7.

Часто при работе с интересующей матрицей мы предпочитаем выносить за скобки скалярное кратное от каждой записи, если это возможно. Например, если нам дана матрица 𝐴=36240−416−8−44−4, легко заметить, что это можно записать как 𝐴=4×(9)4×(6)4×(0)4×(−1)4×(4)4×(−2)4×(−1)4×(1)4×(− 1).

Таким образом, каждая запись имеет коэффициент 4, который можно удалить, получив таким образом 𝐴=4960−14−2−11−1.

В некоторых ситуациях может быть предпочтительнее определить новую матрицу 𝐵=960−14−2−11−1, что позволяет нам написать 𝐴=4𝐵.

Давайте рассмотрим пример, который включает факторизацию скаляра из матрицы.

Пример 3: скалярное умножение

Учитывая матрицу 𝐴=1−1652−4−3−174, какое наибольшее число 𝑘, для которого ни одна запись 𝑘𝐴 не больше 1?

Ответ

Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице.

Учитывая матрицу 𝐴, определенную выше, это означает 𝑘𝐴=𝑘−16𝑘5𝑘2𝑘−4𝑘−3𝑘−𝑘7𝑘4𝑘.

Если 𝑘=0, каждая запись будет нулевой (которая является нулевой матрицей), которая будет удовлетворять условию, что ни одна запись не больше 1. Поскольку мы ищем наибольшее число 𝑘, для которого выполняется это условие, мы можем сосредоточиться на поиске положительного числа 𝑘>0.

Проверка положительных записей, у нас есть 𝑘, 2𝑘, 4𝑘, 5𝑘 и 7𝑘. Из них 7𝑘 должно быть самым большим входом, что означает что данное условие будет выполнено, если 7𝑘≤1. Это приводит к 𝑘≤17. Поскольку это значение 𝑘 положительно, остальные значения −𝑘, −3𝑘, −4𝑘 и −16𝑘 все будут отрицательно и, следовательно, меньше 1,

Так как мы ищем верхний предел значения 𝑘, ответ 𝑘=17.

Скалярное умножение — это операция, регулярно встречающаяся в линейной алгебре. Наряду с сложением это, пожалуй, самая простая алгебраическая операция для понимания. Однако это не означает, что задачу линейной алгебры можно считать простой только потому, что она включает скалярное умножение. Следующие два вопроса проиллюстрируют, как скалярное умножение матриц может предоставить богатые и интересные примеры, которые позволят развить более высокий уровень понимания.

Пример 4. Решение уравнений, использующих скалярное умножение

Рассмотрим матричное уравнение 819−3=𝑚302−1+−1130.

Найдите значение 𝑚, которое решает это уравнение.

Ответ

Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице. Точно так же мы знаем, что можем добавить две матрицы одного порядка путем добавления пар элементов, соответствующих в одну и ту же строку и столбец из двух матриц.

Сначала мы перепишем уравнение после включения скалярного умножения на 𝑚: 819−3=3𝑚02𝑚−𝑚+−1130.

Завершаем сложение в правой части этого уравнения, работая запись за записью, чтобы найти 819−3=3𝑚−112𝑚+3−𝑚.

Напомним, что две матрицы равны, если они имеют одинаковый порядок и каждая пары записей из одной строки и столбца равны. Мы можем видеть, что матрицы имеют одинаковый порядок, так как они обе имеют 2 строки и 2 столбца.

Соответствие каждой паре записей в одной и той же строке и столбце из двух матрицы, получаем 8=3𝑚−1,1=1,9=2𝑚+3,−3=−𝑚.

Окончательное уравнение дает 𝑚=3, и можно проверить, что все данные уравнения также верны, если 𝑚=3, значит, это и должен быть ответ. Это можно проверить, подставив 𝑚=3 обратно в исходную матрицу. уравнения, а затем наблюдая, что обе части уравнения совпадают.

В предыдущем примере мы нашли неизвестную константу в матричном уравнении. Если мы рассмотрим процесс ближе, мы можем заметить, что матричное уравнение приводит к одновременные уравнения. Следовательно, можно использовать матричное уравнение, чтобы найти больше чем одна неизвестная константа. В нашем последнем примере мы рассмотрим матрицу уравнение с тремя неизвестными константами.

Пример 5. Решение уравнений со скалярным умножением

Найдите числа 𝑎, 𝑏 и 𝑐 так, чтобы 𝑎110−1+𝑏1001+𝑐0−110=10−13.

Ответ

Мы начинаем с включения скалярных членов в матрицы, давая 𝑎𝑎0−𝑎+𝑏00𝑏+0−𝑐𝑐0=10−13.

Поскольку добавление матрицы выполняется запись за записью, мы имеем 𝑎+𝑏𝑎−𝑐𝑐−𝑎+𝑏=10−13.

Соответствие каждой паре записей в одной и той же строке и столбце из две матрицы, мы получаем одновременные уравнения 𝑎+𝑏=1,𝑎−𝑐=0,𝑐=−1,−𝑎+𝑏=3.

Третье уравнение дает 𝑐=−1, которое можно подставить во второе уравнение, чтобы показать, что 𝑎=−1. Затем подстановка значения 𝑎 либо в первое, либо в четвертое уравнение дает, что 𝑏=2.

Скалярное умножение имеет множество привлекательных свойств в сочетании с матричным добавление. Если бы мы работали с обычной алгеброй, то мы знали бы, что количества 𝑎, 𝑏 и 𝑐 всегда будет подчиняться правилу 𝑎×(𝑏+𝑐)=𝑎×𝑏+𝑎×𝑐, которое известно как «распределительное свойство». Выясняется, что одно и то же свойство справедливо для сложения матриц и скалярного умножения.

Теорема: Распределительное свойство

Скалярное умножение является «дистрибутивным» в сочетании со сложением матриц. Другими словами, если предположить, что 𝑎 — скалярная константа, а 𝐵 и 𝐶 — матрицы одного порядка, то 𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶.

Продемонстрируем этот результат на примере. Положим 𝑎=3 и определим две матрицы 𝐵=−460872,𝐶=37−566−1.

Затем, 𝐵+𝐶=−460872+37−566−1=−113−514131; и поэтому 𝑎(𝐵+𝐶)=3−113−514131=−339−1542393.

Точно так же мы могли бы выбрать другой маршрут и сначала вычислить 𝑎𝐵=−1218024216,𝑎𝐶=921−151818−3.

Отсюда мы могли бы вычислить, что 𝑎𝐵+𝑎𝐶=−1218024216+921−151818−3=−339−1542393.

Таким образом, в этом примере мы показали, что 𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶. Естественно, что приведенную выше теорему можно доказать строго и без ссылки на какой-либо конкретный пример, хотя здесь мы дали лишь демонстрацию.

Хотя может показаться, что скалярное умножение — тривиальная матрица операции, способность свободно работать с этой концепцией часто является разница между коротким и простым решением проблемы и решение длинное и сложное. Изучая любую конкретную матрицу, обычно рекомендуется проверить, можно ли разложить на множители любое скалярное кратное со всех записей.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

Умножение матрицы 𝐴 на скаляр 𝑘 означает, что каждый элемент матрицы 𝐴 будет умножен на 𝑘.
Когда каждый элемент матрицы имеет общий множитель, мы можем скаляр из матрицы путем обратного скалярного умножения.
Скалярное умножение является дистрибутивным. Другими словами, если задан скаляр 𝑎 и матрицы 𝐵 и 𝐶 одного порядка, 𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶.
Для любой матрицы 𝐴, 1𝐴=𝐴 и 0𝐴=𝑂, где 𝑂 — нулевая матрица того же порядка, что и 𝐴.

матриц: умножение матриц | SparkNotes

Скалярное умножение

Чтобы умножить матрицу на скаляр, то есть на одну константу, переменной или выражению, умножьте все элементы матрицы на скаляр:

Например,

Скалярное умножение является распределительным: ± ( A + B ) = ± A + ± B . Например,

4( + ) = 4 +4

Умножение двух матриц

Чтобы умножить две матрицы, мы сначала должны знать, как умножить строку (а матрица 1×p ) по столбцу (матрица p ×1). Умножить строку на столбец, умножьте первую запись строки на первую вход в столбец. Затем умножьте вторую запись строки на вторая запись столбца и т. д., и добавить все результаты. ответ должен быть одним числом. Например,

[ 8 –1 3 0 ] = 8(2) + (- 1)(6) + 3(- 4) + 0(- 2) = 16 — 6 — 12 + 0 = — 2

Строка может быть умножена на столбец тогда и только тогда, когда строка и столбец столбец имеет одинаковое количество записей. Точно так же две матрицы могут умножаться тогда и только тогда, когда первая матрица имеет одинаковое количество столбцы, так как вторая матрица имеет строки. То есть две матрицы могут перемножаться тогда и только тогда, когда они имеют размеры м × р и р × n . Ответом будет матрица с тем же количеством строк как первая матрица и такое же количество столбцов, как вторая матрица. Другими словами, она будет иметь размерность м × n .

ПУНКТ Чтобы умножить две матрицы, умножьте каждую строку первой матрицы на каждую столбец второй матрицы.

Умножить матрицы: Онлайн калькулятор. Умножение матриц

Лекции по алгебре

Оглавление

Умножение матрицы на скаляр. Сложение и вычитание матриц. Умножение матриц. Транспонирование матриц

Страницы работы

Содержание работы

Похожие материалы

Информация о работе

Объяснение урока: Скалярное умножение матриц

Определение: скалярное умножение

Свойство: мультипликативное тождество и умножение на ноль в Скалярное умножение

Пример 1. Умножение матрицы на скаляр

Ответ

Пример 2. Нахождение скалярного множителя матрицы

Ответ

Пример 3: скалярное умножение

Ответ

Пример 4. Решение уравнений, использующих скалярное умножение

Ответ

Пример 5. Решение уравнений со скалярным умножением

Ответ

Теорема: Распределительное свойство

Ключевые точки

матриц: умножение матриц | SparkNotes

Скалярное умножение

Умножение двух матриц

Добавить комментарий Отменить ответ