«В какой геометрии параллельные прямые пересекаются?» — Яндекс Кью
Популярное
Сообщества
МатематикаГеометрия
Vic Fowles
·
120,1 K
Ответить19УточнитьAndrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 4 февр 2021
Ни в какой. По определению прямые называются параллельными, если они не пересекаются. Точка. Если они пересекаются, то они не параллельные.
Заблуждение возникло в связи с пятвм постулатом, который дает возможность в евклидоаоц геометрии выделчть классы эквивалентномти параллельных прямых, потому что легко выводится, что если прямая l параллельна прямым m и n, то прямы m и n также параллельны.
Так вот в геометрии Лобачевского если прямая l параллельна прямым m и n, то нет никакой гарантии, что сами m и n не пересекаются.
Виталий Авраменко
1 января
«Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной… Читать дальше
Комментировать ответ…Комментировать…
Максим Лапиков
Математика
2,1 K
математик-системный программист, асу тп для аэс. · 8 авг 2018
на память из неевклидовых помню римана и лобачевского, кроме чисто аксиоматических построений, как ни странно, они имеют реальные модели где применяются в пространствах определённой кривизны при проецировании плоскостей на сферы. у римана правда если я ничего не путаю просто все прямые пересекаются, а у лобачевского, что существуют пересекающиеся две прямые параллельные.
Комментировать ответ…Комментировать…
Виталий Авраменко
-2
Психология, философия, религия, математика. · 4 янв
К вопросу к тому, что, и у кого, и где пересекается. Сфера Римана сама, хоть и, не имеет параллельных геодезических. Но построена через пересечение евклидовых прямых над комплексной плоскостью… Для начала, по факту введения бесконечно удалённой точки и прямые пересекаются в неизвестном месте. Но пересекаются… Вот вам чудеса проективной геометрии — по определению… Читать далее
Виталий Авраменко
18 января
А? Кому-то нужно описание в теоретико множественной интерпретации. Со стандартными и нестандартными множествами… Читать дальше
Комментировать ответ…Комментировать…
Kirill Stupakov
155
магистр математики; преподаватель математики в школе и на младших курсах · 18 авг 2018
Ни в какой. По определению, параллельные прямые не имеют точек пересечения.
Теперь давайте по геометриям и заблуждениям. Всюду будут рассматриваться «плоскости», чтобы это ни значило.
Геометрия Евклида. То, что учили в школе, то, что привычнее и почти точно выполняется в повседневной жизни. Выделю те два факта, что будут существенны потом. Первое: в этой геометрии есть… Читать далее
По определению, параллельные прямые не имеют точек пересечения.
Теперь давайте по геометриям и заблуждениям. Всюду будут рассматриваться «плоскости», чтобы это ни значило.
Геометрия Евклида. То, что учили в школе, то, что привычнее и почти точно выполняется в повседневной жизни. Выделю те два факта, что будут существенны потом. Первое: в этой геометрии есть… Читать далее
25,2 K
Последовательность Ч.
4 февраля 2019
Вы написали, что в геометрии Лобачевского бесконечное количество параллельных прямых через одну точку. Не могли бы… Читать дальше
Комментировать ответ…Комментировать…
Алексей В. Д. Старицкий
554
Православный, русский, радиоинженер. Интерес — жизнь. защищаю тех кого люблю, не жалея… · 10 нояб 2020
По здравому смыслу. Возьмите листок плоский бумаги и нарисуйте на ней две параллельные линии. Затем скомкайте лист бумаги произвольным образом. Если лист бумаги и линии условно будут бесконечными, то они могут пересечься между собой и сами с собой бессчётное количество раз. Теорема доказана. Это не совсем классическая геометрия, скорее схоластика.
Затем скомкайте лист бумаги произвольным образом. Если лист бумаги и линии условно будут бесконечными, то они могут пересечься между собой и сами с собой бессчётное количество раз. Теорема доказана. Это не совсем классическая геометрия, скорее схоластика.
1 эксперт не согласен
Andrei Novikov
возражает
4 февраля 2021
это не ответ по определению.
Комментировать ответ…Комментировать…
руслан б.
1
7 мар 2020
Здравствуйте . Не силён в геометрии и математике, но меня всегда смущало выражение » две параллельные прямые не пересекаются». Я считаю что зависит от обстоятельств . Например если проделать опыт : два столба стоят паралельно друг другу . Если их продолжить в обе стороны до бесконечности они ни когда не пересекутся , при условии что я стою и смотрю на них . Если взять… Читать далее
Если взять… Читать далее
1 эксперт не согласен
11,8 K
Andrei Novikov
возражает
4 февраля 2021
ответ не понятийный. Смешивает проективную геометрию в кучу с обычной.
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
2 ответа скрыто(Почему?)
Когда пересекаются параллельные линии? При каких условиях? — Спрашивалка
Виталька
Когда пересекаются параллельные линии? При каких условиях? условие линия
3809
457
2
Ответы
СМ
Санбай Манибай
Геометрия Лобачевского (или гиперболическая геометрия) основана на аксиомах групп I—IV абсолютной геометрии и на следующей аксиоме Лобачевского.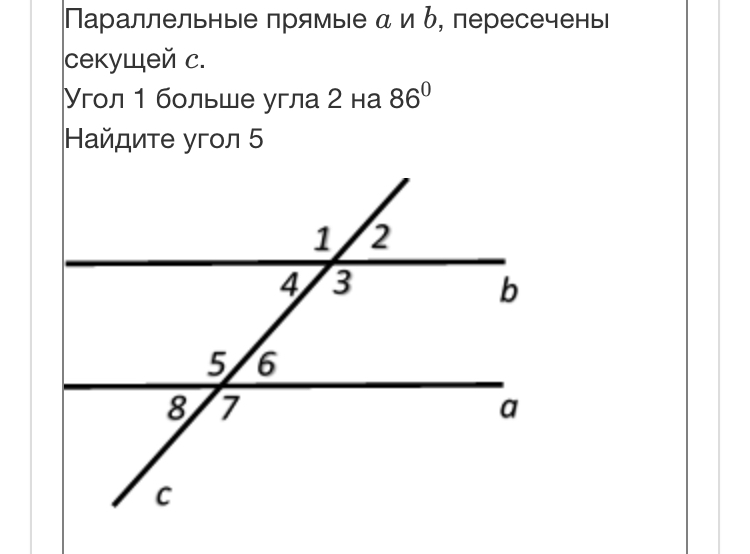
V*. Пусть а — произвольная прямая, а А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не менее двух прямых, проходящих через точку А и не пересекающих прямую а.
 2-1).
2-1).В отличие от определения параллельных прямых по Евклиду в геометрии Лобачевского параллельными к данной прямой называются (только некоторые прямые из тех, которые не пересекают данную прямую. Чтобы ввести это понятие, условимся считать, что все прямые, рассматриваемые нами, являются направленными прямыми. Поэтому мы их будем обозначать двумя буквами, например UV, считая, что точка U предшествует точке V. Предполагается также, что точки U и V выбраны так, что рассматриваемые нами точки на этой прямой лежат между точками U и V.
0
SF
Senior Full Stack Developer
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:
На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
В геометрии Лобачевского вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), так как случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом (аксиомы абсолютной геометрии). Так, например, сферическая геометрия и геометрия Римана, в которых любые две прямые пересекаются, и следовательно, не выполнена ни аксиома о параллельных Евклида, ни аксиома Лобачевского, не совместимы с абсолютной геометрией.
0
To
Torkvemada
1
Александр Наумов
Тут, на просторах Спрашивалки, есть пользователь под кликухой Милан Холик. По его версии лучи от Солнца к Земле идут параллельно. Затем Солнце «как бы висит над облаками» и его лучи (через просветы туч) расходятся под углом в разные стороны. Если мысленно вернуть лучи в точку, откуда они исходят (солнце над облаками), то получается, что когда вышеупомянутый Милан Холик бредит, то параллельные линии пересекаются… на солнце. Слава Милан Холику! Слава! Слава! Аминь…. ШЮТКА
По его версии лучи от Солнца к Земле идут параллельно. Затем Солнце «как бы висит над облаками» и его лучи (через просветы туч) расходятся под углом в разные стороны. Если мысленно вернуть лучи в точку, откуда они исходят (солнце над облаками), то получается, что когда вышеупомянутый Милан Холик бредит, то параллельные линии пересекаются… на солнце. Слава Милан Холику! Слава! Слава! Аминь…. ШЮТКА
0
Viktor Piskov
Паралле́льные прямы́е (от греч. παράλληλος, буквально — «идущий рядом», «идущий вдоль другого») — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.
0
Бактыбек Эркинбаев
. .,две линии пересекаются только при одном условии , если они будут проходит через одной точки…,!!.,параллельные , по теории они никогда не будут пересекаться , на то они и параллельные ..,!! .., параллельные линии пересекаются при условии , если хотя бы одному из них дано такое «право» ..,!!
.,две линии пересекаются только при одном условии , если они будут проходит через одной точки…,!!.,параллельные , по теории они никогда не будут пересекаться , на то они и параллельные ..,!! .., параллельные линии пересекаются при условии , если хотя бы одному из них дано такое «право» ..,!!
0
Glаdiator (Woodland, Са)
Такое возможно наблюдать только в проекции линий, находящихся в разных параллельных плоскостях и следующих в разных направлениях. Параллельные линии, находящиеся в одной плоскости никогда не пересекутся. Это следует из самого определения термина «параллельные линии».
0
…
При условии ,что они преломляются на закруглениях плоскости под определёнными углами они могут даже пересекаться. Например возьмите форму автомобильной покрышки и проведите две параллельные прямые перпендикулярно корду ,вот вы и получите результат вашего поиска.
Например возьмите форму автомобильной покрышки и проведите две параллельные прямые перпендикулярно корду ,вот вы и получите результат вашего поиска.
0
ВВ
Владимир Владимирович
Во-первых, параллельные прямые не могут пересекаться (ни в одной геометрии) по определению параллельности. Во-вторых, в геометрии Лобачевского как раз можно провести через точку, не лежащую на данной прямой, бесконечно много прямых, не пересекающихся с ней.
0
Виталька
Ну ну
1
ВВ
Владимир Владимирович
1
Tr
Traveler
Нельзя достоверно сказать, пересекаются параллельные прямые или нет, если дополнительно не указывать, какой из видов геометрии имеется в виду. ..Эвклида,Лобачевского,Римана.
..Эвклида,Лобачевского,Римана.
0
Goldilocks
))) На всю жизнь запомнила ответ своей одноклассницы на уроке алгебры:
-Кристина, опиши признаки параллельности прямых?
-Если прямые пересекаются, то они параллельны.
0
Виталька
Напутала))))
1
Олег
Бывало еду я по прямой дороге, с двух сторон которой нарисованы параллельные полоски, смотрю вперед и вижу, о чудо! Параллельные прямые пересеклись на горизонте!
0
Виталька
))
1
Олег
Иногда я задаюсь вопросом. Неужели обычные слова и буквы нынче выходят из моды? А как же наш могучий и богатый….
Неужели обычные слова и буквы нынче выходят из моды? А как же наш могучий и богатый….
1
Наталья
У художника да:) если смотреть под другим углом зрения) а так они по определению не пересекаются, параллельные же. Если только рядышком скрещиваются
0
Виталька
))
1
Наталья
1
Виталька
Красотища!)))
1
Наталья
На параллельных плоскостях
1
Виталька
Возможно
1
Ал
Алиса
Не пересекаются в одной плоскости. если менять плоскость наклонять, то визуально в начальной точке может казаться ,что они пересеклись ,но это иллюзия)
если менять плоскость наклонять, то визуально в начальной точке может казаться ,что они пересеклись ,но это иллюзия)
0
Виталька
Ок
1
Ал
Алиса
Без оков надо прочитал или молча или лайк
1
Виталька
Ага
1
ДД
Диво Дивное
но они же не могу пересекаться на то и параллельные прямые Разве что у Лобачевского-через одну точку Но это дебри науки, увы, не мое Я гуманитарий
0
Виталька
Ок
1
Егор🇷🇺
В Эвклидовой геометрии параллельные линии не пересекаются. А в бесконечности при условии не абсолютной паралельности- возможна
А в бесконечности при условии не абсолютной паралельности- возможна
0
NP
N P
ну по теореме никогда, если не учитывать наличие аксиом, по которым все же возможно, и возможность пересечения в бесконечности
0
Виталька
Нееее
1
Снежана
По законам геометрии Лобачевского они могут встретиться в бесконечном пространстве, просто соединиться в общее кольцо
0
Виталька
)))
1
Николай В. Авантюрист
Авантюрист
линии пересекаються с озвездиях-во временах года каждое созездие имеет силуэто 100% я астролог -можешь мне не верить
0
АЛ
Алексей Лушин
Говорят, пространство искривляется. Если долго смотреть в сильный телескоп, увидишь свой затылок. Это я украл где-то.
0
Виталька
Прикольно
1
Володя
Википедия в помощь. Но это не в Эвкалиптовой геометрии, конечно, а в пространстве
Геометрия Лобачевского — Википедия
0
Виталька
Ок
1
Павел Казаков
по неевклидовой геометрии , они пересекаются в бесконечно удаленной точке, ну и .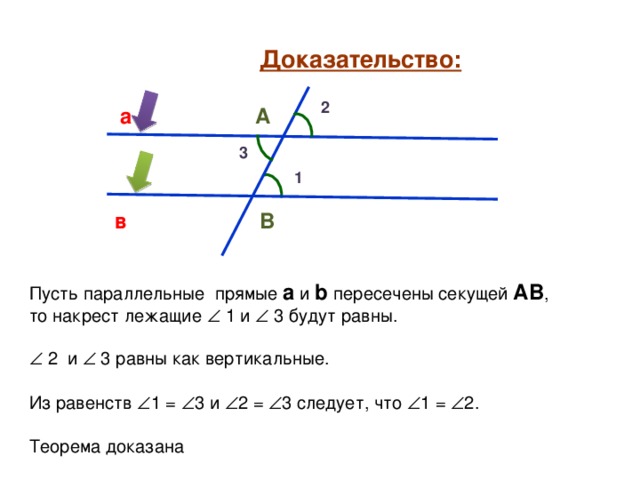 .. в случае искривления пространства
.. в случае искривления пространства
0
Пр
Пррпрполролпрорп
Если точка не лежит на данной прямой, через нее можно провести бесконечно много прямых, но не пересекающихся с ней.
0
Виталька
Ого
1
Ә(
Әруақ (Духи Предков) Ж.р.
Например Земля это сфера. А вернее овал сфера. Допустим мы провели две параллели. На такой форме они пересекутся.
0
Виталька
Агв
1
Ә(
Әруақ (Духи Предков) Ж.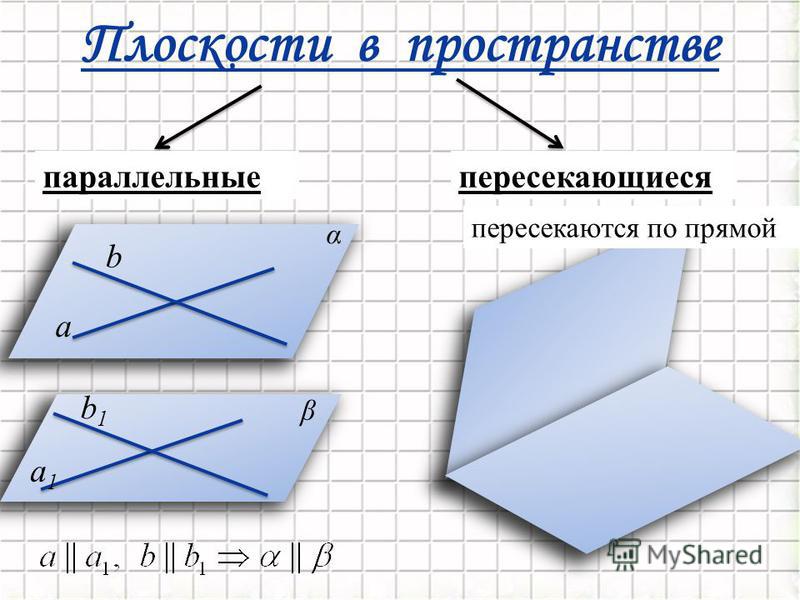 р.
р.
Все зависит от формы!
1
Виталька
Ок
1
Ә(
Әруақ (Духи Предков) Ж.р.
В природе нет параллелей
1
Виталька
Ок
1
Ә(
Әруақ (Духи Предков) Ж.р.
Вот у людей точно бывает параллельно.
1
Виталька
Ага. Душевно
1
Roman Balan
Если плоскость на которой они нарисованы скрутить в спираль! Визуально это будет похоже на двойную синусоиду!
0
Виталька
Ок
1
Ир
Ирина
А они могут пересекаться? Не хочу показаться невежественной, но они не могут пересечься даже в отношениях.
0
Виталька
Ни за что!
1
Ир
Ирина
Значит нет никакого мнения. Туман напустить каждый может.
1
Виталька
Да ну пряяяяям….
1
Ир
Ирина
Пустой разговор.
1
Виталька
Ок
1
Следующая страница
Другие вопросы
что такое креатин. Столько сайтов перечитала, никак не могу понять что именно делает креатин, и для чего он нужен?
Столько сайтов перечитала, никак не могу понять что именно делает креатин, и для чего он нужен?
Как вы думаете кто победит в ответном матче Бавария — Барселона? Пишите ваши прогнозы, очень интересно!
Если парень сменил узкие джинсы на спортивные штаны что это значит?
Помогите узнать имя певицы
Посоветуйте програму для харгэйнера
Как вернуть детей из детдома в семью, если органы опеки и сотрудники детдома всячески препятствуют этому?
Помогите! Может быть кто-то встречал такое платье или имеет представление каким оно должно быть спереди?
Есть ли смысл писать жалобу в управляющую компанию на соседей сверху?
Какая баня лучше всего?
на олимпиаде в беге, как измеряется время? электронный секундомер? а его нажимает судья? а его нажимает судья?
Букмекерские ставки. Объясните пожалуй что значит в букмекерских ставках Фора 0?
как правильнее распределить упражнения на разные группы мышц, какие упр делать в один день. Нужна программа на 4 дня.
мне 14 лет занимаюсь боксом нужно фирменные кросовки адидас около 5 тыщ рубле для тренеровок
Сгорела комната в квартире. Страховку оплачивалиежемесячно. Причина пожара-свечка. Что делать? Можно ли возместить что-
какой велик лучше купить???
геометрия — Как убедить кого-то, что параллельные линии могут соприкасаться/встречаться?
$\begingroup$
Говоря с кем-то, кто знает основы математики, но не очень глубоко, как бы вы объяснили, что параллельные линии могут соприкасаться?
Я имею в виду неевклидову/проективную геометрию.
Редактировать: Почему параллельные прямые на евклидовой плоскости (соответствующие прямым) пересекаются на проективной плоскости?
- геометрия
- проективная геометрия
- неевклидова геометрия
$\endgroup$
17
$\begingroup$
Прямые параллельны, если они лежат в одной плоскости и не пересекаются. В других геометриях параллельных линий может не быть, линии могут не иметь общей точки, но могут иметь общую предельную точку на бесконечности, или они могут просто не пересекаться.
В других геометриях параллельных линий может не быть, линии могут не иметь общей точки, но могут иметь общую предельную точку на бесконечности, или они могут просто не пересекаться.
Возможно, вы подумали о проективной геометрии, где «бесконечно удаленная точка» добавляется к каждому семейству параллельных прямых, а множество всех бесконечно удаленных точек называется «бесконечно удаленной линией».
Приложение
Обычно в формальной геометрии точки, линии и плоскости не определяются. Но постулаты определяют их «базовое» поведение. Постулат, который, по-видимому, согласуется с любой геометрией, гласит:
L1: Даны две различные точки на плоскости, и на этой плоскости имеется ровно одна линия, содержащая их.
«Двойственность» этого постулата равна
DL1: Даны две различные прямые на плоскости, и на этой плоскости есть ровно одна точка, принадлежащая обеим прямым.
Поскольку евклидова геометрия содержит параллельные линии, DL2 неверен. Но проективная геометрия принимает DL2 как постулат. Большой вопрос: «Существует ли геометрия, удовлетворяющая постулатам проективной геометрии?» Да есть.
Но проективная геометрия принимает DL2 как постулат. Большой вопрос: «Существует ли геометрия, удовлетворяющая постулатам проективной геометрии?» Да есть.
Создание такой геометрии действительно очень умно. Вы начинаете с евклидовой плоскости и добавляете к ней точки следующим образом. Выберите любую линию на плоскости. К этой линии и всем параллельным ей линиям вы добавляете одну дополнительную точку, точку в бесконечности. Это установленная вещь. Мы рассматриваем евклидову линию $l$ как набор точек и добавляем к этому набору неевклидову точку $p$, $l’ = l \cup \{p\}$. 92 — \{l\}$. Некоторые линии все равно будут пересекаться. Те, что пересекались в точке удаленной линии, теперь будут параллельны.
$\endgroup$
7
$\begingroup$
Я бы сказал, что если мы встанем рядом друг с другом и оба пойдем прямо на север, мы в конце концов столкнемся друг с другом возле северного полюса
Обратите внимание, как уже отмечалось, ваша предпосылка немного неверна.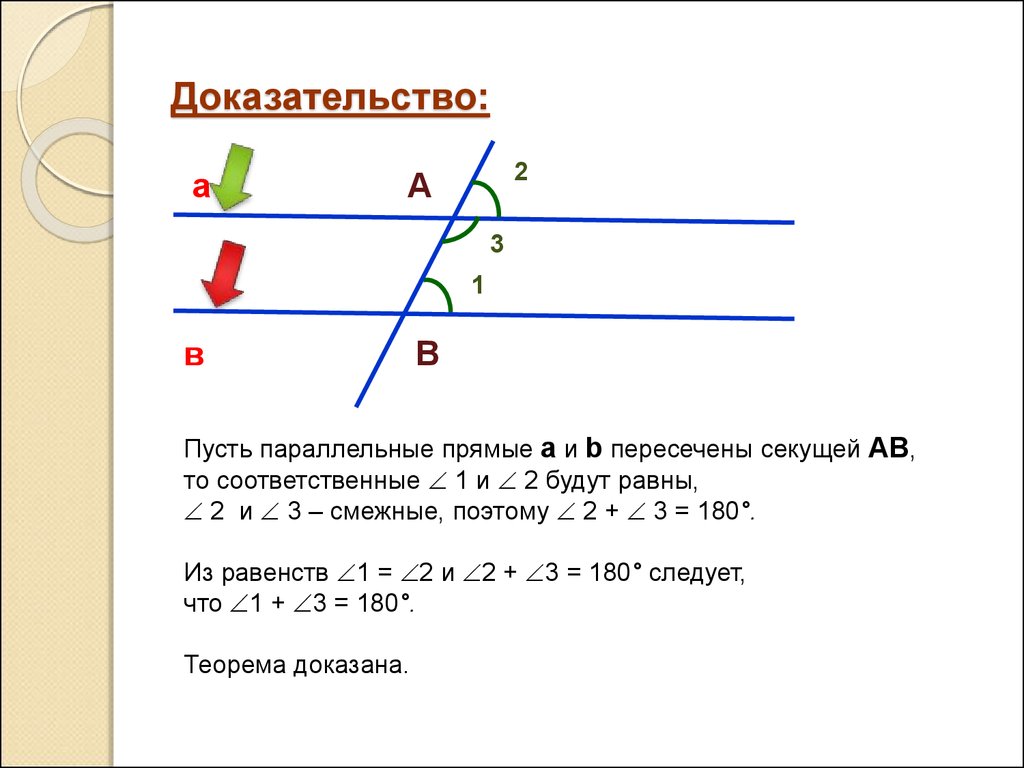 В чем вы можете убедить своего друга, так это в том, что любые две «прямые линии», то есть геодезические, пересекаются на сфере (не параллельные линии), тогда как на плоскости для любой линии существует особое семейство линий, которые никогда ее не касаются.
В чем вы можете убедить своего друга, так это в том, что любые две «прямые линии», то есть геодезические, пересекаются на сфере (не параллельные линии), тогда как на плоскости для любой линии существует особое семейство линий, которые никогда ее не касаются.
$\endgroup$
5
$\begingroup$
Как я уже говорил в комментариях, нельзя убедить кого-то тем, что не соответствует действительности.
ИМО, если кто-то знает основы геометрии, то он должен знать о том, что:
Этот раздел Википедии многого стоит здесь:
В геометрии параллельные линии — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются и не касаются друг друга ни в одной точке, называются параллельными. В более широком смысле линия и плоскость или две плоскости в трехмерном евклидовом пространстве, которые не имеют общей точки, называются параллельными.
Хотя, если вы убеждаете/спорите с кем-то наивным в области геометрии, что Параллели не пересекаются, спросите его, почему люди называют его его/ее именем, а не Джастином Бибером/Селеной Гомес? Ожидаемый ответ: . Потому что это мое имя , и все. Вы получили его / ее. На самом деле параллельные линии не могут встречаться в точке или пересекаться, потому что они определены таким образом, если две линии пересекутся, то они не останутся параллельными линиями.
$\endgroup$
3
$\begingroup$
Когда мне было 16 или около того, мне было скучно решать домашнее задание по математике, поэтому я поиграл с увеличительным стеклом и заметил кое-что интересное:
Если вы посмотрите на бумагу с сеткой через увеличительное стекло, линии останутся параллельными ( это видно, когда они находятся более или менее на «верху стекла»), но все линии сходятся на краю стекла.
(Я пошел к своему старшему брату, который в то время был инженером-первокурсником, и сказал ему, что параллельные линии можно встретить ; но он ответил, что не могут, потому что это аксиома. Несколько лет спустя я узнал, что существует такая вещь, как неевклидова геометрия.)
Заметьте, кстати, что это может потребовать, чтобы вы думали о стакане как о бесконечности.
$\endgroup$
12
$\begingroup$
В своем комментарии @JackyChong обозначил предварительную проблему. Определение «параллели» ясно: линии, которые не пересекаются, значит, нет пересекающихся параллельных линий. Реальный вопрос заключается в определении «линии».
Геодезическая является наиболее естественной для геометрии на сфере. Тогда в этой геометрии нет параллельных прямых.
Для проективной геометрии одним из определений является добавление «бесконечно удаленной точки» к каждой линии, а затем преобразование добавленных точек в «бесконечно удаленную линию».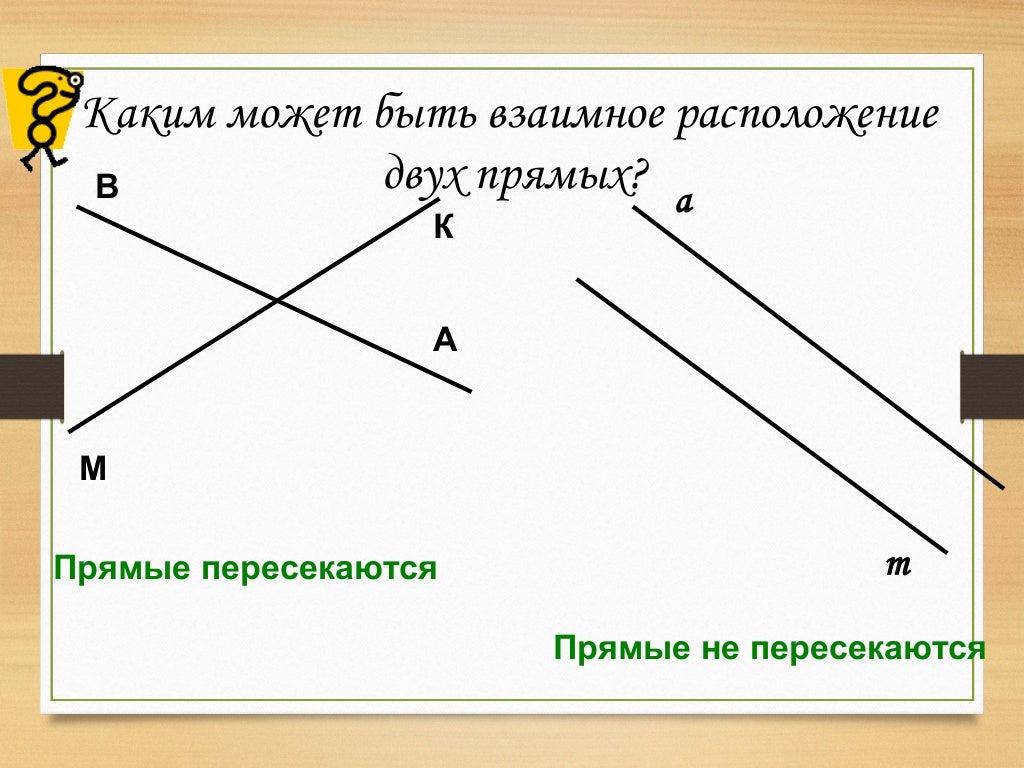 С этими дополнительными точками и линиями нет параллельных линий. Два, параллельные в евклидовой плоскости, имеют общую точку в бесконечности. Здесь помогает аналогия с железнодорожным полотном.
С этими дополнительными точками и линиями нет параллельных линий. Два, параллельные в евклидовой плоскости, имеют общую точку в бесконечности. Здесь помогает аналогия с железнодорожным полотном.
В гиперболической геометрии есть несколько прямых, параллельных заданной прямой, проходящих через точку, не принадлежащую этой прямой. Если вы зайдете так далеко с «человеком, который не знает математики», вы можете показать ему или ей модель Пуанкаре.
$\endgroup$
2
$\begingroup$
Я бы использовал два меридиана на Земле, которые касаются полюсов.
$\endgroup$
2
$\begingroup$
Это вопрос точки зрения 🙂
$\endgroup$
$\begingroup$
Вы можете говорить о поездах. Железнодорожные пути довольно наводящие на размышления.
Железнодорожные пути довольно наводящие на размышления.
$\endgroup$
4
$\begingroup$
Вы не сможете убедить ни одного математика, не говоря уже о своем друге, так как это ложь. Однако они могут столкнуться с идеей, что для чисто теоретических расчетов мы предполагаем, что две параллельные линии могут встретиться в точке в бесконечности. Если вы хотите отправиться в бесконечность, чтобы доказать это, пожалуйста, пришлите открытку, когда доберетесь туда.
$\endgroup$
$\begingroup$
Тот, кто знаком с основами математики, может легко понять это, поскольку согласно определению параллельных прямых
Параллельные прямые: Линии, расстояние между которыми постоянно, называются параллельными прямыми [см. самое верхнее определение]
самое верхнее определение]
Теперь, как мы знаем определение совпадающие прямые также параллельны, так как расстояние между ними является постоянным или $0$. Следовательно, поскольку совпадающие линии касаются друг друга, подразумевается, что параллельные линии также соприкасаются.
Смотрите видео здесь также
$\endgroup$
$\begingroup$
Я начертил бы две параллельные линии на листе бумаги. Затем я сводил все ребра вместе в одну точку и показывал, что параллельные прямые соприкасаются с этой точкой.
$\endgroup$
$\begingroup$
В детстве мама сказала мне фразу, которую я тогда не понял:
Параллельные прямые — это прямые, пересекающиеся в бесконечности.
Это утверждение и его объяснение с помощью искусства (как предложено Педро Тамароффом в комментариях) и демонстрации того, насколько упрощены многие утверждения и доказательства (если человек знает больше математики), является хорошим введением в идею того, что мышление на параллельных линиях как линии, пересекающиеся в бесконечности, имеют смысл и могут быть полезны.
В арте
Это, как вы также можете видеть в ответе Ива Дауста, можно увидеть всякий раз, когда вы смотрите на прямую дорогу, уходящую к горизонту. Например, см. источник на Wikimedia Commons,
Изображение выше показывает причину, по которой эта концепция изначально была концепцией, возникшей в искусстве, поскольку она была действительно полезна для представления того, как мы видим вещи. Поразительное применение этого можно увидеть в церкви Санта-Мария-прессо-Сан-Сатиро, где использовалась проективная геометрия, имитирующая отсутствующее пространство в церкви. Однако есть много других примеров.
В геометрии
В обычной геометрии (т.е. аффинной и евклидовой геометрии) приведенное выше определение или утверждение не имеет смысла, поскольку параллельные прямые не пересекаются. Это может быть определение на плоскости, но обычно (в более высоких измерениях) это результат, полученный из определения параллельных линий как линий с одинаковым направлением.
Однако причина, по которой мы все еще можем понять приведенное выше утверждение о пересечении в бесконечности, заключается в том, что аффинную геометрию можно поместить внутрь проективной геометрии. При этом точки вне аффинного пространства называются «точками на бесконечности», параллельные прямые пересекаются в них и становятся такими же, как пересекающиеся прямые, что упрощает огромное количество утверждений и доказательств, позволяя не различать случаи. Примером может служить теорема Паппа о шестиугольнике.
В заключение
В заключение: не пытайтесь убедить или показать, что параллельные линии соприкасаются. Просто попытайтесь объяснить полезность представления о параллельных линиях как о линиях, пересекающихся в бесконечности. В эпоху Возрождения у вас есть много примеров того, почему это утверждение полезно с точки зрения хорошего представления реальности и перспективы; в математике есть много примеров того, как это действительно полезно для упрощения утверждений и доказательств в геометрии.
$\endgroup$
1
$\begingroup$
В эллиптической геометрии предположение неверно.
В евклидовой геометрии параллельные линии «встречаются» и касаются друг друга на бесконечности, так как их наклон одинаков.
В плоской гиперболической геометрии параллельные линии также могут соприкасаться, но только в бесконечности.
В плоской модели диска Пуанкаре кругового сегмента геодезические параллели пересекаются по касательной только в бесконечно удаленных точках на границе «горизонта» или граничной окружности. Можно увидеть, как линии касаются и перемещаются по границе, указанной в ссылке Wiki.
Poincare Disk_MathWorld
Таким образом, полукруговые геодезические в полуплоскостной модели сходятся в точке $\infty$ на оси x. Анимация также может быть найдена в другом месте, где полукруги касаются оси X, изменяя размер полукруга во время движения.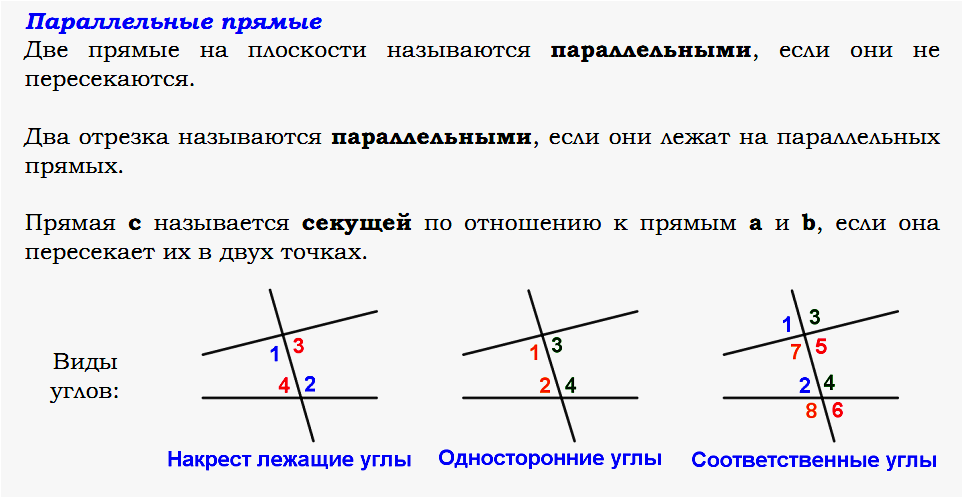
PoincareHalfPlane
Оба примера касаются параллельных линий, касаясь тангенциально/асимптотически в точке бесконечности.
http://math.etsu.edu/multicalc/prealpha/Chap3/Chap3-8/part4.htm
$\endgroup$
$\begingroup$
Один из способов объяснить это — думать о евклидовой плоскости как о изображении (части) объемлющего трехмерного мира. Это соответствует тому, как на самом деле работает наше зрение: свет из трехмерного мира проецируется через хрусталик глаза на поверхность позади нашего глаза.
Более подробно: поместите плоскость в любом месте трехмерного пространства (при условии, что она не проходит через начало координат). Назовите это «картинной плоскостью». Теперь любые 93$ пронзает плоскость изображения ровно в одной точке (при условии, что линия не параллельна плоскости изображения). Любая плоскость , проходящая через начало координат , проходит через плоскость изображения ровно по одной линии (опять же, если плоскость не параллельна плоскости изображения).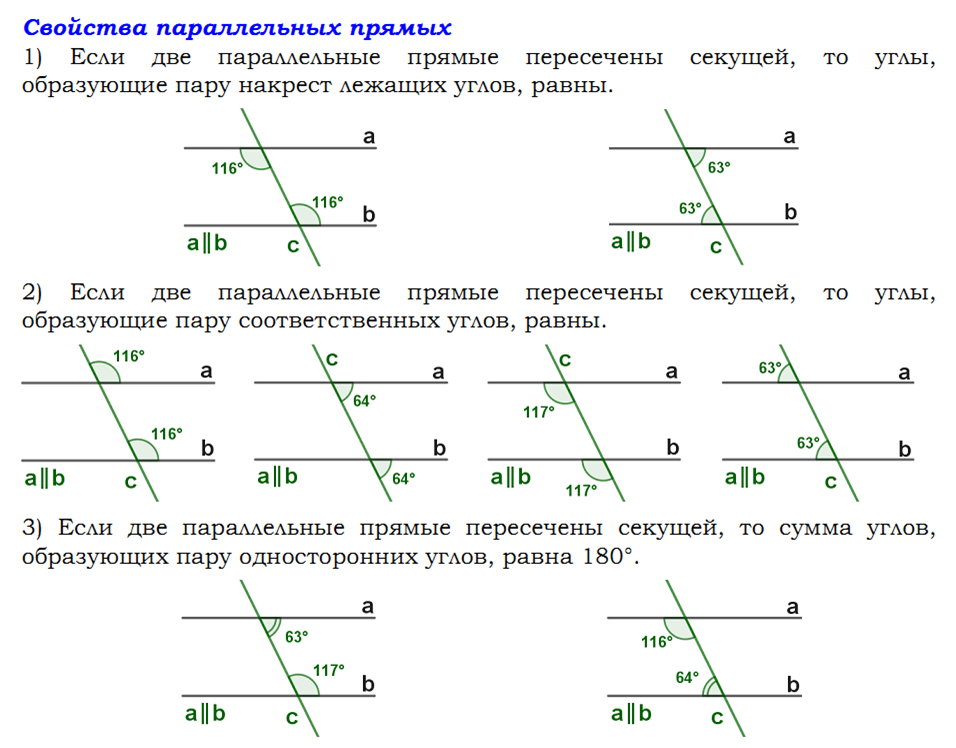 См. ниже (на котором картинная плоскость показана синим цветом).
См. ниже (на котором картинная плоскость показана синим цветом).
Теперь у нас есть словарь: $$\textrm{точка на картинной плоскости} \longleftrightarrow \textrm{линия, проходящая через начало координат в трехмерном пространстве}$$ $$\textrm{линия в картинной плоскости} \longleftrightarrow \textrm{плоскость, проходящая через начало координат в трехмерном пространстве}$$ 93$, которые параллельны картинной плоскости и, следовательно, не соответствуют никаким точкам или линиям на картинной плоскости. Это точки и эту линию можно считать «уходящей в бесконечность», но на самом деле все это означает, что они не имеют изображения в картинной плоскости.
Вы можете увидеть это визуально, держа палец на расстоянии вытянутой руки впереди и на несколько дюймов выше. По мере того, как вы приближаете руку (сохраняя ее высоту), положение кончика пальца кажется «выше» или «дальше» в вашем поле зрения, так как ваши глаза должны все больше и больше напрягаться, чтобы увидеть его.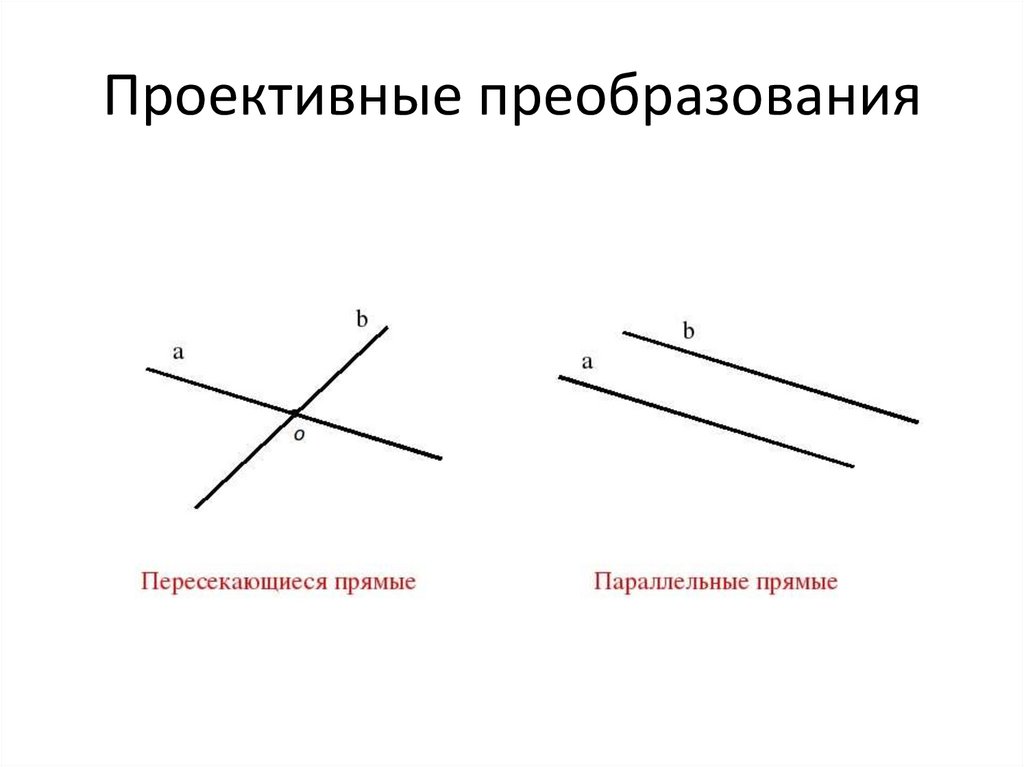 В конце концов, когда кончик пальца оказывается прямо над глазом, палец «исчезает». Конечно, на самом деле он не исчез, но «линия зрения» от кончика пальца до хрусталика вашего глаза параллельна сетчатке, так что кончик пальца не виден. С точки зрения восприятия кончик пальца отодвинулся «бесконечно далеко» в картинной плоскости, но на самом деле он находится всего в паре дюймов в трехмерном пространстве.
В конце концов, когда кончик пальца оказывается прямо над глазом, палец «исчезает». Конечно, на самом деле он не исчез, но «линия зрения» от кончика пальца до хрусталика вашего глаза параллельна сетчатке, так что кончик пальца не виден. С точки зрения восприятия кончик пальца отодвинулся «бесконечно далеко» в картинной плоскости, но на самом деле он находится всего в паре дюймов в трехмерном пространстве.
Однако , мы все знаем, что делать в таких случаях: повернуть голову! Это соответствует выбору новой плоскости изображения с другой ориентацией. Теперь точка, бывшая «в бесконечности», вырисовывается и раскрывается как обычная точка в новой картинной плоскости (и в то же время точки, которые были ранее в поле зрения , никуда не исчезли).
Обратите внимание, что оператор типа
для любых двух различных точек на картинной плоскости существует единственная линия на картинной плоскости, проходящая через данные точки
, который описывает истинный факт о геометрии картинной плоскости, соответствует в этом словаре
.3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».
Конечно, если вы выберете другую плоскость изображения, то линии больше не будут казаться параллельными, и их пересечение будет ясно видно как точка на новой плоскости изображения. Последнее изображение ниже показывает это. На этом изображении оранжевая и желтая плоскости такие же, как и раньше, но синяя плоскость изображения была перемещена и переориентирована; изображения двух плоскостей теперь состоят из непараллельных линий.
Итого:
- Если 2-мерную плоскость понимать как изображение объемлющего 3-мерного пространства, то «точка» — это просто изображение линии, проходящей через начало координат , а «линия» — это просто изображение плоскость через начало координат
- Некоторые «точки» (и «линия», содержащая эту точку) не будут иметь изображения в картинной плоскости, что мы описываем, говоря, что они находятся «в бесконечности»
- Однако нахождение «в бесконечности» является артефактом того, какую плоскость изображения мы используем; изменение плоскостей изображения меняет точки, находящиеся на бесконечности
- Кроме того, параллельность двух «линий» является артефактом плоскости изображения, которую мы используем для их просмотра; линии, которые кажутся параллельными с одной точки зрения, не параллельны с другой точки зрения
- Связь между двумя последними пунктами состоит в том, что «линии», кажущиеся параллельными в одной картинной плоскости , пересекаются с , но точкой пересечения является точка «в бесконечности» относительно картинной плоскости ; изменить перспективу, и точка больше не находится в бесконечности, и линии больше не параллельны.
- Все вышеперечисленное более или менее точно соответствует тому, как работает человеческий глаз, поэтому перспективное искусство может так хорошо обманывать глаз и создавать иллюзию глубины на плоской поверхности.
$\endgroup$
$\begingroup$
Визуально или концептуально параллельные линии сходятся на чрезвычайно большом расстоянии, они НИКОГДА не пересекаются. Меня не волнует, в скольких измерениях вы работаете или в каком геометрическом пространстве вы работаете, если у вас есть линии: L1 и L2, вы всегда можете абстрагировать соответствующий вектор от каждого L1:v1<> и L2:v2<> и если вы примените аркос угла косинуса между двумя векторами, где угол косинуса представляет собой скалярное произведение v1 и v2, деленное на произведение их величин, вы узнаете, параллельны они или нет.
v1<> v2<> mag1 mag2 // где mag1 и mag2 — величины v1 и v2 cosAngle = (v1 точка v2) / (mag1 * mag2) Определяющее значение = arcos(cosAngle) Если определяющее значение == 0, 180, 360, если в градусах или 0, PI или 2PI в радианах тогда векторы параллельны В противном случае они неРедактировать
То же самое можно сказать и об ARC, если две дуги принадлежат двум разным окружностям с разной длиной радиуса, где оба радиуса имеют одинаковое начальное положение; другими словами, концентрические круги, как в яблочко на доске для дартс или доске для стрельбы из лука, или если они разделены на расстоянии, превышающем сумму их радиусов, иначе, если любой из их радиусов имеет разную длину и не имеет одинаковая центральная точка то они могут иметь точку пересечения.
Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются.
Из следующих нескольких изображений параллельными будут считаться только концентрические окружности и эллипсы, остальные либо пересекаются, либо нет.
Они не пересекаются
Они пересекаются
Единственный из них, который можно считать параллельным, — это концентрические круги, поскольку каждая дуга имеет одинаковое расстояние от другого круга.
То же самое можно применить к эллипсам — За исключением того, что они имеют два радиуса разной величины, один для оси x и один для оси y.
Редактировать
Я заметил, что многие использовали терминологию или утверждение, говорящее: «Поместите точку в бесконечность» либо в своих комментариях, либо в своих ответах. Меня это беспокоит, и я удивлен этим. Почему? Я думаю, что невозможно поместить точку в бесконечность, потому что Бесконечность — это концепция, и по определению она считается НАН (не числом).
Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности.
Я думаю, что лучшим или правильным утверждением для этого предположения было бы: «Если поместить точку в точку Конвергенции». Я говорю это, потому что параллельные линии всегда будут параллельны и всегда будут иметь одинаковое расстояние в любой заданной точке этих линий. Теперь из-за того, как работают наши глаза и как мы интерпретируем световые сигналы, параллельные линии будут сходиться на чрезвычайно большом расстоянии. Если бы кто-то сказал поместить точку на линии в месте, приближающемся к Бесконечности, это было бы лучшим утверждением, чем поместить точку в бесконечность, но даже это все равно неверно. Почему?
Подумайте вот о чем: представьте себе, что вы находитесь на плоских равнинах Среднего Запада Соединенных Штатов с очень небольшими холмами, где вы можете практически видеть весь горизонт без помех: Теперь посмотрите вниз на железнодорожные пути, которые оказались практически прямыми с очень минимальные изгибы.
Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности.
$\endgroup$
7
геометрия — Что произойдет, если две бесконечные линии перестанут пересекаться и станут параллельными?
Один неупомянутый момент заключается в том, что есть способ уточнить ваше представление о параллельных прямых, пересекающихся под нулевым углом, но это не означает, что они пересекаются на конечном расстоянии. В этом суть ошибки рассуждения.
Stan Liou упомянул проективную плоскость в комментарии.
Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости.
Существует еще один возможный вид, который может отразить понятие параллельных прямых, пересекающихся под углом $0$, а именно расширенная комплексная плоскость. Можно доказать, что каждая (обобщенная) окружность (включая прямые) отображается в окружность на сфере Римана. Каждая прямая проходит через $\infty$, которая определяется как точка, соответствующая северному полюсу, и, таким образом, каждые две различные прямые пересекаются в двух точках, дважды считая касание. Параллельные линии сопоставляются с окружностями, касающимися северного полюса, а непараллельные линии сопоставляются с окружностями, которые пересекаются под положительным углом на северном полюсе. Оказывается, угол можно определить естественным образом (угол на поверхности сферы), и он удивительным образом согласуется с углом на плоскости, когда пересечение не в $\infty$! [См.
ниже, если вас интересуют доказательства.]
Теперь мы можем рассмотреть, что происходит на сфере Римана, когда у вас есть две линии, как в вашем вопросе, одна из которых постепенно меняется, чтобы стать параллельной другой. Для простоты предположим, что одна из них — это прямая, проходящая через начало координат, так что она отображается в большой круг $C$ через $\infty$. Теперь, куда сопоставляется другая линия? Я выполнил поиск в Google по изображению и был приятно удивлен, обнаружив, что Али Чаглаян уже сделал это здесь.
Предположим, что черная линия — фиксированная, а синяя — та, которую мы меняем. Обратите внимание, что красный круг пересекает $C$ на северном полюсе и в какой-то другой точке $P$. Теперь представьте, что произойдет, если вы повернете синюю линию так, чтобы она стала параллельной черной линии. Красный кружок тоже как бы вращается, и $P$ движется вдоль $C$ все ближе и ближе к северному полюсу. Наконец, когда синяя линия параллельна черной линии, $P$ достигла северного полюса (соответствующего $\infty$) и угол между линиями равен $0$, но теперь оба их пересечения находятся в точке $\infty$.
. Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.


 3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».
3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».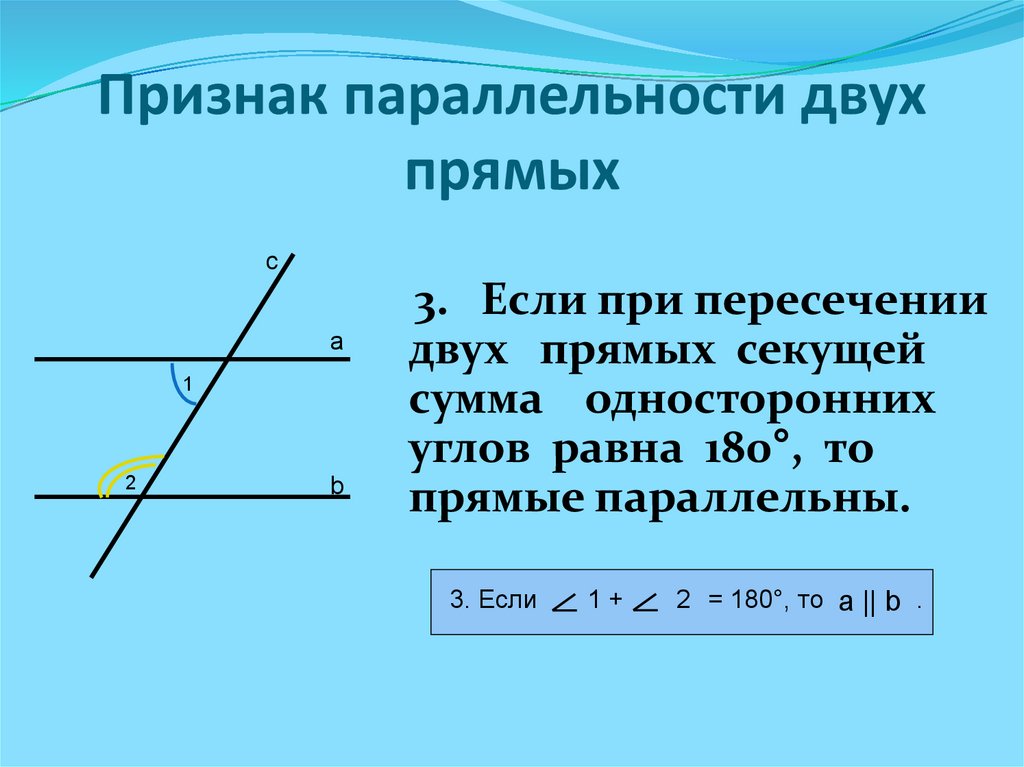
 Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются.
Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются. Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности.
Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности. Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности.
Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности. Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости.
Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости. ниже, если вас интересуют доказательства.]
ниже, если вас интересуют доказательства.] . Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.
. Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.