Алгебра Упрощение тригонометрических выражений
Материалы к уроку
Конспект урока
14. Упрощение тригонометрических выражений
Равенства
Часто они используются при упрощении и доказательстве тригонометрических выражений.
Рассмотрим примеры использования этих формул при упрощении тригонометрических выражений.
( вынесем за скобку общий множитель косинус квадрат тэ, в скобках получим разность единицы и квадрата косинуса тэ, что равно по первому тождеству квадрату синуса тэ. Получим сумму синус четвертой степени тэ произведения косинус квадрат тэ и синус квадрат тэ. общий множитель синус квадрат тэ вынесем за скобки, в скобках получим сумму квадратов косинуса и синуса, что по основному тригонометрическому тождеству равно единице. В итоге получим квадрат синуса тэ).
( Вынесем общий множитель косинус тэ за скобки, а в скобках приведем к общему знаменателю, который представляет собой произведение один минус синус тэ на один плюс синус тэ.
В числителе получим: единица плюс синус тэ плюс единица минус синус тэ, приводим подобные, числитель равен двум после приведения подобных.
В знаменателе можно применить формулу сокращенного умножения (разность квадратов) и получить разность единицы и квадрата синуса тэ, что по основному тригонометрическому тождеству
равно квадрату косинуса тэ. После сокращения на косинус тэ получим конечный ответ : два деленное на косинус тэ).
Рассмотрим примеры использования этих формул при доказательстве тригонометрических выражений.
ПРИМЕР 4.Найти значение выражения tg 2 t + ctg 2 t ,если tg t + ctg t = 6.
( сумма квадратов тангенса тэ и котангенса тэ, если сумма тангенса и котангенса равна шести).
Решение. (tg t + ctg t)2 = 62
tg 2 t + 2 ∙ tg t ∙ctg t + ctg 2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg 2 t + ctg 2 t = 34
Возведем обе части исходного равенства в квадрат:
(tg t + ctg t)2 = 62 ( квадрат суммы тангенса тэ и котангенса тэ равна шести в квадрате).
Вспомним формулу сокращённого умножения: Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a+b)2=a2+2ab+b2 Получим tg 2 t + 2 ∙ tg t ∙ctg t + ctg 2 t = 36 (тангенс квадрат тэ плюс удвоенное произведение тангенса тэ на котангенс тэ плюс котангенс квадрат тэ равно тридцати шести).
Так как произведение тангенса тэ на котангенс тэ равно единице, то tg 2 t + 2 + ctg 2 t = 36 ( сумма квадратов тангенса тэ и котангенса тэ и двух равна тридцати шести),
значит tg 2 t + ctg 2 t = 34 (сумма квадратов тангенса тэ и котангенса тэ равна тридцати четырем). Ответ: 34.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Упрощение тригонометрических выражений по основным формулам тригонометрии.
Часть 1412+
6 месяцев назад
Математика от Баканчиковой296 подписчиков
Геометрия 9 класс. Как применять основные формулы тригонометрии для упрощения тригонометрических выражений в 9 и 10 классах? Сегодня мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в геометрии», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Вы обратим Ваше внимание на то, что чтобы легко упрощать тригонометрические выражения, Вы должны чётко знать 20 основных формул тригонометрии и практически все темы алгебры, включая действия с многочленами, дробями, формулы сокращенного умножения многочленов, законы математики, приведение подобных слагаемых и т.п. А чтобы Вы закрепили и запомнили материал этого урока, мы предлагаем Вам в качестве домашнего задания самостоятельно решить те упражнения, решение которых было показано на этом уроке, а потом сверить получившиеся ответы. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°. Тригонометрические функции в геометрии. Часть 5. Геометрия 9 класс. https://rutube.ru/video/9393cb6043b9878b49883195db02d251/
Как найти противо- и прилежащие катеты по углу и гипотенузе. Как найти площадь треугольника, параллелограмма и трапеции. Тригонометрические функции. Часть 6. Геометрия 9 класс. https://rutube.ru/video/01cfdff903c6c37227f510c5f4bf7984/
Как найти объем пирамиды (конуса) по боковому ребру (образующей) и углу между боковым ребром (образующей) и плоскостью основания. Тригонометрические функции. Часть 7. Геометрия 10-11 класс. https://rutube.ru/video/a246217e2de6f5960fb55a3e77b904d0/
Как найти противо- и прилежащие катеты по углу и другому катету. Как найти площадь треугольника и параллелограмма. Тригонометрические функции. Часть 8. Геометрия 9 класс. https://rutube.ru/video/5b374b4961980532582185a1803b6be0/
Тангенс и котангенс в решении задач по стереометрии.
Объяснение урока: Упрощение тригонометрических выражений
В этом объяснении мы узнаем, как упростить тригонометрическое выражение.
Эти выражения часто упрощаются при применении одного или нескольких тригонометрических тождеств, которые связывают различные тригонометрические и обратные тригонометрические функции и их аргументы. Их мотивация математическая, но они также приложения в реальных задачах.
Тригонометрические тождества имеют несколько реальных применений в различных областях, таких как физика, инженерия, архитектура, робототехника, теория музыки и навигация, и это лишь некоторые из них. В физике их можно использовать в движении снарядов, моделируя механику электромагнитных волн, анализируя переменные и постоянные токи и находя траекторию движения массы вокруг массивного тела под сила тяжести.
Начнем с напоминания о тригонометрических функциях, пифагорейские тождества которых мы рассмотрим в этом толкователе. Учитывать следующий прямоугольный треугольник.
Тригонометрические функции могут быть выражены через отношение сторон треугольника как
sinOHcosAHtanOA𝜃=,𝜃=,𝜃=.
Эти функции удовлетворяют следующему тригонометрическому тождеству: тансинкос𝜃=𝜃𝜃.
Отметим, что эти тригонометрические соотношения определены для острых углов 0𝜃90∘∘, а тригонометрические функции для всех значений 𝜃 определены на единичной окружности.
Предположим, что точка движется по единичной окружности против часовой стрелки. В определенной позиции (𝑥,𝑦) на единичной окружности с углом 𝜃 функция синуса определяется как 𝑦=𝜃sin и функция косинуса как 𝑥=𝜃cos, как показано на диаграмме выше. Другими словами, тригонометрические функции определяются с помощью координат точки пересечения единичной окружности. с конечной стороной 𝜃 в стандартном положении.
Взаимные тригонометрические уравнения определяются в терминах стандартных тригонометрических уравнений следующим образом.
Определение: обратные тригонометрические функции
Функции косеканса, секанса и котангенса определяются как
cscsinseccoscottancossin𝜃=1𝜃,𝜃=1𝜃,𝜃=1𝜃=𝜃𝜃.
Тригонометрические функции являются периодическими, что означает, что если мы добавим целое число, кратное 2𝜋, в радианы или 360∘ на угол 𝜃, значение функции остается прежней: sincoscostantan(360+𝜃)=𝜃,(360+𝜃)=𝜃,(360+𝜃)=𝜃.∘∘∘
Мы можем видеть это непосредственно из определения единичного круга тригонометрических функций. На самом деле, касательная функция периодическая по 𝜋, в радианах, или 180∘, так как у нас есть tantan(180+𝜃)=𝜃.∘
Аналогично, для обратных тригонометрических функций имеем csccscsecseccotcot(360+𝜃)=𝜃,(360+𝜃)=𝜃,(360+𝜃)=𝜃.∘∘∘
Подобно функции тангенса, функция котангенса периодична по 𝜋, в радианы или 180∘, так как у нас есть коткот(180+𝜃)=𝜃.∘
Тригонометрические тождества, которые мы рассмотрим в этом объяснении, выполняются для любого угла 𝜃 в области
функции в градусах или
радианы. В частности, мы можем преобразовать угол между
степени и
радианах по следующему правилу: если у нас есть угол
𝜃степень, мы можем
преобразовать его в радианы через
𝜃=𝜋180𝜃.
radiansdegree
При работе с тригонометрическими выражениями полезно переписать обратные тригонометрические тождества в терминах синуса и косинус для упрощения.
Рассмотрим пример, в котором мы должны использовать обратные тригонометрические функции для определения значения тригонометрическое выражение.
Пример 1. Использование взаимных тождеств для вычисления тригонометрических выражений
Найдите значение 8𝜃×−5𝜃sincsc.
Ответ
В этом примере мы хотим найти значение конкретного выражения, включающего тригонометрические и обратные числа. тригонометрические функции.
Один из способов вычисления тригонометрического выражения состоит в том, чтобы записать его в терминах функций синуса и косинуса, используя следующие определение функции косеканса, входящей в данное выражение: cscsin𝜃=1𝜃.
Следовательно, выражение можно упростить, чтобы дать 8𝜃×−5𝜃=8𝜃×−5=8𝜃×−5𝜃=−40×𝜃𝜃=−40.sincscsinsinsinsinsinsin
Теперь давайте рассмотрим пример, в котором мы упрощаем конкретное тригонометрическое выражение.
Пример 2. Упрощение тригонометрических выражений с использованием тригонометрических тождеств
Упростить coscscsin𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определение функции косеканса, входящей в данное выражение: cscsin𝜃=1𝜃.
Данное тригонометрическое выражение становится coscscsincossinsincos𝜃𝜃𝜃=𝜃×1𝜃×𝜃=𝜃.
В следующем примере мы упростим тригонометрическое выражение, записав его с помощью функций синуса и косинуса.
Пример 3. Упрощение тригонометрических выражений с использованием тригонометрических тождеств
Упрощение tansinsec𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определения для функций тангенса и секанса, которые появляются в данном выражении: тансинкоссеккос𝜃=𝜃𝜃𝜃=1𝜃.
Данное тригонометрическое выражение становится tansinsectansincossincossincossincossin𝜃𝜃𝜃=𝜃𝜃÷1𝜃=𝜃𝜃×𝜃𝜃=𝜃×𝜃𝜃=𝜃.
В следующем примере используется произведение тригонометрических и обратных тригонометрических функций, которое мы можем просто использовать, используя определение обратных функций, а затем переписать окончательный ответ в терминах другой обратной функции.
Пример 4. Упрощение тригонометрических выражений с использованием взаимных тождеств
Simplify cosseccsc𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие
определения функций косеканса и секанса, входящих в данное выражение:
cscsinseccos𝜃=1𝜃,𝜃=1𝜃.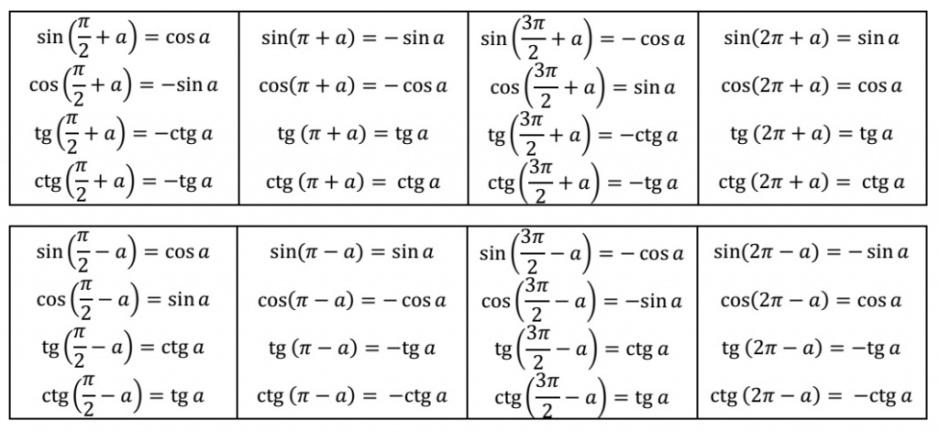
Таким образом, выражение можно упростить как cosseccsccoscossincossin𝜃𝜃𝜃=𝜃×1𝜃×1𝜃=𝜃𝜃.
Теперь, используя определение функции котангенса, коткосин𝜃=𝜃𝜃.
Данное выражение может быть выражено через функцию котангенса как cossecccscossincot𝜃𝜃𝜃=𝜃𝜃=𝜃.
Тригонометрические и обратные тригонометрические функции являются четными и нечетными функциями, поскольку они удовлетворяют свойствам 𝑓(−𝜃)=𝑓(𝜃) для четных функций и 𝑓(−𝜃)=−𝑓(𝜃) для нечетных функций. В частности, функция синуса нечетная, а функция косинуса четно, так как они удовлетворяют sinsincoscos(−𝜃)=−𝜃,(−𝜃)=𝜃, для любого значения 𝜃 в градусах или радианы. Отсюда мы также можем определить четность других тригонометрические функции, которые определяются с их точки зрения. В частности, для касательной функции имеем tansincossincostan(-𝜃)=(-𝜃)(-𝜃)=-𝜃𝜃=-𝜃.
Таким образом, функция тангенса нечетна, и мы можем вывести четность других тригонометрических функций аналогичным образом.
Мы можем обобщить их следующим образом.
Четные и нечетные тождества для тригонометрических функций
Функции косинуса и секанса четны, что означает, что для любого значения 𝜃 в соответствующих областях определения они удовлетворяют тождества coscossecsec(−𝜃)=𝜃,(−𝜃)=𝜃.
А функции синуса, тангенса, косеканса и котангенса нечетны, что означает, что они удовлетворяют следующим тождествам для любого значение 𝜃 в соответствующих доменах: sinsintantancsccsccotcot(-𝜃)=-𝜃,(-𝜃)=-𝜃,(-𝜃)=-𝜃,(-𝜃)=-𝜃.
Теперь давайте рассмотрим пример, в котором мы должны применить четность тригонометрической функции, чтобы просто определить конкретную тригонометрическое выражение.
Пример 5. Упрощение тригонометрических выражений, включающих нечетные и четные тождества
Упростить tancsc(−𝜃)𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции
используя четную/нечетную идентичность.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определение функции косеканса, входящей в данное выражение: cscsin𝜃=1𝜃.
Касательная функция нечетная, поэтому тождество тантан(-𝜃)=-𝜃.
Мы можем переписать функцию тангенса, используя ее определение в терминах функций синуса и косинуса: тансинкос𝜃=𝜃𝜃.
Таким образом, выражение можно упростить как tancsctancscsincossincos(−𝜃)𝜃=−𝜃𝜃=−𝜃𝜃×1𝜃=−1𝜃.
Наконец, мы можем переписать это выражение в терминах функции секущей, определяемой как секкос𝜃=1𝜃.
Таким образом, выражение принимает вид tancscsec(−𝜃)𝜃=−𝜃.
Функция синуса эквивалентна функции косинуса смещением на 90∘ влево, что можно визуализировать, сравнив график обеих функций.
В частности, для углов 𝜃 и 90+𝜃∘: sincoscossin(90+𝜃)=𝜃,(90+𝜃)=−𝜃.∘∘
Мы также можем проиллюстрировать их на единичной окружности, как показано.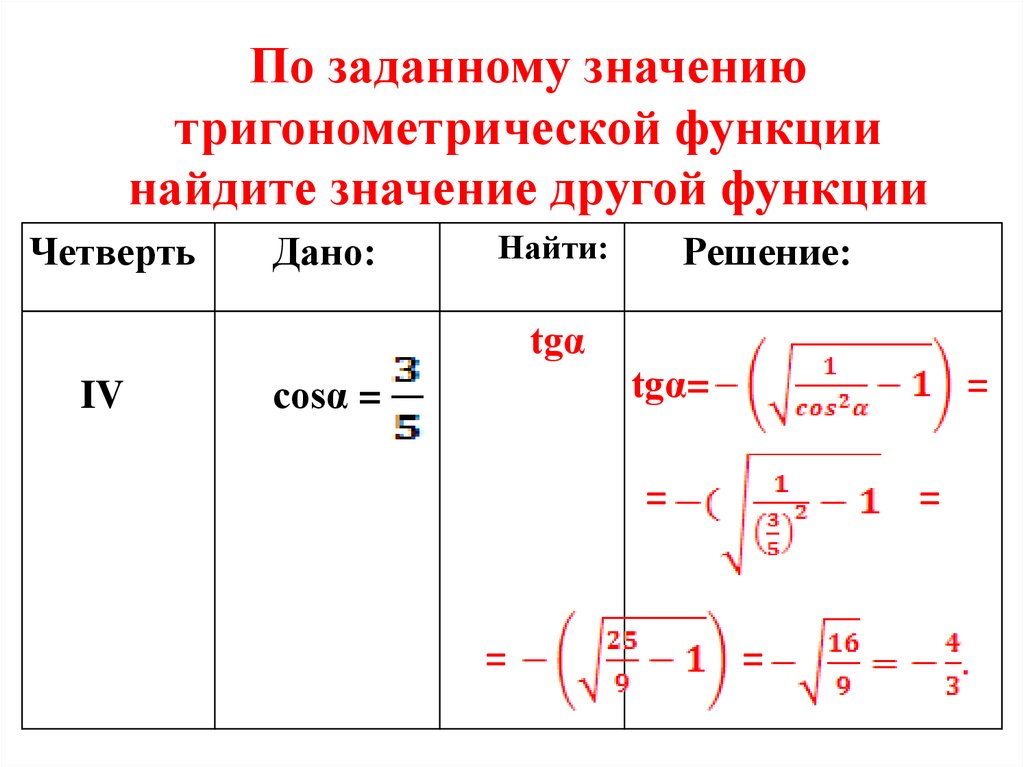
Аналогично, заменяя 𝜃 на −𝜃, мы получаем следующие тождества кофункций для дополнительных углов 𝜃 и 90−𝜃∘: sincoscossin(90−𝜃)=𝜃,(90−𝜃)=𝜃.∘∘
Мы можем проиллюстрировать это, как показано.
На рисунке изображен прямоугольный треугольник с углом 𝐴𝑂𝐵 в стандартном положении, который пересекает единичную окружность в точке 𝐵(𝑥,𝑦) и имеет остроугольную меру 0𝜃90∘∘.
Мы можем комбинировать эти тождества и использовать их для определения тождеств для других тригонометрических функций, определенных в функции синуса и косинуса.
Определение: тригонометрические тождества коррелированных углов
Тригонометрические функции удовлетворяют тождествам кофункций для всех 𝜃 в своих областях определения. В частности, у нас есть sincoscossintancottancscsecseccsc(90±𝜃)=𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=𝜃,(90±𝜃)= ∓𝜃.∘∘∘∘∘∘
Например, для функции касательной имеем
tansincossincossincot(90±𝜃)=(90±𝜃)(90±𝜃)=𝜃∓𝜃=∓𝜃𝜃=∓𝜃.
∘∘∘
Все эти тождества также выполняются в радианах, в частности, заменив 90∘ на 𝜋2 в радианы.
Теперь давайте рассмотрим пример, где мы используем это тождество вместе с четностью тригонометрической функции, чтобы упростить выражение.
Пример 6. Упрощение тригонометрических выражений с использованием коррелированных и четных тождеств
Упростить sinsec𝜋2+𝜃(−𝜃).
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее обратные тригонометрические функции.
Мы также будем использовать тождество коррелированного угла синкос𝜋2+𝜃=𝜃 и даже тождество сексек(−𝜃)=𝜃.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующее определение функции секущей: секкос𝜃=1𝜃.
Используя их, выражение становится sinseccosseccoscos𝜋2+𝜃(−𝜃)=𝜃𝜃=𝜃×1𝜃=1.
Теперь предположим, что мы хотим определить sin(180−𝜃)∘.
Мы можем найти это, многократно используя приведенные выше тождества. Если мы позволим
𝜃=90−𝑥∘, тогда
sinsinsincos(180−𝜃)=(180−[90−𝑥])=(90+𝑥)=𝑥.∘∘∘∘
Теперь, подставляя обратно 𝑥=90−𝜃, получаем sincossin(180−𝜃)=(90−𝜃)=𝜃.∘∘
Аналогично находим coscos(180−𝜃)=−𝜃.∘
Повторно применяя эти тождества или используя единичную окружность, мы также получаем тождества для углов 𝜃 и 𝜃±180∘: sinsincoscos(180±𝜃)=∓𝜃,(180±𝜃)=−𝜃.∘∘
Для 𝜃 и 180−𝜃∘, имеем следующее.
А для 𝜃 и 180+𝜃∘ имеем следующее.
У нас также есть тождества для других тригонометрических функций, которые следуют из тождеств для функций синуса и косинуса, из их определения: tantancotcotcsccscsecsec(180±𝜃)=±𝜃,(180±𝜃)=±𝜃,(180±𝜃)=∓𝜃,(180±𝜃)=-𝜃.∘∘∘∘
В следующем примере используются определения обратных тригонометрических функций вместе с тождествами кофункций в радианах, чтобы упростить выражение.
Пример 7. Использование периодических тождеств и тождеств кофункций для упрощения тригонометрического выражения
Simplify seccot−𝜃(𝜋−𝜃).
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее обратные тригонометрические функции.
Мы также будем использовать кофункцию и коррелированные тождества: seccsccotcot𝜋2−𝜃=𝜃,(𝜋−𝜃)=−𝜃.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определения для функций косеканса и котангенса, которые появляются в числителе и знаменателе: cscsincotcossin𝜃=1𝜃,𝜃=𝜃𝜃.
Числитель выражения можно упростить как secscssin𝜋2−𝜃=𝜃=1𝜃.
И знаменатель как cotcotcossin(𝜋−𝜃)=−𝜃=−𝜃𝜃.
Таким образом, выражение можно упростить как seccotsinsincoscos−𝜃(𝜋−𝜃)=−1𝜃×𝜃𝜃=−1𝜃.
Наконец, мы можем переписать это выражение в терминах функции секущей, определяемой как секкос𝜃=1𝜃.
Таким образом, получаем seccotsec−𝜃(𝜋−𝜃)=−𝜃.
Аналогично, для углов 𝜃 и 270±𝜃∘ имеем
sincoscossintancotcottancscsecseccsc(270±𝜃)=−𝜃,(270±𝜃)=±𝜃.
(270±𝜃)=∓𝜃,(270±𝜃)=∓𝜃,(270±𝜃)=-𝜃,(270±𝜃 )=±𝜃.∘∘∘∘∘∘
Это можно представить следующим образом.
Используя периодичность тригонометрических функций и единичный круг, мы имеем sinsincoscostantancotcsccscsecsec(360±𝜃)=±𝜃,(360±𝜃)=𝜃,(360±𝜃)=±𝜃,(360±𝜃)=±𝜃,(360±𝜃)=±𝜃,(360±𝜃) =𝜃.∘∘∘∘∘∘
Все тождества также выполняются в радианах, заменив 360∘ на 2𝜋 в радианах. Их также можно визуализировать с помощью единичного круга, как показано на рисунке.
Все тождества с коррелированными углами можно визуализировать, используя следующее.
Теперь давайте рассмотрим несколько примеров, где мы должны применить тождества кофункций, чтобы упростить тригонометрическое выражение. В следующем примере мы будем многократно использовать это тождество для функций косинуса и синуса, в градусов.
Пример 8. Упрощение тригонометрических выражений с использованием тождеств кофункций
Упростить sincos𝜃+(270+𝜃)∘.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические функции.
Чтобы упростить данное выражение, мы используем тождество коррелированного угла cossin(270+𝜃)=𝜃.∘
Следовательно, имеем sincossinsinsin𝜃+(270+𝜃)=𝜃+𝜃=2𝜃.∘
В последнем примере мы хотим повторно применить тождества кофункций к функциям тангенса и котангенса, в градусов, чтобы упростить тригонометрическое выражение.
Пример 9. Использование тригонометрических тождеств для упрощения тригонометрического выражения
Упростить сектанту𝜃𝜃(270+𝜃)∘.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Мы также будем использовать тождество коррелированного угла tancot(270+𝜃)=−𝜃.∘
Поскольку по определению функции котангенса мы имеем хлопок𝜃=1𝜃, коррелированное тождество можно записать в терминах касательной функции как tancottan(270+𝜃)=−𝜃=−1𝜃.∘
Следовательно, выражение можно упростить как
сектантансектансектансек𝜃𝜃(270+𝜃)=𝜃𝜃×−1𝜃=−𝜃×𝜃𝜃=−𝜃.
∘
Давайте закончим повторением нескольких важных ключевых моментов из этого объяснения.
Ключевые моменты
- Мы можем выразить тангенс и обратные тригонометрические функции через синус и косинус как tansincoscsscsinseccoscottancossin𝜃=𝜃𝜃,𝜃=1𝜃,𝜃=1𝜃,𝜃=1𝜃=𝜃𝜃. и мы можем использовать их для упрощения тригонометрических выражений.
- Все эти тригонометрические функции либо четные, либо нечетные. В частности, для функций синуса и косинуса имеем коскоссин(-𝜃)=𝜃,(-𝜃)=-𝜃, и аналогично для других тригонометрических функций, следующих из определений. Мы можем использовать четность тригонометрические функции, которые помогут нам упростить тригонометрические выражения.
- Единичный круг позволяет нам определить тождества коррелированных углов для синуса и косинуса.
Например, тождества кофункций (в радианах): sincoscossin𝜋2−𝜃=𝜃,𝜋2−𝜃=𝜃. Соответствующие тождества для касательной и обратной тригонометрических функций находятся по их определениям.
через функции синуса и косинуса. - Нам часто приходится применять более одного тождества или типа тождества, чтобы упростить тригонометрическое выражение.
через функции синуса и косинуса.Тригонометрические тождества — Все тригонометрические тождества с доказательствами
Тригонометрические тождества являются фундаментальным аспектом тригонометрии, изучающей отношения между углами и сторонами треугольников. Эти тождества представляют собой математические уравнения, которые включают тригонометрические функции, такие как синус, косинус и тангенс, и верны для всех значений задействованных переменных.
Тригонометрические тождества полезны для упрощения выражений, решения уравнений и доказательства математических теорем в различных областях науки и техники. Понимание свойств и приложений этих тождеств важно для студентов и специалистов в таких областях, как математика, физика и инженерия.
1. | Что такое тригонометрические тождества? |
| 2. | Взаимные тождества |
| 3. | Пифагорейские тригонометрические тождества |
| 4. | Дополнительные и дополнительные идентификаторы |
| 5. | Тождества суммы и разности |
| 6. | Периодические тождества |
| 7. | Двойные и половинчатые удостоверения |
| 8. | Трёхугольные удостоверения |
| 9. | Идентичности суммы и произведения |
| 10. | Правило синуса и косинуса |
| 11. | Часто задаваемые вопросы о тригонометрических тождествах |
Что такое тригонометрические тождества?
Тригонометрические тождества являются уравнениями, содержащими тригонометрические функции, и справедливы для любого значения вовлеченных переменных при условии, что обе части равенства определены.
Эти уравнения верны для любого значения переменной, которая есть в области.
Тригонометрические тождества связывают 6 тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Давайте узнаем обо всех тригонометрических тождествах подробно, которые упомянуты ниже.
- Взаимные тождества
- Пифагорейские тождества
- Тождества с противоположными углами
- Дополнительные тождества углов
- Дополнительные удостоверения углов
- Тождества суммы и разности
- Периодические удостоверения
- Идентификаторы с двойным и половинным углом
- Трёхугольные удостоверения
- Суммировать идентификаторы продуктов
- Продукт для суммирования идентификаторов
- Закон синусов и закон косинусов
Взаимные тождества
Мы уже знаем, что обратные величины синуса, косинуса и тангенса равны косекансу, секансу и котангенсу соответственно.
Таким образом, взаимные тождества задаются как
- sin θ = 1/cosec θ (OR) cosec θ = 1/sin θ
- cos θ = 1/с θ (ИЛИ) с θ = 1/cos θ
- tan θ = 1/кот θ (OR) кроватка θ = 1/tan θ
Пифагорейские тригонометрические тождества
Тригонометрические тождества Пифагора в тригонометрии выводятся из теоремы Пифагора. Ниже приведены 3 пифагорейских тригонометрических тождества.
- sin 2 θ + cos 2 θ = 1. Это также можно записать как 1 — sin 2 θ = cos 2 θ ⇒ 1 — 9 3 sin 9 2 90 θ
- сек 2 θ — загар 2 θ = 1. Это также можно записать как сек 2 θ = 1 + тангенс 2 θ ⇒ сек 2 θ — 1 = тангенс 2 θ
- csc 2 θ — детская кроватка 2 θ = 1. Это также может быть записано как csc 2 θ = 1 + детская кроватка 2 θ ⇒ csc 2 θ 9 039 детская кроватка
Давайте посмотрим, как доказать эти тождества.
3 Доказательство тождества Пифагора
Рассмотрим прямоугольный треугольник ABC с прямым углом в точке B, как показано ниже.
Применяя к этому треугольнику теорему Пифагора, получаем
Противоположная 2 + Прилежащая 2 = Гипотенуза 2 … (1)
Разделив обе стороны на гипотенузу 2 6 395 2 / Гипотенуза 2 + Смежное 2 / Гипотенуза 2 = Гипотенуза 2 / Гипотенуза 2
Используя определения тригонометрических соотношений, приведенное выше уравнение принимает вид
- 395 2 θ + cos 2 θ = 1
Это одно из пифагорейских тождеств. Таким же образом мы можем вывести два других пифагорейских тригонометрических тождества.
- tan 2 θ + 1 = сек 2 θ (это можно получить, разделив обе части (1) на «Смежные 2 »)
- 1 + кроватка 2 θ = cosec 2 θ (это можно получить, разделив обе части (1) на «Противоположные 2 »)
Дополнительные и дополнительные идентификаторы
Дополнительные углы — это пара двух углов, сумма которых равна 90°.
Дополнение угла θ равно (90 — θ). Тригонометрические отношения дополнительных углов (также известные как тождества кофункций):
- sin (90°-θ) = cos θ
- cos (90°- θ) = sin θ
- загар (90°- θ) = детская кроватка θ
- косек (90°-θ) = сек θ
- сек (90°- θ) = cosec θ
- раскладушка (90°- θ) = загар θ
Дополнительные углы представляют собой пару двух углов, сумма которых равна 180°. Дополнение угла θ равно (180 — θ). Тригонометрические отношения дополнительных углов:
- sin (180°-θ) = sinθ
- cos (180°- θ) = -cos θ
- тангенс (180°- θ) = -тангенс θ
- косек (180°-θ) = косек θ
- сек (180°- θ)= -сек θ
- раскладушка (180°- θ) = -раскладушка θ
Тождества суммы и разности
Тождества суммы и разности включают формулы sin(A+B), cos(A-B), tan(A+B) и т. д.
- sin (A+B) = sin A cos B + cos A sin Б
- sin (A-B) = sin A cos B — cos A sin B
- cos (A+B) = cos A cos B — sin A sin B
- cos (A-B) = cos A cos B + sin A sin B
- тангенс (A+B) = (тангенс A + тангенс B)/(1 — тангенс A тангенс B)
- загар (AB) = (загар A — загар B)/(1 + загар A загар B)
Периодические тождества
Периодические тождества в тригонометрии представляют собой набор тождеств, описывающих периодический характер тригонометрических функций.
Периодическая функция — это функция, которая повторяет свои значения через определенный интервал, известный как ее период. Вот периодические тождества sin, cos и tan.
- грех(х + 2π) = грех(х)
- потому что (х + 2π) = потому что (х)
- тангенс (х + π) = тангенс (х)
Мы можем попытаться вывести их либо с помощью единичного круга, либо с помощью вышеупомянутых тождеств суммы и разности.
Тождества с двойными и половинными углами
Формулы двойного угла: Тригонометрические тождества двойного угла можно получить, используя формулы суммы и разности.
Например, из приведенных выше формул:
sin (A+B) = sin A cos B + cos A sin B
Подставим здесь A = B = θ с обеих сторон, получим:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin 2θ = 2 sinθ cosθ
Таким же образом мы можем вывести другие тождества двойного угла.
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ — sin 2θ
= 2 cos 2 θ — 1
= 1 — 2sin 2 θ - тангенс 2θ = (2тангенс θ)/(1 — тангенс 2 θ)
Формулы половинного угла: Используя одну из приведенных выше формул двойного угла,
cos 2θ = 1 — 2 sin 2 θ
2 sin 2 θ = 1- cos 2θ
sin 2 θ = (1 — cos2θ)/(2)
sin θ = ±√ 2[(1 — cos θ) 2[(1 — cos 2θ) ]
Замена θ на θ/2 с обеих сторон,
sin (θ/2) = ±√[(1 — cos θ)/2]
Это формула половинного угла sin.
Таким же образом можно вывести и другие формулы половинного угла.
- sin (θ/2) = ±√[(1 — cos θ)/2]
- cos (θ/2) = ±√(1 + cos θ)/2
- тангенс (θ/2) = ±√[(1 — cos θ)(1 + cos θ)]
Трехугольные тождества
Тождества тройного угла — это тригонометрические тождества, связывающие значения тригонометрических функций трехкратного угла со значениями тригонометрических функций самого угла. Формула тройного угла для синуса может быть получена следующим образом.
Мы можем записать sin 3x как:
sin (3x) = sin (2x + x)
= sin 2x cos x + cos 2x sin x
Используя формулу двойного угла для синуса,
sin 3x = 2 sin x cos x cos x + cos 2x sin x
Теперь, используя тождество Пифагора и формулу двойного угла для cos,
= 2 sin x (1 — sin 2 x) + ( 1 — 2sin 2 x) sin x
= 2 sin x — 2 sin 3 x + sin x — 2 sin 3 x
= 3 sin x — 4 sin 3 x
3 9 таким образом, мы можем вывести и другие формулы тройного угла.
- sin(3x) = 3sin(x) — 4sin 3 (x)
- cos(3x) = 4cos 3 (x) — 3 cos x
- tan(3x) = (3 tan x — tan 3 x)/(1 — 3tan 2 x)
Идентичности суммы и произведения
Эти тождества используются либо для преобразования «суммы в произведение» или «произведения в сумму» в случае тригонометрических функций.
Сумма тождеств продукта: Эти тождества равны
- sin A + sin B = 2[sin((A + B)/2)cos((A − B)/2)]
- грех А — грех В = 2 [cos ((А + В) / 2) грех ((А — В) / 2)]
- потому что А + потому что В = 2 [потому что ((А + В) / 2) потому что ((А — В) / 2)]
- потому что A — потому что B = -2[sin((A + B)/2)sin((A — B)/2)]
Произведение на сумму тождеств: Эти тождества таковы:
- sin A⋅cos B = [sin(A + B) + sin(A − B)]/2
- потому что A⋅cos B = [cos(A + B) + cos(A − B)]/2
- sin A⋅sin B = [cos(A − B) − cos(A + B)]/2
Правило синусов и косинусов
Тригонометрические тождества, которые мы узнали, выводятся с помощью прямоугольных треугольников.
Есть несколько других тождеств, которые мы используем в случае непрямоугольных треугольников.
Правило синусов: Правило синусов определяет соотношение между углами и соответствующими сторонами треугольника. Для непрямоугольных треугольников нам придется использовать правило синусов и правило косинусов. Для треугольника со сторонами «a», «b» и «c» и соответствующими противоположными углами, равными A, B и C, правило синусов может быть задано как 9.0003
- а/sinA = b/sinB = c/sinC
- sinA/a = sinB/b = sinC/c
- а/б = sinA/sinB; а/с = sinA/sinC; б/с = sinB/sinC
Правило косинуса: Правило косинуса дает отношение между углами и сторонами треугольника и обычно используется, когда даны две стороны и угол между ними. Правило косинуса для треугольника со сторонами «a», «b» и «c» и соответствующими противоположными углами A, B и C, правило синуса может быть указано как,
- а 2 = b 2 + с 2 — 2bc·cosA
- b 2 = c 2 + a 2 — 2ca·cosB
- с 2 = а 2 + b 2 — 2ab·cosC
Важные замечания по тригонометрическим тождествам:
- Чтобы записать тригонометрические отношения дополнительных углов, мы рассмотрим следующие пары: (sin, cos), (cosec, sec) и (tan, cot).
- При записи тригонометрических отношений дополнительных углов тригонометрическое соотношение не изменится. Знак можно определить, используя тот факт, что только sin и cosec положительны во втором квадранте, где угол имеет форму (180-θ).
- Есть 3 формулы для формулы cos 2x. Вы можете запомнить только первое, потому что два других можно получить с помощью тождества Пифагора sin 2 x + cos 2 x = 1.
- Формула половинного угла для tan получается путем применения тождества tan = sin/cos и последующего использования формул половинного угла для sin и cos.
☛ Связанные темы:
- Тригонометрические тождества для класса 12
- Тригонометрические тождества Класс 11
- Тригонометрические тождества Класс 10
Примеры тригонометрических тождеств
Пример 1: Докажите следующее тождество, используя тригонометрические тождества:
[(sin 3θ + cos 3θ)/(sin θ + cos θ)] + sin θ cos θ = 1
Решение:
Мы используем следующее тождество:
a 3 +b 3 = (a+b)(a 2 -ab+b 2 )
Для доказательства тождеств Пифагора это тождество.
Л.Х.С. = [(sin 3θ + cos 3θ)(sin θ + cos θ)] + sin θ cos θ
= [(sin θ + cos θ)(sin 2 θ — sin θ cos θ + cos 2 θ )(sin θ + cos θ) + sin θ cos θ
= (sin 2 θ — sin θ cos θ + cos 2 θ) + sin θ cos θ
= sin 2 θ + cos 2 θ
= 1 = R.H.S.
Ответ: Данное тождество доказано.
Пример 2: Докажите следующее тождество, используя тождества тригонометрии:
(sin θ + cosec θ) 2 + (cos θ + sec θ) 2 = 7 + cottan 5 2 09 9 θ θ
Решение:
Мы используем взаимные тождества и тождества Пифагора, чтобы доказать это тождество.
L H S = (sin 2 θ + cosec 2 θ + 2 sin θ cosec θ) + (cos 2 θ + sec 2 θ + 2 cos θ 9 sec
θ) θ + cos 2 θ + cosec 2 θ + sec 2 θ + 2 + 2= 1 + (1 + ctg 2 θ) + (1 + tan 2 + 2 2
= 7 + загар 2 θ + кроватка 2 θ = правая сторона
Ответ: Данное тождество доказано.
Пример 3: Найдите точное значение sin 75°, используя тождества триго.
Решение:
Мы знаем, что 75° = 30° + 45°
Применим тождество суммы sin, чтобы найти значение sin 75°.
sin (A+B) = sin A cos B + cos A sin B
Замените здесь A = 30° и B = 45° с обеих сторон:
sin (30° + 45°) = sin 30° cos 45°+ cos 30° + sin 45°
sin 75° = (1/2)⋅(√2/2) + (√3/2)⋅(√2/2)
sin 75° = (√ 2 + √6)/4 = (√3 + 1)2√2
Здесь значения sin 30°, cos 45°, cos 30° и sin 45° можно получить с помощью тригонометрической таблицы.
Ответ: sin 75°= (√3 + 1)/2√2
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Практические вопросы по тригонометрическим тождествам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о тригонометрических тождествах
Что такое тригонометрические тождества в тригонометрии?
Тригонометрические тождества — это равенства, включающие тригонометрические функции и истинные для каждого значения вовлеченных переменных таким образом, что обе части равенства определены.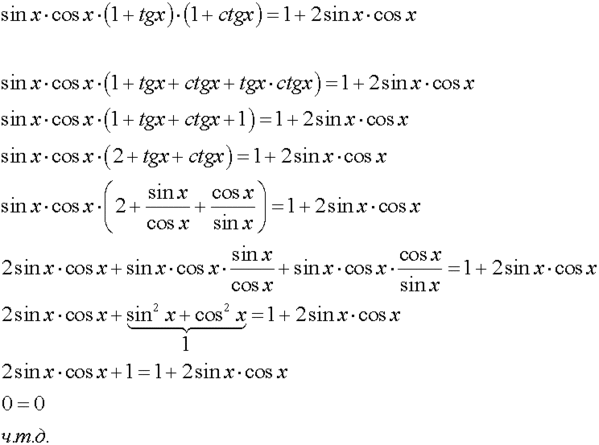
Некоторые важные тождества в тригонометрии задаются следующим образом:
- sin θ = 1/cosec θ
- cos θ = 1/сек θ
- загар θ = 1/кот θ
- sin 2 θ + cos 2 θ = 1
- 1 + тангенс 2 θ = сек 2 θ
- 1 + кроватка 2 θ = cosec 2 θ
Что такое 3 тригонометрических тождества?
Три тригонометрических тождества задаются как
- sin 2 θ + cos 2 θ = 1
- 1 + тангенс 2 θ = сек 2 θ
- 1 + кроватка 2 θ = cosec 2 θ
Для чего используются тригонометрические тождества?
Основные области применения тригонометрических тождеств включают:
- Упрощение выражений: Тригонометрические тождества позволяют нам упростить сложные тригонометрические выражения, заменяя их более простой формой, что может быть полезно при решении тригонометрических уравнений, построении графиков тригонометрических функций и упрощении вычислений. .
- Решение уравнений: Тригонометрические тождества можно использовать для решения тригонометрических уравнений путем преобразования их в более простые формы. Это часто делается с использованием более чем одного тождества, чтобы привести уравнение к более легко решаемой форме.
- Доказательство теорем: Тригонометрические тождества часто используются при доказательстве математических теорем, особенно в геометрии и исчислении. Используя их, математики могут установить справедливость различных геометрических и математических формул.
- Вычисление значений : Тригонометрические тождества используются для вычисления значений тригонометрических функций, таких как синус, косинус и тангенс, для различных углов. Это важно во многих приложениях, таких как навигация, геодезия и инженерия.
.Как доказать тригонометрические тождества?
Тригонометрические тождества можно доказать, используя другие известные пифагорейские и тригонометрические тождества.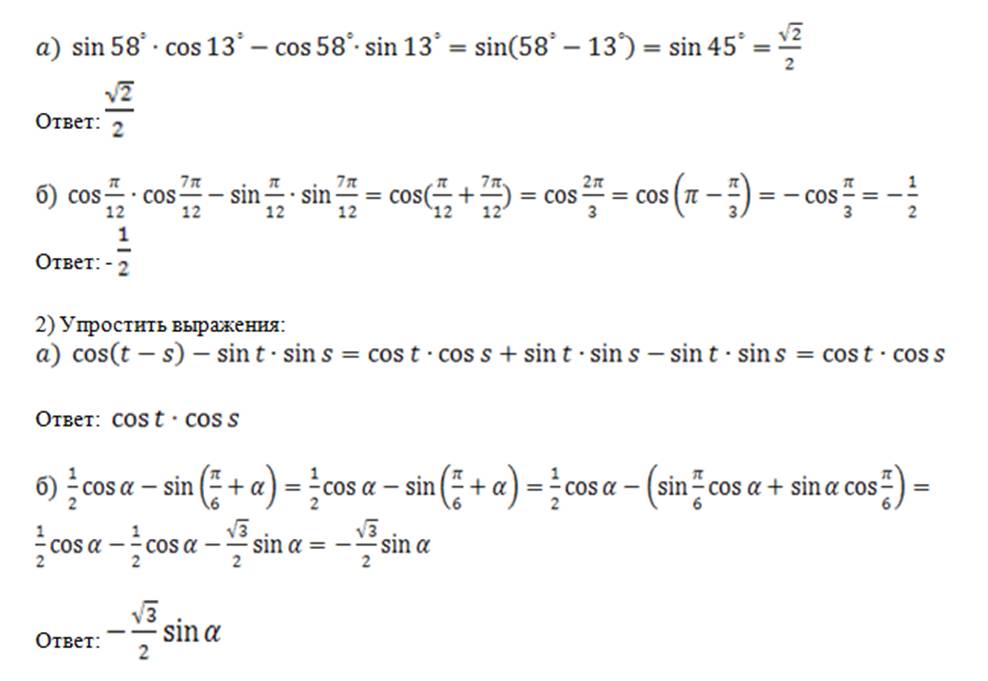
Мы также можем использовать некоторые тригонометрические соотношения и формулы для доказательства тригонометрических тождеств.
Что такое тождества противоположных углов в тригонометрии?
Тождества противоположного угла говорят о том, что происходит с коэффициентами триггера, когда угол отрицательный. Они следующие:
- sin(-x) = — sin x; csc(-x) = — csc х
- cos(-x) = cosx; сек(-х) = сек х
- тангенс(-х) = — тангенс х; детская кроватка (-x) = — детская кроватка x
Эти тождества могут быть получены из определений тригонометрических функций и свойств единичной окружности.
Как вы решаете уравнения с триггерными тождествами?
С помощью тригонометрических тождеств можно решать различные математические задачи. Мы можем преобразовать уравнения в параметрические уравнения, а затем применить тригонометрические тождества для их решения.
Какие тригонометрические тождества мы должны знать?
При решении задач используются все триггерные тождества.