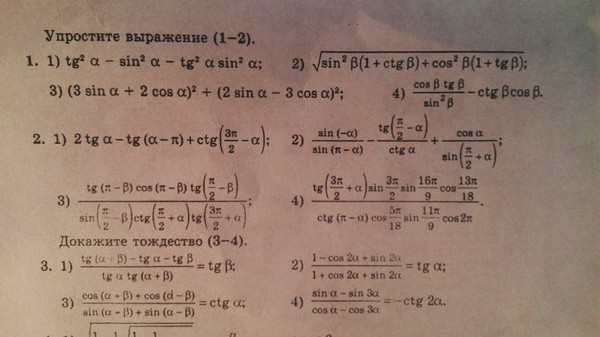Упрощение выражений — видеоурок по математике за 5 класс
Упрощение буквенных выражений позволяет сократить время при решении таких примеров и делать их легче, тем самым за более короткий промежуток времени человек может решить большее количество выражений.
В математической науке нередко возникают примеры, которые записываются в короткой форме, то есть упрощенные.
Определение. Упрощение выражений — преобразования, в которых позволяет заменить выражение равным ему с меньшим числом действий.
Замена на эквивалентное выражение помогает упростить выражение:
Числовые выражения это такие выражения, которые состоят из чисел, знаков действий и скобок по возможности.
Для выявления эквивалентного значения нужно выполнить следующий алгоритм:
Выполнить действия
Воспользоваться свойствами сложения, вычитания, умножения и деления для упрощения вычислений.
Законы суммирования и вычитания:
Обратите внимание. Сочетательное свойство сложения:
К первому числу прибавляют сумму второго и третьего числа для того, чтобы прибавить число к сумме чисел.
а+(b+c)=(a+b)+c
Переместительность свойства сложения
От перемены мест слагаемых сумма не меняется
а+b=b+a
Важно знать. Свойство вычитания суммы из числа:
Каждое число можно отдельно вычесть, чтобы вычесть сумму из числа.
а-(b+c)=a-b-c
Свойства умножения и деления
Распределительный закон умножения:
Для того, чтобы число умножить на сумму, необходимо умножить его на каждое слагаемое по отдельности.
а(b+c)=ab+ac
Сочетательное свойство
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
a(bc)=(ab)c
Запомните. Закон перемещения в умножении:
От перестановки множителей произведение не меняется.
аb=ba
Запомните. Свойства сложения, вычитания, умножения и деления имеют пользу в том, что они позволяют преобразовывать суммы и произведения в удобные выражения для вычислений.
Главный и очевидный плюс сочетательного, переместительных свойств это то, что они используются в упрощении выражений:
7*а*2=7*2*а=14а
Распределительное свойство умножения относительно сложения
10а+5а=15а
Правило. Распределительное свойство умножения относительно сложения:
Распределительное свойство умножения относительно сложения:
Каждое число нужно умножить на множитель и сложить для того, чтобы умножить сумму на число.
(а+b)*c= ac+bc
Выражение:
(5+1)*4=6*4=24
5*4+1*4=20+4=24
Распределительное свойство умножения относительно вычитания:
Важно знать. Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
(а-b)*c=a*c-b*c=ac-bc
(10-2)*3=8*3=24
(10*3)-(2*3)=30-6=24
Иногда используют сочетательный закон умножения:
3y*7*2=(3*7*2)*y=42*y=42y
Упрощение:
6а+18а+13а при а=12
6*12+18*12+13*12=72+216+156=444
Упрощаем:
6a+18a+13a=37а
37*11=407
Алгоритм решения без упрощения:
- Подстановка значения вместо буквы
- Умножение цифр на подставленное значение вместо букв
- Сложение перемноженных значений
- Алгоритм решения с упрощением:
- Суммирование буквенного выражения
- Подстановка значения вместо буквы и перемножение
Самое главное запомнить, что складывать можно складывать только одинаковые буквы.
Также можно вынести а за скобку как при распределительном законе умножения
6а+18а+13а
а*(6+18+13)
a*37=37a
Коэффициент — число, стоящее перед буквенным значением.
Другой пример:
2(6-4х)+15х — 10 = 12 — 8х + 15х — 10 = 7х +2
Вывод. Распределительные законы умножения относительно умножения, сложения и вычитания, а также методы упрощения помогают ускорить процесс решения задач и примеров.
Домашнее задание.
Составьте буквенное выражение по условию задачи и найдите его значение:
Составили 3 букета из роз и 5 букетов из хризантем. В каждом букете по а цветков.
Ответьте на вопросы:
- Сколько всего цветков в букетах роз?
- Сколько всего цветков в букетах хризантем?
- Сколько всего цветков в букетах роз и хризантем? Вычислите при а=7
Поделиться статьей в соцсетях
Остались вопросы?
Наши репетиторы помогут
Остались вопросы?
Разработка урока по математике «Упрощение выражений»
Упрощение выражений
Тип урока: Урок обобщения и систематизации знаний
Цели урока:
Обучающие — повторить, обобщить и систематизировать знания по данной теме, совершенствовать умения и навыки учащихся упрощать выражения,
Развивающие — способствовать развитию математического слуха, речи, счетных навыков и мышления; развивать познавательный интерес через использование межпредметных связей, культуру математической речи, логическое мышление;
Воспитательные — побуждать учащихся к само и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели.

Задачи урока:
Закрепить навыки умения упрощать выражения;
Формировать развитие мышления, счетных навыков;
Возбудить интерес учебными действиями к урокам математики
Основные средства обучения:
компьютер, проектор, карточки, тесты , домашнее задание, презентация
Форма урока: Комбинированный
Ход урока
I. Организационный момент.
слайд 1. Здравствуйте, ребята! Садитесь! Сегодня у нас будет необычный урок.
II. Актуализация знаний.
Слайд 2. 1) Повторение теоретического материала, повторение свойств сложения — работа со слайдом:
a+b = b+a — переместительное свойство сложения
a * b = b * a — переместительное свойство умножения
(a+b)+c = a+(b+c) — сочетательное свойство сложения
(a * b) * c = a * (b * c) — сочетательное свойство умножения
(a+b) * c=ac+bc распределительное свойство умножения относительно сложения
(a-b)c=ac-bc распределительное свойство умножения относительно вычитания
Слайд 3. Где применяли мы эти законы?(Для упрощения) Итак: «Упрощение выражений» — такова тема нашего урока
Где применяли мы эти законы?(Для упрощения) Итак: «Упрощение выражений» — такова тема нашего урока
III. Постановка цели и задач урока. Мотивация учебной деятельности
Упрощение выражений» — такова тема нашего урока. Открыли тетради, записали дату, « Классная работа». Cкажите, а вы знакомы с этой темой? Как вы думаете, зачем нам нужно упрощать выражения? (учащиеся отвечают — повторить способы упрощения выражений, закрепить навыки решения уравнений и задач и т.д.)
Слайд 4,5. 2) Устный счет. Какие трудные примеры? Можно ли их вычислить устно?
Решение каждого примера комментируется (каким свойством вы воспользовались?)
Нужно объяснить, что означают записанные равенства. На корабле а — офицеров, в — матросов.
Что означают следующие равенства?
Решение каждого примера комментируется (каким свойством вы воспользовались?)
125 * 68 * 8 = 68000 —
192 * 135 — 92 *135 = (192 — 92)135= 13500
13 * 101 = (100+1)13=1313 —
199 * 7 = (200-1) 7 = 1393 –
IV. Применение умений и навыков.
Применение умений и навыков.
1.Решение уравнений.
Слайды 6 Решение уравнений (у доски)
Самопроверка. Затем все проверяем решения (на слайде 7)
Задайте по одному вопросу ребятам у доски.
2. Контроль усвоения. Тестирование — слайд 8
У вас на столах лежат листочки с тестами. Подпишите их. Выберите верный ответ и обведите его (Прил. 1)
Приступайте к решению. Время истекло. Проверяем
Вариант 1
1.Укажите верное равенство:
1) (x+4) * 3=x+12; 2) 6(m-10)=6m+60; 3) (2-a) * 8=16-a; 4) 4(k+12)=4k+48
2. Упростить выражение 13 * z * 6
1) 18z 2) 78z, 3) 78, 4) 68
3. Упростить выражение 15х + 12+ 6х:
1) 33х, 2) 15х+ 18, 3) 21х+12, 4) 33
Итог: 423 — шелчок
Вариант 2
1.Укажите верное равенство:
1) (m+7) * 2=m+14; 2) 11(x-10)=11x-110; 3) (15+y) * 3=45+y; 4) 5(12-c)=60+5c
2. Упростить выражение 11 * у * 7
1) 17у 2) 77 3) 77у 4) 117у
3. Упростить выражение 14х- 5+8х:
Упростить выражение 14х- 5+8х:
1) 17х, 2) 22х+5, 3) 27х, 4) 22х-5
Итог: 234 — шелчок
V. Физкультминутка.
Слайд 9. Вы видите примеры с ответами на слайдах, если вы согласны, то поднимаете руки вверх, если нет — опускаете вниз.
Слайд 10. Если вы согласны, то голову наклоняем вниз, если нет — назад
VII. Воспроизведение знаний на новом уровне.
Слайд 11. Встает еще одна проблема. Нужно немного подумать — «Угадай-ка». Угадайте корень уравнения:
Чем вы воспользовались?
3. Применение умений и знаний в жизненной(проблемной) ситуации
Решаем задачи. — слайд 12 Вспомним, как решаются задачи на части
Наверное, у всех есть комнатные растения. Если они начинают портится, то что предпринимают ваши родители? Вот и мы, решим практическую задачу.
Слайд 13. Для приготовления смеси для рассады берут 1 часть торфа, 2 части перегноя и 5 частей земли. Сколько килограммов торфа, перегноя и земли надо взять для приготовления 72 кг смеси для рассады?
Составим план решения задачи. Обозначаем массу 1 части за х кг.
Обозначаем массу 1 части за х кг.
Слайд 13. Что нужно иметь, чтобы приготовить данную смесь? Торф, перегной и землю. Сколько частей торфа? 1 часть — ? кг, сколько перегноя — 2 части — ? кг, земли — 5 частей — ? кг. Всего 72кг.
Слайд 14. Как же решить такую задачу? Обозначаем массу 1 части за х кг.
Торфа — х кг, перегноя — 2х кг, земли — 5х кг. Всего (х+2х+5х)кг, что по условию задачи составляет 72 кг. Составим и решим уравнение: Х+2х+5х=72
К доске пойдет…. решит уравнение и ответит на вопрос задачи (решает за доской). Первые 3 человека, решившие правильно задачу получают дополнительный балл.
Х+2х+5х=72,
9х=72,
х=8 кг — 1 часть — торф
Что нужно еще найти в задаче? Количество земли — 8 * 5 = 40 кг, количество перегноя — 2 * 8=16 кг
Для решения каких практических задач нужны знания сегодняшнего урока? Посмотрите, какую задачу решает кондитер (слайд 15), фармацевт (слайд 16), в химической промышленности (слайд 17), строители (слайд 18) и т.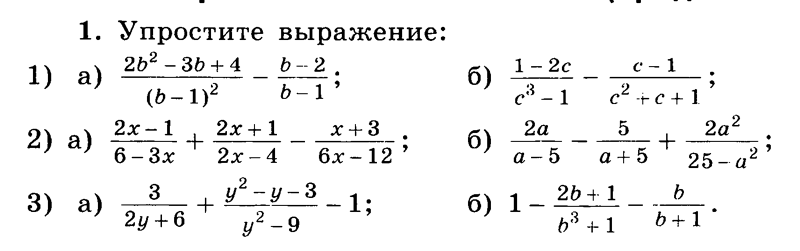 д.
д.
2. Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба?
VI. Итог урока – слайд 20
Подведём итоги нашего занятия: слайд 19
1. Знания, каких законов математики помогло вам справиться с заданиями?
2. В каких прикладных задачах их можно применять?
Домашнее задание. П.14, найти или придумать задачу по теме, карточки
Даю вам творческое задание на дом — спросить у родителей, применяют ли они такие задачи в быту, в профессиональной деятельности, составить их и оформить на листах А4.
Ещё карточки с заданиями (задания карточек по уровням сложности). Решив верно задания, разукрасим лесовика. А также вы получили творческие задания — составить практическую задачу на части. (Приложение 2)
VII/ Рефлексия. У вас на столе есть геометрические фигуры. Если вам урок очень понравился, то положите в сундучок круг, если не очень — квадрат, если вам было неуютно — треугольник.
(Слайд 20) Рефлексия.
Ребята, я прошу вас дать самооценку своей деятельности на уроке.(Каждому выдаётся лицо, ребятам необходимо нарисовать рот)
– Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. | – Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно. | – У меня не было желания работать. Сегодня не мой день. |
Что такое Simplify? Определение, пример, факты
Упростить просто означает сделать это простым. В математике просто или упрощение означает приведение выражения/дроби/задачи к более простой форме. Это упрощает задачу с расчетами и решением. Мы можем —
Давайте разберем пошаговую процедуру упрощения дробей на нескольких примерах.
Знаете ли вы, что вместо того, чтобы исключать общие множители в несколько шагов, мы можем сделать это и в один шаг. Это дает ту же простейшую форму дроби.
Математические выражения представляют собой комбинацию различных чисел и операций. Итак, чтобы упростить их, нам нужно знать правило, известное как порядок операций. Он сообщает нам правильную последовательность, в которой должны выполняться операции при упрощении математического выражения. Мы можем запомнить порядок, используя аббревиатуру PEMDAS.
Simplyfly $1\frac{4}{7}\times 2\frac{4}{33} \div \frac{5}{9}$ Преобразование смешанной дроби в неправильную
1 Упростите выражение: 15 + 10 ÷ 5 = ?17 15 5 10 Правильный ответ: 17 2 Упростить выражение: 4 + (3 x 4 ) ÷ 224 7 10 12 Правильный ответ: 7 3 Какова простейшая форма дроби $\frac{12}{36}$ ?$\frac{3}{9}$ $\frac{1}{3}$ $\frac{3}{4}$ $\frac{1}{36}$ Правильный ответ: $\frac{1}{3}$ 4 Упростим выражение: $18 – [6 – {4 – ( 8 – 6 + 3 )}]$$11$ $20$ $7$ $27$ Правильный ответ: $11$ |
Что такое упрощение ?
Упрощение — это процесс замены математического выражения эквивалентным, более простым, обычно более коротким.
Как упростить математические выражения?
Порядок операций играет важную роль в упрощении математических операций. Правильный порядок операций: слагаемые в скобках, показатели степени, умножение, деление, сложение и, наконец, вычитание. Удобная аббревиатура, которую вы можете использовать, чтобы запомнить это, — PEMDAS.
Как упростить дроби?
Говорят, что дробь имеет простейшую форму, если 1 является единственным общим делителем ее числителя и знаменателя. Таким образом, чтобы упростить дробь, разделите числитель и знаменатель на их наибольший общий делитель.
Это были основные правила и преимущества упрощения в математике. Каждый ребенок должен изучить эту концепцию, так как она позволяет относительно легко решать сложные задачи. Если вы ищете платформу для обучения вашего ребенка математике с помощью веселых игр, попробуйте SplashLearn, зарегистрировавшись бесплатно. Поскольку математика может быть сложной для некоторых детей, веселые игры и головоломки делают ее интересной и гораздо более всеобъемлющей! Чтобы узнать больше о концепциях упрощения и других математических темах, посетите нас по адресу: https://www.