Упрощение выражений с степенями и корнями: Упрощение выражений, содержащих корни и степени

«Корни, степени и логарифмы» (10 класс)

ГЛАВА 2. КОРНИ, СТЕПЕНИ И ЛОГАРИФМЫ

 

Смотри в корень!

Козьма Прутков

 

                Вторая экскурсия на воображаемой машине времени начинается. Мы отправляемся в Древнюю Грецию, и видим, что математиками уже используются выражения квадрат и куб числа при вычислениях площадей и объемов. Далее переносимся в средневековую Францию XIV-VI веков, где учеными применяются степени с дробным показателем, а вот и знаменитый Декарт чертит знак корня с полкой сверху! Однако, нам пора в Англию XVI века к шотландскому математику Дж.Неперу. Что мы видим? Он изобретает таблицу логарифмов, которые, по словам Лапласа, удлинили жизнь вычислителей! Теперь нам пора возвратиться в колледж, где продолжается изучение студентами новых действий с числами!

 

                                                                                                                                         § 5.

Степени с натуральными и целыми показателями

 

1.Действие возведения в степень, понятие и свойства. Познакомимся с пятым алгебраическим действием, широко применяющимся в математике, кроме известных четырех арифметических – возведение числа в степень, которое позволяет упростить действие умножения одинаковых сомножителей.  Рассмотрим определение этого понятия.                                                                                                          Определение: n-ной степенью числа а называют произведение n одинаковых сомножителей, равных а (:

Здесь а называется основанием степени, а n – показателем степени. Обозначается n — ная степень числа а через аⁿ.      

         Например,    .                               Названия второй степени числа – «квадрат», а третьей – «куб» появились еще в глубокой древности и дошли до наших времен.

На практике обычно используются: 

Свойства степеней с натуральным показателем (:

 

;  ;    ;

;  , где ().

 

Пример 1.Вычислить .

Решение:    

Пример 2. Вычислить  .

Решение:  

Пример 3. Вычислить (  

Решение: (  

Пример 4. Вычислить   .

Решение: 

Пример 5. Вычислить    .

Решение:

 

2. Степени с целым показателем. (

Для них справедливы все свойства степеней с натуральным показателем. Рассмотрим определения степени с нулевым и отрицательным показателями (; .

         Определение: нулевая степень числа  равна единице:

 .

         Определение: степень  числа  с отрицательным  показателем равна дроби, у которой в числителе единица, а в знаменателе степень  числа  с показателем, противоположным данному:

.

Нулевая и отрицательная степень числа 0 не определяются!

 

Пример 1. Вычислить  (-3)⁰. 

Решение: По определению степени с нулевым показателем имеем: (-3)⁰=1. 

Пример 2. Вычислить   .

Решение:   

Пример 3. Вычислить     

Решение: Используем то, что 6 = 2×3, и применяя правила действий с целыми степенями:

 

3. Корни. Действие извлечения (отыскания) корня является обратным возведению в степень и рассматривается как шестое алгебраическое действие с числами.                                                                                                         

Определение: если  , где (. Здесь

— подкоренное выражение. n – показатель корня, b называется корнем n—й степени из числа . Таким образом, корнем n—й степени из числа называется каждое число b такое, что его n—я степень равна  

         Например, если , то . Здесь b=2, a=8, n=3. Таким образом,  .                                                                                                                                           Если показатель корня n нечетное число, то для любого действительного числа  существует только одно значение корня степени n. Знак корня

b соответствует знаку числа , стоящего под корнем.

         Пример 1. Вычислить  

         Решение: Здесь число а=27> 0, тогда значение корня из этого числа b=3>0. Имеем    .

         Пример 2. Вычислить  .

         Решение: Имеем Здесь число а=–32<0, тогда значение корня из этого числа b=–2<0. 

         Если показатель корня n четное число, то корни четной степени из отрицательного числа а на множестве действительных чисел не существуют.

         Однако, на множестве мнимых и комплексных чисел корни из отрицательных чисел существуют (см. главу I § 3).

         Для любого положительного числа а корень четной степени n имеет два значения, равные по абсолютной величине и противоположные по знаку

.    

         Пример 1. Вычислить . на множествах действительных

чисел. 

         Решение:  не имеет действительных корней, т.к. под корнем четной степени стоит отрицательное число. 

         Пример 2. Вычислить .

         Решение: .

         Корень из нуля при любом показателе n равен нулю. 

         Современное обозначение корня придумано Рене Декартом в виде знака радикала с полкой: , а показатель корня к этому знаку был введен Исааком Ньютоном в виде:  . Распространение получили корни второй степени (квадратные корни) и третьей степени (кубические  корни) .

         Следует обратить особое внимание на следующие два выражения с корнями из произвольного действительного числа а:

         1) при нечетном n:    ;

         2) при четном n:    .

         Например, , но .

 

         На практике преимущественно выполняются действия с положительными значениями корней, из-за их простоты.  

 

 

 

 

 

4. Арифметический корень. Рассмотрим определение этого понятия и его свойства.                                                                                                           Определение: арифметическим корнем называется положительный корень четной степени из положительного числа.                                                       Например, ;  ;

                                                       

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Как называется алгебраическое действие, заменяющее умножение одинаковых сомножителей?

2. Как определяется степень числа с натуральным показателем?

3. Что такое показатель  и основание степени?

4. Какие свойства имеются у степеней с натуральным показателем?

5. Как определяется степень с нулевым показателем?

6. Как определяется степень с отрицательным показателем?

7. Как понятие корня связано с понятием степени?

8. Как определяется арифметический корень?

9. Какие свойства имеет арифметический корень?

 

§ 6. Степени с рациональными показателями

 

1. Определение и свойства степеней. Известно, что сложение и вычитание можно объединить в алгебраическое сложение, а деление представить, как умножение на число обратное, данному числу. Оказывается и возведение в степень числа с рациональным показателем, возможно представить через корень  из этого числа соответствующей степени. Рассмотрим с этой целью задачу.

   Решение:

       

 

         

         Следовательно, можно дать определение  произвольной степени числа с рациональным показателем, объединив ее с корнем из того же числа.

         Определение:  степенью числа  с рациональным показателем , где  называется число вида:

 .

Эта формула определяет переход от степени с рациональным (дробным) показателем к корню и наоборот.                                                                Например,

 

2.Свойства степеней с рациональными показателями. Для любых рациональных чисел p и q  при положительных основаниях  верны равенства, задающие их свойства:

 

 

         Таким образом, для степеней с рациональным показателем справедливы все свойства степеней с целым показателем.

 

 

 

        

Отметим еще два свойства степеней с рациональными показателями:

        

         1) Пусть r – рациональное число и  b >> 0 , Тогда

   при  r > 0,

 при  r  0.

 

 

         2) Для любых рациональных чисел r и s   из неравенства r > s   следует, что

 при ,

      при .

 

         Вывод: Степени можно сравнивать, если равны их основания или равны их показатели.

 

         Свойства степеней 1) и 2)  используются при сравнении чисел.

Пример 1.

Решение: Представим корни в виде степеней с дробным показателем, а дроби в основаниях степеней приведем к общему знаменателю:

          ;  , тогда по  первому свойству          при   r =>0 получим < , или  < .

 

 

Пример 2.

Сравнить числа:  и   .

 

Решение:  Приведем корень к степени с дробным показателем и основанием 2:

.

По второму свойству степеней при а =2>1 получим:  2¹ >  , или

> .

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Какова связь корня и степени с рациональным показателем?

2. При каком основании определяется степень с рациональным показателем?

3. Какие свойства имеют степени с рациональным показателем?

4. Какие свойства степени с рациональным показателем применяются для сравнения чисел?

5. Возможно ли сравнение степеней с разными основаниями?

6. При каком условии можно сравнивать степени с разными показателями?

 

 

 

§ 7. Степени с действительными показателями

 

1.Понятие степени с действительным показателем. Рассмотрим степень положительного числа  при произвольных действительных показателях. Следует определить степень с иррациональным показателем , где х – иррациональное число. В основу определения кладется последовательное приближение х рациональными числами. Например, для рассматриваются приближения по недостатку и по избытку для  и возводить 3 в соответствующие рациональные степени:

,

,

,

………………

По мере увеличения точности приближения левые и правые части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее число совпадающих десятичных знаков, которые и будут приниматься за рациональное приближение иррационального числа .

         При любом  и любом а > 0 степень  является положительным действительным числом:

 

 

2.Свойства степени с действительным показателем. Рассмотрим выражение степени при нулевом основании:

При таком определении степени с действительным показателем для них справедливы все свойства степеней с рациональным показателем, рассмотренные выше. Доказательства этих свойств рассматриваются в курсе высшей математики.

         При сравнении чисел, являющихся степенями с действительным показателем,  используют также следующие два  их свойства:

         1) если  а > 1 и > 0, то при  следует ;

         2) если  0 <а < 1 и > 0, то при  следует .

         Пример 1. 

         Решение: Сравним показатели  и . , , т.к. 5>1 и 12<18, то по первому свойству  .

         Пример 2.

         Решение: Так как , то . Сравним показатели: так как , то , тогда по второму свойству .

Кроме сравнения чисел важно научиться выполнять действия  над числами и переменными, обозначенными буквами.

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Как определяется степень числа с действительным показателем?

2. Для какого основания определена степень числа с действительным показателем?

3. Как определяется степень числа с иррациональным показателем?

4. Каковы свойства степени с действительным показателем?

5. Как определяется степень с действительным показателем при нулевом основании?

6. Имеет ли смысл степень с действительным показателем при нулевом основании и отрицательном показателе?

 

        

                                                                                                                                           § 8. Преобразование алгебраических выражений

 

1.Виды алгебраических выражений. Из чисел и переменных с помощью алгебраических действий и скобок составляются алгебраические выражения.

         Определение: Алгебраическое  выражение – запись, указывающая алгебраические действия над некоторыми числами и буквами.       Примеры алгебраических выражений:

         1);  2) ;  3) ;  4);

         5) ;  6);  7) ;  8) ;  9) .

 

         Простейшее алгебраическое выражение – одночлен является произведением числовых и буквенных сомножителей.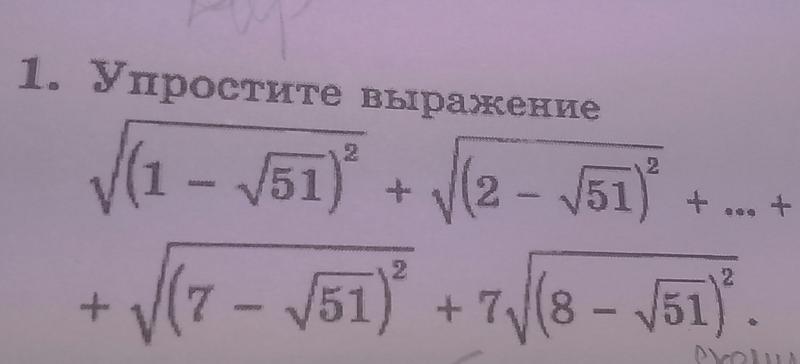

          Алгебраическая сумма одночленов называется  многочленом.

Примерами одночленов и многочленов являются выражения 1), 2) и 3), приведенные выше.

         Алгебраические выражения разделяются на рациональные и иррациональные.

Рациональные алгебраические выражения содержат рациональные действия над буквенными величинами: сложение, вычитание, умножение, деление и возведение в степень с натуральным и целым показателем. Такое выражение обычно представляется как алгебраическая дробь  – частное от деления одночленов или многочленов.

         Иррациональные алгебраические выражения – содержат кроме указанных алгебраических действий знаки радикала или степени с рациональным показателем и действия над ними, поэтому такие выражения часто называют степенными.

Примеры рациональных алгебраических выражений: 1)–5) и 7), а иррациональных выражений: 6), 8) и 9).

 

2.Тождественное преобразование алгебраических выражений. При таком преобразовании исходное выражение заменяется другим тождественно равным ему алгебраическим выражением.

         Например, ;  при  – тождественные преобразования рационального и иррационального алгебраических выражений.

         Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных или букв.

         Тождествами являются все формулы сокращенного умножения, свойства корней и степеней, рассмотренные выше и другие выражения.

         Примеры тождеств: ;  при ;     при .

         Для упрощения различных алгебраических выражений используют формулы сокращенного умножения, разложение многочлена на множители, сокращение дробей и др. способы. Они рассматривались в 9 классе средней школы.

         Цель преобразования любого рационального алгебраического выражения, как правило, представление его в виде дроби, числитель и знаменатель которой –  целые рациональные выражения.

         Например,

         Упростить выражение: :.

         Решение:

         1) ;

         2)=   =;

         3) : = =.  

        

         Преобразования иррациональных алгебраических выражений выполняются с использованием свойств корней, степеней и общих приемов упрощения алгебраических выражений.

         Пример 1.

         Пример 2.

 

         Пример 3.

         Обычно ответ записывается так, чтобы в знаменателе не содержалась иррациональность. Для освобождения от иррациональности в знаменателе дроби  умножается и числитель, и знаменатель на – это выражение называется сопряженным знаменателю , т.е. дополняющим знаменатель до рационального выражения. Получим:

.

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Как определяется алгебраическое выражение?

2. Как называется простейшее алгебраическое выражение?

3. Чем отличается одночлен от многочлена?

4. Какие алгебраические выражения называются рациональными?

5. Каково определение рациональной дроби?

6. Чем отличается рациональное алгебраическое выражение от иррационального?

7. Какова цель преобразования рационального алгебраического выражения?

8. Как освободиться от иррациональности (корней) в знаменателе дроби?

 

                                                                                                                     

§ 9. Логарифмы

 

1. Введение в теорию логарифмов. На рубеже XVI–XVII веков бурно развивающиеся астрономия и физика столкнулись с необходимостью решать математические задачи по определению расстояний до планет, нахождением их размеров, масс и т.д., где требовалось вычислять степени с рациональным показателем. Например, вычислить число 3,2^13,5 более или менее точно было невозможно!

В математике появилась необходимость в решении уравнения , где  — положительные числа.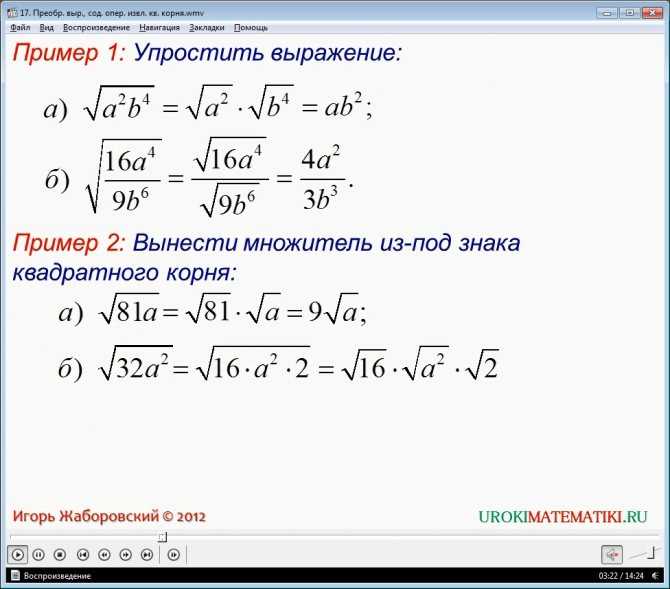 Решение этого уравнения требовалось в задачах по физике, связанных с радиоактивным распадом, движением тел с переменной массой, поглощением средой того или иного вида излучения.

Для выполнения вышеуказанных операций над числами и решения таких уравнений нужен был новый математический аппарат, который позволил бы не только выполнять подобные действия, но и ускорить получение результата вычислений.

Такой аппарат вскоре был изобретен и создателем его был шотландский математик Джон Непер (1550-1617).

 

2. Понятие логарифма числа. В новом математическом аппарате, созданном Непером, основным понятием является логарифм числа.

     Определение: Логарифмом положительного числа b по основанию а (а>0, а¹1) называется показатель степени, которую нужно возвести а, чтобы получить b:

                                     .                                                        (2.1)

Равенство означает, что , таким образом приведенные выражения позволяют находить неизвестный показатель степени, обозначенный логарифмом числа.

Например, , так как ; , так как ; , так как .

На практике формулу (2.1) обычно называют основное логарифмичес-кое тождество.

Например, ;   .

 

3.Натуральные и десятичные логарифмы. Основатель логарифмов Джон Непер за основание логарифмов принял уже известное иррациональное число

е=exp=2,71828… и нашел с точностью до 17-го знака после запятой логарифмы чисел от 1 до 10 000.   Так появились и нашли широкое применение в вычислениях натуральные логарифмы, в основании которых лежит известное число е. Обозначаются натуральные логарифмы символом:

.

         Спустя 20 лет после Непера английский математик Бриггс практически повторил его работу. Он вычислил логарифмы чисел от 1 до 20 000  и от       90 000 до 101 000 с точностью до 14 знака после запятой, но за основание логарифма принял число 10.

         Логарифмы чисел, в основании которых лежит число 10, получили название десятичных и обозначаются так:

.

Они также нашли широкое применение в вычислениях. Десятичные логарифмы любого числа приведены в четырехзначных математических таблицах советского математика Брадиса, соответственно с точностью до

4-го знака после запятой, вполне достаточной для большинства научных вычислений.

         В настоящее время, с появлением вычислительной техники логарифмы вычисляются  обычно с помощью калькуляторов или ПК. Логарифмы с любым положительным основанием обычно приводятся к десятичным или натуральным с помощью свойств логарифмов, рассмотренных ниже.

 

4. Свойства логарифмов. Для вычисления и упрощения выражений, содержащих логарифмы, выполняются действия, основанные на свойствах логарифмов, вытекающих из определения логарифма числа.

         При любых а > 0, а ¹ 1 и положительных х и y выполняются равенства:

 

1. log_a 1= 0,

2. log_a a =1,

3. log_a (х× y) = log_a x + log_a y,

4. log_a (х / y) = log_a x – log_a y,

5. log_ax ^p= p× log_ax,

                       где р – любое действительное число.

Доказываются свойства по основному логарифмическому тождеству. Формулы 1-5 используют для преобразования логарифмических выражений.

Например, вычислить:

        Решение: Применяя формулы 2, 3, 4, 5 получим:

         Для вычисления логарифма с произвольным положительным основанием применяется:

Формула перехода от одного основания логарифма к другому основанию:

 

     ,

здесь а, b, x > 0; а, b ¹ 1. Эта формула также доказывается по основному логарифмическому тождеству.

         Пример 1. Найти  .

         Решение: По свойству 6 имеем: =Пользуясь калькулятором или таблицами, находим , . подставляя в формулу перехода »

         Пример 2. Вычислить  .

         Решение: По свойству 6 имеем: .

 

5.Преобразование показательных и логарифмических выражений. Рассмотрим определения выражений, содержащих степени и логарифмы и применение свойств степеней и логарифмов для решения различных примеров с этими выражениями.

 

Определение: показательными называют выражения, содержащие действия над степенями с показателями, выраженными рациональными числами, буквами и логарифмами.

Например, ;; ; .

         Пример 1. Сравнить числа и .

         Решение: Приведем степени к одному показателю:  ;  , тогда по свойству степеней (см. §2 п.2) при 100>0 имеем >или

>.       

         Пример 2. Вычислить: .

         Решение: По свойству степеней имеем:

Первый множитель преобразуем к основному логарифмическому тождеству:

         1) , 2) .

        

         Пример 3. Найти х :

                                               .

         Решение: Второй множитель преобразуем к основному логарифмическому тождеству:

         .

            . Таким образом, х=22,5.

        

Определение: Логарифмическими называются выражения, содержащие действия над логарифмами, выраженными числами и буквами.

         Например, ; ; .

Над логарифмическими выражениями проводят два основных преобразования:

1) логарифмирование по данному основанию, т.е. нахождение логарифма данного выражения.

2) потенцирование, т.е. нахождение выражения по его логарифму.

Также проводится упрощение логарифмических выражений с использованием свойств логарифмов.

 

         Пример 1: Прологарифмировать по основанию а=5 выражение:

                                               .

         Решение:

Подставляя значение а=5, имеем:

.

         

Пример 2: Найдите х, если: 

Решение: Преобразуем правую часть равенства по свойствам степеней и логарифмов:

,  отсюда  или .

Таким образом, потенцирование – операция обратная логарифмиро-ванию.

 

         Пример 3: Найдите значение выражения: .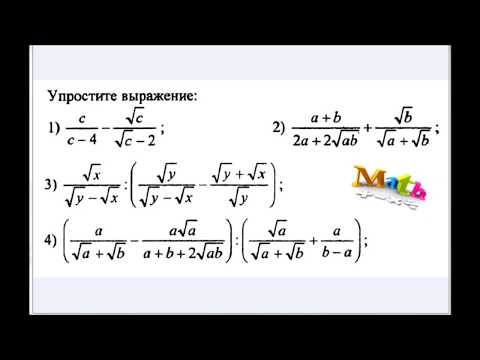

         Решение: Применим свойства логарифмов для преобразования числителя и знаменателя:

 

         .

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Как определяется логарифм числа?

2. Для чего применяются натуральные и десятичные логарифмы?

3. Каковы основные свойства логарифмов?

4. Какое выражение называется показательным?

5. Какое выражение называется логарифмическим?

6. Чем отличается операция логарифмирования от потенцирования?

Иррациональные выражения. Преобразование иррациональных выражений

• Сложение и вычитание корней
• Умножение и деление корней
• Возведение корня в степень
• Извлечение корня
• Сокращение корней
• Приведение корней к общему показателю

Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.

Примеры:

  — иррациональные выражения.

Сложение и вычитание корней

При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.

Примеры:

В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть, имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.

Примеры:

Умножение и деление корней

При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:

При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:

Примеры:

Возведение корня в степень

Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:

Примеры:

При возведении    в  n-ю  степень знак корня отбрасывается, так как возведение числа (или выражения) в  n-ю  степень и извлечение из него корня  n-ой  степени — это взаимно сокращающиеся действия:

Извлечение корня

Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:

,  так как 

Пример.

С помощью таких преобразований можно упростить извлечение корней  4-й,  6-й,  8-й,  9-й  и т. п. степеней из чисел.

Примеры:

Сокращение корней

Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:

так как извлечение корня и возведение в степень — это взаимно сокращающиеся действия, если их показатели равны.

На этом свойстве основано сокращение корней и приведение их к общему показателю.

Сокращение корней — это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.

Примеры:

Приведение корней к общему показателю

Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:

1. Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.

   Рассмотрим три выражения:

   ,

   Так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой. Полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:

2. Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.

   Рассмотрим два выражения:

   ,

   НОК (4, 6) = 12,  значит, для первого выражения дополнительным множителем будет  3,  а для второго  2.  После приведения к общему показателю выражения будут иметь следующий вид:

При умножении и делении иррациональных выражений с разными показателями их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.

Примеры:

Видео с вопросами: Упрощение алгебраических выражений с использованием показателей степени и квадратных корней

Стенограмма видео

Упростите квадратный корень из 100𝑥 в 16 степени.

В этом вопросе значение 𝑛 в нашем 𝑛-м корне опущен. Когда он опущен, мы предполагаем, что оно равно двум, и поэтому мы определяем его как квадратный корень. Итак, мы собираемся упростить это выражение, применяя некоторые свойства корней 𝑛-й, где 𝑛 равно два. Первое свойство, которое мы применяем, выглядит при нахождении произведения 𝑛-х корней. Это говорит нам о том, что когда 𝑛th корень из 𝑎 и 𝑛-й корень из 𝑏 хорошо определены в действительных числах, то 𝑛-й также определен корень из 𝑎, умноженный на 𝑏. Это 𝑛-й корень из 𝑎, умноженный на 𝑛 корень 𝑏. Мы можем опустить это значение 𝑛 и скажем, что эквивалентно квадратному корню из 𝑎, умноженному на квадратный корень из 𝑏, равно квадратный корень из 𝑎𝑏.

Затем мы можем применить это свойство в задний ход. И это позволяет нам отделить квадратный корень из 100𝑥 в 16-й степени и запишите его как квадратный корень из 100 раз квадратный корень из 𝑥 в 16-й степени. И, конечно, если мы знаем нашу квадратные числа наизусть, первую часть этого выражения довольно легко запомнить. оценивать. Квадратный корень из 100 просто равно 10. Но что нам делать с квадратом корень из 𝑥 в 16 степени? Что ж, воспользуемся правилом это применимо, когда 𝑛 — четное целое число, а 𝑎 — действительное число. Это то, что 𝑛-й корень 𝑎 к 𝑛-я степень равна абсолютному значению 𝑎.

Чтобы применить это правило, мы нужно сделать немного манипуляции, и это включает в себя применение одного из наших показательные законы. Это говорит о том, что 𝑥 до восьмого квадрат степени равен 𝑥 в 16-й степени. Таким образом, мы можем эквивалентно написать квадратный корень из 𝑥 в 16-й степени как квадратный корень из 𝑥 в восьмой степени в квадрате. И тогда, по предыдущему свойству, можно сказать, что это на самом деле равно абсолютному значению 𝑥 с точностью до восьмой мощность. Теперь мы можем заменить каждую часть нашего более раннее выражение со значениями 10 и абсолютным значением 𝑥 до восьмого мощность. И мы видим, что мы упростили квадратный корень из 100𝑥 в 16-й степени, умноженный на 10-кратное абсолютное значение 𝑥 в восьмая власть.

Тогда давайте быстро подумаем о что на самом деле говорит нам абсолютное значение. Он принимает ввод, который находится здесь 𝑥 в восьмой степени, и это делает его положительным. Конечно, если 𝑥 — действительное число, тогда 𝑥 в 𝑛-й степени на самом деле будет неотрицательным для четных значений 𝑛. В этом случае наша степень восемь равна даже, поэтому мы можем сказать, что 𝑥 в восьмой степени будет неотрицательным. Оно будет больше или равно ноль, если 𝑥 — действительное число. Это означает абсолютное значение символы на самом деле здесь не нужны, поэтому мы можем еще больше упростить нашу выражение. Когда мы это сделаем, мы обнаружим, что квадрат корень из 100𝑥 в 16-й степени можно упростить в 10 раз 𝑥 в восьмой мощность. 9{\frac{1}{2}}}[/latex]

А поскольку вы знаете, что возведение числа в степень [latex] \frac{1}{2}[/latex] равносильно возведению в квадрат корень этого числа, вы также можете записать его таким образом.

[латекс] \sqrt{3x}=\sqrt{3}\cdot \sqrt{x}[/latex]

Посмотрите на это — любое число под радикалом можно представить как произведение отдельных множителей , каждый под своим радикалом.

Продукт, преобразованный в степенное правило или иногда называемый квадратный корень из правила продукта

Для любых действительных чисел a и b , [latex] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex]. {2}} }[/латекс].

Квадратный корень из правила произведения поможет нам упростить несовершенные корни, как показано в следующем примере.

Пример

Упрощение. [латекс] \sqrt{63}[/латекс]

Показать решение

Окончательный ответ [латекс] 3\sqrt{7}[/латекс] может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три радикальных семи» или «три умножить на квадратный корень из семи».

В следующем видео показано больше примеров того, как упростить квадратные корни, которые не имеют идеальных квадратных корней. 9{2}}[/латекс] [латекс]\влево|х\вправо|[/латекс] [латекс]−5[/латекс] [латекс]25[/латекс] [латекс]5[/латекс] [латекс]5[/латекс] [латекс]−2[/латекс] [латекс]4[/латекс] [латекс]2[/латекс] [латекс]2[/латекс] [латекс]0[/латекс] [латекс]0[/латекс] [латекс]0[/латекс] [латекс]0[/латекс] 92[/latex] всегда будет неотрицательным. Один из советов, чтобы узнать, когда применять абсолютное значение после упрощения любого даже индексированного корня, — посмотреть на конечный показатель степени в ваших переменных терминах. Если показатель степени нечетный, включая [latex]1[/latex], добавьте абсолютное значение. Это относится к упрощению любого корня с четным индексом, как мы увидим в последующих примерах.

В следующем видео вы увидите больше примеров того, как упростить радикальные выражения с помощью переменных.

Мы покажем другой пример, где упрощенное выражение содержит переменные как с нечетными, так и с четными степенями.

В нашем следующем примере мы начнем с выражения, записанного с рациональным показателем. Вы увидите, что вы можете использовать аналогичный процесс — разложение членов на множители и сортировку по квадратам — для упрощения этого выражения.

Вот еще один пример с идеальными квадратами.

Упрощение кубических корней

Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, для упрощения корней более высокого порядка. Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами , чтобы вы могли извлечь из них кубический корень. Нам больше не нужно беспокоиться о том, определили ли мы главный корень, поскольку теперь мы находим кубические корни. Сосредоточьтесь на поиске идентичных трио факторов по мере упрощения. 9{3}}\end{array}[/latex]

Вы также можете пропустить шаг разложения на множители отрицательного числа, когда освоитесь с определением кубов.

В следующем видео мы покажем больше примеров упрощения кубических корней.

Упрощение корней четвертой степени

Теперь давайте перейдем к упрощению корней четвертой степени. Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найдите кубы для кубических корней, степени четырех для четвертых корней и т. д. Вспомните, что когда ваше упрощенное выражение содержит четный индексный радикал и переменный множитель с нечетным показателем, вам нужно применить абсолютное значение.

Альтернативный метод факторизации состоит в том, чтобы переписать выражение с рациональными показателями, а затем использовать правила показателей для упрощения. Вы можете обнаружить, что предпочитаете один метод другому. В любом случае приятно иметь варианты. Мы снова покажем последний пример, используя эту идею.

В следующем видео мы покажем еще один пример того, как упростить корень четвертой и пятой степени.

В нашем последнем примере мы упростим более сложное выражение, [латекс]\dfrac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3] {8{{b}^{4}}}}[/латекс] .