ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме.  Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 34. Сложная функция. 35. Обратная функция. 36.  n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения).  60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 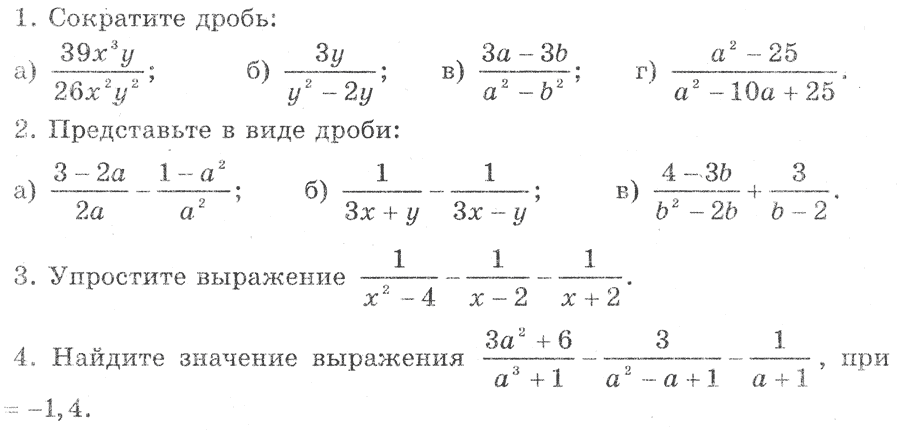 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. 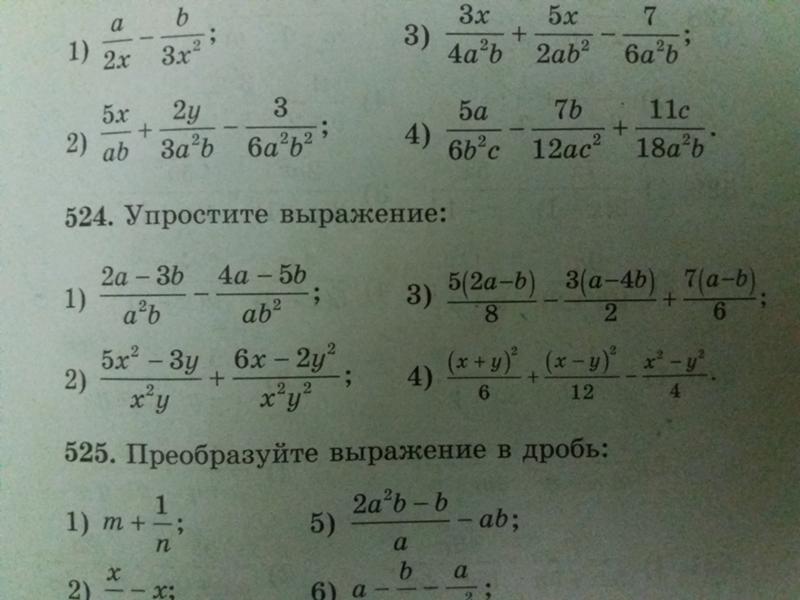 Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Преобразование выражений с дробями: примеры, решения
Давайте рассмотрим основные преобразования, которые могут применимы для выражений с дробями.
Выражения с дробями и дробные выражения
Судя по заявленной в заголовке статьи теме, речь пойдет о преобразовании выражений с переменными числовых выражений, запись которых содержит хотя бы одну дробь.
Отдельные дроби в данном материале мы рассматривать не будем, так как уделили им достаточно внимания в статье «Преобразование дробей: общий взгляд». Остановимся лишь на разнице смысла словосочетаний «дробные выражения» и « выражения с дробями».
Выражение с дробями – это более общее понятие по сравнению с «дробным выражением». Далеко не любое выражение, содержащее дробь, является дробным выражением. Так, например, выражение x2-1 является целым рациональным числом.
Основные тождественные преобразования выражений с дробями: перестановка местами слагаемых и множителей, раскрытие скобок, приведение подобных слагаемых. Все эти приемы мы разбирали для выражений различных видов.
Важно при проведении преобразований соблюдать принятый порядок действий.
Пример 1Упростите выражение 3·x+1×2-4-1-2·x+1×2-4+3.
Решение
Раскроем скобки: 3·x+1×2-4-3-2·x+1×2-4+3. Мы получили выражение, в котором присутствуют подобные слогаемые 3·x+1×2-4 и -2·x+1×2-4, а также −3 и 3. Методом приведения получим дробь x+1×2-4.
Решение можно записать кратко:
3·x+1×2-4-1-2·x+1×2-4+3==3·x+1×2-4-3-2·x+1×2-4+3=x+1×2-4
Ответ: 3·x+1×2-4-1-2·x+1×2-4+3=x+1×2-4.
Пример 2
Представьте выражение 1×2+6·1x+9 в виде квадрата суммы.
Решение
Мы можем записать число 6 как 2·3, а 9 как 32. Тогда исходное выражение примет следующий вид:
1×2+2·3·1x+32
Теперь используем формулу сокращенного умножения квадрат суммы: 1×2+2·3·1x+32=1x+32.
Ответ: 1×2+6·1x+9=1x+32.
Работа с отдельными дробями
Предлагаем вам обсудить преобразование отдельных дробей, которые входят в запись выражения. Это необходимо для того, чтобы в следующем пункте мы могли перейти к выполнению действий с дробями, которые входят в исходное выражение.
С дробями, являющимися частью выражения, можно выполнять все те преобразования, которые мы подробно описали в материале «Преобразование дробей». Любое преобразование должно давать нам тождественную дробь, а исходное выражение при этом должно давать тождественно равное выражение.
Пример 3Преобразовать выражение с дробью x+1+(x-1)2-1x к более простому виду.
Решение
Для начала поработаем с дробью (x-1)2-1x: раскроем скобки, приведем подобные слагаемые в числителе: (x-1)2-1x=x2-2·x+1-1x=x2-2·xx
Вынесем общий множитель x за скобки в числителе и произведем сокращение алгебраической дроби: x2-2·xx=x·(x-2)x=x-2.
Подставим полученный результат вместо дроби в выражение из условия задачи, получим:
x+1+x-2.
Ответ: x+1+(x-1)2-1x=x+1+x-2.
Выполнение действий с дробями
Действия с дробями проводятся в соответствии с общепринятым порядком. Стоит учитывать тот факт, что любое число может быть представлено в виде дроби со знаменателем 1.
Пример 4Упростите выражение x+2·x-1x+2·x+12x.
Решение
Существует несколько вариантов решения данной задачи. В контексте темы мы решим ее методом выполнения действий с дробями:
x+2·x-1x+2·x+12x==x+2·x-x+12x+2·x
Полученное произведение x+2·x запишем в виде дроби для того, чтобы нам проще был провести вычитание дробей:
x+2·x-x+12x+2·x==x+2·x1-x+12x+2·x==x+2·x·x+2·xx+2·x-x+12x+2·x==x+2·xx+2·x-x+12x+2·x==x+2·x-x+12x+2·x=x2+2·x-x2+2·x+1x+2·x==-1x+2·x=-1x+2·x
Для того, чтобы избавиться от иррациональности в знаменателе, можно выполнить еще одно действие:
-1x+2·x=-x+2·xx2+2·x
Ответ: x+2·x-1x+2·x+12x=-x+2·xx2+2·x.
Применение свойств корней, степеней, логарифмов и т.п.
Выражения с дробями могут содержать логарифмы, корни, тригонометрические функции, степени с различными показателями. Для их преобразования могут применяться соответствующие свойства.
Применимо к дробям, стоит выделить свойство логарифма разности logcab=logca-logcb, свойство корня из дроби abn=anbn, свойство модуля частного ab=ab и свойство дроби в степени abp=apbp.
Поясним написанное выше на примерах.
Выражение 4×6-2·2×3+1 можно преобразовать, заменив первую дробь степенью 2×32 на базе свойств степени. Это позволяет нам представить исходное выражение в виде квадрата разности.
В логарифмическом выражении lnx+3x+ln x логарифм дроби можно заменить разностью логарифмов. Далее приводим подобные слагаемые и таким образом упрощаем выражение: lnx+3x+ln x=lnx+3-ln x+ln x=lnx+3.
В тригонометрических выражениям отношение синуса к косинусу можно заменить тангенсом одного и того же угла.
Избавиться от аргумента-дроби можно при переходе от половинного аргумента к целому с использованием соответствующих формул.
Например, 2·sin2x-32=1-cos(x-3).
Как видите, тема эта очень объемная. Для ее подробного изучения мы рекомендуем обратиться к материалам, изложенным в разделах, посвященных преобразованию тригонометрических выражений, иррациональных выражений с использованием свойств корня, выражений с использованием свойств степеней, логарифмических выражений с использованием свойств логарифмов.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Учебник по алгебре для среднего уровня 34
Алгебра для среднего уровня
Урок 34. Сложные дроби
WTAMU > Виртуальная математическая лаборатория > Алгебра для среднего уровня
Цели обучения
После завершения этого руководства вы сможете:
- Упростите сложные дроби.
Введение
Ар дроби тебя расстраивают? Если да, то вы не одиноки. Что ж, тебе повезло. У нас есть еще один учебник, посвященный рациональным выражения (дроби). В этом уроке мы рассмотрим упрощение сложный дроби. Если вам нужен обзор по упрощению и делению рациональный выражения, не стесняйтесь вернуться к Учебник 32: Умножение и деление рациональных выражений . Если вам нужен обзор по нахождению ЖК дробей не стесняйтесь вернуться к Tutorial 33: Сложение и вычитание рациональных выражений . Пришло время начать с этого учебника.
Учебник
Комплексная фракция
Сложная дробь — это рациональное выражение, имеющее
фракция
в его числителе, знаменателе или обоих.
Другими словами, существует хотя бы одна маленькая дробь в рамках общего доля.
Некоторые примеры сложных дробей:
и
Есть два способа упростить сложные дроби. Мы назовем их методом I и методом II.
Метод I
Упрощение сложной дроби
Шаг 1: При необходимости перепишите
числитель и знаменатель так, чтобы они были одной дробью.
Другими словами, вы будете комбинировать все
части числителя
составить одну дробь и все части знаменателя
другой
доля. Если вам нужен обзор по сложению и вычитанию рациональных
выражения, перейдите к Уроку 33:
Добавление
и вычитание рациональных выражений.
Шаг 2. Разделите числитель на
знаменатель
путем умножения числителя на обратную величину знаменателя.
Шаг 3: При необходимости упростите
рациональное выражение.
Если вам нужен обзор по упрощенной рациональной выражения, перейдите к учебнику 32: Умножение и деление рациональных выражений.
Пример 1 : Упростить.
Шаг 1: При необходимости перепишите числитель и знаменатель так, чтобы они были одной дробью.
Комбинируя только числитель, получаем:
*Перезапись дробей на ЖК-дисплее
12
Сложив только знаменатель, получим:
*Перезапись дробей на ЖК-дисплее
8
Складываем их обратно в сложную дробь, получаем:
*Написать числитель над знаменателем
Шаг 2.
Разделите числитель
по знаменателю
умножив числитель на обратную величину знаменателя
И
Шаг 3: При необходимости упростите рациональное выражение.
*Переписать раздел. как мульт. из
взаимный
*Разделить на общий делитель 4
Пример 2 : Упростить .
Шаг 1: При необходимости перепишите числитель и знаменатель так, чтобы они были одной дробью.
Комбинируя только числитель, получаем:
*Перезапишите дроби с ЖК-дисплеем ab
Знаменатель уже записан как одна дробь:
Подставив их обратно в сложную дробь, мы получим:
*Написать числитель над знаменателем
Шаг 2.
Разделите числитель
по знаменателю
умножив числитель на обратную величину знаменателя
И
Шаг 3: При необходимости упростите рациональное выражение.
*Переписать раздел. как мульт. из
взаимный
*Разделите общие делители a и b
Метод II
Упрощение сложной дроби
Шаг 1: Умножьте числитель на
знаменатель
общие сложные дроби
ЖК более мелких фракций.
Вспомним, что при умножении одинаковых
дело в числителе
а в знаменателе получается эквивалентная дробь.
Если вы
нужен обзор по поиску ЖК, вернитесь к Учебник
33: Добавление и вычитание рациональных выражений.
Шаг 2. При необходимости упростите рациональное выражение.
Пример 3 : Упростить.
Шаг 1: Умножьте числитель на знаменатель общие сложные дроби ЖК более мелких фракций.
Знаменатель дроби числителя имеет вид после двух факторы:
*Коэффициент
разность двух квадратов
Знаменатель дроби знаменателя имеет следующее фактор:
Объединение всех различных факторов и использование наивысший показатель, получаем следующий ЖК для всех мелких дробей:
Умножая числитель и знаменатель на ЖКИ мы получить:
*Множ.
число и ден. по ( х + 5)( х — 5)
Шаг 2: При необходимости упростите рациональное выражение.
*Выделить общий множитель из (2 x + 1)
Пример 4 : Упрощение.
Шаг 1: Умножьте числитель на знаменатель общие сложные дроби ЖК более мелких фракций.
Знаменатель дроби числителя имеет вид следующий фактор:
Знаменатель дроби знаменателя имеет следующее факторы:
и и
Объединение всех различных факторов и использование наивысший показатель, получаем следующий ЖК для всех мелких дробей:
Умножая числитель и знаменатель на ЖКИ мы получить:
*Множ.
число и ден. по у в квадрате
Шаг 2: При необходимости упростите рациональное выражение.
*Номер. факторы как разница
из двух квадратов
*Ден. факторы как совершенный
квадратный трехчлен.
*Выделить общий множитель из (3 и + 1)
Пример 5 : Упростить .
На первый взгляд не выглядит сложным
доля. Однако,
как только вы перепишете его с положительными показателями, вы увидите, что мы действительно
имеют сложную дробь.
*Переписать с положительными показателями
Шаг 1: Умножьте числитель на знаменатель общие сложные дроби ЖК более мелких фракций.
Два знаменателя дробей числителя иметь следующее факторы:
а и б
Два знаменателя знаменателя дроби имеют следующие факторы:
и
Объединение всех различных факторов и использование наивысший показатель, получаем следующий ЖК для всех мелких дробей:
Умножая числитель и знаменатель на ЖКИ мы получить:
*Множ.
число и ден. по a в квадрате b в квадрате
Шаг 2: При необходимости упростите рациональное выражение.
*Коэффициент из GCF ab в ном.
Практические задачи
Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
виды проблем. Математика работает так же, как
что-либо
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
это.
Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этого, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой задачи . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1а — 1б: Упростить.
1а.
(ответ/обсуждение
к 1а)
1б.
(ответ/обсуждение
до 1b)
Нужна дополнительная помощь по этим темам?
Перейти к получению
Помощь за пределами
Классная комната в Учебнике 1: Как добиться успеха на уроке математики для
некоторый
больше предложений.
WTAMU > Виртуальная математическая лаборатория > Промежуточная алгебра
Последняя редакция Ким Сьюард 17 июля 2011 г.
Авторское право на все содержимое (C) 2001–2011, WTAMU и Ким Сьюард. Все права защищены.
7.4: Упрощение сложных рациональных выражений
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5162
- OpenStax
- OpenStax
Цели обучения 92+4·5}\).
Если вы пропустили эту проблему, просмотрите [ссылка] .
2-16\). Это выражение было бы неопределенным, если \(x=4\) или \(x=-4\). 9{2}-7 x+12}}{\dfrac{2}{x-4}} \nonumber \]- Ответ
\(\dfrac{1}{2(x-3)}\)
Полосы дробей действуют как символы группировки. Итак, чтобы следовать порядку действий, мы максимально упрощаем числитель и знаменатель, прежде чем мы сможем выполнить деление.
Пример \(\PageIndex{2}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{\dfrac{1}{3}+\dfrac{1}{6}}{\dfrac {1}{2}-\dfrac{1}{3}} \номер\]
Решение
Упростите числитель и знаменатель. Найдите ЖК и сложите дроби в числителе. Найдите ЖК и вычтите дроби в знаменателе.
\[\dfrac{\dfrac{1 \cdot {\color{red}2}}{3 \cdot {\color{red}2}}+\dfrac{1}{6}}{\dfrac{1 \cdot {\color{red}3}}{2 \cdot {\color{red}3}}-\dfrac{1 \cdot {\color{red}2}}{3 \cdot {\color{red} 2}}} \nonumber \]
Упростите числитель и знаменатель.
\[\dfrac{\dfrac{2}{6}+\dfrac{1}{6}}{\dfrac{3}{6}-\dfrac{2}{6}} \nonumber \]
Перепишите сложное рациональное выражение в виде задачи на деление.
\[\dfrac{3}{6} \div \dfrac{1}{6} \nonumber \]
Умножьте первое на обратное значение второго.
\[\dfrac{3}{6} \cdot \dfrac{6}{1} \nonumber \]
Упростить.
\[3 \номер\]
Попробуйте \(\PageIndex{3}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\ dfrac{5}{6}+\dfrac{1}{12}} \nonumber \]
- Ответить
\(\dfrac{14}{11}\)
Попробуйте \(\PageIndex{4}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{\dfrac{3}{4}-\dfrac{1}{3}}{\ dfrac{1}{8}+\dfrac{5}{6}} \nonumber \]
- Ответ
\(\dfrac{10}{23}\)
Мы следуем той же процедуре, когда комплексное рациональное выражение содержит переменные.
Пример \(\PageIndex{3}\): как упростить сложное рациональное выражение с помощью деления
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{x}{y}-\dfrac{y }{x}} \номер \]
Решение
Шаг 1 .
Упростите числитель.
Упростим сумму в знаменателе. числитель и разность в знаменателе.
\[\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{x}{y}-\dfrac{y}{x}} \nonumber \]
Найдите общий знаменатель и сложите дроби в числителе. 9{2}}\right) \nonumber \]
Фактор любых выражений, если это возможно.
\[\dfrac{x y(y+x)}{x y(x-y)(x+y)} \nonumber \]
Удалить общие делители.
\[\dfrac{\cancel {x y}\cancel {(y+x)}}{\cancel {x y}(xy)\cancel {(x+y)}} \nonumber \]
Упростить.
\[\dfrac{1}{x-y} \номер\]
Попробуйте \(\PageIndex{5}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\ dfrac{1}{x}-\dfrac{1}{y}} \nonumber \] 9{2}}} \номер \]
- Ответ
\(\dfrac{a b}{b-a}\)
Здесь мы суммируем шаги.
Как упростить сложное рациональное выражение, записав его в виде деления.
- Перепишите сложное рациональное выражение в виде задачи на деление.
- Разделите выражения.
Пример \(\PageIndex{4}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{n-\dfrac{4 n}{n+5}}{\dfrac{1}{ n+5}+\dfrac{1}{n-5}} \номер\] 9{2}+n}{n+5} \cdot \dfrac{(n+5)(n-5)}{2 n} \nonumber \]
Фактор любых выражений, если это возможно.
\[\dfrac{n(n+1)(n+5)(n-5)}{(n+5) 2 n} \nonumber \]
Удалить общие делители.
\[\dfrac{\отменить {n}(n+1)\отменить {(n+5)}(n-5)}{\отменить {(n+5)} 2 \отменить {n}} \ не число \]
Упрощение.
\[\dfrac{(n+1)(n-5)}{2} \номер\]
Попробуйте \(\PageIndex{7}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{b-\dfrac{3 b}{b+5}}{\dfrac{2} {b+5}+\dfrac{1}{b-5}} \номер\]
- Ответить
\(\dfrac{b(b+2)(b-5)}{3b-5}\)
Попробуйте \(\PageIndex{8}\)
Упростите сложное рациональное выражение, записав его в виде деления: \[\dfrac{1-\dfrac{3}{c+4}}{\dfrac{1}{ c+4}+\dfrac{c}{3}} \nonumber \]
- Ответ
\(\dfrac{3}{c+3}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея
Мы «очищали» дроби, умножая их на ЖК-дисплей, когда решали уравнения с дробями.
Мы можем использовать эту стратегию здесь, чтобы упростить сложные рациональные выражения. Умножим числитель и знаменатель на ЖК всех рациональных выражений.
Давайте посмотрим на сложное рациональное выражение, которое мы упростили одним способом в примере 7.4.2. Здесь мы упростим это, умножив числитель и знаменатель на LCD. Когда мы умножаем на \(\dfrac{LCD}{LCD}\), мы умножаем на 1, поэтому значение остается прежним.
Пример \(\PageIndex{5}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{1}{3}+\dfrac{1}{6}}{\dfrac {1}{2}-\dfrac{1}{3}} \номер \]
Решение
ЖК-дисплей всех дробей в целом выражении равен 6.
Очистите дроби, умножив числитель и знаменатель на этот ЖК-дисплей.
\[\dfrac{{\color{red}6} \cdot\left(\dfrac{1}{3}+\dfrac{1}{6}\right)}{{\color{red}6} \cdot\left(\dfrac{1}{2}-\dfrac{1}{3}\right)} \nonumber \]
Распределить.
\[\dfrac{6 \cdot \dfrac{1}{3}+6 \cdot \dfrac{1}{6}}{6 \cdot \dfrac{1}{2}-6 \cdot \dfrac{ 1}{3}} \nonumber \]
Упрощение.
\[\dfrac{2+1}{3-2} \номер\]
\[\dfrac{3}{1}\nonumber \]
\[3\nonumber \]
Попробуйте \(\PageIndex{9}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{1}{2}+\dfrac{1}{5}}{\dfrac{1}{10}+\dfrac{1}{5}} \nonumber \]
- Ответ
\(\dfrac{7}{3}\)
Попробуйте \(\PageIndex{10}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{1}{4}+\dfrac{3}{8}}{\ dfrac{1}{2}-\dfrac{5}{16}} \nonumber \]
- Ответить
\(\dfrac{10}{3}\)
Мы будем использовать тот же пример, что и в примере 7.4.3. Решите, какой метод работает лучше для вас.
Пример \(\PageIndex{6}\): как упростить сложное рациональное выражение с помощью ЖК-дисплея
Упростить сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{1}{x}+\ dfrac{1}{y}}{\dfrac{x}{y}-\dfrac{y}{x}} \nonumber \]
Решение
Шаг 1 .
Найдите ЖК всех дробей в сложном рациональном выражении.
ЖКИ всех дробей \(xy\).
\[\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{x}{y}-\dfrac{y}{x}} \nonumber \]
Шаг 2 . Умножьте числитель и знаменатель на LCD.
Умножьте числитель и знаменатель на \(xy\).
\[\dfrac{{\color{red}x y} \cdot\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}{{\color{red}x y} \cdot\left(\dfrac{x}{y}-\dfrac{y}{x}\right)} \nonumber \] 9{2}}}{\dfrac{1}{x}+\dfrac{1}{y}} \nonumber \]
- Ответ
\(\dfrac{yx}{x y}\)
Как упростить сложное рациональное выражение с помощью ЖК-дисплея.
- Умножьте числитель и знаменатель на ЖК-дисплей.
- Упростите выражение.
Обязательно начните с факторизации всех знаменателей, чтобы найти ЖК-дисплей.
Пример \(\PageIndex{7}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{2}{x+6}}{\dfrac{4}{x-6 }-\dfrac{4}{x^{2}-36}} \nonumber \] 9{2}-36=(x+6)(x-6) \номер \]
Умножьте числитель и знаменатель на ЖК-дисплей.
\[\dfrac{(x+6)(x-6) \dfrac{2}{x+6}}{(x+6)(x-6)\left(\dfrac{4}{x- 6}-\dfrac{4}{(x+6)(x-6)}\right)} \nonumber \]
Упростите выражение.
Распределить в знаменателе.
\[\dfrac{(x+6)(x-6) \dfrac{2}{x+6}}{{\color{red}(x+6)(x-6)}\left(\ dfrac {4} {x-6} \ right) — {\ color {red} (x + 6) (x-6)} \ left (\ dfrac {4} {(x + 6) (x-6)} \right)} \nonumber \]
Упростить.
\[\dfrac{\cancel{(x+6)}(x-6) \dfrac{2}{\cancel{x+6}}}{{\color{red}(x+6)\cancel{ (x-6)}}\left(\dfrac{4}{x-6}\right)-{\color{red}\cancel{(x+6)(x-6)}}\left(\dfrac {4}{\cancel{(x+6)(x-6)}}\right)} \nonumber \]
Упростить.
\[\dfrac{2(x-6)}{4(x+6)-4} \nonumber \]
Чтобы упростить знаменатель, распределите и объедините одинаковые члены.
\[\dfrac{2(x-6)}{4 x+20} \nonumber \]
Фактор знаменателя.
\[\dfrac{2(x-6)}{4(x+5)} \номер\] 9{2}-7 m+12}}{\dfrac{3}{m-3}-\dfrac{2}{m-4}} \nonumber \]
Решение
Найти ЖК всех фракций в сложном рациональном выражении.
ЖК-дисплей равен \((m−3)(m−4)\).
Умножьте числитель и знаменатель на ЖК-дисплей.
\[\dfrac{(m-3)(m-4) \dfrac{4}{(m-3)(m-4)}}{(m-3)(m-4)\left(\ dfrac{3}{m-3}-\dfrac{2}{m-4}\right)} \nonumber \]
Упростить.
\[\dfrac{\отменить {(м-3)(м-4)}\dfrac{4}{\отменить {(м-3)(м-4)}}}{\отменить {(м-4)}} 3)}(m-4)\left(\dfrac{3}{\cancel {m-3}}\right)-(m-3)\cancel {(m-4)}\left(\dfrac{2 }{\cancel {m-4}}\right)} \nonumber\] 9{2}+13 г+5\вправо)}{3 г}\)
Пример \(\PageIndex{9}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{\dfrac{y}{y+1}}{1+\dfrac{1}{y -1}} \номер \]
Решение
Найдите НЛД всех дробей в комплексном рациональном выражении.
ЖК-дисплей \((y+1)(y−1)\).
Умножьте числитель и знаменатель на ЖК-дисплей.
\[\dfrac{(y+1)(y-1) \dfrac{y}{y+1}}{(y+1)(y-1)\left(1+\dfrac{1}{) у-1}\справа)} \номер\] 9{2}+y} \nonumber \]
Разложите знаменатель на множители и удалите множители, общие с числителем.
\[\dfrac{\cancel {y}(y-1)}{\cancel {y}(y+1)} \nonumber \]
Упростить.
\[\dfrac{y-1}{y+1} \nonumber \]
Попробуйте \(\PageIndex{17}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{ \dfrac{x}{x+3}}{1+\dfrac{1}{x+3}} \nonumber \]
- Ответ
\(\dfrac{х}{х+4}\)
Попробуйте \(\PageIndex{18}\)
Упростите сложное рациональное выражение с помощью ЖК-дисплея: \[\dfrac{1+\dfrac{1}{x-1}}{\dfrac{3}{ x+1}} \nonumber \]
- Ответ
\(\dfrac{х(х+1)}{3(х-1)}\)
Получите доступ к этому онлайн-ресурсу, чтобы получить дополнительные инструкции и попрактиковаться в сложных дробях.
- Сложные дроби
Ключевые понятия
- Как упростить сложное рациональное выражение, записав его в виде деления.
- Упростите числитель и знаменатель.
- Перепишите сложное рациональное выражение в виде задачи на деление.
- Разделите выражения.
- Упростите числитель и знаменатель.
- Как упростить сложное рациональное выражение с помощью ЖК-дисплея.
- Найдите ЛКД всех дробей в сложном рациональном выражении.
- Умножьте числитель и знаменатель на ЖК-дисплей.
- Упростите выражение.
Глоссарий
- сложное рациональное выражение
- Комплексное рациональное выражение — это рациональное выражение, в котором числитель и/или знаменатель содержит рациональное выражение.
Эта страница под названием 7.4: Simplify Complex Rational Expressions распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.