Спецификация тестовых заданий для проведения внутренней мониторинговой работы по математике 5 класс
5 класс 1 полугодие
Спецификация
тестовых заданий для проведения внутренней мониторинговой работы
по математике
5 класс
(промежуточный этап)
Назначение мониторинговой работы: оценка уровня обученности обучающихся за I полугодие 5 класса.
Документы, определяющие содержание работы:
Программа по математике для 5 классов.
Обязательный минимум содержания основного общего образования по предмету математика за курс 5 класса
Работа составлена на основе следующих контрольно-измерительных материалов:
Александрова В. Л. 5 класс. Контрольные работы в новом формате; Московский центр непрерывного математического образования. – М.: Интеллект-Центр, 2011 г.
Гусева И. Л. Тестовые материалы для оценки качества обучения. 5 класс. М.: Интеллект-Центр, 2011 г.
Характеристика структуры и содержания мониторинговой работы.
Работа состоит из трех частей. Часть А состоит из 8-ми заданий: семь заданий на выбор правильного ответа из четырех предложенных и одного задания на соответствие. Часть В состоит из трех заданий, требующих самостоятельного решения заданий. Часть С состоит из двух заданий самостоятельного решения, предназначена для выявления высокого уровня знаний.
Обозначение задания в работе | Проверяемые элементы содержания | Максимальный балл за выполнение задания |
А1 | Классы и разряды. | 1 |
А2 | Шкалы и координаты. | 1 |
А3 | Сложение и вычитание чисел, использование соответствующих терминов. | 1 |
А4 | Умножение и деление чисел, использование соответствующих терминов. | 1 |
А5 | Нахождение значений числовых и буквенных выражений со скобками и без них. | 1 |
А6 | Установление зависимостей между величинами, характеризующими процессы движения (пройденный путь, время, скорость) | 1 |
А7 | Умножение и деление чисел, использование соответствующих терминов. | 1 |
А8 | Площадь геометрической фигуры | 1 |
В1 | Решение текстовых задач арифметическим способом с опорой на таблицы | 2 |
В2 | Использование свойств арифметических действий при выполнении вычислений | 2 |
В3 | Использование свойств арифметических действий при выполнении вычислений. | 2 |
С1 | Решение текстовых задач арифметическим или алгебраическим способом с опорой на краткие записи | 3 |
С2 | Единицы длины (миллиметр, сантиметр, дециметр, метр, километр) Единицы времени (секунда, минута, час, сутки, неделя, месяц, год, век) | 3 |
Система оценивания отдельных заданий и всей работы в целом.
Блок А выявляет знания учащихся базового уровня, блок Б — знания учащихся повышенного уровня и блок С – знания учащихся высокого уровня.
За верное выполнение задания блока А обучающийся получает 1 балл, за верное выполненное задание блока В – 2 балла, за верно выполненное задание блока С – 3 балла. За неверный ответ или его отсутствие 0 баллов. Максимальное количество баллов, которое может набрать обучающийся, верно выполнивший задания – 20 баллов.
Шкала оценивания работы:
Критерий 1
Для получения отметки «3» достаточно правильно выполнить 8 заданий из группы А.
Для получения отметки «4» дополнительно к ним необходимо правильно выполнить любые 2 задания группы В.
Оценка «5» ставится при обязательном выполнении 7 заданий из группы А, 2 заданий группы В, одного задания из группы С.
Критерий 2
«5» — 16 баллов
«4» — 12-15 баллов
«3» — 11 – 8 баллов
«2» — менее 8 баллов
Кодификатор для тестовой работы
Обозначение задания в работе | Проверяемые элементы содержания |
А1 | Классы и разряды. |
А2 | Шкалы и координаты. |
А3 | Сложение и вычитание чисел, использование соответствующих терминов. |
А4 | Умножение и деление чисел, использование соответствующих терминов. |
А5 | Нахождение значений числовых и буквенных выражений со скобками и без них. |
А6 | Установление зависимостей между величинами, характеризующими процессы движения (пройденный путь, время, скорость) |
А7 | Умножение и деление чисел, использование соответствующих терминов. |
А8 | Площадь геометрической фигуры |
В1 | Решение текстовых задач арифметическим способом с опорой на таблицы |
В2 | Использование свойств арифметических действий при выполнении вычислений |
В3 | Использование свойств арифметических действий при выполнении вычислений. |
С1 | Решение текстовых задач арифметическим или алгебраическим способом с опорой на краткие записи |
С2 | Единицы длины (миллиметр, сантиметр, дециметр, метр, километр) Единицы времени (секунда, минута, час, сутки, неделя, месяц, год, век) |
Промежуточный этап мониторинга
I вариант
Часть А
Что означает цифра 8 в записи числа 1 780 025?
8 сотен тысяч
8 десятков тысяч
8 единиц тысяч
8 десятков миллионов
На каком рисунке правильно изображены точки Р (9) и А (5)?
На сколько число 4265 меньше числа 15 104?
на 11 161 3) на 10 849
на 10 839 4) на 10 939
Выберите верное утверждение:
произведение нескольких чисел зависит от выбора порядка множителей
при делении числа на нуль получается нуль
чтобы найти неизвестный делитель надо делимое разделить на частное
чтобы найти неизвестный множитель надо произведение умножить на известный множитель
Упростите выражение : 16-( 3 + у )
19 – у 2) 13 у 3) 13 + у 4) 13 — у
В ящике было у кг яблок, а в корзине – на 2 кг больше.
Сколько яблок было в ящике и в корзине вместе? Составьте выражение по условиям задачи и упростите его.
2у кг 2) (2у + 2) кг 3) 4у кг 4) (у + 2) кг
Выберите уравнение, корнем которого является число 8:
х * 13 = 108
У * 12 = 96
У : 12 = 96
96 : а = 8
Найдите на рисунке равные фигуры.
Часть В
За 5 ч велосипедист проехал 75 км, а автомобилист за 4 ч проехал 360 км. Во сколько раз скорость велосипедиста меньше скорости автомобилиста?
Вычислите:
5 * 43 – (122 : 16)2
Решите уравнение: 216: (15 – х) = 18
Часть С
Запишите решение задачи. Если из задуманного числа вычесть 17, а затем к разности прибавить 21, то получиться 46. Найдите задуманное число.
Что больше и во сколько раз: шесть сантиметров или двадцать миллиметров?
Промежуточный этап мониторинга
II вариант
Часть А
Сколько всего тысяч в числе 364 891
4 3) 360
300 4) 364
На каком рисунке правильно изображены точки В (8), С (4)?
На сколько число 2638 меньше числа 13 105?
на 1543 3) на 10 467
на 10 477 4) на 11 467
Выберите верное утверждение:
чтобы найти неизвестный множитель надо известный множитель умножить на произведение
при делении числа на один получается нуль
чтобы найти неизвестное делимое надо делитель разделить на частное
произведение нескольких чисел не зависит от выбора порядка множителей
Упростите выражение : 20 — (7 + а )
13 + а 2) 27 — а 3) 13 — а 4) 13а
В первый день турист прошел n км, а во второй – на 5 км больше, чем в первый день.
Какое расстояние прошел турист за два дня? Составьте выражение по условиям задачи и упростите его.
(2n + 5) км 2) 5n км 3) 7n км 4) (n + 5) км
Выберите уравнение, корнем которого является число 9:
х * 12 = 108
у : 11 = 99
9 * а = 108
225 : с = 9
Найдите на рисунке фигуры с равной площадью.
Часть В
За 3 ч катер проехал 72 км, а ракета за 5 ч прошла 480 км. Во сколько раз скорость ракеты больше скорости катера?
Вычислите:
(182 : 36)2 + 53 * 4
Решите уравнение: (х – 8) •12 = 132
Часть С
Если к задуманному числу прибавить 37, а потом из суммы вычесть 91, то получиться 46. Найдите задуманное число.
Что больше и во сколько раз два часа или сорок минут?
Результаты внутреннего мониторинга
Класс: 5
Дата проведения: 23.
12.2015
Предмет: математика
Количество учащихся в классе: 5
Количество выполнявших работу: 5
За верное выполнение задания блока А обучающийся получает 1 балл, за верное выполненное задание блока В – 2 балла, за верно выполненное задание блока С – 3 балла. За неверный ответ или его отсутствие 0 баллов. Максимальное количество баллов, которое может набрать обучающийся, верно выполнивший задания, – 20 баллов.
№ п/п | Ф И обучающегося | Номер задания Проверяемые элементы содержания | Оценка | |||||||||||||
А 1 Классы и разряды | А 2 Шкалы и координаты | А 3 Сложение и вычитание чисел, использование соответствующих терминов. | А 4 Умножение и деление чисел, использование соответствующих терминов. | А 5 Нахождение значений числовых и буквенных выражений со скобками и без них. | А 6 Установление зависимостей между величинами, характеризующими процессы движения (пройденный путь, время, скорость) | А 7 Умножение и деление чисел, использование соответствующих терминов. | А 8 Площадь геометрической фигуры | В 1 Решение текстовых задач арифметическим способом с опорой на таблицы | В 2 Использование свойств арифметических действий при выполнении вычислений | В 3 Использование свойств арифметических действий при выполнении вычислений. | С 1 Решение текстовых задач арифметическим или алгебраическим способом с опорой на краткие записи | С 2 Единицы длины (миллиметр, сантиметр, дециметр, метр, километр) Единицы времени (секунда, минута, час, сутки, неделя, месяц, год, век) | Количество баллов | |||
1 | Ансимова Дарья | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | — | — | — | 3 | 2 |
2 | Бакулин Станислав | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 3 | 10 | 3 |
3 | Бочкарёва Ульяна | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 2 | 1 | 0 | 8 | 3 |
4 | Швайгерт Эрик | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 2 | 0 | 2 | 2 | 2 | 15 | 4 |
5 | Кузьминова Татьяна | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 5 | 2 |
Анализ мониторинговой работы обучающихся
5 класса по математике
Критерии оценивания:
Критерий 1
Для получения отметки «3» достаточно правильно выполнить 8 заданий из группы А.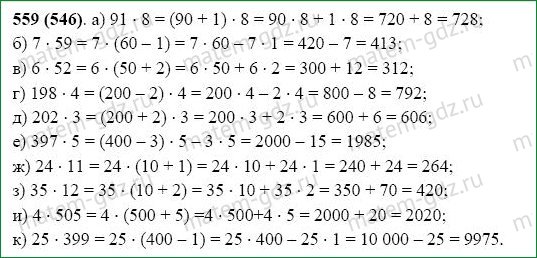
Для получения отметки «4» дополнительно к ним необходимо правильно выполнить любые 2 задания группы В.
Оценка «5» ставится при обязательном выполнении 7 заданий из группы А, 2 заданий группы В, одного задания из группы С.
Критерий 2
«5» — 16 баллов
«4» — 12-15 баллов
«3» — 11 – 8 баллов
«2» — менее 8 баллов
Анализ ошибок
Обозначение задания в работе | Проверяемые элементы содержания | % выполнения |
А1 | Классы и разряды. | 100 |
А2 | Шкалы и координаты. | 40 |
А3 | Сложение и вычитание чисел, использование соответствующих терминов. | 80 |
А4 | Умножение и деление чисел, использование соответствующих терминов. | 40 |
А5 | Нахождение значений числовых и буквенных выражений со скобками и без них. | 40 |
А6 | Установление зависимостей между величинами, характеризующими процессы движения (пройденный путь, время, скорость) | 20 |
А7 | Умножение и деление чисел, использование соответствующих терминов. | 80 |
А8 | Площадь геометрической фигуры | 20 |
В1 | Решение текстовых задач арифметическим способом с опорой на таблицы | 40 |
В2 | Использование свойств арифметических действий при выполнении вычислений | 0 |
В3 | Использование свойств арифметических действий при выполнении вычислений. | 40 |
С1 | Решение текстовых задач арифметическим или алгебраическим способом с опорой на краткие записи | 20 |
С2 | Единицы длины (миллиметр, сантиметр, дециметр, метр, километр) Единицы времени (секунда, минута, час, сутки, неделя, месяц, год, век) | 40 |
Практические математические вопросы для практики: упрощение алгебраического выражения
Praxis Core: 1001 практический вопрос для чайников
Изучить книгу Купить на Amazon
Некоторые алгебраические выражения на экзамене Praxis Core могут показаться пугающими, и вы даже можете отказаться от них и двигаться дальше. Однако, как вы увидите из следующих практических вопросов, для их решения можно использовать несколько простых приемов, таких как разложение на множители и комбинирование одинаковых терминов.
Практические вопросы
- Which of the following is the simplified form of the expression 8 x 2 y – 5 xy 2 + 12 xy 2 – 3 x 2 y ?
А. 5 x 2 y 2 + 7 x 2 y B. 3 x 2 y + 9 xy 2 C.
- Что из следующего является упрощенной формой
Ответы и пояснения
- Правильный ответ: вариант (С).
Вы можете комбинировать подобные термины, чтобы упростить выражение. Подобные термины имеют одинаковые переменные, и каждая переменная имеет один и тот же показатель степени в каждом из подобных терминов.Чтобы объединить одинаковые термины, сложите их коэффициенты; комбинации переменных и показателей, которые являются общими для терминов, идут справа от новых коэффициентов:
- Правильный ответ: вариант (D).
Разложите числитель и знаменатель на множители. Затем отмените любое выражение, которое является множителем числителя и знаменателя.
Вы можете комбинировать подобные термины, чтобы упростить выражение. Подобные термины имеют одинаковые переменные, и каждая переменная имеет один и тот же показатель степени в каждом из подобных терминов.Об этой статье
Эта статья взята из книги:
- Praxis Core: 1,001 практических вопросов для чайников,
Об авторах книги:
Карла Киркланд, основатель и генеральный директор Kirkland Group, образовательного консалтинга фирма, уже более 20 лет помогает преподавателям готовить своих учеников к стандартизированным тестам.
Чан Кливленд, исполнительный вице-президент Kirkland Group, преподаватель английского языка, который разработал ресурсы по словесности для нескольких школьных округов.
Эту статью можно найти в категории:
- Praxis ,
Понимание парадокса дня рождения – BetterExplained
23 человека . В комнате всего из 23 человек вероятность того, что по крайней мере у двух человек день рождения совпадет, составляет 50 на 50. В комнате на 75 человек с вероятностью 99,9% совпадут как минимум два человека.
Положите калькулятор и вилы, я не говорю ересь. Парадокс дня рождения странен, нелогичен и совершенно верно . Это всего лишь «парадокс», потому что наш мозг не может справиться с суммирующей силой экспонент. Мы ожидаем, что вероятности будут линейными, и учитываем только те сценарии, в которых участвуем (кстати, оба предположения ошибочны).
Давайте посмотрим, почему возникает парадокс и как он работает.
Проблема 1: Экспоненты не интуитивны
Мы изучили математику и статистику, но не будем себя обманывать: это неестественно.
Вот пример: какова вероятность выпадения 10 орлов подряд при подбрасывании монеты? Нетренированный мозг может подумать так: 910$ или около 0,001.
Но даже после тренировки нас снова ловят. При процентной ставке 5% мы удвоим наши деньги за 14 лет, а не за «ожидаемые» 20 лет. Вы естественным образом вывели правило 72-х, узнавая о процентных ставках? Возможно нет. Понять составной экспоненциальный рост с помощью нашего линейного мозга сложно.
Проблема 2: Люди немного эгоистичны
Посмотрите новости. Обратите внимание, сколько негативных новостей является результатом действий без учета других. Я оптимист и 9От 0022 до есть надежда для человечества, но это отдельный разговор :).
В комнате с 23 людьми вы думаете о 22 сравнениях, где ваш день рождения сравнивается с чьим-то еще? Вероятно.
Вы думаете о сравнениях 231 , когда кого-то, кто не вы, сравнивают с кем-то другим, кто не вы? Ты понимаешь, что их так много? Возможно нет.
Тот факт, что мы пренебрегаем в 10 раз большим количеством сравнений, которые не включают нас, помогает нам понять, почему может произойти «парадокс».
Хорошо, хорошо, люди ужасны: покажите мне математику!
Вопрос: Каковы шансы, что у двух человек в группе из 23 человек день рождения совпадает?
Конечно, мы могли бы перечислить пары и подсчитать все возможные совпадения. Но это сложно: совпадений может быть 1, 2, 3 или даже 23!
Это все равно что спросить: «Какова вероятность того, что при 23 подбрасываниях монеты выпадет один или несколько орлов?» Есть так много возможностей: решка при первом броске, или 3-м, или последнем, или 1-м и 3-м, 2-м и 21-м, и так далее.
923, но поработайте со мной здесь), есть 99% шанс иметь хотя бы одну голову . Не знаю, 1 решка, или 2, или 15, или 23: у нас есть решки, и это главное. Если мы вычтем вероятность проблемного сценария из 1, мы получим вероятность хорошего сценария.
Тот же принцип применим и к дням рождения. Вместо того, чтобы найти все способы, которыми мы совпадаем, находят шанс того, что все разные, «проблемный сценарий» . Затем мы берем противоположную вероятность и получаем шанс на совпадение. Это может быть 1 совпадение, или 2, или 20, но кто-то совпал, что нам и нужно найти.
Объяснение: подсчет пар (приблизительная формула)
Из 23 человек у нас получается 253 пары:
(Если хотите, освежите в памяти комбинации и перестановки).
Вероятность того, что 2 человека имеют разные дни рождения:
Имеет смысл, верно? При сравнении дней рождения одного человека с днем рождения другого в 364 из 365 сценариев они не совпадут.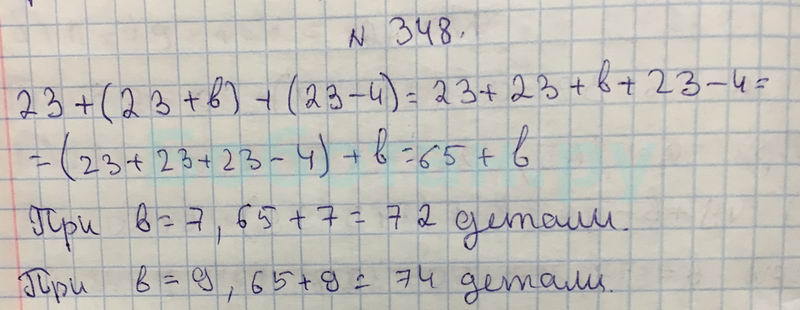
Отлично.
Но провести 253 сравнения и сделать так, чтобы они все были разными, это все равно, что получить орёл 253 раза подряд — вам приходилось каждый раз уворачиваться от «решки». Давайте получим приблизительное решение, представив, что сравнение дней рождения похоже на подбрасывание монеты. (См. Приложение A для точного расчета.)
Мы используем показатели степени, чтобы найти вероятность:
Наши шансы получить один промах довольно высоки (99,7260%), но когда вы используете этот шанс сотни раз, шансы сохранить эту серию падают. Быстрый.
Вероятность совпадения: 1 – 49,95% = 50,05%, или чуть больше половины! Если вы хотите найти вероятность совпадения для любого количества людей, используйте формулу:
Интерактивный пример
Я не верил, что нам нужно всего 23 человека. Математика работает, но реально ли это?
Ещё бы. Попробуйте пример ниже: выберите количество предметов (365), количество людей (23) и проведите несколько испытаний.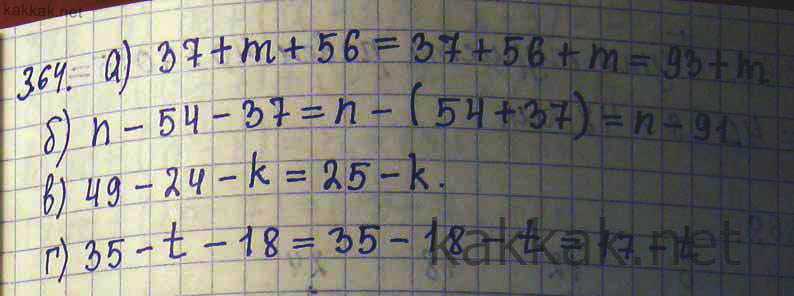
Во время испытаний вы увидите теоретическое совпадение и фактическое совпадение. Вперед, нажмите кнопку (или просмотрите страницу целиком).
По мере того, как вы проводите все больше и больше испытаний (продолжайте нажимать!), фактическая вероятность должна приближаться к теоретической.
Примеры и выводы
Вот несколько уроков парадокса дня рождения:
- $\sqrt{n}$ — это примерно то число, которое вам нужно, чтобы иметь 50%-й шанс совпадения с n предметами. $\sqrt{365}$ составляет около 20. Это используется в криптографии для атаки на день рождения.
- Несмотря на то, что существует 2 128 (1e38) GUID, у нас есть только 2 64 (1e19) для использования до 50% вероятности столкновения. А 50% — это очень, очень много.
- Вам нужно всего 13 человек, чтобы подобрать буквы алфавита, чтобы вероятность совпадения составила 95%. Попробуйте выше (людей = 13, предметов = 26).
- Экспоненциальный рост быстро снижает вероятность выбора уникальных предметов (он же увеличивает шансы совпадения). Помните: экспоненты не интуитивны, а люди эгоистичны!
Помните: экспоненты не интуитивны, а люди эгоистичны!После долгих размышлений парадокс дня рождения, наконец, пришел ко мне. Но я все же проверю интерактивный пример, чтобы убедиться.
Приложение A: Объяснение повторного умножения (точная формула)
Помните, мы предполагали, что дни рождения независимы? Ну, это не так.
Если Человек A и Человек B совпадают, и Человек B и C совпадают, мы знаем, что A и C также должны совпадать. Результат сопоставления A и C зависит от их результатов с B, поэтому вероятности не являются независимыми. (Если бы A и C были действительно независимыми, вероятность совпадения составила бы 1/365, но мы знаем, что совпадение гарантировано на 100 %.)
При подсчете пар мы относились к совпадениям дней рождения как к подбрасыванию монеты, умножая одну и ту же вероятность снова и снова. . Это предположение не совсем верно, но его достаточно для небольшого числа людей (23) по сравнению с размером выборки (365). Маловероятно, что несколько человек совпадут и испортят независимость, так что это хорошее приближение.
Маловероятно, но может случиться. Давайте посчитаем реальные шансы того, что каждый человек выберет другой номер:
- Первый человек имеет 100% вероятность того, что выпадет уникальный номер (конечно)
- Второй имеет шанс (1 – 1/365) (все, кроме 1 числа из 365)
- Третий имеет шанс (1 – 2/365) (все числа, кроме 2)
- 23-й номер имеет (1–22/365) (все номера, кроме 22)
Умножение выглядит довольно уродливо:
9x$ равно:, поэтому
Используя наш удобный ярлык, мы можем переписать большое уравнение так:
Но мы помним, что сложение чисел n + n = 1 к n) /2. Не путайте это с n(n-1)/2, что равно C(n,2) или количеству пар из n элементов. Они выглядят почти одинаково!
Прибавляя 1 к 22, мы получаем (22 * 23)/2:
Уф. Это приближение очень близко, подставьте ниже свои цифры: 92 / (2 \cdot 365)} \примерно 1$ .
Приложение B: Общая формула дня рождения
Давайте обобщим формулу для выбора n человек из T всего предметов (вместо 365):
) и решить для n :
Вуаля! Если вы возьмете $\sqrt{T}$ предметов (на 17% больше, если вы хотите быть разборчивым), у вас будет примерно 50-50 шансов получить совпадение.