Упростите выражение примеры решения: Упрощение выражений — примеры решений

2. Найти значение выражения , если .

3. Упростите выражение и вычислите его значение при .

4. Упростите выражение и вычислите его значение при .

5. Упростите выражение и вычислите его значение при .

6. Упростите выражение .

7. При всех допустимых и найти численное значение выражения

.

8. При всех допустимых упростить выражение:

.

9. При всех допустимых и упростить выражение:

.

10. .

11. .

12. .

Многие уравнения и неравенства часто сводятся к решению линейных и квадратных уравнений и неравенств соответственно. Поэтому кратко повторим основные подходы к их решению.

Корень (решение) уравнения – число, которое при подстановке его в уравнение вместо переменной, превращает данное уравнение в верное равенство.

Решить уравнение, — значит, найти все его корни (решения) или доказать, что корней (решений) нет.

Равносильные уравнения – уравнения, множества корней (решений) которых совпадают, в частности, если оба уравнения не имеют корней, то они равносильны.

Замечание: 1. Если каждый корень уравнения является в то же время корнем уравнения , полученного после некоторых преобразований из уравнения , то уравнение называют следствием уравнения .

2. Если каждое из двух уравнений является следствием другого из них, то такие уравнения являются равносильными.

Линейные уравнения – уравнения вида , где и — некоторые числа, — переменная.

Эти уравнения имеют три различных случая решения (рассмотрим на примерах):

Пример. (умножим обе части уравнения на 12).

,

,

,

. (единственное решение).

Пример. , решений нет.

Пример. ; любое

удовлетворяет последнему уравнению, а значит и исходному. (бесконечно много

решений).

Квадратные уравнения – уравнения вида , где и — некоторые числа, — переменная, при этом (при уравнение превращается в линейное.) Если или , а также в случае одновременного равенства нулю этих коэффициентов квадратное уравнение называют неполным и решают стандартными способами разложения на множители.

Пример. или ; или .

Пример. .

Для решения полного квадратного уравнения используют обычную формулу корней квадратного уравнения:

.

Возможны три случая:

1. ; уравнение имеет два различных действительных корня , ;

2. ; уравнение имеет два одинаковых действительных корня ;

3. ; уравнение не имеет действительных корней.

Замечание. Для решения приведенного квадратного уравнения, , , часто используют теорему Виета:

, .

Пример. .

Рациональные (дробно-рациональные) уравнения.

Определение: Функция вида , где ; — некоторый действительные числа, называется целой рациональной функцией.

Целым рациональным уравнением называется уравнение вида , где — целая рациональная функция.

Теорема 1. Для того чтобы несократимая дробь была корнем многочлена с целыми коэффициентами, необходимо, чтобы число было делителем свободного члена , а число — делителем старшего коэффициента .

Теорема 2. (Теорема Безу) Остаток от деления многочлена на двучлен равен значению мног4очлена при , то есть .

При делении многочлена на двучлен имеем равенство

.

Оно справедливо, в частности, при , то есть .

Пример. Решить уравнения: 1) ; 2) ;

3) ; 4) .

Пример. Решить уравнение .

Решение: Поскольку коэффициенты уравнения – целые числа, то попробуем найти хотя бы один целый корень. Делителями свободного члена являются числа . Подстановкой легко убедиться, что — корень уравнения. Проведем деление многочленов «уголком»:

Получили .

Аналогично, убеждаемся, что — корень многочлена , проведем деление:

Таким образом, исходное уравнение можно записать в виде:

,

Что равносильно совокупности двух уравнений:

Дискриминант второго уравнения отрицательный, значит, оно не имеет действительных корней. Итак, является корнем исходного уравнения.

Для самостоятельного решения:

Решить уравнение:

Ответ: -1, 2.

Дробно-рациональным уравнением называется уравнение вида , где — многочлены.

Решение дробно-рационального уравнения сводится к нахождению корней уравнения и проверке того, что они удовлетворяют условию , то есть рациональное уравнение равносильно системе:

Пример.

Решить уравнения 1) ;

2) .

Пример. Решить уравнение .

Решение: Область определения уравнения:

.

Далее будем работать на области определения уравнения. Умножим обе части уравнения на и получим уравнение:

,

.

Пример. Решить уравнение .

Решение: Область определения уравнения:

.

Далее будем работать на области определения уравнения. Заметим, что ; . Сделаем замену . Тогда исходное уравнение перепишем следующим образом:

,

, ,

,

Обратная замена:

.

Пример. Решить уравнение .

Решение: Непосредственно проверкой устанавливаем, что не является корнем данного уравнения. Тогда вынесем из каждой скобки и перейдем к равносильному уравнению:

,

.

Сделаем замену: . Отсюда:

или .

,

Пример. Решить уравнение .

Решение: Сгруппируем множители в левой части уравнения так, чтобы при перемножении были равны первый коэффициент и свободный член:

Далее аналогично примеру 10. Так как не является корнем уравнения, вынесем его за скобки:

Замена: , или .

.

Пример. Решить уравнение .

Решение: Так как не является корнем уравнения, разделим обе части уравнения на , получим уравнение, равносильное данному:

.

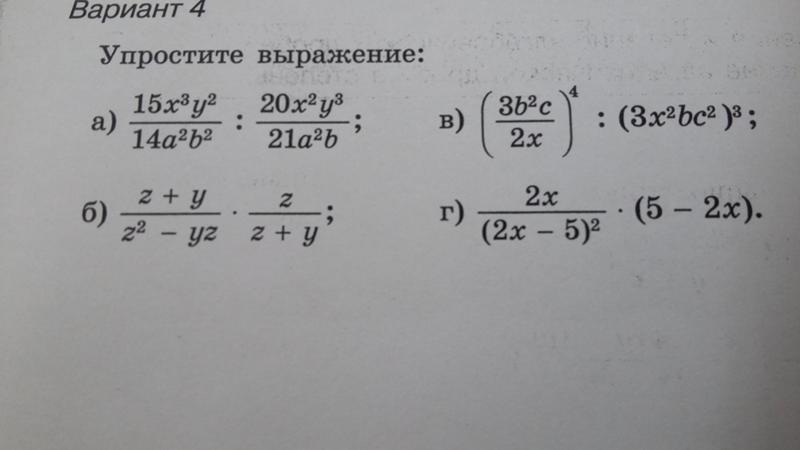
Сгруппируем члены этого уравнения:

.

Введем замену: , , .

или .

.

Для самостоятельного решения:

1. Решить уравнение:

(Примечание: замена ).

Ответ: -2, 1.

2. Решить уравнение: .

(Примечание: замена ).

Ответ: .

Рациональные (дробно-рациональные) неравенства. Метод интервалов для рациональных функций.

Важнейшим методом решения неравенств является метод интервалов. В 9 классе изучается метод интервалов, прежде всего для многочленов. Он основан на том, что двучлен положителен при и отрицателен при , то есть меняет знак при переходе через точку .

Заметим, что

1. двучлен в нечетной степени ведет себя так же, как ,

2. двучлен в четной степени ведет себя по-другому: он не меняет знак при переходе через точку .

3. квадратичный трехчлен, имеющий положительный коэффициент при и отрицательный дискриминант, всегда положителен и может быть опущен при решении любого неравенства.

4. при переходе через точку может изменить знак только один множитель, , выражение при переходе через точку знак не меняет.

Пример. а. Решить неравенство ,

б.

Решение: а. Для решения строгого неравенства наносим на числовую ось нули функции кружочками («дырками»). Далее расставляем знаки, учитывая замечание выше:

Ответ: .

б. Вспомним, что по определению,

.

Для решения нестрогих неравенств наносим нули функции на числовую ось точками. Затем расставляем знаки в промежутках.

Ответ: .

Метод интервалов легко распространяется на рациональные функции.

Рациональной называется функция, которая может быть представлена в виде частного двух многочленов, то есть в виде .

Неравенства называются рациональными, если их правые и левые части являются рациональными функциями.

Заметим, что , поэтому метод интервалов применяется к дроби точно так же, как и к многочленам. Для нестрого же неравенства имеем:

.

При решении нестрогих рациональных неравенств нули числителя наносятся на числовую ось точками, а нули знаменателя — «дырками».

Пример. Решить неравенство .

Решение: Приведем неравенство к стандартному виду и разложим числитель и знаменатель на множители. Затем решаем методом интервалов:

, , ,

Ответ: .

Пример. Найти сумму целых решений неравенства .

Решение: Решим неравенство методом интервалов:

. Видно, что целыми решениями являются числа: -2, -1. 3. 4. Их сумма равна 4.

Ответ: 4.

Для самостоятельного решения:

1. Решить неравенства:

2. Укажите длину промежутка, который является решением неравенства:

Ответ: 9.

3. Найти произведение всех целых решений неравенства: .

Ответ: .

Математика для блондинок: Как упростить выражение

Комментарии к этой странице переполнены и у меня нет возможности отвечать. Свои вопросы и пожелания оставляйте здесь.

Вот очередная просьба о спасении утопающего в тригонометрии. Есть набор тригонометрических символов, а что с ними делать — не понятно. Как упростить выражение? Рецепт очень простой — нужно использовать те формулы, которые вы учите сейчас. Или те формулы, которые вы учили когда-то, но напрочь забыли. Вот описание выражений.

Теперь перепишем выражения, которые нужно упростить, в более удобоваримом виде.

Не знаю, как вас, а меня красота математики иногда просто завораживает. Но не в этом случае — не люблю задачи, составленные людьми. Мы с блондинками недавно решали пример на упрощение: под корнем квадратным четыре выражения в скобках перемножаются между собой, каждая скобка содержит сумму из трех тригонометрических функций. Я даже сам сперва испугался такого монстра. Любопытство и вера в мудрость математики победили. Я начал перемножать скобки. Огромное выражение таяло, как снег весной, в результате сокращений. В итоге мы получи произведение двух тригонометрических функций. Даже блондинкам это понравилось: «Вау! Супер!» — так звучал их вердикт.

Процесс упрощения математических выражений очень похож на то, чему учат курсы кройки и шитья. Вырезаем один фрагмент и заменяем его другим. При этом математическими формулами мы пользуемся, как выкройками. Все формулы разрезаются по знаку равенства. Вместо того куска формулы, который присутствует в математическом выражении, мы вставляем другой кусок, который находится с противоположной стороны знака равенства.

Посмотрим на наших примерах, как это делается. Прежде всего, нужно определить, какие именно формулы необходимо использовать для упрощения выражений. В процессе обучения чаще всего используются те формулы, которые вы учили совсем недавно. В повседневной жизни для этих целей используйте справочники.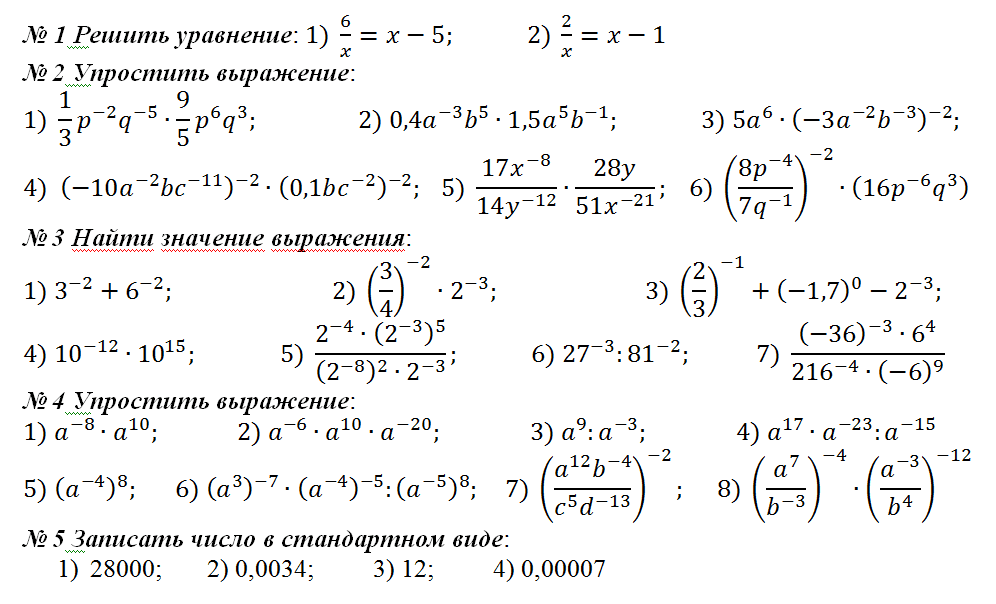 Сейчас мы используем основные тригонометрические тождества.

Вместо квадратов синуса и косинуса ставим единицу в наше выражение. У нас получилось новое тригонометрическое тождество, только угол у нас обозначен по-другому — бетта вместо альфа. В результате наше выражение превращается в единицу, деленную на косинус угла бетта в квадрате. Вместо этого можно записать секанс бетта в квадрате (по определению тригонометрических функций).

Для упрощения второго выражения необходимо немного преобразовать основные тригонометрические тождества. Используем обычные арифметические правила переноса слагаемых и сомножителей из одной части равенства в другую. Зеленые стрелочки справа показывают, из какого тождества получена нужная нам формула. Заменяем котангенс в знаменателе на тангенс в числителе. Мы избавляемся от дроби и получаем тангенс в квадрате. По теореме Пифагора в тригонометрическом виде заменяем единицу минус косинус альфа в квадрате на квадрат синуса альфа. Из определения тригонометрических функций заменяем тангенс на отношение синуса к косинусу. Сокращаем нашу дробь и получаем синус альфа в квадрате.

Как бы математики не гордились своей высшей математикой, но вся она построена на банальной кройке и шитье. Решение дифференциалов, интегралов и прочей ерунды сводится к поиску подходящих формул и преобразовании выражений до удобоваримого вида, которое принято называть «решение». Всё отличие математики высшей от математики обычной заключается в количестве формул, которые используются при решении. В высшей математике их ну очень много.

Если вы научитесь в уме жонглировать основными формулами, если вы научитесь в предлагаемых выражениях видеть куски, содержащие основные формулы, тогда с математикой у вас не будет никаких проблем. Вы будете решать всё, что от вас потребуют. Умение распознавать хорошо замаскированную суть и интуитивное видение решения — это то, что вы получите в результате тренировок по упрощению математических выражений.

Я столько всего пишу о математике, что пора уже собирать разрозненные мысли в одну книгу «Математика для блондинок». Потом можно издать книгу за свой счет и вы получите перевод абстрактной математики на человеческий язык. Как разложить борщ по тригонометрическим функциям? Такое в принципе возможно или нет? Есть ещё масса не менее интересных вопросов, ответы на которые вы сможете получить.

Но проблема заключается в финансировании моей работы над математикой. Если я занят зарабатыванием денег, тогда я не занимаюсь математикой. Если я занимаюсь математикой — я не зарабатываю себе на жизнь. Такова формула жизни. Если вам нужна «Математика для блондинок», тогда окажите мне материальную помощь. Если вы не будете перечислять денег, тогда я с чистой совестью буду заниматься другими делами. А что делать вам? Покупайте оценки у учителей, нанимайте репетиторов или усердно зубрите математику. Так делают все.

Алгебраические выражения — определение, типы, упрощение, примеры

Алгебраические выражения зародились в 9 веке. Вначале это было скорее в форме утверждений, а вовсе не математических. Например, алгебраические уравнения раньше записывались так: «Пять умноженных на 3 дают 18, что равно 5x + 3 = 18. Этот тип уравнения, который не был математическим, был вавилонской алгеброй. Алгебра развивалась со временем и с появлением различных форм. Все началось с египетской алгебры, затем появилась вавилонская алгебра, затем греческая геометрическая алгебра, затем диофантова алгебра, за ней последовала индуистская алгебра, затем арабская алгебра, а затем абстрактная алгебра. Сегодня самая простая и удобная форма алгебры преподается в классах для лучшего понимания.

Что такое алгебраические выражения?

Алгебраические выражения — это выражения, полученные из комбинации переменных, констант и математических операций, таких как сложение, вычитание, умножение, деление и т. д. Алгебраическое выражение состоит из членов, в уравнении может присутствовать один или несколько членов. Давайте узнаем об основных терминах, используемых в алгебраических выражениях.

Алгебраические термины, константы, переменные и коэффициенты

 

В алгебраическом выражении фиксированные числа называются константами. Константы не имеют присоединенных к ним переменных. Например, 3x – 1 имеет константу -1. Переменные — это неизвестные значения, присутствующие в алгебраическом выражении. Например, 4y + 5z имеет y и z в качестве переменных. Коэффициенты — это фиксированные значения (действительные числа), прикрепленные к переменным. Они умножаются на переменные. Например, 5x ² + 3 имеет 5 в качестве коэффициента x ² . Терм может быть константой, переменной или их комбинацией. Каждый термин отделяется либо сложением, либо вычитанием. Например, термины 3x + 5, 3x и 5.

Типы алгебраических выражений

Существуют различные типы алгебраических выражений в зависимости от количества членов.

Тип алгебраического выражения0043 Мономиальное	Мономиальное алгебраическое выражение — это алгебраическое выражение, которое имеет только один член.	2xy, 5y 3 , 7a, 2b и т. д.	6x + 8y, 3a 2 + 2ab и т. д.
Трехчленный	Трехчленное алгебраическое выражение — это алгебраическое выражение, содержащее три непохожих члена или три монома.	x + y + z, 11x 2 -5y + z и т. Д.
Полиномиальная	Alynomial Algebraic Expression является алкогольными выражениями, которая имеет два или более нуженные. показатели переменной.	3x + 4y + 5z, ax 3 + bx 2 + cx + d и т. д.
Полиномиальное	Полиномиальное алгебраическое выражение — это алгебраическое выражение, которое имеет один или более членов. Здесь показатель степени переменной также может быть отрицательным.	x + y -2 , 5x 2 + 6Z -1

Упрощающие алгебраические выражения

Упрощающие алкогольные выражения и очень основы. Во-первых, поймите, что такое похожие и непохожие термины. Однородные термины имеют один и тот же знак, а разные термины имеют противоположные знаки. Чтобы упростить данное алгебраическое выражение, сначала найдите члены, имеющие одинаковую мощность. Затем, если термины похожи на термины, добавьте их; если они разные термины, найти различие между терминами. Наиболее упрощенной формой алгебраического выражения является та, в которой не повторяются одинаковые степенные члены.

Например, давайте упростим 4x ⁵ + 3x ³ — 8x ² + 67 — 4x ² + 6x ³ . выражение принимает вид 4x ⁵ + (3x ³ + 6x ³ ) — (8x ² — 4x ² ) + 67. Теперь, упростив выражение, получаем окончательный ответ: 4x5 6 5 + 9x ³ – 12x ² + 67. В этом члене нет повторяющихся членов с одинаковой мощностью.

Сложение алгебраических выражений

Когда операция сложения выполняется над двумя алгебраическими выражениями, одинаковые члены складываются только с подобными членами, т. е. складываются коэффициенты подобных членов.

Пример: сложите (25x + 34y + 14z) и (9x − 16y + 6z + 17).

Решение:

(25x + 34y + 14z) + (9x − 16y + 6z + 17)

Записав вместе подобные слагаемые, мы получим

= −1 ) + (14з + 6з) + 17

Складывая подобные члены, получаем

= 34x + 18y + 20z + 17.

Следовательно, (25x + 34y + 14z) + (9x − 16y + 6z + 17) = 34x + 18y + 20z + 17.

Вычитание алгебраических выражений

Чтобы вычесть алгебраическое выражение из другого, мы должны добавить аддитивную обратную величину второго выражения к первому выражению.

Пример: Вычтите (5b ² + 6b + 8) из (3b ² − 5b).

Решение:

(5b ² + 6b + 8) − (3b ² − 5b)

= (5b ² + 6b + 8) + (−3b ^{2 9003) = (−3b 2 9003) 5b 2 − 3b 2 ) + (6b + 5b) + 8 = 2b 2 + 11b + 8}

Умножение алгебраических выражений

Когда операция умножения выполняется над двумя алгебраическими выражениями умножьте каждый член первого выражения на каждый член второго выражения, а затем объедините все произведения.

Пример: Умножить (3x + 2y) на (4x + 6y − 8z)

Решение:

(3x + 2y)(4x + 6y − 8z) = 3x(4x) + 3x(6y) ) − 3x(8z) + 2y(4x) + 2y(6y) − 2y(8z)

= 12x ² + 18xy − 24xz + 8xy + 12y ² − 16yz

+ 9 12x 90 ² + 26xy − 16yz − 24xz

Деление алгебраических выражений

Когда нам нужно разделить алгебраическое выражение от другого, мы можем разложить на множители и числитель, и знаменатель, затем сократить все возможные члены и упростить остальные , или мы можем использовать метод длинного деления, когда мы не можем разложить алгебраические выражения на множители.

Пример: Решите: (x ² + 5x + 6)/(x + 2)

Решение:

= (x ² + 5x + 2)/(x + 6)

(х ² + 5х + 6) = (х + 2) (х + 3)

= [(х + 2) (х + 3)]/(х + 2)

= (х + 3)

Алгебраические формулы

Общие алгебраические формулы, которые мы используем для решения выражений или уравнений:

1. (х + а) (х + b) = х аб
2. (a + b) ² = a ² + 2ab + b ²
3. (a – b) ² = a ² – 2ab + b ²
4. (a + b ) ² + (а – б) ² = 2 (а ² + б ² )
5. (а + б) ² – (а – б) ^{2 8 8 аб 902 = 4 91 а 2} – b ² = (a – b)(a + b)
6. (a + b + c) ² = a ² + b ² + c ² + 2b + 2ab + 2ка
7. (а + б) ³ = а ³ + б ³ + 3аб(а + б)
8. (а – б) ³ = а ³ – 3 аб(5 а – б)
9. а ³ – б ³ = (а – б)(а ² + аб + б ² )
10. а ³ + б ^{)(a 2 – ab + b 2 )}
11. a ³ + b ³ + c ³ – 3abc = (a + b + c)(a 5 b + c)(a 5 b 1 + с ² — AB — BC — CA))

Решающие примеры по алгебраическим выражениям

Проблема 1: Узнайте постоянную из следующих выражений алгебраических – 6

9 + y ⁵

Ответ: 

а во втором случае 9является константой.

Problem 2: Find out the number of terms present in the following expressions,

1. 4x ² + 7x – 8
2. 5y ⁷ – 12

Answer:

Термины отделяются друг от друга знаком сложения или вычитания. Следовательно, в первом случае 3 термина, а во втором случае 2 термина.

Задача 3: Упростить алгебраический член, z ⁵ + Z ³ — Y ⁶ + 7Z ⁵ — 8Y ⁶ + 34 + 10Z ³

Решение:

В выражении, есть термины, и это. мощность и одна и та же переменная, которые повторяются, сначала сведите их вместе,

(z ⁵ + 7z ⁵ ) + (z ³ + 10z ³ ) – (y ⁶ – 6 8y ^{) + 34.}

Теперь упростим выражение,

8z ⁵ + 11z ³ – 9y ⁶ + 34.

Задача 4: Сложить (13x ² + 11), ( – 25x ^{+ 9 – 3 2 x 2 и 926016 ).}

Решение:

(13x ² + 11) + ( — 25x ² + 26x + 42) + (–33x — 29)

= 13x ² — 25x ^{2 9001 + = 13x 2 — 25x 2 9001 +. 26x – 33x + 11 + 42 – 29}

Теперь складываем одинаковые члены

= –12x ² – 7x + 24

Следовательно, (13x ² + 11) + ( – 25x ² + 26x + 42) + (–33x – 29) = –12x ² – 7x + 24.

Задача 5. Решить (5x + 6z + 4y ) ² + (3г – 7х) ² .

Решение:

Дано,

(5x + 4y + 6Z) ² + (3y — 7x) ²

Из алгебраических формулов, у нас

(A + b + c) c) c). ² = а ² + b ² + с ² + 2ab + 2bc + 2ca

(а – б) ² = а ² – 2аб + б ²

= (5х) ² + (4у) ² ) + (6х) 2 ^{(4y) + 2(4y)(6z) + 2(6z)(5x) + [(3y) 2 – 2(3y)(7x) + (7x) 2 ]}

= 25x ² + 16y ² + 36z ² + 40xy + 48yz + 60zx +9y2 – 42xy + 49x ²

Теперь соединим подобные термины.

= 74x ² + 25y ² + 36z ² – 2xy + 48yz + 60zx

Следовательно, (5x + 4y + 6z) ² + (3y – 7x) ² = 74x ² + 25y ² + 36z ² – 2xy + 60zy + 60zy

Часто задаваемые вопросы об алгебраических выражениях

Вопрос 1: Какие существуют типы алгебраических выражений?

Ответ:

Три основных типа алгебраических выражений:

• Одночлен: Одночлен — это выражение, которое имеет только один ненулевой член. 2xy, 5y3, 7a, 2b и т. д. — некоторые примеры мономов.
• Биномиальное: Биномиальное выражение — это выражение, содержащее два ненулевых члена. Например, 2a + 3 имеет два монома 2a и 3 и, следовательно, является биномом.
• Многочлен: Многочлен — это выражение, которое имеет более двух ненулевых, непохожих членов. Например, x-4y+ 8z имеет три монома x, 4y и z, следовательно, это многочлен.

Вопрос 2: Все ли алгебраические выражения являются полиномами?

Ответ:

Не все алгебраические выражения являются полиномами, но все полиномы являются алгебраическими выражениями, т. е. существуют некоторые алгебраические выражения, которые не являются полиномами. Пример: πx + 1 — алгебраическое выражение, но не многочлен.

Вопрос 3: Как определяются алгебраические выражения?

Ответ:

Алгебраическое выражение представляет собой представление чисел с использованием таких букв, как x, y, z и т. д., без указания их фактических значений. Это математическое утверждение, которое мы получаем, когда арифметические операции, такие как сложение, вычитание, умножение или деление, выполняются над переменными и константами. Проще говоря, алгебраическое выражение — это математическое выражение, в котором переменные объединены с помощью основных арифметических операций.

Пример: Возраст Рама в три раза больше возраста Акаши, а их общий возраст равен 48 годам. Выразите это в виде алгебраического уравнения.

Решение: Пусть возраст Акаши равен х. Тогда возраст Рама равен 3x

3x + x = 48

4x = 48

Вопрос 4: Что такое переменные в алгебраическом выражении?

Ответ:

В алгебраическом выражении переменная — это символ, который не имеет фиксированного значения. Например, в уравнении 3x + 7 = 0 x — это переменная, которая может принимать любое значение. В математике a, b, m, n, x, y, z и т. д. являются некоторыми примерами переменных.

Упрощение алгебраических выражений — примеры и практические задачи

Алгебраические выражения можно упростить, используя распределительное свойство для удаления круглых скобок. Затем мы объединяем одинаковые члены, то есть члены с одинаковыми переменными и одинаковыми показателями. Наконец, мы добавляем постоянные члены.

В этой статье мы кратко рассмотрим упрощение алгебраических выражений. Кроме того, мы рассмотрим несколько примеров упрощения с ответами, чтобы полностью освоить эту тему.

АЛГЕБРА

Актуально для …

Изучение примеров упрощения алгебраических выражений.

См. примеры

Содержание

АЛГЕБРА

Актуально для …

Изучение примеров упрощения алгебраических выражений.

См. примеры

Краткое описание упрощения алгебраических выражений

Упрощение алгебраических выражений позволяет нам получать более простые выражения, с которыми можно легко работать.

Чтобы упростить алгебраические выражения, мы можем применить свойство дистрибутивности, чтобы удалить круглые скобки и другие знаки группировки, и мы можем комбинировать подобные термины.

Распределяющее свойство

Распределяющее свойство говорит нам, как устранить знаки группировки путем распределения умножения числа на все внутренние члены в скобках:

Объединить подобные члены

Подобные члены — это алгебраические термины, в которых возводятся одни и те же переменные к той же мощности.