Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3.
А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел.
Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Пример 2Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Пример 3Представьте выражение со степенями 9-b3·π-12 в виде произведения.
Решение
Представим число 9 как степень 32 и применим формулу сокращенного умножения:
9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1
Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения.
Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а
- ar·as=ar+s;
- ar:as=ar−s;
- (a·b)r=ar·br;
- (a:b)r=ar:br;
- (ar)s=ar·s.
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.
Ответ: a2,5·(a2)−3:a−5,5=a2.
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Найти значение степенного выражения 313·713·2123.
Решение
Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.
Есть еще один способ провести преобразования:
313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21
Ответ: 313·713·2123=31·71=21
Пример 6
Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.
Решение
Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.
Ответ: t3−t−6.
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2
Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a0,3:
a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a
б) Обратим внимание на знаменатель:
x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162
Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.
е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.
Пример 9Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.
Получаем:
30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)
б) Здесь наличие одинаковых множителей неочевидно.
Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14
Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10Выполните действия x12+1×12-1-x12-1×12+1·1×12.
Решение
Начнем с вычитания дробей, которые располагаются в скобках.
Приведем их к общему знаменателю:
x12-1·x12+1
Вычтем числители:
x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12
Теперь умножаем дроби:
4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12
Произведем сокращение на степень x12, получим 4×12-1·x12+1.
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.
Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1
Пример 11Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение
Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.
Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.
Переходим от последнего произведения к дроби x138x2,7+1.
Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2.
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12Представьте выражение x19·x·x36 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞).
На этом множестве мы имеем право перейти от корней к степеням:
x19·x·x36=x19·x·x1316
Используя свойства степеней, упростим полученное степенное выражение.
x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13
Ответ: x19·x·x36=x13.
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.
Теперь поделим обе части равенства на 72·x.
Это выражение на ОДЗ переменной x принимает только положительные значения:
5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0
Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.
Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Упрощение показателей — математика для старших классов
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Алгебра II » Математические отношения и основные графики » Экспоненты » Упрощение показателей
Упростите следующее выражение.
Возможные ответы:
Правильный ответ:
Объяснение:
При делении с показателями степени показатель в знаменателе вычитается из показателя степени в числителе. Например: .
В нашей задаче каждое слагаемое можно трактовать таким образом. Помните, что отрицательный показатель степени можно перенести в знаменатель.
Теперь упростим цифры.
Сообщить об ошибке
Упростите следующее выражение.
Возможные ответы:
Правильный ответ:
Объяснение:
Нам дано: .
Вспомните, что когда мы умножаем показатели степени с одним и тем же основанием, мы сохраняем основание одним и тем же и складываем показатели степени.
Итак, имеем.
Сообщить об ошибке
Упростите следующее выражение.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, что когда мы делим степени с одинаковым основанием, мы сохраняем основание одним и тем же и вычитаем степени.
Итак, имеем.
Напомним также, что для отрицательных показателей
.
Таким образом, .
Сообщить об ошибке
Упростите следующее выражение степени:
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с перестройки терминов в числителе и знаменателе, чтобы показатели были положительными:
Умножение Экспоненты:
Упрощение:
.
выражение:
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала упростите второй термин, а затем объедините два:
Отчет о ошибке
Решение для:
Возможные ответы:
Нель предоставленная информация.
Правильный ответ:
Объяснение:
Перепишите каждую часть уравнения, чтобы использовать только основание 2:
Это уравнение может быть истинным только в том случае, если показатели равны.
Итак:
С каждой стороны отменяем, и перемещая в левую сторону, получаем:
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала составим уравнение: . Упрощение этого результата дает .
Сообщить об ошибке
Какое наибольшее положительное целое число , такое что является множителем ?
Возможные ответы:
10
20
5
16
8
Правильный ответ:
16
Объяснение:
. Таким образом, равно 16.
Сообщить об ошибке
Упорядочить следующее от меньшего к большему:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, необходимо упростить каждый из вариантов ответа.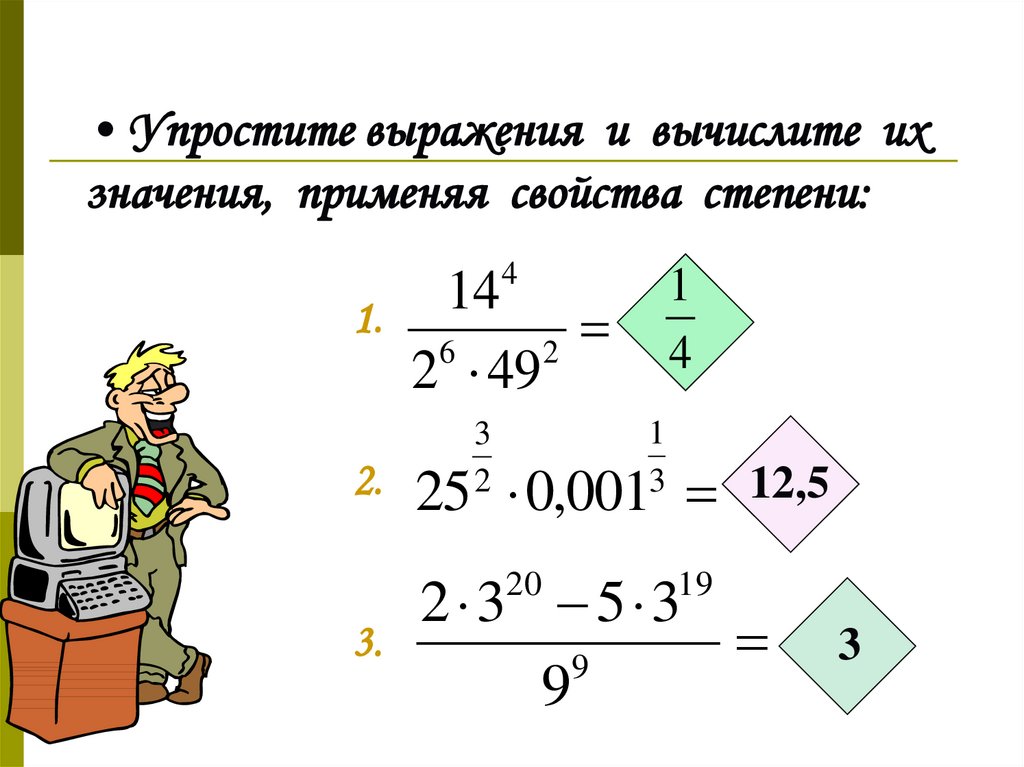
Вместо того, чтобы полностью упрощать, приведите все члены к такой форме, чтобы их показатель степени был равен 100. Тогда их можно будет легко сравнить.
, , , и .
Таким образом, упорядочение от меньшего к большему: .
Отчет о ошибке
Упростите выражение:
Возможные ответы:
нельзя упростить
Правильный ответ:
. Объяснение:
Начните с распределения показателя степени через круглые скобки. Правило степени диктует, что показатель степени, возведенный в другую степень, означает, что два показателя степени умножаются:
Любые отрицательные степени можно преобразовать в положительные степени в знаменателе дроби:
Подобные члены можно упростить, вычитая степень знаменателя из степени числителя:
5 Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Учитесь по концепции
Объяснение урока: Упрощение экспоненциальных выражений с помощью целочисленных показателей
В этом объяснении мы узнаем, как выполнять операции и упрощения над выражениями, которые включают целые показатели степени.
Чтобы помочь нам понять, как упростить выражения, включающие целые показатели степени, мы вспомним, как вычислять степень. Давайте сначала вспомните, как оценить степень с положительным целым показателем степени.
Определение: вычисление степени
Для степени с основанием 𝑎, где 𝑎∈ℝ−0 и показателем 𝑛 где 𝑛∈ℤ, то 𝑎=𝑎×𝑎×𝑎×⋯×𝑎.кратно
Далее мы вспомним, как оценивать степень с нулевым или отрицательным основанием.
Законы: правила для нулевых и отрицательных показателей
- Закон для нулевых показателей: 𝑎=1, где 𝑎∈ℝ−0
- Закон для отрицательных показателей: 𝑎=1𝑎𝑎=1𝑎,или где 𝑎∈ℝ−0 и 𝑛∈ℤ
Используя это определение вместе с порядком операций, мы можем упростить числовые и алгебраические выражения с целыми числами экспоненты. Мы сделаем это в нашем первом примере.
Пример 1. Вычисление выражения, включающего целочисленные показатели степени
Вычислить 10×25×420×5.
Ответ
Чтобы вычислить 10×25×420×5, мы можем записать степени в развернутом виде а затем сократите общие множители в числителе и знаменателе.
Напомним, что расширенная форма — это когда мы записываем степень с основанием 𝑎, где 𝑎∈ℝ−0, и показателем степени 𝑛, где 𝑛∈ℤ, как 𝑎=𝑎×𝑎×𝑎×⋯×𝑎.
В нашем примере это даст нам 10×25×420×5=10×10×10×10×10×25×25×420×20×5×5×5×5×5.
Мы можем сократить общие множители, записав сначала числитель и знаменатель как произведения простых множителей, а затем сократив. Это дает нам 10×25×420×5=10×10×10×10×10×25×25×420×20×5×5×5×5×5=2×5×2×5×2 ×5×2×5×2×5×5×5×5×5×2×22×2×5×2×2×5×5 ×5×5×5×5=2×5×5×2×21=200.
Следовательно, 10×25×420×5=200.
Иногда при упрощении выражений с целыми показателями нам нужно использовать для этого законы показателей. Давайте Вспомните законы показателей.
Правило: Законы экспонент
Ниже приведены правила экспонент с вещественными основаниями и целочисленными экспонентами:
- Правило произведения: 𝑎×𝑎=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ
- Факторное правило: 𝑎÷𝑎=𝑎, где 𝑎∈ℝ−0, 𝑚∈ℤ и 𝑛∈ℤ
- Сила правила произведения: (𝑎𝑏)=𝑎𝑏, где 𝑎, 𝑏∈ℝ−0 и 𝑛∈ℤ
- Мощность частного правила: 𝑎𝑏=𝑎𝑏, где 𝑎, 𝑏∈ℝ−0 и 𝑛∈ℤ
- Силовое правило: (𝑎)=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ
В нашем следующем примере мы будем использовать правила показателей степени, чтобы упростить выражение с квадратными корнями.
Напомним, что для
𝑎≥0, √𝑎=𝑎. Мы также будем использовать это в следующем примере.
Пример 2. Упрощение числовых выражений, содержащих квадратные корни, с использованием законов экспонент
Ответ
Чтобы упростить выражение √3×−√3√3, мы можем использовать законы показателей. Начнем с упрощения числителя √3×−√3.
Поскольку основания разные, полезно записать −√3 как −1×√3 и использовать силу правила произведения, которое гласит (𝑎𝑏)=𝑎𝑏, где 𝑎, 𝑏∈ℝ−0 и 𝑛∈ℤ. Для −1×√3 это дает нам −1×√3=(−1)√3.
Подставляя обратно в числитель, получаем √3(−1)√3 .
Для степеней с основанием √3 мы можем использовать правило произведения, которое гласит 𝑎×𝑎=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ. Затем это дает нам
Поскольку 15 — нечетный показатель, то (−1)=−1, что дает нам (−1)√3=−1×√3=−√3.
Подставляя обратно в выражение, получаем
√3×−√3√3=−√3√3.
Далее, мы можем использовать правило отношения для показателей, которое утверждает 𝑎÷𝑎=𝑎, где 𝑎∈ℝ−0, 𝑚∈ℤ и 𝑛∈ℤ.
Применяя это, мы получаем −√3√3=−√3÷√3=−√3=−√3.
Чтобы упростить − √3, мы можем записать это как произведение квадратов, а затем использовать правило 𝑎>0,√𝑎=𝑎.
Это дает нам −√3=−√3×√3×√3×√3×√3×√3=−3×3×3×3×3×3= −729.
Следовательно, √3×−√3√3 упрощенно -729.
Обратите внимание, что мы также можем вычислить -√3, используя степенное правило, следующим образом: −√3=−√3=−√3=−(3)=−729.×
В следующем примере мы рассмотрим, как упростить алгебраическую выражения, использующие законы показателей.
Пример 3. Использование законов экспонент для вычисления алгебраических выражений
Упростить 4×4(4)×16.
Ответ
Чтобы упростить выражение 4×4(4)×16, нужно использовать
законы показателей.
Во-первых, мы начнем с упрощения числителя, 4×4. Для этого воспользуемся правилом произведения для показатели, в котором говорится, что 𝑎×𝑎=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ. Этот дает нам 4×4=4=4.
Далее упростим знаменатель, (4)×16. Для того, чтобы применить правила для степени, нам нужно, чтобы основания были одинаковыми. Таким образом, мы хотим написать 16 с основанием 4. Так как 16 4, то мы можем написать 16=4.
Чтобы еще больше упростить это, мы можем использовать степенной закон для показателей степени, который гласит, что (𝑎)=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ. Этот затем дает нам 4=4=4.×
Подставляя 4 обратно в знаменатель, теперь имеем (4)×16=(4)×4.
Поскольку основания теперь одинаковы, мы можем снова использовать правило произведения для показателей степени, чтобы упростить знаменатель.
Это дает нам
(4)×4=4=4.
Подставляя 4 в числитель и 4 в знаменатель нашего исходного выражение дает нам 4×4(4)×16=44.
Поскольку у нас есть деление, мы можем использовать правило отношения для показателей степени, чтобы еще больше упростить выражение. Это правило гласит, что 𝑎÷𝑎=𝑎, где 𝑎∈ℝ−0, 𝑚∈ℤ и 𝑛∈ℤ. Затем это дает нам 44=4=4=4.()
Вычисляя 4, получаем 4×4×4×4=256. Поэтому, 4𝑥×4(4)×16=256.
Далее мы рассмотрим пример, в котором законы показателей используются вместе с обычными алгебраическими методами для упрощения.
Пример 4. Упрощение рациональных алгебраических выражений с использованием законов показателей
Упростить 6×6×6×6×6×66+6+6+6+6+6.
Ответ
Чтобы упростить 6×6×6×6×6×66+6+6+6+6+6, нам нужно рассмотреть, какие законы экспоненты могут использоваться и когда.
Так как числитель выражения содержит произведения степеней одного и того же основания, то мы можем использовать правило произведения. Этот правило гласит 𝑎×𝑎=𝑎, где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ.
Следовательно, для числителя получаем 6×6×6×6×6×6=6=6.0005
Так как знаменатель выражений содержит сложение степеней с основанием, то нам нужно быть осторожными, чтобы не неправильно применить правило произведения. Вместо этого мы можем собрать подобные термины, сложив число 6, что дает нам 6 лотов по 6 следующим образом: 6+6+6+6+6+6=6(6).
Поскольку мы умножаем 6 на 6, то мы можем снова применить правило произведения, чтобы получить 6(6)=6.
Подставляя числитель и знаменатель обратно в выражение, получаем 6×6×6×6×6×66+6+6+6+6+6=66.0005
Так как и числитель, и знаменатель имеют одинаковое основание, то мы можем применить правило частного для показателей степени.
Это правило гласит
𝑎÷𝑎=𝑎,
где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ.
Следовательно, применяя это, мы получаем 66=6÷6=6=6=6.()
Следовательно, 6×6×6×6×6×66+6+6+6+6+6=6.
В следующем примере мы будем использовать законы показателей для упрощения алгебраических выражений с двумя разными основаниями.
Пример 5. Упрощение алгебраических дробей с использованием свойств показателей степени
Упростить 𝑥𝑦𝑥𝑦()()().
Ответ
Чтобы упростить выражение 𝑥𝑦𝑥𝑦()()(), мы можем использовать законы показателей. Поскольку законы применяются только к экспонентам с одинаковыми основаниями, полезно переписать выражение в виде произведения двух дробей, имеющих числители и знаменатели с одинаковым основанием.
Это дает нам 𝑥𝑦𝑥𝑦=𝑥𝑥×𝑦𝑦.()()()()()()
Взяв первую дробь, 𝑥𝑥()(), мы можем упростить ее, используя
частное правило для показателей, которое утверждает
𝑎÷𝑎=𝑎,
где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ.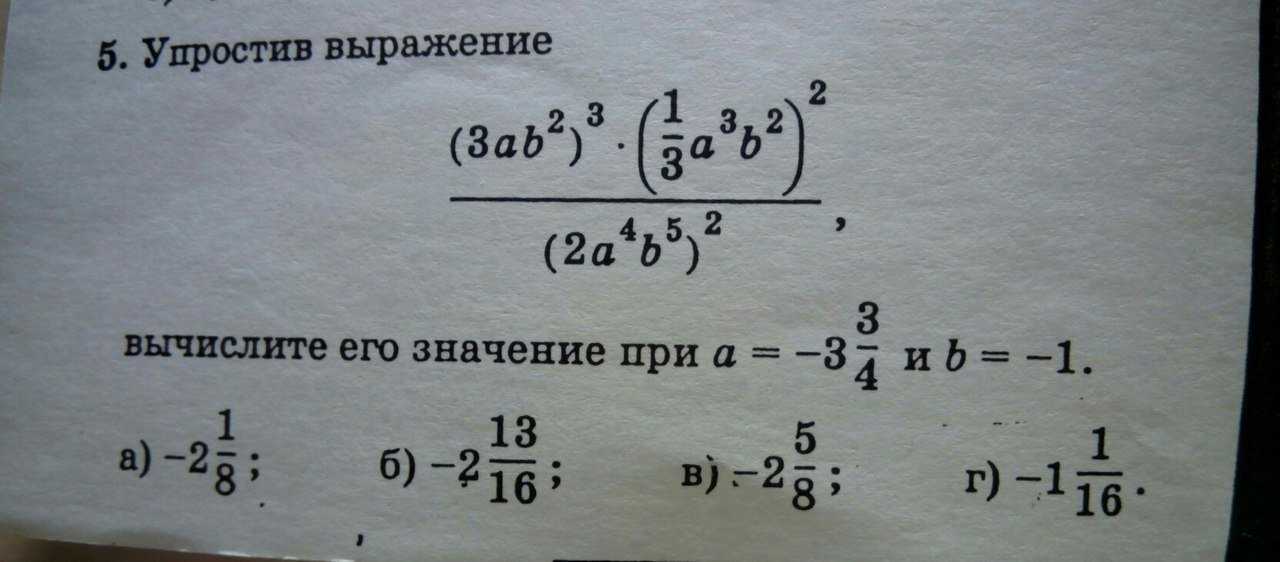
Это дает нам 𝑥𝑥=𝑥=𝑥=𝑥.()()()()
Далее мы воспользуемся тем же законом для упрощения второй знаменатель, 𝑦𝑦(), давая нам 𝑦𝑦=𝑦=𝑦.()()
Подстановка 𝑥 и 𝑦 обратно в 𝑥𝑥×𝑦𝑦()() мы получаем 𝑥𝑥×𝑦𝑦=𝑥×𝑦=𝑥𝑦.()()()
В последнем примере мы обсудим, как упростить алгебраическое выражение, используя законы показателей и удаляя общие факторы, являющиеся силами.
Пример 6. Использование законов экспонент для нахождения неизвестного в заданном уравнении
Найдите значение 𝑎, для которого 2−2=𝑎×2.
Ответ
Чтобы найти значение 𝑎 в уравнении 2−2=𝑎×2, нам понадобится левая часть уравнения должна быть в виде правой части. Другими словами, мы хотим, чтобы он был в форме 𝑏×2=𝑎×2, что означает 𝑏=𝑎. Для этого мы должны сначала манипулировать степени в левой части так, чтобы они записывались как 2.
Для 2 мы можем использовать правило произведения для показателей степени, которое гласит
𝑎×𝑎=𝑎,
где 𝑎∈ℝ−0 и 𝑚, 𝑛∈ℤ.