Как написать уравнение касательной и нормали к кривой?
Как написать уравнение касательной и нормали к кривой?
Уравнение касательной имеет вид y−y0=y′tx′t(x−x0)илиx−x0x′t=y−y0y′t. Соответственно, уравнение нормали записывается как y−y0=−x′ty′t(x−x0)илиx−x0y′t=−y−y0x′t.
Как составить уравнение касательной к графику функции?
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Что называется касательной к графику функции?
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Что такое касательная к окружности?
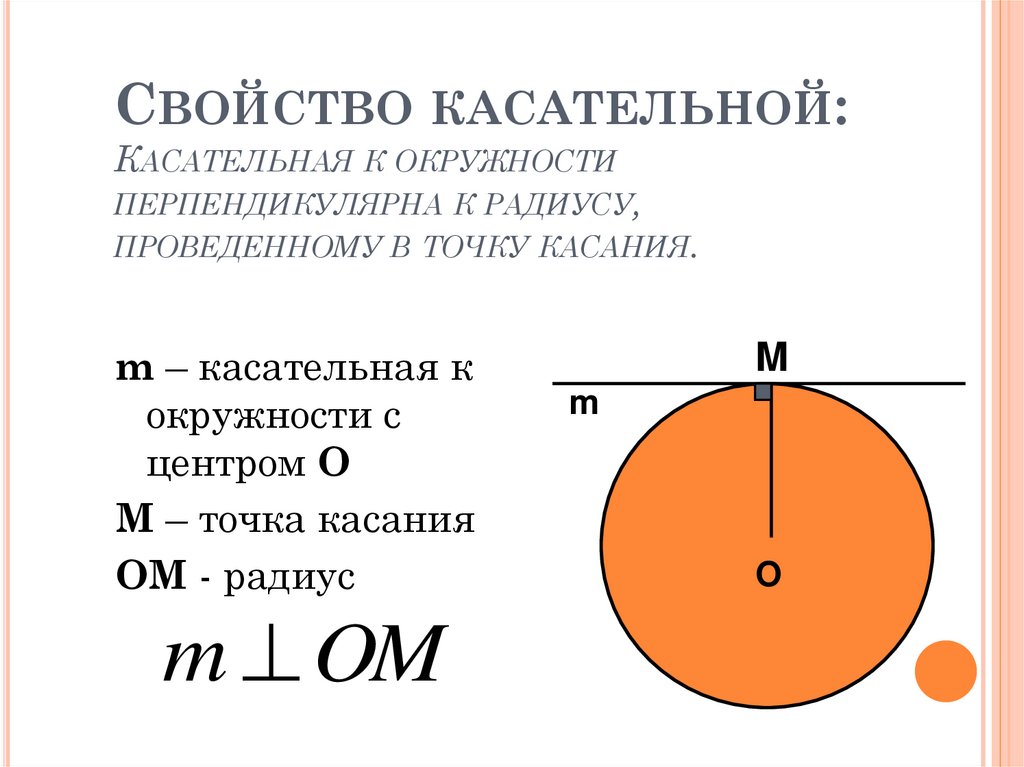
Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку.
В каком случае прямая и окружность пересекаются?
Говорят, что прямая и окружность пересекаются, если они имеют ровно две общие точки. В этом случае прямая называется секущей к окружности. Окружность и прямая касаются, если они имеют ровно одну общую точку. В этом случае прямая называется касательной к окружности, а общая точка прямой и окружности – их точкой касания.
Как могут располагаться прямая и окружность?
На плоскости прямая и окружность могут 1. пересекаться ; 2. касаться ; 3. не иметь общих точек вообще.
Как могут располагаться две прямые?
Две прямые на плоскости могут располагаться либо паралельно друг другу, либо пересекаться, ну или — совпадать.
Каким образом могут располагаться Прямая и плоскость в пространстве?
5. Как могут располагаться в пространстве прямая и плоскость? Прямая может лежать в плоскости, может пересекаться с плоскостью в некоторой точке, может быть параллельна плоскости.
Какое взаимное расположение прямой и окружности?
если расстояние от центра окружности до прямой меньше радиуса окружности (d прямая и окружность имеют две общие точки. Так как OH = r, то точка H лежит на окружности и, следовательно, является общей точкой прямой a и окружности (рис. …
Как Взаимное расположение прямой и окружности зависит от радиуса окружности и расстояния от центра окружности до прямой?
Вывод: Если расстояние от центра окружности до прямой равно радиусу, прямая касается окружности и имеет одну общую т очку с окружностью. Если расстояние от центра окружности до прямой больше радиуса, окружность и прямая не имеют общих точек.
Каким может быть взаимное расположение прямых в пространстве?
Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут быть пересекающимися, параллельными и скрещивающимися. Две различные прямые называются пересекающимися, если они имеют общую точку. Точка пересечения единственна: если две прямые имеют две общие точки, то они совпадают.
Две различные прямые называются пересекающимися, если они имеют общую точку. Точка пересечения единственна: если две прямые имеют две общие точки, то они совпадают.
Что такое взаимное расположение двух окружностей?
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: … II. Не пересекающиеся окружности не имеет общих точек.
Как называется общая точка двух окружностей?
Две окружности, имеющие две общие точки, называются пересекающимися. Их круги (ими ограниченные) пересекаются по области, называемой двойным круговым сегментом. Углом между двумя пересекающимися (или касающимися) окружностями называется угол между их касательными, проведенными в общей точке пересечения (или касания).
Каким может быть взаимное положение прямой и окружности двух окружностей?
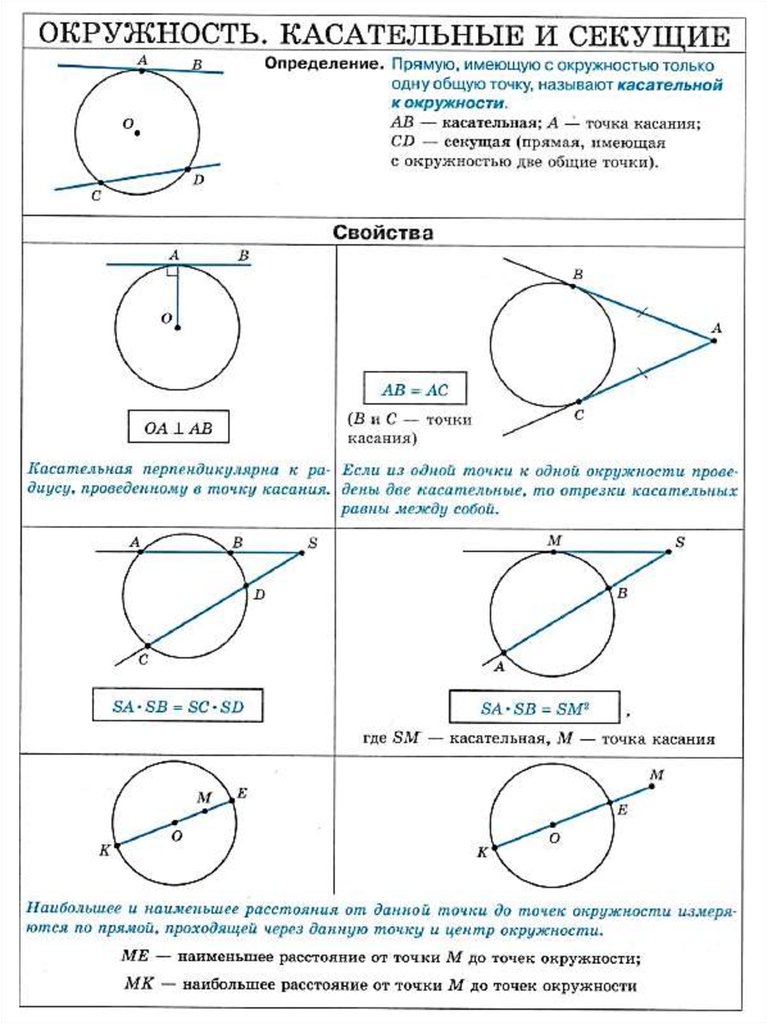
1. прямая может касаться окр-ти, может пересекать окр-ть, может не касаться окр-ти. 2. касательная перпендикулярна к радиусу; отрезки касательных,проведенных из одной точки,не лежащей в и на окр-ти, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
2. касательная перпендикулярна к радиусу; отрезки касательных,проведенных из одной точки,не лежащей в и на окр-ти, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Когда окружности пересекаются?
Если две окружности имеют только одну общую точку, то говорят, что они касаются . Если две окружности имеют только одну общую точку, то говорят, что они касаются. Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Как понять что окружности пересекаются?
Окружности пересекаются, если расстояние между центрами меньше либо равно сумме радиусов иначе окружности не пересекаются.
Когда окружности касаются?
Говорят, что две окружности касаются, если они имеют одну общую точку. Окружности касаются внутренним образом, если одна из них расположена внутри другой. Окружности касаются внешним образом, если они расположены вне друг друга.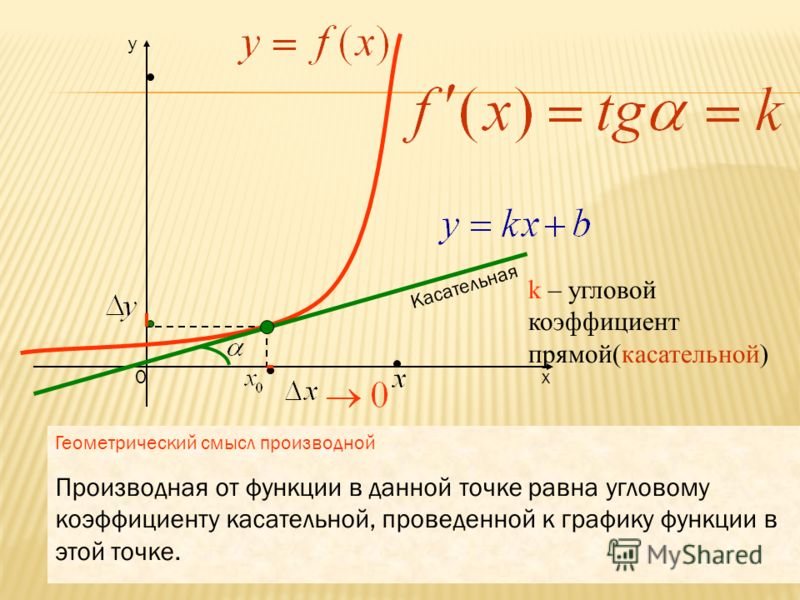
Что такое концентрические окружности?
Концентрические окружности – это окружности, которые имеют общий центр.
Касательная прямая к окружности
Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. Касательные прямые к окружностям служат предметом рассмотрения ряда теорем и играют важную роль во многих геометрических построениях и доказательствах.
Касательные прямые к одной окружности
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических преобразованиях, таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C.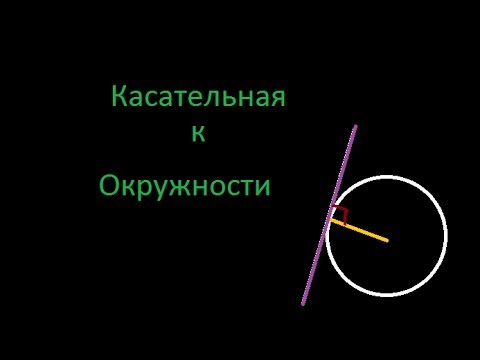 Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
A B ¯ + C D ¯ = B C ¯ + D A ¯ . {displaystyle {overline {AB}}+{overline {CD}}={overline {BC}}+{overline {DA}}.}
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a. Но каждая сторона четырёхугольника состоит из двух таких отрезков
Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a. Но каждая сторона четырёхугольника состоит из двух таких отрезков
A B ¯ + C D ¯ = ( a + b ) + ( c + d ) = B C ¯ + D A ¯ = ( b + c ) + ( d + a ) {displaystyle {overline {AB}}+{overline {CD}}=(a+b)+(c+d)={overline {BC}}+{overline {DA}}=(b+c)+(d+a)} ,
что и доказывает утверждение.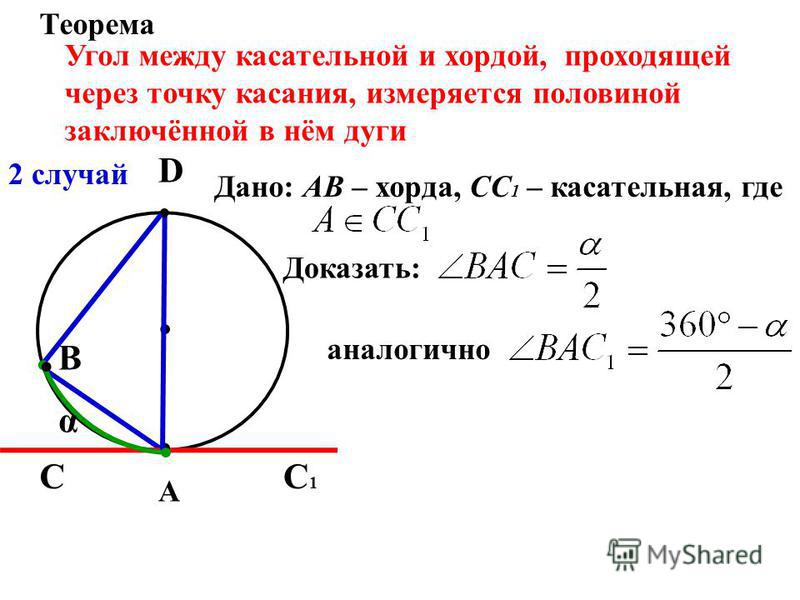
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.
Эта теорема и обратная к ней имеют различные применения. Например, из теоремы немедленно следует, что ни в какой прямоугольник не может быть вписана окружность, если только это не квадрат, а также что можно вписать окружность в любой ромб, хотя в общем случае вписать в параллелограмм окружность нельзя.
Касательные прямые к двум окружностям
Для двух окружностей в общем случае имеется четыре различные прямые, касательные к обоим окружностям, если одна окружность не лежит в другой, но в вырожденных случаях может быть любое число касательных от нуля до четырёх. Эти случаи описаны ниже. Из четырёх касательных прямых две являются внешними касательными, когда окружности оказываются лежащими по одну сторону от касательной прямой. Для двух других прямых, внутренних касательных, окружности оказываются лежащими по разные стороны от касательной прямой. Внешние касательные пересекаются в центре внешней гомотетии, в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.
Внешние касательные пересекаются в центре внешней гомотетии, в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.
Внешняя касательная
Красные прямые, соединяющие точки T1 и T3, T2 и T4, являются внешними касательными двух окружностей.
Внутренняя касательная
Внутренние касательные — это касательные, которые пересекают отрезок, соединяющий центры окружностей. Заметим, что внутренние касательные не существуют в случае пересекающихся окружностей.
Построение
Касательные к двум окружностям могут быть построены с помощью нахождения центров гомотетии, как описано выше, а затем построения касательных, проходящих через эти центры. Можно также построить касательные прямые и касательные точки прямо, как описано ниже.
Можно также построить касательные прямые и касательные точки прямо, как описано ниже.
Элементарная геометрия
Пусть O1 и O2 — два центра двух окружностей C1 и C2 и пусть r1 и r2 — их радиусы, при этом r1 > r2. Другими словами, окружность C1 будем считать большей из двух окружностей. Два различных способа можно использовать для построения внешних и внутренних касательных прямых.
Внешние касательные
Рисуем новую окружность C3 с радиусом r1 − r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиусов обеих окружностей C1 и C2 на одно и то же число r2, в результате чего окружность C2 превращается в точку. Через две точки касания на окружности C3 можно провести два луча из центра O1. Эти лучи пересекают C1 в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.
Эти лучи пересекают C1 в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.
Внутренние касательные
Рисуем новую окружность C3 с радиусом r1 + r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиуса окружности C2 до нуля с одновременным увеличением радиуса C1 на ту же константу r2. Два радиальных луча можно провести из центра O1 через точки касания на C3. Эти лучи пересекают C1 в искомых точках касания. Искомые внутренние касательные перпендикулярны радиальным лучам и пересекают лучи в найденных точках, так что их можно построить вышеуказанным методом.
Фактически это то же самое построение, что и для внешних касательных, если принять, что радиус меньшей окружности отрицателен.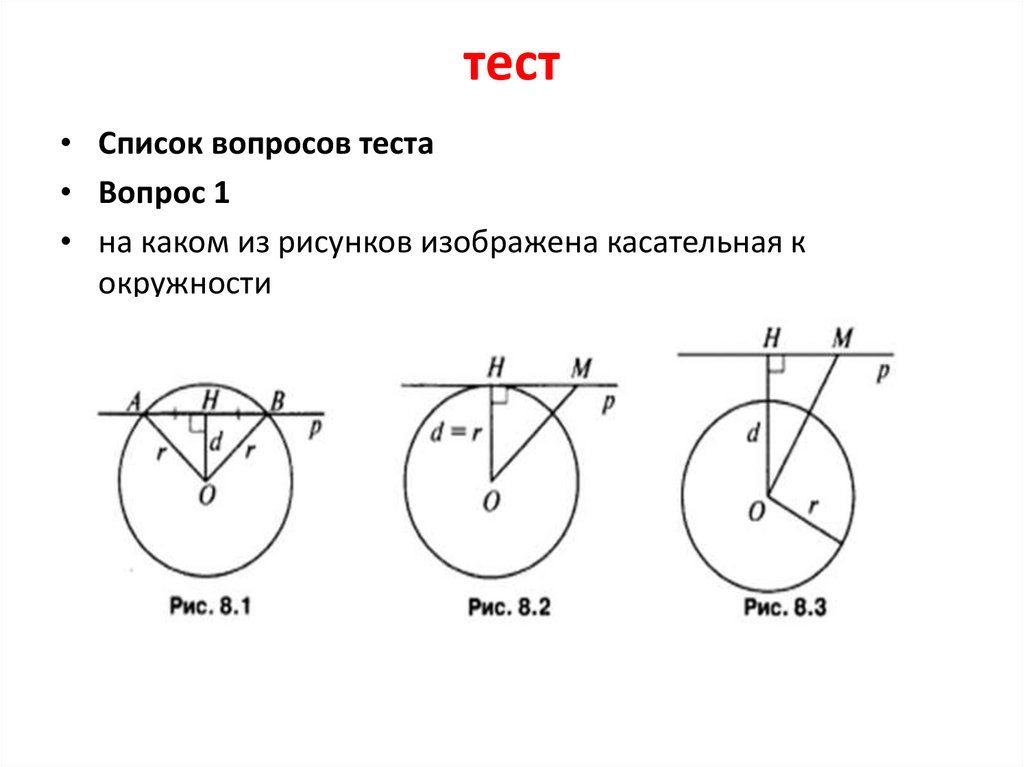
Аналитическая геометрия
Пусть окружности имеют центры c1 = (x1,y1) и c2 = (x2,y2) и радиусы r1 и r2 соответственно. Пусть касательная прямая имеет уравнение a x + b y + c = 0 , {displaystyle ax+by+c=0,} с нормализацией a2 + b2 = 1, тогда расстояние от центров окружностей до прямой вычисляется по формулам:
ax1 + by1 + c = r1 и ax2 + by2 + c = r2.
Вычтем первое уравнение из второго, получим
aΔx + bΔy = Δr
где Δx = x2 − x1, Δy = y2 − y1 и Δr = r2 − r1.
Если d = ( Δ x ) 2 + ( Δ y ) 2 {displaystyle d={sqrt {(Delta x)^{2}+(Delta y)^{2}}}} — расстояние от c1 до c2, мы можем нормализовать, сделав замену X = Δx/d, Y = Δy/d и R = Δr/d для упрощения уравнений, что даёт уравнения aX + bY = R и a2 + b2 = 1. Решаем их и получаем два решения (k = ±1) для двух внешних касательных линий:
Решаем их и получаем два решения (k = ±1) для двух внешних касательных линий:
a = RX − kY√(1 − R2) b = RY + kX√(1 − R2) c = r1 − (ax1 + by1)
Геометрически это соответствует вычислению угла, образованного касательной и прямой, проведённой через центры, а затем линия центов поворачивается для получения уравнения касательной. Угол можно вычислить с помощью тригонометрии из прямоугольного треугольника, вершинами которого являются (внешний) центр гомотетии, центр окружности и точка касания. Гипотенуза лежит на прямой центров, радиус является катетом, противоположным углу, а прилегающий к углу катет лежит на касательной прямой.
(X, Y) — это единичный вектор, направленный от c1 в c2, в то время как R равен cos θ {displaystyle cos heta } , где θ {displaystyle heta } — угол между линией центров и касательной. {2}}}} (в зависимости от знака θ {displaystyle heta } , что эквивалентно направлению вращения), и приведённые выше уравнения являются вращением (X, Y) на ± θ , {displaystyle pm heta ,} с помощью матрицы вращения
{2}}}} (в зависимости от знака θ {displaystyle heta } , что эквивалентно направлению вращения), и приведённые выше уравнения являются вращением (X, Y) на ± θ , {displaystyle pm heta ,} с помощью матрицы вращения
( R ∓ 1 − R 2 ± 1 − R 2 R ) {displaystyle {egin{pmatrix}R&mp {sqrt {1-R^{2}}}pm {sqrt {1-R^{2}}}&Rend{pmatrix}}} k = 1 — это касательная прямая справа от окружностей, если смотреть из c1 в направлении c2. k = −1 — это касательная прямая справа от окружностей, если смотреть из c2 в направлении c1.
k = −1 — это касательная прямая справа от окружностей, если смотреть из c2 в направлении c1.
Все рассуждения выше предполагают, что радиусы окружностей положительны. Если r1 положителен, а r2 отрицателен, то c1 будет лежать слева от каждой прямой, а c2 — справа, и две касательные прямые пересекутся. Таким путём можно получить все четыре решения. Смена знака обоих радиусов приводит к обмену вариантов k = 1 и k = −1.
Векторы
В общем случае точки касания t1 и t2 для любой из четырёх касательных прямых к окружностям с центрами в v1 и v2 и с радиусами r1 и r2 получаются путём решения четырёх уравнений:
( t 2 − v 2 ) ⋅ ( t 2 − t 1 ) = 0 ( t 1 − v 1 ) ⋅ ( t 2 − t 1 ) = 0 ( t 1 − v 1 ) ⋅ ( t 1 − v 1 ) = r 1 2 ( t 2 − v 2 ) ⋅ ( t 2 − v 2 ) = r 2 2 {displaystyle {egin{aligned}(t_{2}-v_{2})cdot (t_{2}-t_{1})&=0(t_{1}-v_{1})cdot (t_{2}-t_{1})&=0(t_{1}-v_{1})cdot (t_{1}-v_{1})&=r_{1}^{2}(t_{2}-v_{2})cdot (t_{2}-v_{2})&=r_{2}^{2}end{aligned}}}
Эти уравнения выражают тот факт, что касательная прямая перпендикулярна радиусам, а точки касания лежат на соответствующих окружностях.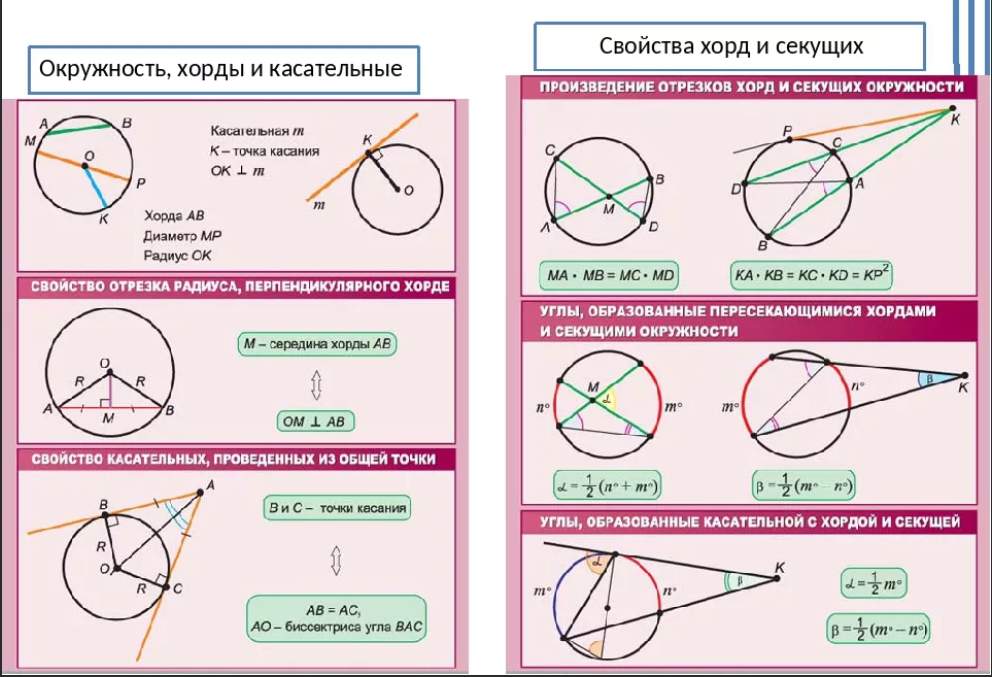
Эти четыре квадратных уравнения с двумерными векторными переменными в общем случае дают четыре пары решений.
Вырожденные случаи
Две различные окружности могут иметь, в зависимости от взаимного расположения, от нуля до четырёх прямых, касающихся обеих окружностей. Варианты можно классифицировать по расстоянию между центрами и радиусам.
- Если окружности не соприкасаются ( d > r 1 + r 2 {displaystyle d>r_{1}+r_{2}} ), что является общим положением, имеются четыре касательные, касающиеся одновременно обеих окружностей.
- Если окружности соприкасаются ( d = r 1 + r 2 {displaystyle d=r_{1}+r_{2}} ) — имеют одну точку внешнего касания — они имеют две внешних общих касательных и одну внутреннюю, проходящую через точку касания окружностей.
 Эта общая касательная прямая имеет кратность два.
Эта общая касательная прямая имеет кратность два. - Если окружности пересекаются в двух точках ( | r 1 − r 2 | < d < r 1 + r 2 {displaystyle |r_{1}-r_{2}|<d<r_{1}+r_{2}} ), у них нет внутренних общих касательных и есть две внешние касательные прямые.
- Если окружности касаются друг друга изнутри ( d = | r 1 − r 2 | {displaystyle d=|r_{1}-r_{2}|} ) — имеется одна точка внутреннего касания — у них нет внутренних общих касательных и имеется одна общая внешняя касательная, проходящая через точку касания окружностей, и эта прямая имеет кратность два.

- Если одна окружность полностью внутри другой ( d < | r 1 − r 2 | {displaystyle d<|r_{1}-r_{2}|} ), у них нет общих касательных, поскольку любая касательная к внутренней окружности будет секущей к внешней.
И наконец, если окружности совпадают, любая касательная прямая к одной окружности будет общей касательной.
Далее понятие общей касательной прямой можно расширить на случай окружностей отрицательного радиуса (которые образованы теми же самыми точками x 2 + y 2 = ( − r ) 2 , {displaystyle x^{2}+y^{2}=(-r)^{2},} но «наизнанку»). В этом случае, если радиусы имеют противоположные знаки (одна окружность имеет положительный радиус, другая — отрицательный) внешний и внутренний центры гомотетии меняются местами и внешние и внутренние общие касательные меняются местами. Если же радиусы имеют один и тот же знак (оба радиуса положительны или оба отрицательны), то понятия «внешний» и «внутренний» имеют обычный смысл.
В этом случае, если радиусы имеют противоположные знаки (одна окружность имеет положительный радиус, другая — отрицательный) внешний и внутренний центры гомотетии меняются местами и внешние и внутренние общие касательные меняются местами. Если же радиусы имеют один и тот же знак (оба радиуса положительны или оба отрицательны), то понятия «внешний» и «внутренний» имеют обычный смысл.
Общие касательные можно определить для окружностей с нулевым радиусом. В этом случае окружность с нулевым радиусом трактуется как двойная точка, а потому любая прямая, проходящая через эту точку, пересекает её с кратностью два. Если окружность имеет радиус ноль, общая касательная прямая — это просто касательная прямая к окружности, проходящая через точку, но считается эта прямая дважды. Если обе окружности имеют нулевой радиус, то общая касательная прямая — это прямая, проходящая через две точки, и эта прямая имеет кратность четыре.
Заметим, что в этих вырожденных случаях внешний и внутренний центры гомотетии остаются (внешний центр уходит в бесконечность, если радиусы равны), за исключением случая, когда окружности совпадают (в этом случае внешний центр не определён), или когда обе окружности имеют нулевой радиус (в этом случае отсутствует внутренний центр).
Приложения
Задача о ремённой передаче
Внутренние и внешние касательные полезны при решении задачи о ремённой передаче, которая заключается в вычислении длины ремня, который плотно бы прилегал к колёсам передачи. Если считать ремень математической кривой с пренебрежительно малой толщиной и если колёса передачи находятся точно в одной плоскости, задача сводится к суммированию отрезков касательных с соответствующими длинами дуг. Если ремень натянут на колёса с пересечением, необходимо рассматривать внутренние касательные. Если же ремень натянут без пересечения, необходимо рассматривать внешние касательные. Последний случай иногда называется задачей шкивов.
Касательные прямые к трём окружностям: теорема Монжа
Для трёх окружностей C1, C2 и C3 существует три пары окружностей (C1C2, C2C3 и C1C3). Поскольку каждая пара окружностей имеет два центра гомотетии, всего получим шесть центров гомотетии.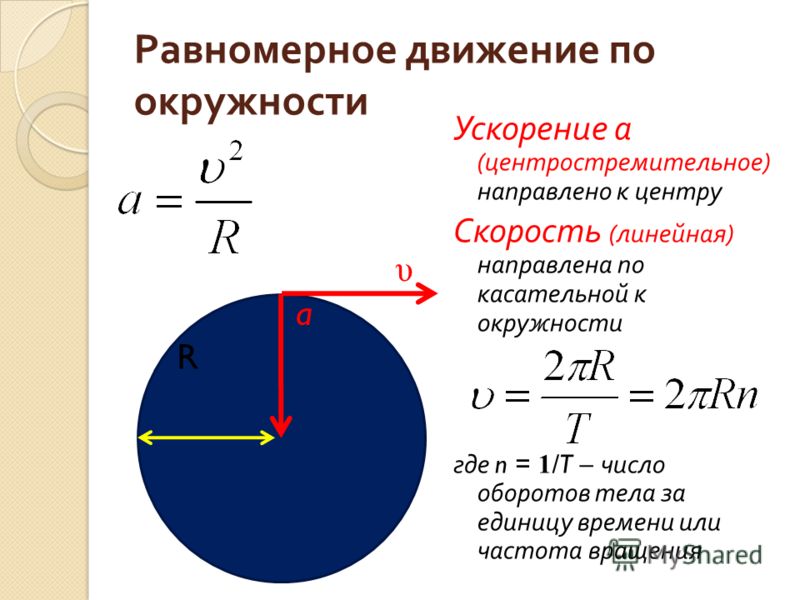 Гаспар Монж показал в начале 19-го века, что эти шесть точек лежат на четырёх прямых, и на каждой прямой лежат три точки.
Гаспар Монж показал в начале 19-го века, что эти шесть точек лежат на четырёх прямых, и на каждой прямой лежат три точки.
Касательные прямые и бильярд
Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).
Задача Аполлония
Много частных случаев задачи Аполлония используют нахождение окружностей, касающихся одной или нескольких прямых. В простейшем из этих случаев строится окружность, касающаяся трёх заданных прямых (задача LLL). Центр любой такой окружности должен лежать на биссектрисе угла в точке пересечения любой пары этих прямых. В каждой точке пересечения прямых есть две биссектрисы. Пересечения этих биссектрис дают центры окружностей, являющихся решением. В общем случае существует четыре таких окружностей для треугольника, образованного пересечением трёх прямых — вписанная окружность и три вневписанных.
В каждой точке пересечения прямых есть две биссектрисы. Пересечения этих биссектрис дают центры окружностей, являющихся решением. В общем случае существует четыре таких окружностей для треугольника, образованного пересечением трёх прямых — вписанная окружность и три вневписанных.
Анимация, показывающая инверсное преобразование задачи Аполлония. Синяя и красная окружности увеличиваются, пока не коснутся, и при инверсии относительно серой окружности переходят в две параллельные прямые. Жёлтые решения получаются путём перемещения вдоль этих прямых до касания зелёной окружности.
В общем случае задачу Аполлония можно свести к более простой задаче построения окружности, касающейся одной окружности и двух параллельных прямых (это сам по себе частный случай LLC). Чтобы это сделать, увеличиваем пропорционально две из этих трёх заданных окружностей вплоть до их касания. Инверсия относительно окружности подходящего радиуса с центром в точке касания переводит эти две окружности в две параллельные прямые, а третью окружность — в другую окружность. Таким образом, решение может быть найдено путём перемещения окружности постоянного радиуса между двумя параллельными прямыми, пока не получим касание с преобразованной третьей окружностью. Обратная инверсия даст решения исходной задачи.
Таким образом, решение может быть найдено путём перемещения окружности постоянного радиуса между двумя параллельными прямыми, пока не получим касание с преобразованной третьей окружностью. Обратная инверсия даст решения исходной задачи.
Обобщения
Понятие касательной прямой к одной и более окружностям можно обобщить несколькими путями. В первую очередь, свойство парности касательных прямых и точек касания можно обобщить до полюса и полярной прямой, когда полюс может находиться в любом месте, не обязательно на окружности. Во-вторых, объединение двух окружностей является особым (приводимым) случаем плоской кривой четвёртой степени, а внешние и внутренние касательные прямые являются касательными к двум точкам этой кривой. В общем случае плоская кривая четвёртой степени имеет 28 прямых, касающихся её дважды.
Третье обобщение относится скорее к касательным окружностям, а не к касательным прямым. Касательную прямую можно рассматривать как касательную окружность с бесконечным радиусом. В частности, внешние касательные прямые к двум окружностям можно рассматривать как частные случаи из семейства окружностей, касающихся с внутренней или внешней стороны обеих окружности, в то время как внутренние касательные прямые можно рассматривать как частные случаи семейства окружностей, касающихся с внутренней стороны одной окружности и с внешней стороны другой) .
В частности, внешние касательные прямые к двум окружностям можно рассматривать как частные случаи из семейства окружностей, касающихся с внутренней или внешней стороны обеих окружности, в то время как внутренние касательные прямые можно рассматривать как частные случаи семейства окружностей, касающихся с внутренней стороны одной окружности и с внешней стороны другой) .
В геометрии Мёбиуса или инверсной геометрии прямые рассматриваются как окружности с центром «в бесконечности» и для любой прямой и для любой окружности существует преобразование Мёбиуса, которое переводит одну фигуру в другую. В геометрии Мёбиуса касание прямой и окружности становится особым случаем касания двух окружностей. Эта эквивалентность развивается далее в сферической геометрии Ли.
{2} = 20\) с центром в \(O(0;0)\). {2}\]
{2}\]Касательная — это прямая линия, которая касается окружности окружности только в одном месте.
Касательная \(AB\) касается окружности в точке \(D\).
Радиус окружности \(CD\) перпендикулярен касательной \(AB\) в точке касания \(D\).
\begin{align*} CD & \perp AB \\ \text{and } C\hat{D}A &= C\hat{D}B = \text{90} ° \end{align*}
Произведение градиента радиуса и градиента касательной равно \(-\text{1}\). 9{2}\]
Нарисуйте эскиз
Центр круга равен \((-3;1)\), а радиус равен \(\sqrt{17}\) единицам.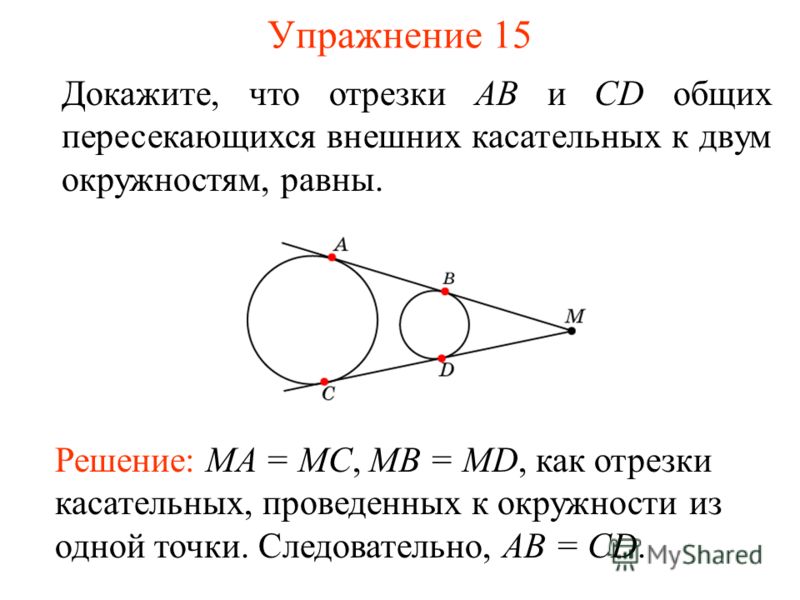
Определить градиент радиуса \(CF\)
\begin{align*} m_{CF} &= \cfrac{y_{2} – y_{1}}{x_{2}- x_{ 1}}\\ &= \cfrac{5 – 1}{-2 + 3}\\ &= 4 \end{align*}
Определить градиент касательной
Пусть градиент касательной равен \ (м\).
\begin{align*} m_{CF} \times m &= -1 \\ 4 \times m &= -1 \\ \следовательно m &= – \cfrac{1}{4} \end{align* }
Определите уравнение касательной к окружности
Запишите уравнение прямой линии в форме точки градиента и подставьте \(m = – \cfrac{1}{4}\) и \(F(-2; 5)\).
\begin{align*} y – y_{1} &= m (x – x_{1}) \\ y – y_{1} &= – \cfrac{1}{4} (x – x_{1 }) \\ \text{Подстановка } F(-2;5): \quad y – 5 &= – \cfrac{1}{4} (x – (-2)) \\ y – 5 &= – \ cfrac{1}{4} (x + 2) \\ y &= – \cfrac{1}{4}x – \cfrac{1}{2} + 5 \\ &= – \cfrac{1}{4 }x + \cfrac{9}{2} \end{align*} 9{2} = 26\) в точках \(P\) и \(Q\).
- Вычислите координаты \(P\) и \(Q\).
- Нарисуйте окружность и прямую в одной системе координат.
 Обозначьте точки \(P\) и \(Q\).
Обозначьте точки \(P\) и \(Q\). - Определить координаты \(H\), середины хорды \(PQ\).
- Если \(O\) является центром окружности, покажите, что \(PQ \perp OH\).
- Определите уравнения касательных к окружности в точках \(P\) и \(Q\).
- Определите координаты \(S\), точки пересечения двух касательных. 9{2} + 4x – 5 &= 0 \\ (x – 1)(x + 5) &= 0 \\ \следовательно, x = 1 &\text{ или } x = -5 \\ \text{Если } x = 1 \quad y &= 1 + 4 = 5 \\ \text{If } x = -5 \quad y &= -5 + 4 = -1 \end{align*}
Это дает точки \(P (-5;-1)\) и \(Q(1;5)\).
Начертить эскиз
Определить координаты средней точки \(H\)
\begin{align*} H(x;y) &= ( \cfrac{x_{1} + x_{2 }}{2}; \cfrac{y_{1} + y_{2}}{2} ) \\ &= ( \cfrac{1 – 5}{2}; \cfrac{5 – 1}{2}) \\ &= ( \cfrac{-4}{2}; \cfrac{4}{2} ) \\ &= (-2; 2 ) \end{align*}
Показать, что \(OH\) перпендикулярно \(PQ\)
Нам нужно показать, что произведение двух градиентов равно \(-\text{1}\).
 Из данного уравнения \(PQ\) мы знаем, что \(m_{PQ} = 1\).
Из данного уравнения \(PQ\) мы знаем, что \(m_{PQ} = 1\).\begin{align*} m_{OH} &= \cfrac{2 – 0}{-2 – 0} \\ &= – 1 \\ & \\ m_{PQ} \times m_{OH} &= – 1 \\ & \\ \следовательно PQ & \perp OH \end{align*}
Определить уравнения касательных в точках \(P\) и \(Q\)
Касательная в точке \(P\) :
Определить градиент радиуса \(OP\):
\begin{align*} m_{OP} &= \cfrac{-1 – 0}{- 5 – 0} \\ &= \cfrac{ 1}{5} \end{align*}
Касательная окружности перпендикулярна радиусу, поэтому мы можем написать:
\begin{align*} \cfrac{1}{5} \times m_{P } &= -1 \\ \поэтому m_{P} &= – 5 \end{align*}
Замените \(m_{P} = – 5\) и \(P(-5;-1)\) в уравнение прямой.
\begin{align*} y – y_{1} &= – 5 (x – x_{1}) \\ \text{Substitute } P(-5;-1): \quad y + 1 &= – 5 (x + 5) \\ y &= -5x – 25 – 1 \\ &= -5x – 26 \end{align*}
Касательная в \(Q\):
Определить градиент радиуса \(OQ\):
\begin{align*} m_{OQ} &= \cfrac{5 – 0}{1 – 0} \\ &= 5 \end{align*}
Касательная окружности перпендикулярна радиусу, поэтому мы можем написать:
\begin{align*} 5 \times m_{Q} &= -1 \\ \поэтому m_{Q} &= – \cfrac{1}{5} \end{align*}
Замените \(m_{Q} = – \cfrac{1}{5}\) и \(Q (1;5)\) в уравнение прямой.

\begin{align*} y – y_{1} &= – \cfrac{1}{5} (x – x_{1}) \\ \text{Подстановка } Q(1;5): \quad y – 5 &= – \cfrac{1}{5} (x – 1) \\ y &= – \cfrac{1}{5}x + \cfrac{1}{5} + 5 \\ &= – \cfrac {1}{5}x + \cfrac{26}{5} \end{align*}
Уравнения касательных: \(y = -5x – 26\) и \(y = – \cfrac{1 {5}x + \cfrac{26}{5}\).
Определите координаты \(S\)
Приравняйте два линейных уравнения и найдите \(x\):
\begin{align*} -5x – 26 &= – \cfrac{1}{5} x + \cfrac{26}{5} \\ -25x – 130 &= – x + 26 \\ -24x &= 156 \\ x &= – \cfrac{156}{24} \\ &= – \cfrac {13}{2} \\ \text{Если } x = – \cfrac{13}{2} \quad y &= – 5 ( – \cfrac{13}{2} ) – 26 \\ &= \cfrac {65}{2} – 26 \\ &= \cfrac{13}{2} \end{align*}
Это дает точку \(S ( – \cfrac{13}{2}; \cfrac{13}{2} )\).
Покажите, что \(S\), \(H\) и \(O\) лежат на прямой
Нам нужно показать, что существует постоянный градиент между любыми двумя из трех точек. Мы уже показали, что \(PQ\) перпендикулярна \(OH\), поэтому мы ожидаем, что градиент линии, проходящей через \(S\), \(H\) и \(O\), будет \(- \текст 1}\).

\begin{align*} m_{SH} &= \dfrac{\cfrac{13}{2} – 2}{- \cfrac{13}{2} + 2} \\ &= – 1 \end{ align*}\begin{align*} m_{SO} &= \dfrac{\cfrac{13}{2} – 0}{- \cfrac{13}{2} – 0} \\ &= – 1 \end {выравнивание*} 9{2} = 80\), учитывая, что оба параллельны прямой \(y = \cfrac{1}{2}x + 1\).
Нарисуйте эскиз
Касательные к окружности, параллельные линии \(y = \cfrac{1}{2}x + 1\), должны иметь градиент \(\cfrac{1}{ 2}\). Из эскиза мы видим, что есть две возможные касательные.
Определить координаты \(A\) и \(B\)
Чтобы определить координаты \(A\) и \(B\), надо найти уравнение прямой, перпендикулярной \(y = \cfrac{1}{2}x + 1\) и проходящей через центр окружности. Эта перпендикулярная линия будет пересекать окружность в точках \(A\) и \(B\). 9{2} &= 16 \\ \поэтому x &= \pm 4 \\ \text{If } x = 4 \quad y &= – 2(4) + 1 = – 7 \\ \text{If } x = -4 \quad y &= – 2(-4) + 1 = 9 \end{align*}
Это дает точки \(A(-4;9)\) и \(B(4;-7) \).
Определить уравнения касательных к окружности
Касательная в точке \(A\):
\begin{align*} y – y_{1} &= \cfrac{1}{2} (x – x_{1}) \\ y – 9 &= \cfrac{1}{2} (x + 4 ) \\ y &= \cfrac{1}{2} x + 11 \end{align*}
9{2}} = \sqrt{9} = 3 \end{align*}
Примечание: из скетча видно, что \(F\) должна иметь отрицательную \(y\)-координату, поэтому берем отрицательный квадратный корень.
 Точно так же \(H\) должна иметь положительную \(y\)-координату, поэтому мы берем положительный квадратный корень.
Точно так же \(H\) должна иметь положительную \(y\)-координату, поэтому мы берем положительный квадратный корень.Это дает точки \(F(-3;-4)\) и \(H(-4;3)\).
Касательная в \(F\):
\begin{align*} m_{FG} &= \cfrac{-1 + 4}{-7 + 3} \\ &= – \cfrac{3} {4} \end{align*}\begin{align*} y – y_{1} &= m (x – x_{1}) \\ y – y_{1} &= – \cfrac{3}{4 } (x – x_{1}) \\ y + 1 &= – \cfrac{3}{4} (x + 7) \\ y &= – \cfrac{3}{4}x – \cfrac{21 }{4} – 1 \\ y &= – \cfrac{3}{4}x – \cfrac{25}{4} \end{align*}
Касательная в \(H\):
\begin{align*} m_{HG} &= \cfrac{-1 – 3}{-7 + 4} \\ &= \cfrac{4}{ 3} \end{align*}\begin{align*} y + 1 &= \cfrac{4}{3} (x + 7 ) \\ y &= \cfrac{4}{3}x + \cfrac{ 28}{3} – 1 \\ y &= \cfrac{4}{3}x + \cfrac{25}{3} \end{align*}
Запишите окончательный ответ
Уравнения касательных к окружности равны \(y = — \cfrac{3}{4}x — \cfrac{25}{4}\) и \(y = \cfrac{4}{3}x + \cfrac{25}{3} }\).
youtube.com/embed/WmBT-hY48mc» frameborder=»0″ allowfullscreen=»allowfullscreen»> 9029{c}\)\(a_{b}\)
\(\sqrt{a}\)
\(\sqrt[b]{a}\)
\(\frac{a}{ б}\)
\(\cfrac{a}{b}\)
\(+\)
\(-\)
\(\times\)
\(\div\)
\(\pm\)
\(\cdot\)
\(\amalg\)
\(\ast\)
\(\barwedge\)
\(\bigcirc\)
\( \bigodot\)
\(\bigoplus\)
\(\bigotimes\)
\(\bigsqcup\)
\(\bigstar\)
\(\bigtriangledown\)
\(\bigtriangleup\)
\(\blacklozenge\)
\(\blacksquare\)
\(\blacktriangle\)
2 \(\
3) \(\bullet\)
\(\cap\)
\(\cup\)
\(\circ\)
\(\circledcirc\)
\(\dagger\)
\( \ddagger\)
\(\diamond\)
\(\dotplus\)
\(\lozenge\)
\(\mp\)
\(\ominus\)
\(\oplus \)
\(\oslash\)
\(\otimes\)
\(\setminus\)
\(\sqcap\)
\(\sqcup\)
\(\square\)
\(\star\)
\(\triangle\)
\(\triangledown\)
\(\triangleleft\)
\(\Cap\)
\(\Cup\)
\( \upplus\)
\(\vee\)
\(\veebar\)
\(\клин\)
\(\wr\)
\(\следовательно\)
\(\left ( a \right )\)
\(\left \| a \right \|\)
\(\влево [ a \вправо ]\)
\(\влево \{ a \вправо \}\)
\(\влево \lceil a \вправо \rceil\)
\(\влево \ lfloor a \right \rfloor\)
\(\left ( a \right )\)
\(\vert a \vert\)
\(\leftarrow\)
\(\leftharpoondown\)
\(\leftharpoonup\)
\(\leftrightarrow\)
\(\leftrightharpoons\)
\(\mapsto\)
\(\rightarrow\)
\(\rightharpoondown\)
\( \правый гарпунвверх\)
\(\rightleftharpoons\)
\(\to\)
\(\Leftarrow\)
\(\Leftrightarrow\)
\(\Rightarrow\)
\(\overset{a}{ \leftarrow}\)
\(\overset{a}{\rightarrow}\)
\(\приблизительно \)
\(\asymp\)
\(\cong \)
\(\dashv \)
\(\doteq \)
\(= \)
\(\equiv \)
\(\frown \)
\(\geq \)
\(\geqslant \)
\(\гг\)
\(\gt \)
\(| \)
\(\leq \)
\(\leqslant \)
\(\ll \)
\(\lt \)
\( \models\)
\(\neq \)
\(\ngeqslant \)
\(\ngtr \)
\(\nleqslant \)
\(\nless \)
\(\not \equiv \)
\(\overset{\underset{\mathrm{def}}{}}{=} \)
\(\parallel \)
\(\perp \)
\(\prec \)
\(\preceq \)
\(\сим\)
\(\simeq\)
\(\smile\)
\(\succ\)
\(\succeq\)
\(\vdash\)
\(\in\)
\ (\ni \)
\(\notin \)
\(\nsubseteq \)
\(\nsupseteq \)
\(\sqsubset \)
\(\sqsubseteq \)
\(\ sqsupset \)
\(\sqsupseteq \)
\(\subset \)
\(\subseteq \)
\(\subseteqq \)
\(\supset \)
\\supseteq )\(\supseteqq \)
\(\emptyset\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\)
\(\mathbb{R}\)
\(\mathbb{C}\)
\(\alpha\)
\(\beta\)
\(\gamma\)
\(\delta \)
\(\эпсилон\)
\(\дзета\)
\(\эта\)
\(\тета\)
\(\йота\)
\(\каппа\)
\(\lambda\)
\(\mu\)
\(\nu\)
\(\xi\)
\(\pi\)
\(\rho\)
\(\sigma\)
\(\tau\)
\(\upsilon\)
\(\phi\)
\(\chi\)
\(\psi\)
\(\omega\)
\(\Gamma\)
\(\Delta\)
\(\Theta\)
\( \Lambda\)
\(\Xi\)
\(\Pi\)
\(\Sigma\)
\(\Upsilon\)
\(\Phi\)
\(\Psi \)
\(\Омега\)
\((а)\)
\([а]\) 9{} a\)
Редактировать математику с помощью TeX:
Предварительный просмотр математики:
Касательная к окружности
Мы знаем, что круги и линии — это две разные формы, которые имеют очень мало общего.
 Но что происходит, когда они встречаются или пересекаются в какой-то одной точке? Это приводит к касательной. Касательная к окружности – это прямая, которая касается окружности в одной точке. Точка касания — это место, где окружность встречается с точкой. Касательная также перпендикулярна радиусу окружности, по которой она пересекается. Его можно рассматривать для любой изогнутой формы. Касательная – это линия, имеющая свое уравнение. В этой главе мы изучим касательную к окружности в различных других формах. Мы также увидим уравнение касательной к окружности и формулу касательной к окружности.
Но что происходит, когда они встречаются или пересекаются в какой-то одной точке? Это приводит к касательной. Касательная к окружности – это прямая, которая касается окружности в одной точке. Точка касания — это место, где окружность встречается с точкой. Касательная также перпендикулярна радиусу окружности, по которой она пересекается. Его можно рассматривать для любой изогнутой формы. Касательная – это линия, имеющая свое уравнение. В этой главе мы изучим касательную к окружности в различных других формах. Мы также увидим уравнение касательной к окружности и формулу касательной к окружности.Определение касательной к окружности
Линия, соединяющая две близкие точки из точки на окружности, называется касательной. Простыми словами можно сказать, что прямые, которые пересекают окружность ровно в одной единственной точке, являются касательными. Только одна касательная может быть в точке окружности. Точка, в которой касательная касается окружности, называется точкой касания.
 Точка пересечения окружности и прямой перпендикулярна радиусу. Поскольку он играет жизненно важную роль в геометрическом построении, с ним связано множество теорем, которые мы обсудим далее в этой главе.
Точка пересечения окружности и прямой перпендикулярна радиусу. Поскольку он играет жизненно важную роль в геометрическом построении, с ним связано множество теорем, которые мы обсудим далее в этой главе.(изображение скоро будет загружено)
Здесь точка O — радиус, точка P — точка касания.
Различные условия касания
Только когда линия касается кривой в одной точке, она считается касательной. Или же он считается только линией. Следовательно, мы можем определить касательную на основе точки касания и ее положения по отношению к окружности.
Когда точка лежит на окружности
Когда точка лежит внутри окружности
Когда точка лежит вне окружности
Когда точка лежит на окружности
(изображение скоро будет загружено)
Здесь из рисунка видно, что к окружности проходит только одна касательная точка, лежащая на окружности.

Когда точка лежит внутри круга
(изображение скоро будет загружено)
На рисунке выше точка P находится внутри круга. Теперь все прямые, проходящие через точку P, пересекают окружность в двух точках. следовательно, нельзя провести касательную к окружности, проходящей через точку, лежащую внутри окружности.
Когда точка лежит вне круга
(изображение скоро будет загружено)
Из приведенного выше рисунка следует, что из точки P, лежащей вне круга, есть две касательные к кругу.
Свойства касательной
Всегда помните следующие пункты о свойствах касательной
Линия касательной никогда не пересекает окружность и не входит в нее; он касается только круга.
Точка пересечения селезенки и окружности перпендикулярна радиусу
Касательный отрезок к окружности равен от той же внешней точки.

Касательная и хорда образуют угол, угол в точности подобен касательной, вписанной с противоположной стороны хорды.
Уравнение касательной к окружности
Ниже приведено уравнение касательной к окружности
Уравнение касательной к окружности sin θ= a
Касательная к уравнению окружности x2+ y2=a2 в точке (x1, y1) равна xx1+yy1= a2
Касательная к уравнению окружности x2+ y2=a2 для прямой y = mx +c равна y = mx ± a √[1+ m2] y1) is xx1+yy1= a2
Формула касательной к окружности
Чтобы понять формулу касательной, посмотрите на диаграмму, приведенную ниже.
(изображение скоро будет загружено)
Здесь у нас есть окружность с P в качестве внешней точки.
 Из внешней точки P окружность имеет касательную в точках Q и S. Прямая линия, которая разрезает кривую на две или более частей, называется секущей. Итак, здесь секущая равна PR, а в точке Q точка R пересекает окружность, как показано на диаграмме выше. Итак, теперь мы получаем формулу тангенса-секанса
Из внешней точки P окружность имеет касательную в точках Q и S. Прямая линия, которая разрезает кривую на две или более частей, называется секущей. Итак, здесь секущая равна PR, а в точке Q точка R пересекает окружность, как показано на диаграмме выше. Итак, теперь мы получаем формулу тангенса-секансаPR/PS = PS/ PQ
PS² = PQ.PR
Теоремы касательных к окружности
Теорема 1
Радиус получается при соединении центра и точки касания. Касательная в общей точке окружности лежит под прямым углом к радиусу. Диаграмма ниже пояснит то же самое, где AB \[\perp\] OP
(изображение будет загружено в ближайшее время)
Теорема 2
Из одной внешней точки к окружности проведены только две касательные, имеющие равные касательные сегменты. Касательный сегмент — это линия, соединяющая внешнюю точку и точку касания. Согласно приведенной ниже диаграмме AC = BC
(изображение скоро будет загружено)
Примеры формулы касательной к окружности
Пример 1
В приведенной ниже окружности точка O — это радиус, PT — касательная, а OP — радиус.
 Если PT — касательная, то OP перпендикулярна PT.
Если PT — касательная, то OP перпендикулярна PT.Если OP = 3 единицы и PT = 4 единицы. Найдите длину OT
Решение: поскольку радиус перпендикулярен касательной в точке касания, OP \[\perp\] PT
Следовательно, ∠P — прямой угол в треугольнике OPT, а треугольник OPT — прямоугольный треугольник.
Теперь по теореме Пифагора находим ОТ.
(OP)² + (PT)² = (OT)²
3² + 4² = (OT)²
9 + 16 = (OT)²
25 = (OT)²
5 = OT
Поскольку длина не может быть отрицательной, длина OT составляет 5 единиц.
Пример 2
На приведенной ниже диаграмме PA и PB касаются окружности. Найдите значение
∠OAP
∠AOB
∠OBA
-
∠ASB
Длина ОП, ПБ = 7 см (дана)
(изображение скоро будет загружено)
Решение:
♂оап = 90 ° (тангенс перпендикулярно радиусу)
↑AOB + ♂ = 180 °
retAOB + 48 °
↑AOB + 48 °
.

 Эта общая касательная прямая имеет кратность два.
Эта общая касательная прямая имеет кратность два.
 Обозначьте точки \(P\) и \(Q\).
Обозначьте точки \(P\) и \(Q\).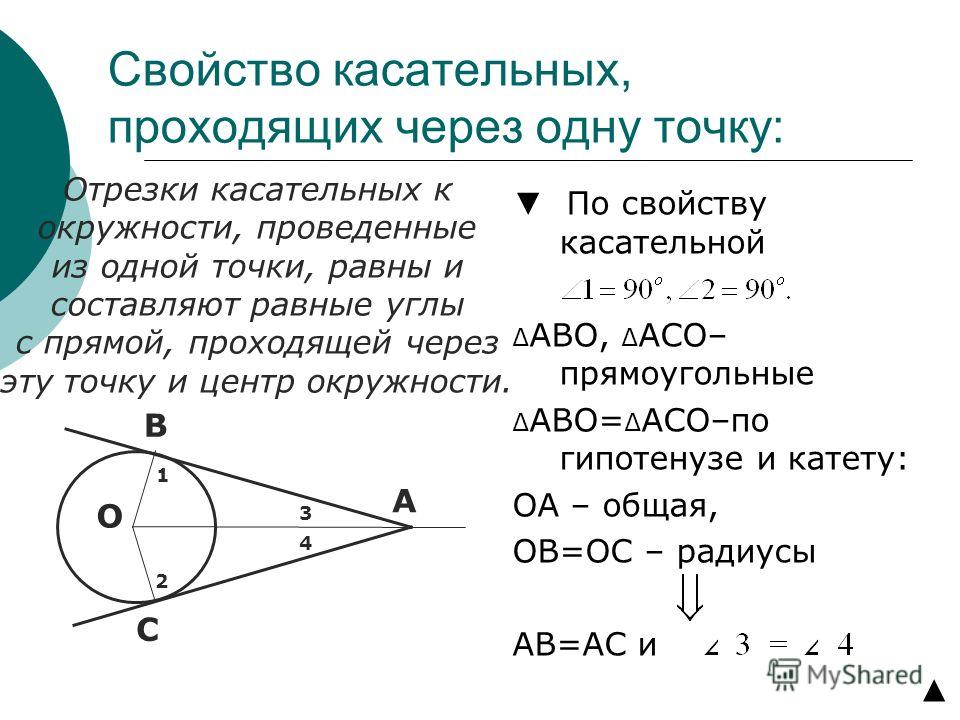 Из данного уравнения \(PQ\) мы знаем, что \(m_{PQ} = 1\).
Из данного уравнения \(PQ\) мы знаем, что \(m_{PQ} = 1\).

 Точно так же \(H\) должна иметь положительную \(y\)-координату, поэтому мы берем положительный квадратный корень.
Точно так же \(H\) должна иметь положительную \(y\)-координату, поэтому мы берем положительный квадратный корень. Но что происходит, когда они встречаются или пересекаются в какой-то одной точке? Это приводит к касательной. Касательная к окружности – это прямая, которая касается окружности в одной точке. Точка касания — это место, где окружность встречается с точкой. Касательная также перпендикулярна радиусу окружности, по которой она пересекается. Его можно рассматривать для любой изогнутой формы. Касательная – это линия, имеющая свое уравнение. В этой главе мы изучим касательную к окружности в различных других формах. Мы также увидим уравнение касательной к окружности и формулу касательной к окружности.
Но что происходит, когда они встречаются или пересекаются в какой-то одной точке? Это приводит к касательной. Касательная к окружности – это прямая, которая касается окружности в одной точке. Точка касания — это место, где окружность встречается с точкой. Касательная также перпендикулярна радиусу окружности, по которой она пересекается. Его можно рассматривать для любой изогнутой формы. Касательная – это линия, имеющая свое уравнение. В этой главе мы изучим касательную к окружности в различных других формах. Мы также увидим уравнение касательной к окружности и формулу касательной к окружности. Точка пересечения окружности и прямой перпендикулярна радиусу. Поскольку он играет жизненно важную роль в геометрическом построении, с ним связано множество теорем, которые мы обсудим далее в этой главе.
Точка пересечения окружности и прямой перпендикулярна радиусу. Поскольку он играет жизненно важную роль в геометрическом построении, с ним связано множество теорем, которые мы обсудим далее в этой главе.

 Из внешней точки P окружность имеет касательную в точках Q и S. Прямая линия, которая разрезает кривую на две или более частей, называется секущей. Итак, здесь секущая равна PR, а в точке Q точка R пересекает окружность, как показано на диаграмме выше. Итак, теперь мы получаем формулу тангенса-секанса
Из внешней точки P окружность имеет касательную в точках Q и S. Прямая линия, которая разрезает кривую на две или более частей, называется секущей. Итак, здесь секущая равна PR, а в точке Q точка R пересекает окружность, как показано на диаграмме выше. Итак, теперь мы получаем формулу тангенса-секанса Если PT — касательная, то OP перпендикулярна PT.
Если PT — касательная, то OP перпендикулярна PT.