Уравнение касательной к плоскости и нормали к поверхности онлайн: Касательная плоскость к поверхности онлайн

Содержание

Касательная плоскость к поверхности онлайн

Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M₀(x₀,y₀,z₀) – фиксированная точка на поверхности σ, т.е. z₀ = f(x₀,y₀). Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.

Решение онлайн
Видеоинструкция

Функция задана в явном виде

z = f(x,y)

в точке M₀(;)

Функция задана в неявном виде f(x,y,z)

F(x,y,z) =

в точке M(;;)

Дополнительно находить уравнение нормали

Правила ввода функций:

Все переменные выражаются через x,y,z

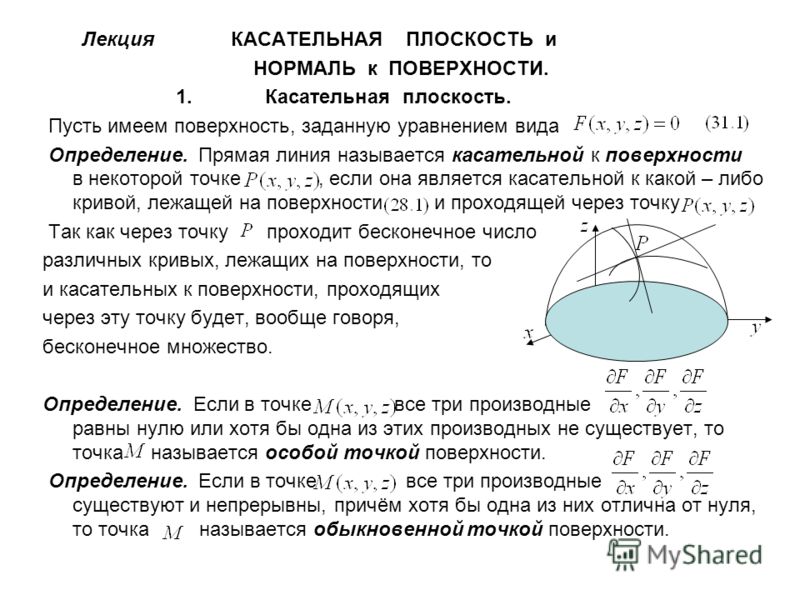
Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M₀(x₀,y₀,z₀) имеет вид:

z – z₀ = f’_x(x₀,y₀)(x – x

0) + f’_y(x₀,y₀)(y – y₀)

Вектор называется вектором нормали к поверхности σ в точке М₀. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М₀ называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M₀(x₀,y₀,z₀), где z₀ = f(x₀,y₀), имеют вид:

Пример №1. Поверхность задана уравнением x³+5y. Найти уравнение касательной плоскости к поверхности в точке M₀(0;1). 3+5*y:
f'_x(x,y) = (x³+5•y)'_x = 3•x²

f’_x(x,y) = (x³+5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f'_x(0;1) = 0
f'_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0

Пример №2. Поверхность задана неявным образом y²-1/2*x³-8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f'_x(1;0;1) = ^-3/₁₆
f'_y(1;0;1) = 0

Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z - 1 = ^-3/₁₆(x - 1) + 0(y - 0) или ³/₁₆•x+z-¹⁹/₁₆ = 0

Пример.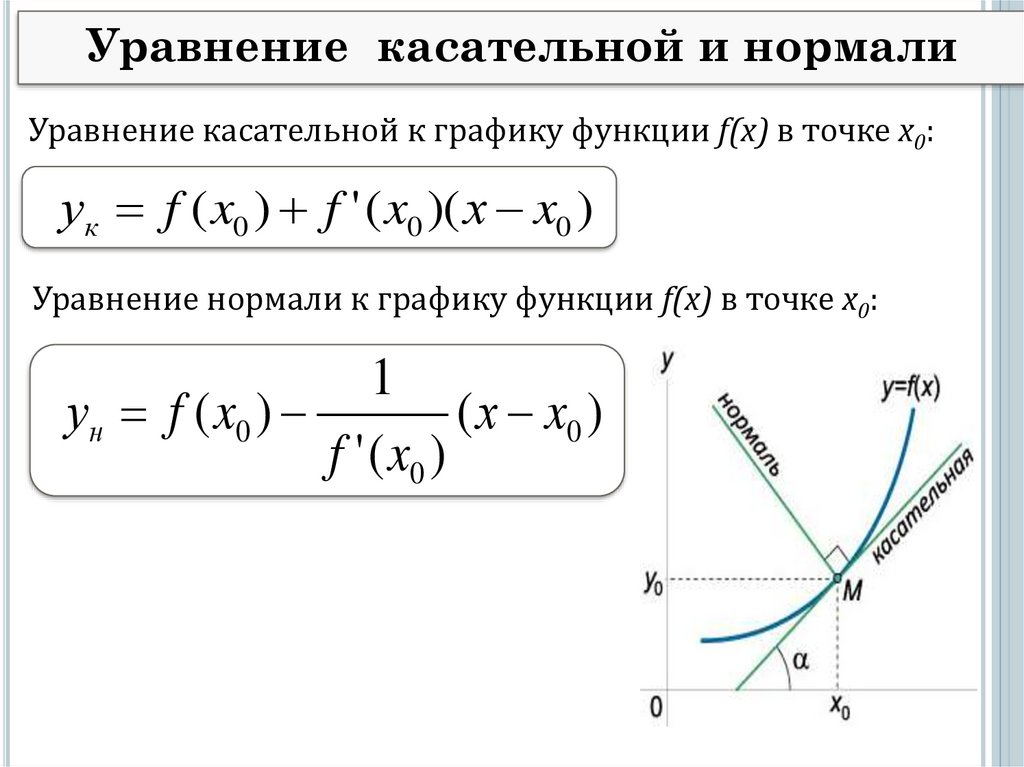 Поверхность σ задана уравнением z= y/x + xy – 5x³. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x³:
f_x’(x, y) = (y/x + xy – 5x³)’_x = – y/x² + y – 15

x²;
f_y’ (x, y) = (y/x + xy – 5x³)’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

z= y/x + xy – 5x³

z₀ = 2/(-1) + (–1) 2 – 5 (–1)³ = 1.

В точке М₀(–1, 2, 1) значения частных производных:
f_x’(М₀) = –1/(-1)² + 2 – 15(–1)² = –15; f_y’(М₀) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М₀

:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y +4 15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М₀: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .

Пример №1. Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).

2:
f’_x(x,y) = (x²+3•x•y•+y²)’_x = 2•x+3•y³
f’_x(x,y) = (x²+3•x•y•+y²)’_y = 9•x•y²
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x² + y² в точке (1;-1;3).
Скачать решение

Касательная плоскость и нормаль к поверхности: вывод уравнений, примеры

Понятие касательной плоскости и нормали к поверхности
Вывод уравнений касательной плоскости и нормали к поверхности
Примеры нахождения уравнений касательной плоскости и нормали к поверхности

Определение.

Касательной плоскостьью к поверхности z = f(x,y) в точке P0(x0,y0,f(x0,y0)) называется плоскость, содержащие все касательные к поверхности, проведённые в точке P0.

Определение. Нормалью к поверхности в точке P называется прямая, проходящая через эту точку перпендикулярно касательной плоскости, проведённой через точку P.

Чтобы найти уравнения касательной плоскости и нормали к поверхности, нужно выполнить следующее:

найти частные производные функции, которой задана поверхность;
найти значения найденных частных производных в точке P0;
найденные значения частных производных и координаты точки P0 подставить в уравнения касательной плоскости и нормали в общем виде.

Прежде чем решать примеры, выведем уравнения касательной плоскости и нормали к поверхности: их вывод может быть включён в экзаменационные билеты.

Пусть дана поверхность z = f(x,y) и точка P0(x0,y0,f(x0,y0)) на этой поверхности.

Чтобы получить уравнение касательной плоскости, достаточно составить уравнение плоскости, на которой находятся две касательные прямые, проведённые через точку P0(x0,y0,f(x0,y0)). Одна из касательных прямых пусть будет параллельна плоскости xOz

, другая — параллельна плоскости yOz (поэтому x — константа). Уравнения этих прямых будут следующими:

где z0 = f(x0,y0)

Из аналитической геометрии известно, что уравнение плоскости, проходящей через точку P0(x0,y0,z0), будет следующим:

A1(x − x0) + B1(y − y0) + C1(z − z0) = 0

или

z − z0 = A(x − x0) + B(y − y0),

где

, .

В последнем уравнении A и B — произвольные константы. Эта плоскость перпендикулярна вектору нормали .

Принимая в уравнении плоскости y = y0, получим уравнение пучка прямых, проходящих через точку P0(x0,y0,z0) и лежащих в плоскости y = y0:

Чтобы касательная прямая принадлежала этому пучку прямых, должно быть .

Принимая в уравнении плоскости x = x0, получим уравнение пучка прямых, проходящих через точку P0(x0,y0,z0) и лежащих в плоскости x = x0:

Чтобы касательная прямая принадлежала этому пучку прямых, должно быть .

Подставляя полученные коэффициенты A и B в уравнение плоскости, получаем уравнение касательной плоскости:

Это и есть уравнение касательной плоскости к поверхности z = f(x,y) в точке P0(x0,y0,z0).

Так как вектор перпендикулярен касательной плоскости к поверхности, то он параллелен нормали и может служить вектором её направления. Таким образом, уравнение нормали к поверхности z = f(x,y) в точке P0(x0,y0,z0):

Рассмотрим также случай, когда уравнение поверхности дано в неявной форме:

Это уравнение определяет неявную функцию z = f(x,y), частные производные которой в точке P0(x0,y0,z0)

при условии, что , а . Подставляя эти производные в уравнение касательной плоскости, получаем

Перенеся все слагаемые в левую часть и умножив на , получаем уравнение касательной плоскости для случая, когда поверхность задана в неявном виде:

Соответствующие уравнения нормали к поверхности:

Пример 1. Составить уравнения касательной плоскости и нормали к поверхности

в точке .

Решение. Функция, которой задана поверхность:

Найдём частные производные этой функции:

Вычислим значения частных производных в точке :

Найденные значения частных производных и координаты точки подставим в уравнения касательнной плоскости и нормали к поверхности. Получаем уравнение касательной плоскости:

Уравнение нормали:

Нет времени вникать в решение? Можно заказать работу!

Пример 2. Составить уравнения касательной плоскости и нормали к поверхности

в точке P0(x0,y0,z0), если y0 = 1, z0 = 0.

Решение. Эта задача уже посложнее, так как в ней не дано x0 и эту координату требуется найти. Для этого подставим y0 и z0 в уравнение поверхности:

Найдём частные производные функции, которой задана поверхность:

Вычислим значения частных производных в точке P0(x0,y0,z0):

Найденные значения частных производных и координаты точки подставим в уравнения касательнной плосоксти и нормали к поверхности. Получаем уравнение касательной плоскости:

Уравнение нормали:

Пример 3. Составить уравнения касательной плоскости и нормали к поверхности

которая параллельна плоскости .

Решение. Сначала нужно найти точку поверхности, проведённая через которую касательная плоскость будет параллельна заданной плоскости. Если касательная плоскость и данная плоскость параллельны, то векторы нормалей будут коллинеарны.

Вектором нормали касательной плоскости будет , где . Вектором нормали данной плоскости является .

Если векторы коллинеарны, то их координаты пропорциональны, то есть

Так как частные производные

то получим

или

Чтобы найти координаты точки M, к последним равенствам нужно присоединить уравнение поверхности. В результате получим систему уравнений, которую и решаем:

Таким образом,

следовательно,

Вот мы и нашли две точки и , проведённая через которые касательная плоскость параллельна данной плоскости.

Вычислим значения частных производных в точке :

Теперь уже можем составить уравнение касательной плоскости, проведённой через точку :

Вычислим значения частных производных в точке :

И, наконец, уравнение касательной плоскости, проведённой через точку :

К началу страницы

Пройти тест по теме Функции нескольких переменных

Поделиться с друзьями

Производные

Что такое производная
Найти производную: алгоритм и примеры решений
Производные произведения и частного функций
Производная суммы дробей со степенями и корнями
Производные простых тригонометрических функций
Производная сложной функции
Производная логарифмической функции
Уравнение касательной и уравнение нормали к графику функции
Дифференциал функции
Дифференциал сложной функции, инвариантность формы дифференциала
Правило Лопиталя

Функции нескольких переменных

Функция двух и более переменных. Её область определения
Поверхности второго порядка
Частные производные
Производная по направлению, градиент функции
Экстремумы функции двух переменных
Условные экстремумы и функция Лагранжа
Вычисление двойных интегралов
Вычисление тройных интегралов

Калькулятор касательной плоскости — Найти уравнение (шаг за шагом)

Онлайн-калькулятор касательной плоскости поможет вам эффективно определить касательную плоскость в заданной точке кривой. Более того, он может точно обрабатывать математические функции с 2 и 3 переменными и обеспечивает пошаговое решение. Возможность быстро вычислить касательную плоскость с помощью этого калькулятора, не выполняя все шаги дифференциального исчисления, значительно экономит время.

Кроме того, вы также получите теоретическую основу и найдете несколько решенных примеров в качестве бонуса.

Что такое касательная плоскость?

Как известно, производная $\frac{dy}{dx}$ функции $f(x)$ в определенной точке представляет собой касательную в этой точке. Вы можете рассчитать касательную к поверхности с помощью нашего Калькулятора касательной. Точно так же частная производная $frac{∂y}{∂x}$ функции $f(x)$ в конкретной точке представляет касательную плоскость в этой точке. В какой-то момент он будет содержать все касательные линии, которые касаются кривизны рассматриваемой функции в этой точке, как показано на рисунке ниже.

Условие касательной плоскости:

Функция, образующая поверхность, должна быть дифференцируемой в точке, чтобы эта плоскость могла там существовать.

Уравнение касательной плоскости:

Пусть S — поверхность, определяемая дифференцируемой функцией $z = f(x,y) $, которая включает 2 переменные, и пусть $P_o = (x_o, y_o)$ быть точкой в области определения f. Тогда уравнение касательной плоскости к S в точке Po задается следующим образом: $$
Аналогично, общее уравнение касательной плоскости в точке $P_o=(x_o, y_o, z_o)$ к поверхности S, определяемой математической функцией $z = f(x,y,z)$, которая включает 3 переменных приведено ниже:
$$z = f(x_o, y_o, z_o) + f_x(x_o, y_o, z_o)(x − x_o) + f_y(x_o, y_o, z_o)(y − y_o) + f_z(x_o) , y_o, z_o)(z − z_o)$$

Как найти уравнение касательной плоскости?

Вам необходимо выполнить следующие шаги, чтобы найти уравнение касательной плоскости к поверхности, заданной функцией. Этот калькулятор касательной плоскости также дает аналогичное решение за долю времени.

Проверка предварительных требований:

Убедитесь, что у вас есть математическая функция поверхности и координаты точки на этой поверхности, где вы хотите вычислить уравнение.

Решение частных дифференциалов:

Частичное дифференцирование математической функции рассматриваемой поверхности. Подробные расчеты можно увидеть из примеров, показанных в следующем разделе.

Вычисление частных дифференциалов в точке:

Рассчитайте значение частично дифференцированной функции в заданных точках для нахождения уравнения касательной плоскости, как показано в следующих примерах.

Решаемые примеры:

Следующие примеры наглядно иллюстрируют, как можно определить требуемое уравнение с помощью вышеупомянутых шагов.

Наш калькулятор касательной плоскости также следует той же процедуре, что и в этих примерах, и вы можете получить точно такой же результат за считанные секунды.

Пример-1: 92\) имеем:
$fx(x,y) = 2x$$
$$fy(x,y) = 2y$$
Итак, уравнение касательной плоскости в точке $(1, 2,5)$:
$$2(1)(x−1)+2(2)(y−2)−z+5 = 0$$
$$= 2x+4y−z−5=0 $$

Пример-2:

Найдите уравнение касательной плоскости к поверхности, заданной функцией $f(x,y)=sin(2x)cos(3y)$ в точке $ (π/3,π/4)$.

Решение:

Сначала вычислим $fx(x,y)$ и $fy(x,y)$, затем вычислим требуемое уравнение касательной плоскости, используя общее уравнение \ (z=f(x_o,y_o)+fx(x_o,y_o)(x-x_o)+fy(x_o,y_o)(y-y_o)\) с $xo = \frac{π}{3}$ и $yo = \frac{π}{4}$:
$$f_x(x,y) = 2cos(2x)cos(3y)$$
$$f_y(x,y) = −3sin(2x)sin(3y)$$
$$f(\frac{π {3}, \ frac {π} {4}) = sin (2 (\ frac {π} {3})) cos (3 (\ frac {π} {4})) = (\ frac {\ sqrt {3}}{2})(\frac{-\sqrt{2}}{2}) = \frac{-\sqrt{6}}{2}$$
$$f_x(\frac{π}{ 3},\frac{π}{4}) = 2cos(2(\frac{π}{3}))cos(3(\frac{π}{4})) = 2(\frac{-1} {2})( \frac{-√2}{2}) = \frac{\sqrt{2}}{2}$$
$$f_y(\frac{π}{3},\frac{π} {4}) = 2\sqrt{2} — 3sin(2(\frac{π}{3}))sin(3(\frac{π}{4})) = -3(3\sqrt{2} )(2\sqrt{2}) = −36\sqrt{4}$$

Теперь подставим эти значения в общее уравнение: 92$$
Тогда наша поверхность является поверхностью уровня $w = 36$. Следовательно, нормаль к поверхности равна:
$$∇w = (2x, 4y, 6z)$$
В точке P имеем $∇w|P = (2, 8, 18)$. Используя точечную нормальную форму, уравнение касательной плоскости имеет вид:
$$2(x − 1) + 8(y − 2) + 18(z − 3) = 0, \text { или эквивалентно} 2x + 8y + 18z = 72$$

Как пользоваться калькулятором касательной плоскости:
С помощью этого онлайн-калькулятора можно эффективно и быстро рассчитать уравнение касательной плоскости, выполнив следующие шаги:
Вы можете переключаться между расчетом с 2 переменными и расчетом с 3 переменными, нажимая соответствующие вкладки в верхней части полей ввода.
Ввод:
Сначала введите нужную математическую функцию в поле ввода под названием «Введите функцию».
Затем просто введите координаты в зависимости от количества переменных в функции.
Выходы:
Калькулятор определяет уравнение касательной плоскости, касающейся поверхности (образованной заданной математической функцией) в координатных точках. Он также предоставляет пошаговое решение, предполагающее дифференциацию всех соответствующих деталей.
Часто задаваемые вопросы:
Какая основная математическая основа используется для определения касательной плоскости?
Частичное дифференцирование в основном используется для определения уравнения, управляющего плоскостью. Этот калькулятор касательной плоскости основан на той же математической концепции и дает точные результаты за считанные секунды.
Касательная плоскость лежит в двумерном или трехмерном пространстве?
Касательные линии лежат в двумерном пространстве, но касательные плоскости представляют собой комбинацию всех касательных линий, касающихся поверхности в определенной точке, следовательно, они лежат в трехмерном пространстве.
В чем разница между касательным вектором и касательной плоскостью?
Касательный вектор — это отдельная линия, которая едва касается поверхности (определяемой математической функцией) в точке, тогда как касательная плоскость — это комбинация всех касательных векторов, касающихся поверхности в определенной точке.
Какая связь между касательной плоскостью и нормальной линией?
Касательная плоскость едва касается поверхности кривой и проходит параллельно ей, тогда как нормаль проходит через поверхность и перпендикулярно ей.
Вывод:
Выполнение всех этих расчетов вручную — очень утомительный процесс. Этот онлайн-калькулятор уравнения касательной плоскости является удобным ресурсом, который дает точные результаты в кратчайшие сроки, даже при работе с 3 переменными функциями. Математическая основа, используемая в бэкэнд-расчетах, точно такая же, как и в ручном процессе.
Ссылки:
Из Википедии – Касательные
Из образовательного блога Openstax – Касательные плоскости и линейные приближения
Из онлайн-ресурсов Libretexts — Касательная плоскость к поверхности
Касательные плоскости — Учебные пособия по исчислению
Касательные плоскости и линейная аппроксимация — Учебное пособие по исчислению HMC
Точно так же, как мы можем визуализировать прямую, касающуюся кривой в точке в двухмерном пространстве, в трехмерном пространстве мы можем изобразите плоскость , касающуюся поверхности в точке.
Рассмотрим поверхность, заданную выражением $z = f (x, y)$. Пусть $(x_0, y_0, z_0)$ — любая точка на этой поверхности. Если $f (x, y)$ равно дифференцируемая в точке $(x_0, y_0)$, то поверхность имеет касательную плоскость в точке $(x_0, y_0, z_0)$.
Уравнение касательной плоскости в точке $(x_0, y_0, z_0)$ задается как $$f_x (x_0, y_0)(x – x_0) + f_y (x_0, y_0)(y – y_0) – (z – z_0 ) = 0. $$
Примечания
Напомним, что уравнение плоскости, содержащей точку $(x_0 , y_0 , z_0 )$ и нормаль к вектору ${\bf n} = (a, b, c)$, равно $$ a(x – x_0 ) + b(y – y_0 ) + c(z – z_0 ) = 0. $$ вывод уравнения для касательной плоскости просто включает в себя доказательство того, что касательная плоскость нормальна к вектору ${\bf n} = (f_x (x_0, y_0), f_y (x_0, y_0), -1)$.
Для поверхностей $F (x, y, z) = 0$, которые нелегко решить относительно $z$, уравнение касательной плоскости в точке $(x_0 , y_0 , z_0 )$ имеет вид $$ F_x ( x_0 , y_0 , z_0 )(x – x_0 ) + F_y (x_0 , y_0 , z_0 )(y – y_0 ) + F_z (x_0 , y_0 , z_0 )(z – z_0 ) = 0 $$ при условии, что $\nabla F ( x_0, y_0, z_0) \neq 0$. Обратите внимание, что если мы положим $F (x, y, z) = f (x, y) – z$, мы получим уравнение, данное для касательной плоскости к $z = f (x, y)$ в точке $(x_0, у_0, z_0)$. 93(-2) + 2 = -14. \end{выравнивание*}
Таким образом, касательная плоскость имеет вектор нормали $ {\bf n} = (48, -14, -1) $ в точке $(1, -2, 12)$ и уравнение касательной плоскости определяется выражением $$ 48(x – 1) – 14 (y – (-2)) – (z – 12) = 0.$$ упрощение, $$ 48x – 14y – z = 64. $$
Линейная аппроксимация
Касательная плоскость к поверхности в точке остается близкой к поверхности вблизи точки. Фактически, если $f (x, y)$ дифференцируема в точке $(x_0 , y_0 )$, то касательная плоскость к поверхности $z = f (x, y)$ при $(x_0, y_0)$ обеспечивает хорошее приближение к $f (x, y)$ вблизи $(x_0, y_0)$:
$\qquad$ Решение $f_x (x_0, y_0)(x – x_0) + f_y (x_0, y_0)(y – y_0) – (z – z_0) = 0$ для $z$, $$ z = z_0 + f_x (x_0, y_0) (x – x_0) + f_y (x_0, y_0) (y – y_0). $$ $\qquad$ Так как $z_0 = f (x_0, y_0)$, мы имеем, что $$ z = f (x_0, y_0) + f_x (x_0, y_0) (x – x_0) + f_y (x_0, y_0) (y – y_0). $$ $\qquad$ Вблизи $(x_0 , y_0 )$ поверхность близка к касательной плоскости. Таким образом, $$ f (x, y) \ приблизительно f (x_0, y_0) + f_x (x_0, y_0) (x – x_0) + f_y (x_0, y_0) (y – y_0). $$ Мы называем это линейная аппроксимация или локальная линеаризация $f (x, y)$ вблизи $(x_0 , y_0 )$.
Примечания
Линейная аппроксимация на самом деле представляет собой просто полином Тейлора со многими переменными степени 1 для $f (x, y)$ около $(x_0, y_0)$. Это точно только около $(x_0, y_0)$. Лучшее приближение можно получить, используя полиномы Тейлора более высокого порядка.
Эти концепции можно распространить на функции более чем двух переменных: $$ f (x, y, z) \ приблизительно f (x_0, y_0, z_0)+f_x (x_0, y_0, z_0)(x-x_0)+f_y (x_0, y_0, z_0)(y-y_0)+f_z (x_0, y_0, z_0)(z-z_0) $$ где $f (x, y, z)$ дифференцируема в $(x_0, y_0, z_0)$. 92 + 2г$ вблизи $x = 1,\quad y = -2$ есть $$ f (x, y) \ приблизительно 48x – 14y – 64. $$ Это, конечно, точно при $x = 1, \quad y = -2$: $$ f (1, -2) = 12 = 48(1) – 14(-2) – 64. $$ При $x = 1,1$ и $y = -1,9$ согласно линейному приближению $$ f (1,1, -1,9) \ приблизительно 48(1,1) – 14(-1,9) – 64 = 15,4, $$ что действительно очень близко к точному значению $f (1,1, -1,9) = 15,41964$.
Ключевые понятия
Касательная плоскость к поверхности
Пусть $(x_0 , y_0 , z_0 )$ — любая точка на поверхности $z = f (x, y)$. Если $f (x, y)$ дифференцируема в $(x_0, y_0)$, то поверхность имеет касательную плоскость в точке $(x_0, y_0, z_0)$, определяемую выражением $$ f_x (x_0, y_0)(x – x_0) + f_y (x_0, y_0)(y – y_0) – (z – z_0) = 0. $$
Линейная аппроксимация поверхности
Если $f (x, y)$ дифференцируема в $(x_0, y_0)$, то вблизи $(x_0, y_0)$ $$ f (x, y) \ приблизительно f (x_0, y_0) + f_x (x_0, y_0) (x – x_0) + f_y (x_0, y_0) (y – y_0).
No related posts.