Що таке периметр прямокутника: Як знайти периметр прямокутника, що таке периметр прямокутника

Периметр прямокутника. Як знайти периметр прямокутника

Периметр прямокутника можна вважати однією з найважливіших характеристик цієї геометричної фігури. Він визначається як загальна відстань, пройдена навколо зовнішньої сторони прямокутника.

Периметр, в основному, дає нам довжину двовимірної фігури. У випадку квадрата, у якого всі сторони мають однакову довжину, периметр дорівнює чотирикратній довжині однієї з його сторін.

Тут ми дізнаємося про формулу периметра прямокутника і використаємо її для вирішення різних задач.

Навігація по сторінці.

1. Формула периметра прямокутника.
2. Периметр прямокутника – приклади з відповідями.
3. Блок-схема алгоритму знаходження периметра прямокутника.

Формула периметра прямокутника.

Периметр прямокутника визначається як сума довжин усіх його сторін. Тобто, для прямокутника  зображеного на рисунку нижче, матимемо: , де  – периметр прямокутника.

Проте, виходячи з того, що прямокутник має по дві пари рівних сторін, то при знаходженні периметра достатньо суму довжин двох його суміжних сторін (довжина плюс ширина) помножити на два. Тобто, знову-таки, повертаючись до прямокутника , матимемо: .

Зауваження: якщо позначити довжину та ширину прямокутника буквами  та  відповідно, то формула периметра перепишеться у більш звичній буквенній формі: .

Периметр прямокутника – приклади з відповідями.

У наступних прикладах для отримання відповіді використовується формула для периметра прямокутника. Незважаючи на те, що кожен приклад має рішення, рекомендується спробувати розв’язати вправи самостійно, перш ніж дивитися відповідь.

Приклад 1: знайти периметр прямокутника з основою  і висотою .

Отже, за умовою маємо, що довжина та ширина прямокутника дорівнює  і  відповідно. Використавши формулу  периметра із заданими значенням матимемо:

Таким чином, периметр прямокутника дорівнює .

Приклад 2: знайти периметр прямокутника з основою  і висотою .

Зазначимо, що у цьому випадку довжина і ширина прямокутника дорівнює  та .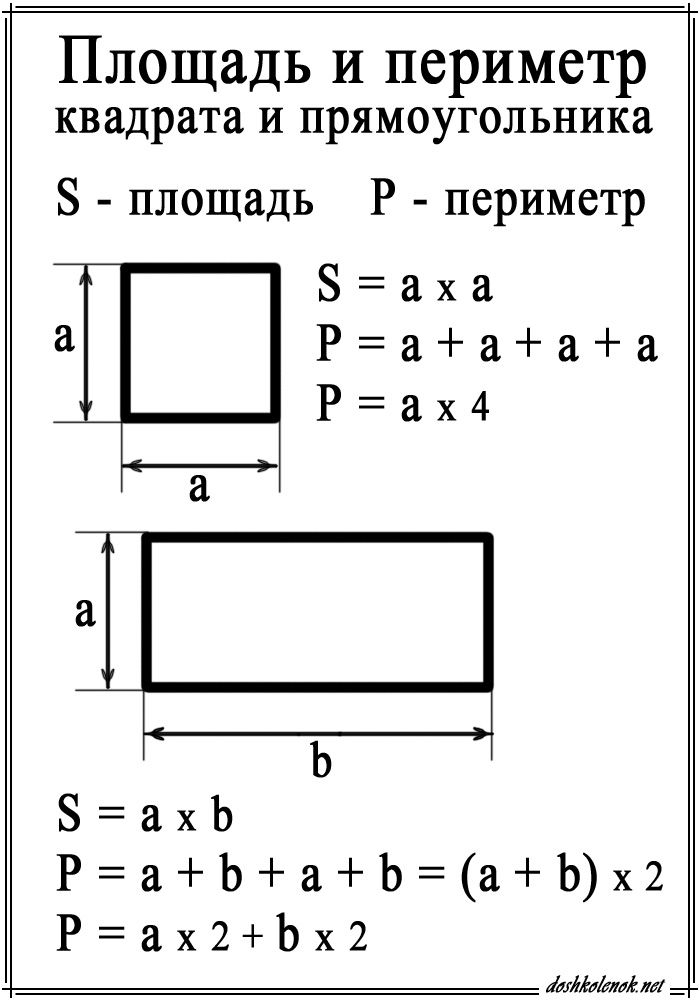 Тому, замінивши  та  у формулі периметра заданим значенням отримаємо:

Отже, периметр прямокутника дорівнює .

Приклад 3: периметр прямокутника дорівнює , а його основа . Яка довжина його висоти?

Зазначимо, що у цьому випадку ми повинні знайти ширину прямокутника, знаючи периметр та основу. Отже, використовуючи ту ж формулу, підставляємо задані значення та знаходимо висоту :

Звідси, довжина висоти прямокутника дорівнює .

Приклад 4: знайти основу прямокутника з висотою  і периметром .

Знову-таки, скориставшись формулою , підставляємо задані значення і знаходимо довжину прямокутника:

Отже, основа прямокутника дорівнює .

Приклад 5: бісектриса одного з кутів прямокутника  ділить його сторону навпіл. Знайти периметр прямокутника, якщо його менша сторона дорівнює .

Отже, врахувавши те, що за умовою, , отримаємо: .

Скориставшись далі формулою обчислення периметра прямокутника, знайдемо розв’язок задачі:

Таким чином, периметр прямокутника  дорівнює .

Дивіться також:

Хочете дізнатися більше про прямокутник? Перегляньте ці сторінки:

1. Прямокутник і його властивості.
2. Діагональ прямокутника – формули та приклади
3. Площа прямокутника – формули та приклади.

Блок-схема алгоритму знаходження периметра прямокутника

Ми в соціальних мережах

Як пишеться периметр прямокутника. Що таке периметр і його застосування на практиці

Прямокутник володіє багатьма відмітними особливостями, виходячи з яких, вироблені правила обчислення його різних числових характеристик. Отже, прямокутник:

Плоска геометрична фігура;
чотирикутник;
Фігура, у якій протилежні сторони рівні і паралельні, всі кути прямі.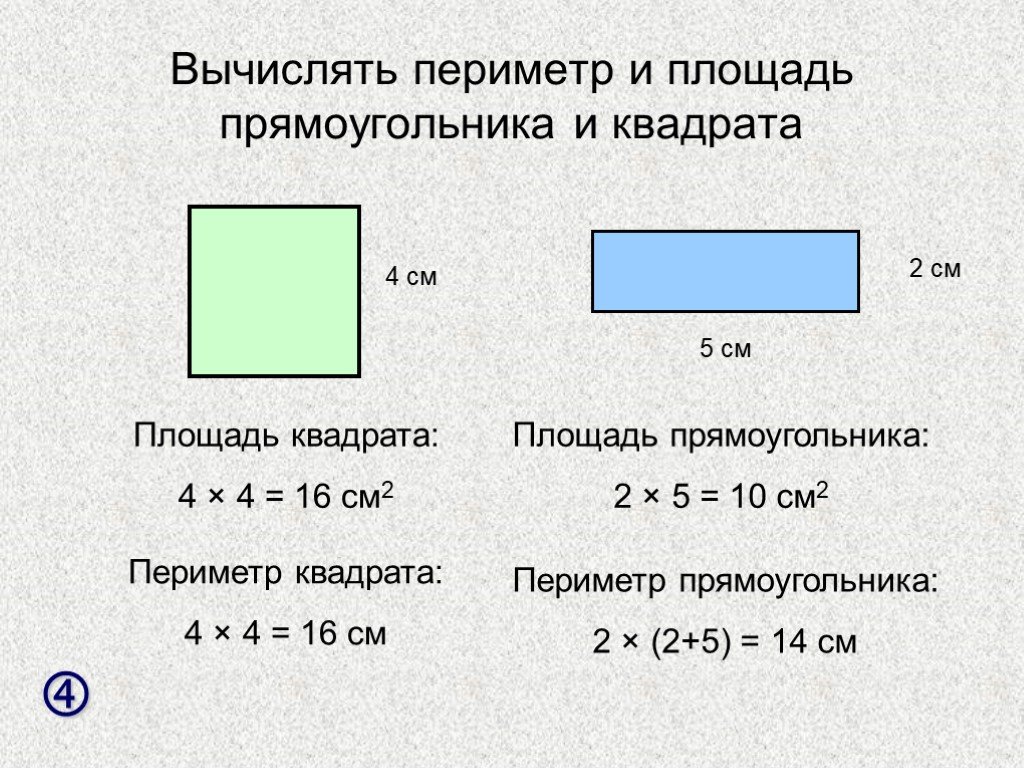

Периметр — це загальна довжина всіх сторін фігури.

Обчислення периметра прямокутника — досить просте завдання.

Все, що вам потрібно знати, це ширину і довжину прямокутника. Оскільки прямокутник має дві рівні довжини і дві рівні ширини, вимірюється тільки одна сторона.

Периметр прямокутника дорівнює подвоєною сумі 2-х його сторін довжини і ширини.

P \u003d (a + b) 2, де a — довжина прямокутника, b — ширина прямокутника.

Так само периметр прямокутника можна знайти за допомогою суми всіх сторін.

P \u003d a + a + b + b, де а довжина прямокутника, b — ширина прямокутника.

Периметр квадрата — це довжина сторони квадрата, помножена на 4.

P \u003d a 4, де a — довжина сторони квадрата.

Доповнення: Знаходження знайти площі і периметра прямокутників

У програмі навчання за 3 клас передбачено вивчення багатокутників і їх особливостей. Для того щоб зрозуміти, як знайти периметр прямокутника і площа, розберемося, що мається на увазі під цими поняттями.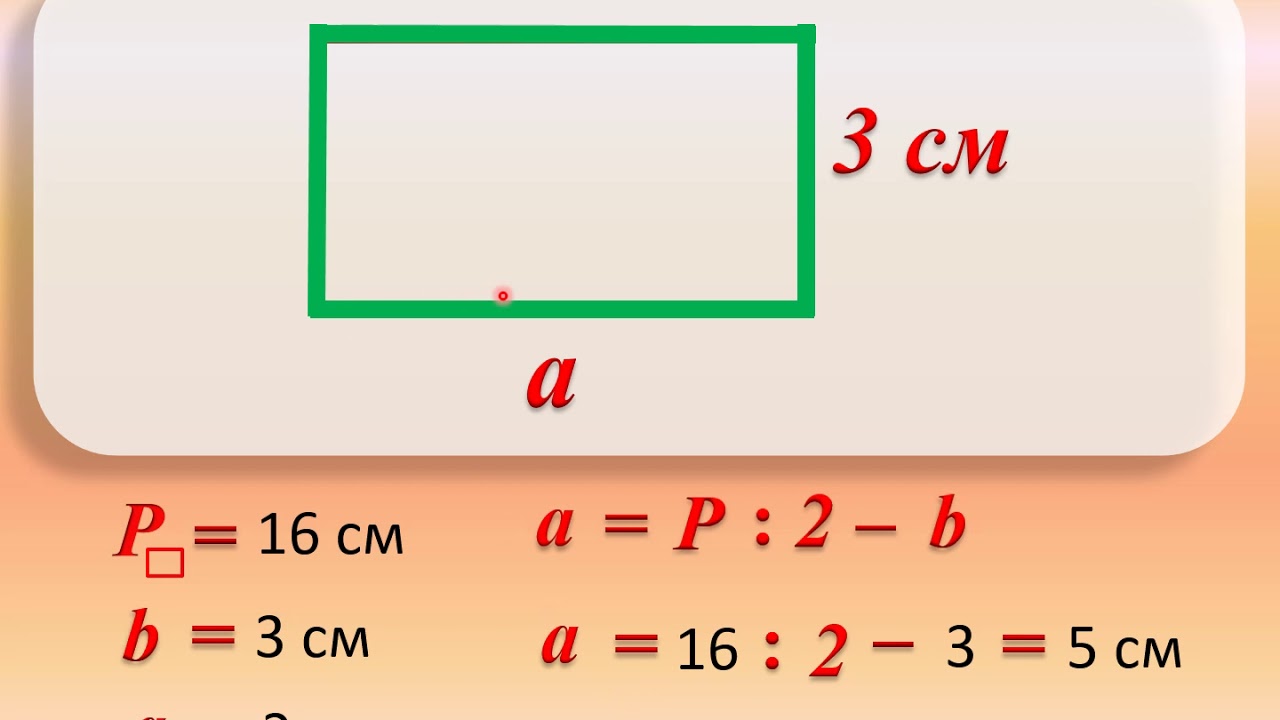

Основні поняття

Знаходження периметра і площі вимагає знання деяких термінів. До них відносяться:

1. Прямий кут. Утворюється з 2 променів, що мають спільний початок у вигляді точки. При знайомстві з фігурами (3 клас) прямий кут визначають за допомогою кутника.
2. Прямокутник. Це чотирикутник, всі кути якого є прямими. Його сторони називають довжиною і шириною. Як відомо, протилежні сторони цієї фігури рівні.
3. Квадрат. Є чотирикутником, усі сторони якого рівні.

При знайомстві з багатокутниками їх вершини можуть називатися АВСД. У математиці прийнято називати точки на кресленнях буквами латинського алфавіту. У назві багатокутника перераховують всі вершини без пропусків, наприклад, трикутник ABC.

обчислення периметра

Периметр багатокутника — це сума довжин всіх його сторін. Ця величина позначається латинською буквою P. Рівень знань для запропонованих прикладів — 3 клас.

Завдання №1: «Накресліть прямокутник 3 см шириною і 4 см завдовжки з вершинами ABCD. Знайдіть периметр прямокутника ABCD ».

Формула буде виглядати так: P \u003d AB + BC + CD + AD або P \u003d AB × 2 + BC × 2.

Відповідь: P \u003d 3 + 4 + 3 + 4 \u003d 14 (см) або P \u003d 3 × 2 + 4 × 2 \u003d 14 (см).

Завдання №2: «Як знайти периметр прямокутного трикутника ABC, якщо значення сторін рівні 5, 4 і 3 см?».

Відповідь: P \u003d 5 + 4 + 3 \u003d 12 (см).

Завдання №3: «Знайдіть периметр прямокутника, одна сторона якого дорівнює 7 см, а інша на 2 см довший».

Відповідь: P \u003d 7 + 9 + 7 + 9 \u003d 32 (см).

Завдання №4: «Змагання з плавання проходили в басейні, периметр якого складає 120 м. Скільки метрів проплив учасник змагань, якщо ширина басейну 10 м?».

У цьому завданню стоїть питання, як знайти довжину басейну. Для вирішення знайдіть довжини сторін прямокутника. Ширина відома. Сума довжин двох невідомих сторін повинна скласти 100 м. 120-10 × 2 \u003d 100. Щоб дізнатися відстань, яку подолав плавець, потрібно розділити отриманий результат на 2. 100: 2 \u003d 50.

Відповідь: 50 (м).

обчислення площі

Складнішою величиною є площа фігури. Для її вимірювання використовують мірки. Еталоном серед мірок є квадрати.

Площа квадрата зі стороною 1 см дорівнює 1 см². Квадратний дециметр позначений як дм², а квадратний метр — м².

Області застосування одиниць вимірювання можуть бути такими:

1. У см² вимірюють маленькі предмети, наприклад фотографії, обкладинки підручників, аркуші паперу.
2. У дм² можна виміряти географічну карту, віконне скло, картину.
3. Для вимірювання статі, квартири, земельної ділянки використовують м².

Якщо накреслити прямокутник 3 см завдовжки і 1 см шириною і розбити на квадрати зі стороною 1 см, то в ньому поміститься 3 квадрата, а значить, його площа складе 3 см². Якщо прямокутник розбитий на квадрати, знайдемо периметр прямокутника також без труднощів. В даному випадку він дорівнює 8 см.

Інший спосіб порахувати кількість квадратів, що вміщаються в фігуру, — це використання палетки.

Накреслимо на кальці квадрат площею 1 дм², що становить 100 см². Помістимо кальку на фігуру і порахуємо число квадратних сантиметрів в одному ряду. Після цього з’ясуємо кількість рядів, а потім перемножимо значення. Значить, площа прямокутника — це твір його довжини і ширини.

Способи порівняння площ:

1. На око. Іноді досить просто поглянути на предмети, оскільки в деяких випадках і неозброєним оком видно, що одна фігура займає більше місця, як, наприклад, підручник, що лежить на столі поруч з пеналом.
2. Накладення. Якщо фігури збігаються при накладанні, їх площі рівні. Якщо ж одна з них повністю поміщається всередині другої, то її площа менше. Місця, які займає зошитових листом і сторінкою з підручника, можна порівняти, наклавши їх один на одного.
3. За кількістю мірок. Фігури при накладенні можуть і не збігатися, однак мати однакову площу. Порівняти в цьому випадку можна, підрахувавши кількість квадратів, на які розбита фігура.
4. Числа. Порівнюються чисельні значення, виміряні однією і тією ж міркою, наприклад, в м².

Приклад №1: «Швачка пошила дитяче ковдру з квадратних різнокольорових клаптиків. Один клаптик довжиною 1 дм, в ряду по 5 штук. Скільки дециметрів стрічки знадобиться швачці для обробки країв ковдри, якщо відома площа 50 дм²? ».

Щоб вирішити задачу, потрібно відповісти на питання, як знайти довжину прямокутника. Далі знайдемо периметр прямокутника, складеного з квадратів. З завдання ясно, що ширина ковдри — 5 дм, обчислюємо довжину, розділивши 50 на 5, і отримуємо 10 дм. Тепер знайдіть периметр прямокутника зі сторонами 5 і 10. P \u003d 5 + 5 + 10 + 10 \u003d 30.

Відповідь: 30 (м).

Приклад №2: «На розкопках виявлено ділянку, де можуть перебувати стародавні скарби. Скільки території доведеться досліджувати вченим, якщо відомий периметр 18 м і ширина прямокутника 3 м? ».

Визначимо довжину ділянки, виконавши 2 дії. 18-3 × 2 \u003d 12. 12: 2 \u003d 6. Шукана територія буде також дорівнює 18 м² (6 × 3 \u003d 18).

Відповідь: 18 (м²).

Таким чином, знаючи формули, обчислити площу і периметр не складе труднощів, а наведені вище приклади допоможуть попрактикуватися у вирішенні математичних задач.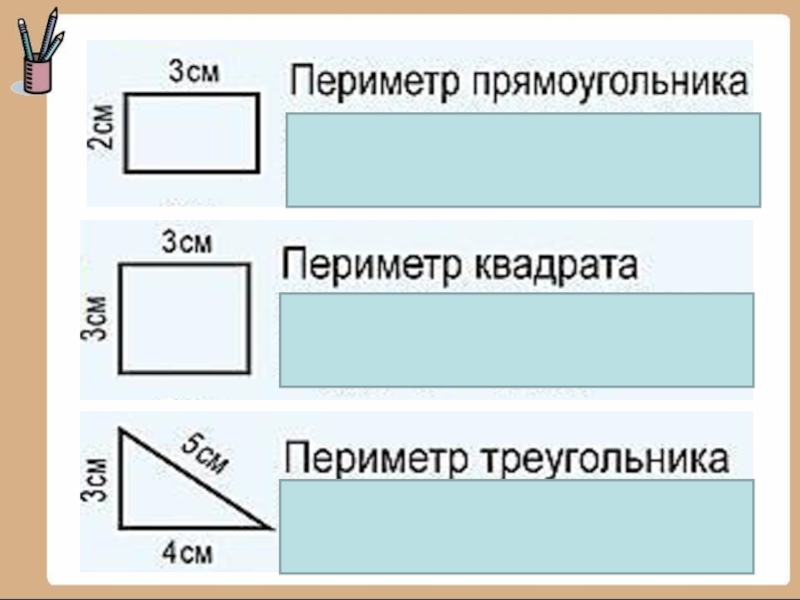

На цьому занятті ми познайомимося з новим поняттям — периметр прямокутника. Ми сформулюємо визначення цього поняття, виведемо формулу для його обчислення. Також повторимо сполучний закон додавання і розподільний закон множення.

На даному уроці ми познайомимося з периметром прямокутника і його обчисленням.

Розглянемо наступну геометричну фігуру (рис. 1):

Мал. 1. Прямокутник

Дана фігура — прямокутник. Згадаймо, які відмінні риси прямокутника ми знаємо.

Прямокутник — це чотирикутник, у якого чотири прямих кута і сторони попарно рівні.

Що в нашому житті може мати прямокутну форму? Наприклад, книга, кришка столу або земельну ділянку.

Розглянемо наступну задачу:

Завдання 1 (рис. 2)

Навколо земельної ділянки будівельникам знадобилося поставити паркан. Ширина цієї ділянки — 5 метрів, довжина — 10 метрів. Забір якої довжини вийде у будівельників?

Мал. 2. Ілюстрація до задачі 1

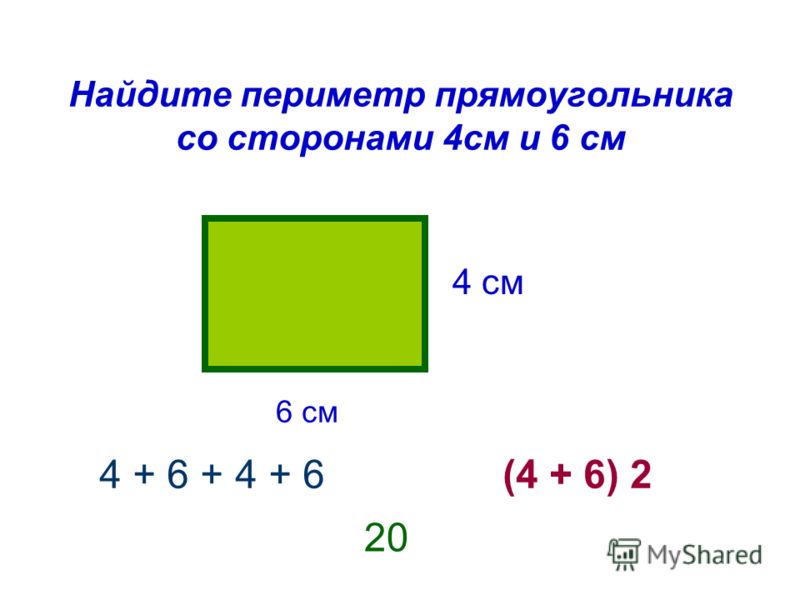
Забір ставлять по межах ділянки, тому, щоб дізнатися довжину забору, потрібно знати довжину кожної зі сторін. У даного прямокутника сторони рівні: 5 метрів, 10 метрів, 5 метрів, 10 метрів. Складемо вираз для підрахунку довжини паркану: 5 + 10 + 5 + 10. Скористаємося переместітельним законом складання: 5 + 10 + 5 + 10 \u003d 5 + 5 + 10 + 10. В даному вираженні є суми однакових доданків (5 + 5 і 10 + 10). Замінимо суми однакових доданків творами: 5 + 5 + 10 + 10 \u003d 5 · 2 + 10 · 2. Тепер скористаємося розподільним законом множення щодо складання: 5 · 2 + 10 · 2 \u003d (5 + 10) · 2.

Знайдемо значення виразу (5 + 10) · 2. Спочатку виконуємо дію в дужках: 5 + 10 \u003d 15. А потім повторюємо число 15 два рази: 15 · 2 \u003d 30.

Відповідь: 30 метрів.

периметр прямокутника — сума довжин всіх його сторін. Формула для підрахунку периметра прямокутника:, Тут a — довжина прямокутника, а b — ширина прямокутника. Сума довжини і ширини називається напівпериметр. Щоб з напівпериметр отримати периметр, потрібно його збільшити в 2 рази, тобто помножити на 2.

Скористаємося формулою периметра прямокутника і знайдемо периметр прямокутника зі сторонами 7 см і 3 см: (7 + 3) · 2 \u003d 20 (см).

Периметр будь-якої фігури вимірюється в лінійних одиницях.

На даному уроці ми познайомилися з периметром прямокутника і формулою його обчислення.

Твір числа і суми чисел дорівнює сумі творів даного числа і кожного з доданків.

Якщо периметр — це сума довжин всіх сторін фігури, то напівпериметр — сума однієї довжини і однієї ширини. Ми знаходимо напівпериметр, коли працюємо за формулою знаходження периметра прямокутника (коли ми виконуємо перша дія в дужках — (a + b)).

Список літератури

1. Александрова Е.І. Математика. 2 клас. — М .: Дрофа, 2004.
2. Башмаков М.І., Нефедова М.Г. Математика. 2 клас. — М .: Астрель, 2006.
3. Дорофєєв Г.В., Міракова Т.І. Математика. 2 клас. — М .: Просвещение, 2012.

1. Festival.1september.ru ().
2. Nsportal.ru ().
3. Math-prosto.ru ().

Домашнє завдання

1. Знайти периметр прямокутника, у якого довжина 13 метрів, а ширина — 7 метрів.
2. Знайти напівпериметр прямокутника, якщо його довжина — 8 см, а ширина — 4 см.
3. Знайти периметр прямокутника, якщо його напівпериметр — 21 дм.

периметр— це сума довжин всіх сторін багатокутника.

• Для обчислення периметра геометричних фігур використовуються спеціальні формули, де периметр позначається буквою «P». Назва фігури рекомендується писати маленькими буквами під знаком «P», щоб знати чий периметр ти знаходиш.
• Периметр вимірюється в одиницях довжини: мм, см, м, км тощо

Відмінні риси прямокутника

• Прямокутник — це чотирикутник.
• Всі паралельні сторони рівні
• Всі кути \u003d 90º.
• Наприклад в повсякденному житті прямокутник може зустрічатися у вигляді — книги, монітора, кришки від столу або двері.

Як обчислити периметр прямокутника

Існує 2 способи його знаходження:

• 1 спосіб. Складаємо все боку. P \u003d a + а + b + b
• 2 спосіб. Скласти ширину і довжину, і помножити на 2. P \u003d (a + b) · 2. АБО Р \u003d 2 · а + 2 · b.Сторони прямокутника, які лежать один проти одного (протилежні), називаються довжиною і шириною.

«A» — довжина прямокутника, довша пара його сторін.

«B» — ширина прямокутника, коротша пара його сторін.

Приклад завдання на підрахунок периметра прямокутника:

Обчисліть периметр прямокутника, є його ширина дорівнює 3 см., А довжина — 6.

Запам’ятай формули обчислення периметра прямокутника!

напівпериметр— це сума однієї довжини і однієї ширини .

• Напівпериметр прямокутника —коли виконуєш перша дія в дужках — (A + b).
• Щоб з напівпериметр отримати периметр, потрібно його збільшити в 2 рази, тобто помножити на 2.

Як знайти площу прямокутника

Формула площі прямокутника S \u003d a * b

Якщо в умові відома довжина одного боку і довжина діагоналі, то площа знайти можна, використовуючи в таких завданнях, теорему Піфагора, вона дозволяє знайти довжину сторони прямокутного трикутника якщо відомі довжини двох інших сторін.

• : A 2 + b 2 \u003d c 2, Де a і b — сторони трикутника, а з — гіпотенуза, найдовша сторона.

Пам’ятай!

1. Всі квадрати — прямокутники, але не всі прямокутники — квадрати. Так як:
   • прямокутник — це чотирикутник з усіма прямими кутами.
   • квадрат — прямокутник, у якого всі сторони рівні.
2. Якщо ти знаходиш площа, відповідь завжди буде в квадратних одиницях (мм 2, см 2, м 2, км 2 і т.д.)

Часто на просторах інтернету можна знайти глузування з приводу того, як знання з математики — інтеграли, диференціали, тригонометричні функції і інші розділи предмета — не допомагають полегшити життя людини. Такі жарти даремні, адже як виручає уміння правильно розраховувати периметр квадрата, прямокутника і інших геометричних фігур в будівельних роботах. Витрата матеріалу: плитки, шпалер, підлогового покриття — не визначити без розуміння елементарних математичних формул і геометричних фігур.

властивості квадрата

Будь-які обчислення в математиці базуються на властивостях об’єкта. Щоб відповісти на питання: «Чому дорівнює периметр квадрата?» — рекомендується згадати відмінні характеристики цієї фігури.

1. Рівність усіх боків.
2. Наявність чотирьох кутів величиною 90 градусів.
3. Паралельність сторін.
4. Поворотна симетрія. При обертанні фігури її вид залишається незмінним.
5. Можливість описати і вписати коло.
6. Діагоналі при перетині ділять один одного навпіл.
7. Площа фігури характеризує заповнене квадратом місце в двомірному просторі.
8. Периметр фігури не що інше, як сума довжин його сторін.
9. З попереднього властивості випливає, що одиницями вимірювання величини периметра будуть одиниці довжини: м, см, дм і інші.

Для підрахунку плінтусів для завершення ремонту в квадратному приміщенні, необхідно знати довжину кімнати. Для цього необхідно порахувати її периметр.

периметр

У перекладі з грецької мови слово означає «вимірювати навколо».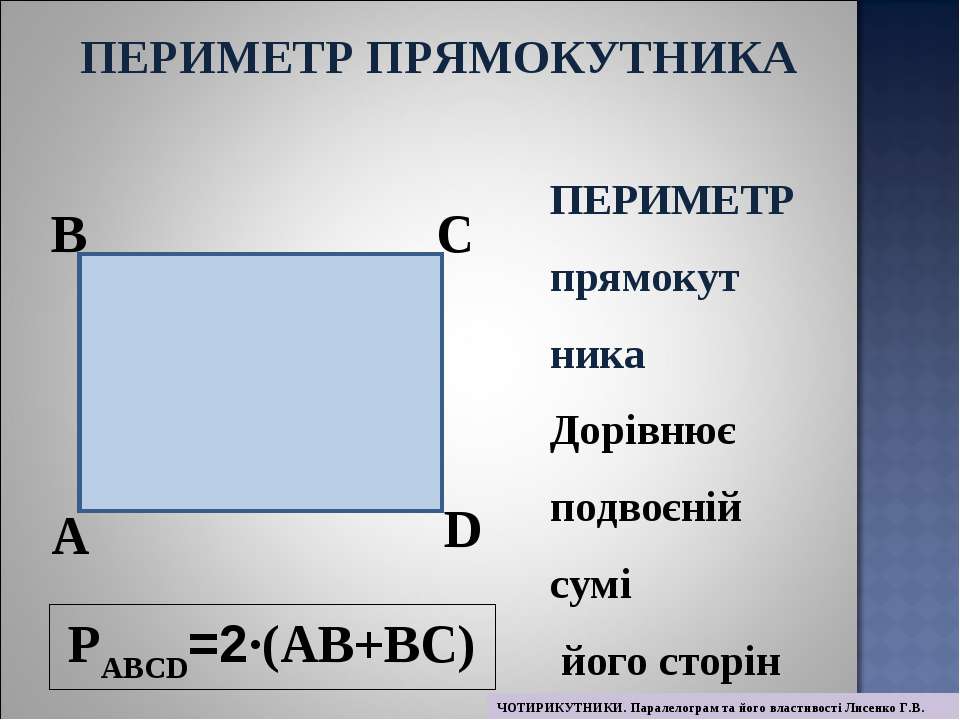 Термін застосуємо до всіх замкнутим фігурам: квадрату, окружності, прямокутника, трикутника, трапеції і іншим. Знання по визначенню периметра елементарних фігур необхідні для вирішення складних геометричних задач з об’єктами неправильної форми. Наприклад, для розрахунку плінтусів в кімнату плануванням типу «Г», або як ще називають, «чобітком», потрібно визначити периметр квадрата і прямокутника. Адже форма приміщення складається з цих елементарних фігур.

Загальноприйняте позначення такої величини — буква Р. Кожній фігурі з урахуванням її властивостей притаманна своя формула для визначення периметра.

властивості прямокутника

1. Рівність протилежних сторін.
2. Рівність діагоналей.
3. Можливість описати коло.
4. Висоти прямокутника рівні його сторонам.
5. Сума кутів дорівнює 360 градусів, і всі кути прямі.
6. Паралельність протилежних сторін.
7. Перпендикулярність прилеглих сторін.
8. Сума квадратів діагоналей прямокутника дорівнює сумі квадратів його сторін.
9. Перетинаючись, діагоналі ділять один одного навпіл.
10. Неможливість вписати в фігуру окружність.

периметр квадрата

Залежно від встановлених (відомих) параметрів квадрата, існують різні формули для визначення його периметра. Простим завданням є розрахунок периметра при встановленій довжині його боку (с). В цьому випадку Р \u003d з + з + з + з або 4 * с. Наприклад, довжина сторони квадрата 7 см, тоді периметр фігури буде 28 см (4 * 7).

У першому випадку все зрозуміло, але як знайти периметр квадрата, знаючи його площу? І тут все гранично ясно. Оскільки площа фігури визначається множенням одного боку на іншу, а у квадрата всі сторони рівні, необхідно витягти корінь з відомої величини. Приклад: є квадрат з площею 25 дм 2. Корінь з 25 дорівнює 5 — ця величина характеризує довжину сторони квадрата. Тепер, підставляючи знайдену величину — 5 дм 2 — в первісну формулу периметра, можна вирішити задачу. Відповіддю буде значення в 20 дм. Тобто 4 помножили на 5, отримали шукану величину.

Квадрат і коло

З властивостей розглянутої фігури випливає, що в квадрат можна вписати коло і також її описати навколо фігури.

Перший варіант — знаходження периметра по радіусу описаного кола. Вписаним вважається квадрат, вершини якого знаходяться на колі. Радіус кола дорівнює 1/2 довжини діагоналі. Виходить, що діаметр дорівнює діагоналі. Тепер необхідно розглянути прямокутний трикутник, який вийшов в результаті поділу діагоналлю квадрата. Рішення завдання зводиться до знаходження сторін цього трикутника. ВС — це відома величина, діаметр описаного кола. Припустимо, він дорівнює 3 см. Теорема Піфагора у випадку з рівними сторонами трикутника, буде виглядати так: 2с 2 \u003d 3 2. У формулі позначення з — це довжина сторони трикутника і квадрата; 3 — відома величина гіпотенузи. Звідси, з \u003d √9 / 2. Знаючи сторону квадрата, його периметр порахувати не проблема.

Особливістю вписаного кола є поділ сторін квадрата навпіл. Тому радіус дорівнює половині довжини сторони квадрата. Тоді сторона з \u003d 2 * радіус. Периметр квадрата в цьому випадку дорівнює 4 * 2 * радіус або 8 радіусів кола.

периметр прямокутника

Сама елементарна формула визначення периметра прямокутника через відомі величини його сторін виглядає так: Р \u003d 2 (а + b), де а і b — довжини сторін фігури.

Діагональ прямокутника аналогічно квадрату ділить фігуру навпіл, утворюючи прямокутний трикутник. Однак завдання ускладнюється тим, що сторони цього трикутника нерівні. У випадку з відомою величиною однієї зі сторін і діагоналі, другу можна знайти, слідуючи теоремі Піфагора: д 2 \u003d а 2 + в 2, де а і в — сторони фігури, а д — діагональ.

Якщо невідома жодна зі сторін, тоді в справу вступають знання тригонометрії: синуси, косинуси і інші функції.

Знаходження периметра по описаного кола і відомому діаметру зводиться до того, що діаметр дорівнює довжині діагоналі фігури. Далі рішення задачі визначається за наявністю відомих величин. Якщо дані кути, тоді через тригонометричні функції. Якщо дана сторона, відповідь буде знайдено через теорему Піфагора.

Прямокутник і тригонометричні функції

Для наочності наведено приклади розв’язання задач. Дано: прямокутник АВСД; довжина діагоналі ( d) 20 см; кут ф — 30 °. Знайти периметр фігури.

З тригонометрії необхідно згадати наступне: синус кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузи. Синус 30 ° (існують таблиці, за якими можна визначити значення тригонометричних функцій для правильних кутів) дорівнює 1/2. Виходить 1/2 \u003d відношенню до до d. Невідома величина в дорівнюватиме d/ 2 \u003d 20/2 \u003d 10 см.

Для розрахунку периметра слід знайти другу сторону фігури. Можна через теорему Піфагора, так як відомі довжини гіпотенузи і одного з катетів або знову через ставлення сторін для косинуса кута.

косинус кута ф виражається як відношення прилеглого катета до гіпотенузи дорівнює √3 / 2.

√3/2=n / d, n \u003d (d* √3) / 2 або 10 * √3. Після вилучення кореня з 3, отримуємо довжину сторони трикутника: 10 * 1,73 \u003d 17,3 см.

Периметр дорівнює 2 (17,3 + 10) \u003d 2 * 27,3 \u003d 54,6 см.

Периметр і ставлення сторін

У шкільній програмі зустрічаються завдання з геометрії, коли довжини сторін прямокутника виражені їх ставленням один до одного. Розгляд вирішення такого завдання представлено нижче.

Відомо, що сума довжин всіх сторін прямокутника, тобто його периметр, дорівнює 84 см. Відношення довжини (д) до ширини (ш) — 3: 2. Знайти сторони фігури.

Рішення: нехай довжина буде 3х, а ширина 2х, згідно співвідношенню з умови задачі. Формула периметра прямокутника з отриманими даними довжин сторін буде наступною: 3х + 3х + 2х + 2х \u003d 84. Далі, 10х \u003d 84, х \u003d 8,4 см. Підставивши х в вираз довжини і ширини прямокутника, можна знайти шукані величини. Довжина буде: 3 * 8,4 \u003d 25,2 см; ширина: 2 * 8,4 \u003d 16,8 см.

Стаття присвячена вирішенню найбільш часто зустрічаються завдань у шкільній програмі. І це далеко не всі способи знаходження периметра квадрата і прямокутника.

клас: 2

мета: ознайомити з прийомом знаходження периметра прямокутника.

завдання:формувати вміння розв’язувати задачі, пов’язані з перебуванням периметра фігур, виробляти вміння креслити геометричні фігури, закріпити вміння обчислювати, застосовуючи з переместительное властивість складання, розвивати навик усного рахунку, логічне мислення, виховувати пізнавальну активність і вміння працювати в колективі.

устаткування:ІКТ (мультимедійний проектор, презентація до уроку), картинки з геометричними фігурами для физминутки, модель магічного квадрата, в учнів — моделі геометричних фігур, маркерні дошки, лінійки, підручники, зошити.

ХІД УРОКУ

1. Організаційний момент

Перевірка готовності до уроку. Привітання.

Починається урок,
Він піде хлопцям на користь.
Постарайтеся все зрозуміти —
І уважно вважати.

2. Усний рахунок

а) Використання магічних фігур. ( Додаток 1 )

— Заповнимо клітини магічного квадрата, назвіть його особливості (сума чисел по горизонталях, вертикалях і діагоналях рівні) і визначте чарівне число. (39)

По ланцюжку діти заповнюють квадрат на дошці і в зошитах.

б) Знайомство з властивостями магічних трикутників. ( Додаток 2 )

— Суми чисел в кутах, що утворюють трикутник рівні. Знайдемо чарівні числа у трикутника. Визнач пропущене число. Відзнач його на маркерні дошки.

3. Підготовка до вивчення нового матеріалу

— Перед Вами геометричні фігури. Назвіть їх одним словом. (Чотирикутники).
— Розділіть їх на 2 групи. ( додаток 3 )
— Що таке прямокутники. (Прямокутники — чотирикутники, у яких всі кути прямі.)
— Що можна дізнатися, знаючи довжини сторін чотирикутників? Периметр — сума довжин сторін фігур.
— Знайдіть периметр білої фігури, жовтої.
— Чому у прямокутників відомі не всі сторони?
— Які властивості у протилежних сторін прямокутників? (У прямокутника протилежні сторони рівні).
— Якщо протилежні сторони рівні, чи треба вимірювати всі сторони? (Ні.)
— Правильно, досить виміряти довжину і ширину.
— Як обчислити зручним способом? (Учні працюють усно з коментуванням.)

4. Вивчення нової теми

— Прочитайте тему нашого уроку: «Периметр прямокутника». ( додаток 4 )
— Допоможіть знайти периметр даної фігури, якщо її довжина дорівнює — а, А ширина — в.

Бажають знаходять Р у дошки. Учні в зошитах записують рішення.

— Як записати це по-іншому?

Р \u003d а + а + в + в,
Р \u003d а х 2 + в х 2,
Р \u003d ( а + в) Х 2.

— Ми отримали формулу знаходження периметра прямокутника. ( додаток 5 )

5. Закріплення

Стор. 44 № 2.

Діти читають і записують умова, питання, креслять фігуру, знаходять Р різними способами, записують відповідь.

6. Физминутку. сигнальні картки

Скільки клітинок зелених,
Стільки виконаємо нахилів.
Стільки разів руками вип’ємо.
Стільки разів ногами тупни.
Скільки тут у нас гуртків,
Стільки зробимо стрибків.
Ми сядемо стільки раз,
Настільки підтягнемося зараз.

7. Практична робота

— У Вас на партах лежать в конвертах геометричні фігури. Як ми їх назвемо?
— Що таке прямокутники?
— Що ви знаєте про протилежних сторонах прямокутників?
— Виміряйте сторони фігур за варіантами, знайдіть периметр різними способами.
— Перевіряємо у сусіда.

взаимопроверка зошитів.

— Прочитайте: Як знайшли периметр? Що можна сказати про периметрах даних фігур? (Вони рівні).
— Накресліть прямокутник з таким же Р, але іншими сторонами.

Р 1 \u003d (2 + 6) х 2 \u003d 16 Р 1 \u003d 2 х 2 + 6 х 2 \u003d 16
Р 1 \u003d 2 + 2 + 6 + 6 \u003d 16
Р 2 \u003d 3 + 3 + 5 + 5 \u003d 16 Р 2 \u003d (3 + 5) х 2 \u003d 16
Р 3 \u003d 4 + 4 + 4 + 4 \u003d 16 Р 4 \u003d 1 + 1 + 7 + 7 \u003d 16

8. Графічний диктант

Зліва 6 клітин. Поставили крапку. Починаємо рух. 2 — вправо, 4 — вправо вниз, 10 — вліво, 4 — вправо вгору. Яка фігура? Перетвори її в прямокутник. Добудуй. Знайди Р різними способами.

Р \u003d (5 + 2) х 2 \u003d 14.
Р \u003d 5 + 5 + 2 + 2 \u003d 14.
Р \u003d 5 х 2 + 2 х 2 \u003d 14.

9. Пальчикова гімнастика

Множили, множили.
Дуже, дуже ми втомилися.
Наші пальчики сплетём і з’єднаємо долоні.
А потім, як тільки можемо, міцно міцно стиснемо.
На дверях висить замок.
Хто його відкрити не зміг?
Ми замочком постукали,
Ми замочок покрутили,
Ми замочок покрутили і відкрили.

(Слова супроводжуються рухами)

10. Складання і рішення задачі за умовою(додаток 8 )

Довжина прямокутника — 12 дм
Ширина — на 3 дм м.
Р -?
У першій дії знайдемо ширину: 12 — 3 \u003d 9 (дм) — ширина
Знаючи довжину і ширину, дізнаємося Р одним із способів.
Р \u003d (12 + 9) х 2 \u003d 42 дм

11. Самостійна робота

12. Підсумок уроку

— Чого вчилися. Як знаходили Р прямокутника?

13.Оценіваніе

Оцінюються відповіді учнів біля дошки і вибірково в процесі самостійної роботи.

14.Домашнее завдання

С. 44 № 5 (з поясненнями).

Периметр прямоугольника | ChiliMath

Периметр прямоугольника равен расстоянию вокруг прямоугольника . Периметром прямоугольного цветника считается длина забора, окружающего сад. Мы вычисляем периметр прямоугольника, получив сумму всех его сторон.

---

Как известно, у прямоугольника четыре стороны и четыре прямых угла. Однако по сравнению с квадратом не все его стороны равны. Две пары противоположных сторон прямоугольника имеют равные размеры. То есть длина одной стороны равна длине другой стороны, а ширина одной стороны равна ширине другой стороны.

Примечание. Количество делений указывает на конгруэнтность сторон.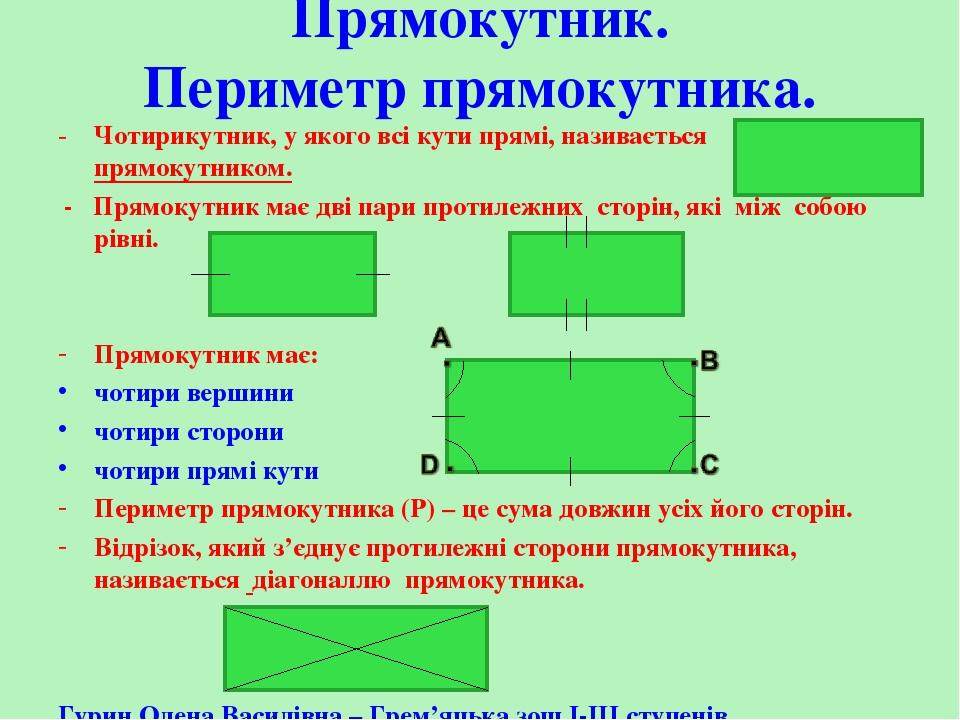 Также помните, что длина (l) — самая длинная сторона, а ширина (w) — самая короткая.

Найдем периметр прямоугольника, сложив все измерения его сторон. Если мы запишем это уравнением, оно будет выглядеть так:

P = l + w + l + w

где P обозначает периметр, l длину и w ширину

Однако, поскольку противоположные стороны прямоугольники конгруэнтны, уравнение можно просто записать как P = 2l + 2w.

Как вы могли заметить, длина и ширина в формуле умножаются на два, а затем складываются вместе, а не записываются дважды.

---

Примеры нахождения периметра прямоугольника

Нет лучшего способа попрактиковаться в использовании этой формулы и узнать больше о периметре прямоугольника, чем рассмотреть несколько примеров. Хорошо, начнем!

Пример 1 : Найдите периметр прямоугольника.

Прямоугольник выше имеет длина 16 км и ширина 11 км . Несмотря на то, что нам не известны размеры всех четырех сторон, мы знаем, что две другие стороны также имеют размеры 16 км и 11 км соответственно. Как? Потому что противоположные стороны прямоугольника равны. Другими словами, нам нужно знать только длину и ширину, чтобы вычислить периметр прямоугольника.

Теперь воспользуемся формулой для периметра прямоугольника и подставим 16 вместо L и 11 вместо W.

периметр прямоугольника равен 54 км .

---

Пример 2 : Какой длины прямоугольник ниже, если его периметр равен 154 футам , а его ширина равна 25 футам ?

Иногда возникает проблема, связанная с отсутствием одного из измерений. В этой задаче нас просят найти длину прямоугольника, а не вычислять его периметр. Найти недостающую длину или ширину легко, если у вас есть измерение одного из измерений и периметра прямоугольника.

Чтобы найти недостающую длину, все, что нам нужно сделать, это использовать формулу периметра прямоугольника, заменить P на 154 и W на 25, а затем найти L.

Отлично! Длина прямоугольника 52 фута.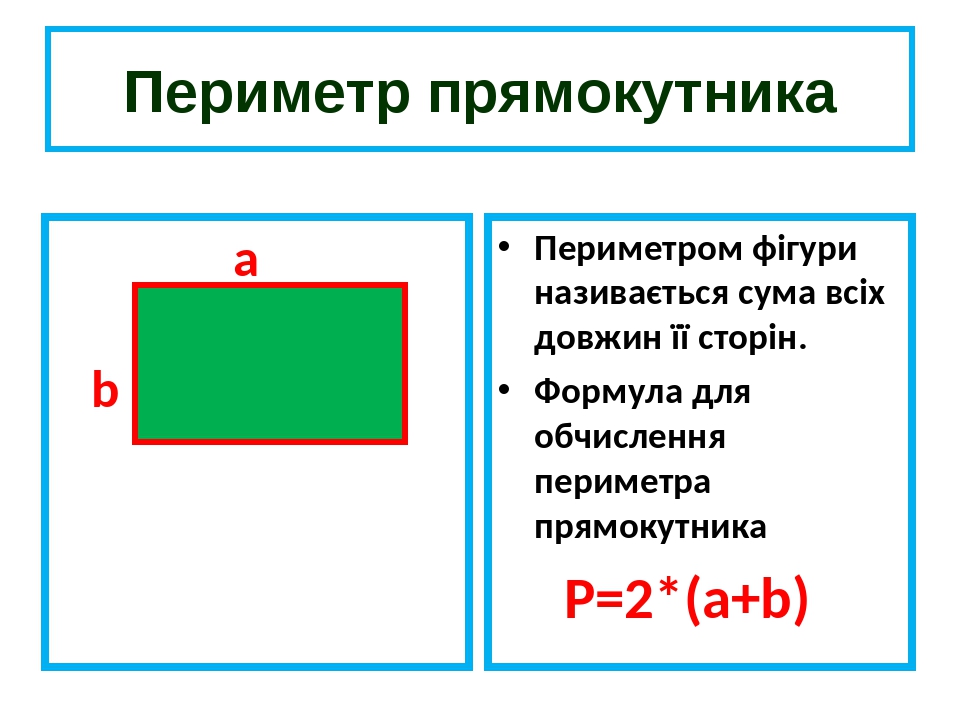 Однако, прежде чем мы завершим эту задачу, давайте убедимся, что наши длина и ширина действительно дадут нам периметр 154 фута. Снова используя формулу, мы имеем

P = 2L + 2W

154 = 2\влево( {52} \вправо) + 2\влево( {25} \вправо)

154 = 104 + 50

154 = 154

И да, это так! Следовательно, длина прямоугольника равна 52 футам .

---

Пример 3 : Если длина и ширина прямоугольника ниже уменьшены на 4 дюйма , найдите периметр нового прямоугольника.

В этом примере нас просят уменьшить размеры нашего исходного прямоугольника на 4 дюйма, затем, используя эти новые размеры, мы найдем периметр нового прямоугольника.

Шаг 1 : Уменьшите длину и ширину исходного (текущего) прямоугольника на 4 дюйма.

• Длина:

Д = 37 \color{- 4}

Д = 33

• Ширина:

Вт = 14 \цвет{красный}{- 4}

W = 10

Мы получили размеры нового прямоугольника. Длина теперь составляет 33 дюйма, а новая ширина — 10 дюймов.

Шаг 2 : Вычислите периметр нового прямоугольника, используя новые длину и ширину.

• Подставьте 33 вместо L и 10 вместо W в формулу периметра прямоугольника.

Вот оно! Периметр для нашего нового прямоугольника равен 86 дюймам .

---

Пример 4 : длина прямоугольника в раз больше его ширины . Каков периметр прямоугольника с шириной 6,8 см ?

Прежде чем приступать к каким-либо вычислениям, давайте сначала определим и интерпретируем фрагменты информации, данные нам в задаче.

• Ширина (Ш): 6,8\,см

• Длина (Д): Двойная ширина → 6,8\влево(2\вправо) = {13,6\,см}

Теперь, когда мы есть наши длина и ширина, мы можем действовать как обычно, чтобы найти периметр прямоугольника.

Периметр прямоугольника равен 40,8 см .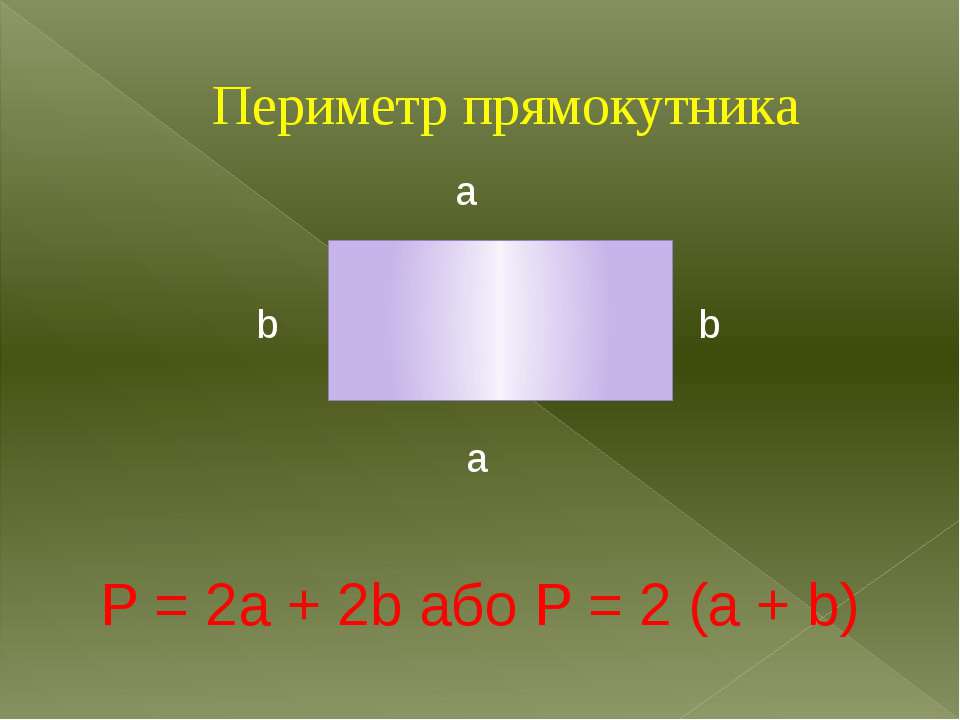

---

Пример 5: У нашего соседа есть прямоугольный бассейн длиной 36 футов . Если периметр пула составляет 108 футов , какой ширины бассейн?

В этой задаче отсутствует одно из измерений, как и в одном из наших предыдущих примеров. В этом случае измерение ширины бассейна неизвестно. Чтобы получить лучшее представление о проблеме, давайте сначала нарисуем ее, используя предоставленную нам информацию.

Теперь найдем ширину по формуле периметра прямоугольника.

Я оставляю на ваше усмотрение проверить, действительно ли наши длина и ширина дадут нам периметр в 108 футов.

Бассейн нашего соседа 18 футов шириной .

---

Пример 6 : Саманта хочет поместить рамку вокруг своей фотографии с кошкой. Изображение 14 дюймов на 18 дюймов . Сколько границ нужно Саманте?

Начнем снова с определения доступных нам частей информации.

Вот размеры фотографии Саманты.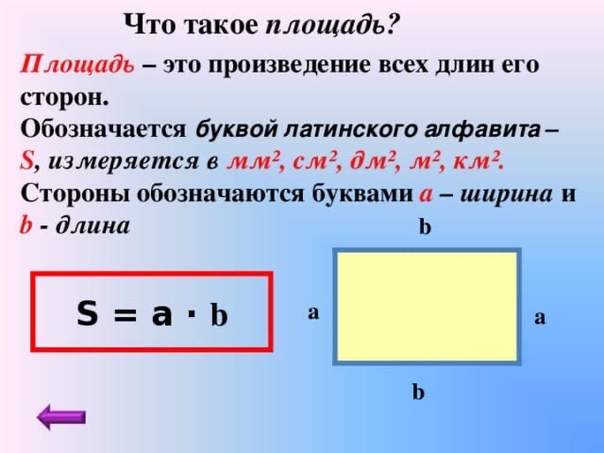

Длина :

Д = 18 дюймов.

Ширина :

Вт = 14 дюймов.

Поскольку она хочет обвести прямоугольную картинку рамкой, мы сразу понимаем, что имеем дело с задачей, связанной с периметром прямоугольника. Чтобы узнать, сколько границ ей нужно, нам нужно просто применить формулу для нахождения периметра прямоугольника.

Прекрасно! Саманте нужно 64 дюйма рамки , чтобы обклеить ее фотографию с кошкой.

---

Вас также может заинтересовать:

Периметр прямоугольника Словесные задачи

Площадь прямоугольника

Периметр квадрата

Периметр прямоугольника с формулами и диаграммой

Периметр любой двумерной геометрической фигуры — это расстояние, пройденное вокруг ее края. В этой статье мы узнаем, как найти периметр прямоугольника с помощью формул и примеров.

Что такое периметр прямоугольника

Периметр прямоугольника — это общее расстояние, пройденное вокруг края прямоугольника.

Поскольку прямоугольник является четырехсторонней фигурой, его периметр также определяется как сумма четырех сторон.

Периметр – это общая мера длины или расстояния. Выражение периметра в линейных единицах. Таким образом, единицей измерения периметра прямоугольника являются ярды, футы, дюймы, метры или любая другая линейная единица.

Формула

Формула для нахождения периметра прямоугольника приведена ниже:

Периметр прямоугольника

Вывод

Поскольку периметр четырехугольника (геометрическая фигура с 4 сторонами) равен сумме всех сторон, поэтому , периметр (P) равен,

P = сумма всех четырех сторон = w + w + l + l = 2(w + l), где w = ширина, а l = длина.

Таким образом, мы получаем стандартную формулу периметра прямоугольника (P) = 2(w + l)

Как найти периметр прямоугольника

Основные шаги для вычисления периметра прямоугольника по его длине (l ) и ширина (w) следующие:

• Запишите формулу Периметра прямоугольника 2(w + l).
• Подставьте значения длины (l) и ширины (w) в формулу.
• Запишите ответ в линейных единицах.

Давайте решим несколько примеров, чтобы лучше понять концепцию.

Решенные примеры

Найдите периметр прямоугольного сада длиной 10 м и шириной 6 м.

Решение:

Как известно,
P = 2(w + l), здесь w = 6 м, l = 10 м
= 2 х (10 + 6)
= 32 м.

Сколько кружев понадобится Джону, чтобы украсить простыню длиной 150 дюймов и 95 дюймов в ширину?

Решение:

Длина шнурка равна периметру (P) простыни.
Как мы знаем,
P = 2(w + l), здесь w = 95 дюймов, l = 150 дюймов
= 2 x (95 + 150)
= 490 дюймов
Итак, Джону нужно кружево 490 дюймов для украшения простыни.

Нахождение периметра прямоугольника, когда известны ДИАГОНАЛЬ и любая ОДНА СТОРОНА

Найдите периметр прямоугольника с диагональю 9 футов и длиной 8 футов.

Решение:

Здесь мы будем использовать формулу 305 + l ² ), где d = диагональ, l = длина
Как мы знаем,
P = 2l + 2√(d ² – l ² ), где d = 9 футов, а l = 8 футов
= 2 x 8 + 2 x √ (9 ² – 8 ² )
≈ 24,25 фута

Найдите периметр прямоугольника шириной 16 дюймов и диагональю 32 дюйма.

Решение:

Здесь мы будем использовать формулу 305 + l ² ), где d = диагональ, w = ширина
Как мы знаем,
P = 2w + 2√(d ² – w ² ), где w = 16 дюймов, d = 32 дюйма
= 2 x 16 + 2√(32 ² – 16 ² )
≈ 87,42 дюйма

Нахождение периметра прямоугольника, когда известны ПЛОЩАДЬ и любая ОДНА СТОРОНА 900 05

Найдите периметр прямоугольного бассейна, площадь которого составляет 700 кв. футов и имеет ширину 100 футов.

Решение:

Здесь мы будем использовать формулу P = 2w + 2A/w , чтобы найти периметр (P) как A = w × l и P = 2(w + l), где w = ширина , l = длина, A = площадь.
Как известно,
P = 2w + 2A/w, здесь w = 100 футов, а A = 700 кв. футов.
= 2 × 100 + 2 × (700/100)
= 214 футов. Найдите периметр прямоугольника, площадь которого 3750 кв.см, а длина 75см.

Решение:

Здесь мы будем использовать формулу P = 2l + 2A/l , чтобы найти периметр (P) как A = w × l и P = 2(w + l),
Где w = ширина, l = длина, A = площадь.
Как известно,
P = 2l + 2A/l, здесь l = 75 см, а A = 3750 кв. см
= 2 × 75 + 2 × (3750/75)
= 250 см 291

Найти длина парка, если длина парка в два раза больше его ширины, а периметр равен 390 ярдам.

Решение:

Здесь мы будем использовать формулу l = P/2 – w, которую мы получаем из формулы P = 2(w + l), где l = длина, P = периметр, w = ширина.