Парная линейная регрессия. Задачи регрессионного анализа
- Понятие линейной регрессии. Парная линейная регрессия
- Уравнение парной линейной регрессии и метод наименьших квадратов
- Анализ качества модели линейной регрессии
- Интерпретация коэффициентов уравнения парной линейной регрессии
- Задачи регрессионного анализа
- Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо
величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x),
когда каждому значению независимой переменной x соответствует одно определённое значение
величины y, при линейной регрессии одному и тому же значению x могут соответствовать
в зависимости от случая различные значения величины 
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
y = ax + b,
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади
кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором
приближении к прямой, хотя и не на самой прямой.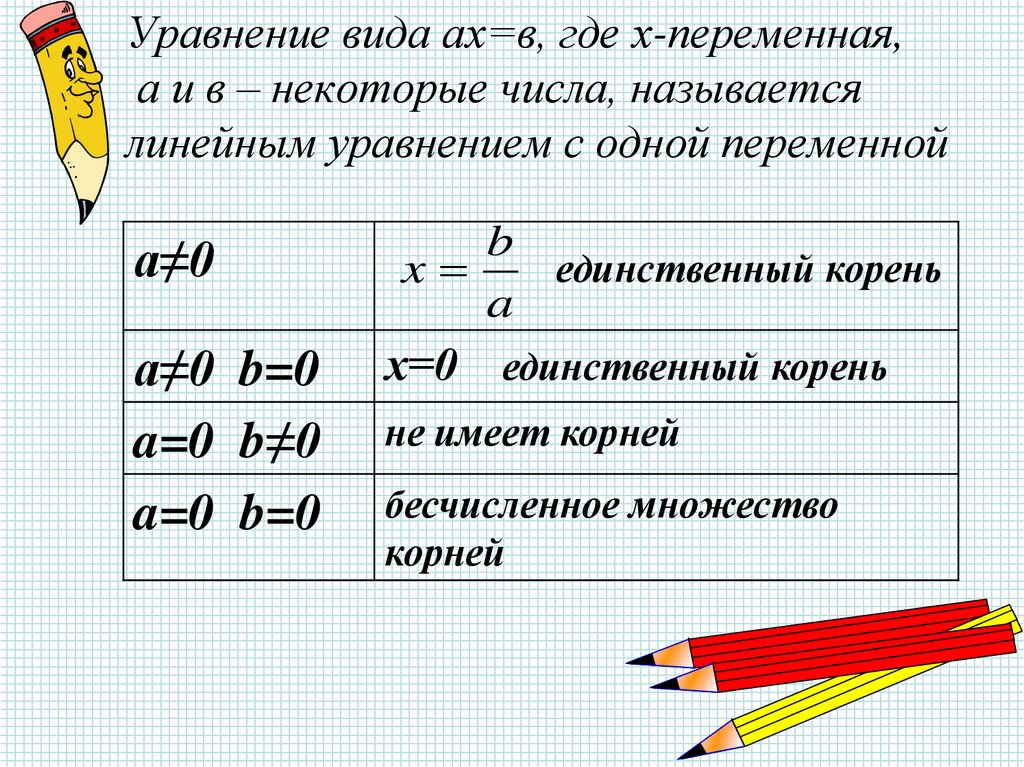
Если точки корреляционной диаграммы соединить ломанной
линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то
полученная прямая будет прямой теоретической регрессии. На рисунке ниже
она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
где
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
или
где
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:
- прямая парной линейной регрессии проходит через точку ;
- среднее значение отклонений равна нулю: ;
- значения и не связаны: .
Пройти тест по теме Теория вероятностей и математическая статистика
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2.
Найти уравнение парной линейной регрессии для выборки из
6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Правильное решение и ответ.
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации
принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице.
Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
где
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
Правильное решение и ответ.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
где
—
остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится
к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593, SSE = 10 459,587, SSR = 53 311,007.
Можем убедиться, что выполняется закономерность SSR = SST — SSE:
63770,593-10459,587=53311,007.
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной
регресии.
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение.
Подставляем в уравнение парной линейной регрессии xi = 20000
и получаем прогноз потребления при доходе в 20 000 у.е. yi = 17036,4662.
Подставляем в уравнение парной линейной регрессии xi = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. yi = 4161,9662.
Если доход не меняется, то xi = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям
независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не
влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы,
то есть линейной зависимости Y от X нет.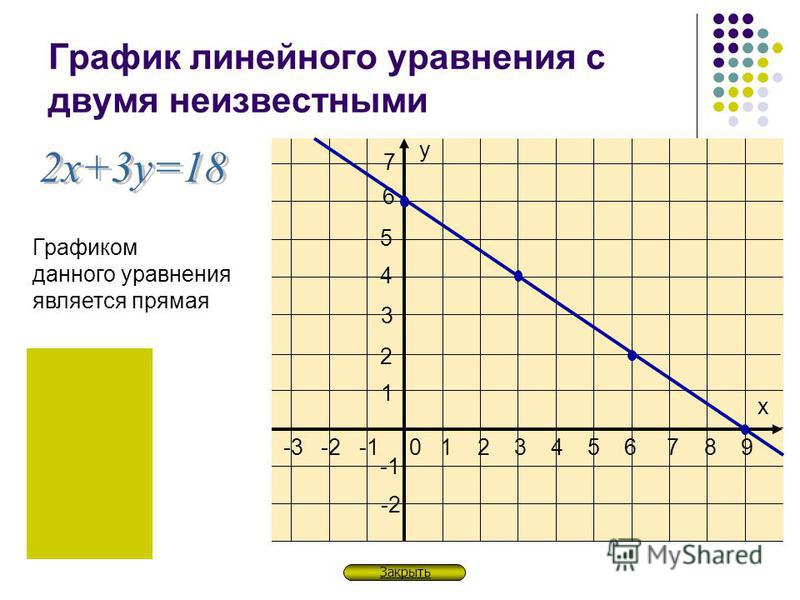
Нулевую гипотезу
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2,
где — стандартная погрешность коэффициента направления прямой линейной регресии b1.
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном
потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и
проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b1:
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пройти тест по теме Теория вероятностей и математическая статистика
К началу страницы
| Назад | Листать | Вперёд>>> |
Всё по теме «Математическая статистика»
Характеристики выборки и генеральной совокупности: среднее значение, дисперсия, погрешности выборки
Доверительный интервал для математического ожидания
Распределение Стьюдента и малые выборки
Проверка статистических гипотез
Корреляционная зависимость, коэффициент корреляции
Множественная корреляция, её коэффициент.
Частная корреляция
Множественная линейная регрессия. Улучшение модели регрессии
Дисперсионный анализ: соединение теории и практики
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1.
Для характеристики зависимости у от х рассчитать параметры следующих функций:
А) линейной;
Б) степенной;
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x2 | y2 | ||
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
| 8,4988 | 11,1431 | х | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .
Так как
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x)2 | (lg y)2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
| 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х | |
| 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | ||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
| 8,4988 | 11,1431 | 0,000640820 | х | х | х | |
| 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Получено уравнение:
Индекс корреляции:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
Формула линейного уравнения — Выводы, формулы, примеры
Используя формулу линейного уравнения, мы преобразуем данную ситуацию в математические утверждения, иллюстрирующие взаимосвязь между неизвестными (переменными) из предоставленной информации. Линейное уравнение – это уравнение прямой линии, также известное как уравнения первого порядка.
Мы используем линейные уравнения для решения наших повседневных задач. Давайте подробно разберем формулу линейного уравнения в следующих разделах.
Что такое формула линейного уравнения?
Уравнение с максимальным порядком 1 и уравнение прямой называется линейным уравнением. Формула линейного уравнения может быть записана в простой форме, т. е. y = mx + b, где x и y — переменные, m — наклон линии, а b — точка пересечения с осью y. Наклон определяет направление линии и ее крутизну. Значение y, когда x равно 0, называется точкой пересечения y, потому что (0,y) — это точка, в которой линия пересекает ось y. Следовательно, формула линейного уравнения имеет вид:
y = mx + b
где,
- x и y две переменные
- b — точка пересечения с осью Y
- м — уклон линии
Формула линейного уравнения
Применяя формулу линейного уравнения (y= mx+b), уравнение прямой линии с точкой пересечения по оси y (0, 2) с наклоном m = 4 определяется как y = 4x +2.
Линейное уравнение с одной и двумя переменными может быть представлено во многих формах, где линия может быть определена в плоскости (x, y). Некоторые из распространенных форм:
| Форма линейного уравнения | Формула | Пояснение |
| Общая форма | топор + бай = с | , где а ≠ 0; а, b, с — действительные числа. м = -а/б |
| Форма пересечения уклонов | у = мх + б | , где y и x – точки на плоскости (x,y), m – наклон линии (известный как градиент), b – точка пересечения (постоянная величина) |
Форма из двух пунктов | \(у-у_{1} = м (х-х_{1})\) | , где \((x_{1},y_{1})\) и \((x_{2}, y_{2})\) – две точки на прямой, м = \(\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\) и \(x_{1}\) ≠ \(x_{2}\) |
| Форма перехвата | х/\(х_{0}\) + у/\(у_{0}\)= 1 | , где \(x_{0}\) = x-пересечение \(y_{0}\) = y-пересечение |
| Вертикальная линия | х = р | p — точка пересечения с х |
| Горизонтальная линия | г = д | q — точка пересечения с осью y |
Линейные уравнения могут быть решены для определенной переменной методом подстановки или исключения или графически.
Давайте посмотрим на линейные уравнения на следующем графике, как показано ниже:
Вывод формулы линейного уравнения
Давайте посмотрим, как формула линейного уравнения определяется на графике по прямой или наклонной линии. Наклон – это линия, равная отношению изменения координаты y к изменению координаты x.
Уравнение прямой линии задается следующим образом: y = mx + b
Где m – наклон линии, b – точка пересечения с осью y, x и y – координаты осей x и y. , соответственно.
Когда прямая параллельна оси x, то координата x будет равна нулю. Следовательно, y = b
Когда прямая линия параллельна оси Y, координата Y будет равна нулю. Таким образом,
mx + b = 0
x = -b/m
Таким образом, наклон показывает подъем линии на плоскости вместе с пройденным расстоянием по оси x.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.
С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Примеры использования формулы линейного уравнения
Пример 1. В копилке Джейка 11 монет (только четвертаки или десять центов) номиналом 1,85 сингапурских доллара. Сколько десятицентовиков и четвертаков в копилке?
Решение: Предположим, что:
Количество монет = x
Количество четвертей = у
Поскольку всего 11 монет, x + y = 11 ⇒ y = 11 – x → (1)
Общая стоимость денег в копилке составляет 1,85 доллара США.
Мы знаем, что 100 центов = 1 доллар, 1 квартер = 1 доллар и 10 десятицентовиков = 1 доллар. (2)
10x + 25(11 − x) = 185 (Подставив (1) в (2))
10x + 275 − 25x = 185
−15x + 275 = 185
−15x = −90 9000
x = 6
Подставим это в (1): y = 11 — 6 = 5
Следовательно, количество монет = 6; Количество четвертей = 5
Пример 2. Джон получает уравнение прямой линии 3x + 4y = 15.
Помогите ему найти наклон.
Решение: Дано 3x + 4y = 15
Это уравнение имеет общий вид: ax+by = c
в уравнении 3x + 4y = 15, a = 3 и b = 4
Используя формула линейного уравнения, мы получаем наклон как m = -a/b
m = -3/4
Таким образом, наклон этой прямой равен m = -3/4
Пример 3: Найдите значение y из уравнений 2x + 4y = 20, когда x = 24
Решение:
Подставьте значение x в уравнение и найдите y.
Дано, х = 24 и 2х + 4у = 20 Формулы уравнений
Что такое формула линейного уравнения?
Формула линейного уравнения получается на основе того, в какой форме находится уравнение прямой.
Что такое формула для расчета линейного уравнения?
Формула для расчета линейного уравнения на склоне:
y = mx + b
где,
- x и y — две переменные
- b — точка пересечения y
- м — уклон линии
Какие формы используются в формуле линейного уравнения?
Различные формы, используемые в формуле линейного уравнения, где линия может быть построена на графике как по оси X, так и по оси Y:
- Общая форма
- Форма пересечения уклонов
- Балловая форма
- Форма перехвата
- Двухточечная форма
Что такое стандартная форма формулы линейного уравнения?
Стандартная форма формулы линейного уравнения состоит из переменной и константы.
Формула: ax + b = 0, где a ≠ 0, а x — переменная.
Одновременные линейные уравнения | Решатель | Решенные примеры
Одновременные линейные уравнения с двумя переменными включают две неизвестные величины для представления реальных задач.
Это помогает установить взаимосвязь между количествами, ценами, скоростью, временем, расстоянием и т. д., что приводит к лучшему пониманию проблем.
Мы все используем одновременные линейные уравнения в нашей повседневной жизни, даже не подозревая об этом.
В этом мини-уроке мы подробно узнаем о решениях линейных уравнений, состоятельных и несовместных уравнениях, однородных линейных уравнениях, решателе одновременных уравнений, примере одновременного уравнения и т. д. в этом мини-уроке.
1. | Что вы подразумеваете под одновременными линейными уравнениями? |
| 2. | Советы и рекомендации |
| 3. | Решенные примеры одновременных линейных уравнений |
| 4. | Сложные вопросы по одновременному линейному уравнению |
| 5. | Интерактивные вопросы по линейному уравнению |
Два линейных уравнения с двумя или тремя переменными, которые решают вместе для нахождения общего решения, называются одновременными линейными уравнениями.
Например, мы можем визуализировать решение линейной системы уравнений, нарисовав 2 линейных графика и найдя их точку пересечения.
Красная точка представляет решения для уравнения 1 и уравнения 2. Пересечение – это уникальная точка (2,1) – это искомое решение, которое будет удовлетворять обоим уравнениям
Линейное уравнение Калькулятор
Этот решатель уравнений одновременно найдет нетривиальное решение при вводе коэффициентов x и y и константы.
Как решать одновременные линейные уравнения?
Следующие методы могут быть использованы для нахождения решения линейной системы уравнений, давайте посмотрим на пример совместного уравнения.
1. Метод подстановкиРассмотрим следующую пару линейных уравнений:
\[\begin{array}{l}x + 2y = 6\;\;\;\; & …(1)\\ х — у = 3\;\;\;\; & …(2)\end{array}\]Преобразуем первое уравнение, чтобы выразить \(x\) через \(y\), следующим образом:\[\begin{array}{l}x + 2y = 6\\ \Стрелка вправо \;\;\;x = 6 — 2y\end{массив}\]
Это выражение для \(x\) теперь можно подставить во второе уравнение, так что у нас останется уравнение только с \(y\):
\[\begin{align}& x — y = 3\\ &\Стрелка вправо \;\;\;6 — 2y -y = 3\\ &\Стрелка вправо \;\;\;-3y = 3 — 6\\ &\Стрелка вправо \;\;\;y = \ frac{-3}{-3}\\ &\Rightarrow \;\;\;y = 1\end{align}\]
Получив значение \(y\), мы можем снова подключить его к любое из двух уравнений, чтобы узнать \(x\).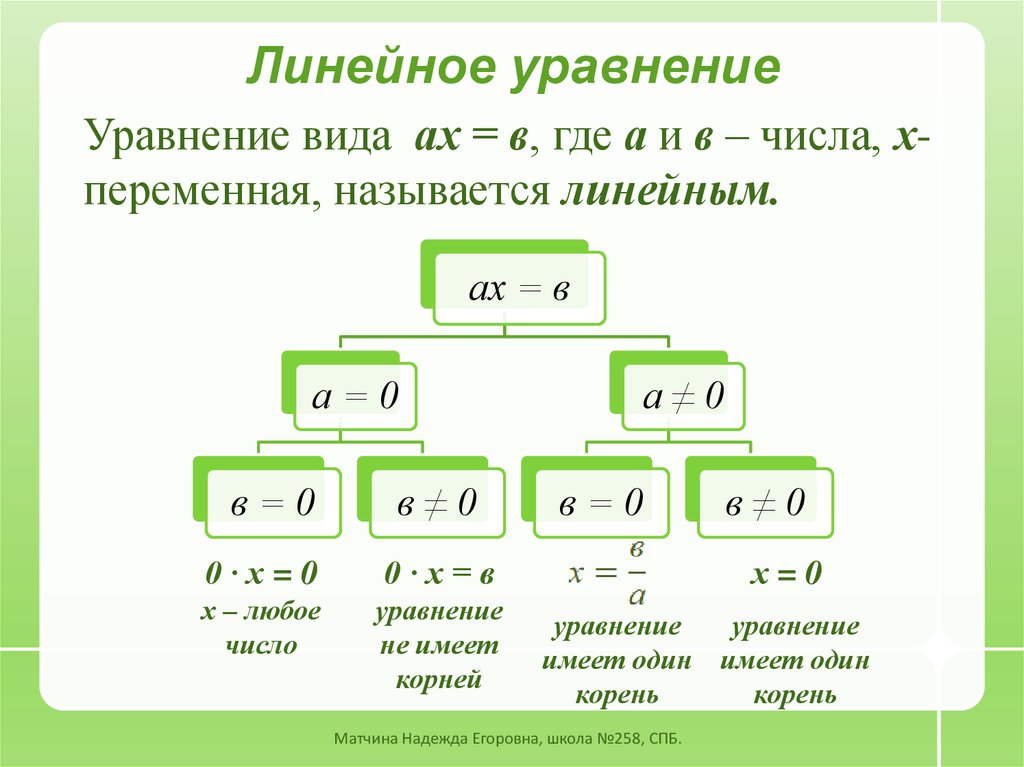
Подставим это в первое уравнение:
\[\begin{array}{l}x + 2y = 6\\ \Стрелка вправо \;\;\;x + 2 \times 1 = 6\\ \Стрелка вправо \;\;\;x = 6 — 2 = 4\\ \Rightarrow \;\;\;x = 4\end{array}\]
Окончательное нетривиальное решение:
\[x = 4,\;y = 1\]
It Должно быть ясно, почему этот процесс называется заменой. Мы выражаем одну переменную через другую, используя одно из двух уравнений, и подставляем это выражение во второе уравнение.
2. Метод исключенияРассмотрим следующую пару линейных уравнений:
\[\begin{array}{l} 2x + 3y — 7 = 0\\ 3x + 2y — 3 = 0 \end{array}\]
Коэффициенты x в двух уравнениях равны 2 и 3 соответственно . Умножим первое уравнение на 3, а второе уравнение на 2, чтобы коэффициенты при x в двух уравнениях стали равными:
\[\begin{array}{l}\left\{ \begin{array}{ l}3 \times \left( {2x + 3y — 7 = 0} \right)\\2 \times \left( {3x + 2y — 3 = 0} \right)\end{array} \right.\\ \Стрелка вправо \;\;\;6x + 9y — 21 = 0\\\qquad6x + 4y — 6 = 0\end{массив}\]
Теперь вычтем два уравнения, а это значит, что мы вычтем левые части двух уравнений и правые части двух уравнений, и равенство все равно сохранится (это должно быть очевидно: если я = II и III = IV, то I – III будет равно II – IV):
\[\begin{array}{l}\left\{ \begin{array}{l}\,\,\, \,6x + 9y — 21 = 0\\\,\,\,\,6x + 4y — 6 = 0\\\подчеркнуть { — \,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,} \\\,\,\,\,\,\,0 + 5y\,\,\, — 15 = 0\end{массив} \right.
\\ \Стрелка вправо \;\;\;5y = 15\\ \Стрелка вправо \;\;\;y = 3\end{массив}\]
Обратите внимание, что x исключается, и у нас остается уравнение только с y. Получив значение y, мы действуем, как и раньше, — подставляем его в любое из двух уравнений. Подставим это в первое уравнение:
\[\begin{array}{l}2x + 3y — 7 = 0\\ \Стрелка вправо \;\;\;2x + 3\left( 3 \right) — 7 = 0\\ \Стрелка вправо \;\;\;2x + 9 — 7 = 0\\ \Стрелка вправо \;\;\;2x = -2\\ \Стрелка вправо \;\;\;x = -1\end{ array}\]
Таким образом, решение:
\[x = -1,\;y = 3\]
3. Графический методВ качестве примера рассмотрим следующую пару линейных уравнений:
\[\begin{array}{l} x — y = 0\\ x + y — 4 = 0\end{array }\]
Проведем соответствующие линии на тех же осях:
Точка пересечения \(A\left( {2,\,\,2} \right)\), значит \( x = 2, \; \; y = 2\) является решением пары линейных уравнений (2). Фактически, это единственное решение пары , так как две непараллельные прямые не могут пересекаться более чем в одной точке.
Советы и рекомендации
Решенные примеры
| Пример 1 |
Суммарный вес Фабии и Валериана составляет 60 фунтов, а разница равна 2. Найдите веса Фабии и Валериана.
Решение
Пусть вес Фабии и Валериана будет \(x\) фунтов и \(y\) фунтов соответственно.
Таким образом, одновременные уравнения имеют вид \[\begin{array}{l}x + y = 60\;\;\;\; & …(1)\\ х — у = 2\;\;\;\; & …(2)\end{array}\]
Преобразуем первое уравнение, чтобы выразить \(x\) через \(y\), следующим образом:\[\begin{array}{l} x + y = 60\\ \Rightarrow \;\;\;x = 60 — y\end{array}\]
Это выражение для \(x\) можно теперь подставить во второе уравнение, так что мы останется уравнение только в \(y\):
\[\begin{align}& x — y = 2\\ &\Rightarrow \;\;\;60 — y -y = 2\\ &\ Стрелка вправо \;\;\;-2y = 2 — 60\\ &\Стрелка вправо \;\;\;y = \frac{-58}{-2}\\ &\Стрелка вправо \;\;\;y = 29\end{align}\]
Получив значение \(y\), мы можем подставить его обратно в любое из двух уравнений, чтобы узнать \(x\).
Подставим его в первое уравнение:
\[\begin{array}{l}x + y = 60\\ \Стрелка вправо \;\;\;x + 29 = 60\\ \Стрелка вправо \;\;\; x = 60 — 29\\ \Rightarrow \;\;\;x = 31\end{array}\]
Окончательное решение:
\[x = 31,\;y = 29\]
| Таким образом, вес Фабии и Валериана составляет 31 фунт и 29 фунтов соответственно. |
| Пример 2 |
Можете ли вы помочь Алексу найти двузначное число, в котором цифра единиц в три раза больше цифры десятков, и если к числу добавить 36, цифры меняются местами.
Решение
Пусть в разряде единиц стоит цифра \(x\).
И цифра в разряде десятков будет \(y\)
Тогда \(x = 3y\) и число \(= 10y + x\)
Число, полученное путем перестановки цифр, равно \(10x + y\).
Если к номеру добавить \(36\), цифры меняются местами,
Следовательно, мы имеем \[10y + x + 36 = 10x + y\]
\[10у — у + х + 36 = 10х + у — у\]
\[9у + х — 10х + 36 = 10х — 10х\]
\[9у — 9х + 36 = 0 \]
\[9(х — у) = 36\]
\[х — у = \фрак{36}{9}\]
\[x — y += 4 …. (i) \]
Подставляя значение x = 3y в уравнение (i), получаем
\[3у — у = 4\]
\[ 2г = 4\]
\[ y = \frac{4}{2}\]
\[ y = 2\]
Подставив значение \(y = 2\) в уравнение (i), мы получим
\[ х — 2 = 4 \]
\[ х = 4 + 2 \] 90 153
\[ x = 6\]
| Следовательно, число, которое ищет Алекс, равно 62. |
Сложные вопросы
Решенный кроссворд по одновременным линейным уравнениям
Интерактивные вопросы Вот несколько упражнений для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Давайте суммируем
Мини-бессмысленный нацелился на увлекательную концепцию одновременных линейных уравнений. Математическое путешествие по одновременным уравнениям начинается с того, что уже известно учащемуся, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
О CuemathНаша команда экспертов по математике в Cuemath стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.
Часто задаваемые вопросы по Синхронные линейные уравнения
1. Какова степень линейного уравнения?
Степень линейного уравнения равна 1
2. Сколько существует типов линейных уравнений?
Три основные формы линейных уравнений: форма точки-наклона, стандартная форма и форма пересечения.
3. Что такое линейные уравнения?
Линейное уравнение – это уравнение, в котором переменная(ые) имеет(е) показатель степени 1
Пример: \[2 х = 23 \]
\[ x — y = 5\]
4. Как решить систему линейных уравнений?
У нас есть разные методы решения системы линейных уравнений:
Графический метод
Метод замены
Метод перекрестного умножения
Метод исключения
Метод детерминантов
5.
