| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.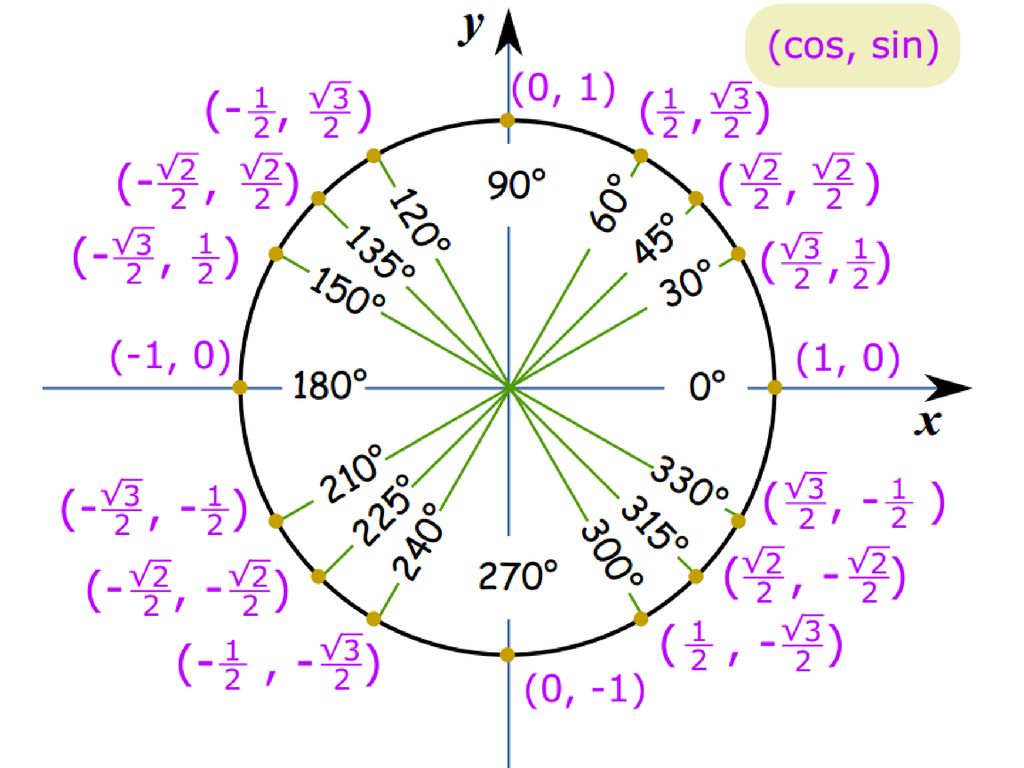 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Мультиметр iCarTool IC-M113 / Инструменты / iXBT Live
Это младший из новой линейки мультиметров iCarTool. Его
возможности не самые большие, но, тем не менее, прибор может найти свою нишу. В
обзоре проверим весь функционал и найдем все плюсы и минусы.
Его
возможности не самые большие, но, тем не менее, прибор может найти свою нишу. В
обзоре проверим весь функционал и найдем все плюсы и минусы.
Начнем с заявленных характеристик.
Мультиметр может измерять:
- Напряжение – постоянное и переменное
- Сопротивление, в том числе в режиме прозвонки
- Частоту
- Емкость
- Падение напряжения на полупроводнике
- Определять фазу сетевом кабеле и искать скрытую проводку.
Да, этот мультиметр не измеряет ток. Это существенный минус,
но у этого минуса есть и положительная сторона: при работе с этим прибором
невозможно устроить большой «бабах», случайно сунув щупы в розетку в режиме амперметра.
В мультиметре нет предохранителей– входное сопротивление прибора достаточно
велико, чтоб большой ток через него не прошел в любом случае. А раз так, то провода
щупов могут быть тонкими и эластичными – это не повлияет на точность измерений.
Что касается дополнительных возможностей, делающих работу комфортной – это подсветка экрана, графическая шкала, фонарик, функция фиксации показаний и главное – автоматический выбор типа измерения. Т.е. прибор сам должен угадывать, что вы хотите измерить – напряжение, сопротивление или просто прозваниваете цепь.
Обычная картонная коробка, на обратной стороне перечисление возможностей прибора.
Внутри сам прибор в пластиковом ложементе. Под ним инструкция, щупы и пара батареек ААА.
Да, питания от ААА. И это хорошее решение – такие батарейки чаще всего оказываются под рукой и они достаточно емкие, чтобы долго не беспокоиться о замене. А если прибор приобретался, чтобы возить в машине и использовать изредка, можно разориться на литиевые элементы ААА, такие не боятся морозов и сохранят заряд дольше, чем служит сама машина (срок хранения до 20 лет).
Документация на мультиметр слегка избыточна. Опустив
ритуальные оговорки и предупреждения и оставив только нужное, можно было
изложить все вчетверо короче.
Внешний осмотр прибора оставляет приятное впечатление. Корпус из качественного пластика, детали подогнаны превосходно. Ничего нигде не топорщится и не скрипит. В отличие от старших моделей, резинового бампера у IC-M113 нет, но прибор довольно легкий и я не представляю себе, с какой высоты его нужно уронить, чтобы расколоть корпус. На лицевой стороне большой экран, сверху окошко индикаторного светодиода. Внизу 4 кнопки управления, на нижнем торце два гнезда для щупов.
Пиктограммы напоминают возможности прибора. Верхний ряд на желтом фоне: напряжение постоянное и переменное, сопротивление, прозвонка. Выбор из этого набора может быть автоматическим (а может быть и ручным).
Строкой ниже на сером фоне пиктограммы с функциями, выбор из которых осуществляется кнопкой FUNC.
Ниже технические надписи:
Экран на 4000 отсветов. Еще указано, что мультиметр
рассчитан на напряжения до 600 вольт, сертифицирован для работ категории 3. Последнее
означает, что он годится для ремонта всего, что по схеме ниже квартирного электрощита
с входным автоматом и счетчиком. Пиктограмма квадрат в квадрате – знак того, что
у прибора двойная изоляция и/или усиленная защита. СЕ — знак соответствия
нормам Евросоюза
Пиктограмма квадрат в квадрате – знак того, что
у прибора двойная изоляция и/или усиленная защита. СЕ — знак соответствия
нормам Евросоюза
Восклицательный знак в треугольнике – рекомендация перед работой ознакомиться с инструкцией. Завершают композицию пиктограмм подписи над гнездами для щупов. Справа – красненький INPUT, слева – черненький COM.
На обратной стороне крышка батарейного отсека, наклейка соответствия стандартам таможенного союза, наклейка технического контроля, серийного номера и окошко для светодиода фонарика.
Крышка батарейного отсека так точно подогнана, что не разглядев никаких щелей по периметру я, пытаясь ее открыть, вместо одного винта этой крышки открутил еще пару винтов, скрепляющих корпус.
Крышку я в итоге кое-как вытряхнул. А корпус не распался только благодаря тому, что в батарейном отсеке остались еще два винта. Ну хорошо, раз уж такое дело, отвинчиваем и их.
Внутри одна плата. Основной чип – в «капельке».
Рядом – драйвер экрана. Для защиты входной цепи предусмотрен
термистор. Обращает на себя внимание реле с двумя парами контактов.
Для защиты входной цепи предусмотрен
термистор. Обращает на себя внимание реле с двумя парами контактов.
Вокруг него не смыт флюс, есть он и вокруг проводов, но по остальной поверхности платы флюс смыт – видимо реле и провода припаивались вручную. Кое-где есть огрехи пайки.
Вынимаем плату из корпуса:
Экран подключен через токопроводящую резину. Рядом с резинкой дополнительный винтик, чтоб контакт был лучше и не пропадал при прогибе платы.
Кнопки как в пультах дистанционного управления, пятачки из токопроводящей резины замыкают лабиринты дорожек на плате.
Больше ничего интересного нет, собираем обратно.
Пожалуй, это основная функция прибора.
Для проверки измерения постоянного напряжения я взял
источник опорного напряжения на микросхеме AD584LH. Схема
выдает тестовые напряжения 2.5, 5, 7.5 и 10 вольт. Максимальная ошибка от 2.5
до 5 мВ, это от 0,1% до 0,05%. Для сравнения, заявленная точность
мультиметра 0,5% плюс три единицы младшего разряда.
Смотрим 2,5 В:
Показания: 2,507 В.
Допустимая ошибка прибора: 2,5*0,005 + 0,003 = 0,0155 В.
Как видим, прибор укладывается с двукратным запасом, даже без учета погрешности ИОНа.
Диапазон 5 В:
Показания: 5,01 В
И считать не обязательно: укладываемся даже в пределы предыдущего диапазона.
Теперь 7,5 В:
Показания: 7,50 В
Точнее не бывает. Немного обидно, конечно, что не используется весь диапазон шкалы. Лидирующий ноль можно было бы опустить и добавить еще один разряд после запятой. Видимо таков предел не экрана, а АЦП прибора. На практике сотых долей вольта должно хватить для любых работ, не связанных с разработкой высокоточной аппаратуры.
10 вольт:
Показания: 10,01.
Результат с запасом остается в границах допустимых значений.
Производитель заявляет, что мультиметр измеряет среднеквадратичное значение переменного напряжения – поддерживает измерения «True RMS».
Дело в том, что если мы имеем дело с переменным напряжением
(да и током), то возникает вопрос, как его измерять. Можно по максимальному,
пиковому значению. Но оно иногда достигается лишь на бесконечно короткий миг и
по нему некорректно судить о том, что происходит все остальное время. Чаще
всего под переменным напряжением понимают среднеквадратичное его значение.
«Среднее» — понятно из школьного курса: поделили на кусочки, каждый измерили,
все сложили, результат поделили на количество кусочков и вот оно – среднее
арифметическое. Среднеквадратичное – это почти то же самое. Но теперь мы
вычисляем среднее арифметическое среди квадратов значений в каждом фрагменте, а
потом из этого среднего арифметического квадратов извлекаем корень. Зачем такая
затейливая математика? Именно так мы получаем постоянный уровень (напряжения,
тока), равный по энергетике измеряемому переменному.
Можно по максимальному,
пиковому значению. Но оно иногда достигается лишь на бесконечно короткий миг и
по нему некорректно судить о том, что происходит все остальное время. Чаще
всего под переменным напряжением понимают среднеквадратичное его значение.
«Среднее» — понятно из школьного курса: поделили на кусочки, каждый измерили,
все сложили, результат поделили на количество кусочков и вот оно – среднее
арифметическое. Среднеквадратичное – это почти то же самое. Но теперь мы
вычисляем среднее арифметическое среди квадратов значений в каждом фрагменте, а
потом из этого среднего арифметического квадратов извлекаем корень. Зачем такая
затейливая математика? Именно так мы получаем постоянный уровень (напряжения,
тока), равный по энергетике измеряемому переменному.
Для проверки, как с такими измерениями обстоят дела у мультиметра IC-M113, я сделал небольшой генератор сигналов. Заодно проверим карманный осциллограф, который тоже способен измерить среднеквадратичное значение напряжения.
В качестве генератора я использовал плату с микроконтроллером
esp32. Она способна не только оцифровывать аналоговый сигнал, но и генерировать
его, двумя встроенными в чип восьмибитными цифро-аналоговыми преобразователями.
Для тестирования я запрограммировал четыре сигнала: меандр, пилу, обратную
пилу, треугольник и, конечно же, классическую синусоиду. Диапазон, напряжений, который
может выдать контроллер без помощи операционного усилителя, ограничен 3,3
вольтами. Отрицательные напряжения недоступны. Таким образом, на выходе
контроллера у нас получается не столько переменное, сколько пульсирующее
напряжение. Установка в цепь разделительного конденсатора решает эту проблему.
Но амплитуда нашего, теперь уже по-настоящему переменного напряжения,
уменьшится в два раза, т.е. станет порядка 1,6 вольт. Для начала попробуем подать
на приборы максимальное значение сигнала с генератора:
Она способна не только оцифровывать аналоговый сигнал, но и генерировать
его, двумя встроенными в чип восьмибитными цифро-аналоговыми преобразователями.
Для тестирования я запрограммировал четыре сигнала: меандр, пилу, обратную
пилу, треугольник и, конечно же, классическую синусоиду. Диапазон, напряжений, который
может выдать контроллер без помощи операционного усилителя, ограничен 3,3
вольтами. Отрицательные напряжения недоступны. Таким образом, на выходе
контроллера у нас получается не столько переменное, сколько пульсирующее
напряжение. Установка в цепь разделительного конденсатора решает эту проблему.
Но амплитуда нашего, теперь уже по-настоящему переменного напряжения,
уменьшится в два раза, т.е. станет порядка 1,6 вольт. Для начала попробуем подать
на приборы максимальное значение сигнала с генератора:
3,2 – считает осциллограф, 3,167 – мультиметр. Приемлемое
расхождение. Можно начинать подавать тестовые сигналы. Частоту выберем
максимально удобную для генерации и измерения: 100 Гц.
Синус:
Осциллограф показывает 1,08 В, мультиметр – 1,088 В, а сколько должно быть на самом деле?
Не буду утомлять вас математикой, поверьте на слово: действующее значение сигнала синусоидальной формы в корень из 2 раз меньше пикового значения, т.е. в нашем случае
(3,167/2)/sqrt(2) = 1,12 В.
Ну что же, мультиметр оказался даже ближе к истинному значению!
Ошибка:
((1,12 — 1,088)/1,12)*100% = 2,9%
Техническая документация на мультиметр устанавливает допустимую ошибку в диапазоне до 4 вольт как +/- 0,8% от измеряемой величины плюс три единицы младшего разряда. В нашем случае это будет:
(1,12 * 0,008)+0,003 = 0,012 В.
А у нас получилось
1,12 — 1,088 = 0,032 В.
Не уложились.
Следующий сигнал – пила. Прямая и обратная должны давать одинаковые значения напряжения, разумеется.
Осциллограф – 0,88 В., мультиметр – 0,882 В. Очень близко. А как в теории?
Действующее значение меньше пикового в корень из трех раз. Считаем:
Считаем:
(3,167/2)/sqrt(3) = 0,914 В.
Ошибка:
((0,914 — 0,882)/0,914)*100% = 3,5%
Допустимая ошибка:
0,914 * 0,008 + 0,003 = 0,01 В.
А у нас
0,914 — 0,882 = 0,032 В.
Втрое больше. Снова не уложились.
Сигнал треугольной формы:
Осциллограф – 0,88 В., мультиметр – 0,889 В.
Теоретически значение должно быть точно такое же, как в случае пилообразного сигнала: 0,914 В.
Ошибка мультиметра:
0,914 — 0,889 = 0,025 В.
Уже лучше.
Наконец — самое сложное. Меандр. При всей видимой простоте, обычный меандр – совокупность бесконечного количества гармоник разной частоты. И качественно его передать и измерить – задача не такая уж тривиальная.
Двуполярный меандр:
Осциллограф — 1,52 В., мультиметр – 1,533 В.
Его действующее значение равно амплитудному:
3,167/2 = 1,584 В.
Ошибка:
1,584 — 1,533 = 0,051 В.
Допустимая ошибка:
1,584*0,008 + 0,003 = 0,016 В.
Снова немного вышли за рамки.
Попробуем однополярный меандр.
Т.е. избавимся от блокировочного конденсатора, чем поднимем график над нулевым значением напряжения. Теперь у нас импульсы с напряжением 3,167 В и частотой 100 Гц. По длительности импульсы равны паузам, иначе говоря – коэффициент заполнения равен 0,5. Это совершенно контринтуитивно, но действующее значение такого сигнала не будет половиной от амплитуды. Оно будет меньше амплитуды в корень из двух раза, как в случае синусоиды!
3.167/sqrt(2) = 2,239 В.
Осциллограф относительно близок – 2,28 В. А вот мультиметр схалтурил: 1,533 В. Очевидно, внутренние алгоритмы прибора посчитали сигнал биполярным меандром, и провели все последующие вычисления исходя из этого.
Но может быть, надо принудительно переключить его в режим измерения постоянного напряжения? Пробуем:
Нет, и 1,624 В все еще не может считаться релевантным измерением.
Какой промежуточный итог можно подвести? Все плохо? Ни разу же не вписались в установленные производителем допустимые ошибки?
И да, и нет.
Главное, что мультиметр действительно отличает разные формы напряжения. Отличает пилу от синусоиды, треугольник от меандра. Так что да, он действительно измеряет среднеквадратичное значение. И будучи засунутым в розетку 220 не покажет амплитудные 310 вольт.
Что же касается точности до третьего знака после запятой – я не могу себе представить ситуацию, когда она могла бы пригодиться в реальной жизни. Аналоговые датчики, драйвера электродвигателей – для разбирательства с ними часто бывает нужно измерение напряжения. Высокая точность нужна, к примеру, для диагностики ДМРВ, при снятии напряжения с низкоомного шунта. Но это все постоянное напряжение. При переменном или пульсирующем токе, бывает, нужно измерить коэффициент заполнения, это довольно распространенный и весьма помехозащищенный способ связи датчика с приемником. Измерение частоты бывает нужно.
А если понадобилось измерение с такой точностью именно
действующего значения переменного напряжения произвольной формы – тогда вашим
настольным прибором должен быть осциллограф, и никак иначе.
Да, и не будем обижаться на маленький мультиметр за то, что он «не раскусил» однополярный меандр. Все-таки это скорее импульсный сигнал, а не переменный.
Перейдем к следующему тесту: какой диапазон частот доступен для измерения переменного напряжения? В этот раз я взял готовый генератор сигналов. Он может быть не такой точный, как на базе esp32, но в нем быстрее настраивать частоту.
Убедившись, что обе пилы и треугольник мультиметр воспринимает одинаково (что совершенно справедливо), а однополярный меандр тестировать смысла нет, я решил ограничиться тремя сигналами: синусом, треугольником и меандром. Амплитуду установил в 2,5 В для синуса и треугольника и 5 В для меандра. Заявленный производителем диапазон частот для измерения переменного напряжения 40 Гц ‑ 1 КГц.
Тем не менее, прибор начинает уверенно показывать значение переменного напряжения, не перепрыгивая то и дело в режим постоянного, уже с частоты в 17 Гц, а меандр – даже с 13 Гц.
Но измерения я проводил с 20 Гц. Вот что у меня получилось:
Вот что у меня получилось:
Как видно из графиков – даже до 2 КГц измерения более-менее релевантны. И только при измерении меандра прибор начинает заметно занижать вольтаж уже с 1000 Гц.
Ну а после 8-10 КГц прибор совсем не может разобраться, что же мы измеряем и начинает скакать по шкалам в поисках правды.
По этому тесту можно подытожить: измерения остаются осмысленным занятием до 1000‑2000 Гц, в зависимости от формы сигнала.
Большинство современных резисторов имеют допуск в 1%. Заявленная погрешность измерения тоже 1% (плюс 5 единиц младшего разряда). Подготавливаем набор резисторов, смотрим на результат:
1 КОм. Уложились в 4 единицы младшего разряда, даже без процента. Очень хорошо!
10 КОм. Две единицы.
Для проверки низких сопротивлений я просто замкнул щупы мультиметра:
Даже сопротивление самих щупов скомпенсировано!
Итог: сопротивление измеряет вполне адекватно.
Здесь все просто: чем быстрее прибор реагирует на замкнутые
щупы – тем лучше. В идеале, чтоб вообще моментально. Поэтому я снял видео:
В идеале, чтоб вообще моментально. Поэтому я снял видео:
Надо отметить, что прибор до начала теста был переключен из автоматического режима в режим прозвонки. Так он мог ориентироваться намного быстрее, что я от него хочу.
Заявленный диапазон – до 4МГц, точность – 1% плюс три младшие единицы.
Берем в качестве генератора прибор М328 и смотрим:
10 Гц:
Отклонение 0,2%.
1 КГц:
Отклонение 0,4%
Частота 10 КГц:
Отклонение 0,4%.
Далее сложнее. Заявлено определение частоты до 4 МГц. Возможно, у меня на такой частоте получился слабый сигнал, но 4 МГц прибор не взял. Максимальная частота порядка 3,3 МГц, но и она определяется не сразу. Я записал видео о том, как это происходит:
У меня нет идеальных конденсаторов для поверки измерителей
емкости. (А часто приходится
измерять до пикофарада?) Я взял несколько типовых конденсаторов и посмотрел,
насколько будут повторяться результаты нескольких измерений и насколько быстро
будут измеряться большие емкости. Малые конденсаторы измеряются адекватно,
электролитики – тоже, хотя чем больше емкость, тем дольше времени требуется для
измерения.
(А часто приходится
измерять до пикофарада?) Я взял несколько типовых конденсаторов и посмотрел,
насколько будут повторяться результаты нескольких измерений и насколько быстро
будут измеряться большие емкости. Малые конденсаторы измеряются адекватно,
электролитики – тоже, хотя чем больше емкость, тем дольше времени требуется для
измерения.
Время измерения электролитиков на 2-3 мФ — 9-20 секунд. Предел прибора – 4 мФ.
Иногда бывает нужно измерить это падение для поиска наилучшего диода. Иногда – чтобы проверить светодиод.
Однако, при проверке у меня ни один светодиод не загорелся, мультиметр неизменно показывал «0L». В то время, как другой мультиметр все точно измерил.
В чем может быть дело?
Оказалось, что дело в напряжении проверки. Его не хватает,
чтобы проверять светодиоды. Может быть, его хватит, чтоб запустить инфракрасный
светодиод, но и это не факт.
Может быть, его хватит, чтоб запустить инфракрасный
светодиод, но и это не факт.
У токоизмерительных клещей IC-M206D напряжение тестирования диодов 3,3 вольта, а у мультиметра IC-M113 всего 1,84 вольта.
Но обычные диоды и диоды Шоттки мультиметр измеряет хорошо:
Ищем фазу:
Нашли!
Ищем провод:
И его нашли!
И фонарик работает.
Подсветка экрана – отличная вещь: с ней показания читаются намного лучше. У нее есть свое автоотключение, но его можно отменить, правда только вместе с отменой авоотключения самого прибора. В инструкции сказано как это сделать.
Плюсы:
- Качественный корпус
- ААА как источник питания
- Безопасность для малоопытного пользователя
- Компактность
- Подсветка экрана
- Автоматический выбор типа измерений можно отключить
- Качественные, «взрослые» щупы
Минусы:
- Отсутствует измерение тока
- Подтормаживает автоматический режим работы
- В режиме проверки диодов невозможно проверить светодиоды
- Неидеальная точность измерения переменного напряжения
- Отсутствие чехла в комплекте
Итоги
В общем и целом, прибор понравился. Да, он не умеет мерить
ток. Он не подойдет в качестве основного прибора для радиолюбителя или
автоэлектрика. Но у профессионалов так не бывает, чтоб один прибор был на все
случаи жизни. Этот мультиметр поместится в карман и поможет быстро найти
пропавшую фазу в щите. Проверит диодный мост в генераторе. Найдет проводку под
штукатуркой. Подсветит блок предохранителей под капотом, найдет горелый. Проверит
подозрительную батарейку. Да часто ли вообще нужен амперметр для домашнего
мастера? Большую часть типовых работ домашнего мастера выполнит и этот малыш. И
лишь иногда придется снимать с полки его массивного полнофункционального
коллегу.
Да, он не умеет мерить
ток. Он не подойдет в качестве основного прибора для радиолюбителя или
автоэлектрика. Но у профессионалов так не бывает, чтоб один прибор был на все
случаи жизни. Этот мультиметр поместится в карман и поможет быстро найти
пропавшую фазу в щите. Проверит диодный мост в генераторе. Найдет проводку под
штукатуркой. Подсветит блок предохранителей под капотом, найдет горелый. Проверит
подозрительную батарейку. Да часто ли вообще нужен амперметр для домашнего
мастера? Большую часть типовых работ домашнего мастера выполнит и этот малыш. И
лишь иногда придется снимать с полки его массивного полнофункционального
коллегу.
Функция синус-квадрата — исчисление
Эта статья о конкретной функции из подмножества действительных чисел в действительные числа. В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 личности
- 4 График
- 5 Дифференциация
- 5.
 1 Первая производная
1 Первая производная - 5.2 Вторая производная
- 5.3 График функции с производной
- 5.
- 6 Точки и интервалы интереса
- 6.1 Критические точки
- 6.2 Интервалы увеличения и уменьшения
- 6.3 Локальные экстремальные значения
- 6.4 Интервалы подбарабанья вверх и вниз
- 6.5 Точки перегиба
- 7 Интеграция
- 7.1 Первая первообразная
- 7.1.1 Использование формулы косинуса двойного угла
- 7.1.2 Использование интегрирования по частям
- 7.2 График функции с первообразной
- 7.3 Определенные интегралы
- 7.4 Модифицированные версии
- 7.5 Высшие производные
- 7.1 Первая первообразная
- 8 Серия Power и серия Taylor
- 8.1 Расчет ряда мощностей
- 8.2 Полиномы Тейлора как аппроксимации
- 9 Предельные вычисления
- 9.1 Нулевой порядок
- 9.2 Пределы высшего порядка
Определение
Эта функция, обозначенная , определяется как композиция функции квадрата и функции синуса.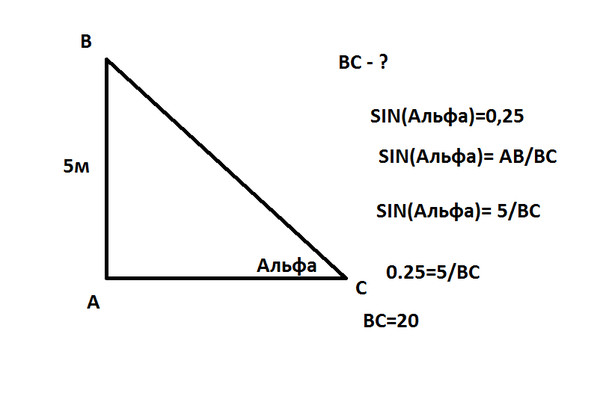 В явном виде это карта:
В явном виде это карта:
Для краткости пишем как .
Ключевые данные
| Элемент | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. е. все |
| диапазон | , то есть абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | , т. е. |
| локальное максимальное значение и точки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых кратных . |
| локальное минимальное значение и точки достижения | Все локальные минимальные значения равны 0 и достигаются при целых кратных . |
| точки перегиба (обе координаты) | нечетных кратных , со значением 1/2 в каждой точке. |
| производная | , то есть функция синуса двойного угла. |
| вторая производная | |
| производная | раз выражение, которое равно или , в зависимости от остатка по модулю |
| первообразная | |
| среднее значение за период | 1/2 |
| выражение как синусоидальная функция плюс постоянная функция | |
| важные симметрии | четная функция (следует из комбинации четной функции с нечетной функцией четной, функция квадрата четная, а функция синуса нечетная) в более общем смысле, зеркальная симметрия относительно любой вертикальной линии формы , целое число.  Также полуоборотная симметрия относительно всех точек формы . |
| Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз | Для каждого целого числа интервал от до подразделяется на четыре части: : возрастание и вогнутость вверх : возрастание и вогнутость вниз : уменьшение и вогнутость вниз, : уменьшение и вогнутость вверх |
| серия Power и серия Taylor | Степенной ряд около 0 (который, следовательно, также является рядом Тейлора) равен Это глобально сходящийся степенной ряд. |
Личности
У нас есть следующие важные личности с участием:
- , связывая это с функцией квадрата косинуса.
- или эквивалентно .
График
Вот график на интервале , выполненный в масштабе:
Вот увеличенный вид графика между и . Пунктирная горизонтальная линия указывает среднее значение:
Точки с красными точками обозначают точки перегиба, а точки с черными точками обозначают локальные экстремальные значения.
Вот изображение, показывающее функцию (синяя) и функция квадрата косинуса (фиолетовая) с пунктирной линией. На картинке показано, что:
Дифференцирование
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного косинуса угла
У нас есть:
Мы можем сделать это двумя способами.
Используя цепное правило для дифференцирования, мы имеем:
По формуле двойного синуса угла это то же самое, что и .
В качестве альтернативы, используя формулу двойного косинуса угла, мы перепишем:
Дифференцируя, получаем:
Вторая производная
Снова продифференцировав производную, получим:
График функции с производной
Заполните позже
Точки и интервалы интереса
Критические точки
Рассмотрим .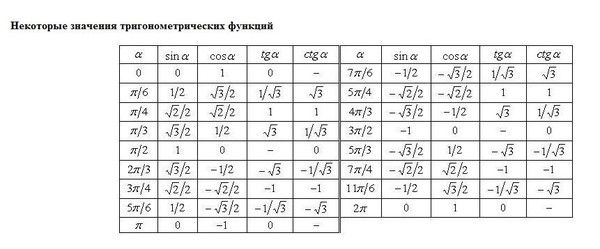 Как было подсчитано ранее, имеем:
Как было подсчитано ранее, имеем:
Это равно нулю именно в точках, где , поэтому . Другими словами, критические точки возникают при целых кратных .
Интервалы возрастания и убывания
Функция положительна при , при и отрицательна при , при . Делим на 2, получаем:
- возрастает на интервалах вида , .
- убывает на интервалах вида , .
Локальные экстремальные значения
Из информации об интервалах возрастания и убывания делаем вывод, что:
- достигает своих локальных максимальных значений в точках вида , и все значения равны 1.
- достигает своих локальных минимальных значений в точках вида , , и все значения равны 0.
Интервалы вогнутости вверх и вниз
Вторая производная есть функция . Это положительно для и отрицательно для , где . Таким образом, мы получаем:
- вогнут на промежутках вида , с .
- вогнуто вниз на интервалах вида , с .
Точки перегиба
Из определения интервалов, где вогнутость вверх и вогнутость вниз, мы обнаруживаем, что точками перегиба являются точки с -координатой, нечетно кратной . Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .
- В точках с функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
- В точках с функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интегрирование
Первая первообразная
ЧТО ИСПОЛЬЗУЕМ : формула косинуса двойного угла, рекурсивная версия интегрирования по частям, интегрирование линейного преобразования функции
Используя формулу косинуса двойного угла интеграция:
Для интегрирования используем метод интегрирования линейного преобразования функции для получения . Подключив его, мы получим:
Использование интегрирования по частям
Переписываем и используем интегрирование по частям в его рекурсивной версии:
Теперь перепишем и получим:
Установив выбор первообразной таким образом, чтобы вышеприведенное выполнялось без каких-либо свободно плавающих констант, мы получаем:
Переставляя, получаем:
Это дает:
Итак, общая первообразная:
Используя формулу синуса двойного угла, мы можем убедиться, что это соответствует предыдущему ответу.
Для заданной непрерывной функции на связном множестве первообразные, полученные разными методами, должны отличаться на константу . В некоторых случаях первообразные могут быть точно равными, но это не обязательно вообще .
См. Нулевая производная подразумевает локальную постоянную
График функции с первообразной
На рисунке ниже мы изображаем (синий) и функцию (фиолетовый). Это уникальная первообразная, которая принимает значение 0 в 0. Остальные первообразные можно получить, сдвинув фиолетовый график по вертикали:
Черные точки соответствуют локальным экстремумам для , а красные точки соответствуют точкам перегиба первообразной. Как и следовало ожидать, каждая черная точка находится на той же вертикальной линии, что и красная точка, поскольку точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. В дальнейшем:
- Первообразная везде возрастает, потому что везде неотрицательна и равна нулю только в изолированных точках.

- Первообразная вогнута на тех интервалах, где является возрастающей, т. е. на интервалах вида as изменяется по целым числам.
- Первообразная вогнута вниз на тех интервалах, где убывающая, т. е. на интервалах вида as меняется по целым числам.
Определенные интегралы
Часть в первообразной означает, что линейная часть первообразной имеет наклон , а это связано с тем, что имеет среднее значение на любом интервале длины, равной периоду. На самом деле ясно, что функция является синусоидальной функцией относительно .
Итак, имеем:
где целое число.
Среднее значение для интервала длины, равного кратному периоду, равно . Таким образом, для очень больших интервалов среднее значение очень близко к 1/2, даже если оно не обязательно должно быть ровно 1/2. Конкретно:
Преобразованные версии
На основе интегрирования мы можем также интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
Таким образом, мы видим, что среднее значение этой функции также на любом интервале длины, кратной периоду. Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:
Высшие первообразные
Можно проводить антидифференцировку более одного раза. Первообразная представляет собой сумму многочлена степени и тригонометрической функции с периодом .
Степенной ряд и ряд Тейлора
Расчет степенного ряда
Мы можем использовать идентификатор:
вместе со степенным рядом функции косинуса, чтобы найти степенной ряд для .
Степенной ряд функции косинуса везде сходится к функции и равен:
Серия мощности для:
Серия мощности для:
Разделив на 2, получим степенной ряд для:
Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
Полиномы Тейлора как аппроксимации
Обратите внимание, что, поскольку это четная функция, все ее полиномы Тейлора также являются четными полиномами. На рисунке ниже мы рассматриваем графики и его второй, четвертой и шестой тейлоровских аппроксимаций.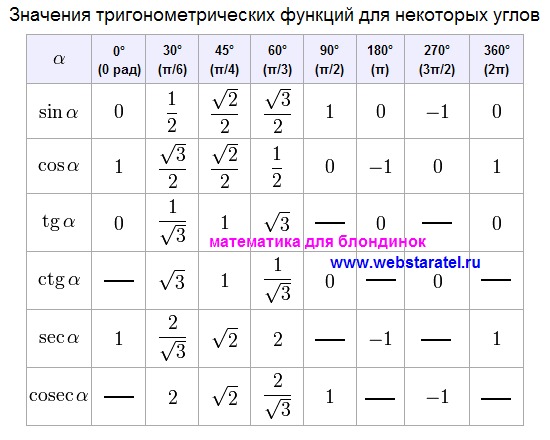
- Второй полином Тейлора , равный третьему полиному Тейлора , равен .
- Четвертый полином Тейлора , который равен пятому полиному Тейлора , равен .
- Шестой полином Тейлора , который равен седьмому полиному Тейлора , равен .
Предельные вычисления
Порядок нуля
Из степенного ряда получаем следующий предел:
Таким образом, порядок нуля в нуле равен 2, а остаток равен 1.
Этот лимит можно вычислить разными способами:
| Наименование метода расчета предела | Подробнее |
|---|---|
| Простая манипуляция с использованием | |
| Использование правила Лопиталя | |
| Использование серии Power | Имеем , значит получаем . Принимая предел как дает 1. |
Пределы высшего порядка
У нас есть предел:
Этот лимит можно вычислить разными способами:
| Наименование метода расчета предела | Подробнее |
|---|---|
| Использование и | У нас есть . Первый предел равен, а второй предел равен 2 из заданных данных. Получаем таким образом. |
| Использование правила Лопиталя | . |
| Использование серии Power | У нас есть , значит , значит предел равен 1/3. |
Функция синус-квадрат — Исчисление
Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 личности
- 4 График
- 5 Дифференциация
- 5.1 Первая производная
- 5.2 Вторая производная
- 5.3 График функции с производной
- 6 Точки и интервалы интереса
- 6.
 1 Критические точки
1 Критические точки - 6.2 Интервалы увеличения и уменьшения
- 6.3 Локальные экстремальные значения
- 6.4 Интервалы подбарабанья вверх и вниз
- 6.5 Точки перегиба
- 6.
- 7 Интеграция
- 7.1 Первая первообразная
- 7.1.1 Использование формулы косинуса двойного угла
- 7.1.2 Использование интегрирования по частям
- 7.2 График функции с первообразной
- 7.3 Определенные интегралы
- 7.4 Модифицированные версии
- 7.5 Высшие первообразные
- 7.1 Первая первообразная
- 8 Серия Power и серия Taylor
- 8.1 Расчет ряда мощностей
- 8.2 Полиномы Тейлора как аппроксимации
- 9 Предельные вычисления
- 9.1 Нулевой порядок
- 9.2 Пределы высшего порядка
Определение
Эта функция, обозначенная , определяется как композиция функции квадрата и функции синуса. В явном виде это карта:
Для краткости пишем как .
Ключевые данные
| Элемент | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. е. все |
| диапазон | , то есть абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | , т. е. |
| локальное максимальное значение и точки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых кратных . |
| локальное минимальное значение и точки достижения | Все локальные минимальные значения равны 0 и достигаются при целых кратных . |
| точек перегиба (обе координаты) | нечетных кратных , со значением 1/2 в каждой точке. |
| производная | , то есть функция синуса двойного угла. |
| вторая производная | |
| производная | раз выражение, которое равно или , в зависимости от остатка по модулю |
| первообразная | |
| среднее значение за период | 1/2 |
| выражение как синусоидальная функция плюс постоянная функция | |
| важные симметрии | четная функция (следует из комбинации четной функции с нечетной функцией четной, функция квадрата четной, функция синуса нечетной) в более общем смысле, зеркальная симметрия относительно любой вертикальной линии формы , целое число.  Также полуоборотная симметрия относительно всех точек формы . |
| Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз | Для каждого целого числа интервал от до подразделяется на четыре части: : возрастание и вогнутость вверх : возрастание и вогнутость вниз : уменьшение и вогнутость вниз, : уменьшение и вогнутость вверх |
| Степенной ряд около 0 (который, следовательно, также является рядом Тейлора) равен Это глобально сходящийся степенной ряд. |
Личности
У нас есть следующие важные личности с участием:
- , связывая это с функцией квадрата косинуса.
- или эквивалентно .
График
Вот график на интервале , выполненный в масштабе:
Вот увеличенный вид графика между и . Пунктирная горизонтальная линия указывает среднее значение:
Точки с красными точками обозначают точки перегиба, а точки с черными точками обозначают локальные экстремальные значения.
Вот изображение, показывающее функцию (синяя) и функция квадрата косинуса (фиолетовая) с пунктирной линией. На картинке показано, что:
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного косинуса угла
У нас есть:
Мы можем сделать это двумя способами.
Используя цепное правило для дифференцирования, мы имеем:
По формуле двойного синуса угла это то же самое, что и .
В качестве альтернативы, используя формулу двойного косинуса угла, мы перепишем:
Дифференцируя, получаем:
Вторая производная
Снова продифференцировав производную, получим:
График функции с производной
Заполните позже
Точки и интервалы интереса
Критические точки
Рассмотрим . Как было подсчитано ранее, имеем:
Как было подсчитано ранее, имеем:
Это равно нулю именно в точках, где , поэтому . Другими словами, критические точки возникают при целых кратных .
Интервалы возрастания и убывания
Функция положительна при , при и отрицательна при , при . Делим на 2, получаем:
- возрастает на интервалах вида , .
- убывает на интервалах вида , .
Локальные экстремальные значения
Из информации об интервалах возрастания и убывания делаем вывод, что:
- достигает своих локальных максимальных значений в точках вида , и все значения равны 1.
- достигает своих локальных минимальных значений в точках вида , , и все значения равны 0.
Интервалы вогнутости вверх и вниз
Вторая производная есть функция . Это положительно для и отрицательно для , где . Таким образом, мы получаем:
- вогнут на промежутках вида , с .
- вогнуто вниз на интервалах вида , с .
Точки перегиба
Из определения интервалов, где вогнутость вверх и вогнутость вниз, мы обнаруживаем, что точками перегиба являются точки с -координатой, нечетно кратной .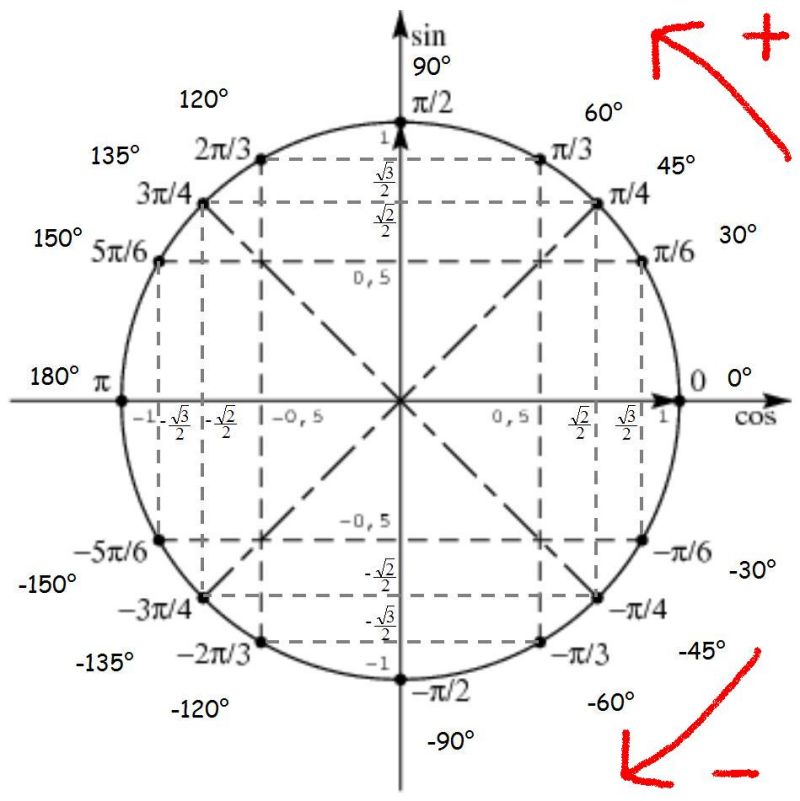 Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .
- В точках с функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
- В точках с функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интегрирование
Первая первообразная
ЧТО ИСПОЛЬЗУЕМ : формула косинуса двойного угла, рекурсивная версия интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
Теперь мы можем выполнить интеграцию:
Для интегрирования используем метод интегрирования линейного преобразования функции для получения . Подключив его, мы получим:
Использование интегрирования по частям
Переписываем и используем интегрирование по частям в его рекурсивном варианте:
Теперь перепишем и получим:
Установив выбор первообразной таким образом, чтобы вышеприведенное выполнялось без каких-либо свободно плавающих констант, мы получаем:
Переставляя, получаем:
Это дает:
Итак, общая первообразная:
Используя формулу синуса двойного угла, мы можем убедиться, что это соответствует предыдущему ответу.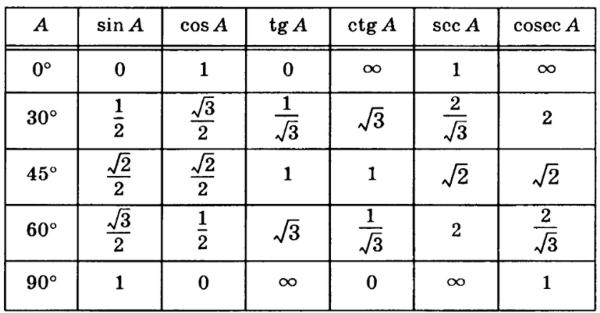
Для заданной непрерывной функции на связном множестве первообразные, полученные разными методами, должны отличаться на константу . В некоторых случаях первообразные могут быть точно равны, но это вообще не надо .
См. Нулевая производная подразумевает локальную постоянную
График функции с первообразной
На рисунке ниже мы изображаем (синий) и функцию (фиолетовый). Это уникальная первообразная, которая принимает значение 0 в 0. Остальные первообразные можно получить, сдвинув фиолетовый график по вертикали:
Черные точки соответствуют локальным экстремумам для , а красные точки соответствуют точкам перегиба первообразной. Как и следовало ожидать, каждая черная точка находится на той же вертикальной линии, что и красная точка, поскольку точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. В дальнейшем:
- Первообразная везде возрастает, потому что везде неотрицательна и равна нулю только в изолированных точках.

- Первообразная вогнута на тех интервалах, где является возрастающей, т. е. на интервалах вида as изменяется по целым числам.
- Первообразная вогнута вниз на тех интервалах, где убывающая, т. е. на интервалах вида as меняется по целым числам.
Определенные интегралы
Часть в первообразной означает, что линейная часть первообразной имеет наклон , и это связано с тем, что имеет среднее значение на любом интервале длины, равной периоду. На самом деле ясно, что функция является синусоидальной функцией относительно .
Итак, имеем:
где целое число.
Среднее значение для интервала длины, равного кратному периоду, равно . Таким образом, для очень больших интервалов среднее значение очень близко к 1/2, даже если оно не обязательно должно быть ровно 1/2. Конкретно:
Преобразованные версии
На основе интегрирования мы можем также интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
Таким образом, мы видим, что среднее значение этой функции также на любом интервале длины, кратной периоду . Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:
Высшие первообразные
Можно проводить антидифференцировку более одного раза. Первообразная представляет собой сумму многочлена степени и тригонометрической функции с периодом .
Степенной ряд и ряд Тейлора
Расчет степенного ряда
Мы можем использовать тождество:
вместе со степенным рядом функции косинуса, чтобы найти степенной ряд для .
Степенной ряд функции косинуса везде сходится к функции и равен:
Серия мощности для:
Серия мощности для:
Разделив на 2, получим степенной ряд для:
Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
Полиномы Тейлора как аппроксимации
Обратите внимание, что, поскольку это четная функция, все ее полиномы Тейлора также являются четными полиномами. На рисунке ниже мы рассматриваем графики и его второй, четвертой и шестой тейлоровских аппроксимаций.

 1 Первая производная
1 Первая производная
 1 Критические точки
1 Критические точки