ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2. 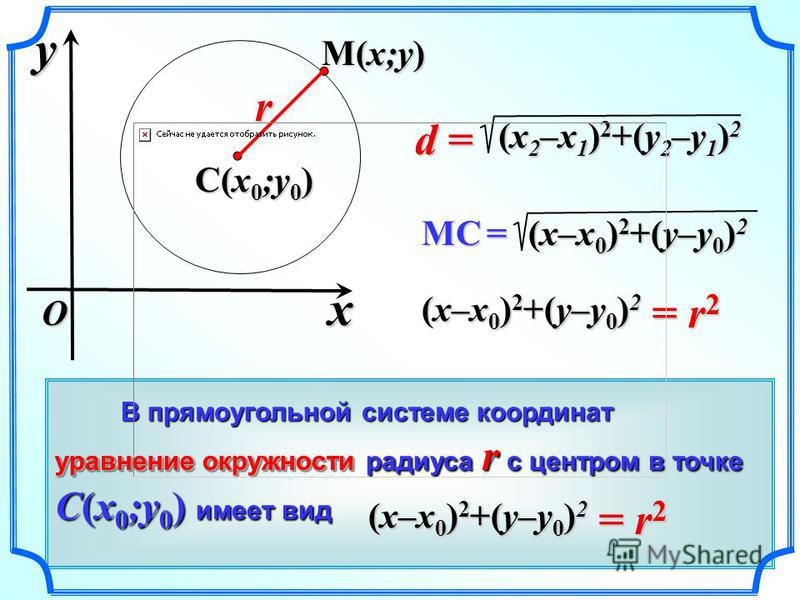 Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
6. Параметрические уравнения окружности и эллипса.
Возьмем окружность: x2+y2=R2
Параметрическое уравнение окружности
{X=Rcos(t)
{Y=Rsin(t)
Если t принадлежит [0,2П],
то точка М(х, у) принадлежит окружности.
Параметрическое уравнение эллипса:
Y=b*sin(t)
x2/a2+b2sin2 (t)/b2=0
x=a*cos(t), т.к знак cos(t) и знак x во всех четвертях совпадают.
0≤t≤2П, {x=a cos(t)
{y=b sin(t)
7. Связь между параметрами эллипса в случае b>a.
Если a<b, то b2=a2+c2, c2=b2-a2
E=c/b
a/b=√(1-E2)
Эллипс вытянут вдоль оси Оу.
8. Определение и вывод канонического уравнения гиперболы
Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Для вывода канонического уравнения гиперболы используется такая же система координат, как и для эллипса. (см билет №3)
√((x+c)
(√((x+c) 2+y2))2=(√((x-c) 2+y2) ±2a) 2
x2+2xc+c2+y2=x2-2xc+c2+y2±4a√((x-c) 2+y2)+4a2
4cx-4a2=±4a√((x-c) 2+y2)
c2x2-2cxa2+a4=a2(x2-2cx+c2+y2)
c2x2+a4=a2x2+a2c2+a2y2
(c2-a2)x2-a2y2=a2(c2-a2)
c2-a2>0
т.
к. c>a
c2-a2=b2
b2x2-a2y2=a2b2 : a2b2
x2/a2—y2/b2=1 – каноническое уравнение гиперболы
9. Исследование формы гиперболы по ее каноническому уравнению. Уравнение асимптот гиперболы
Т.к уравнение содержит только x2 и y2, то, как и в случае эллипса, доказывается, что гипербола имеет две оси симметрии (Ох и Оу) и центр симметрии в точке О.
Выразим из уравнения у.
x2/a2-1=y2/b2
y2=b2x2/a2-b2
y=±b/a√(x2-a2)
x2≥a2
|x|≥a
y=0 при x=±a
x≠0 ни при каких y
F (±c, 0) – фокусы гиперболы.
График гиперболы в первой четверти: y=b/a*√(x2-a2)
Найдем асимптоту гиперболы:
y=kx+h
k=lim(x=>+∞) b√(x-a)/(ax)= lim(x=>+∞) b|x|√(1-a2/x2)/(ax)= lim(x=>+∞) b/a√1=b/a
h= lim(x=>+∞) (b/a√(x2-a2)-b/a*x)=b/a lim(x=>+∞) (√(x2-a2)-x) = b/a lim(x=>+∞) ((x2-a2-x2)/( √ (x2-a2)+x)=b/a * -a2/∞=0
Прямая y=b/a
*x является асимптотой
гиперболы в первой и третьей четверти.
Очевидно, что прямая y=-b/a
*x является асимптотой во
второй и четвертой координатных
четвертях.
Числа а и b называют вещественной и мнимой полуосями соответственно. Числа 2а и 2b – вещественной и мнимой осями.
10. Параметры гиперболы; связь между ними.
Числа а и b называют вещественной и мнимой полуосями соответственно. Числа 2а и 2b – вещественной и мнимой осями.
Из определения b2 следует, что b2=c2-a2, c2=a2+b2
Если b=a, то гипербола называется равносторонней, прямоугольник гиперболы становится квадратом и его диагонали, т.е. асимптоты гиперболы, перпендикулярны. В этом случае их можно принять за новые оси координат. В результате получится «школьная» гипербола.
11. Эксцентриситет гиперболы. Оптическое свойство гиперболы
Эксцентриситетом гиперболы называют величину, равную отношению расстояния между фокусами к большей оси гиперболы.
E=2c/2aE=c/a, E≥1
c2=a2+b2
c=√(a2+b2)
E=√(1+b2/a2), E2=1+b2/a2, b2/a2=E2-1, b/a=√(E2-1)
Если Е=1, то это означает, что c=a,
b=0.
В этом случае гипербола
вырождается в отрезок на прямой Ox
(-∞,-a] и [a,+
∞).
Если E=∞, b/a∞. Гипербола превращается в две прямые, перпендикулярные оси Ox и проходящие через вершины действительной оси гиперболы.
Если E=√2, то a=b, гипербола называется равносторонней, прямоугольник гиперболы вырождается в квадрат, асимптоты взаимно перпендикулярны.
Оптическое свойство гиперболы: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Окружность — Параметрическое уравнение
В этом уроке будет рассмотрено параметрическое уравнение окружности .
Подобно параметрическому уравнению линии, эта форма поможет нам найти координаты любой точки на окружности, связав координаты с «параметром».
Параметрическое уравнение для стандартного круга
Рассмотрим следующий круг, центр которого находится в точке O(0, 0) , а радиус равен r .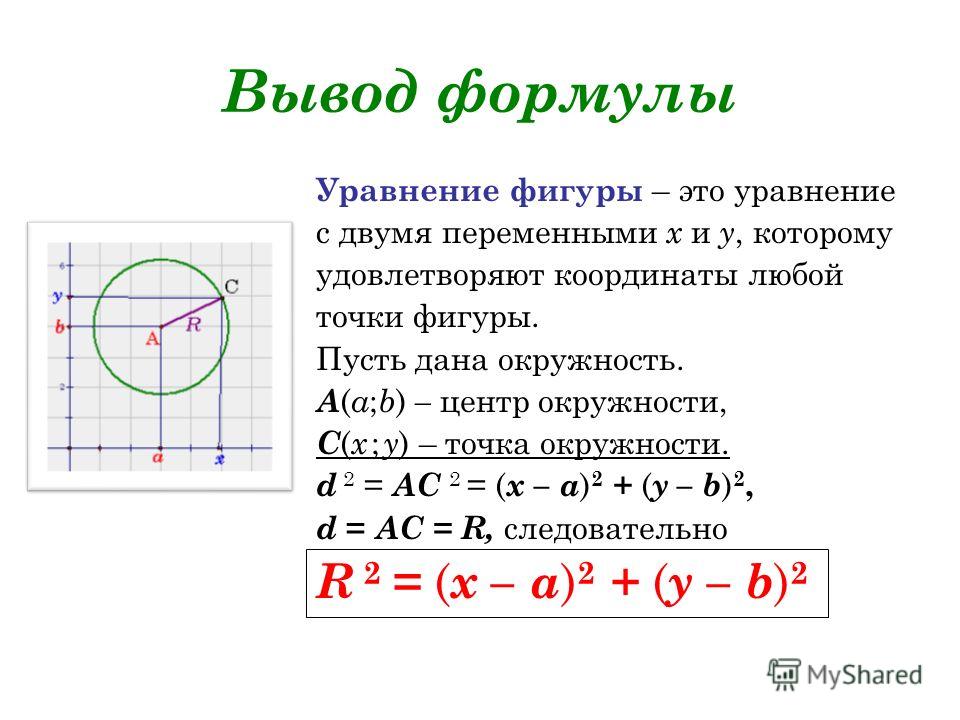
Пусть P(x, y) — любая точка на окружности, такая, что OP образует угол θ с осью X . С помощью тригонометрии получим:
x = rcosθ
y = rsinθ
И все! Мы получили то, что называется параметрическим уравнением окружности. Здесь θ — это параметр, представляющий угол, образованный OP с осью X .
Другими словами, для всех значений θ , точка (rcosθ, rsinθ) лежит на окружности x 2 + y 2 = r 2 . Или любая точка на окружности равна (rcosθ, rsinθ) , где θ — параметр.
Мы также можем получить параметрическое уравнение окружности, центр которой не лежит в начале координат.
Параметрическое уравнение общей окружности
Рассмотрим общее уравнение окружности:
x 2 + y 2 + 2gx + 2fy + c = 0
Можно записать как 2 = g 2 + f 2 – c )
Снова пусть P(x, y) будет любой точкой на окружности такой, что CP составляет угол 04 с 04 Х -ось.
В этом случае получим
x + g = rcosθ
y + f = rsinθ
Это дает нам
x = — g + rcosθ
y = -f + rsinθ
и, это параметрическое уравнение круга . х 2 + у 2 + 2gx + 2fy + с = 0 .
Вот симуляция, демонстрирующая параметрическое уравнение окружности.
Вы можете перетащить ползунок, чтобы изменить значение θ и наблюдать за точкой (rcosθ, rsinθ) . Всегда ли он лежит на окружности?
Краткий обзор урока
- Параметрическое уравнение окружности
- Параметрическое уравнение окружности x 2 + y 2 + 2gx + 2fy + c = 0 равно x = -g + rcosθ , y = -f + 0rsin04.
Здесь θ — параметр, представляющий угол, образуемый линией, соединяющей точку (x, y) с центром, с осью X .
Это урок. Увидимся в следующем!
Узнать больше о параметрическом уравнении окружности.
Здесь у нас есть окружность радиуса c с центром, совпадающим с началом системы координат. Теперь рассмотрим точку на окружности P, имеющую координаты (xp,yp). Проведем линию, соединяющую эту точку с центром окружности. Из рисунка видно, что эта линия образует угол Ɣ с осью x. Теперь мы проведем линию, параллельную оси Y, к оси X от точки (xp, yp).
Мы также проведем линию от точки (xp,yp) до оси Y, параллельной оси X. Теперь у нас есть прямоугольная фигура в нашем представлении круга.
Теперь давайте посмотрим на треугольник OPM, значение sinƔ в этом треугольнике даст нам,
⇒ sinƔ = PM/OP
⇒ PM = (sinƔ) x OP
Теперь посмотрим в треугольнике OPN значение угла NPO равно Ɣ, потому что они являются альтернативными углами между двумя параллельными прямыми.
Теперь cosƔ в этом треугольнике даст нам
⇒ cosƔ = PN/OP
⇒ PN = (cosƔ) x OP
Здесь, поскольку четырехугольник OMPN является прямоугольником,
⇒ PN = OM
Поскольку длина OM дает нам координату x ( xp,yp), мы можем сказать, что
⇒ xp = (cosƔ) x OP
Из рисунка выше видно, что OP — это радиус окружности, поэтому мы можем сказать, что
⇒ xp = (cosƔ) x c
Точно так же мы можем видеть, что длина PM даст нам длину координаты y (xp,yp).
⇒ yp = (sinƔ) x c
Мы выразили xp и yp через Ɣ. Таким образом, теперь мы можем записать координату (xp,yp) как ( (cosƔ) x c, (sinƔ) x c).
Поскольку точка, которую мы выбрали, была случайной точкой на окружности, мы можем выразить все точки окружности как функцию Ɣ.
Итак, мы можем сказать, что x = c (cosƔ)
и y = c (sinƔ)
Это параметрическое уравнение окружности.
Теперь, если мы подставим значения x и y в неявную форму уравнения окружностей, мы получим
( c (cosƔ) – p)2 + (c (sinƔ) – q)2
⇒ c2 (( cosƔ – p)2 + ( sinƔ – q)2) = c2
Где c – радиус окружности .
Это показывает, что параметрическое уравнение окружности согласуется с неявной формой уравнения окружности.
Примечание. В параметрической форме уравнения окружности мы успешно устранили переменную второй степени в неявной форме уравнения окружности с помощью тригонометрических функций.
Теперь уравнение окружности зависит только от значения Ɣ, которое изменяется от 0 до 2π радиан.
Эта Ɣ называется параметрической переменной уравнения окружности.
Свойства параметрического уравнения окружности- Параметрическое уравнение окружности можно представить с помощью одной переменной.
- Параметрическая переменная имеет значение в диапазоне [0,2π] радиан.
- Мы можем вывести неявное, а также явное уравнение окружности из параметрического уравнения окружности.
- Процесс преобразования уравнения окружности из параметрического в явный вид уравнения называется имплицитацией.
Окружность — это совокупность точек, находящихся на равном расстоянии от общей точки, которую мы называем центром окружности. Мы можем выразить уравнение окружности в параметрической, явной и неявной формах.
Мы используем параметрическую форму уравнения окружности, чтобы выразить уравнение окружности как функцию одной переменной. Эта единственная переменная представляет собой угол, который радиус образует с осью x.