Вычитание векторов
Вам уже знакомы правила сложения векторов.
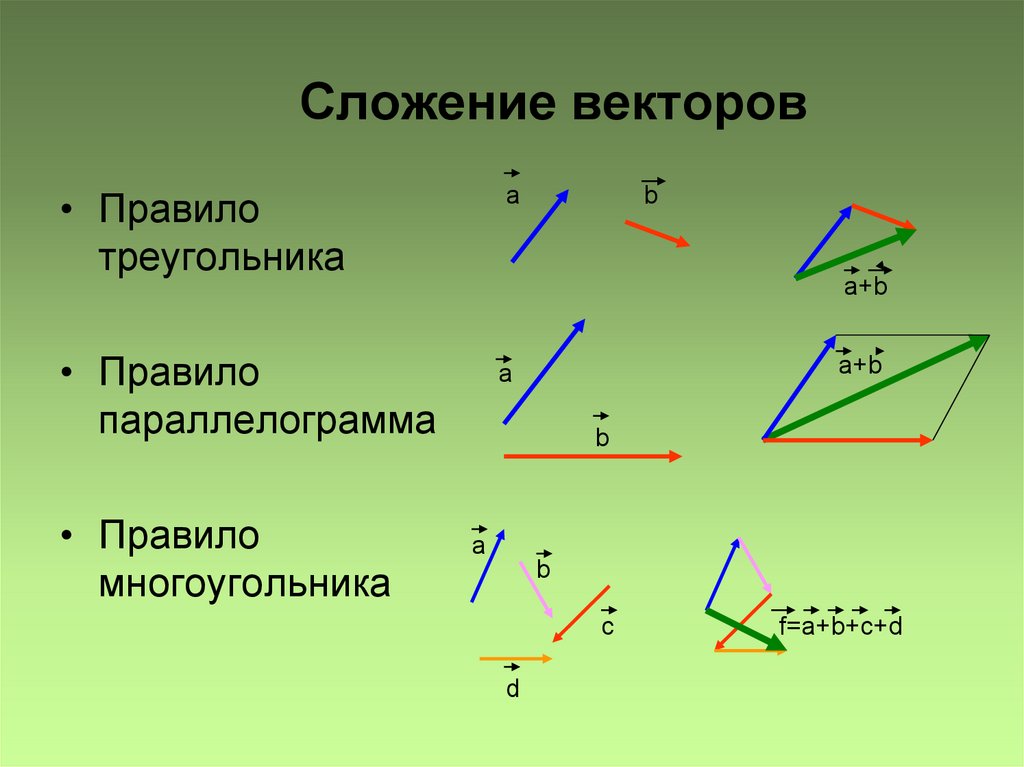
Чтобы сложить неколлинеарные векторы и по правилу треугольника, нужно от некоторой точки А отложить вектор , равный вектору . Далее от точки B отложить вектор , равный вектору . Вектор является вектором суммы двух векторов и .
Для сложения этих же векторов можно использовать правило параллелограмма. При этом нужно отложить от произвольной точки А векторы и , равные векторам и соответственно, и построить на них параллелограмм ABCD. Тогда вектор равен сумме векторов и .
Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего.
Так
же вам известны законы сложения векторов: переместительный и сочетательный.
На этом уроке поговорим о разности двух векторов. Её обозначают так .
Разностью векторов и называют такой вектор , сумма которого с вектором равна вектору .
Чтобы получить представление о разности двух векторов, решим задачу.
Задача. По данным векторам и построить вектор .
Построение
.
Вектор — искомый.
Эту задачу можно решить другим способом.
Но перед тем как его привести введём понятие вектора, противоположного данному.
Для произвольного ненулевого вектора вектор будет противоположным, если:
Вектор, противоположный вектору , обозначается так . И говорят «вектор минус a».
Очевидно, что сумма вектора с противоположным ему равна нулевому вектору .
Запишем
теорему о разности двух векторов.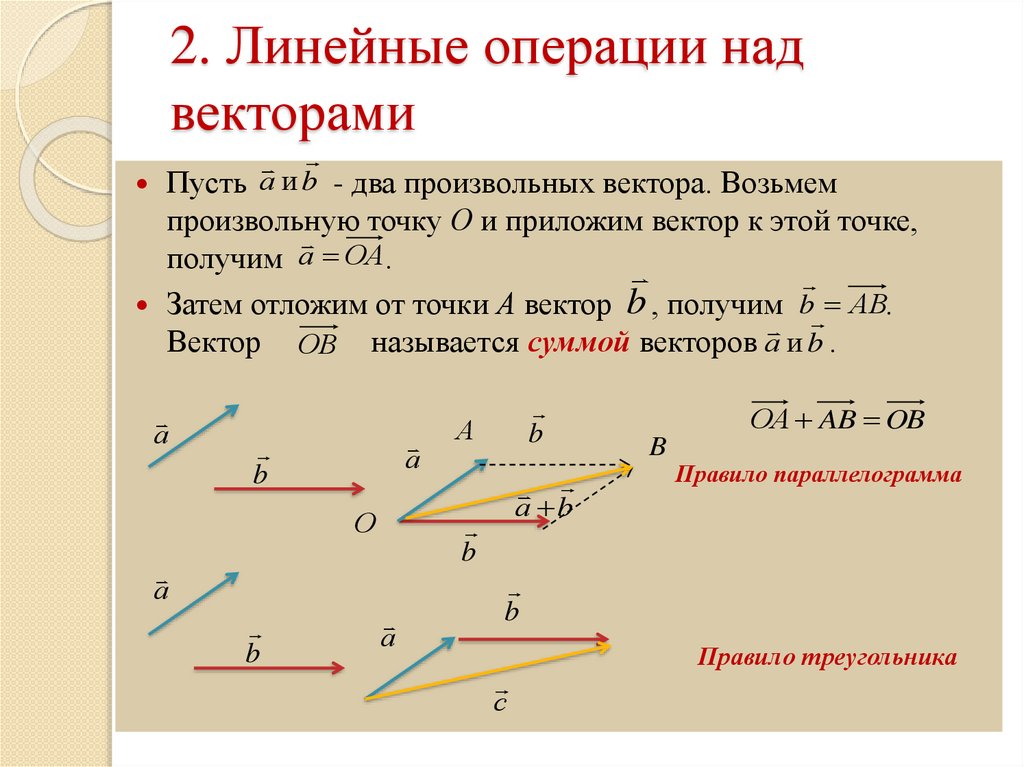
Для любых векторов и справедливо равенство .
Докажем данную теорему.
Доказательство.
Что и требовалось доказать.
Опираясь на эту теорему, приведём ещё одно решение задачи на построение разности векторов .
Способ
Отметим произвольную точку О и от неё отложим вектор . Далее отложим от точки А вектор .
По правилу треугольника сумма .
А значит, пользуясь теоремой о разности двух векторов, можем сделать вывод о том, что разность векторов . И вектор — искомый.
Итак, можем сделать вывод, что вектор разности двух векторов можно строить двумя способами.
Можно
от некоторой точки О отложить векторы и , равные векторам . При этом вектором их
разности будет вектор ,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.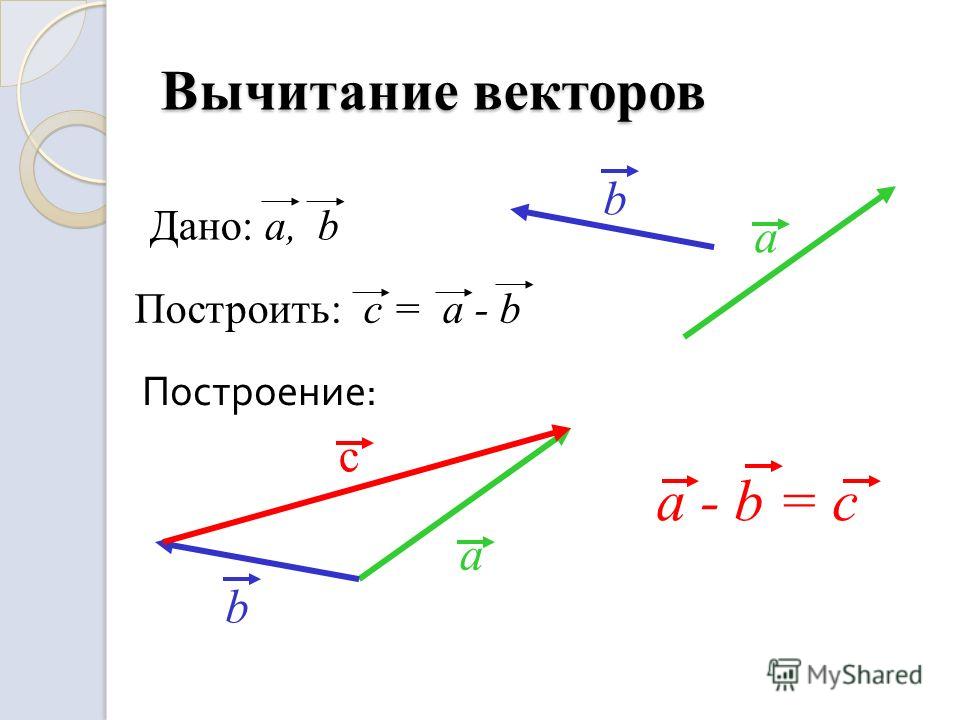
Так же, пользуясь теоремой о разности двух векторов, разность векторов можно представить в виде суммы вектора .
Тогда, отложив от некоторой точки О вектор , равные вектору , а от точки А — вектор , равный вектору , по правилу треугольника получим вектор .
Он является вектором суммы вектора . И, соответственно, вектором разности векторов .
Задача. Начертить попарно неколлинеарные векторы , и . Построить на них векторы: , , , , и .
Построение.
Для начала построим векторы, противоположные данным.
Векторы являются противоположными, если их длины равны и они противоположно направлены.
Выберем точки А, B и C, от которых будем откладывать противоположные векторы.
Далее через каждую из этих точек проведём прямые параллельные векторам , и соответственно.
От
отмеченных точек на проведённых прямых можно изобразить векторы, равные данным,
и, противоположные данным. Нам нужны те, которые противоположны векторам , и соответственно.
Нам нужны те, которые противоположны векторам , и соответственно.
Так мы построили векторы , и .
Задача. Сторона квадрата равна . Найти и .
Построение.
Решение.
По теореме Пифагора:
Ответ: ; .
Подведём итоги нашего урока.
Сегодня вы познакомились с понятием противоположного вектора. Противоположные векторы имеют равные длины и противоположно направлены.
Мы ввели понятие разности двух векторов. Разностью векторов , называют такой вектор , сумма которого с вектором равна вектору .
Для построения вектора разности мы выделили два способа.
Можно от некоторой точки О отложить векторы и , равные векторам и . При этом вектором их разности будет вектор, направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так
же, пользуясь теоремой о разности двух векторов, разность векторов и можно представить в
виде суммы вектора и
вектора, противоположного вектору .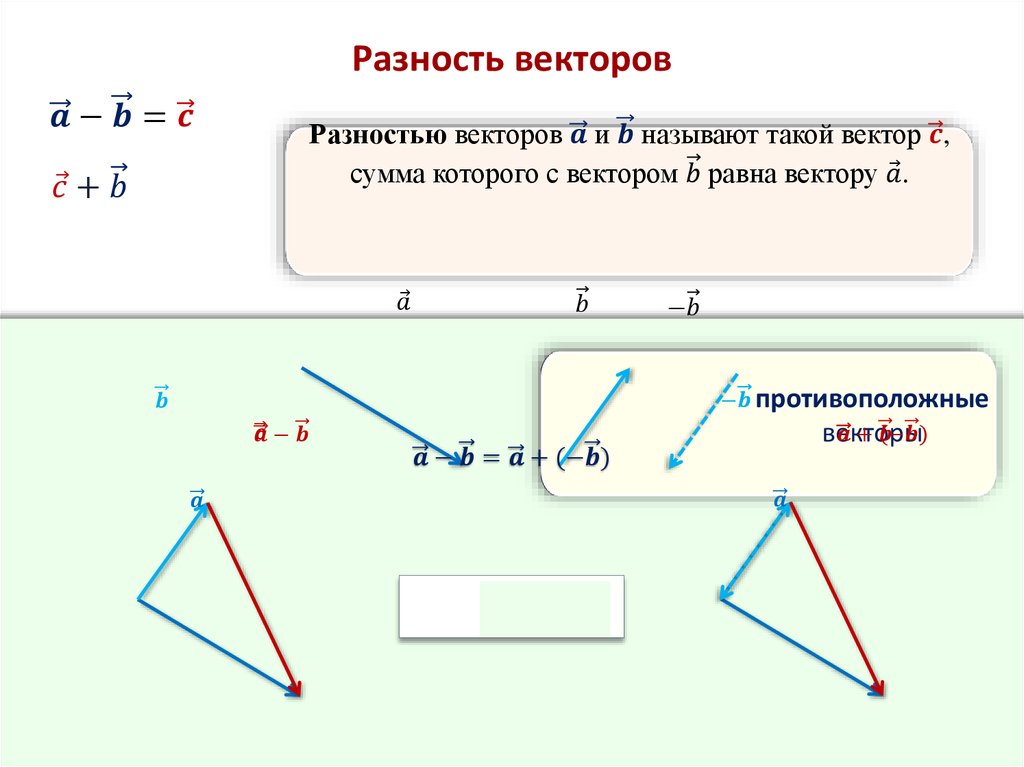
Тогда, отложив от некоторой точки О вектор , равный вектору , а от точки А — вектор , равный вектору , по правилу треугольника получим вектор .
Он является вектором суммы вектора и вектора, противоположного вектору . И, соответственно, вектором разности векторов и .
Теперь вы владеете не только правилами сложения, а ещё и правилом вычитания векторов.
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4. Скользящие и приложенные векторные величины. 5. Модуль вектора. 6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. 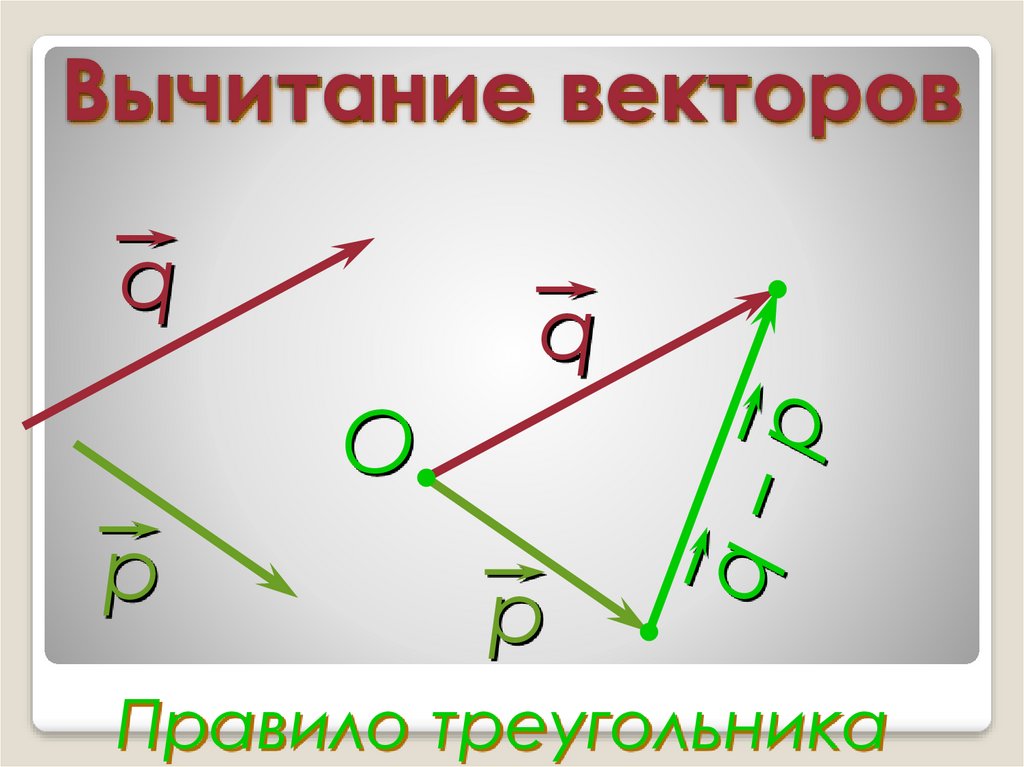 Проекции векторов на ось Проекции векторов на ось§ 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме. 4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов.  7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. 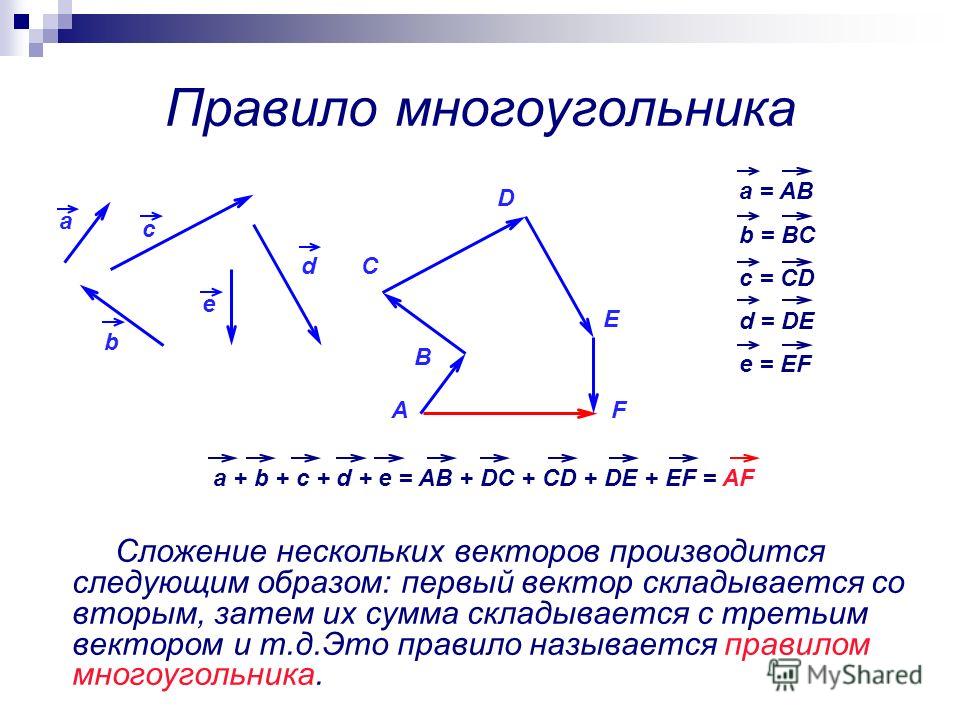 Разложение вектора (a, b, c) (m x n) по векторам a, b, c. Разложение вектора (a, b, c) (m x n) по векторам a, b, c.3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 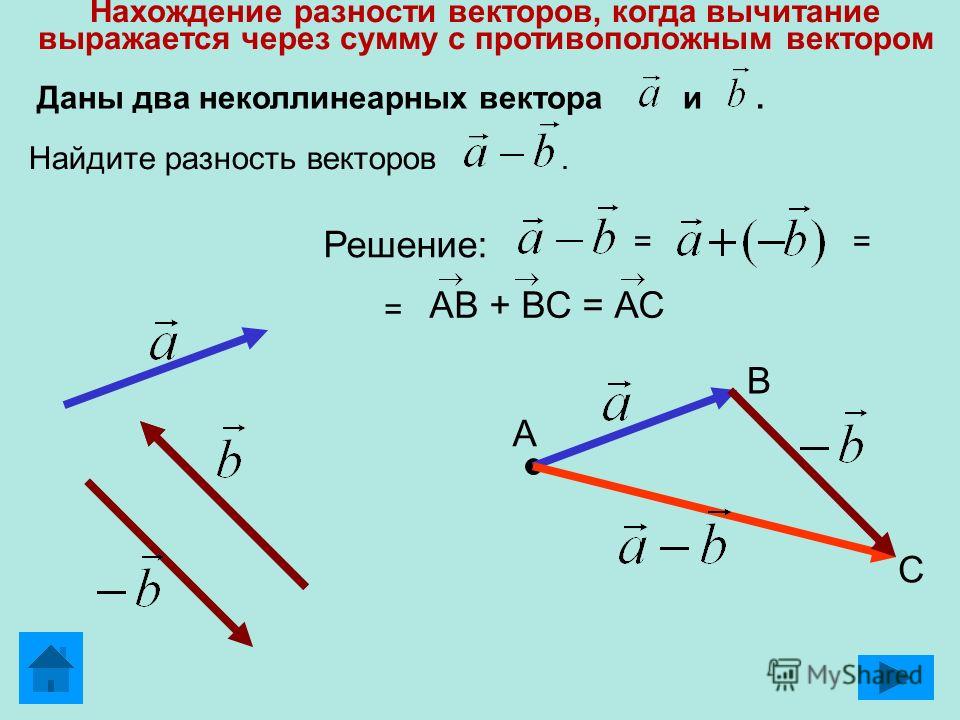 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ § 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2.  Система дифференциальных уравнений движения сопровождающего трехгранника. Система дифференциальных уравнений движения сопровождающего трехгранника.3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. Круг кривизны § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть.  4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. 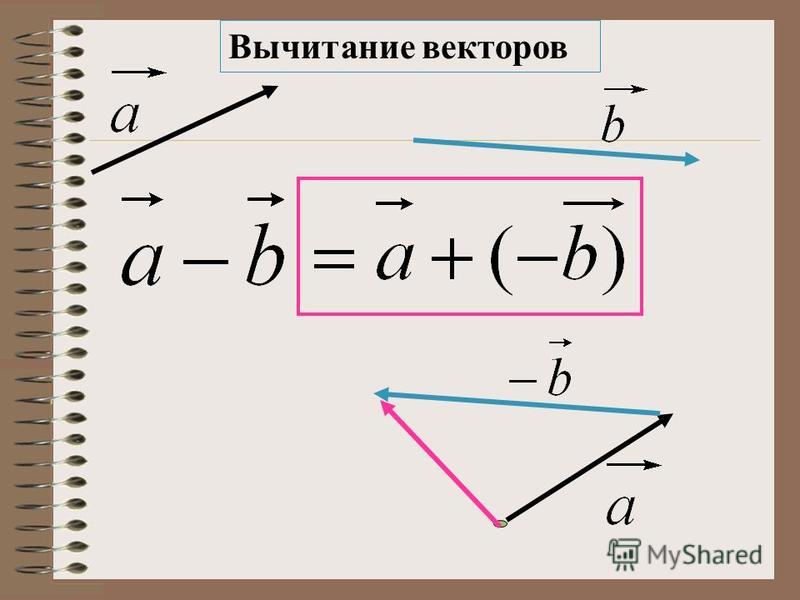 Градиент поля Градиент поля2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2. Криволинейный интеграл от линейной формы по произвольной кривой. 3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 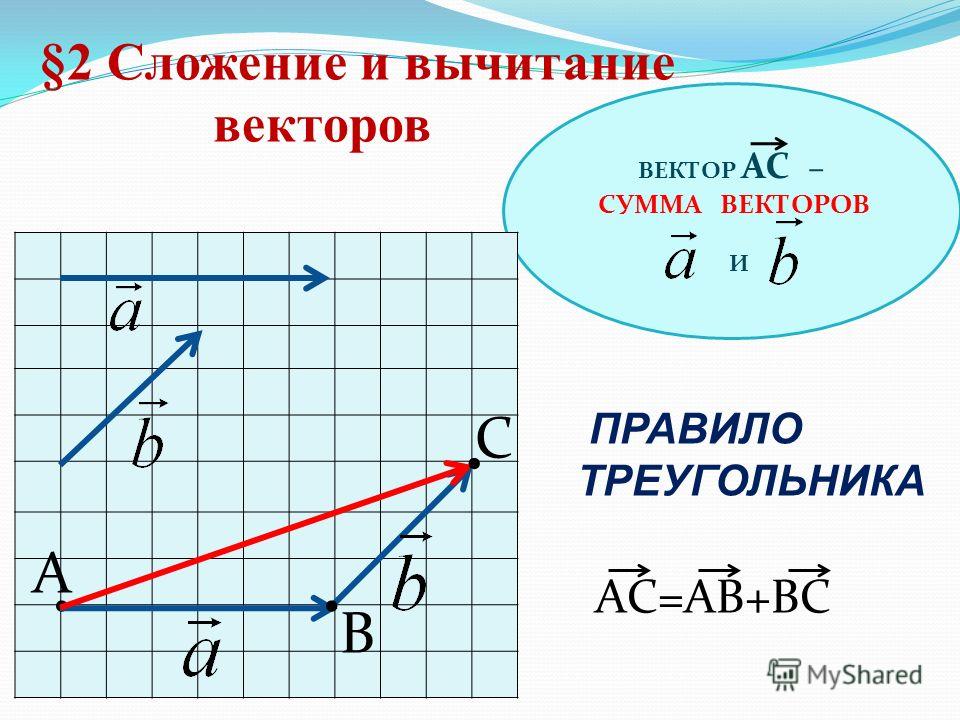 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ § 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. 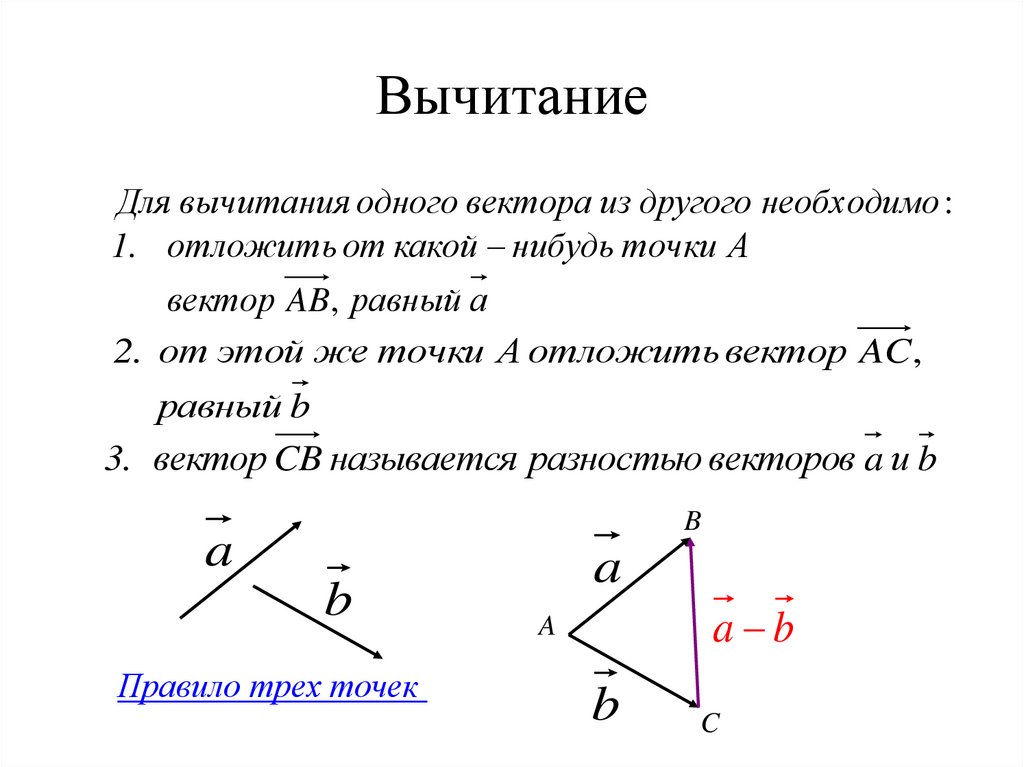 Вычисление потенциала. Вычисление потенциала.9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ § 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 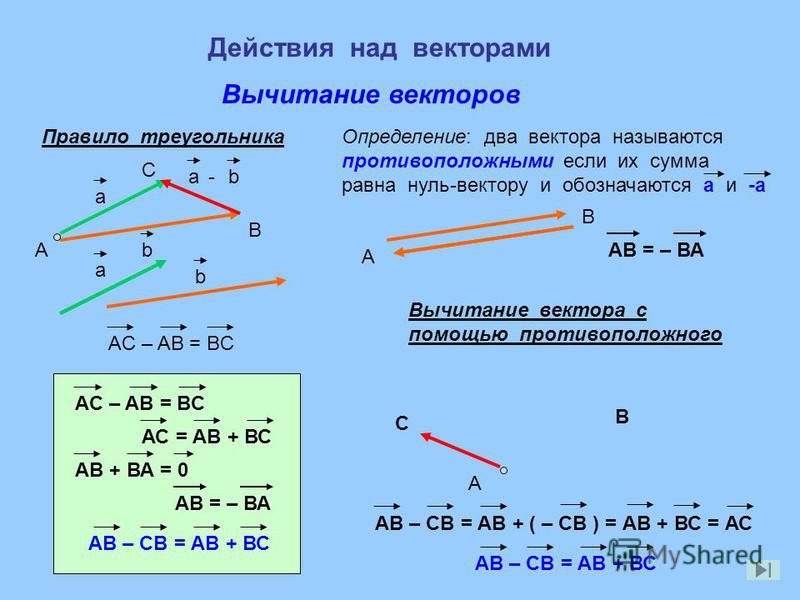 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах. § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Графические методы – физика колледжа
Глава 3 Двумерная кинематика
Резюме
- Понимание правил сложения, вычитания и умножения векторов.
- Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.

Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.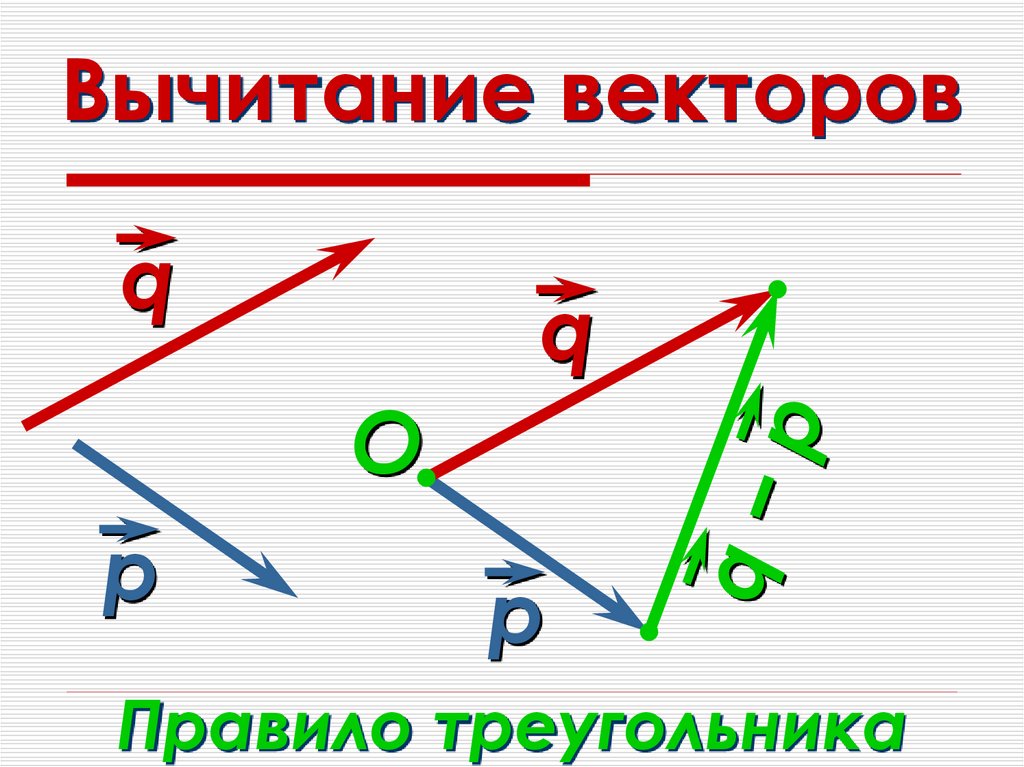 1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что полужирный символ, такой как [latex]\textbf{D}[/latex] , обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]{D},[/латекс], а его направление — [латекс]{\тета}.[/латекс]
1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что полужирный символ, такой как [latex]\textbf{D}[/latex] , обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]{D},[/латекс], а его направление — [латекс]{\тета}.[/латекс]
ВЕКТОРА В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором [latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]{F},[/латекс], а направление переменной будет задано углом [латекс]{\тета}.[/латекс ]
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D .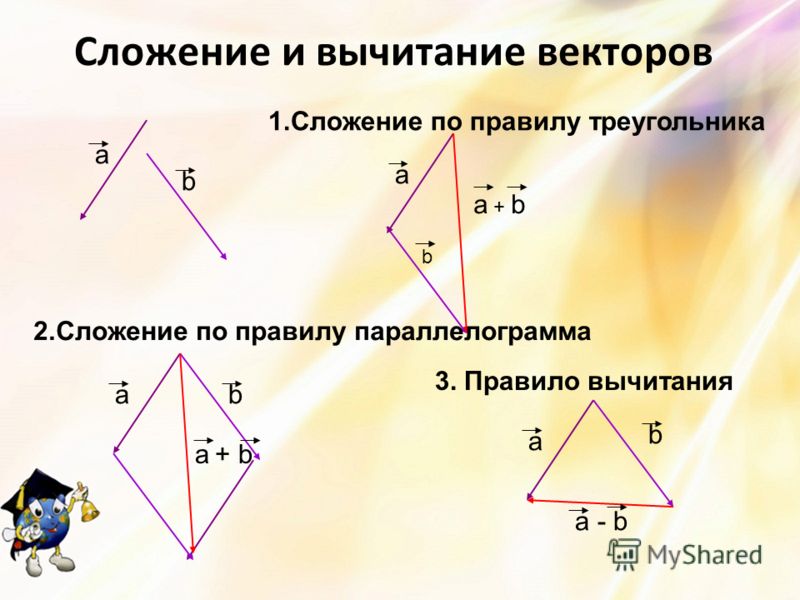 С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.
С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север.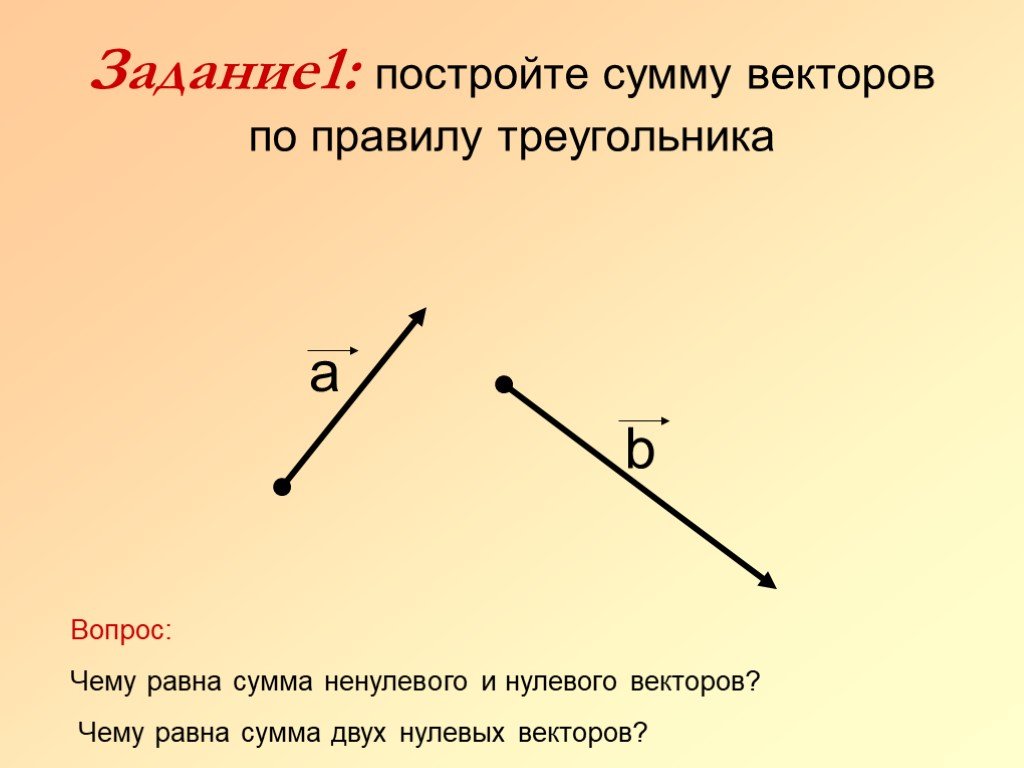 Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .
Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5.Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6. Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7.Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9{\circ}}[/latex] к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически стрелкой, обозначив первый [latex]\textbf{A},[/latex], второй [latex]\textbf{B},[/latex] и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого [latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 8.(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9. (3) Нарисуйте результирующий вектор [латекс]\textbf{R}.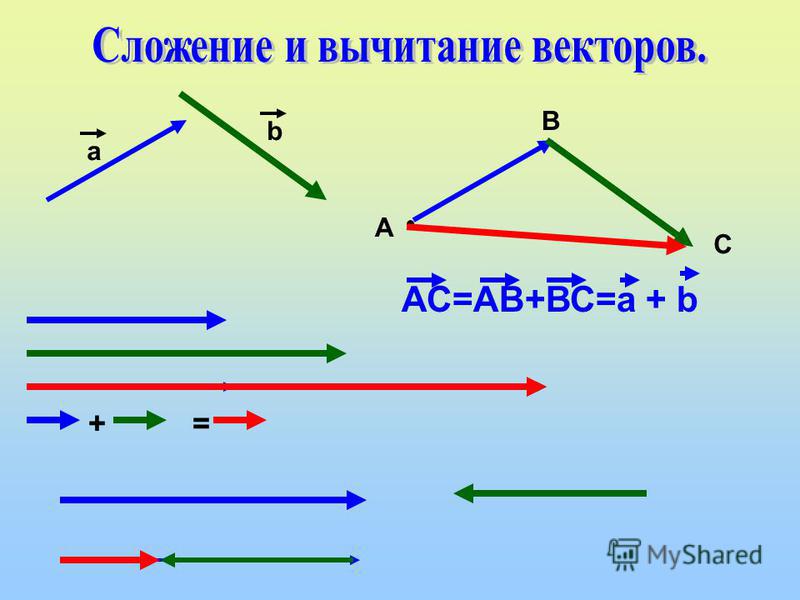 [/latex]
[/latex]
(4) Используйте линейку для измерения величины [латекс]\ textbf{R},[/latex] и транспортир для измерения направления [latex]\textbf{R}.[/latex] Несмотря на то, что направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9{\circ}}[/latex] к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Рисунок 12. Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[latex]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это справедливо и для сложения обычных чисел— вы получите тот же результат, если вы добавите, например, [латекс]{2+3}[/латекс] или [латекс]{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс] из [латекс]\текстбф{А},[/латекс], записанного [латекс]{\текстбф{А}-\текстбф{В }}[/latex] , мы должны сначала определить, что мы подразумеваем под вычитанием.0021 отрицательный вектора [latex]\textbf{B}[/latex] определяется как [latex]{-\textbf{B}};[/latex], то есть графически отрицательный любой вектор имеет той же величины, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]{-\textbf{B}},[/latex ] но указывает в противоположном направлении.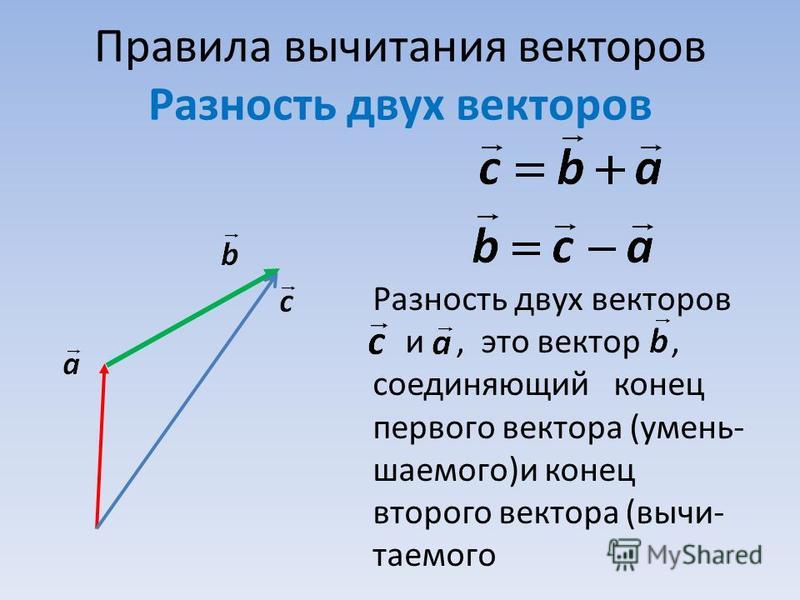 По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора [latex]\textbf{B}[/latex] из вектора [latex]\textbf{A}[/latex] просто определяется как сложение [latex]{-\ textbf{B}}[/latex] в [latex]\textbf{A}.[/latex] Обратите внимание, что вычитание векторов — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
[латекс]{\textbf{A}-\textbf{B}=\textbf{A}+(-\textbf{B})}.[/latex]
Это аналогично вычитанию скаляров (где, например, [латекс]{5-2=5+(-2)}[/латекс] ). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.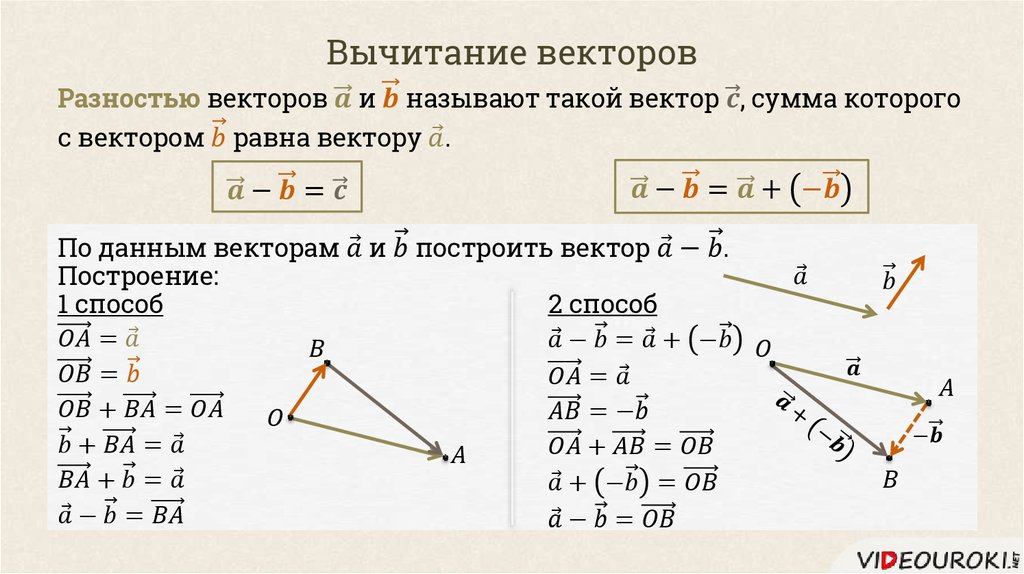 {\circ}}[/latex] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
{\circ}}[/latex] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап пути с помощью вектора [latex]\textbf{A},[/latex] и второй этап пути с помощью вектора [latex] \textbf{B}.[/latex] Док находится в месте [latex]{\textbf{A}\:+\:\textbf{B}}.[/latex] Если женщина по ошибке путешествует в напротив 9{\circ}}[/latex] к югу от востока. Мы представляем это как [латекс]{-\textbf{B}},[/латекс], как показано ниже. Вектор [latex]{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [latex]{\textbf{A}+(-\textbf{B})},[/latex] или [latex]{\textbf{A}-\textbf{B}} .[/latex]
Рисунок 15. Мы выполним сложение векторов, чтобы сравнить местоположение дока, [latex]{\textbf{A}+\textbf{B}},[/latex] с местоположением в которую по ошибке прибывает женщина, [латекс]{\textbf{A}+(-\textbf{B})}. [/latex]
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex]\textbf{A}[/latex] и [latex]{-\textbf{B}}.[ /latex]
(2) Разместите векторы «голова к хвосту».
(3) Нарисуйте результирующий вектор [latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.}[/latex] к югу от востока. 9{\circ}}[/latex] к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли [латекс]{3 \times 27,5\text{ м}},[/latex] или 82,5 м, в направлении [латекс] {66,0 ^ {\ circ}} [/ латекс] к северу от востока. Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор [latex]\textbf{A}[/latex] умножается на скаляр [latex]{c},[/latex]
- величина вектора становится абсолютной величиной [latex]{cA},[/latex]
- , если [latex]{c}[/latex] положительный, направление вектора не меняется,
- , если [latex]{c}[/latex] имеет отрицательное значение, направление меняется на противоположное.
В нашем случае [латекс]{с=3}[/латекс] и [латекс]{\текстбф{А}=27,5\текст{м}}.[/латекс] Во многих случаях векторы умножаются на скаляры. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x – и y , или компонентов север-юг и восток-запад. 9{\circ}}[/latex] к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод сложения векторов [latex]\textbf{A}[/latex] и [latex]\textbf{B}[/latex] включает рисование векторов на графике и их сложение с использованием прямого метод хвоста.
 Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно. - графический метод вычитания вектора [latex]\textbf{B}[/latex] из [latex]\textbf{A}[/latex] включает добавление противоположного вектора [latex]\textbf{B},[/latex ] который определяется как [latex]{-\textbf{B}}.[/latex] В этом случае [latex]{\textbf{A}-\textbf{B}=\textbf{A}+(-\ textbf{B})=\textbf{R}}.[/latex] Затем обычным способом используется метод сложения головы к хвосту для получения результирующего вектора [latex]\textbf{R}.[/ латекс]
- Сложение векторов коммутативно , такое что [латекс]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора.
 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора. - Если вектор [latex]\textbf{A}[/latex] умножить на скалярную величину [latex]{c},[/latex], величина произведения будет равна [latex]{cA}.[/ латекс] Если [латекс]{с}[/латекс] положительный, направление произведения указывает в том же направлении, что и [латекс]\текстбф{А};[/латекс], если [латекс]{с}[/латекс] ] отрицательно, направление произведения указывает в направлении, противоположном направлению [латекс]\текстбф{А}.[/латекс]
- компонент (двумерного вектора)
- часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов 90 336
- коммутативный
- относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 336
- направление (вектора)
- ориентация вектора в пространстве
- голова (вектора)
- конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
- метод «голова к хвосту»
- метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора
- величина (вектора)
- длина или размер вектора; величина является скалярной величиной
- результат
- сумма двух или более векторов
- результирующий вектор
- векторная сумма двух или более векторов
- скаляр
- количество с величиной, но без направления
- хвост
- начальная точка вектора; напротив наконечника или наконечника стрелки
Сложение и вычитание векторов
Сложение двух (или более) векторов вместе всегда приводит к другому вектору, называемому результирующим .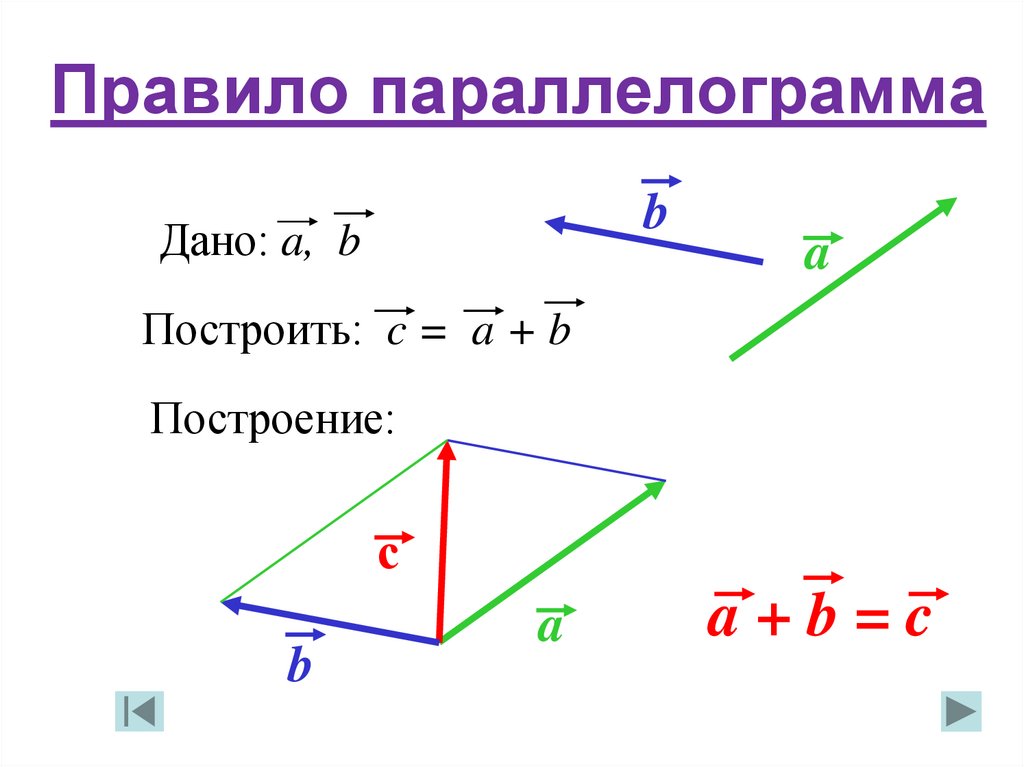 Складываемые вместе векторы известны как компоненты результирующего вектора. Однако если векторы компонентов не действуют в одном и том же направлении с самого начала, направление равнодействующей будет отличаться от направления любого из ее компонентов. Кроме того, абсолютная величина результирующего (т. е. его величина без учета знака) обычно будет меньше, чем сумма абсолютных величин векторов его компонентов (если только вектора компонентов не равны 9).0021 все действуют в одном направлении). Вы, наверное, уже знаете, что любой вектор на двумерной плоскости можно описать с помощью его компонентов x и y , и что эти компоненты сами по себе являются векторами. Чтобы наглядно представить, что это значит, представьте, что вы идете три километра на восток, а затем четыре километра на север. Всего вы прошли семь километров, но как далеко вы от того места, откуда начали, по прямой?
Складываемые вместе векторы известны как компоненты результирующего вектора. Однако если векторы компонентов не действуют в одном и том же направлении с самого начала, направление равнодействующей будет отличаться от направления любого из ее компонентов. Кроме того, абсолютная величина результирующего (т. е. его величина без учета знака) обычно будет меньше, чем сумма абсолютных величин векторов его компонентов (если только вектора компонентов не равны 9).0021 все действуют в одном направлении). Вы, наверное, уже знаете, что любой вектор на двумерной плоскости можно описать с помощью его компонентов x и y , и что эти компоненты сами по себе являются векторами. Чтобы наглядно представить, что это значит, представьте, что вы идете три километра на восток, а затем четыре километра на север. Всего вы прошли семь километров, но как далеко вы от того места, откуда начали, по прямой?
Как далеко вы от точки происхождения?
Глядя на приведенную выше диаграмму, ответ (пять километров) можно найти достаточно легко, применив теорему Пифагора.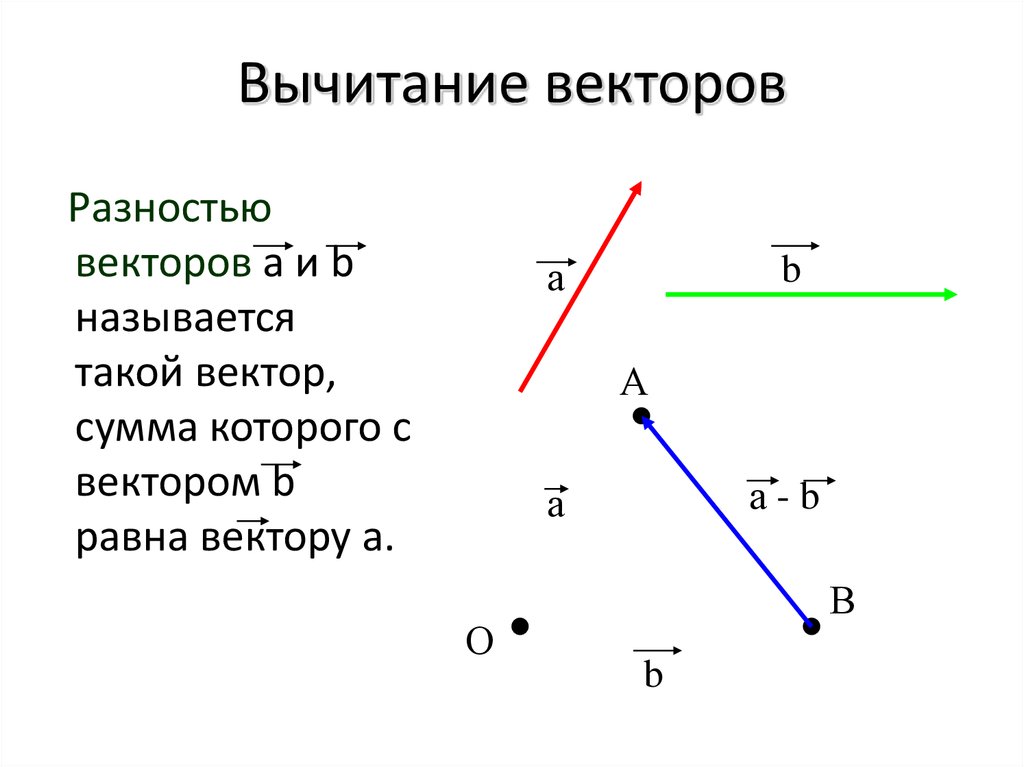 Каждый этап вашего путешествия (три километра на восток и четыре километра на север) представляет собой отдельный вектор . Два вектора образуют стороны прямоугольного треугольника, для которого отрезок линии, соединяющий точку, в которой вы начали, и точку, в которой вы закончили (т.е. равнодействующее ) становится гипотенузой. Вот расчет:
Каждый этап вашего путешествия (три километра на восток и четыре километра на север) представляет собой отдельный вектор . Два вектора образуют стороны прямоугольного треугольника, для которого отрезок линии, соединяющий точку, в которой вы начали, и точку, в которой вы закончили (т.е. равнодействующее ) становится гипотенузой. Вот расчет:
расстояние от начала координат = √3 2 + 4 2 = 5
Итак, хотя на самом деле вы прошли семь километров, на самом деле вы находитесь всего в пяти километрах от исходной точки. Это, конечно, совершенно логично, поскольку кратчайшее расстояние между двумя точками всегда является прямой линией. Мы можем использовать этот вид визуального представления, чтобы найти результат сложения любого набора векторов. На иллюстрации ниже показаны два свободных вектора, а и б .
Бесплатные векторы a и b
Если мы хотим визуализировать, что происходит, когда мы складываем эти векторы вместе, мы можем переместить один из векторов (не меняя его направление) так, чтобы его конец касался кончика стрелки, принадлежащей другому вектору. На самом деле не имеет значения, какой вектор мы выберем для перемещения — результат будет тот же (что касается сложения скалярных значений, сложение векторов равно коммутативный и ассоциативный ). Чтобы показать, что это так, на рисунке ниже показаны оба возможных сценария. В каждом случае результат отображается зеленой стрелкой.
На самом деле не имеет значения, какой вектор мы выберем для перемещения — результат будет тот же (что касается сложения скалярных значений, сложение векторов равно коммутативный и ассоциативный ). Чтобы показать, что это так, на рисунке ниже показаны оба возможных сценария. В каждом случае результат отображается зеленой стрелкой.
Графическое представление сложения векторов
Мы можем сделать что-то очень похожее, чтобы представить вычитанием одного вектора из другого. Если мы хотим вычесть вектор b из вектора a , например, мы просто меняем направление вектора b , чтобы создать новый вектор с именем -b , и следуем той же процедуре, что и ранее, то есть перемещаем вектор -b так, чтобы его хвост касался наконечник стрелки, принадлежащий вектору a . Однако обратите внимание, что, как и для скалярных значений, вычитание не является ни коммутативным, ни ассоциативным.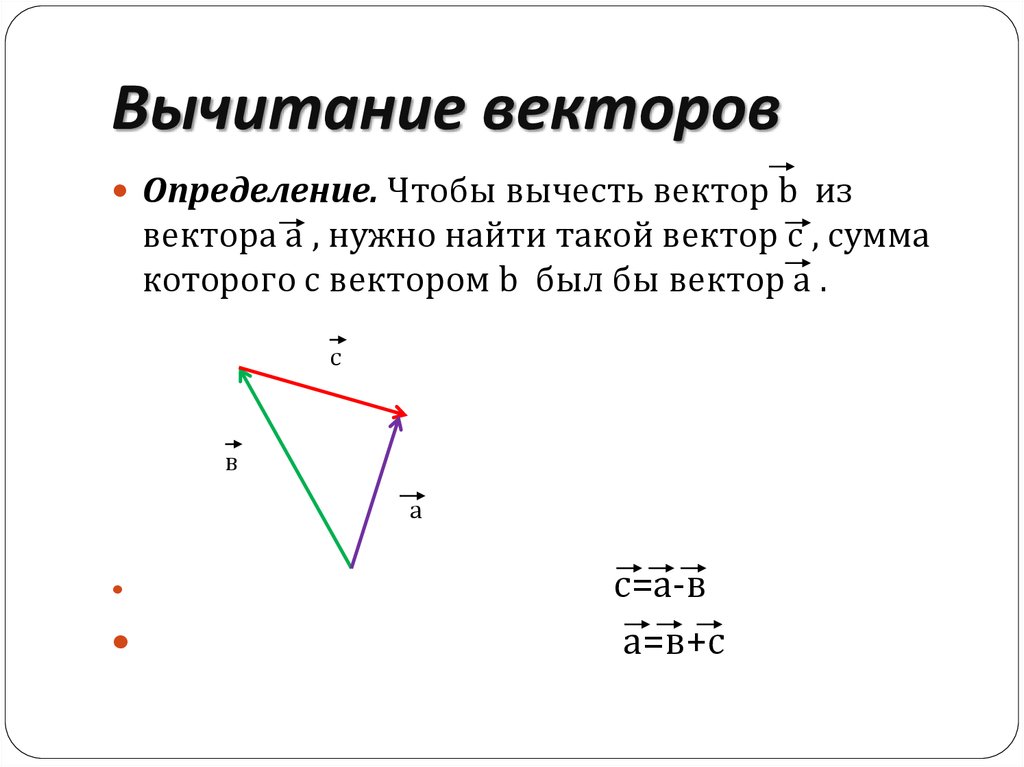 Мы не получим того же результата, если вместо этого вычтем вектор a из вектора b . Чтобы продемонстрировать это, оба сценария проиллюстрированы ниже. Обратите внимание, что хотя величина равнодействующей одинакова в обоих случаях, ее направление , когда вектор a вычитается из вектора b , полностью противоположно направлению вектора, который получается в результате вычитания вектора b из вектора в .
Мы не получим того же результата, если вместо этого вычтем вектор a из вектора b . Чтобы продемонстрировать это, оба сценария проиллюстрированы ниже. Обратите внимание, что хотя величина равнодействующей одинакова в обоих случаях, ее направление , когда вектор a вычитается из вектора b , полностью противоположно направлению вектора, который получается в результате вычитания вектора b из вектора в .
Вычитание векторов некоммутативно и неассоциативно.
Следует отметить, что если мы хотим вычесть один вектор из другого, мы можем просто изменить направление вычитаемого вектора, а затем сложить два вектора вместе. Еще один момент, который следует отметить, это то, что результирующая идет от выбранной точки происхождения до конечной точки напрямую . Векторы-компоненты (то есть векторы, которые мы складываем вместе) создают непрямой путь из одной и той же начальной точки в одну и ту же конечную точку. Таким образом, логически сумма 9Компоненты 0021 x двух добавляемых векторов должны равняться компоненте x результирующей, а сумма компонентов y векторов должна равняться компоненте y результирующей. Это означает, что мы можем выразить сложение векторов с помощью чисел, вместо того чтобы рисовать диаграмму каждый раз, когда мы хотим сложить векторы вместе. Давайте снова выполним наше исходное сложение векторов, на этот раз используя сложение матриц, чтобы найти x и y компоненты результирующего:
Таким образом, логически сумма 9Компоненты 0021 x двух добавляемых векторов должны равняться компоненте x результирующей, а сумма компонентов y векторов должна равняться компоненте y результирующей. Это означает, что мы можем выразить сложение векторов с помощью чисел, вместо того чтобы рисовать диаграмму каждый раз, когда мы хотим сложить векторы вместе. Давайте снова выполним наше исходное сложение векторов, на этот раз используя сложение матриц, чтобы найти x и y компоненты результирующего:
| a + b = | 4 | + | 1 | = | 5 | ||||||
| 1 | 2 | 3 |
Если мы хотим вычесть вектор b из вектора a , мы просто инвертируем значения компонентов x и y для вектора b , как показано здесь:
| a — b = | 4 | + | -1 | = | 3 | ||||||
| 1 | -2 | -1 |
Точно так же мы можем вычесть вектор a из вектора b , инвертируя значения компонентов x и y для вектора a :
| b — a = | 1 | + | -4 | = | -3 | ||||||
| 2 | -1 | 1 |
Если вы сверите полученные здесь результаты с приведенными выше иллюстрациями, вы сможете увидеть, что они согласуются с результатами, которые мы получили, используя визуальное представление сложения векторов. Пока вы это делаете, вы также можете убедиться, что 9Компоненты 0021 x и y , указанные для векторов a и b , верны (вы можете сделать это, подсчитав количество квадратов в каждом из горизонтальных и вертикальных направлений между концами стрелки, представляющей вектор и его наконечник). Ради удобства мы использовали целые значения для компонентов x и y всех векторов. В реальной жизни значение компонента часто будет иметь дробную часть, но принцип тот же. Добавлять векторы относительно легко, если вы знаете значения x и y компоненты каждого вектора.
Пока вы это делаете, вы также можете убедиться, что 9Компоненты 0021 x и y , указанные для векторов a и b , верны (вы можете сделать это, подсчитав количество квадратов в каждом из горизонтальных и вертикальных направлений между концами стрелки, представляющей вектор и его наконечник). Ради удобства мы использовали целые значения для компонентов x и y всех векторов. В реальной жизни значение компонента часто будет иметь дробную часть, но принцип тот же. Добавлять векторы относительно легко, если вы знаете значения x и y компоненты каждого вектора.
Хотя мы пока добавили только два вектора вместе, процесс работает одинаково хорошо для любого количества векторов. Рассмотрим сценарий, показанный ниже, который показывает четыре свободных вектора. Как вы думаете, что получится, если сложить их все вместе?
Что получится в результате сложения этих векторов?
Конечно, мы могли бы найти ответ, используя визуальный метод, который мы использовали ранее, но давайте сначала попробуем сложение векторов, используя численный метод.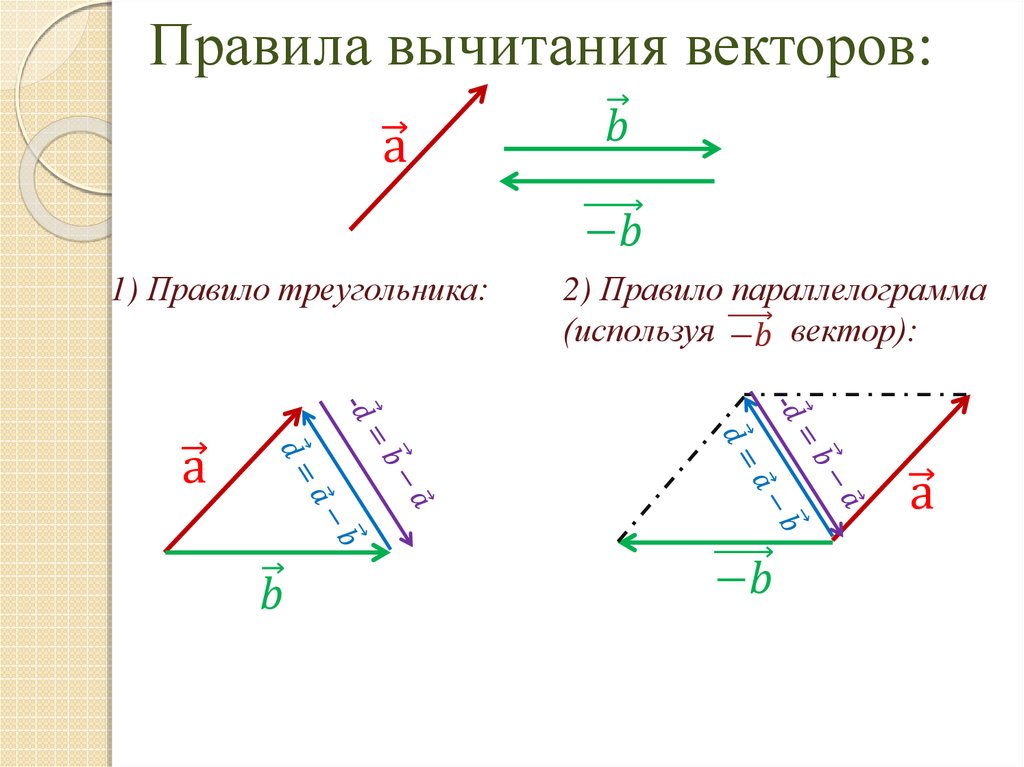 Нам нужно знать 9Компоненты 0021 x и y для каждого вектора, которые мы можем найти путем подсчета квадратов. Вот список векторов с их компонентами x и y в виде вектора-строки:
Нам нужно знать 9Компоненты 0021 x и y для каждого вектора, которые мы можем найти путем подсчета квадратов. Вот список векторов с их компонентами x и y в виде вектора-строки:
a = (-4, 2)
b = (2, 1)
c = (5, -1)
d = (-3, -2)
Теперь у нас есть необходимая информация, мы можем представить все в матричной форме:
| a + b + c + d = | -4 | + | 2 | + | 5 | + | -3 | = | 0 | ||||||||||
| 2 | 1 | -1 | -2 | 0 |
Согласно приведенному выше расчету, сложение векторов a , b , c и d дают результат, для которого оба компонента x и y равны нулю. Единственный вывод, который мы можем сделать из этого, состоит в том, что если мы будем двигаться по каждому из векторов по очереди, в каком бы порядке мы ни выбрали (помня, что порядок не имеет значения при добавлении векторов), то мы всегда будем возвращаться в точку, где мы начал. Это действительно так, как показано на рисунке ниже. Вы можете играть с различным порядком этих векторов, но они всегда будут возвращаться к одной и той же точке. Обратите внимание, что вектор, для которого оба 9Компоненты 0021 x и y равны нулю, называется нулевым вектором (или нулевым вектором ).
Единственный вывод, который мы можем сделать из этого, состоит в том, что если мы будем двигаться по каждому из векторов по очереди, в каком бы порядке мы ни выбрали (помня, что порядок не имеет значения при добавлении векторов), то мы всегда будем возвращаться в точку, где мы начал. Это действительно так, как показано на рисунке ниже. Вы можете играть с различным порядком этих векторов, но они всегда будут возвращаться к одной и той же точке. Обратите внимание, что вектор, для которого оба 9Компоненты 0021 x и y равны нулю, называется нулевым вектором (или нулевым вектором ).
Результатом сложения этих векторов является нулевой вектор (0, 0)
Сложение векторов работает одинаково для трех измерений (или любого количества измерений, если уж на то пошло). На приведенной ниже диаграмме показаны три вектора: a , b и c . Также показан результат, полученный путем сложения этих векторов.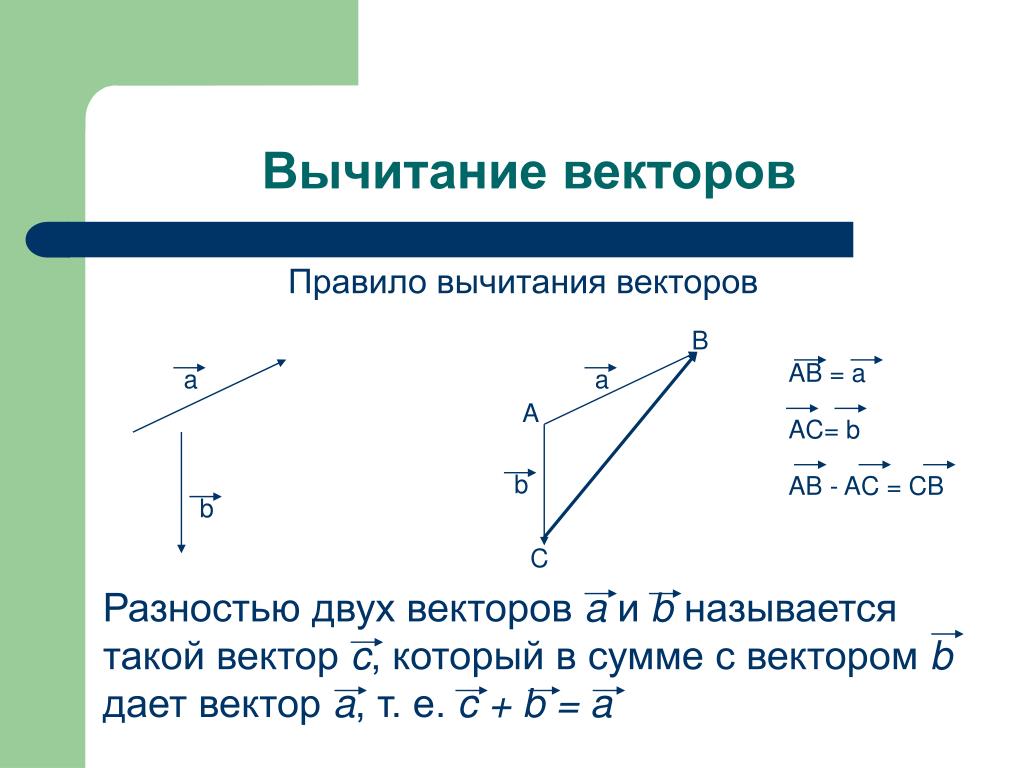 Обратите внимание, что относительное направление осей выбрано несколько произвольно. При работе в среде компьютерной графики принято считать, что горизонтальная ось равна 9.0021 x — ось, а вертикальная ось — y — ось. Тогда ось z является осью, перпендикулярной обеим осям x и y . Положительные значения z выходят за пределы экрана (по направлению к пользователю), а отрицательные значения z выходят за пределы экрана (от пользователя).
Обратите внимание, что относительное направление осей выбрано несколько произвольно. При работе в среде компьютерной графики принято считать, что горизонтальная ось равна 9.0021 x — ось, а вертикальная ось — y — ось. Тогда ось z является осью, перпендикулярной обеим осям x и y . Положительные значения z выходят за пределы экрана (по направлению к пользователю), а отрицательные значения z выходят за пределы экрана (от пользователя).
Результатом является сумма векторов a , b и c
Для тех, кто интересуется такими вещами, приведенная выше диаграмма была создана с использованием GeoGebra 5.0 Beta , которая на момент написания все еще находилась в стадии разработки. Это программное обеспечение находится в свободном доступе под Стандартной общественной лицензией GNU (веб-сайт: www.geogebra.org). Векторная арифметика показана ниже и очень похожа на то, что мы уже видели.

 Книга окажется полезной и в условиях заочного обучения.
Книга окажется полезной и в условиях заочного обучения.

 Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.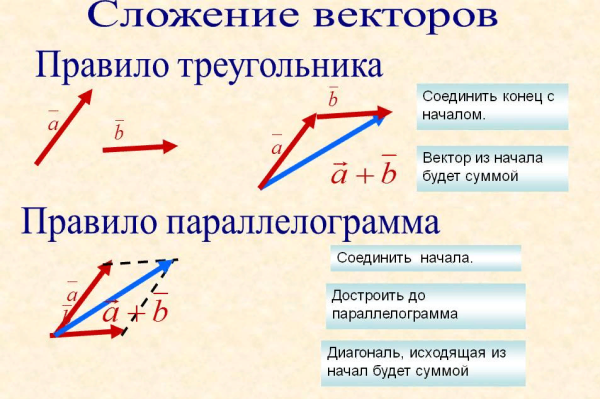 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.