Метаматериалы помогут решать уравнения со скоростью света
Американские физики спроектировали компактный оптический аналоговый вычислитель, который практически мгновенно решает дифференциальные и интегральные уравнения. В его основе лежит метаматериал с субволновым распределением диэлектрической проницаемости, а решение кодируется в рассеянной на нем волне. Исследование опубликовано в Physical Review Letters.
Классические компьютеры неразрывно ассоциируются с цифровой электроникой. Цифровой подход основан на представлении информации в виде единиц и нулей и ее обработке с помощью битовых операций. Такой подход естественен при сложении или вычитании целых и даже рациональных чисел. Он же применяется и при обработке аналоговых сигналов, которые представляют собой функции одной или нескольких переменных. В этом случае необходимо производить аналогово-цифровые преобразования.
Вместе с тем существует другой подход, основанный на использовании аналоговых компьютеров.
В нем обработка аналоговой информации производится вычислителем напрямую. Благодаря этому аналоговый подход обладает преимуществом в скорости при работе с функциями, например, дифференцировании, интегрировании или решении дифференциальных уравнений. Строго говоря, первые вычислительные машины были именно аналоговыми, в частности, механическими (например, Антикитерский механизм). Их ключевым недостатком стало отсутствие универсальности, и, в конце концов, во второй половине ХХ века аналоговые компьютеры уступили своё место цифровым устройствам, чья вычислительная мощность на тот момент росла согласно закону Мура.
В наши дни закон Мура сильно замедлился. В поисках способов ускорения вычислений физики и инженеры все чаще стали смотреть в сторону аналоговых компьютеров. Этому способствует бурный прогресс в области создания материалов, по-новому взаимодействующих со светом. Например, мы уже рассказывали, как ученые создали оптические и терагерцовые аналоговые нейронные сети. Ключевым недостатком этих технологий стал их большой размер, что не позволяет реализовать их на чипе.
Для решения этой проблемы Андреа Алу (Andrea Alù) с коллегой из Городского университета Нью-Йорка предложили использовать метаматериалы. С помощью численных симуляций они показали, что сконструированные на их основе микрометровые аналоговые вычислители способны почти мгновенно решать дифференциальные и интегро-дифференциальные уравнения с высокой точностью и устойчивостью, если облучать их светом определенной частоты.
Некоторые математические операции проще проводить в одну сторону, чем в другую. Типичный пример — это дифференцирование или интегрирование. На практике мы чаще всего сталкиваемся с необходимостью восстановить исходные данные по набору наблюдаемых данных, произведя вычисления в «сложную» сторону. Решение таких обратных задач занимает важное место в целом ряде прикладных наук.
Применение оптического аналогового вычислителя к этой проблеме основано на представлении входных и выходных решений в виде разложения по импульсам. Вычислитель проектируется таким образом, чтобы связать эти коэффициенты согласно некоторому оператору, который содержит в себе всю информацию о задаче.
Для реализации на практике невозможно сохранить бесконечность такого разложения: его приближенность должна быть сбалансирована с требуемой точностью восстановления.
Авторы предложили использовать в качестве входных и выходных данных электромагнитные волны, которые рассеиваются вычислителем, представляющим собой структуру, чья диэлектрическая проницаемость зависит от координаты некоторым заранее настроенным образом. Их задачей было описать профиль этой структуры в зависимости от того, какое уравнение вычислитель будет решать.
Для демонстрации работоспособности этого принципа, физики ограничились двумерным представлением. Оно предполагает, что все волны имеют цилиндрический волновой фронт, а диэлектрическая проницаемость зависит только от двух координат. Выбрав поляризацию волн, перпендикулярную плоскости, авторы свели электромагнитную задачу к скалярной. В этом случае входные и выходные данные имели вид одномерных функций полярного угла.
Исследователи раскладывали рассеянные и падающие волны по функциям Ханкеля первого и второго рода, соответственно.
Это позволило описывать данные в виде столбцов, а само математическое преобразование в виде матрицы. Для того чтобы сопоставить этой матрице некоторое распределение диэлектрической проницаемости, физики решали задачу оптимизации для целевой функции, собранной из ошибок преобразования для всех компонент разложения.
В качестве примера физики спроектировали вычислитель, который решает дифференциальное уравнение второго порядка, а также интегральное уравнение Фредгольма второго рода. В их модели рабочая частота волн, раскладываемых по пяти гармоникам, составила 135 терагерц, радиус структуры был равен одному микрометру, а информация считывалась с радиуса, равного 1,6 микрометра. В результате вычислений они восстанавливали пространственный профиль для диэлектрических проницаемостей, равный 1 и 12. Работоспособность профиля авторы проверяли методом конечных элементов, сравнивая волны на выходе с точным решением уравнений.
Результаты симуляций показали, что сделанных приближений достаточно для хорошего воспроизведения решений.
Модель показала устойчивость даже тогда, когда авторы добавили шум к частоте и к распределению диэлектрической проницаемости. Физики отмечают, что если расширить описанный метод до трехмерного случая, это позволит решать задачи для двумерных функций. В данный момент они работают над экспериментальной реализацией предложенного аналогового вычислителя в рамках оптики и акустики.
Ранее мы уже рассказывали, как покрытие стен офиса метаповерхностями превратило его в аналоговый вычислитель дискретного двумерного преобразования Фурье, работающего на частотах Wi-Fi.
Марат Хамадеев
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Как научиться решать простые и сложные уравнения
Как научиться решать простые и сложные уравнения
Уважаемые родители!
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для многих смежных дисциплин. В послешкольной жизни реальной необходимостью становится непрерывное образование, что требует базовой общешкольной подготовки, в том числе и математической.
В начальной школе закладываются не только знания по основным темам, но и развивается логическое мышление, воображение и пространственные представления, а также формируется интерес к данному предмету.
Соблюдая принцип преемственности, мы сделаем упор на важнейшую тему, а именно «Взаимосвязь компонентов действий при решении составных уравнений».
С помощью данного урока можно без труда научиться решать усложненные уравнения. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений.
Многих, родителей ставит в тупик вопрос – как же заставить детей научиться решать простые и сложные уравнения. Если уравнения простые — это еще пол беды, но ведь бывают и сложные – например интегральные. Кстати, для сведения, есть и такие уравнения, над решением которых бьются лучшие умы нашей планеты и за решение которых выдаются очень весомые денежные премии. Например, если вспомнить Перельмана и невостребованную им денежную премию в размере нескольких миллионов.
Однако вернемся для начала к простым математическим уравнениям и повторим виды уравнений и названия компонентов. Небольшая разминка:
_________________________________________________________________________
РАЗМИНКА
Найди лишнее число в каждом столбике:
2) Какого слова не хватает в каждом столбике?
3) Соедините слова из первого столбика со словами из 2 столбика.
«Уравнение» «Равенство»
4) Как вы объясните, что такое «равенство»?
5) А «уравнение»? Это равенство? Что в нем особенного?
слагаемое сумма
уменьшаемое разность
вычитаемое произведение
множитель равенство
делимое
уравнение
Вывод: Уравнение – это равенство с переменной, значение которой надо найти.
_______________________________________________________________________
Предлагаю каждой группе написать на листке фломастером уравнения: (на доску)
1 группе — с неизвестным слагаемым; 2 группе — с неизвестным уменьшаемым; 3 группе – с неизвестным вычитаемым; 4 группе – с неизвестным делителем; 5 группе – с неизвестным делимым; 6 группе – с неизвестным множителем. | 1 группа х + 8 = 15 2 группа х – 8 = 7 3 группа 48 – х = 36 4 группа 540 : х = 9 5 группа х : 15 = 9 6 группа х * 10 = 360 |
Один из группы должен на математическом языке прочитать свое уравнение и прокомментировать их решение, т. е. проговорить выполняемую операцию с известными компонентами действий (алгоритм).
Вывод: Умеем решать простые уравнения всех видов по алгоритму, читать и записывать буквенные выражения.
_____________________________________________________________________________
Предлагаю решить задачу, в которой появляется новый тип уравнений.
Х + 2кг 5кг и 3 кг | С какой величиной связан рисунок? Составьте и запишите по этому рисунку уравнение: Подберите для полученного уравнения подходящее уравнение: х + а = в а : х = в х : а = в х * а = в х – а = в а – х = в |
Вывод: Познакомились с решением уравнений, в одной из частей которых содержится числовое выражение, значение которого надо найти и получить простое уравнение.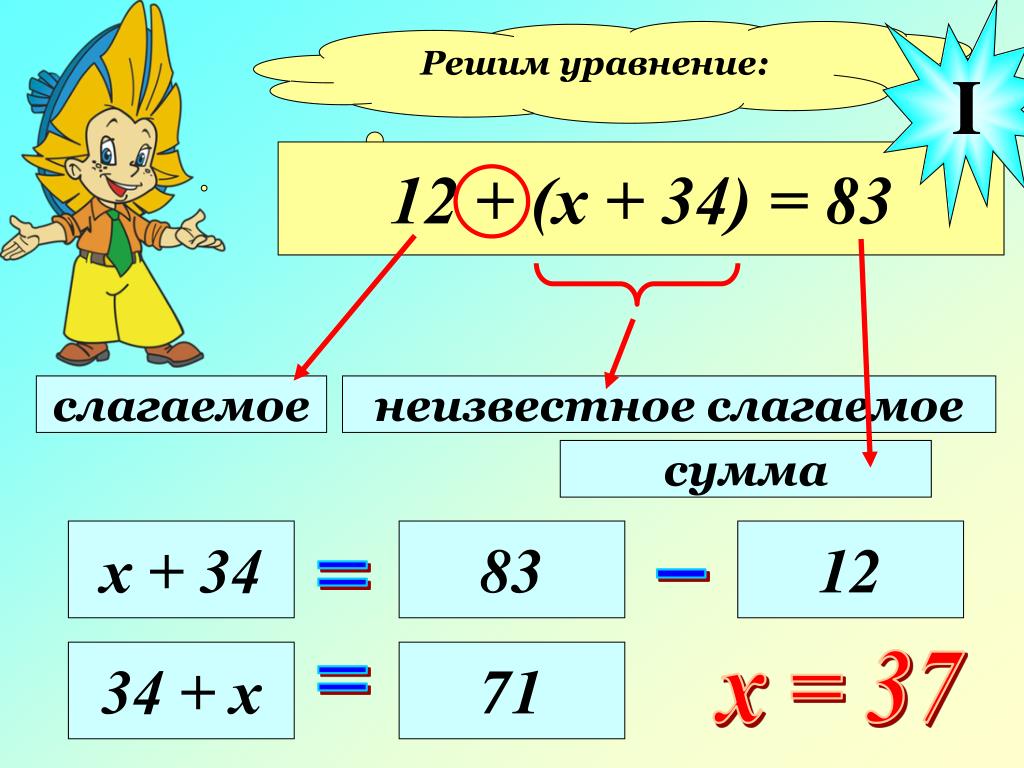
________________________________________________________________________
Рассмотрим еще один вариант уравнения, решение которого сводится к решению цепочки простых уравнений. Вот один из введения составных уравнений.
а + в * с (х – у) : 3 2 * d + (m – n) Являются ли уравнениями записи? Почему? Как называют такие действия? Прочитайте их, называя последнее действие: | Нет. Это не уравнения, т. к. в уравнении должен быть знак «=». Выражения а + в * с — сумма числа а и произведения чисел в и с; (х – у) : 3 — частное разности чисел х и у; 2 * d + (m – n) — сумма удвоенного числа d и разности чисел m и n. |
Предлагаю каждому записать на математическом языке предложение:
Произведение разности чисел х и 4 и числа 3 равно 15.
Запишите на математическом языке предложение: произведение разности чисел х и 4 и числа 3 равно 15 | (х – 4) * 3 = 15 |
ВЫВОД: Возникшая проблемная ситуация мотивирует постановку цели урока: научиться решать уравнения в которых неизвестный компонент является выражением. Такие уравнения являются составными уравнениями.
__________________________________________________________________________
А может нам помогут уже изученные виды уравнений? (алгоритмы)
На какое из известных уравнений похоже наше уравнение? Х * а = в
ОЧЕНЬ ВАЖНЫЙ ВОПРОС: Чем является выражение в левой части – суммой, разностью, произведением или частным?
(х – 4) * 3 = 15 (Произведением)
Почему? (т.к. последнее действие – умножение)
Вывод: Такие уравнения еще не рассматривались. Но можно решить, если на выражение х – 4 наложить карточку (у — игрек), и получится уравнение, которое легко можно решить, используя простой алгоритм нахождения неизвестного компонента.
При решении составных уравнений необходимо на каждом шаге осуществлять выбор действия на автоматизированном уровне, комментируя, называя компоненты действия.
↓
↓
↓
↓
| (у – 5) * 4 = 28 |
Вывод: В классах с разной подготовкой эта работа может быть организована по-разному.
В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
_____________________________________________________________________________
ЗАКЛЮЧЕНИЕ:
Когда речь идёт о чём-нибудь очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два — четыре!».
А ведь прежде чем додуматься до того, что дважды два — четыре, людям пришлось учиться много, много тысяч лет.
Многие правила из школьных учебников арифметики и геометрии были известны древним грекам две с лишним тысячи лет назад.
Всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись.
А чем дальше, тем больше и точнее нужно было считать. С каждым десятилетием математика становилась всё нужнее людям.
Трудно представить, как жили бы люди, если бы не умели считать, измерять, сравнивать. Этому учит математика.
Сегодня Вы окунулись в школьную жизнь, побывали в роли учеников и я предлагаю Вам, уважаемые родители, оценить свои умения по шкале.
Мои умения | Дата и оценка |
Компоненты действий. | |
Составление уравнения с неизвестным компонентом. | |
Чтение и запись выражений. | |
Находить корень уравнения в простом уравнении. | |
Находить корень уравнения, в одной из частей которых содержится числовое выражение. | |
Находить корень уравнения, в которых неизвестный компонент действия является выражением. |
Решение уравнений — документация по SymPy 1.11
НаверхПереключить боковую панель оглавления
Пакет Python SymPy может символически решать уравнения, дифференциальные уравнения, линейные уравнения, нелинейные уравнения, матричные задачи, неравенства, Диофантовы уравнения и вычисление интегралов. SymPy также может решать численно.
92 + у = 2, х — у = 4\)\(\{(х = -3, у = -7), (х = 2, у = 2)\}\)
Численное решение уравнения
\(\cos(x) = x \)
\( х \приблизительно 0,739085133215161\)
Алгебраическое решение обыкновенного дифференциального уравнения
\(у»(х) + 9у(х)=0 \)
\( х = 1, у = 0\)
Алгебраическое решение матричной задачи
\( \left[\begin{array}{cc} 1 & 1\\1 & -1\end{array}\right] \left[\begin{array}{cc} x\\y\end{ array}\right] = \left[\begin{array}{cc} 2\\0\end{array}\right] \)
\( \left[\begin{array}{cc} x\\y\end{массив}\right] = \left[\begin{array}{cc} 1\\1\end{массив}\right ]\)
\( \{(х = 2, у = 1), (х = 5, у = 1)\}\)
Примечание: SymPy имеет функцию с именем solve() который предназначен для поиска корней уравнения или системы уравнений.
SymPy solve() может быть или не быть тем, что вам нужно для конкретной проблемы,
поэтому мы рекомендуем вам использовать ссылки на этой странице, чтобы узнать, как «решить» вашу проблему.
И хотя общеупотребительным разговорным выражением является, например, «решить интеграл»,
в терминологии SymPy это будет «вычислить интеграл».
Математическая головоломка: Поможешь медведю решить это уравнение?
Головоломка
Опубликовано
Это алгебраическое уравнение с заполнением пробелов требует, чтобы вы выяснили, какой арифметический символ находится где. Можете ли вы решить это?
К Кортни Мур | Fox News
Художник-график проверяет все знания математического порядка операций со строкой чисел и отсутствующими арифметическими символами.
Гергели Дудас из Будапешта, Венгрия, поделился с Fox News Digital новой визуальной математической задачей, в которой мультяшный медведь пытается выяснить, какие арифметические символы стоят между четырьмя цифрами, написанными на зеленой доске.
Маленькая птичка с красным галстуком-бабочкой, похоже, доставила медведю проблемы в пустынном лесу.
ЗАДАЧА ДЛЯ МОЗГОВ: ЭТА «СЛОЖНАЯ» МАТЕМАТИЧЕСКАЯ ГОЛОВОЛОМКА, ВДОХНОВЛЕННАЯ ПРИРОДОЙ, МОЖЕТ ЗАСТАВИТЬ ВАС, ЕСЛИ БУДЕТ НЕВНИМАТЕЛЬНЫМ
Четыре варианта арифметических символов, предложенных Дудасом для математической задачи на заполнение пробелов, включают сложение, вычитание, умножение и деление, но необходимы только три символа.
Между тем, четыре цифры, написанные на доске, включают 10, 5, 6 и 4.
При правильном объединении сумма математической задачи равна 8.
Сможете ли вы решить каждое математическое уравнение?
Подсказка: вам нужно будет вернуться к школьному уроку по порядку действий — круглые скобки, показатели степени, умножение, деление, сложение и вычитание (PEMDAS) — чтобы выяснить, какие арифметические символы стоят между каждым числом.
ЧАШКА КОФЕ ЗАДАЧА ДЛЯ МОЗГОВ: МОЖЕТЕ ЛИ ВЫ РЕШИТЬ ЭТУ МАТЕМАТИЧЕСКУЮ ЗАГАДКУ?
Некоторым может показаться, что решить математическую задачу сложно, так как в ней нет круглых скобок, но задачу все же можно решить, если знать, в каком направлении двигаться.
Дудас поделился своей искусной математической задачей в своих аккаунтах в социальных сетях в понедельник, 8 мая, и, судя по комментариям, оставленным под его публикацией, большинство из них смогли решить ее на Facebook.
«Заняло минуту, мои математические навыки такого типа немного заржавели», — написал один из пользователей Facebook.
«Это было легко… не забывайте порядок действий», — написал другой пользователь.
«Даже не пытался. Математика, использующая более одного символа, не была другом», — признал один из пользователей Facebook с поражением.
ЗАДАЧА ДЛЯ МОЗГОВ: ПОМНИТЕ ПЕМДАСА? ПОПРОБУЙТЕ РЕШИТЬ ЭТО МАТЕМАТИЧЕСКОЕ УРАВНЕНИЕ
Нужна помощь в решении математической задачи?
См. решение на веб-сайте Дудаса: dudolfsolutions.blogspot.com/2023/05/equation-solution.html.
Если вас не убедило решение Дудаса, ресурс «Использование порядка операций без скобок», опубликованный платформой онлайн-обучения Study.
Нажмите здесь, чтобы подписаться на нашу новостную рассылку Lifestyle
Dudás — комический автор и художник, который опубликовал несколько книг по иллюстрациям, в том числе «Bear’s Springtime Book of Hidden Things» и «Медвежья Книга Скрытых вещей: Рождественские «Ищи и найди: Рождественская книга для детей».
Его обычная работа в стиле «ищи и найди» была представлена на миниатюрных принтах, кофейных кружках и различных других товарах. Иногда Дудас публикует сложные математические задачи на своем веб-сайте и в социальных сетях.
У Дудаса более 167 000 преданных подписчиков в Facebook, более 49 000 подписчиков в Instagram, более 8 300 подписчиков в Twitter и сотни подписчиков в Pinterest.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ ПРИЛОЖЕНИЕ FOX NEWS
Хотите попробовать еще одну головоломку? Проверьте свои навыки с помощью этой головоломки «ищи и найди».