Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел.  8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами.  30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49.  3. 3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени.  130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения.  149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 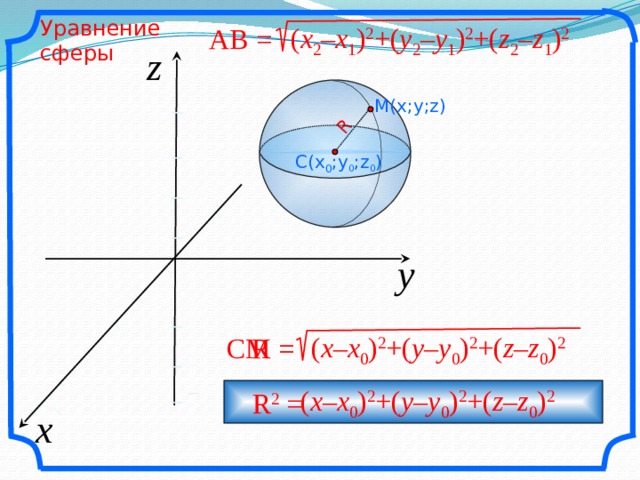 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. 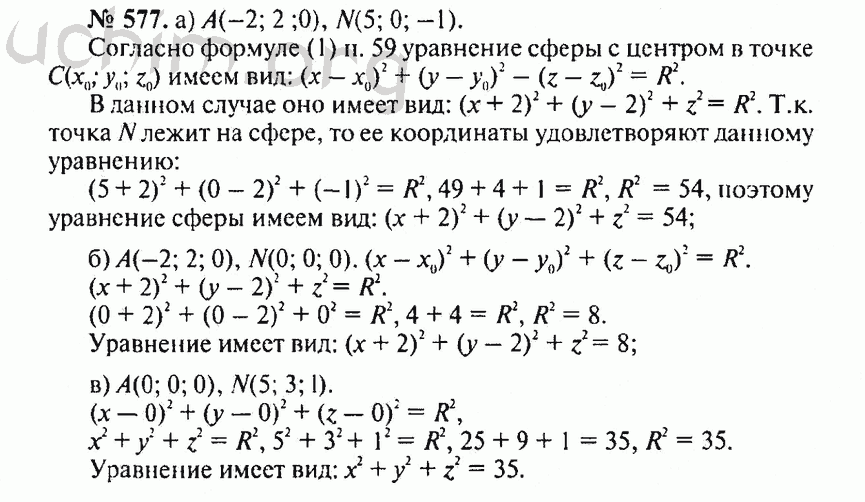 Неравенства и системы неравенств с двумя переменными. Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21.  Производная и ее применения Производная и ее применения209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных. Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22.  23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 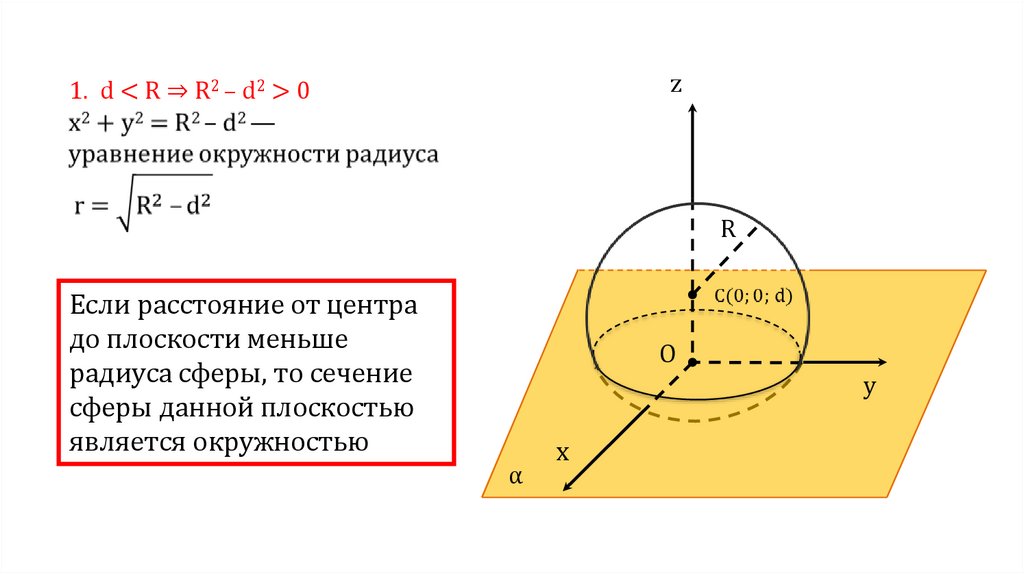 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76.  Понятие движения. Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
Сфера и шар. Уравнение сферы
На этом уроке мы вспомним понятия сферы и шара. Дадим их определения. Рассмотрим их основные элементы. А также выведем уравнение сферы радиуса с центром в точке .
Итак, рассмотрим понятия сферы и шара. В окружающем мире предметы имеют очень разнообразные формы. Среди них встречаются так называемые «круглые тела». Особое место среди круглых тел занимает шар.
Итак, шар – это геометрическое тело.
Форму, близкую к форме шара, имеют шарики мороженного, снежный ком, бусинки, светильники.
Некоторые архитектурные сооружения.
Декоративным растениям также придают форму шара.
Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Как окружность, есть граница круга, так и сфера – это граница шара.
Представление о сфере дают полые круглые предметы, например, мячи (футбольный, баскетбольный, волейбольный и т.д.), шарики для украшения ёлки, мыльные пузыри.
А также ставший популярным видом отдыха в наше время «аквазорбинг». Зорб даёт представление о сфере.
Сфера входит в число наиболее привлекательных пространственных фигур. Использование в строительстве и архитектуре конструкций, имеющих форму сферы, придает сооружениям особое величие и служит подтверждением тому, что сфера – достаточно гармоничная геометрическая фигура.
Чтобы уяснить разницу между понятиями шар и сфера, давайте внимательно посмотрим на экран.
Перед вами изображены воздушный шар и бильярдный шар. Отметим,
что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со
сферой, а во втором с полноценным шаром со своим содержимым внутри.
Отметим,
что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со
сферой, а во втором с полноценным шаром со своим содержимым внутри.
Определение:
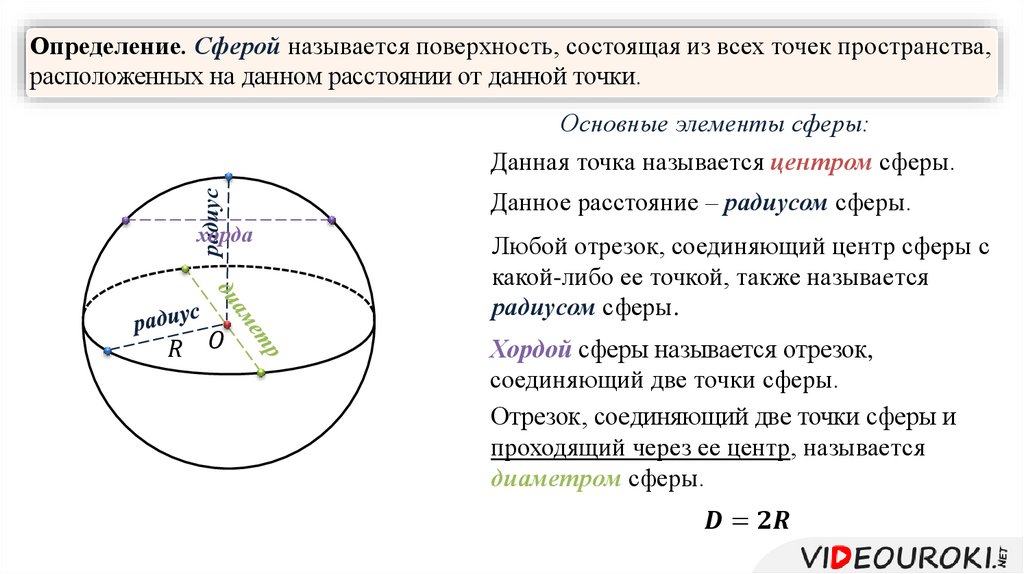
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
А теперь назовём основные элементы сферы.
Данная точка называется центром сферы (в нашем случае это точка О), а данное расстояние – радиусом сферы. Радиус сферы часто обозначают латинской буквой .
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Все радиусы одной сферы равны между собой.
Хордой сферы называется отрезок, соединяющий две точки сферы.
Отрезок, соединяющий две точки сферы и проходящий
через её центр, называется диаметром сферы. Любой диаметр сферы равен
двум радиусам .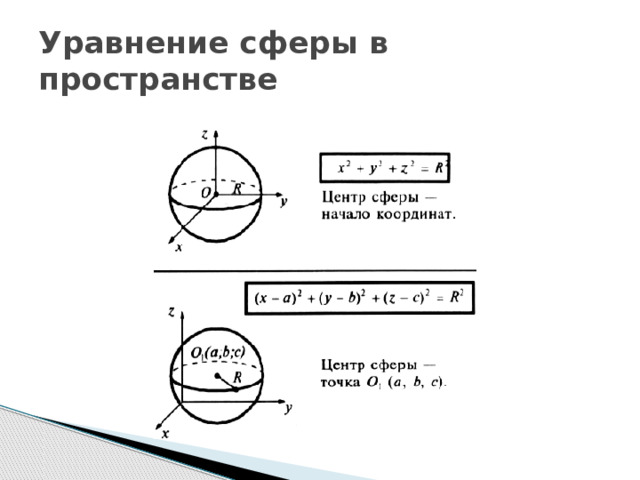
Тело, ограниченное сферой, называется шаром.
Определение:
Шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Центр, радиус, хорда и диаметр сферы называются также центром, радиусом, хордой и диаметром шара.
Т.е. отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара.
Отрезок, соединяющий две точки сферы называется хордой шара.
Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам .
Рассмотрим чертёж.
Перед нами математическое изображение шара. Точка О –
это центр шара. Все точки поверхности шара одинаково удалены от
центра шара. Понятно, что шар радиуса с
центром О содержит все точки пространства, расположенные от точки О на
расстоянии, не превышающем (включая
саму точку О), и не содержит других точек.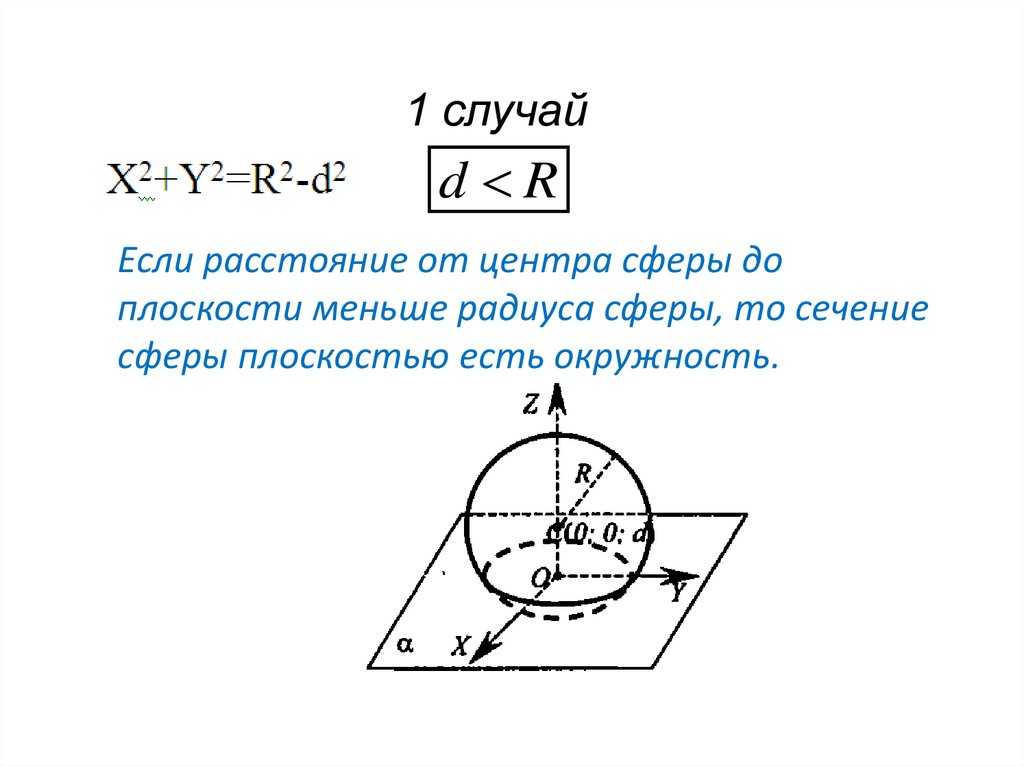
Хотелось бы обратить внимание на то, что шар может быть получен путём вращения полукруга вокруг его диаметра.
При этом сфера образуется в результате вращения полуокружности вокруг её диаметра.
Задача: отрезок – хорда сферы, не проходящая через центр сферы . Вычислите расстояние от центра сферы до середины хорды , если радиус сферы равен см, а длина хорды равна см.
Решение: обозначим середину хорды точкой .
Рассмотрим . Он равнобедренный, т.е. , так как . А как мы знаем, все радиусы одной сферы равны между собой. Отсюда, (см).
Теперь рассмотрим . Он прямоугольный, так как отрезок является серединным перпендикуляром проведённым к хорде . Его катет (см).
Воспользовавшись теоремой Пифагора найдём катет ,
который как раз таки и есть расстояние от центра сферы до середины хорды .
Получаем, что (см).
Запишем ответ.
Перейдём к уравнению сферы.
Для начала вспомним, что уравнение с тремя переменными , , называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
Напомним, что уравнение плоскости, проходящей через точку и перпендикулярной к ненулевому вектору имеет следующий вид:
где
Теперь давайте выведем уравнение сферы радиуса с центром в точке .
Напомним, что расстояние от произвольной точки до точки вычисляется по формуле:
Если точка лежит на данной сфере, то расстояние , или , т.е. координаты точки удовлетворяют уравнению:
Если же точка не
лежит на данной сфере, то расстояние ,
или ,
т.е. координаты точки не
удовлетворяют уравнению сферы.
Следовательно, в прямоугольной системе координат уравнение сферы радиуса с центром в точке :
Если уравнение относительно прямоугольных координат определяет поверхность в пространстве, то ею является сфера.
Задача: напишите уравнение сферы с центром в точке радиусом равным см.
Решение: запишем уравнение сферы в общем виде, где , и – координаты центра сферы.
Подставим заданные координаты центра сферы в уравнение. Получим, что уравнение данной нам сферы выглядит так:
Запишем ответ.
Задача: найдите координаты центра и радиус сферы, заданной уравнением: .
Решение: запишем уравнение сферы в общем виде, где , и – координаты центра сферы.
Тогда не трудно заметить, что координаты центра сферы будут равны 2, — 1, 0.
А радиус заданной сферы равен .
Не забудем записать ответ.
Задача: какую поверхность определяет уравнение
?
Решение: запишем уравнение сферы в общем виде, где , и – координаты центра сферы.
Преобразуем наше уравнение.
Разделим почленно это уравнение на 4.
Получим, .
Затем выделим полные квадраты. Получим, .
Преобразуем слагаемые получившегося выражения. Получим, .
Теперь сравним последнее уравнение с уравнением сферы в общем виде. Заметим, что исходное уравнение определяет сферу с центром в точке и .
Запишем ответ.
Итоги:
На этом уроке мы вспомнили понятия сферы и шара. Узнали,
что сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки. А шар – это совокупность
всех точек пространства, находящихся от центра на расстоянии, не больше
заданного. Назвали основные элементы сферы и шара. А также вывели уравнение
сферы радиуса с
центром в точке .
А также вывели уравнение
сферы радиуса с
центром в точке .
Калькулятор уравнения сферы
Создано Кришной Нелатуру
Отредактировано Стивеном Вудингом
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое уравнение сферы?
- Как вывести уравнение сферы
- Расширенная форма уравнения сферы
- Уравнение сферы по концам любого диаметра
- Уравнение сферы по ее центру и любой известной точке на ее поверхности
- Как использовать этот калькулятор уравнения сферы
Наш калькулятор уравнения сферы поможет вам написать уравнение сферы в стандартной форме или расширенной форме , если вы знаете центр и радиус сферы. Кроме того, вы можете найти уравнение сферы, если вы знаете ее центр и любую точку на ее поверхности или если вы знаете конечных точек любого из ее диаметров . Этот калькулятор также может найти центр и радиус сферы из ее уравнения.
Этот калькулятор также может найти центр и радиус сферы из ее уравнения.
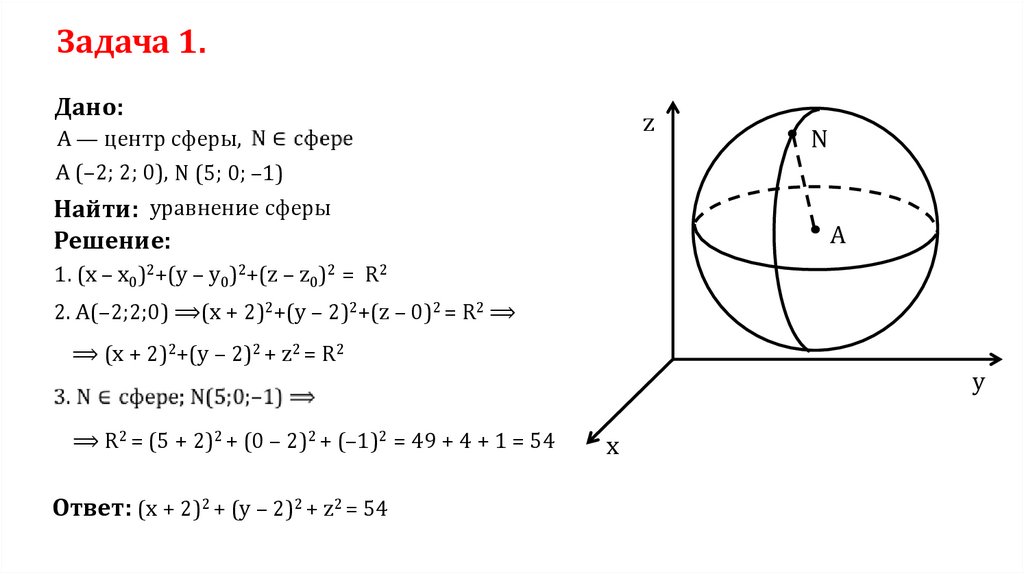
Вам интересно, что такое стандартное уравнение сферы или как найти центр и радиус сферы, используя это уравнение? Возможно, вы сталкивались с уравнением сферы, которое не похоже на общее уравнение? Вам интересно, как знание конечных точек диаметра или центра и точки на сфере может помочь вам найти уравнение сферы? Возьмите свой любимый напиток и продолжайте читать эту статью; мы решим эти вопросы вместе! 92(x−h)2+(y−k)2+(z−l)2=r2
где:
- (x,y,z)(x,y,z)(x,y,z) ) – координаты любой точки, лежащей на поверхности сферы;
- (h,k,l)(h,k,l)(h,k,l) – Координаты центра сферы; и
- ррр – Радиус сферы.
 92 = 36(x−7)2+(y+12)2+(z+4)2=36, то его центр будет (7,−12,−4)\small(7,-12,-4 )(7,−12,−4).
92 = 36(x−7)2+(y+12)2+(z+4)2=36, то его центр будет (7,−12,−4)\small(7,-12,-4 )(7,−12,−4).Как вывести уравнение сферы
Теперь, когда мы знаем стандартное уравнение сферы, давайте узнаем, как оно появилось:
- Первое, что нужно понять, это то, что уравнение сферы представляет всех точек лежащие на равном расстоянии от центра точки. Другими словами, любая точка, которая находится на расстоянии rrr от точки (h,k,l)(h,k,l)(h,k,l), лежит на сфере. Звучит знакомо? Уравнение окружности работает точно так же! Перейдите к нашему калькулятору уравнения окружности и посмотрите, сможете ли вы обнаружить больше сходства! 92\\
\end{align*}((x−h)2+(y−k)2+(z−l)2
)2⟹(x−h)2+(y−k)2+(z− l)2=(r)2=r2
И, вуаля! Вот так мы получили стандартное уравнение сферы ! Стоит повторить, что каждая точка SSS, удовлетворяющая этому уравнению, лежит на поверхности сферы.
Расширенная форма уравнения сферы
Иногда вы можете столкнуться с уравнением сферы, которое отличается от стандартной формы , которую мы обсуждали до сих пор.
 В общем случае такие уравнения должны выглядеть следующим образом: 92+Ex+Fy+Gz+H = 0x2+y2+z2+Ex+Fy+Gz+H=0
В общем случае такие уравнения должны выглядеть следующим образом: 92+Ex+Fy+Gz+H = 0x2+y2+z2+Ex+Fy+Gz+H=0где:
- EEE – Сумма всех коэффициентов членов xxx;
- FFF – Сумма всех коэффициентов членов yyy;
- GGG – сумма всех коэффициентов членов zzz; и
- HHH – Сумма всех констант.
На первый взгляд это уравнение может показаться пугающим, но если вы присмотритесь повнимательнее; это просто расширенная версия стандартной формы , к которой мы привыкли. Давайте воспользуемся методом заполнения квадратов, чтобы вернуться от расширенной версии к более простой стандартной форме: 92}{4}-Н} \end{align*}hklr2or: r=−2E=−2F=−2G=4E2+4F2+4G2−H=4E2+4F2+4G2−H
Нужна помощь в заполнении квадратов? Вам поможет наш комплектующий квадратный калькулятор.
В этом калькуляторе уравнения сферы вы можете просто выбрать опцию расширенной формы в качестве типа уравнения и ввести соответствующие значения EEE, FFF, GGG и HHH, чтобы получить уравнение в стандартной форме, его центр и радиус, и другие релевантная информация.

Уравнение сферы из концов любого диаметра
Теперь, когда вы знаете, что такое уравнение сферы, давайте обсудим, как его получить в тех случаях, когда у вас нет под рукой необходимых параметров. Предположим, вы знаете только конечных точек любого из диаметров сферы и не имеете информации о центральной точке или радиусе. У вас все еще есть способ сформулировать его уравнение.
Диаметр сферы AB с конечными точками A(x1,y1,z1)A(x_1,y_1,z_1)A(x1,y1,z1) и B(x2,y2,z2)B(x_2,y_2,z_2) )B(x2,y2,z2).Предположим, что диаметр ABABAB сферы имеет конечные точки A(x1,y1,z1)A(x_1,y_1,z_1)A(x1,y1,z1) и B(x2,y2,z2)B(x_2) ,y_2,z_2)B(x2,y2,z2). Ясно, что центр C(h,k,l)C(h,k,l)C(h,k,l) задается серединой ABABAB, которая определяется как: 92}r=(x1−h)2+(y1−k)2+(z1−l)2
Затем мы можем вставить этот центр и радиус в стандартное уравнение сферы .
Уравнение сферы из ее центра и любой известной точки на ее поверхности
Сфера с центром (h,k,l)(h,k,l)(h,k,l) и точкой P(px,py, pz)P(p_x,p_y,p_z)P(px,py,pz) на его поверхности.
Аналогично случаю выше, если мы знаем центр (h,k,l)(h,k,l)(h,k,l) и любую точку P(px,py,pz)P(p_x, p_y,p_z)P(px,py,pz) на сфере, мы можем использовать 92}r=(px−h)2+(py−k)2+(pz−l)2
Опять же, мы можем напрямую подставить значения центра и радиуса в стандартный уравнение сферы.
Как пользоваться этим калькулятором уравнения сферы
Вы можете использовать этот калькулятор уравнения сферы, чтобы найти уравнение сферы или найти центр и радиус сферы, в зависимости от переменных, которые вы уже знаете:
Если у вас есть центр и радиус , введите их непосредственно в поля координаты центра и радиуса , чтобы получить уравнение сферы в стандартной форме и расширенной форме .
Если вы знаете уравнение сферы в стандартной форме , выберите тип стандартного уравнения в поле Выберите уравнение .
 2r2 в поле RRR, чтобы вычислить центр и радиус сферы.
2r2 в поле RRR, чтобы вычислить центр и радиус сферы.Если вы знаете уравнение сферы в расширенной форме , выберите тип расширенного уравнения в поле Выберите уравнение . Введите значения коэффициентов x-члена в поле EEE, коэффициентов y-члена в поле FFF, коэффициентов z-члена в поле GGG и оставшегося постоянного члена в поле HHH, чтобы вычислить центр и радиус сфера.
Если вы знаете конечных точек любого диаметра сферы, выберите «Известные конечные точки диаметра AB» из поля Выберите уравнение и введите конечные точки, чтобы получить уравнение сферы вместе с ее центром и радиусом.
Если вы знаете центр и любую точку на сфере , выберите «Известная точка на сфере P(px,py,pz)P(p_x,p_y,p_z)P(px,py,pz) » из поля Выберите уравнение и введите координаты точки и координаты центра, чтобы получить уравнение сферы и ее радиус.

Как только вы узнаете радиус сферы, получить другие важные свойства, такие как площадь, не составит труда. Этот калькулятор оценит площадь поверхности и объем сферы для вашего удобства.
Если у вас возникли проблемы с калькулятором, в частности , если инструмент игнорирует ваши вводы , попробуйте обновить калькулятор и снова ввести значения в этом конкретном режиме калькулятора. Вы можете сделать это, нажав на циркуляр перезагрузить значок в самом низу инструмента.
Krishna nelaturu
Select Уравнение
(x-h) ² + (y-k) ² + (z-l) ² = r
Центральные координаты
X-координата
Y-координата
z-координат
z-координата
z-координата
z-координата
z-координата
z-координата
Радиус
Диаметр
Площадь поверхности
Объем
Посмотреть 39 похожих калькуляторов координатной геометрии 📈
Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… 36 еще
Окружность, площадь поверхности и формула объема
В геометрии сфера представляет собой набор всех точек в трехмерном пространстве, находящихся на одинаковом расстоянии (радиус) от данной точки (центра), или результат вращения окружность вокруг одного из его диаметров.
 Компоненты и части сферы аналогичны компонентам круга. Некоторые реальные примеры сфер включают футбольный мяч, баскетбольный мяч, модель земного шара и т. д. Поскольку сфера является трехмерным объектом, она имеет площадь поверхности и объем. Ниже приведено изображение сферы, показывающее радиус, диаметр и центр сферы.
Компоненты и части сферы аналогичны компонентам круга. Некоторые реальные примеры сфер включают футбольный мяч, баскетбольный мяч, модель земного шара и т. д. Поскольку сфера является трехмерным объектом, она имеет площадь поверхности и объем. Ниже приведено изображение сферы, показывающее радиус, диаметр и центр сферы.Части сферы: Мы знаем, что сфера — это трехмерный объект круглой формы. Итак, прежде чем перейти к уравнению сферы и другим вещам, связанным со сферой. Сначала мы узнаем о некоторых важных частях сферы, а именно:
- Радиус сферы: Это расстояние от точного центра сферы до любой точки на поверхности сферы.
- Диаметр сферы: Это самый длинный отрезок, который можно провести между двумя точками на сфере. Его длина вдвое больше радиуса сферы, т. е. диаметр = 2\(r\).
- Окружность сферы: Определяется как длина большого круга сферы. Большой круг — это тот, который содержит диаметр сферы.
 Это максимально возможный круг, который можно нарисовать внутри сферы.
Это максимально возможный круг, который можно нарисовать внутри сферы.
- Площадь поверхности сферы: Это область, покрытая поверхностью сферического объекта в трехмерном пространстве. 9{2}\). Это известно как стандартная форма уравнения сферы. Уравнение сферы в диаметральной форме
Диаметральная форма сферы означает, что уравнение сферы при заданных концах диаметра. Итак, уравнение сферы, крайние диаметры которой равны \(A(x_{1},y_{1},z_{1})\) и \(B(x_{2},y_{2},z_{2} )\) задается как
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})+(z-z_{1 })(z-z_{2})=0\).
Уравнение сферы в цилиндрических координатах 9{2}\), Уравнение сферы в параметрической формеОбщая форма параметрического уравнения сферы:
\((x,y,z) = (acos\theta sin\phi , asin\theta sin\phi, acos\phi)\),
где a — постоянный радиус, \(\theta\in [0,2\pi)\) — долгота и \(\phi\in [0,\pi]\) — совместная высота.

Поскольку поверхность сферы двумерна, параметрические уравнения обычно имеют две переменные (т. е. \(\theta\) и \(\phi\)). 9{2})=0\).
Окружность сферыОкружность сферы — это длина окружности наибольшего возможного круга внутри сферы (большой круг). Он также известен как большой круг, который содержит центр и диаметр сферы. Он измеряется в линейных единицах, таких как мм, см, м, дюйм или фут. На приведенном ниже рисунке показана длина окружности сферы.
Формула для нахождения длины окружности сферы:
Длина окружности (C) = 2\(\pi\)r, где \(\pi\) = 22/7 = 3,141, а r = радиус.
Площадь поверхности сферыПлощадь поверхности сферы — это площадь, покрытая внешней поверхностью сферы. Мы знаем, что сфера имеет полностью изогнутую форму, поэтому площадь криволинейной поверхности равна общей площади сферы (т.е. площади поверхности). Она также известна как площадь боковой поверхности сферы.
 {3}\), где \(\pi\) = 22/7 = 3,141 и r = радиус. 9{2}&2x_{4} &2y_{4} &2z_{4} &1 \\\end{vmatrix}\) = 0,
{3}\), где \(\pi\) = 22/7 = 3,141 и r = радиус. 9{2}&2x_{4} &2y_{4} &2z_{4} &1 \\\end{vmatrix}\) = 0,Решая приведенный выше определитель, мы получаем уравнение сферы, проходящей через четыре точки (т.е. \( (x_{1},y_{1},z_{1})\), \((x_{2},y_{2},z_{2})\), \((x_{3},y_{ 3},z_{3})\) и \((x_{4},y_{4},z_{4})\)).
Разница между кругом и сферойРазница между кругом и сферой приведена ниже:
Круг Сфера 9{2}-5x-5y-3z=0\). Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы об уравнении сферыВ.1 Как найти центр сферы из уравнения?
Ответ 1 9{2}&2x_{4} &2y_{4} &2z_{4} &1 \\
\end{vmatrix}\) = 0.

 В общем случае такие уравнения должны выглядеть следующим образом: 92+Ex+Fy+Gz+H = 0x2+y2+z2+Ex+Fy+Gz+H=0
В общем случае такие уравнения должны выглядеть следующим образом: 92+Ex+Fy+Gz+H = 0x2+y2+z2+Ex+Fy+Gz+H=0

 2r2 в поле RRR, чтобы вычислить центр и радиус сферы.
2r2 в поле RRR, чтобы вычислить центр и радиус сферы.
 Компоненты и части сферы аналогичны компонентам круга. Некоторые реальные примеры сфер включают футбольный мяч, баскетбольный мяч, модель земного шара и т. д. Поскольку сфера является трехмерным объектом, она имеет площадь поверхности и объем. Ниже приведено изображение сферы, показывающее радиус, диаметр и центр сферы.
Компоненты и части сферы аналогичны компонентам круга. Некоторые реальные примеры сфер включают футбольный мяч, баскетбольный мяч, модель земного шара и т. д. Поскольку сфера является трехмерным объектом, она имеет площадь поверхности и объем. Ниже приведено изображение сферы, показывающее радиус, диаметр и центр сферы.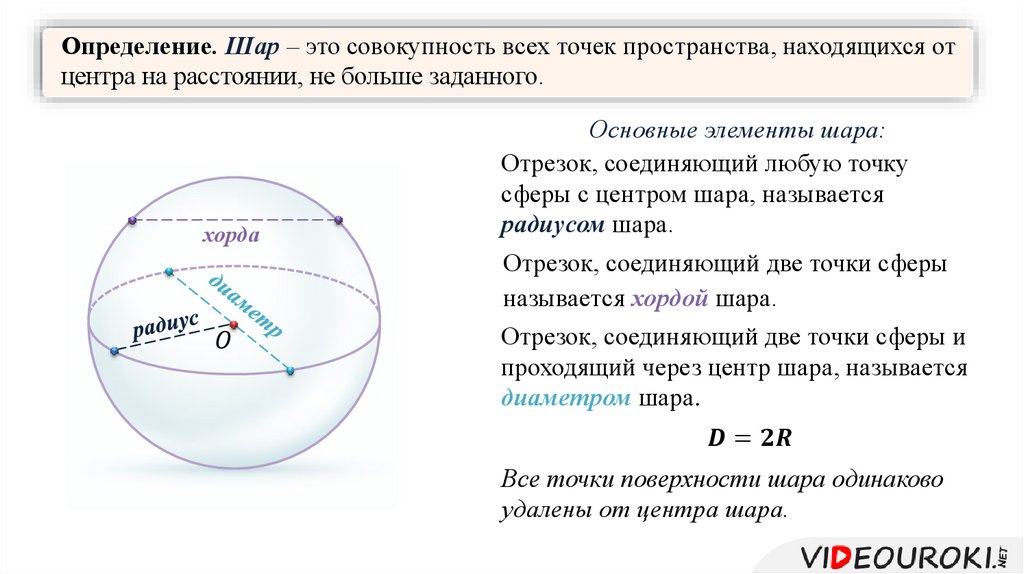 Это максимально возможный круг, который можно нарисовать внутри сферы.
Это максимально возможный круг, который можно нарисовать внутри сферы.
 {3}\), где \(\pi\) = 22/7 = 3,141 и r = радиус. 9{2}&2x_{4} &2y_{4} &2z_{4} &1 \\\end{vmatrix}\) = 0,
{3}\), где \(\pi\) = 22/7 = 3,141 и r = радиус. 9{2}&2x_{4} &2y_{4} &2z_{4} &1 \\\end{vmatrix}\) = 0,