Обратные тригонометрические функции и их свойства. 10 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
10 класс
Обратные тригонометрические функции
и их свойства
2015-2016 учебный год
Содержание
• Функция y = arcsin x и ее свойства
• Функция y = arccos x и ее свойства
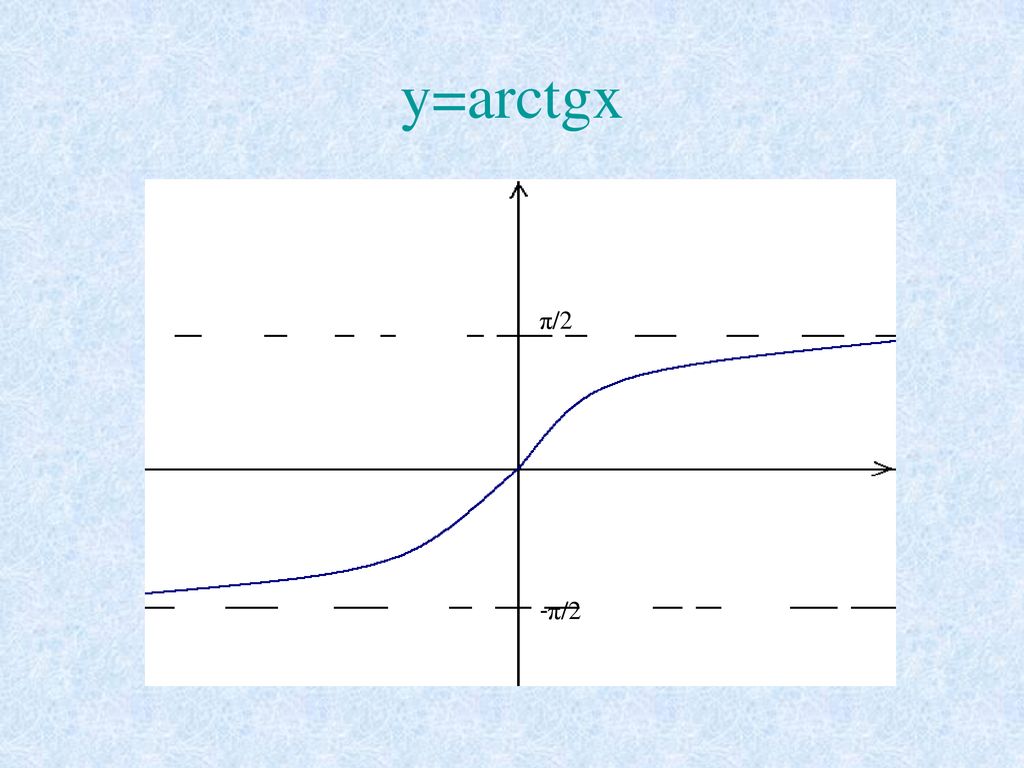
• Функция y = arctg x и ее свойства
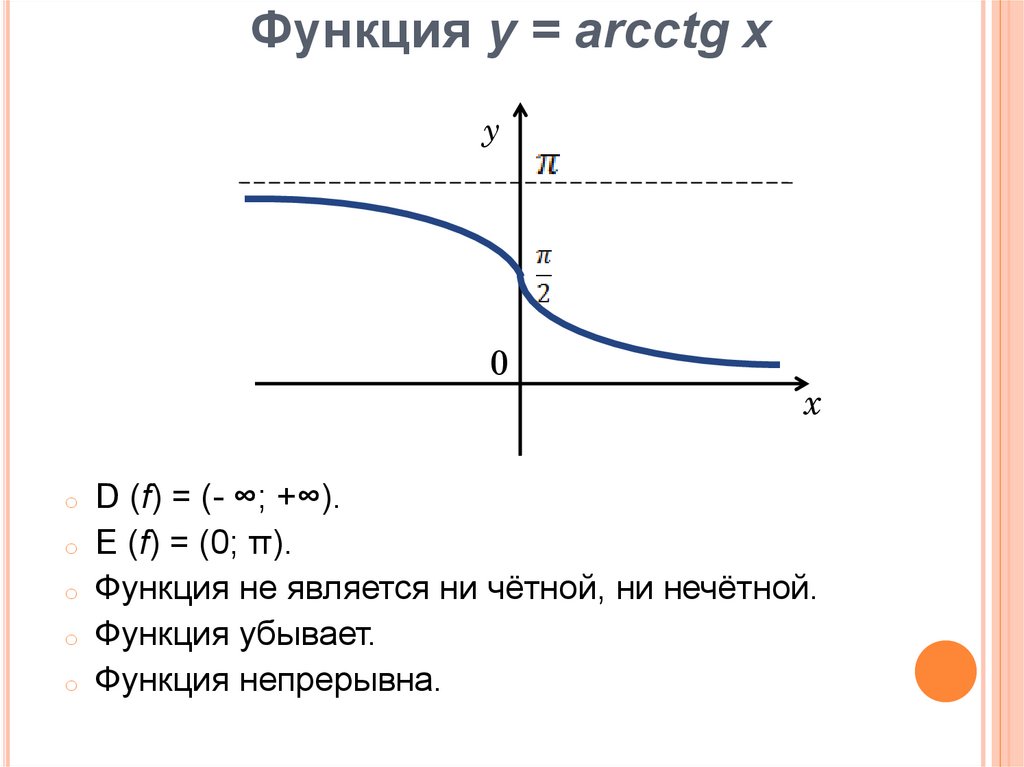
• Функция y = arcctg x и ее свойства
Функция y=arcsinx и ее свойства
Если |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2; π/2], синус которого
Если |а| ≤ 1, то
arcsin а = t
sin t = а,
-π/2 ≤ t ≤ π/2;
sin (arcsin a) = a
Функция y=arcsinx и ее график
у
π/2
y=arcsin x
y=sin x
х
-1
0
-π/2
1
π
Функция y=arcsinx и ее свойства
1. D(y) = [-1; 1].
2. E(y) = [-π/2; π/2].
3. arcsin (-x) = — arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
Функция y=arccosx и ее свойства
Если |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где -1 ≤ а ≤ 1
Функция y=arccosx и ее график
у
y=arccosx
π
π/2
Y=cos x
-1
π
0
1
х
Функция y=arccosx и ее свойства
1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
Функция y=arctgx и ее свойства
arctg а – это такое число из интервала (-π/2;
π/2), тангенс которого равен а.
arctg а = t
tg t = а,
-π/2 < t < π/2;
tg (arctg a) = a
Функция y=arctgx и ее график
у
π/2
y=arctg x
π/4
х
-1
0
-π/4
-π/2
y=tg x
1
π
Функция y=arctgx и ее свойства
1. D(y) = (- ; + ).
2. E(y) = (-π/2; π/2).
3. arctg (-x) = — arctg x – функция нечетная.
4. Функция возрастает на (- ; + ).
5. Функция непрерывна.
Функция y=arcctgx и ее свойства
arcсtg а – это такое число из интервала (0;
π), котангенс которого равен а.
arcсtg а = t
сtg t = а,
0 < t < π;
сtg (arcсtg a) = a
arcctg (-a) = π – arcctg a
Функция y=arcctgx и ее график
у
y=сtg x
y=arcсtg x
π/2
-π
-π/2
0
π/2
π
х
Функция y=arcctgx и ее свойства
1. D(y) = (- ; + ).
2. E(y) = (0; π).
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на (- ; + ).
5. Функция непрерывна.
English Русский Правила
Блог для уроків інформатики: Тригонометричні рівняння
Тригонометричні рівняння
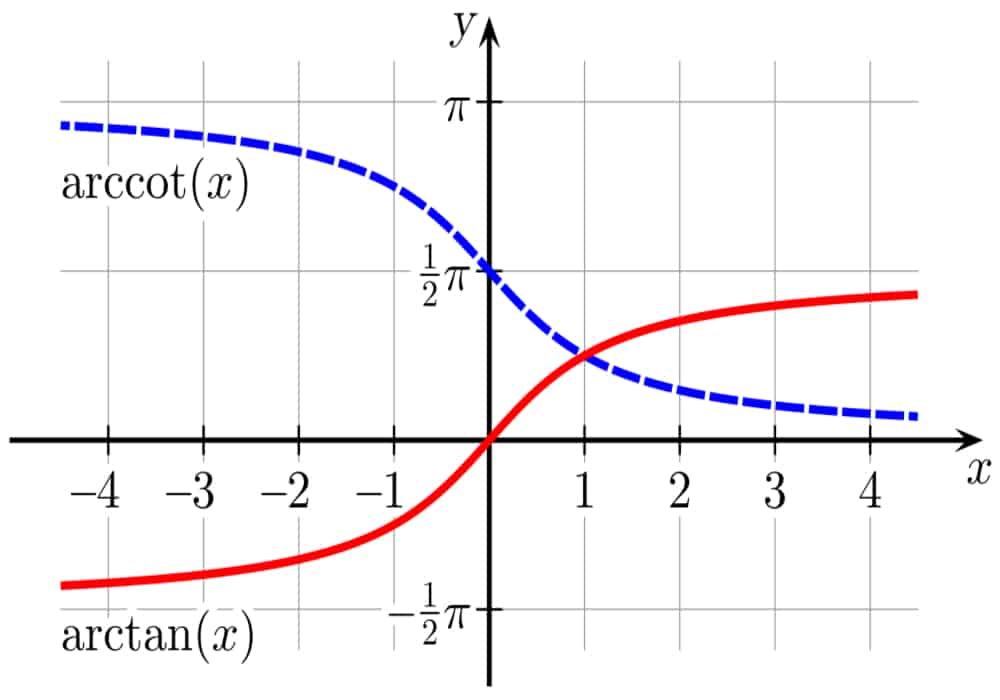
Арктангенс
Арктангенс, y = arcsin x, определен при и имеет множество значений .
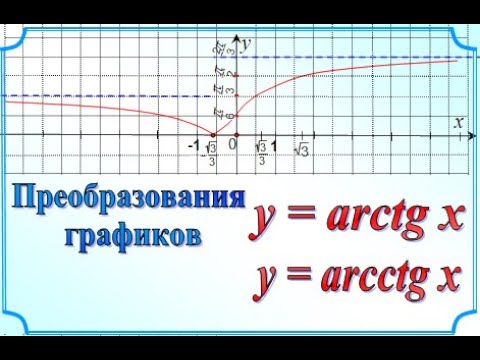
График функции арктангенс
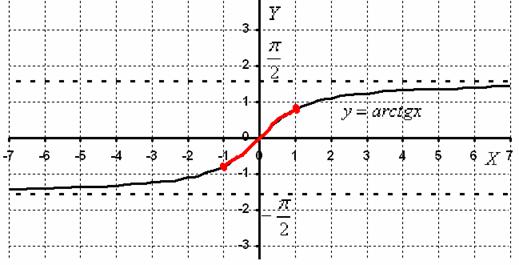
График функции y = arctg xГрафик арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс
Арккотангенс, y = arcctg x, определен при и имеет множество значений .
График функции арккотангенс
График функции y = arcctg xГрафик арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна.
Такое определение называют главным значением арккотангенса.Четность
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg xФункция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) =π – arcctg x ≠ ± arcctg x.
Свойства — экстремумы, возрастание, убывание
Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arcctg x | ||
| Область определения | – ∞ ≤ x ≤ ∞ | – ∞ ≤ x ≤ ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.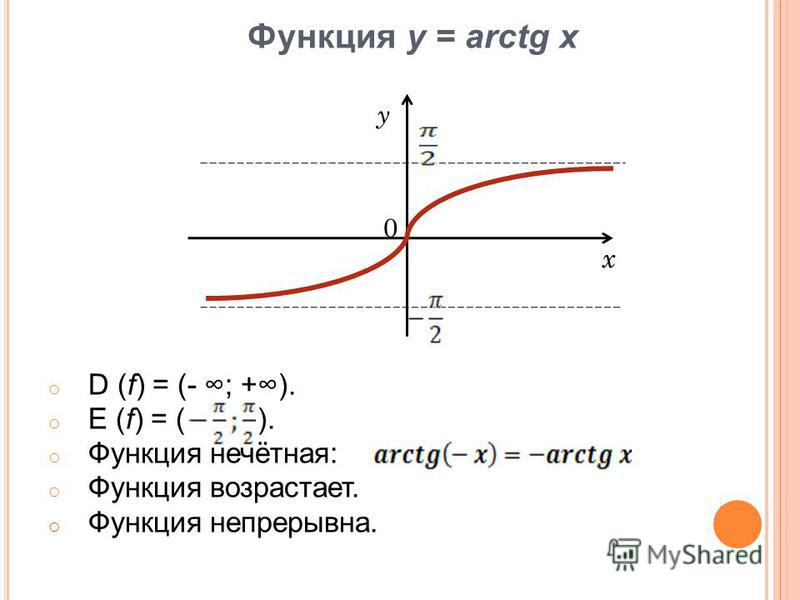
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | 120° | ||
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
Арксинус
Арксинус, y = arcsin x определен при и имеет множество значений .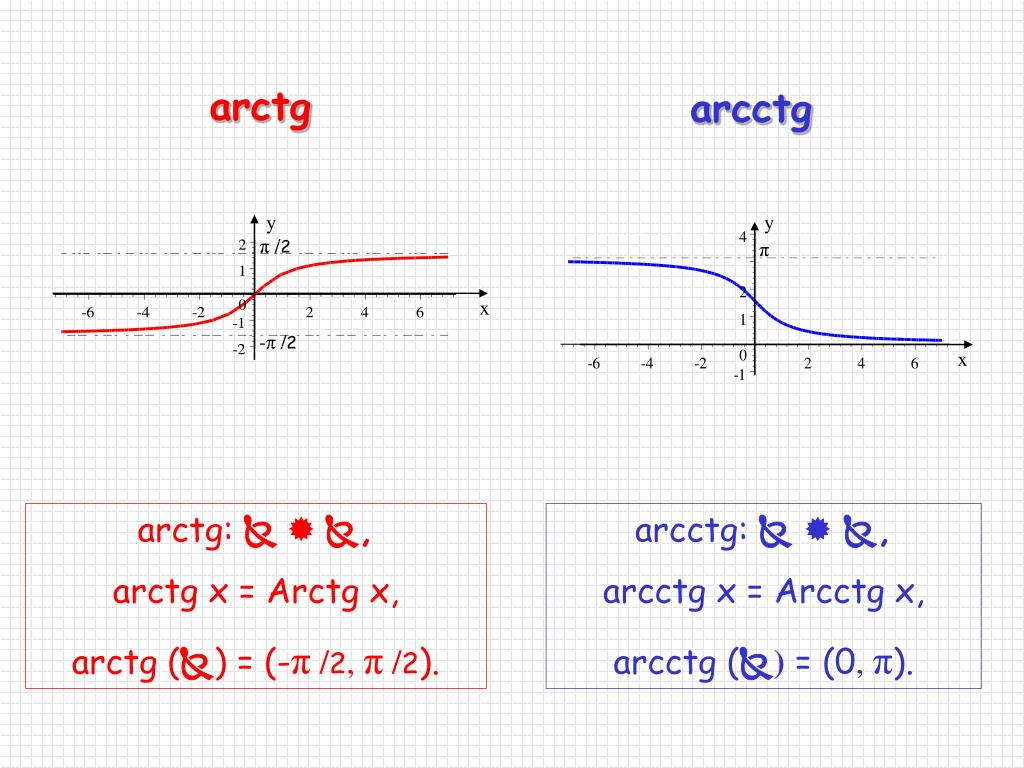
График функции арксинус
График функции y = arcsin xГрафик арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, y = arccos x определен при и имеет множество значений .
График функции арккосинус
График функции y = arccos xГрафик арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin xФункция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) =π – arccos x ≠ ± arccos x Свойства — экстремумы, возрастание, убывание
| y = arcsin x | y = arccos x | |
| Область определения | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.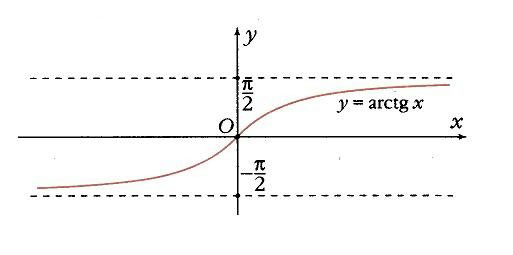
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | 150° | ||
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
Главная страница
Подписаться на: Комментарии к сообщению (Atom)
Если f(x)= arctan x, g(x)=0,9x и x выражено в радианах, то для скольких значений x f(x)=g(x)?
Тригонометрические функции
Кайла К.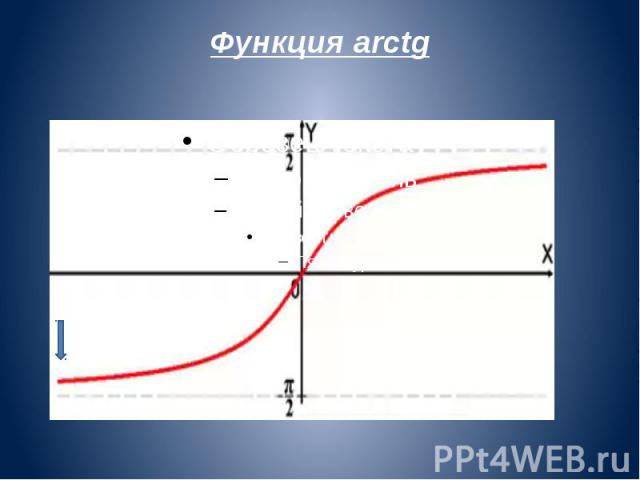
Учитывая, что arctan x = 0,9x, как получить обратный тангенс переменной, который дал бы результат, в 0,9 раз превышающий переменную?
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джон П. ответил 10.05.15
Репетитор
5,0 (173)
Знающий преподаватель математики, естественных наук, SAT, ACT — выпускник Гарварда с отличием
Об этом репетиторе ›
Об этом репетиторе ›
Это интересный вопрос. На самом деле я не уверен, как решить это, работая с реальным уравнением (arctan x = 0,9x).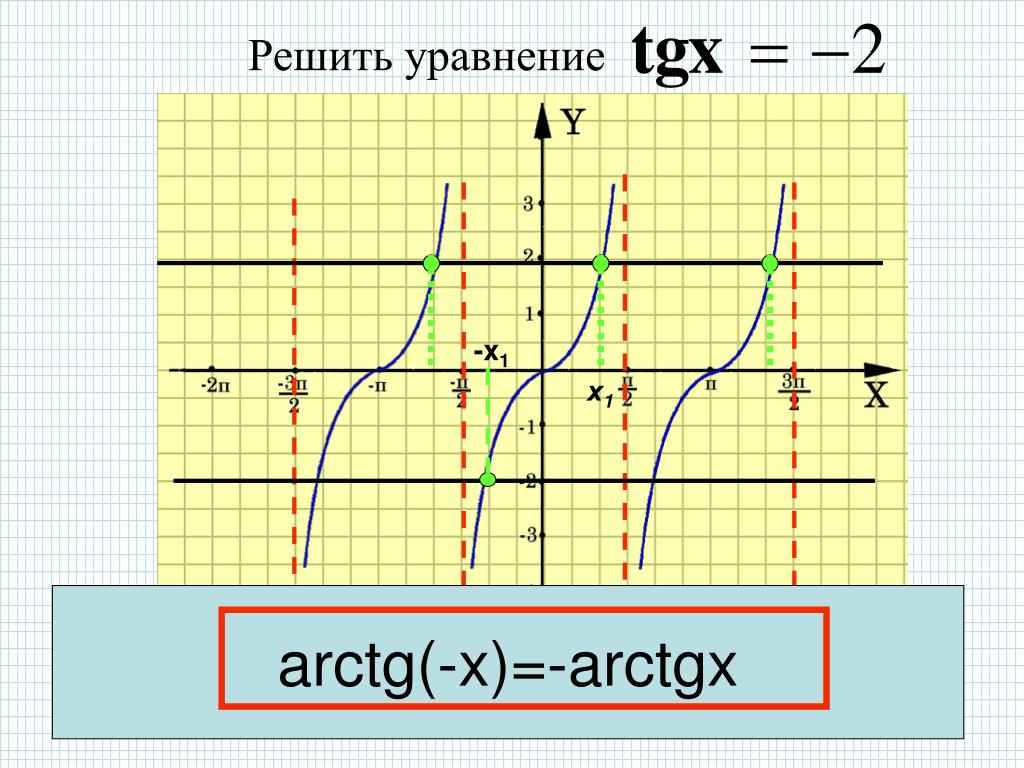
Однако я могу увидеть ответ, построив график двух функций.
Если построить график y = arctan x и y = 0,9x, то места, где графики пересекаются, будут местами, где две функции равны.
Когда вы сделаете это, вы увидите, что функция арктангенса начинается с (0,0) и поднимается вправо (и падает влево) с наклоном 1, но наклон постепенно уменьшается и приближается к 0 по мере приближения функции к своим горизонтальным асимптотам при y = π/2 и y = -π/2.
График y = 0,9x — это линия, которая также начинается в точке (0,0) и выходит из начала координат с наклоном чуть меньше 1 (0,9) вдоль всей линии. Это говорит о том, что сразу после того, как график арктангенса покидает начало координат, он идет выше справа и ниже слева, чем график y = 0,9x, но затем линия вскоре пересекает график арктангенса.
Итак, я вижу три места, где две функции равны: (0,0) и два места, которые пересекают графики — одно справа от начала координат, а другое слева.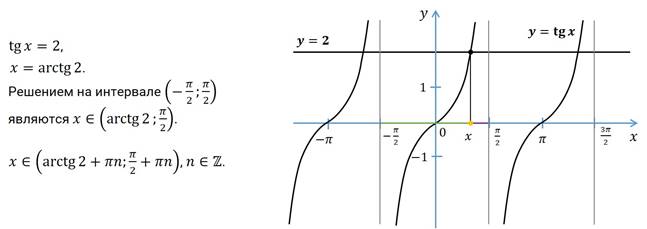
Голосовать за 1 голос против
Подробнее
Отчет
Роберт Л. ответил 10.05.15
Репетитор
4,8 (45)
The Math Whisperer — Математика и смежные темы 92 Мне снова нужно извлечь квадратный корень, и я получаю ответы ± 0,565. Если вы подключите это к уравнению (используя радианы), вы получите довольно близкое решение.
арктангенса 0,565 = 0,514 0,514/0,565 = 0,9097, что близко.
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Урок по Arctan Graph — Образование
Рой — 12 марта 2021 г. в онлайн-образовании
Об арктангенсе и графике арктангенсаПеревернутый тангенс, называемый арктангенсом или сокращенно арктангенсом, обычно обозначается как тангенс-1 (некоторая функция). Чтобы быстро отличить его, у нас есть два варианта:
1.
) Используйте политику простого дериватива.
2.) Получите производную политику, а затем примените правило.
В этом уроке мы покажем производную регуляцию для tan-1(u) и tan-1( ). Есть четыре экземпляра проблемы, чтобы помочь вашему пониманию.
3.) В конце урока мы увидим, как получается правило побочного продукта.
Производное арктана(u).Производный регламент для Arctan ( u) предлагается как:
производный arctan( u).
U является характеристикой одиночной переменной, а также значок «штрих» обозначает производную относительно этой переменной. Вот несколько примеров функции одной переменной u.
и = х.
и, u = неправильно(x).
и = у3–3у + 4,
Производное от Arctan (x) и Arctan Graph Производное правило Arctan (x) — это правило Arctan (u), но при каждом изменении u на x. Учитывая, что производная от x равна просто 1, числитель сокращается до 1. Правило производной для Arctan (x) таково.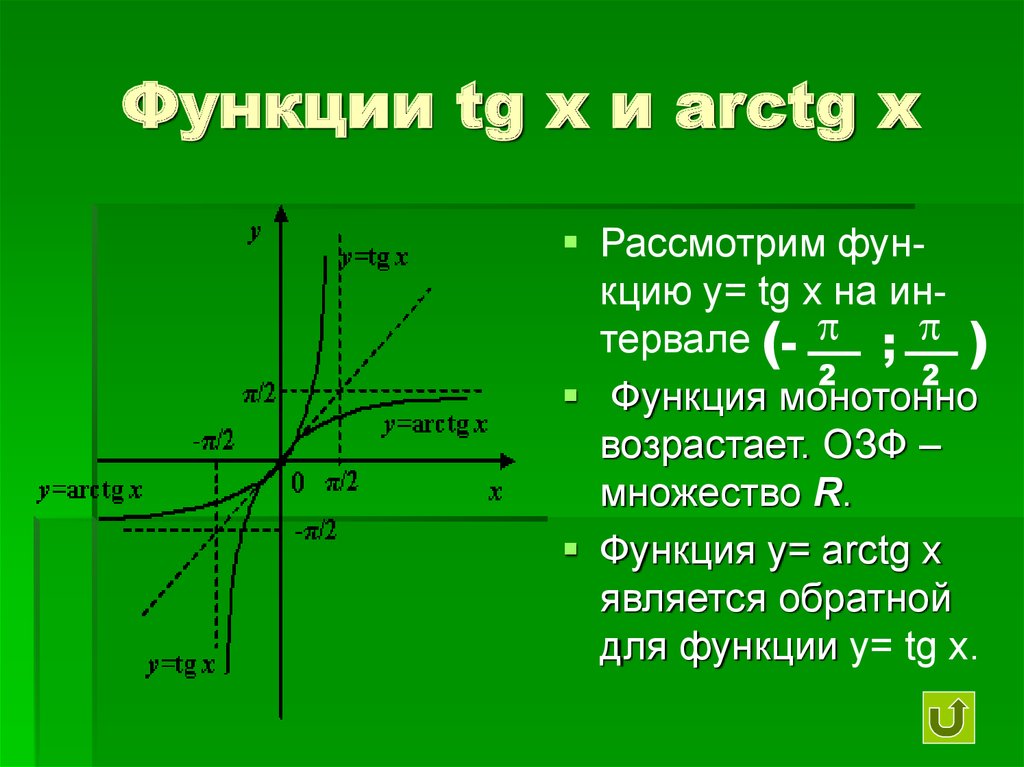
Где’ обозначает производную по x.
ЗадачиПроизводные их от Arctan (2x).
Найдите производную по x от тангенса – 1 (2x).
Решение:
производная от арктан(2x) вариант.
Производное арктана ( 1/x).
Найдите производную по x от tan − 1( 1/x).
Раствор :
раствор производного арктана (1overx).
Они были производными от Arctan ( 4x).
Определите побочный продукт относительно x тангенса − 1(4x).
Раствор :
Производное арктана (4x) раствор.
Производное арктана (x2 + 1).
Найдите побочный результат x tan − 1(x2 + 1).
Решение:
производная от arctan(xsquaredplus1)
Что делает Arctan дифференцируемым? Арктангенс является дифференцируемым признаком, поскольку он является производным от каждого фактора своей области.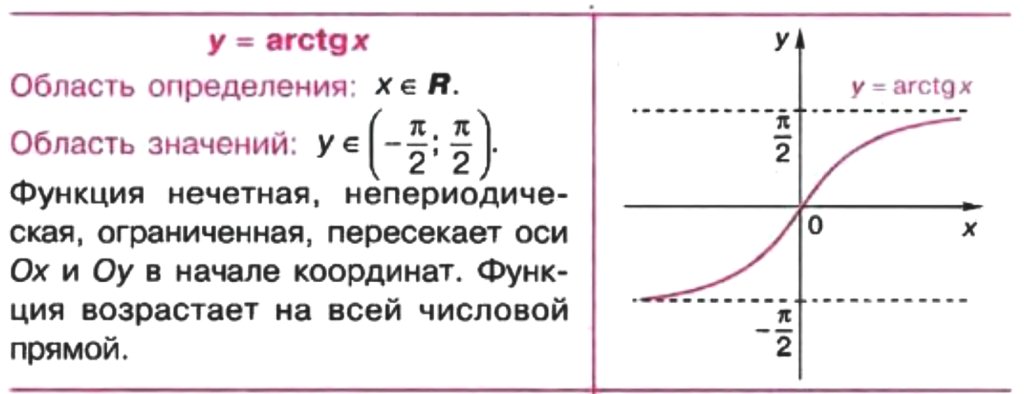
На фотографии ниже показан одиночный период графика Арктана (x). Кривая непрерывна и не имеет острых краев.
Если на графике есть острый угол, побочный продукт в этой точке не указан. Таким образом, если вы найдете функцию, карта которой имеет острые края, она не будет дифференцируема по каждому фактору своего доменного имени.
Диаграмма Арктана ( х).Функция f(x) = arctan(x), построенная для одного периода.
Свидетельство производного правила.Так как арктангенс обратен тангенсу, мы понимаем, что арктангенс является обратной характеристикой тангенса. Следовательно, мы можем подтвердить побочный продукт арктангенса (x), связав его как обратную функцию отклонения. Вот действия по получению производного регулирования Arctan (x).
1.) y = arctan(x), поэтому x = tan(y).
2.) dx/dy [x = tan(y)] = sec2(y).
3.) Использование эффекта суммы квадратов: sec2(y) = 1 + tan2(y).