НОУ ИНТУИТ | Лекция | Нечеткие множества
< Лекция 6 || Лекция 6: 123456789
Аннотация: В лекции представлены методы моделирования экономических задач с использованием нечетких множеств в среде Mathcad. Введены основные понятия теории нечетких множеств. На примерах показаны операции над множествами, расчет свойств. Рассмотрены оригинальные задачи, в которых применен нечетко-множественный подход в процессе принятия решения. Техника моделирования реализована с помощью матриц программы Mathcad.
Ключевые слова: множества, нечеткая логика, значение, нечеткое число, принятия решений, Универсальное множество, Пустое множество, единица, функция, функция принадлежности, подмножество, элемент множества, запись, объединение, нечеткое множество, ПО, представление, неравенство, отрезок, график, операции, мера, расстояние, метрика, индекс, массив, анализ, представление данных, матрица, алгоритм, операторы, стоимость, выражение, прибыль, доходность, NPV, информация, фирма, затраты, входные данные
6.1 Нечетко-множественное моделирование
При моделировании широкого класса реальных объектов возникают необходимость принимать решения в условиях неполной нечеткой информации. Современным перспективным направлением моделирования различного вида неопределенностей является теория нечетких множеств. В рамках теории нечетких множеств разработаны методы формализации и моделирования рассуждений человека, таких понятий как «более или менее высокий уровень инфляции», «устойчивое положение на рынке», «более ценный» и т.д.
Впервые понятие нечетких множеств предложил американский ученый Л.
А.Заде (1965 г ). Его идеи послужили развитию нечеткой логики . В отличие от стандартной логики с двумя бинарными состояниями (1/0, Да/Нет, Истина/Ложь), нечеткая логика позволяет определять промежуточные значения между стандартными оценками. Примерами таких оценок являются: «скорее да, чем нет», «наверное да», «немного вправо», «резко влево» в отличие от стандартных: «вправо» или «влево», «да». В теории нечетких множеств введены нечеткие числа как нечеткие подмножества специализированного вида, соответствующих высказываниям типа «значение переменной примерно равно а». В качестве примера рассмотрим треугольное нечеткое число, где выделяются три точки: минимально возможное, наиболее ожидаемое и максимально возможное значение фактора. Треугольные числа – это самый часто используемый на практике тип нечетких чисел, причем, чаще всего их используют в качестве прогнозных значений параметра. Например, ожидаемое значение инфляции на следующий год. Пусть наиболее вероятное значение – 10%, минимально возможное – 5%, а максимально возможное – 20%, тогда все эти значения могут быть сведены к виду нечеткого подмножества или нечеткого числа A: А: (5, 10, 20)
intuit.ru/2010/edi»>С введением нечетких чисел оказалось возможным прогнозировать будущие значения параметров, которые меняются в установленном расчетном диапазоне. Вводится набор операций над нечеткими числами, которые сводятся к алгебраическим операциям с обычными числами при задании определенного интервала достоверности (уровня принадлежности). Применение нечетких чисел позволяет задавать расчетный коридор значений прогнозируемых параметров. Тогда ожидаемый эффект оценивается экспертом также как нечеткое число со своим расчетным разбросом (степенью нечеткости).Нечеткая логика, как модель человеческих мыслительных процессов, встроена в системы искусственного интеллекта и в автоматизированные средства поддержки принятия решений (в частности, в системы управления технологическими процессами).
6.2 Основные понятия теории нечетких множеств
Множество — неопределяемое понятие математики.
Георг Кантор (1845 – 1918) – немецкий математик, чьи работы лежат в основе современной теории множеств, дает такое понятие: «…множество — это многое, мыслимое как единое».
Множество, включающее в себя все объекты, рассматриваемые в задаче, называют универсальным множеством. Универсальное множество принято обозначать буквой . Универсальное множество является максимальным множеством в том смысле, что все объекты являются его элементами, т.е. утверждение в рамках задачи всегда истинно. Минимальным множеством является пустое множество – , которое не содержит ни одного элемента. Все остальные множества в рассматриваемой задаче являются подмножествами множества . Напомним, что множество называют подмножеством множества , если все элементы являются также элементами . Задание множества — это правило, позволяющее относительно любого элемента универсального множества однозначно установить, принадлежит множеству или не принадлежит. Другими словами, это правило, позволяющее определить, какое из двух высказываний, или , является истинным, а какое ложным.
Характеристической функцией множества называют функцию , заданную на универсальном множестве и принимающую значение единица на тех элементах множества , которые принадлежат , и значение нуль на тех элементах, которые не принадлежат :
| ( 6.1) |
В качестве примера рассмотрим универсальное множество и два его подмножества: — множество чисел, меньших 7, и — множество чисел, немного меньших 7. Характеристическая функция множества имеет вид
(
6. 2) |
Множество в данном примере является обычным множеством.
Записать характеристическую функцию множества , используя лишь 0 и 1, невозможно. Например, включать ли в числа 1 и 2? «намного» или «ненамного» число 3 меньше 7? Ответы на эти и подобные им вопросы могут быть получены в зависимости от условий задачи, в которой используются множества и , а также от субъективного взгляда того, кто решает эту задачу. Множество называется нечетким множеством. При составлении характеристической функции нечеткого множества решающий задачу (эксперт) может высказать свое мнение относительно того, в какой степени каждое из чисел множества принадлежит множеству . В качестве степени принадлежности можно выбрать любое число с отрезка . При этом означает полную уверенность эксперта в том, что — столь же полную уверенность, что говорит о том, что эксперт затрудняется в ответе на вопрос, принадлежит ли множеству или не принадлежит.
Функцией принадлежности нечеткого множества называют функцию , которая
- устанавливает значения степени принадлежности нечеткому множеству каждого из элементов универсального множества и принимает значения на отрезке .
- позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству .
Такую функцию называют функцией принадлежности нечеткому множеству . — Максимальное значение функции принадлежности , присутствующее в множестве — верхняя грань — называется супремум. Функция принадлежности отражает субъективный взгляд специалиста на задачу, вносит индивидуальность в ее решение.
Характеристическую функцию обычного множества можно рассматривать как функцию принадлежности этому множеству, но в отличие от нечеткого множества, принимает лишь два значения: 0 или 1.
Нечетким множеством называют пару , где — универсальное множество, — функция принадлежности нечеткого множества .
Несущим множеством или носителем нечеткого множества называют подмножество множества , состоящее из элементов, на которых .
Точкой перехода нечеткого множества называют элемент множества , на котором .
В рассматриваемом примере, где , — множество чисел, меньших 7, — множество чисел, немного меньших 7, субъективно выбираем значения для множества , которые будут составлять функцию принадлежности . В таблице 6.1 представлены функции принадлежности и для и .
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0,5 | 0,6 | 0,8 | 0,9 | 0 | 0 | 0 | 0 |
intuit.ru/2010/edi»>Часто используется более компактная запись конечных или счетных нечетких множеств. Так, вместо приведенного выше табличного представления подмножеств и , эти подмножества можно записать следующим образом:В приведенных равенствах указаны значения функции принадлежности для соответствующих элементов множества , знак "+" означает объединение одноэлементных подмножеств , для которых значения функции принадлежности больше нуля. Такое объединение называют несущим множеством или носителем соответствующего нечеткого множества. Так, несущее множество для состоит из чисел: .
Нечеткое множество записывают в виде (1.2), если , и в виде (1.3), если непрерывно.
Общая форма записи нечеткого подмножества для случаев, когда U дискретно имеет вид:
(
6. 3) |
В общем случае нечеткое множество B с непрерывным носителем U обозначается
| ( 6.4) |
В выражениях (6.3) и (6.4), как правило, указываются лишь элементы несущего множества. Использование символа интеграла не означает интегрирования, но предполагает, объединение по всем элементам несущего множества . Знак интеграла показывает, что несущее множество является частью числовой оси.
Элемент множества , на котором значение функции принадлежности равно 0.5, называют точкой перехода. Точкой перехода для множества в рассмотренном выше примере является .
Удобно представление нечетких множеств в виде графиков функций принадлежности (рис.6.1).
Рис. 6.1. Функции принадлежности обычного множества и нечеткого множества B
< Лекция 6 || Лекция 6: 123456789
Множеества и операции над ними
1.
Множества и операции над нимиМНОЖЕСТВА И ОПЕРАЦИИНАД НИМИ
В математике часто приходится рассматривать
те или иные группы объектов как единое.
Все эти различные совокупности называют
множествами.
Обозначают: А,В,С…, пустое-_____
Объекты, из которых состоит множество,
называют его элементами.
В математике мы рассматриваем
принадлежность объектов к
рассматриваемому множеству: принадлежит
или не принадлежит множеству.
________________________
Множества бывают конечными и бесконечными.
4. Множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству либо не
МНОЖЕСТВО ОПРЕДЕЛЯЕТСЯ СВОИМИЭЛЕМЕНТАМИ,
Т.Е. МНОЖЕСТВО ЗАДАНО, ЕСЛИ О ЛЮБОМ
ОБЪЕКТЕ МОЖНО СКАЗАТЬ, ПРИНАДЛЕЖИТ ОН
ЭТОМУ МНОЖЕСТВУ ЛИБО НЕ ПРИНАДЛЕЖИТ.
Способы задания множеств:
перечисление элементов множества
указание характеристического свойства
5. Отношения между множествами:
ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ:1.
2.
3.
4.
Множества, имеющие общие элементы,
пересекаются
Элементы одного множества В являются
элементами другого множества А. Говорят
множество В является подмножеством
множества А.
Множества равны, если множество А –
подмножество В, В подмножество А
Непересекающиеся множества.
6. Задания:
ЗАДАНИЯ:при помощи кругов Эйлера изобразите
отношения между объектами:
А — множество треугольников, В- множество
прямоугольных треугольников
А – прямые, В – отрезки
А – однозначные числа, В – двузначные числа,
С — натуральные числа.
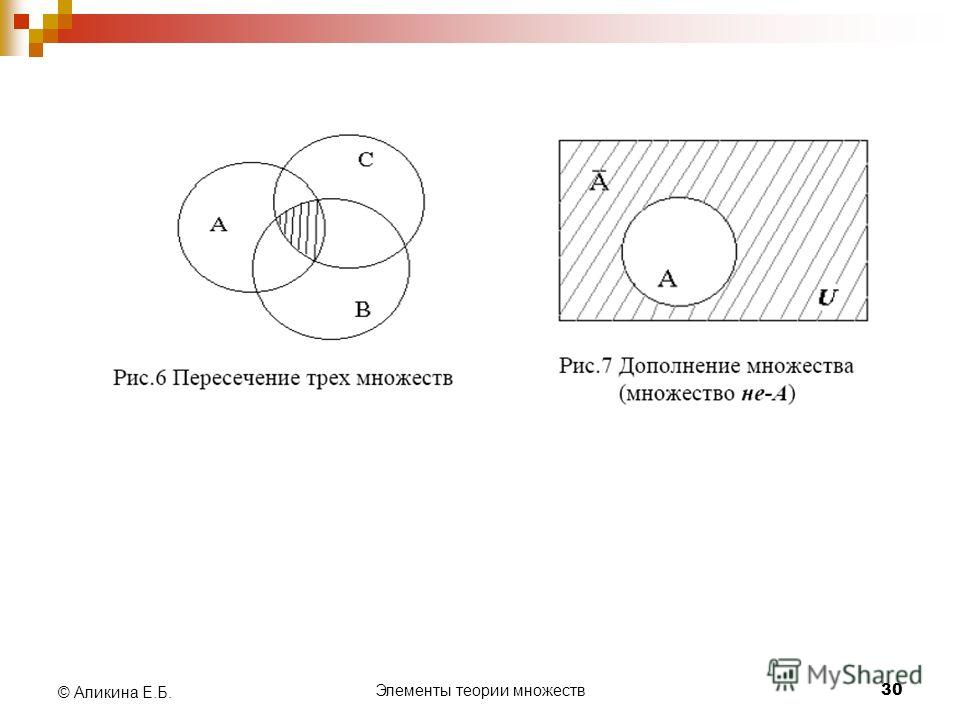
7. Операции над множествами:
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ:Из элементов двух и более множеств можно
образовать новые множества.
Пусть даны два множества: А=2,4,6,8;
В=5,6,7,8,9. Образуем множество С, в которое
включим общие элементы множеств А и В.
Полученное множество называют
пересечением множеств А и В.
8. Операции над множествами:
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ:Пересечением множеств А и В называется
множество, содержащее только такие
элементы, которые принадлежат множеству А
и множеству В.
9. Операции над множествами
ОПЕРАЦИИ НАД МНОЖЕСТВАМИЧто значит 2+3?
К двум кружочкам добавить еще 3.
Мы выполнили операцию объединения двух
множеств, не имеющих общих элементов.
10. Операции над множествами
ОПЕРАЦИИ НАД МНОЖЕСТВАМИОбъединением множеств А и В называется
множество, содержащее только такие
элементы, которые принадлежат множеству А
или множеству В.
11. Задания:
ЗАДАНИЯ:Найдите объединение и пересечение множеств,
если:
А) А =26, 39, 5, 58, 17, 81, В= 17, 26, 58
Б) А=a, b, c, d, e, f,
B= b, e, f, k, l
Назовите все множества, о которых идет речь в
задаче:
— У школы посадили 4 липы и 3 березы. Сколько
всего деревьев посадили?
— На каждой тарелке 5 яблок. Сколько яблок на 3
тарелках?
12. Операции над множествами
ОПЕРАЦИИ НАД МНОЖЕСТВАМИЧто значит 5-3=2?
От 5 кружков убираем 3 кружка. Сколько
осталось? В чем суть приема?
(Из данного множества, в котором а элементов, удаляют
подмножество, содержащее b элементов.
Тогда воставшейся части множества a-b элементов.)
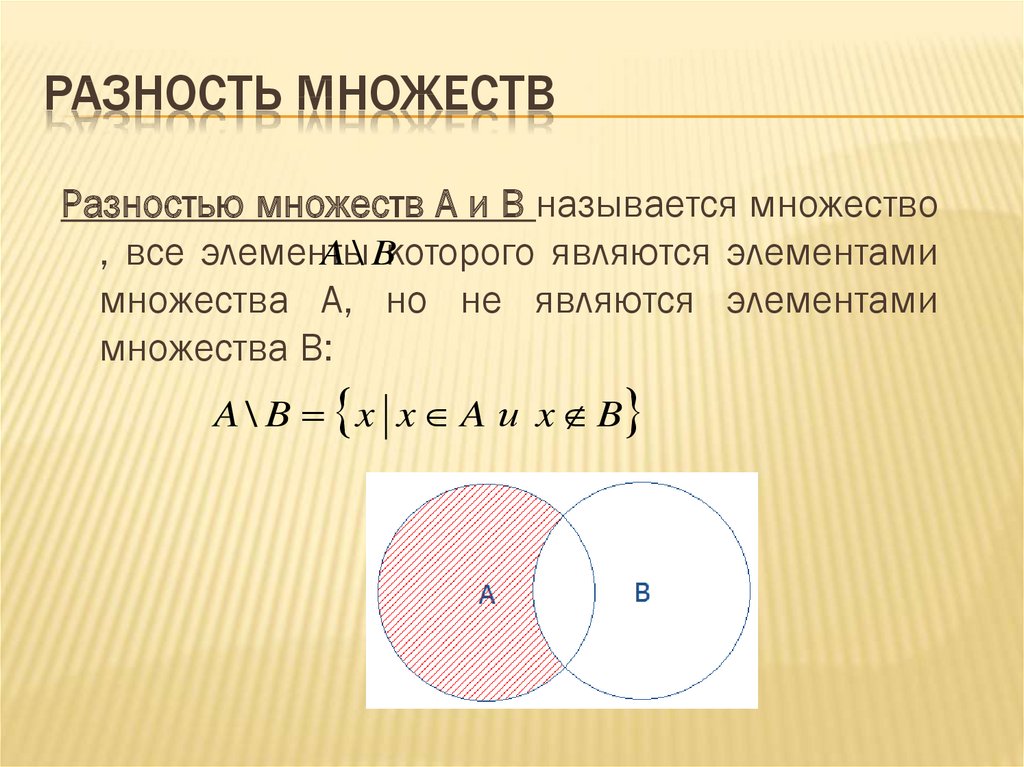
Та часть, которая осталась после удаления из
множества А подмножества В называют
дополнением множества В до множества А.
13. Операции над множествами
ОПЕРАЦИИ НАД МНОЖЕСТВАМИПусть В является подмножеством А.
Дополнением множества В до множества А
называется множество, содержащее только те
элементы множества А, которые не
принадлежат множеству В.
14. Задания:
ЗАДАНИЯ:Найдите дополнение множества С до
множества Д, если: С=41,42,
Д=40,41,42,43,44
У Коли 10 значков, он подарил товарищу 2
значка. Сколько значков осталось у Коли?
У Винни-Пуха 6 воздушных шаров, а у
Пяточка на 2 шара меньше. Сколько
воздушных шаров у Пяточка?
15. Разбиение множества на классы
РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫКлассификация – это действие распределения объектов
по классам на основании сходства объектов внутри
класса и их отличия от объектов других классов.
Любая классификация связана с расчленением
некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х1, Х2,
Х3 …, если:
1) Подмножества Х1,Х2, Х3… попарно не
пересекаются
2) Объединение подмножеств Х1, Х2, Х3 … совпадает
с множеством Х.
16. Можно ли:
МОЖНО ЛИ:множество Х треугольников разбить на три
класса: остроугольные, прямоугольные,
тупоугольные.
множество Х треугольников разбить на три
класса: равнобедренные, равносторонние,
разносторонние
17. Задание:
ЗАДАНИЕ:Покажите, что решение задачи связано с
разбиением заданного множества на попарно
непересекающиеся подмножества:
1) 12 флажков разделили ребятам, по 2 флажка
каждому. Сколько ребят получили флажки?
2) Для игры в волейбол 12 ребят разбились на 2
команды. Сколько ребят в каждой команде?
18. Задание:
ЗАДАНИЕ:Используя цифры 1, 2, 3 составить все
возможные двузначные числа.
19. Декартово умножение множеств
ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВВ процессе выполнения задания мы образовали
новое множество, элементами которого
являются упорядоченные пары чисел. Это
новое множество называют декартовым
произведением множеств А и В
20. Декартово умножение множеств
ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВДекартовым произведением множеств А и В
называется множество пар, первая компонента
которых принадлежит множеству А, а вторая
компонента множеству В.
Операцию, при помощи которой находят
декартово произведение, называют
декартовым умножением множеств.
Получая различные декартовы произведения,
мы должны следить, чтобы получить все его
элементы, не пропуская ни одного.
В математике определена теорема:
Если множество А содержит m элементов, а
множество В — n элементов, то декартово
произведение АхВ содержит m*n элементов.
22. Задание:
ЗАДАНИЕ:сколько элементов в декартовом произведении
АхА, если А=а,b, c, d, e.
используя цифры 4,2,8, запишите все
возможные двузначные числа так, чтобы одна
и та же цифра в записи числа не повторялась.
Комбинаторные задачи – это задачи, связанные
с составлением из элементов конечных
множеств по некоторым правилам различных
комбинаций.
Дополнение множества — определение, свойства, примеры решения
Дополнение множества — это множество, включающее все элементы универсального множества, отсутствующие в данном множестве. Допустим, A — это множество всех монет, которое является подмножеством универсального множества, содержащего все монеты и банкноты, поэтому дополнением множества A является множество банкнот (в которое не входят монеты).
В этой статье мы подробно обсудим дополнение множества, его определение вместе со свойствами, решенными примерами и практическими вопросами.
| 1. | Что такое дополнение набора? |
2. | Дополнение набора диаграмм Венна |
| 3. | Свойства дополнения набора |
| 4. | Дополнение к набору примеров |
| 5. | Часто задаваемые вопросы о дополнении набора |
Что такое дополнение набора?
Если универсальное множество (U) имеет подмножество A, то дополнение множества A, представленное как A’, отлично от элементов множества A, которое включает элементы универсального множества, но не элементы множества A. Здесь A’ = {x ∈ U : x ∉ A}. Другими словами, дополнением множества A является разность между универсальным множеством и множеством A.
Дополнение множества Символ
Дополнение любого множества представлено как A’, B’, C’ и т. д. Другими словами , можно сказать, что если универсальное множество есть (U) и подмножество универсального множества (A) задано, то разность универсального множества (U) и подмножества универсального множества (A) есть дополнение подмножества , т.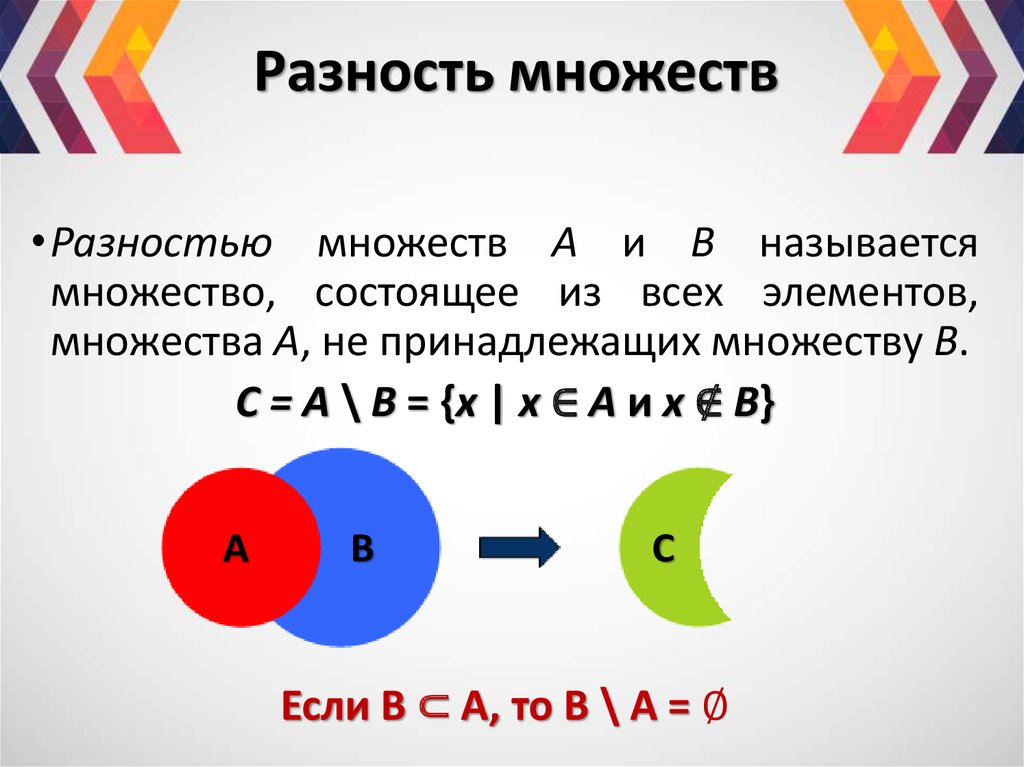
е. А’ = U — А.
Пример дополнения множества
Если универсальное множество состоит из всех простых чисел до 25 и множество A = {2, 3, 5}, то дополнение множества A отлично от элементов множества A.
- Шаг 1: Отметьте универсальный набор и набор, для которого нужно найти дополнение. U = {2, 3, 5, 7, 11, 13, 17, 19, 23}, А = {2, 3, 5}.
- Шаг 2: Вычтите, то есть (U — A). Здесь,
У — А = А’
= {2, 3, 5, 7, 11, 13, 17, 19, 23} — {2, 3, 5}
= {7, 11, 13, 17, 19, 23}
Дополнение набора диаграмм Венна
Для лучшего понимания взгляните на приведенную ниже диаграмму Венна дополнения множества, которая ясно показывает дополнение множества A, то есть A’. Здесь А’ не является частью множества А, и множество А также не является частью А’. A и A’ являются подмножествами U.
Свойства дополнения набора
Ниже приведены свойства дополнения множества, которые включают в себя законы дополнения, закон двойного дополнения, закон пустого множества и универсального множества, а также закон Деморгана.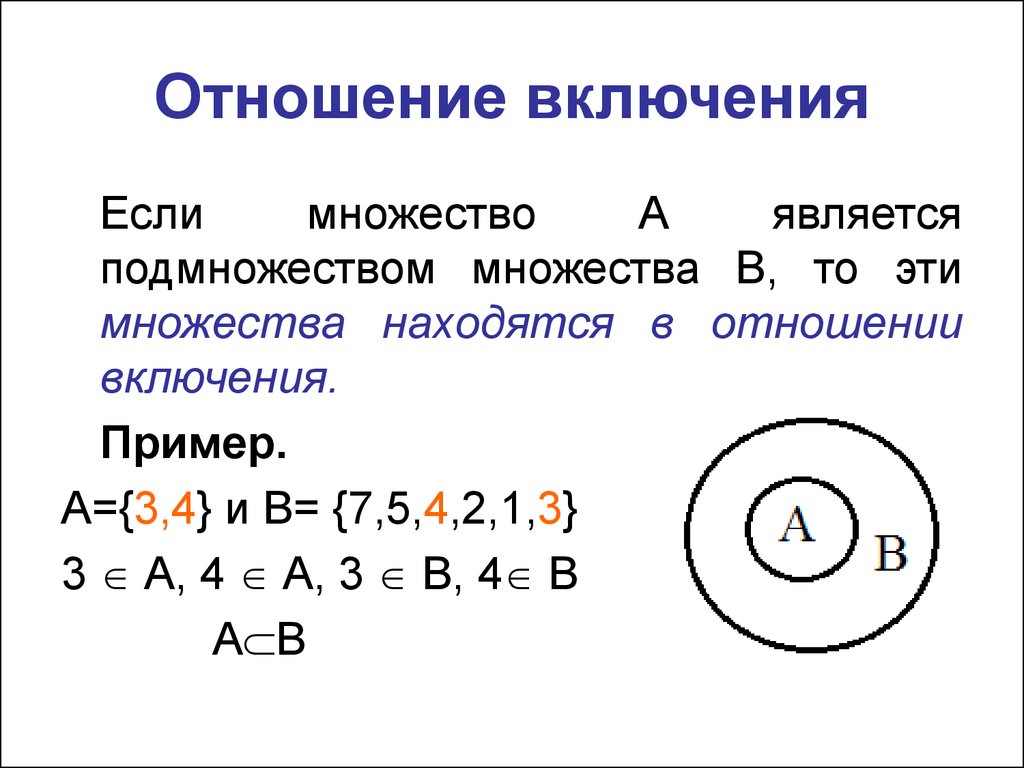
Законы дополнений
- Если A является подмножеством универсального множества, то A’ также является подмножеством универсального множества, поэтому объединение A и A’ представляет собой универсальное множество, представленное как A ∪ A’ = U
- Пересечение множеств A и A’ дает пустое множество «∅», представленное как A ∩ A’ = ∅
Например, если U = {1 , 2 , 3 , 4 , 5 } и A = {4 , 5} и B = {1, 2}
А’ = {1, 2, 3} и В’ = {3, 4, 5}
А ∪ А’ = U знак равно {1, 2, 3, 4, 5}
Кроме того, A ∩ A’ = ∅
Закон двойного дополнения
- В этом законе дополнением дополняемого множества является исходное множество, (A’)’ = A
- Дополнение множества A′, где само A′ является дополнением A, двойное дополнение A, таким образом, является самим A.
В предыдущем примере U = {1, 2, 3, 4, 5} и A = {4, 5}, тогда A’ = {1, 2, 3}.
Дополнение A’ = (A’)’ = {4, 5}, равное множеству A.
Закон Пустого множества и универсального множества
- Дополнением универсального множества является пустое множество или нулевое множество (∅), а дополнением пустого множества является универсальное множество.
- Поскольку универсальное множество содержит все элементы, а пустое множество не содержит элементов, поэтому их дополнение прямо противоположно друг другу, представленному как ∅’ = U И U’ = ∅
В приведенном выше примере множество U = {1, 2, 3, 4, 5}, которое содержит все элементы множества A, а множество B как универсальное множество содержит все элементы, поэтому U’ = ∅ (пустое множество) и ∅’ = {1, 2, 3, 4, 5}.
Закон Де Моргана
Вот законы Де Моргана, в которых говорится о дополнении.
- Дополнение объединения двух множеств равно дополнению множеств и их пересечению. (A U B)’ = A’ ∩ B’ (закон союза Де Моргана).
- Дополнение пересечения двух множеств равно дополнению множеств и их объединению. (A ∩ B)’ = A’ UB’ (закон пересечения Де Моргана).
Взяв приведенный выше пример для доказательства закона Де Моргана, U = {1 , 2 , 3 , 4 , 5 } и A = {4 , 5} и B = {1, 2}. Таким образом,
Закон Союза Де Моргана: (AU B) = {1, 2, 4, 5} и (AU B)’ = {3} и, таким образом, A’ ∩ B’ = {3}, поскольку A’ = {1 , 2 , 3 } и B’ = {3, 4, 5}, поэтому (AU B)’ = A’ ∩ B’ = {3}.
Закон пересечения де Моргана: (A ∩ B) = ∅ (пусто), (A ∩ B)’ = {1, 2, 3, 4, 5} и, таким образом, A’ U B’ = {1, 2, 3, 4, 5}, так как A’ = {1, 2, 3} и B’ = {3, 4, 5}, поэтому (A ∩ B)’ = A’ U B’
Важные примечания о дополнении набора:
- Дополнением универсального набора является пустое множество или нулевое множество.
- Набор пересечений содержит элементы, общие для обоих наборов.
- Объединение двух множеств — это множество, содержащее все элементы, входящие в A или B или в оба.
☛ Связанные темы:
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о дополнении набора и связанных с ним темах.
- Наборы Formula
- Диаграмма Венна Формула
- Набор обозначений Builder
Часто задаваемые вопросы о дополнении набора
Что такое дополнение набора?
Дополнение множества A определяется как множество, содержащее элементы, присутствующие в универсальном множестве, но не в множестве A.
Например, множество U = {2,4,6,8,10,12} и множество A = {4,6,8}, то дополнение множества A, A′ = {2,10,12}.
Как найти дополнение к набору?
Если задано универсальное множество (U) и задано другое множество A, содержащее некоторые элементы универсального множества, то мы можем найти дополнение множества A, представив его как A’. Элементы, которые не являются частью множества A, но частью множества U, будут элементами множества A’, являющегося дополнением множества A. Здесь A’ = {x ∈ U: x ∉ A}.
Каково дополнение набора А, если универсальный набор — это набор букв английского алфавита, а набор А — набор согласных в английском алфавите?
Если универсальное множество состоит из всех алфавитов и множество А содержит все согласные, то дополнением множества А, то есть А’, будет множество гласных английских алфавитов.
Что такое дополнение пересечения множеств?
Дополнением пересечения множеств называется множество элементов, входящих в универсальное множество U, но не входящих в множество пересечений.
Например, предположим, что множество U = множество натуральных чисел меньше 10 и элементы множества X = {1, 2, 5, 6}, а множество Y = {1, 3, 4, 5, 6}. Таким образом, пересечение множества X и Y или X ∩ Y = {1, 5, 6} и дополнение (X ∩ Y) или (X ∩ Y)’ = {2, 3, 4, 7, 8, 9}.
Легко доказать, что дополнение пересечения двух множеств равно объединению дополнения каждого из множеств.
Что такое дополнение к пустому набору или нулевому набору?
Пустое множество означает, что в множестве нет элементов, поэтому дополнением к пустому множеству или нулевому множеству является универсальное множество, содержащее все элементы.
Что входит в состав универсального набора?
Универсальный набор содержит все возможные элементы, а нулевой набор вообще не содержит элементов. Таким образом, дополнением универсального множества является нулевое множество.
Дополнение | Математические вкусности
Форма поиска
Поиск
На предыдущих уроках мы узнали, что набор — это группа объектов, и что диаграммы Венна можно использовать для иллюстрации как отношений набора, так и логических отношений.
Пример 1: Дано = {учащиеся школы Кьюл} и A = {ученики класса миссис Глоссер}. Какова совокупность всех учащихся школы Кьюл, которые не учатся в классе миссис Глоссер?
Анализ: Связь между этими наборами показана на диаграмме Венна ниже.
Ответ: Заштрихованная область снаружи A представляет всех учащихся школы Кьюла, которые не учатся в классе миссис Глоссер.
В примере 1 заштрихованная область представляет собой дополнение набора A . Дополнение A , обозначаемое A ‘ , состоит из всех учащихся школы The Kewl, которые не учатся в классе миссис Глоссер. Напомним, что Универсальный набор — это набор всех рассматриваемых элементов, обозначенных заглавными буквами, и что все остальные наборы являются подмножествами универсального набора. Теперь мы можем определить дополнение множества.
Определение: Дополнение множества A , обозначаемое как A’ , представляет собой множество элементов, принадлежащих , но не принадлежащих A .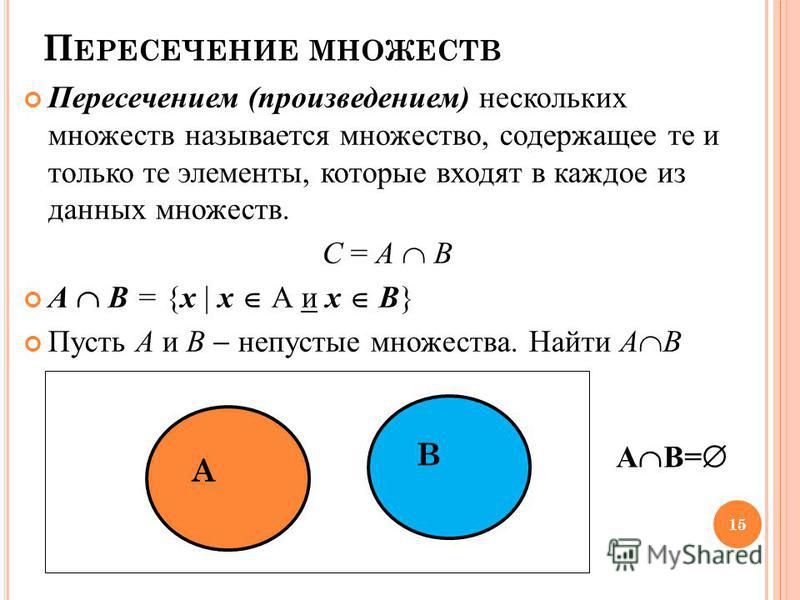
Дополнение набора A обозначается A ‘ , Вы также можете сказать «дополнение A в » или «A-простое число». Теперь мы можем пометить наборы в примере 1, используя это обозначение.
Пример 1: Дано = {учащиеся школы Кьюл} и A = {ученики класса миссис Глоссер}. Какова совокупность всех учащихся школы Кьюл, которые не учатся в классе миссис Глоссер?
Анализ: Связь между этими наборами показана на диаграмме Венна ниже.
Ответ: Заштрихованная область снаружи A представляет A ‘ , то есть всех учащихся школы Кьюл, которые не учатся в классе миссис Глоссер.
Еще один способ представить дополнение множества следующим образом: заданное множество A , дополнение A является множеством всех элементов универсального множества , которых нет в A . Используя нотацию построителя наборов, мы можем написать:
А ‘ = { х | x и x A }
Найдем дополнение набора чисел.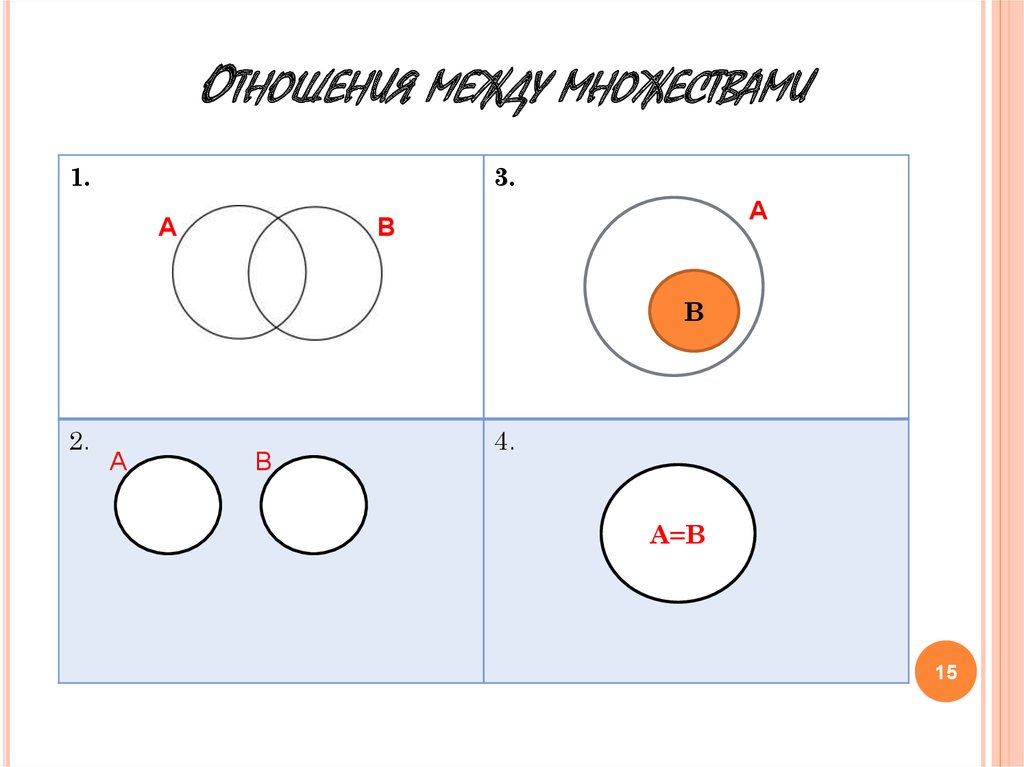
Пример 2: Учитывая = {одиночные цифры} и B = {0, 1, 4, 5, 6, 7, 8}, найдите дополнение B .
Ответ: B ‘ = {2, 3, 9}
Таким образом, B ‘ не входят во все числа,0202 В . Используя нотацию построителя множеств, мы можем написать: B ‘ = { x | x и x B }
В примерах с 3 по 5 универсальным набором является английский алфавит.
Пример 3: Дано = {a, b, c, … , x, y, z} и X = {a, b, c, d, e}, найти х ‘ .
Анализ: X’ будет состоять из всех букв английского алфавита, которых нет в X. Это показано на диаграмме Венна ниже.
Ответ: x ‘ = {F, G, H, … , X, Y, Z}
Пример 4: . в, … , х, у, z} , X = {а, б, в, г, д} и Y = {д, е, ж}, найдите Y ‘.
Анализ: Y’ будет состоять из всех букв английского алфавита, которых нет в Y. Это показано на диаграмме Венна ниже. .
Ответ: Y ‘ = {a, b, c, d, h, i, j, … , x, y, z} Пример 5 9 0 015 9000 Дано = {a, b, c, … , x, y, z} , P = {a, b, c, d, e} и Q = {x, y, z }, найдите Q’.
Анализ: Q’ состоит из всех букв алфавита, которых нет в Q . Это показано на диаграмме Венна ниже. .
Ответ: Q ‘ = {a, b, c, d, e, f, g, h … , u, v90, w} В приведенных выше примерах множество и его дополнение не имеют общих элементов. Объединение набора и его дополнения является Универсальным Набором. Пересечение множества и его дополнения является нулевым множеством. Эти утверждения приведены ниже:
Советы:
Notation Alert
Существует несколько различных способов представления дополнения множества, как показано ниже.
Все эти обозначения имеют одинаковое значение. Однако для целей этого учебного модуля мы решили использовать A’ , , читаемый как A-prime.
Давайте рассмотрим несколько примеров дополнения, которые включают нотацию построения множеств и бесконечные множества.
Пример 6: Если = {n | n и -6 < n < 7 } и B = { y | — четное число; -5 < y < 6 }, то каково дополнение B ?
Ответ: B ‘ = {-5, -3, -1, 1, 3, 5, 6}
Пример 7: Дано = {Общее число> 1: 10201. } и C = {простые числа}, найдите C ‘ .
Анализ: C’ будет состоять из всех счетных чисел больше 1, которые не являются простыми . Это показано на диаграмме Венна ниже.
Ответ: C ‘ = {составные номера}
Суммирование: Указанный набор a , комплемент A является набором всех элементов.
нет в A . Дополнение множества A обозначается как A’ и читается как A-prime . Формальное определение дополнения показано ниже.
А ‘ = { х | x и x A }
Упражнения
Указания: прочитайте каждый вопрос ниже. Вы можете нарисовать диаграмму Венна, чтобы найти ответ на каждое упражнение. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
| 1. | Если = {учащиеся, которые посещают школу} и X’ = {учащиеся, которые не ездят на автобусе}, то что из следующего является setX? |
| X = {учащиеся, которые не ездят на велосипедах} X = {учащиеся, которые не ходят пешком} X = {учащиеся, которые ездят на автобусе} Ничего из вышеперечисленного.  ОКНО РЕЗУЛЬТАТОВ: |
| 2. | Если = { k | k и 1 ≤ K ≤ 10 } и P = {1, 3, 5, 7, 9}, то какое из следующих P является дополнением множества? |
| P’ = {2, 4, 6, 8, 10} P’ = {0, 2, 4, 6, 8} P’ = {0, 2, 4, 6, 8, 10} Все вышеперечисленное. ОКНО РЕЗУЛЬТАТОВ: |
| 3. | дано = {A, B, C, … , X, Y, Z} , M = {A, B, C} и N. = {c, d, e}, найти N’. |
| N’ = {a, b, c, d, e} N ‘ = {а, б, е, ж, з, и, к, … , х, у, г} N’ = {а, б, в, … , x, y, z} Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 4. | Если = { n | — 7 < n < 8 } и P = { — 6, — 4, — 2, 4, 6}, то что из следующего является дополнением множества P? |
| P’ = { — 5, — 3, — 1, 1, 3, 4, 5, 6, 7} P’ = { — 3, 8 906 5 — 1, 0, 1, 2, 3, 4, 5, 7} P’ = { — 5, — 3, — 1, 0, 1, 2, 3, 5 , 7} Все вышеперечисленное ОКНО РЕЗУЛЬТАТОВ: |
5. |