все виды решений и график
Рассмотрим уравнение x^2=a, где в качестве а, может выступать произвольное число. Существует три случая решения этого уравнения, в зависимости от значения, которое принимает число а (а0).
Рассмотрим каждый из случаев в отдельности.
Примеры различных случаев уравнения x^2=a
x^2=a, при a<0
Так как квадрат любого действительного числа не может быть отрицательным числом, уравнение x^2=a, при a
x^2=a, при a=0
В данном случае уравнение имеет один корень. Этим корнем является число 0. Так как уравнение можно переписать в виде х*х=0, то еще иногда говорят, что данное уравнение имеет два корня, которые равны между собой и равны 0.
x^2=a, при a>0
В этом случае уравнение x^2=a, при aРешается оно следующим образом. Сначала переносим а в левую часть.
x^2 – a = 0;
Из определения квадратного корня следует, что a можно записать в следующем виде: a=(√a)^2. Тогда уравнение можно переписать следующим образом:
x^2 – (√a)^2 = 0.
В левой части видим формулу разности квадратов, разложим её.
(x+√a)*(x-√a)=0;
Произведение двух скобок равно нулю, если хотя бы одна из них равна нулю. Следовательно,
x+√a=0;
x-√a=0;
Отсюда, x1=√a x2=-√a.
Данное решение можно проверить и построив график.
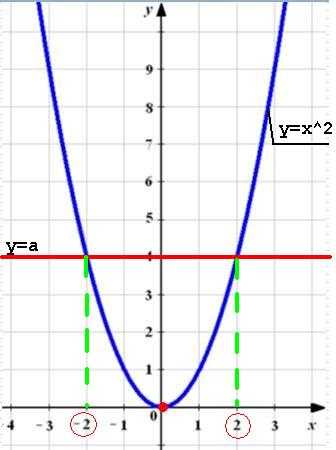
Для примера сделаем это для уравнения x^2 = 4.
Для этого необходимо построить два графика y=x^2 и y=4. И посмотреть координаты х их точек пересечения. Корни должны получиться 2 и -2. На рисунке все наглядно видно.
Нужна помощь в учебе?
Предыдущая тема: Квадратные корни: арифметический квадратный корень
Следующая тема:   Нахождение приближенных значений квадратного корня: изучаем на примере
Все неприличные комментарии будут удаляться.
www.nado5.ru
Решите уравнение x^2+4*y=0 (х в квадрате плюс 4 умножить на у равно 0)
Найду корень уравнения: x^2+4*y=0
Виды выражений
Решение
Подробное решение[LaTeX]
Это уравнение видаa*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$x_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 4 y$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (4*y) = -16*y
Уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
$$x_{1} = 2 \sqrt{- y}$$
$$x_{2} = — 2 \sqrt{- y}$$ Быстрый ответ
[LaTeX]
_________________ _________________
4 / 2 2 /atan2(-im(y), -re(y))\ 4 / 2 2 /atan2(-im(y), -re(y))\
x1 = - 2*\/ im (y) + re (y) *cos|---------------------| - 2*I*\/ im (y) + re (y) *sin|---------------------|
\ 2 / \ 2 /$$x_{1} = — 2 i \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )} — 2 \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )}$$
_________________ _________________
4 / 2 2 /atan2(-im(y), -re(y))\ 4 / 2 2 /atan2(-im(y), -re(y))\
x2 = 2*\/ im (y) + re (y) *cos|---------------------| + 2*I*\/ im (y) + re (y) *sin|---------------------|
\ 2 / \ 2 /$$x_{2} = 2 i \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )} + 2 \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )}$$
www.kontrolnaya-rabota.ru
Решите уравнение x*n+x^2=y (х умножить на n плюс х в квадрате равно у)
Найду корень уравнения: x*n+x^2=y
Виды выражений
Решение
Подробное решение[LaTeX]
Перенесём правую часть уравнения влевую часть уравнения со знаком минус.
Уравнение превратится из
$$n x + x^{2} = y$$
в
$$- y + n x + x^{2} = 0$$
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$x_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = n$$
$$c = — y$$
, то
D = b^2 - 4 * a * c =
(n)^2 - 4 * (1) * (-y) = n^2 + 4*y
Уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
$$x_{1} = — \frac{n}{2} + \frac{1}{2} \sqrt{n^{2} + 4 y}$$
$$x_{2} = — \frac{n}{2} — \frac{1}{2} \sqrt{n^{2} + 4 y}$$ Быстрый ответ
[LaTeX]
/ ___________________________________________________________ \ ___________________________________________________________
| / 2 / / 2 2 \\| / 2 / / 2 2 \\
| 4 / 2 / 2 2 \ |atan2\4*im(y) + 2*im(n)*re(n), re (n) - im (n) + 4*re(y)/|| 4 / 2 / 2 2 \ |atan2\4*im(y) + 2*im(n)*re(n), re (n) - im (n) + 4*re(y)/|
| \/ (4*im(y) + 2*im(n)*re(n)) + \re (n) - im (n) + 4*re(y)/ *sin|---------------------------------------------------------|| \/ (4*im(y) + 2*im(n)*re(n)) + \re (n) - im (n) + 4*re(y)/ *cos|---------------------------------------------------------|
re(n) | im(n) \ 2 /| \ 2 /
x1 = - ----- + I*|- ----- - ------------------------------------------------------------------------------------------------------------------------------| - ------------------------------------------------------------------------------------------------------------------------------
2 \ 2 2 / 2 $$x_{1} = i \left(- \frac{1}{2} \sqrt[4]{\left(2 \Re{n} \Im{n} + 4 \Im{y}\right)^{2} + \left(\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (2 \Re{n} \Im{n} + 4 \Im{y},\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2} \right )} \right )} — \frac{\Im{n}}{2}\right) — \frac{1}{2} \sqrt[4]{\left(2 \Re{n} \Im{n} + 4 \Im{y}\right)^{2} + \left(\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (2 \Re{n} \Im{n} + 4 \Im{y},\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2} \right )} \right )} — \frac{\Re{n}}{2}$$
/ ___________________________________________________________ \ ___________________________________________________________
| / 2 / / 2 2 \\| / 2 / / 2 2 \\
| 4 / 2 / 2 2 \ |atan2\4*im(y) + 2*im(n)*re(n), re (n) - im (n) + 4*re(y)/|| 4 / 2 / 2 2 \ |atan2\4*im(y) + 2*im(n)*re(n), re (n) - im (n) + 4*re(y)/|
| \/ (4*im(y) + 2*im(n)*re(n)) + \re (n) - im (n) + 4*re(y)/ *sin|---------------------------------------------------------|| \/ (4*im(y) + 2*im(n)*re(n)) + \re (n) - im (n) + 4*re(y)/ *cos|---------------------------------------------------------|
re(n) | im(n) \ 2 /| \ 2 /
x2 = - ----- + I*|- ----- + ------------------------------------------------------------------------------------------------------------------------------| + ------------------------------------------------------------------------------------------------------------------------------
2 \ 2 2 / 2 $$x_{2} = i \left(\frac{1}{2} \sqrt[4]{\left(2 \Re{n} \Im{n} + 4 \Im{y}\right)^{2} + \left(\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (2 \Re{n} \Im{n} + 4 \Im{y},\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2} \right )} \right )} — \frac{\Im{n}}{2}\right) + \frac{1}{2} \sqrt[4]{\left(2 \Re{n} \Im{n} + 4 \Im{y}\right)^{2} + \left(\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (2 \Re{n} \Im{n} + 4 \Im{y},\left(\Re{n}\right)^{2} + 4 \Re{y} — \left(\Im{n}\right)^{2} \right )} \right )} — \frac{\Re{n}}{2}$$
www.kontrolnaya-rabota.ru
Однородные уравнения — Решение дифференциальных уравнений
Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.
101. Решить уравнение: (x + 2y)dx — x dy = 0.
102. Решить уравнение: (x — y)dx + (x + y)dy = 0.
103. Решить уравнение: (y2 — 2xy)dx + x2dy = 0.
104. Решить уравнение: 2x3y’ = y(2x2 — y2).
105. Решить уравнение: y2 + x2y’ = xyy’.
106. Решить уравнение: (x2 + y2)y’ = 2xy.
107. Решить уравнение: xy’ — y = x tg(y/x).
108. Решить уравнение: xy’ = y — xey/x.
109. Решить уравнение: xy’ — y = (x + y)ln((x + y)/x).
110. Решить уравнение: xy’ = y cos ln(y/x).
111. Решить уравнение: (y + sqrt(xy))dx = x dy.
112. Решить уравнение: xy’ = sqrt(x2 — y2) + y.
113. Решить уравнение: (2x — 4y + 6)dx + (x + y — 3)dy = 0.
114. Решить уравнение: (2x + y + 1)dx — (4x + 2y — 3)dy = 0.
115. Решить уравнение: x — y — 1 + (y — x + 2)y’ = 0.
116. Решить уравнение: (x + 4y)y’ = 2x + 3y — 5.
117. Решить уравнение: (y + 2)dx = (2x + y — 4)dy.
118. Решить уравнение: y’ = 2((y + 2)/(x + y — 1))2.
119. Решить уравнение: (y’ + 1)ln((y + x)/(x + 3)) = (y + x)/(x + 3).
120. Решить уравнение: y’ = (y + 2)/(x + 1) + tg((y — 2x)/(x + 1)).
121. Решить уравнение: x3(y’ — x) = y2.
122. Решить уравнение: 2x2y’ = y3 + xy.
123. Решить уравнение: 2x dy + (x2y4 + 1)y dx = 0.
124. Решить уравнение: y dx + x(2xy + 1)dy = 0.
125. Решить уравнение: 2y’ + x = 4 sqrt(y).
126. Решить уравнение: y’ = y2 — 2/x2.
127. Решить уравнение: 2xy’ + y = y2sqrt(x — x2y2).
128. Решить уравнение: 2/3 xyy’ = sqrt(x6 — y4) + y2.
129. Решить уравнение: 2y + (x2y + 1)xy’ = 0.
131. Найти кривую, у которой точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.
132. Найти кривую, у которой расстояние любой касательной от начала координат равно абсциссе точки касания.
133. При каких α и β дифференциальное уравнение y’ = axα + byβ
134. Пусть k0 — корень уравнения f(k) = k. Показать, что: 1) если f'(k0) < 1, то ни одно решение уравнения y’ = f(y/x) не касается прямой y = k0x в начале…
xn--e1avkt.xn--p1ai
