Определение область определения функции – ?

StudyPort.Ru — Область определения

Областью определения функции называется множество тех значений х, при которых функция определена. Иными словами, это те значения х, при которых функция «бывает».

Иногда область определения задается непосредственно уже при задании функции.

Например: при . Здесь областью определения (ОДЗ) является промежуток [1;5]. При других значениях х функция не определена.

Однако, не всегда ОДЗ задана так непосредственно.

Чаще всего (для функций заданных аналитически), ОДЗ находят исходя из того, возможно ли при тех или иных значениях х произвести все операции, которые указаны в формуле.

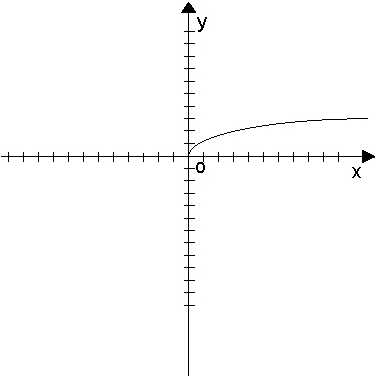
Пример: ОДЗ функции  — промежуток [0;?). При всех других значениях х функция не определена (функции «не бывает»). Например, не существует действительного значения выражения .

При графическом изображении этой функции график будет находиться только в области допустимых значений, и ни на точку не выйдет за эти пределы.

При табличном способе задания функции областью допустимых значений являются только те значения х, которые заданы в таблице.

Например:

Областью определения функции, заданной табличным способом –

является множество ОДЗ =   {3;5.1;10;12.5;13;20}

Пример1: Найти ОДЗ функции .

Квадратный корень можно извлечь только из положительных или равных 0 чисел, значит ОДЗ:

Ответ: ОДЗ = [2;+?).

Пример 2: Найти ОДЗ функции .

Основание логарифма должно быть положительным и отличным от 1.
.

studyport.ru

Область определения функции — это… Что такое Область определения функции?

Область определения функции — множество, на котором задаётся функция.

Определение

Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения

.

Более формально, пусть задано отображение , которое отображает множество в , то есть: ; тогда

• множество называется областью определения функции
• и обозначается , или (от англ. domain «область»).

Обычно предполагается, что , из-за чего понятие области определения выглядит тавтологией: «область определения функции — это область, где определена функция». Для того, чтобы придать чёткий смысл данному понятию, рассматривается некоторое более широкое множество, которое называется областью отправления, и тогда область определения функции  — это такое подмножество множества (которое и есть область отправления функции), где для каждого элемента определено значение функции .

Этот факт коротко записывают в виде: .

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида ;
• а, также, комплекснозначные функции комплексного переменного это функции вида ,

где и  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции совпадает с областью отправления ( или ).

Гармоническая функция

Область определения функции : представляет собой комплексную плоскость без нуля

и не совпадает с областью отправления (вся комплексная плоскость).

Дробно-рациональные функции

Область определения дробно-рациональной функции вида

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

.

Эти точки называются полюсами функции .

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана

функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть  — семейство отображений из множества в множество . Тогда можно определить отображение вида . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку , то можно определить функцию , которая принимает в «точке» то же значение, что и сама функция в точке .

См. также

Литература

• Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• ISBN 5-02-014844-X
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
• А. Н. Колмогоров «Что такое функция» // «Квант». — М.: «Наука», 1970. — В. 1. — С. 27-36. — ISSN 0130-2221.

ushakov.academic.ru

Область определения функции — Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Если на множестве задана функция, которая отображает множество в другое множество, то множество называется областью определения или областью задания функции.

Более формально, если задана функция , которая отображает множество в , то есть: , то

• множество называется областью определения^[1] или областью задания^[2] функции и обозначается или (от англ. domain — «область»).

Иногда рассматривают функции, определенные на подмножестве некоторого множества . В этом случае множество иногда называют областью отправления функции ^[3].

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции[править]

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида ;
• а также комплекснозначные функции комплексного переменного вида ,

где и  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение[править]

Область определения функции совпадает с областью отправления ( или ).

Гармоническая функция[править]

Область определения функции представляет собой комплексную плоскость без нуля

и не совпадает с областью отправления (вся комплексная плоскость).

Дробно-рациональные функции[править]

Область определения функции вида

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

.

Эти точки называются полюсами функции .

Так, например, определен на всех точках, где знаменатель не обращается в ноль, то есть, где . Таки образом является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера[править]

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал[править]

Пусть  — семейство отображений из множества в множество . Тогда можно определить отображение вида . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку , то можно определить функцию , которая принимает в «точке» то же значение, что и сама функция в точке .

• Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
• Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
• В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
• Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65 — 69. — 528 с.
• А. Н. Колмогоров «Что такое функция» // «Квант». — М.: «Наука», 1970. —. —. — ISSN 0130-2221.

www.wikiznanie.ru

Область определения функции Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Содержание

• 1 Определение
• 2 Примеры
  • 2.1 Числовые функции
    • 2.1.1 Тождественное отображение
    • 2.1.2 Гармоническая функция
    • 2.1.3 Дробно-рациональные функции
  • 2.2 Мера
  • 2.3 Функционал
• 3 См. также
• 4 Примечания
• 5 Литература

Определение[ | ]

Если на множествеX{\displaystyle X} задана функция, которая отображает множество X{\displaystyle X} в другое множество, то множество X{\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f\colon X\to Y}, то

• множество X{\displaystyle X} называется областью определения^[1] или областью задания^[2] функции f{\displaystyle f} и обозначается D(f){\displaystyle D(f)} или domf{\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматривают функции, определенные на подмножестве D{\displaystyle D} некоторого множества X{\displaystyle X}. В эт

ru-wiki.ru

Область определения функции — Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Определение

Если на множествеX{\displaystyle X} задана функция, которая отображает множество X{\displaystyle X} в другое множество, то множество X{\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f\colon X\to Y}, то

• множество X{\displaystyle X} называется областью определения^[1] или областью задания^[2] функции f{\displaystyle f} и обозначается D(f){\displaystyle D(f)} или domf{\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматривают функции, определенные на подмножестве D{\displaystyle D} некоторого множества X{\displaystyle X}. В этом случае множество X{\displaystyle X} иногда называют областью отправления функции f{\displaystyle f}^[3].

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} };
• а также комплекснозначные функции комплексного переменного вида f:C→C{\displaystyle f\colon \mathbb {C} \to \mathbb {C} },

где R{\displaystyle \mathbb {R} } и C{\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f(x)=x{\displaystyle f(x)=x} совпадает с областью отправления (R{\displaystyle \mathbb {R} } или C{\displaystyle \mathbb {C} }).

Гармоническая функция

Область определения функции f(x)=1/x{\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:

domf=C∖{0}{\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}},

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции

Область определения функции вида

f(x)=a0+a1x+⋯+amxmb0+b1x+⋯+bnxn{\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b0+b1x+⋯+bnxn=0{\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0}.

Эти точки называются полюсами функции f{\displaystyle f}.

Так, например, f(x)=2xx2−4{\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x2−4≠0{\displaystyle x^{2}-4\neq 0}. Таким образом domf{\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F={f∣f:X→R}{\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X{\displaystyle X} в множество R{\displaystyle \mathbb {R} }. Тогда можно определить отображение вида F:F→R{\displaystyle F\colon \mathbb {F} \to \mathbb {R} }. Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x0∈ X{\displaystyle x_{0}\in ~X}, то можно определить функцию F(f)=f(x0){\displaystyle F(f)=f(x_{0})}, которая принимает в «точке» f{\displaystyle f} то же значение, что и сама функция f{\displaystyle f} в точке x0{\displaystyle x_{0}}.

См. также

Примечания

Литература

• Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
• Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
• В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
• Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65 — 69. — 528 с.
• А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — Вып. 1. — С. 27-36. — ISSN 0130-2221.

wikipedia.green