Что такое синус в тригонометрии?
Что такое синус в тригонометрии?
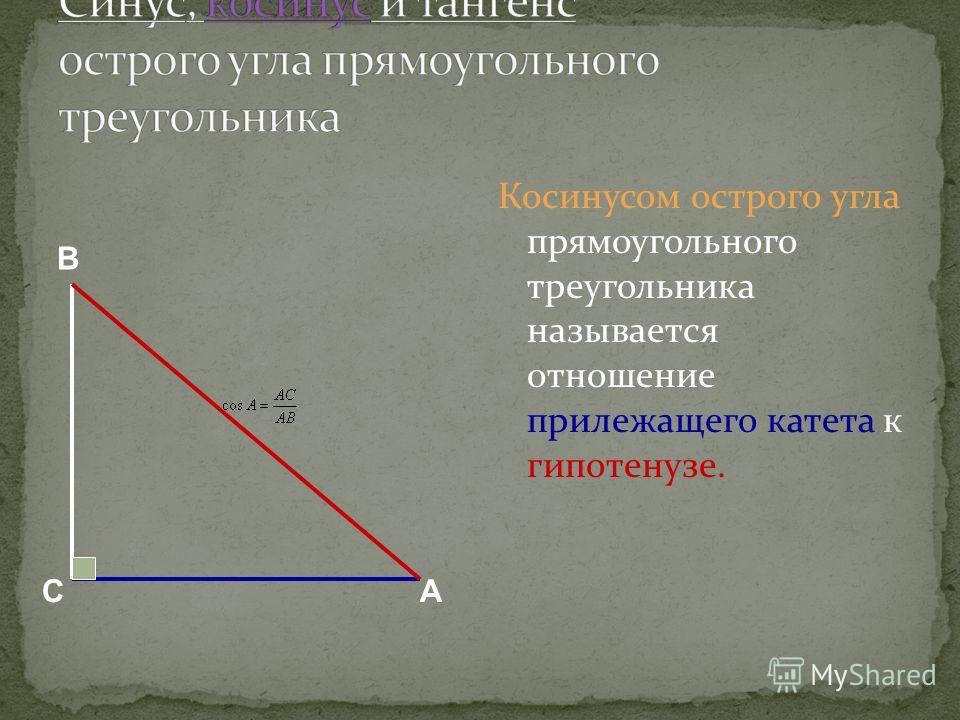
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. … Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Почему синус называется синусом?
Слово «синус» — латинского происхождения. Слово «синус» хорошо известно врачам в значении «пазуха», «впадина». … Однако ни одно из этих многочисленных значений не имеет никакого отношения к синусу в тригонометрии.
Как называется отношение синуса к косинусу?
Тангенс угла – отношение синуса угла к его косинусу. Котангенс угла отношение косинуса угла к его синусу.
Как найти синус угла с?
Для вычисления синуса угла с необходимо разделить катет на гипотенузу: sin∠BAC=BCAB.
Как найти синус угла на окружности?
Чтобы найти синус и косинус угла, нужно:
- Провести единичную окружность с центром, совпадающим с вершиной угла.

- Найти точку пересечения этого угла с окружностью.
- Её «иксовая» координата – это косинус искомого угла.
- Её «игрековая» координата – это синус искомого угла.
Как найти синус угла ромба?
у ромба все стороны равны, а периметр это сумма всех сторон, то одна сторона ромба будет равна 48:4, т. е. 12. Синус угла равен площадь робма разделить на квадрат стороны, т.
Как найти синус угла тупого?
AB=CD=y. Синусом угла альфа на единичной окружности называется ордината точки, полученной из точки P при повороте вокруг точки O на угол альфа. Это — одна из формул приведения. Все формулы приведения рассматриваются в курсе алгебры 10 класса.
Как найти синус с помощью тангенса?
Тригонометрические формулы
- При известном синусе или косинусе числа можно найти его тангенс или котангенс: tg a = sin a/cos a.
- Можно найти синус числа, если известен его косинус и наоборот: sin2 a + cos2 a = 1.

- Найти тангенс можно через синус при известном косинусе: 1 + tg2 a = 1/cos2 a.
Как найти косинус тангенс и синус угла?
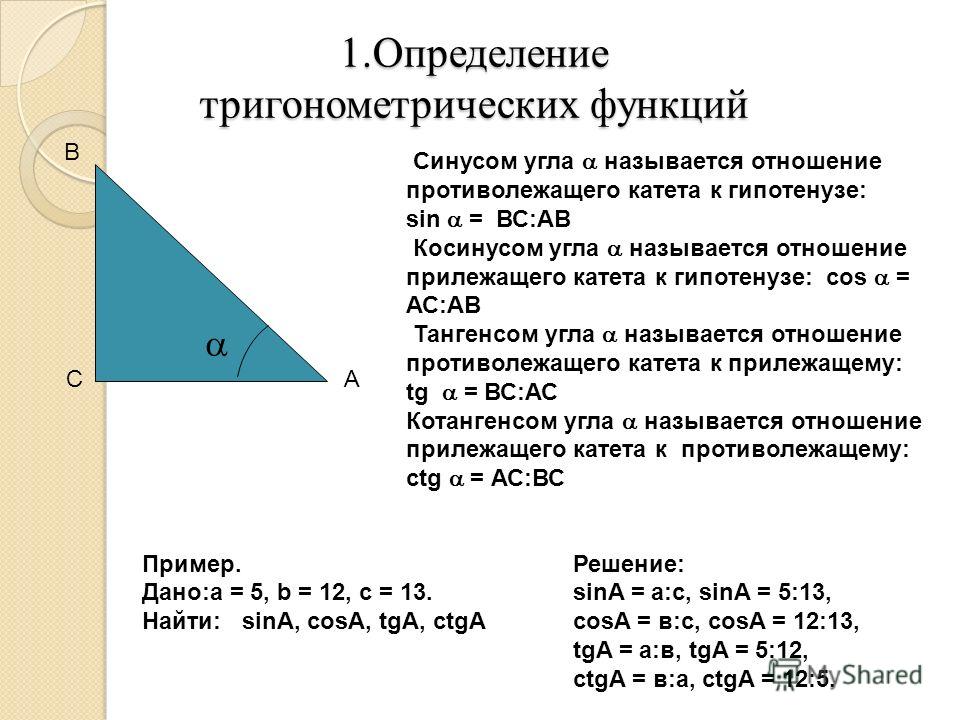
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
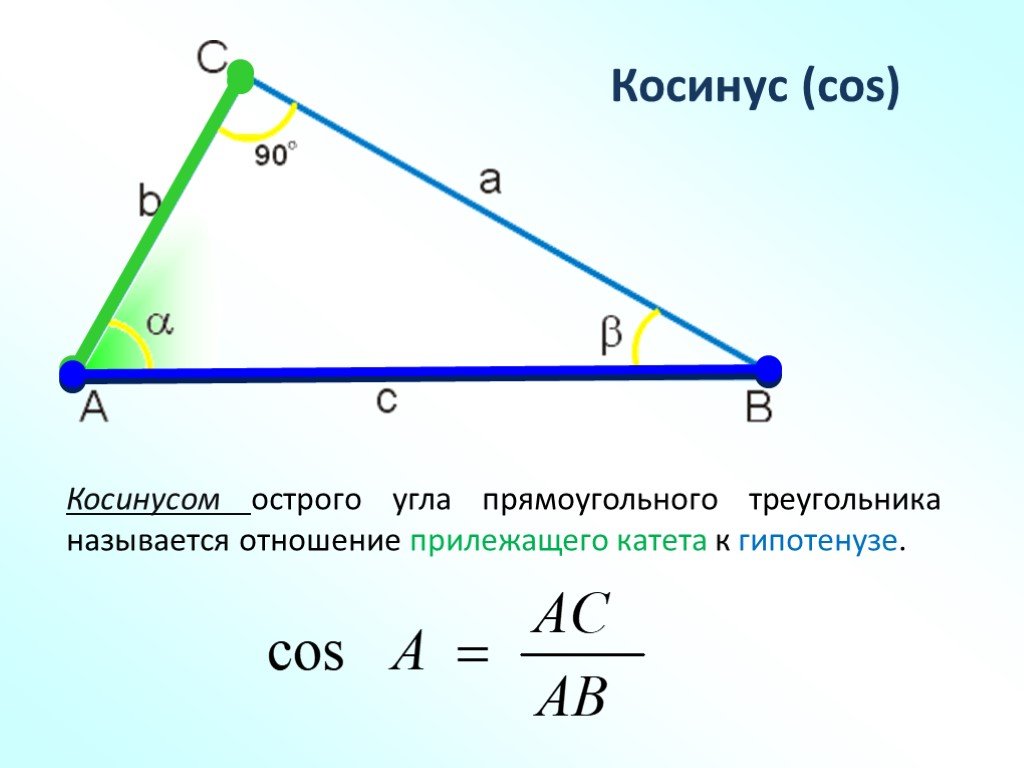
- Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
- Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Как можно найти тангенс?
Представляет собой соотношение катетов прямоугольного треугольника. То есть, tg(А)=ВС/АС, где ВС – противолежащий к углу (А) катет, АС – прилежащий катет.
Что такое тангенс угла?
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе. … Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
Как найти тангенс угла А в прямоугольном треугольнике?
прилежащим — BC. Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета. Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета. Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Чему равен синус угла в 45 градусов?
синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)
Что называется синусом?
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. … Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Как найти с помощью гипотенузы и тангенса найти катеты?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как найти гипотенузу зная катет и угол 90?
Подставьте данные и найденные значения в теорему синусов, чтобы найти гипотенузу: катет «а»/синус угла «A» = гипотенуза «с»/синус угла «С». При этом sin 90˚ = 1. Таким образом, уравнение упрощается до: а/sinA = с/1 или с = а/sinA. Разделите длину катета «а» на синус угла «А», чтобы найти длину гипотенузы.
Как найти один из катетов по теореме Пифагора?
Катет — одна из двух сторон, образующих прямой угол. Формула Теоремы Пифагора выглядит так: a2 + b2 = c2, где a, b — катеты, с — гипотенуза….Из этой формулы можно вывести следующее:
- a = √c2 − b. …
- b = √c2 − a. …
- c = √a2 + b.
Как найти гипотенузу если известны катеты?
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы.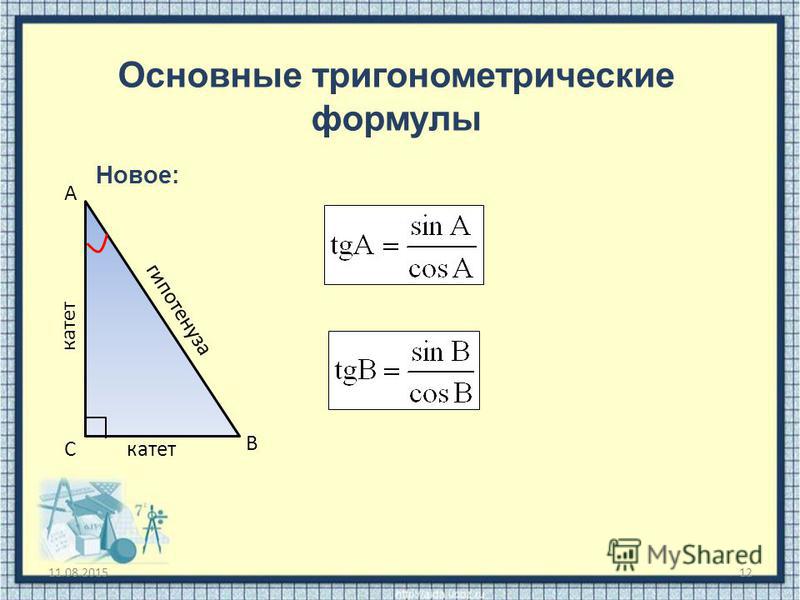
Как найти гипотенузу в треугольнике?
Гипотенуза (греч. ὑποτείνουσα, натянутая) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Как найти стороны в прямоугольном треугольнике?
По теореме Пифагора, для того чтобы вычислить гипотенузу прямоугольного треугольника, нужно извлечь квадратный корень из суммы квадратов катетов. Катетами считаются стороны a и b, образующие друг с другом прямой угол, а гипотенузой – сторона, лежащая напротив него.
Что такое катет и гипотенуза в геометрии?
Катет — одна из двух сторон прямоугольного треугольника, образующих прямой угол. Противолежащая прямому углу сторона называется гипотенузой. Для непрямоугольного треугольника катеты не существуют. … косинус α — отношение катета, прилежащего углу α, к гипотенузе.
Как определить прилежащий катет и противолежащий?
В прямоугольном треугольнике гипотенуза — это самая длинная сторона, «противолежащий катет» — это сторона, лежащая напротив данного угла, а «прилежащий катет» — это катет, образующий данный угол вместе с гипотенузой. Стороны прямоугольного треугольника имеют специальные названия.
Как найти угол если известен катет и гипотенуза?
Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b. Пример. Угол А равен 45 градусов, гипотенуза равна 10 см.
Как обозначается катет в геометрии?
Катеты — это стороны прямоугольного треугольника, которые образуют прямой угол. Как любая сторона треугольника, катет обозначается или двумя заглавными латинскими буквами (по концам соответствующего отрезка) или одной маленькой латинской буквой. Например, на рисунке 1 катеты АС и СВ. На рисунке 2 катеты а и b.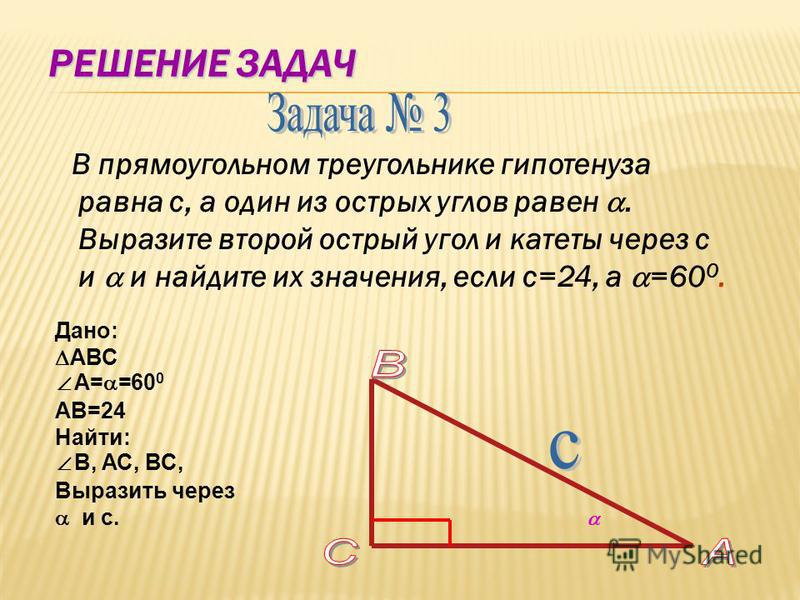
Как обозначается гипотенуза в геометрии?
КАК ОБОЗНАЧАЕТСЯ ГИПОТЕНУЗА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА Как правило, буквой «с», а его катеты «а» и «б».
Как найти катет лежащий против угла в 30 градусов?
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Синус. Что это такое?
25.10.2016 Категория: Образование и наука Подкатегория: Математика Популярность
Тригонометрия является разделом математики, изучающим тригонометрические функции, а также их использование на практике. К таким функциям относятся синус, косинус, тангенс и котангенс.
Синус – это тригонометрическая функция, отношение величины противолежащего катета к величине гипотенузы.
Синус в тригонометрии.
Как уже сказано выше, синус имеет непосредственное отношение к тригонометрии и тригонометрическим функциям. Его функция определяется тем, чтобы
- помогать высчитать угол, при условии известности величин сторон треугольника;
- помогать высчитать величины стороны треугольника, при условии известности угла.

Необходимо помнить, что величина синуса будет всегда одинакова для любых размеров треугольника, поскольку синус – это не измерение, а соотношение.
Следовательно, для того чтобы не высчитывать эту постоянную величину при каждом решении той или иной задачи, были созданы специальные тригонометрические таблицы. В них величины синусов, косинусов, тангенсов и котангенсов уже просчитаны и закреплены. Обычно эти таблицы приводятся на форзаце учебников по алгебре и геометрии. Также их можно найти в Интернете.
Синус в геометрии.
Геометрия требует наглядности, поэтому, чтобы понять на практике, что такое синус угла, нужно нарисовать треугольник с прямым углом.
Допустим, что стороны, образующие прямой угол, названы а, в, противоположный им угол – х.
Обычно в заданиях указана длина сторон. Допустим, а=3, в=4. В таком случае соотношение сторон будет выглядеть как ¾.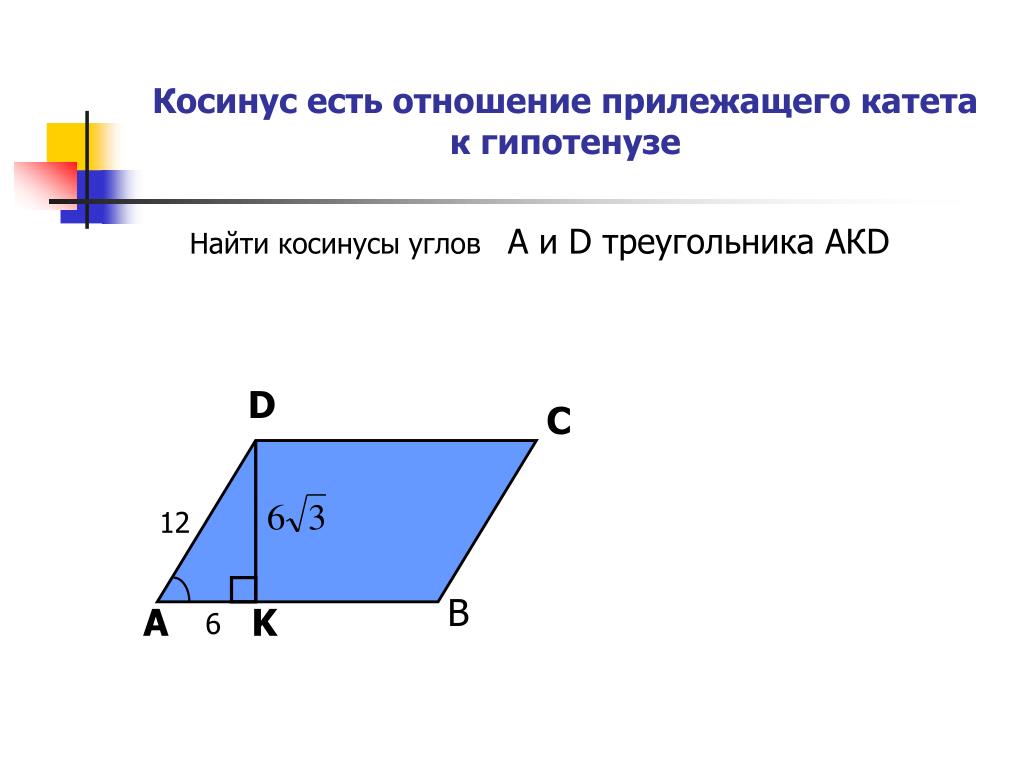
При этом видоизменении сработал закон тригонометрии: длины сторон треугольника изменились, а их отношение – нет.
Тот факт, что при изменении длины сторон треугольника во сколько угодно раз и при сохранении величины угла х, соотношение между его сторонами всё равно останется неизменным, заметили ещё древние ученые. В нашем случае длина сторон могла измениться так: а/в = ¾, при удлинении стороны а до 6 см, а в – до 8 см получаем: m/n = 6/8 = 3/4.
Соотношения сторон в прямоугольном треугольнике в связи с этим получили названия:
- синус угла х – это отношение противолежащего катета к гипотенузе: sinx = а/с;
- косинус угла х – это отношение прилежащего катета к гипотенузе: сosx = в/с;
- тангенс угла х – это отношение противолежащего катета к прилежащему: tgx = а/в;
- котангенс угла х – это отношение прилежащего катета к противолежащему: ctgx = в/а.

Похожие статьи
Видео-урок: Нахождение сторон с помощью косинусного отношения
Стенограмма видео
В этом видео мы увидим
как использовать отношение косинуса для вычисления длины либо соседнего, либо
гипотенуза в прямоугольном треугольнике. Итак, прежде всего, напоминание о том, что
отношение косинусов равно. у меня вот на скрине схема
прямоугольного треугольника. И я выбрал один из других
два угла обозначить как 𝜃. Затем я обозначил три стороны
этого треугольника с их названиями относительно этого угла 𝜃. Итак, у нас есть гипотенуза. У нас все наоборот. А у нас соседний. Отношение косинуса или cos, как это
часто сокращенно, является отношением между соседним и гипотенузой этого
треугольник. Таким образом, его определение состоит в том, что из-за
угол 𝜃 равен прилежащему, деленному на гипотенузу. И если вы используете SOHCATOA для
помочь вам с тригонометрией, то это часть CAH этого.
Вот и наша первая проблема.
Нам дан чертеж
прямоугольный треугольник. Мы видим, что нам дали
длина одной стороны и одного угла. И нас просят вычислить 𝑥,
что является длиной другой стороны. Так что для меня первый шаг к любому
Задача, связанная с тригонометрией, состоит в том, чтобы обозначить три стороны треугольника
их метки по отношению к этому углу 28 градусов. Таким образом, используя первый из каждого из
эти слова, вы можете видеть, что у меня есть гипотенуза, противоположное и
соседний. Теперь, глядя на эти три стороны,
вы можете видеть, что у меня есть шесть сантиметров, которые являются гипотенузой. И я хочу вычислить 𝑥, что
является соседним. Так что у меня есть 𝐴 и 𝐻, участвующие в
это соотношение.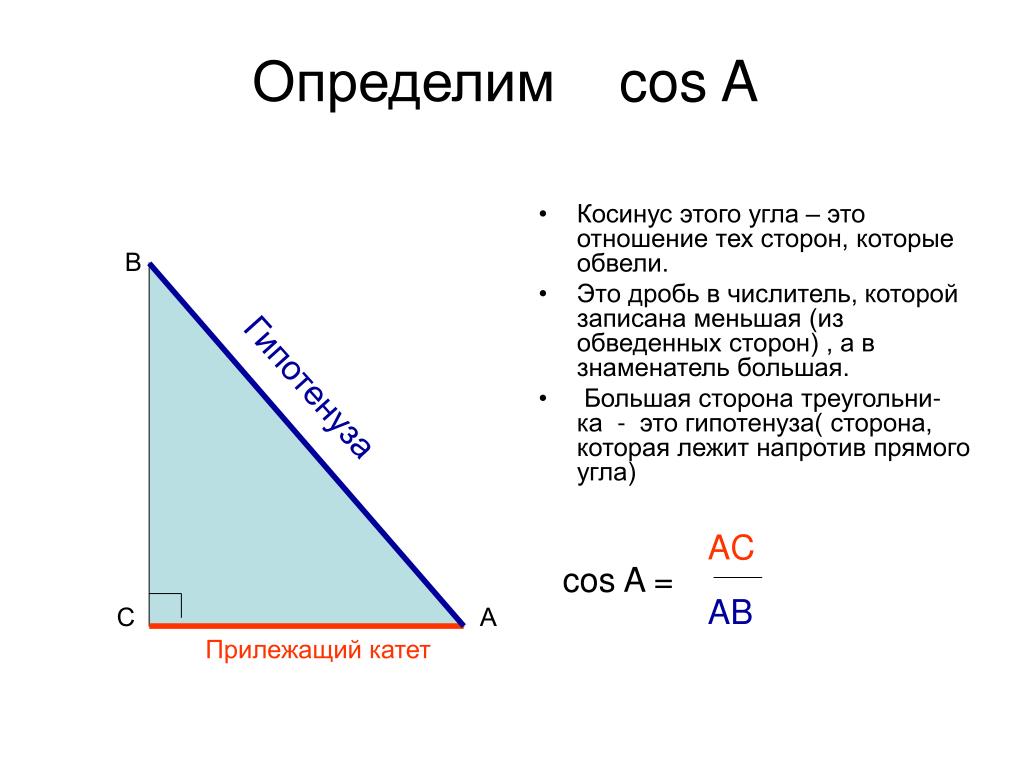
Итак, я припоминаю определение
соотношение кос. И это то, что
соседнее, деленное гипотенузой. То, что я собираюсь сделать, это то, что
Я запишу это соотношение. Но я собираюсь заполнить
информация мне известна. Так что я заменю 𝜃, что означает
угол, с 28. Я заменю соседний на
𝑥, потому что это его буква на диаграмме. И я собираюсь заменить
гипотенуза с шестью. Итак, это дает мне, потому что 28 равно
до 𝑥 более шести. Теперь это уравнение, которое я
ищет решение, чтобы определить значение 𝑥. Итак, первый шаг, который нужно сделать в этом,
ну в знаменателе шестерка. Поэтому мне нужно умножить обе части
это уравнение на шесть.
Теперь я оценю это с помощью
мой калькулятор, убедившись, что он находится в режиме градусов, потому что угол в вопросе был
указывается в градусах. Итак, оценивая это, я понимаю, что 𝑥
равно 5,29768. Вопрос попросил меня найти это
значение с точностью до десятых. Поэтому мне нужно округлить свой ответ. И поэтому у меня это 𝑥 есть
равно 5,3. Итак, краткое изложение, в этом
вопрос тогда, что мы сделали, мы определили, что это было отношение косинуса, которое нам нужно
обозначив стороны треугольника. Затем мы записали это соотношение, но
используя информацию в этом конкретном вопросе, а затем решить полученный
уравнение, чтобы найти недостающее значение 𝑥.
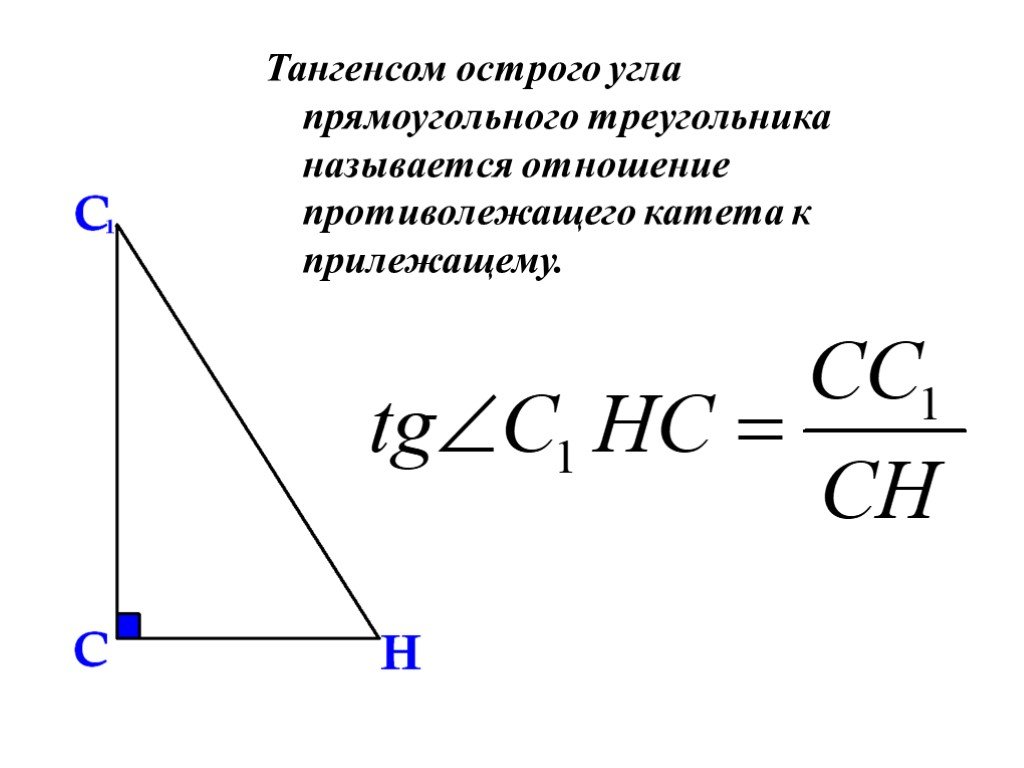
Верно, вот второй пример мы собираемся посмотреть.
В нем сказано: рассчитайте длину гипотенуза треугольника 𝐴𝐵𝐶 с точностью до двух знаков после запятой. И мы видим, что нам дано схема прямоугольного треугольника, где у нас есть длина одной стороны и размер одного из других углов.
Итак, как и раньше, мой первый шаг —
обозначьте три стороны метками по отношению к этому углу 65 градусов. Итак, у нас есть их ярлыки. И снова мы видим, что это
отношение косинуса, которое нам понадобится, потому что мне дана длина соседнего
сторона. Это 5,1 миллиметра. И это гипотенуза, которую я хочу
рассчитать. Итак, 𝐴 и H, помните,
коэффициент косинуса. Итак, как и прежде, что я собираюсь сделать
я собираюсь выписать отношение косинусов. Но я собираюсь заполнить
информация мне известна. Итак, 𝜃 станет 65. Соседнее станет
5.
Итак, мой первый шаг в решении этой
уравнение будет состоять в том, чтобы умножить обе части уравнения на 𝐵𝐶. Так что это дает мне 𝐵𝐶
умножить на cos 65 равно 5,1. Теперь я хочу потренироваться 𝐵𝐶. Итак, следующий шаг — разделить оба
стороны уравнения на cos 65. Cos 65 — это просто число. Так что это совершенно нормально для меня
что. Это дает мне тогда, что 𝐵𝐶
равно 5,1 относительно 65. На этом этапе я собираюсь
используйте мой калькулятор, чтобы оценить это. И это говорит мне, что 𝐵𝐶
равно 12,067 и так далее.
Итак, наконец, мне нужно округлить это отвечать. И мне нужно включить единицы которые будут миллиметрами. Итак, мой окончательный ответ заключается в том, что длина гипотенузы 𝐵𝐶 равна 12,07 миллиметра.
Итак, процесс ответа на этот вопрос был очень похож на предыдущий. Мы обозначили три стороны, определили необходимость коэффициента косинуса, мы записали его, используя информацию в вопрос, а затем решить полученное уравнение. Уравнение было чуть больше на этот раз сложно, потому что длина, которую мы искали, была в знаменателе дроби. Таким образом, это включало два шага по порядку решить ее, а не одну.
Верно, наш следующий пример выглядит немного отличается.
Нам дан круг. И нам говорят, что 𝐴𝐵
диаметр этого круга.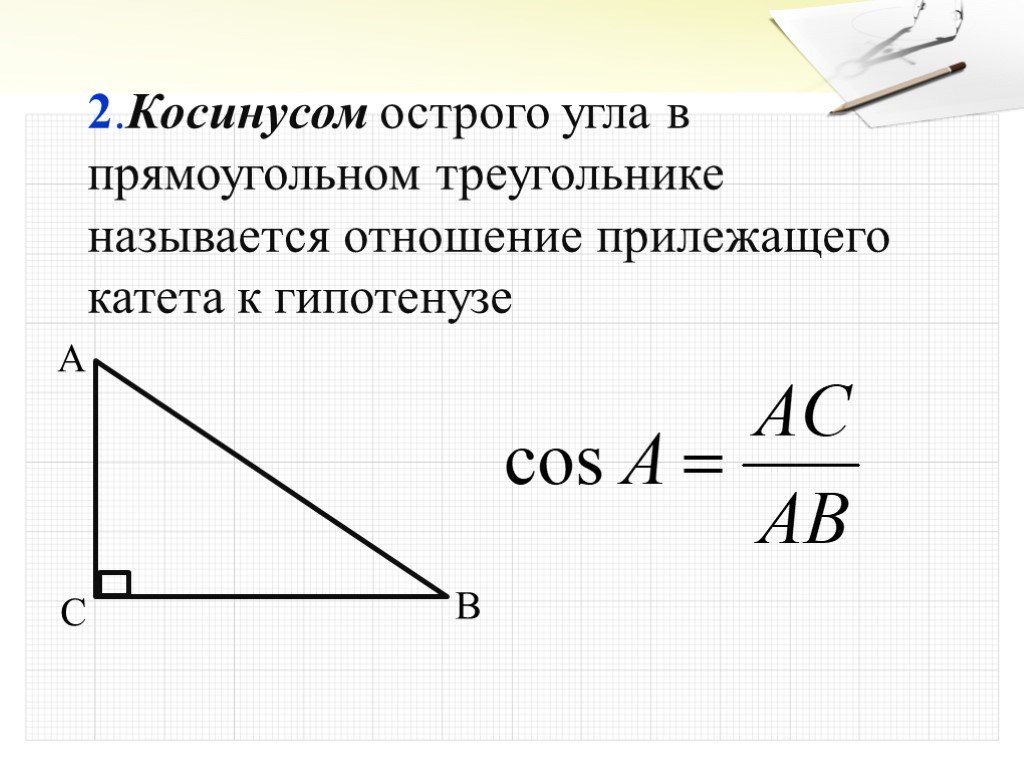 Затем нас просят рассчитать
радиус этой окружности с точностью до сотых.
Затем нас просят рассчитать
радиус этой окружности с точностью до сотых.
Теперь мы видим, что в этом
круг, у нас есть треугольник. И у нас есть один из углов
треугольник, который составляет 40 градусов и длина одной стороны, которая составляет четыре сантиметра. Вопрос в том, хорошо ли это
прямоугольный треугольник? Потому что если это так, то мы можем применить
тригонометрия к этой задаче. Теперь, чтобы увидеть, что это в
на самом деле прямоугольный треугольник, вам нужно сделать соединение с некоторой работой в
другой раздел математики. А это площадь круга
теоремы. Одна из ключевых теорем круга
говорит нам, что если у вас есть такой сценарий, то угол, который находится на
длина окружности равна половине угла в центре. Здесь угол в центре равен
прямая линия. Итак, 180 градусов. И, следовательно, угол при
окружность, угол 𝐴𝐶𝐵, составляет половину этого. Так это 90 градусов, что означает
что этот угол здесь на самом деле прямой угол.
Так это 90 градусов, что означает
что этот угол здесь на самом деле прямой угол.
Если вы, возможно, изучали темы в
другого порядка и вы еще не встречались с теоремами о кругах, то вы ожидаете, что
прямой угол, который будет отмечен на диаграмме для вас. Но в конце концов, как только вы встретите
теоремы круга, вы могли бы вывести это для себя. Итак, это говорит нам о том, что мы делаем
иметь прямоугольный треугольник. И поэтому мы можем использовать
тригонометрии для решения этой задачи. Поэтому мой первый шаг будет
обозначить три стороны этого треугольника их именами, противоположную,
смежные, а гипотенуза — по отношению к углу 40 градусов. Итак, что мы видим, мы знаем
длина соседнего. Если мы хотим вычислить радиус
этого круга, то нам нужно вычислить длину 𝐴𝐵, то есть диаметр,
а потом пополам. Итак, нам снова нужно знать
гипотенуза. Таким образом, A и 𝐻 участвуют, что
говорит нам, что это отношение косинусов, которое нам нужно.
Таким образом, A и 𝐻 участвуют, что
говорит нам, что это отношение косинусов, которое нам нужно.
Как и в предыдущих вопросах,
мы снова напишем соотношение косинусов правильно, но заполнив информацию в
этот конкретный вопрос. Итак, у нас есть этот угол
что 40 равно четырем, прилежащее к 𝐴𝐵, гипотенузе. Теперь то, что мы хотим сделать, это
решите это уравнение, чтобы определить значение 𝐴𝐵. Так что это очень похоже на то, что мы
видел в предыдущем примере. 𝐴𝐵 находится в знаменателе этого
дробная часть. Итак, прежде всего нам нужно умножить
обе части уравнения на 𝐴𝐵. И это дает мне 𝐴𝐵
умножить на cos 40 равно четырем. Следующим шагом мне нужно
разделите обе части этого уравнения на cos 40. Итак, у меня 𝐴𝐵 равно четырем
выше cos 40. Сейчас я не буду оценивать это
совсем еще потому, что вопрос просил меня вычислить радиус круга.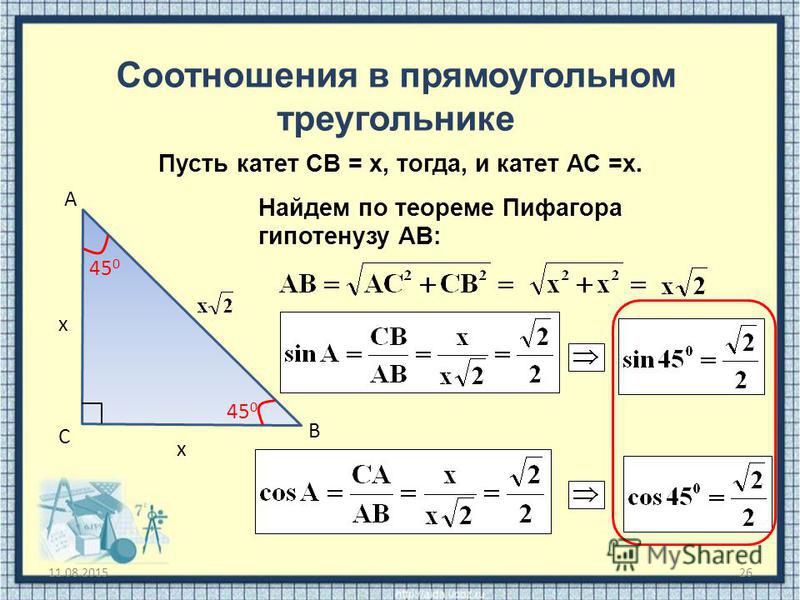 А 𝐴𝐵 — это диаметр. Поэтому мне нужно вдвое уменьшить это, чтобы
ответить на вопрос.
А 𝐴𝐵 — это диаметр. Поэтому мне нужно вдвое уменьшить это, чтобы
ответить на вопрос.
Итак, 𝑟, который я использую для обозначения
радиус круга равен четырем на cos 40, умноженному на половину. И я воспользуюсь своим калькулятором сейчас, чтобы
оцените это, что говорит мне, что 𝑟 равно 2,6108 и так далее. Теперь вопрос попросил меня найти
этот радиус с точностью до сотых. Поэтому я округлю свой ответ. Итак, мы имеем, что радиус
окружность равна 2,61 сантиметра. Таким образом, в этом вопросе актуальным
процесс очень похож на то, что мы уже видели ранее. Единственная разница заключалась в том, что это
время мы объединяли наши знания тригонометрии с нашими знаниями круга
теоремы, а также используя теоремы о круге, чтобы определить, что угол
𝐴𝐶𝐵 было 90 градусов. И, следовательно, мы могли бы применить
тригонометрия к задаче.
Хорошо, последний вопрос, который мы собираемся смотреть на это вопрос noncalculator.
Итак, у нас есть схема прямоугольный треугольник. И нам говорят использовать данные в таблице для расчета 𝐵𝐶. И в таблице мы видим, что нам даны значения отношений синуса, косинуса и тангенса для этого угла 35 градусов.
Итак, занимаясь тригонометрией, вы
почти всегда иметь доступ к калькулятору, потому что он нужен вам для того, чтобы
чтобы сообщить вам значения этих отношений синуса, косинуса и тангенса. Есть определенные углы,
так что 30 градусов, 45 градусов и 60 градусов, для которых эти значения довольно просты
коэффициенты в пересчете на сурды. И так можно заниматься тригонометрией
без калькулятора. Но большую часть времени мы делаем
нужно это. Однако этот вопрос получил
обойти потребность в калькуляторе, дав нам значения sin, cos и tan в пределах
сам вопрос. И поэтому мы посмотрим, как использовать эти
через минуту. Первый шаг тогда, как это, вероятно,
с помощью тригонометрии состоит в том, чтобы обозначить три стороны относительно этого угла в 35°.
градусов. Итак, у нас есть три ярлыка
здесь. И снова, как и во всех примерах
в этом видео мы можем видеть, что это отношение косинуса нам понадобится, потому что мы
имеют длину гипотенузы 𝐻. И мы хотим рассчитать 𝐵𝐶
который является соседним. Итак, 𝐴 и 𝐻 говорят нам, что это
нужное нам отношение косинусов.
И поэтому мы посмотрим, как использовать эти
через минуту. Первый шаг тогда, как это, вероятно,
с помощью тригонометрии состоит в том, чтобы обозначить три стороны относительно этого угла в 35°.
градусов. Итак, у нас есть три ярлыка
здесь. И снова, как и во всех примерах
в этом видео мы можем видеть, что это отношение косинуса нам понадобится, потому что мы
имеют длину гипотенузы 𝐻. И мы хотим рассчитать 𝐵𝐶
который является соседним. Итак, 𝐴 и 𝐻 говорят нам, что это
нужное нам отношение косинусов.
Итак, как и в предыдущих вопросах, мы
собираемся выписать соотношение косинусов, но заполнив информацию для этого
вопрос, поэтому замените угол на 35, замените соседний на 𝐵𝐶 и
заменив гипотенузу на 10. Тогда мы имеем, что cos 35 равен
равно 𝐵𝐶 больше 10. Теперь мне нужно решить это уравнение
для 𝐵𝐶. Так что я собираюсь умножить обе стороны
уравнения на 10. А у меня 𝐵𝐶 равно 10
cos 35. Вот где информация
возникает вопрос, потому что помните, что у нас нет калькулятора. Но, взглянув на таблицу, мы можем
см., что у нас есть значение cos 35 здесь. это 0,819. Так что я могу использовать это значение в этом
этап в вопросе. Итак, это говорит мне, что 𝐵𝐶 равно
до 10 умножить на 0,819. И это прямо
умножение делать без калькулятора. Итак, у нас есть длина 𝐵𝐶
составляет 8,19 см.
Так что я собираюсь умножить обе стороны
уравнения на 10. А у меня 𝐵𝐶 равно 10
cos 35. Вот где информация
возникает вопрос, потому что помните, что у нас нет калькулятора. Но, взглянув на таблицу, мы можем
см., что у нас есть значение cos 35 здесь. это 0,819. Так что я могу использовать это значение в этом
этап в вопросе. Итак, это говорит мне, что 𝐵𝐶 равно
до 10 умножить на 0,819. И это прямо
умножение делать без калькулятора. Итак, у нас есть длина 𝐵𝐶
составляет 8,19 см.
Это не точное значение
потому что cos 35 не совсем 0,819; это более длинное десятичное число. Но нам это дано только
три десятичных знака. Итак, это значение для 𝐵𝐶, это
с точностью до двух знаков после запятой или до ближайшей сотой. Так что этот вопрос просто дает
один из примеров того, как вы можете использовать тригонометрию, когда у вас нет доступа к
калькулятор.
В общем, мы вспомнили определение отношения косинуса как прилежащего деления на гипотенузу. И мы видели, как это применить отношение к четырем различным вопросам, где мы хотим рассчитать либо прилежащей или гипотенузе в прямоугольном треугольнике.
Тригонометрические отношения
Тригонометрическое отношение связывает длины двух сторон . Рассмотрим прямоугольный треугольник △ABC. Один из них был назван θ.
Поскольку он противоположен , BC является прямоугольным треугольником. Остальные стороны — the — можно назвать относительно отмеченного θ. Поскольку AB находится рядом с ∠θ, она называется смежной стороной . И наоборот, поскольку AC лежит напротив ∠θ, его называют противоположной стороной.
Тригонометрические отношения можно использовать для определения неизвестных длин сторон или углов в прямоугольных треугольниках.
Для θ a , синус θ является между длинами и .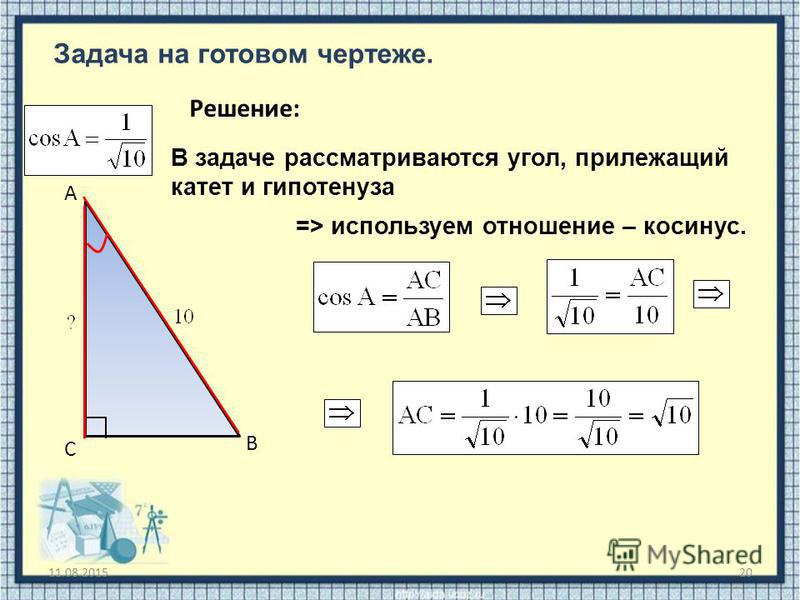
Синус θ записывается как sinθ.
sinθ=гипотенузаПротивоположная
Это тригонометрическое соотношение определяет отношение противолежащего катета к гипотенузе. Он не дает указаний о длине отдельных сторон.
Следует отметить, что для заданного угла, при изменении размеров противолежащего катета и гипотенузы, если их отношение останется прежним, то и синус останется прежним.
Для θ a , косинус θ равен между длинами и .
Косинус θ записывается как cosθ.
cosθ = Гипотенуза Смежный
Хотя это тригонометрическое соотношение выражает отношение прилежащей стороны к гипотенузе, оно не указывает фактические измерения их длин.
Следует отметить, что для заданного угла при изменении длин прилежащего катета и гипотенузы, если их отношение останется прежним, то и косинус останется прежним.
Для θ a , тангенс θ равен между длинами и .
Тангенс θ записывается как tanθ.
tanθ=AdjacentOpposite
Тригонометрическое отношение выражает отношение между противолежащей стороной и прилежащей стороной. Он не дает никаких указаний на фактическое измерение длин сторон.
Следует отметить, что для заданного угла при изменении длин смежной и противолежащей сторон, если их отношение останется прежним, то и касательная останется прежней.
Для θ a косеканс θ — это разница между длинами и .
Косеканс θ записывается как csc(θ).
csc(θ)=противоположная гипотенуза
Это тригонометрическое соотношение устанавливает отношение между гипотенузой и противоположным катетом к определенному углу. Он не дает указаний о длинах сторон.
Он не дает указаний о длинах сторон.
Когда длины противолежащего катета и гипотенузы изменяются для заданного угла, если их отношение остается неизменным, то и косеканс останется прежним. Также обратите внимание, что косеканс θ — это синус θ.
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧cscθ=opphyp∣∣sinθ=hypopp∣∣∣ ⇒ cscθ=sinθ1
Для θ a , секанс θ равен между длинами и .
Секанс θ записывается как sec(θ).
сек(θ)=соседняя гипотенуза
Это тригонометрическое соотношение устанавливает отношение между гипотенузой и прилежащим катетом к определенному углу. Он не дает указаний о длинах сторон.
Когда длины смежного катета и гипотенузы изменяются для заданного угла, если их отношение остается прежним, то и секущая остается неизменной. Также обратите внимание, что секанс θ равен косинусу θ.