Отношение катетов в прямоугольном треугольнике – Прямоугольный треугольник. Определения и свойства

– Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и катету).

Свойства прямоугольного треугольника

 1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора: , где – катеты, – гипотенуза.

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты  и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

И, думаю, будет полезна  таблица формул для треугольника.

egemaximum.ru

Свойства прямоугольного треугольника. Формулы прямоугольного треугольника.

Прямоугольный треугольник

Треугольник с прямым углом \(90°\) называют прямоугольным треугольником.

Самая длинная сторона  треугольника называется гипотенузой, а две другие стороны — катеты.

Свойства прямоугольного треугольника — это свойства, определяющие прямоугольный треугольник.

• Если угол \(α\) равен \(30°\) градусов, то \(2a = c\).

• Площадь прямоугольного треугольника можно измерить с помощью формулы:

 \(S = \frac{1}{2}×a×b\),

где \(a\) и  \(b\) можно рассматривать как две стороны треугольника. Эта формула используется только для прямоугольного треугольника.

• Теорема Пифагора утверждает, что если \(c\)- гипотенуза, а  \(a\) и  \(b\) — две стороны треугольника, то в соответствии с теоремой Пифагора:

\( c^2=a^2+b^2\)

         Квадрат гипотенузы равен сумме квадрата двух других сторон треугольника.

• Радиус вписанной окружности прямоугольного треугольника можно найти по формуле:

\(r = \frac{a+b-c}{2}\)

• Радиус описанной окружности прямоугольного треугольника можно рассчитать по формуле:

\(r=\frac{c}{2}\),

где \(c\) — гипотенуза прямоугольного треугольника.

• Проекции катетов треугольника на гипотенузу:

\(b^2=q*c\)

\(a^2=p*c\)

\(h^2=q*p\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Прямоугольные треугольники — урок. Геометрия, 7 класс.

Свойства прямоугольного треугольника

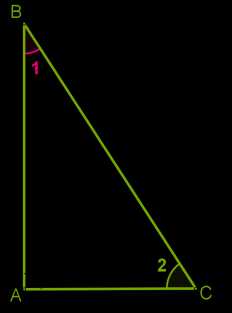
Сумма двух острых углов прямоугольного треугольника равна 90°.\( \)

Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника∡\(1 +\)∡\(2 =\)90°.

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета против угла в \(\)30°\(\)).

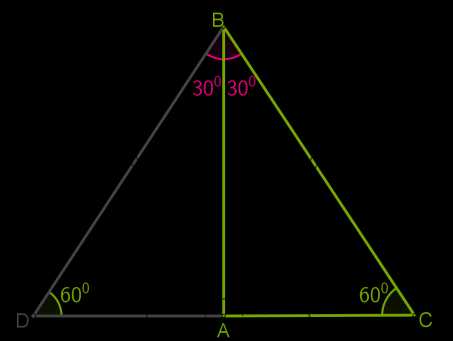
Рассмотрим прямоугольный треугольник \(ABC\), в котором∡\(A\) — прямой, ∡\(B =\)30°и значит, что ∡\(C =\)60°.

Докажем, что \(BC = 2 AC\).
Приложим к треугольнику \(ABC\) равный ему треугольник \(ABD\) как показано на рисунке.

Получим треугольник \(BCD\), в котором∡\(B =\)∡\(D =\)60°, поэтому \(DC = BC\). Но \(DC = 2 AC\). Следовательно, \(BC = 2 AC\).

Справедливо и обратное суждение.

Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

www.yaklass.ru

Прямоугольный треугольник формулы — Математическая шкатулка

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

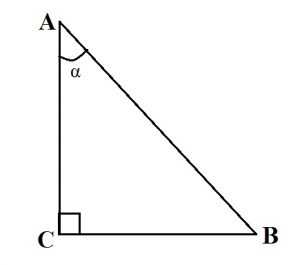
1. Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
2. Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
3. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.  AB² = AC² + CB²

Прямоугольный треугольник:  формулы площади и проекции

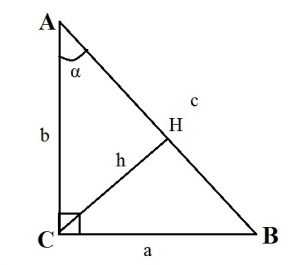
1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH² = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое  между гипотенузой и проекцией этого катета на гипотенузу:  CA² = AB·AH;  CB² = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты.  S = (hc):2.

Прямоугольный треугольник:  формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.                 cosα  = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.           sinα = BC:AB.
3. Тангенс  острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.    tgα  = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.    ctgα  = AC:BC.
5. Основное тригонометрическое тождество:  cos²α + sin²α = 1.
6. Теорема косинусов: b² = a² + c² – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник:  формулы для описанной окружности

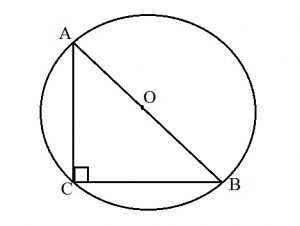
1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник:  формулы для вписанной  окружности

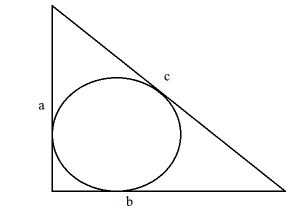
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b  -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из  сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

Решение:

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Ответ: AB = 28.

ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)

mathembox.xyz

Соотношение между сторонами и углами прямоугольного треугольника

Будем рассматривать прямоугольный треугольник $ABC$ c прямым углом $C$ (рис. 1).

Рисунок 1. Прямоугольный треугольник

Будем рассматривать угол $A$. Тогда катет $BC$ будет называться противолежащим катетом, а катет $AC$ прилежащим к углу $A$.

Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника

Определение 1

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе данного треугольника.

Определение 2

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе данного треугольника.

Определение 3

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету данного треугольника.

Определение 4

Синусом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету данного треугольника.

То есть, имеем:

Из формул (1) и (2) очевидно, что

Проверим теперь следующее тождество:

Подставим формулы (1) и (2), получим

Из теоремы Пифагора мы знаем, что ${BC}^2+{AC}^2={AB}^2$, следовательно

Тождество (5) называется основным тригонометрическим тождеством.

Основные значения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника

Вычислим значения синуса, косинуса, тангенса и котангенса для ${30}^{{}^\circ },\ {45}^{{}^\circ }$ и ${60}^{{}^\circ }$. Для этого вспомним следующую теорему.

Теорема 1

Катет прямоугольного треугольника, лежащий напротив угла в ${30}^{{}^\circ }$, равняется половине гипотенузы этого треугольника.

Пусть для начала у нас $\angle A={30}^{{}^\circ }$. Так как треугольник прямоугольный, то $\angle B={60}^{{}^\circ }$.

По теореме 1, имеем $AB=2BC$.

Используя основное тригонометрическое тождество (5), получим:

Теперь нетрудно найти тангенсы и котангенсы этих углов.

Пусть теперь $\angle A={45}^{{}^\circ }$. Тогда $\angle B={45}^{{}^\circ }$, то есть прямоугольный треугольник — равнобедренный. По теореме Пифагора ${BC}^2+{AC}^2={AB}^2$, следовательно, ${AB}^2={2BC}^2=2{AC}^2$, то есть

Тогда

Сведем все полученные данные в таблицу (таблица 1).

Рисунок 2. Основные значения синусов, косинусов, тангенсов и котангенсов

Пример задачи на нахождение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Пример 1

Найти значение синуса, косинуса, тангенса и котангенса угла $A$, если $AB=5,\ BC=4,\ AC=3.$

Решение.

Все решение задачи будем производить с помощью определений 1-4. Получим:

spravochnick.ru

Проекции катетов на гипотенузу | Треугольники

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

или

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

или

www.treugolniki.ru

Тригонометрические функции в прямоугольном треугольнике

Тригонометрические функции являются математическими функциями от угла. Они очень важны при изучении курса геометрии, а также при исследовании множества периодических процессов. Тригонометрические функции определяют, обычно, как отношения длины определенных отрезков в единичной окружности или сторон прямоугольного треугольника. Что касается более современных определений, то они выражают тригонометрические функции, как решение, например, дифференциальных уравнений или через суммы рядов. Все это позволяет расширить область определения тригонометрических функций на произвольные числа, а в некоторых случаях даже на комплексные.

В настоящее время выделяют шесть основных тригонометрических функций:

• косинус;
• синус;
• тангенс;
• котангенс;
• секанс;
• косеканс;

Все эти функции связаны между собой определенными уравнениями. Но поговорим конкретнее о тригонометрических функциях в прямоугольном треугольнике. Для начала определим основные стороны данного треугольника, а именно:

• гипотенуза – сторона, которая лежит напротив прямого угла (90 градусов), а также самая длинная в треугольнике.
• противолежащий катет – катет, что лежит напротив заданного угла;
• прилегающий катет – катет, что является стороной угла.

И, конечно же, не надо забывать о самом угле, допустим, а. Однако, стоит отметить, что угол а ни в коем случае не должен быть прямым.

Итак, свяжем стороны треугольника и его угол в тригонометрические функции:

• Косинус угла – это отношение прилежащего к углу катета к гипотенузе;
• Синус угла – отношение противолежащего катета к гипотенузе;
• Тангенс – это отношение противолежащего катета к прилегающему;
• Котангенс – отношения прилежащего катета к противолежащему;
• Косеканс угла – отношение гипотенузы к катету, что лежит напротив угла;
• Секанс – отношение гипотенузы к катету, который прилегает.

mateshka.ru