Уравнения корни квадратные: Квадратные уравнения — урок. Алгебра, 8 класс.

Формула расчета корней квадратного уравнения. Квадратные уравнения

Просто. По формулам и чётким несложным правилам. На первом этапе

надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно. Самое главное — правильно

определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения.

Выражение под знаком корня называется дискриминант . Как видим, для нахождения икса, мы

используем только a, b и с . Т.е. коэффициенты из квадратного уравнения . Просто аккуратно подставляем

значения a, b и с в эту формулу и считаем. Подставляем со своими знаками!

Например , в уравнении:

а =1; b = 3; c = -4.

Подставляем значения и записываем:

Пример практически решён:

Это ответ.

Самые распространённые ошибки — путаница со знаками значений

a, b и с . Вернее, с подстановкой

отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы

с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой пример решить:

Здесь a = -6; b = -5; c = -1

Расписываем все подробно, внимательно, ничего не упуская со всеми знаками и скобками:

Часто квадратные уравнения выглядят слегка иначе. Например, вот так:

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок.

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду.

Что это означает?

Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с.

Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

Избавьтесь от минуса. Как? Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример.

Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета .

Для решения приведённых квадратных уравнений, т.е. если коэффициент

x 2 +bx+c=0,

тогда x 1 x 2 =c

x 1 +x 2 =− b

Для полного квадратного уравнения, в котором a≠1 :

x 2 + b x+ c =0,

делим все уравнение на а:

→ →

где x 1 и x 2 — корни уравнения.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте

уравнение на общий знаменатель.

Вывод. Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего

уравнения на -1.

3. Если коэффициенты дробные — ликвидируем дроби умножением всего уравнения на соответствующий

множитель.

4. Если икс в квадрате — чистый, коэффициент при нём равен единице, решение можно легко проверить по

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

1. Линейное уравнение

Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х 1,2 = (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а

Также можно определить визуально количество корней, не вычисляя дискриминант. Для этого нужно найти вершину параболы и определить в какую сторону направлены ветви. Определить координату x вершины можно по формуле: х 0 = -b / 2a. В этом случае координата y вершины находится простой подстановкой значения х 0 в изначальное уравнение.

Квадратное уравнение x 2 — 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (-8) 2 — 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

3. Тригонометрические уравнения

Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi.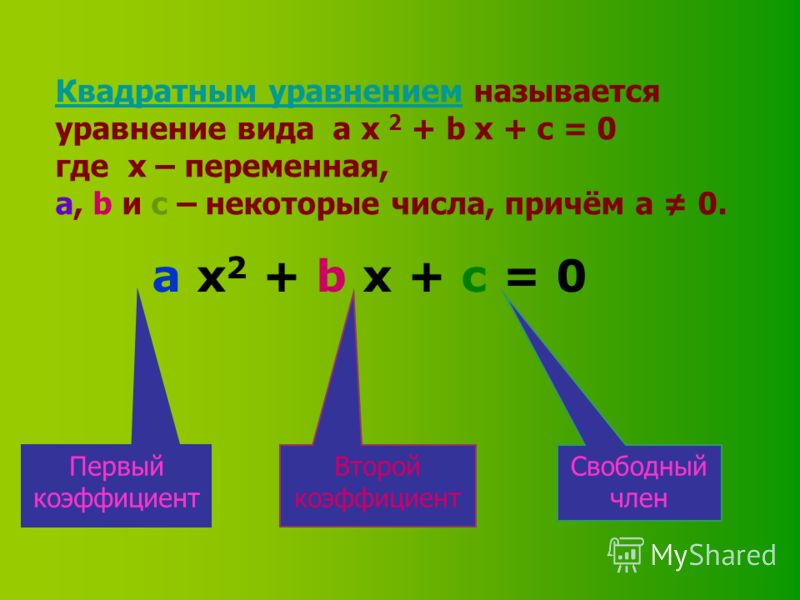 Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Видеоурок 2: Решение квадратных уравнений

Лекция: Квадратные уравнения

Уравнение

Уравнение — это некое равенство, в выражениях которого имеется переменная.

Решить уравнение — значит найти такое число вместо переменной, которое будет приводить его в верное равенство.

Уравнение может иметь одно решение или несколько, или же не иметь его вообще.

Для решения любого уравнения его следует максимально упростить до вида:

Линейное: a*x = b;

Квадратное: a*x 2 + b*x + c = 0.

То есть любые уравнение перед решением нужно преобразовать до стандартного вида.

Любое уравнение можно решить двумя способами: аналитическим и графическим.

На графике решением уравнения считаются точки, в которых график пересекает ось ОХ.

Квадратные уравнения

Уравнение можно назвать квадратным, если при упрощении оно приобретает вид:

a*x 2 + b*x + c = 0.

При этом a, b, c являются коэффициентами уравнения, отличающиеся от нуля. А «х» — корень уравнения. Считается, что квадратное уравнение имеет два корня или могут не иметь решения вообще. Полученные корни могут быть одинаковыми.

«а» — коэффициент, который стоит перед корнем в квадрате.

«b» — стоит перед неизвестной в первой степени.

«с» — свободный член уравнения.

Если, например, мы имеем уравнение вида:

2х 2 -5х+3=0

В нем «2» — это коэффициент при старшем члене уравнения, «-5» — второй коэффициент, а «3» — свободный член.

Решение квадратного уравнения

Существует огромное множество способов решения квадратного уравнения. Однако, в школьном курсе математики изучается решение по теореме Виета, а также с помощью дискриминанта.

Решение по дискриминанту:

При решении с помощью данного метода необходимо вычислить дискриминант по формуле:

Если при вычислениях Вы получили, что дискриминант меньше нуля, это значит, что данное уравнение не имеет решений.

Если дискриминант равен нулю, то уравнение имеет два одинаковых решения. В таком случае многочлен можно свернуть по формуле сокращенного умножения в квадрат суммы или разности. После чего решить его, как линейное уравнение. Или воспользоваться формулой:

Если же дискриминант больше нуля, то необходимо воспользоваться следующим методом:

Теорема Виета

Если уравнение приведенное, то есть коэффициент при старшем члене равен единице, то можно воспользоваться теоремой Виета .

Итак, предположим, что уравнение имеет вид:

Корни уравнения находятся следующим образом:

Неполное квадратное уравнение

Существует несколько вариантов получения неполного квадратного уравнения, вид которых зависит от наличия коэффициентов.

1. Если второй и третий коэффициент равен нулю (b = 0, с = 0) , то квадратное уравнение будет иметь вид:

Данное уравнение будет иметь единственное решение. Равенство будет верным только в том случае, когда в качестве решения уравнения будет ноль.

Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a, b и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1: Решить 2x 2 +8 x –192=0

а=2 b=8 c= –192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2: Решить x 2 –22 x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3: Решить x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а x 2 + bx + c =0 выполняется равенство

a + b + с = 0, то

— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство

a + с = b , то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001 x 2 –4995 x – 6=0

Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит

Пример 2: 2501 x 2 +2507 x +6=0

Выполняется равенство a + с = b , значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а ± b+c ≠ 0, то используется прием переброски, например:

2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1 = 5 х 2 = 0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.

Навигация по странице.

Что такое уравнение?

Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения :

Определение.

Уравнение – это равенство, содержащее неизвестное число, которое надо найти.

Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p , t , u и т.п., но наиболее часто используются буквы x , y и z .

Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.

Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8 , y=3 и т. п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3 , z−2=5 , 3·t=9 , 8:x=2 .

Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18 и x+3·(x+2·(x−2))=3 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8 , 7−3=z+1 или 3·x−4=2·(x+12) .

Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений , изучающиеся в школе.

В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:

Определение.

Уравнением называют равенство, содержащее переменную, значение которой нужно найти.

Например, уравнение x+3=6·x+7 – уравнение с переменной x , а 3·z−1+z=0 – уравнение с переменной z .

На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.

Определение.

Уравнения с одной, двумя, тремя и т.д. переменными – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.

Например, уравнение 3,2·x+0,5=1 – это уравнение с одной переменной x , в свою очередь уравнение вида x−y=3 – это уравнение с двумя переменными x и y . И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27 . Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x , y и z .

Что такое корень уравнения?

С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.

Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a в уравнение a+1=5 подставить число 2 , то получится неверное числовое равенство 2+1=5 . Если же мы в это уравнение подставим вместо a число 4 , то получится верное равенство 4+1=5 .

На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.

Определение.

Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.

Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.

Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5 . Согласно озвученному определению корня уравнения, число 4 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5 , а число 2 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5 .

На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.

Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5 имеет корень 4 , а уравнение 0·x=5 не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x , мы получим неверное равенство 0=5 .

Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4 имеет единственный корень 6 , корнями уравнения x 2 =9 являются два числа −3 и 3 , уравнение x·(x−1)·(x−2)=0 имеет три корня 0 , 1 и 2 , а решением уравнения x=x является любое число, то есть, оно имеет бесконечное множество корней.

Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках. Например, если корнями уравнения являются числа −1 , 2 и 4 , то пишут −1 , 2 , 4 или {−1, 2, 4} . Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x , и корнями этого уравнения являются числа 3 и 5 , то можно записать x=3 , x=5 , также переменной часто добавляют нижние индексы x 1 =3 , x 2 =5 , как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N , целых чисел Z , действительных чисел R . Например, если корнем уравнения с переменной x является любое целое число, то пишут , а если корнями уравнения с переменной y является любое действительное число от 1 до 9 включительно, то записывают .

Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.

Определение.

Решением уравнения с двумя, тремя и т.д. переменными называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.

Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7 . Подставим в него вместо x число 1 , а вместо y число 2 , при этом имеем равенство 1+2=7 . Очевидно, оно неверное, поэтому, пара значений x=1 , y=2 не является решением записанного уравнения. Если же взять пару значений x=4 , y=3 , то после подстановки в уравнение мы придем к верному равенству 4+3=7 , следовательно, эта пара значений переменных по определению является решением уравнения x+y=7 .

Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.

Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7 . Решение этого уравнения x=4 , y=3 кратко можно записать как (4, 3) .

Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений .

Список литературы.

• Математика . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.

Формулы корней квадратных уравнений, разложение на множители

В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.

Квадратные уравнения

Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.

Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.

Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.

Различают два вида уравнений:

• Приведённые — это случай, когда в квадратном равенстве a = 1.
• Непривёденные если a ≠ 1.

При этом x² — приведённое, а уже при 5x² оно станет непривёденным.

Понятие дискриминант

Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.

Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:

• Если D меньше нуля, то действительных корней нет.
• В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
• Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.

Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:

• 9х²-6х+1=0,
• D = (-6)² 4 × 9 ×1 = 0,
• D эквивалентен нулю,
• x = -6/2×9 = 1/3.

Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.

Разные квадратные уравнения

Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.

Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.

Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.

Следовательно оно бывает только трёх видов:

• Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
• ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а &lt, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
• ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.

Из истории математики

Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.

Это показал древнегреческий учёный Диофант. Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.

Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.

После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.

Уравнения	х1 и х2	х1+х2	х1×х2
х² -6х + 8 = 0	2 и 4	6	8
x²+x-12=0	-4 и 3	-1	-12
x²-4x-5=0	-3 и -2	-5	6
x²-4x-5=0	-1 и 5	4	-5

Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.

Теорему можно сформулировать так.

Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.

формулы вычисления. Формула нахождения корней квадратного уравнения

Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.

Что такое квадратный корень?

В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y² = x.

Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x < 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.

Приведем два простых примера:

√9 = 3, поскольку 3² = 9; √(-9) = 3i, поскольку i² = -1.

Итерационная формула Герона для нахождения значений корней квадратных

Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.

Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).

Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:

a_n+1 = 1/2(a_n+x/a_n), где lim_n->∞(a_n) => x.

Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a₀ (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a₀)² было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a₁, которое уже будет ближе к искомому значению. После этого необходимо уже a₁ подставить в выражение и получить a₂. Эту процедуру следует повторять до получения необходимой точности.

Пример применения итерационной формулы Герона

Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a₀).

Приведем простой пример: необходимо вычислить √11. Выберем a₀ = 3, так как 3² = 9, что ближе к 11, чем 4² = 16. Подставляя в формулу, получим:

a₁ = 1/2(3 + 11/3) = 3,333333;

a₂ = 1/2(3,33333 + 11/3,33333) = 3,316668;

a₃ = 1/2(3,316668 + 11/3,316668) = 3,31662.

Дальше нет смысла продолжать вычисления, поскольку мы получили, что a₂ и a₃ начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.

В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.

Уравнения второго порядка

Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.

Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.

Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x²), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.

Нахождения корней квадратного уравнения (формула)

Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:

Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x₁ отличается от расчета x₂ только знаком перед корнем квадратным. Подкоренное выражение, которое равно b² — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x₁ и x₂.

Теорема Виета или некоторые свойства корней уравнений второго порядка

В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:

x₁ + x₂ = -b / a и x₁ * x₂ = c / a.

Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.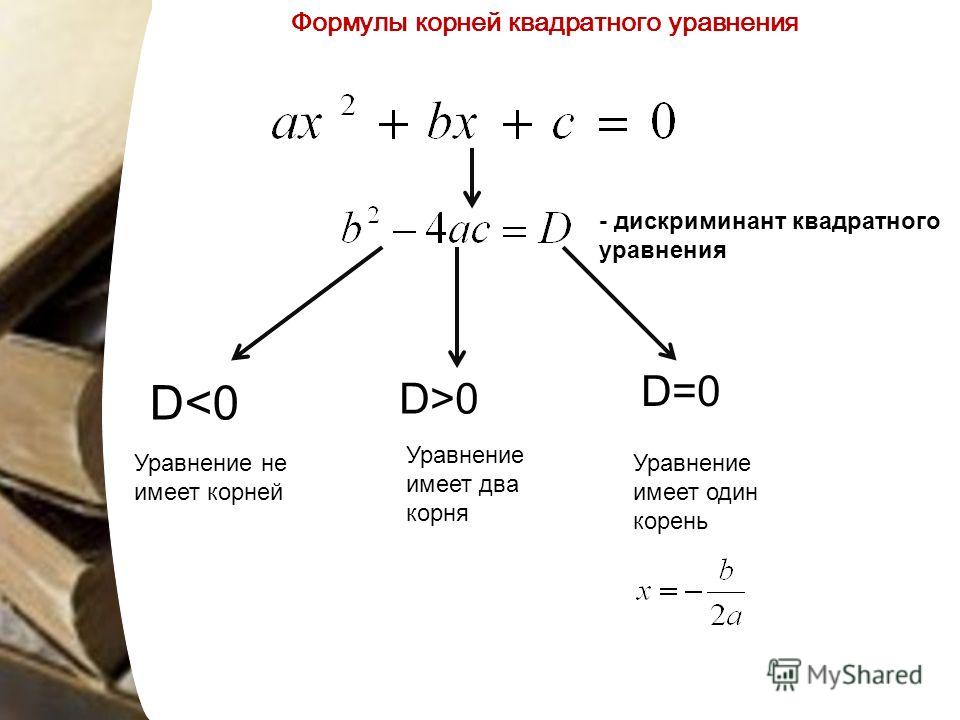

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.

Задача на закрепление полученных знаний

Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:

x₁ + x₂ = -b / a = 4;

x₁ * x₂ = c / a = -13.

Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:

x² — 4x — 13 = 0.

Воспользуемся формулой с дискриминантом, получим следующие корни:

x_1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.

То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.

Теперь воспользуемся рассмотренной формулой квадратного корня: a₀ = 4, тогда:

a₁ = 1/2(4 + 17/4) = 4,125;

a₂ = 1/2(4,125 + 17/4,125) = 4,1231.

В вычислении a₃ нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x_1,2, получим:

x₁ = (4 + 8,246)/2 = 6,123 и x₂ = (4 — 8,246)/2 = -2,123.

Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.

9.6 Решение уравнений с квадратными корнями — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

• Решение радикальных уравнений
• Использование квадратных корней в приложениях

Приготовься 9.

15

Прежде чем начать, пройдите этот тест на готовность.

Упрощение: ⓐ 99 ⓑ 9292.
Если вы пропустили эту задачу, просмотрите Пример 9.1 и Пример 1.19.

Приготовься 9.16

Решите: 5(x+1)−4=3(2x−7)5(x+1)−4=3(2x−7).
Если вы пропустили эту проблему, просмотрите пример 2.42.

Приготовься 9.17

Решить: n2−6n+8=0n2−6n+8=0.
Если вы пропустили эту проблему, просмотрите пример 7.73.

Решение радикальных уравнений

В этом разделе мы будем решать уравнения, в которых переменная стоит под основанием квадратного корня. Уравнения такого типа называются радикальными уравнениями.

Радикальное уравнение

Уравнение, в котором переменная стоит под корнем квадратного корня, называется радикальным уравнением.

Как обычно, при решении этих уравнений то, что мы делаем с одной частью уравнения, мы должны делать и с другой его частью. Поскольку возведение величины в квадрат и извлечение квадратного корня являются «противоположными» операциями, мы возведем обе стороны в квадрат, чтобы удалить знак радикала и найти переменную внутри.

Но помните, что когда мы пишем aa, мы имеем в виду главный квадратный корень. Так что a≥0a≥0 всегда. Когда мы решаем радикальные уравнения, возводя обе части в квадрат, мы можем получить алгебраическое решение, которое сделает отрицательное значение аа. Это алгебраическое решение не было бы решением исходного радикального уравнения; это посторонний раствор. Мы видели посторонние решения и при решении рациональных уравнений.

Пример 9,74

Для уравнения x+2=xx+2=x:

ⓐ Является ли x=2x=2 решением? ⓑ Является ли x=−1x=−1 решением?

Решение

ⓐ Является ли x=2x=2 решением?

Пусть х = 2.
Упрощение.
	2 — это решение.

ⓑ Является ли x=−1x=−1 решением?

Пусть х = -1.
Упрощение.
	−1 не является решением.
	−1 является посторонним решением уравнения.

Попытайся 9.147

Для уравнения x+6=xx+6=x:

ⓐ Является ли x=−2x=−2 решением? ⓑ Является ли x=3x=3 решением?

Попытайся 9.148

Для уравнения −x+2=x−x+2=x:

ⓐ Является ли решение x=−2x=−2? ⓑ Является ли x=1x=1 решением?

Теперь посмотрим, как решить радикальное уравнение. Наша стратегия основана на соотношении между извлечением квадратного корня и возведением в квадрат.

Fora≥0,(a)2=aFora≥0,(a)2=a

Пример 9,75

Как решать радикальные уравнения

Решите: 2x−1=72x−1=7.

Решение

Попытайся 9.149

Решите: 3x−5=53x−5=5.

Попытайся 9.150

Решите: 4x+8=64x+8=6.

Как

Решите радикальное уравнение.

1. Шаг 1. Выделите радикал на одной стороне уравнения.
2. Шаг 2. Возведите в квадрат обе части уравнения.
3. Шаг 3. Решите новое уравнение.
4. Шаг 4. Проверьте ответ.

Пример 9,76

Решите: 5n−4−9=05n−4−9=0.

Решение

Чтобы выделить радикал, добавьте 9 с обеих сторон.
Упрощение.
Возведите в квадрат обе части уравнения.
Решите новое уравнение.
Проверьте ответ.
	Решение n = 17.

Попытайся 9.151

Решите: 3m+2−5=03m+2−5=0.

Попытайся 9.152

Решите: 10z+1−2=010z+1−2=0.

Пример 9,77

Решить: 3у+5+2=53у+5+2=5.

Решение

Чтобы выделить радикал, вычтите 2 с обеих сторон.
Упрощение.
Возведите в квадрат обе части уравнения.
Решите новое уравнение.
Проверьте ответ.
	Решение y=43y=43.

Попытайся 9.153

Решите: 3p+3+3=53p+3+3=5.

Попытайся 9.154

Решите: 5q+1+4=65q+1+4=6.

Когда мы используем подкоренной знак, мы имеем в виду главный или положительный корень. Если уравнение имеет квадратный корень, равный отрицательному числу, то это уравнение не имеет решения.

Пример 9,78

Решите: 9k−2+1=09k−2+1=0.

Решение

Чтобы изолировать радикал, вычтите 1 с обеих сторон.
Упрощение.
Поскольку квадратный корень равен отрицательному числу, уравнение не имеет решения.

Попытайся 90,155

Решите: 2r−3+5=02r−3+5=0.

Попытайся 9.156

Решите: 7s−3+2=07s−3+2=0.

Если одна часть уравнения двучленная, мы используем формулу биномиальных квадратов, когда возводим ее в квадрат.

Биномиальные квадраты

(a+b)2=a2+2ab+b2(a−b)2=a2−2ab+b2(a+b)2=a2+2ab+b2(a−b)2=a2−2ab+b2

Не забудьте средний термин!

Пример 9,79

Решить: p−1+1=pp−1+1=p.

Решение

Чтобы изолировать радикал, вычтите 1 с обеих сторон.
Упрощение.
Возведите в квадрат обе части уравнения.
Упростите, затем решите новое уравнение.
Это квадратное уравнение, поэтому с одной стороны получаем ноль.
Фактор правой стороны.
Использовать свойство нулевого продукта.
Решите каждое уравнение.
Проверьте ответы.
	Решения: p = 1, p = 2.

Попытайся 9.157

Решите: x−2+2=xx−2+2=x.

Попытайся 9.158

Решите: y−5+5=yy−5+5=y.

Пример 9,80

Решить: r+4−r+2=0r+4−r+2=0.

Решение

	г+4-г+2=0г+4-г+2=0
Изолировать радикал.	г+4=г-2г+4=г-2
Возведите в квадрат обе части уравнения.	(г+4)2=(г-2)2(г+4)2=(г-2)2
Решите новое уравнение.	г+4=г2-4г+4г+4=г2-4г+4
Это квадратное уравнение, поэтому с одной стороны получаем ноль.	0=r2-5r0=r2-5r
Фактор правой стороны.	0=г(г-5)0=г(г-5)
Использовать свойство нулевого продукта.	0=r0=r−50=r0=r−5
Решите уравнение.	г=0р=5р=0р=5
Проверьте ответ.
	Решение r=5r=5.
	r=0r=0 — постороннее решение.

Попытайся 9.159

Решить: m+9−m+3=0m+9−m+3=0.

Попытайся 9.160

Решить: n+1−n+1=0n+1−n+1=0.

Если перед корнем стоит коэффициент, его тоже нужно возвести в квадрат.

Пример 9,81

Решите: 33x−5−8=433x−5−8=4.

Решение

	33x−5−8=433x−5−8=4
Изолировать радикал.	33x−5=1233x−5=12
Возведите в квадрат обе части уравнения.	(33x−5)2=(12)2(33x−5)2=(12)2
Упростите, затем решите новое уравнение.	9(3x−5)=1449(3x−5)=144
Распределить.	27x−45=14427x−45=144
Решите уравнение.	27х=18927х=189
	х=7х=7
Проверьте ответ.
	Решение x=7x=7.

Попытайся 9.161

Решите: 24a+2−16=1624a+2−16=16.

Попытайся 9.162

Решите: 36b+3−25=5036b+3−25=50.

Пример 9,82

Решите: 4z−3=3z+24z−3=3z+2.

Решение

	4z-3=3z+24z-3=3z+2
Крайние термины изолированы.	4z-3=3z+24z-3=3z+2
Возведите в квадрат обе части уравнения.	(4z-3)2=(3z+2)2(4z-3)2=(3z+2)2
Упростите, затем решите новое уравнение.	4z-3=3z+2z-3=2z=54z-3=3z+2z-3=2z=5
Проверьте ответ.
Мы оставляем вам показать, что 5 чеков!	Решение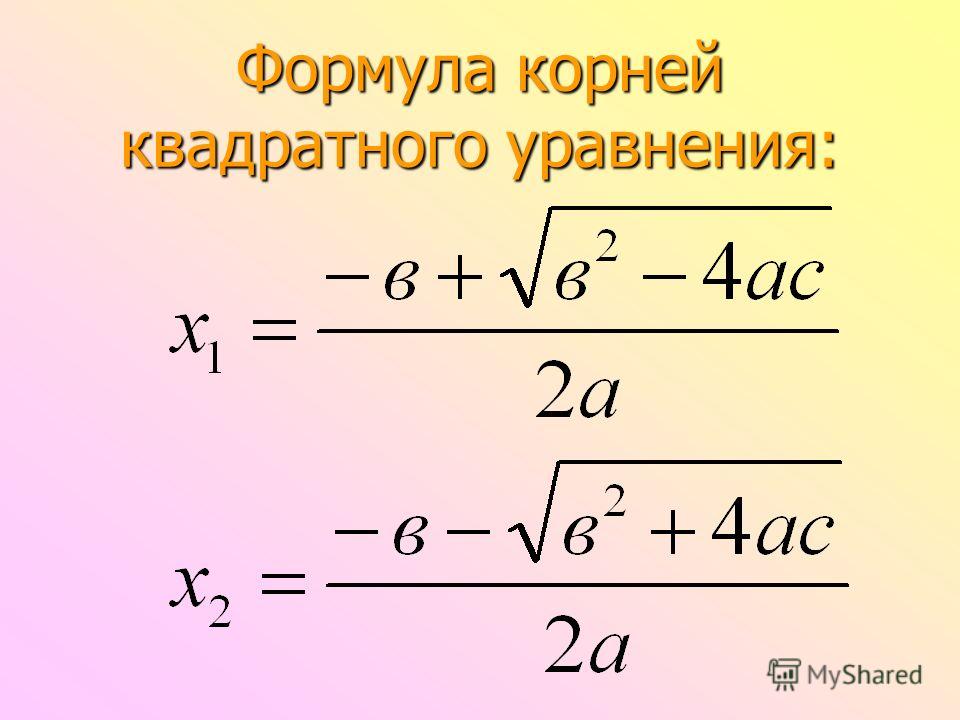 z=5. z=5.

Попытайся 9.163

Решите: 2x−5=5x+32x−5=5x+3.

Попытайся 9.164

Решите: 7y+1=2y−57y+1=2y−5.

Иногда после возведения в квадрат обеих частей уравнения у нас все еще есть переменная внутри радикала. Когда это происходит, мы повторяем Шаг 1 и Шаг 2 нашей процедуры. Мы изолируем радикал и снова возводим в квадрат обе части уравнения.

Пример 9,83

Решите: m+1=m+9m+1=m+9.

Решение

	м+1=м+9м+1=м+9
Радикал с правой стороны изолирован. Подровняйте обе стороны.	(м+1)2=(м+9)2(м+1)2=(м+9)2
Упрощение — будьте очень осторожны при умножении!	м+2м+1=м+9м+2м+1=м+9
В уравнении все еще есть радикал. Поэтому мы должны повторить предыдущие шаги. Изолировать радикал.	2м=82м=8
Квадрат с обеих сторон.	(2м)2=(8)2(2м)2=(8)2
Упростите, затем решите новое уравнение.	4м=644м=64
	м=16м=16
	Проверьте ответ.
Мы предоставляем вам показать, что m=16m=16 чеков!	Решение: m=16.m=16.

Попытайся 9.165

Решить: х+3=х+5х+3=х+5.

Попытайся 9.166

Решите: m+5=m+16m+5=m+16.

Пример 9,84

Решите: q−2+3=4q+1q−2+3=4q+1.

Решение

	q−2+3=4q+1q−2+3=4q+1
Радикал с правой стороны изолирован. Подровняйте обе стороны.	(q−2+3)2=(4q+1)2(q−2+3)2=(4q+1)2
Упрощение.	q−2+6q−2+9=4q+1q−2+6q−2+9=4q+1
В уравнении все еще есть радикал. Поэтому мы должны повторить предыдущие шаги. Изолировать радикал.	6q−2=3q−66q−2=3q−6
Квадрат с обеих сторон.	(6q−2)2=(3q−6)2(6q−2)2=(3q−6)2
Упростите, затем решите новое уравнение.	36(q−2)=9q2−36q+3636(q−2)=9q2−36q+36
Распределить.	36q−72=9q2−36q+3636q−72=9q2−36q+36
Это квадратное уравнение, поэтому с одной стороны получаем ноль.	0=9q2−72q+1080=9q2−72q+108
Фактор правой стороны.	0=9(q2-8q+12)0=9(q2-8q+12)
	0=9(q−6)(q−2)0=9(q−6)(q−2)
Использовать свойство нулевого продукта.	q-6=0q-2=0q=6q=2q-6=0q-2=0q=6q=2
Чеки оставляются вам. (Оба решения должны работать.)	Решения: q=6 и q=2. Решения: q=6 и q=2.

Попытайся 9.167

Решите: y−3+2=4y+2y−3+2=4y+2.

Попытайся 9.168

Решите: n−4+5=3n+3n−4+5=3n+3.

Использование квадратных корней в приложениях

По мере прохождения курсов в колледже вы столкнетесь с формулами, содержащими квадратные корни, во многих дисциплинах. Мы уже использовали формулы для решения геометрических задач.

Мы будем использовать нашу стратегию решения задач для приложений геометрии с небольшими изменениями, чтобы получить план решения приложений с формулами из любой дисциплины.

Как

Решение приложений с формулами.

1. Шаг 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. При необходимости нарисуйте рисунок и подпишите его с помощью данной информации.
2. Шаг 2. Определите , что мы ищем.
3. Шаг 3. Назовите то, что мы ищем, выбрав переменную для ее представления.
4. Шаг 4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
5. Шаг 5. Решите уравнение , используя хорошие методы алгебры.
6. Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
7. Шаг 7. Ответьте на вопрос полным предложением.

Мы использовали формулу A=L·WA=L·W, чтобы найти площадь прямоугольника с длиной L и шириной W . Квадрат – это прямоугольник, у которого длина и ширина равны. Если мы возьмем s за длину стороны квадрата, площадь квадрата будет s2s2.

Формула A=s2A=s2 дает нам площадь квадрата, если мы знаем длину стороны. Что, если мы хотим найти длину стороны для данной площади? Затем нам нужно решить уравнение для s .

A=s2Возьмите квадратный корень из обеих сторон. A=s2Упростите.A=sA=s2Возьмите квадратный корень из обеих сторон.A=s2Упростите.A=s

Мы можем использовать формулу s=As=A, чтобы найти длину стороны квадрата для данной площади.

Площадь квадрата

Мы покажем это в следующем примере.

Пример 9,85

Майк и Лишель хотят сделать квадратный внутренний дворик. У них достаточно бетона, чтобы замостить площадь в 200 квадратных футов. Используйте формулу s=As=A, чтобы найти длину каждой стороны патио. Округлите ответ до ближайшей десятой доли фута.

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и подпишите ее с помощью данной информации.
	А = 200 квадратных футов
Шаг 2. Определите , что вы ищете.	Длина стороны квадратного патио.
Шаг 3. Назовите то, что вы ищете, выбрав переменную для ее представления.	Пусть с = длина стороны.
Шаг 4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените данную информацию.
Шаг 5. Решите уравнение , используя хорошие методы алгебры . Округлить до одного десятичного знака.
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
Это достаточно близко, потому что мы округлили квадратный корень из . Подходит ли патио со стороной 14,1 фута? Да.
Шаг 7. Ответьте на вопрос полным предложением.	Каждая сторона патио должна быть 14,1 фута.

Попытайся 9.169

Кэти хочет посадить квадратную лужайку перед своим двором. У нее достаточно дерна, чтобы покрыть площадь в 370 квадратных футов. Используйте формулу s=As=A, чтобы найти длину каждой стороны ее лужайки. Округлите ответ до ближайшей десятой доли фута.

Попытайся 9.170

Серджио хочет сделать квадратную мозаику в качестве инкрустации для стола, который он собирает. У него достаточно плитки, чтобы покрыть площадь в 2704 квадратных сантиметра. Используйте формулу s=As=A, чтобы найти длину каждой стороны его мозаики. Округлите ответ до десятых долей сантиметра.

Другое применение квадратных корней связано с гравитацией.

Падающие объекты

На Земле, если объект падает с высоты hh футов, время в секундах, необходимое для достижения земли, определяется по формуле

т=ч5т=ч5

Например, если объект падает с высоты 64 фута, мы можем найти время, необходимое для достижения земли, подставив в формулу h=64h=64.

Извлеките квадратный корень из 64.
Упростите дробь.

Объекту, упавшему с высоты 64 фута, потребуется 2 секунды, чтобы достичь земли.

Пример 9,86

Кристи уронила солнцезащитные очки с моста на высоте 400 футов над рекой. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось солнцезащитным очкам, чтобы достичь реки.

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что вы ищете.	Время, за которое солнцезащитные очки достигают реки.
Шаг 3. Назовите то, что вы ищете, выбрав переменную для ее представления.	Пусть t = время.
Шаг 4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
Шаг 5. Решите уравнение , используя хорошие методы алгебры .
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
5=5✓5=5✓
5 секунд кажутся разумными? Да.
Шаг 7. Ответьте на вопрос полным предложением.	Солнечным очкам потребуется 5 секунд, чтобы попасть в воду.

Попытайся 9.171

Вертолет сбросил спасательный пакет с высоты 1296 футов. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось пакету, чтобы достичь земли.

Попытайся 9.172

Мойщик окон уронил швабру с платформы на высоте 196 футов над тротуаром Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось швабре, чтобы добраться до тротуара.

Полицейские, расследующие автомобильные аварии, измеряют длину следов заноса на тротуаре. Затем они используют квадратный корень, чтобы определить скорость в милях в час, которую двигала машина перед тем, как затормозить.

Следы заноса и скорость автомобиля

Если длина следов заноса составляет d фут, то скорость s автомобиля до включения тормозов можно найти по формуле

с=24ds=24d

Пример 9,87

После автомобильной аварии следы заноса одной машины составили 190 футов. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

Решение

Шаг 1. Прочтите проблему.
Шаг 2. Определите , что мы ищем.	Скорость автомобиля.
Шаг 3. Имя то, что мы ищем.	Пусть s = скорость.
Шаг 4. Переведите число в уравнение, написав соответствующую формулу.
Замените данную информацию.
Шаг 5. Решите уравнение .
Округлить до 1 знака после запятой.
Шаг 6. Проверьте ответ в задаче. 67,5≈?24(190)67,5≈?24(190) 67,5≈?456067,5≈?4560 67,5≈?67,5277…67,5≈?67,5277…
Является ли скорость 67,5 миль в час приемлемой?	Да.
Шаг 7. Ответьте на вопрос полным предложением.	Скорость автомобиля составляла примерно 67,5 миль в час.

Попытайся 9.173

Следователь ДТП измерил следы заноса автомобиля. Длина следов заноса составляла 76 футов. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

Попытайся 9.174

Следы заноса автомобиля, попавшего в аварию, были длиной 122 фута. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

Раздел 9.6 Упражнения

Практика ведет к совершенству

Решение радикальных уравнений

В следующих упражнениях проверьте, являются ли заданные значения решениями.

389.

Для уравнения x+12=xx+12=x: ⓐ Является ли x=4x=4 решением? ⓑ Является ли x=−3x=−3 решением?

390.

Для уравнения −y+20=y−y+20=y: ⓐ Является ли y=4y=4 решением? ⓑ Является ли y=−5y=−5 решением?

391.

Для уравнения t+6=tt+6=t: ⓐ Является ли t=−2t=−2 решением? ⓑ Является ли t=3t=3 решением?

392.

Для уравнения u+42=uu+42=u: ⓐ Является ли u=−6u=−6 решением? ⓑ Является ли u=7u=7 решением?

В следующих упражнениях решите.

393.

5г+1=45г+1=4

394.

7z+15=67z+15=6

395.

5x−6=85x−6=8

396.

4x−3=74x−3=7

397.

2м-3-5=02м-3-5=0

398.

2n−1−3=02n−1−3=0

399.

6в-2-10=06в-2-10=0

400.

4и+2-6=04и+2-6=0

401.

5q+3−4=05q+3−4=0

402.

4м+2+2=64м+2+2=6

403.

6n+1+4=86n+1+4=8

404.

2u−3+2=02u−3+2=0

405.

5v−2+5=05v−2+5=0

406.

3z−5+2=03z−5+2=0

407.

2м+1+4=02м+1+4=0

408.

ⓐ u−3+3=uu−3+3=u
ⓑ x+1−x+1=0x+1−x+1=0

409.

ⓐ v−10+10=vv−10+10=v
ⓑ y+4−y+2=0y+4−y+2=0

410.

ⓐ r-1-r=-1r-1-r=-1
ⓑ z+100-z+10=0z+100-z+10=0

411.

ⓐ s-8-s=-8s-8-s=-8
ⓑ w+25-w+5=0w+25-w+5=0

412.

32x−3−20=732x−3−20=7

413.

25x+1−8=025x+1−8=0

414.

28r+1−8=228r+1−8=2

415.

37y+1−10=837y+1−10=8

416.

3u−2=5u+13u−2=5u+1

417.

4v+3=v−64v+3=v−6

418.

8+2р=3р+108+2р=3р+10

419.

12с+6=10-4с12с+6=10-4с

420.

ⓐ а+2=а+4а+2=а+4
ⓑ б-2+1=3б+2б-2+1=3б+2

421.

ⓐ r+6=r+8r+6=r+8
ⓑ s−3+2=s+4s−3+2=s+4

422.

ⓐ u+1=u+4u+1=u+4
ⓑ n−5+4=3n+7n−5+4=3n+7

423.

ⓐ х+10=х+2х+10=х+2
ⓑ у-2+2=2у+4у-2+2=2у+4

424.

2у+4+6=02у+4+6=0

425.

8и+1+9=08и+1+9=0

426.

а+1=а+5а+1=а+5

427.

d−2=d−20d−2=d−20

428.

6с+4=8с-286с+4=8с-28

429.

9п+9=10п-69п+9=10п-6

Использование квадратных корней в приложениях

В следующих упражнениях решите. Округление до одного десятичного знака.

430.

Ландшафтный дизайн Рид хочет иметь квадратный садовый участок на заднем дворе. У него достаточно компоста, чтобы покрыть площадь в 75 квадратных футов. Используйте формулу s=As=A, чтобы найти длину каждой стороны его сада. Округлите ответ до ближайшей десятой доли фута.

431.

Ландшафтный дизайн Винс хочет сделать квадратный внутренний дворик во дворе. У него достаточно бетона, чтобы замостить площадь в 130 квадратных футов. Используйте формулу s=As=A, чтобы найти длину каждой стороны его внутреннего дворика. Округлите ответ до ближайшей десятой доли фута.

432.

Гравитация Создавая праздничные украшения, Рене уронила лампочку с вершины 64-футового дерева. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось лампочке, чтобы достичь земли.

433.

Гравитация Самолет сбросил сигнальную ракету с высоты 1024 фута над озером. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось, чтобы ракета достигла воды.

434.

Гравитация Дельтапланер сбросил свой сотовый телефон с высоты 350 футов. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось сотовому телефону, чтобы коснуться земли.

435.

Гравитация Строитель уронил молоток во время строительства пешеходной дорожки Гранд-Каньона на высоте 4000 футов над рекой Колорадо. Используйте формулу t=h5t=h5, чтобы найти, сколько секунд потребовалось молоту, чтобы достичь реки.

436.

Расследование несчастных случаев 908:80 Следы заноса автомобиля, попавшего в аварию, составляли 54 фута. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

437.

Расследование несчастного случая Длина следов заноса автомобиля, попавшего в аварию, составляет 216 футов. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

438.

Расследование ДТП Следователь ДТП измерил следы заноса одного из автомобилей, попавших в аварию. Длина следов заноса составляла 175 футов. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

439.

Расследование несчастного случая Следователь измерил следы заноса одного из автомобилей, попавших в аварию. Длина следов заноса составляла 117 футов. Используйте формулу s=24ds=24d, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.

Письменные упражнения

440.

Объясните, почему уравнение вида x+1=0x+1=0 не имеет решения.

441.

1. ⓐ Решить уравнение r+4−r+2=0r+4−r+2=0.
2. ⓑ Объясните, почему одно из найденных «решений» на самом деле не было решением уравнения.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Изучив этот контрольный список, что вы сделаете, чтобы стать уверенным в выполнении всех задач?

Упрощение квадратных корней – методы и примеры

Квадратный корень – это операция, обратная возведению в квадрат числа . Квадратный корень числа x обозначается знаком радикала √x или x ^1/2 . Квадратный корень из числа x таков, что число y является квадратом x, что упрощает запись как y ²  = x.

Например, квадратный корень из 25 представляется как √25 = 5. Число, квадратный корень которого вычисляется, называется подкоренным числом. В этом выражении √25 = 5, число 25 является подкоренным числом.

Иногда вы получаете сложные выражения с несколькими радикалами, и вас просят упростить их.

Для этого существует множество способов, в зависимости от количества радикалов и значений под каждым радикалом. Мы увидим их один за другим.

Чтобы упростить выражение, содержащее квадратный корень, находим множители числа и группируем их по парам.

Например, число 16 имеет 4 экземпляра множителей, поэтому мы берем число два из каждой пары и ставим его перед корнем, окончательно отброшенным, т. е. √16 = √(2 x 2 x 2 x 2) = 4,

Упрощение извлечения квадратного корня из числа включает несколько методов. В этой статье описаны некоторые из этих методов.

Упрощение, когда радикалы одинаковы

Вы можете складывать или вычитать сами квадратные корни, только если значения под знаком радикала равны. Затем добавьте или вычтите коэффициенты (числа перед знаком радикала) и сохраните исходное число знака радикала.

Пример 1

Выполните следующие операции

1. 2√3 + 3√3 = (2 +3) √3

= 5√3

1. 4√6 – 2√6 = (4 – 2) √6

= 6

• 5√2 + √2 = (5+ 1) √2

= 6√2

Упрощение под одним радикалом , вычитание и умножение целых чисел под знаком.

Пример 2

Упростите следующие выражения:

• √ (5 x20)

= √100

= 10

• √ (30 + 6)

= √36

= 6

• √ (30 — 5)

=. √25

= 5

• √(3 + 8)

= √11

Упрощение, когда радикальные значения различны различные квадратные корни.

Пример 3

Выполните следующие операции:

• √50 + 3√2

= √ (25 x 2) + 3√2

= 5√2 + 3√2

= 8√2

• √300 + √12

= √(100 x 3) + √(4 x 3)

= 10√3 + 2√3

= 12√3

Пример 4

Умножить:

• √2 x √8 = √16

= 4

• √x ³ + √x ⁵

= √x ⁸ = x ⁴

. корень из суммы чисел с 12 равен 5.

Решение

Напишите выражение этой задачи, квадратный корень из суммы n и 12 равен 5
√(n + 12) = квадратный корень из суммы.

√(n + 12) = 5
Наше уравнение, которое нужно решить сейчас:
√(n + 12) = 5
Каждая сторона уравнения возведена в квадрат:
[√(n + 12)]² = 5²
[√(n + 12)] x [√(n + 12)] = 25
√[(n + 12) x √(n + 12)] = 25
√(n + 12)² = 25
n + 12 = 25
Вычесть 12 из обеих частей выражения
n + 12 – 12 = 25 – 12
n + 0 = 25 – 12
n = 13

Example 6

Simplify

1. √4,500
2. √72

 

Solution

93г\sqrt{x}$

6. Что из следующего показывает упрощенное выражение для $2 + 9 – \sqrt{15}−2$?

$9 – 2\sqrt{15}$

$9 – \sqrt{15}$

$9+ \sqrt{15}$

$9+ 2\sqrt{15}$

7. Что из следующего показывает упрощенное выражение для $3\times 4 + \sqrt{169}$?

$-1$

$16$

$20$

$25$

8. Что из следующего показывает упрощенное выражение для $\sqrt{25} \times \sqrt{16} + \sqrt{36}$?

14$

26$

36$

56$

9. Что из следующего показывает упрощенное выражение для $\sqrt{81} \times 12 + 12$?

33$

66$

120$

240$

10. Что из следующего показывает упрощенное выражение для $\sqrt{36} + \sqrt{47} – \sqrt{16}$?

$2 – \sqrt{47}$

$2 + \sqrt{47}$

$4 – \sqrt{47}$

$4 +\sqrt{47}$

11. Что из следующего показывает упрощенное выражение для $6 + \sqrt{36} + 25−2$?

25$

33$

35$

70$

12. Что из следующего показывает упрощенное выражение для $4(5) + \sqrt{9} − 2$?

18$

21$

25$

35$

13. Что из следующего показывает упрощенное выражение для $15 + \sqrt{16} + 5$?

16$

24$

30$

36$

14. Что из следующего показывает упрощенное выражение для $3\left(2\right)+\sqrt{25}+10$?

11$

13$

21$

23$

15. Что из следующего показывает упрощенное выражение для $4(7) + \sqrt{49} − 12$?

27$

30$

33$

47$

16. Что из следующего показывает упрощенное выражение для $2(4) + \sqrt{9} − 8$?

3$

6$

9$

12$

17. Что из следующего показывает упрощенное выражение для $3(7) + \sqrt{25} + 21$?

21$

37$

31$

47$

18. Что из следующего показывает упрощенное выражение для $8(3) – \sqrt{27}$?

$24-3\sqrt{3}$

$21\sqrt{3}$

$27\sqrt{3}$

$24 + 3\sqrt{3}$

19. Какова площадь прямоугольного треугольника с гипотенузой длиной $100$ см и шириной $60$ см?

80$ см²

300$ см²

400$ см²

800$ см²

20. Ахмед и Том встретились на встрече. Ровно в 16:00 их пути разошлись: Том ехал строго на юг со скоростью 60 долларов в час, а Ахмед — на восток со скоростью 30 долларов в час. На каком расстоянии был Том от Ахмеда в 16:30? 93$ см³

22. Что из следующего показывает диаметр круга площадью $300\pi$ см²?

$3\sqrt{10}$ см

$10\sqrt{3}$ см

$20\sqrt{3}$ см

$40\sqrt{3}$ см

 

Предыдущий урок | Главная страница | Следующий урок

Уравнения с квадратными корнями — Magoosh GMAT

Уравнения с квадратными корнями. Тест иногда дает нам решить уравнение, включающее квадратный корень. В таком уравнении переменная будет стоять под радикалом. Так, например, это будет уравнение с квадратными корнями. Квадратный корень из х плюс 3 равен х минус 3. Мы решим это позже в видео.

В, так что это тип уравнения, о котором мы будем говорить в этом уроке. Конечно, мы извлекаем квадратный корень, возводя его в квадрат, и нам всегда разрешается возводить в квадрат обе стороны. Иногда для простейших радикальных уравнений все, что нам нужно сделать, это возвести в квадрат обе части.

Так, например, если бы у нас было что-то вроде квадратного корня из х плюс 2 равно 3. Ну, просто возведите в квадрат обе стороны. Мы получаем x плюс 2 слева, мы получаем 9 справа, вычитаем, и мы получаем x равно 7. Фантастика. Но это уравнение было слишком простым, чтобы его можно было увидеть в тесте.

На самом деле тест не преподнесет нам что-то простое на блюдечке с голубой каемочкой, он будет немного сложнее. Прежде чем мы продолжим, давайте подумаем об этом. Всегда ли верно для любого значения k, что если мы возьмем квадратный корень из k в квадрате, мы вернемся к k. Другими словами, квадратный корень отменяет возведение в квадрат и всегда возвращает нас туда, откуда мы начали, всегда ли это так?

И, конечно же, нет. Уравнение верно для положительных чисел и для 0, но не для отрицательных значений k. Например, если k равно отрицательному числу 4, то, конечно, при возведении его в квадрат мы получим положительное число 16. Отрицательное число 4 в квадрате равно положительному числу 16,9. 0005

Извлекая квадратный корень из 16, мы получаем 4. Другими словами, мы не возвращаемся к исходному начальному числу. Так что это важно. Это говорит о том, что мы можем столкнуться с некоторыми проблемами, когда возникают отрицательные значения. Так что это на нашем радаре.

Что происходит, когда мы получаем отрицательные значения, в частности, когда вещь под радикалом является отрицательной? Мы должны обратить на это внимание. Получается, что в радикальных уравнениях надо учитывать посторонние корни. Когда мы делаем всю нашу алгебру правильно, включая возведение в квадрат обеих частей уравнения, алгебра может привести к ответам, которые на самом деле не работают в исходном уравнении.

Это посторонние корни. Так что хочу подчеркнуть, речь идет не об ошибке, другими словами, даже если мы делаем всю алгебру правильно, просто в силу того, что мы возводим в квадрат, мы получаем лишние корни, посторонние корни, которые на самом деле не те, решить исходное уравнение. Важно понимать, что в радикальном уравнении будут возникать посторонние корни, даже если вы сделаете всю алгебру правильно.

Теперь мы можем посмотреть на уравнение, которое мы получили в начале. Итак, вот уравнение с самого начала. Так что, конечно, что мы сделаем, так это возведем обе стороны в квадрат. Конечно, тот бином в квадрате справа. Мы, мы са, мы превращаем это в х в квадрате минус 6х плюс 9. Возможно, вы помните схему квадрата разности.

Затем мы соберем все на одну сторону, так что мы получим квадратное число, равное 0. Мы учтем это. Это очень легко учитывать. И мы получаем два корня, 1 и 6. Теперь, как обычно, с алгеброй, как вы думаете, все в порядке, мы должны закончить. Мы нашли значение х.

Но с радикальными уравнениями нужно быть осторожным. Знаем ли мы, что оба эти корня работают? Может быть, они оба, или, может быть, один из них является посторонним корнем. Итак, мы должны проверить наши ответы. Мы должны проверить каждый ответ, который мы нашли, чтобы убедиться, что он работает, потому что прямо сейчас, просто глядя на них, 1 и 6, мы не знаем.

Это оба корня? Являются ли они оба посторонними корнями? Работают ли они в исходном уравнении? Единственный способ выяснить это — подключить их. Итак, вот исходное уравнение. Вот корни, которые мы нашли из алгебры.

Итак, прежде всего, мы проверим первый. X равно 1. Подключите его к левой стороне. Мы получаем квадратный корень из 1 плюс 3, квадратный корень из 4, который равен 2. Подставляем его в правую часть, мы получаем 1 минус 3, что отрицательно 2. Таким образом, две стороны уравнения не равны, одна сторона равна 2, одна сторона равна минус 2,

Значит, этот корень не работает. Теперь проверим другой. Подключим его к левой стороне, получим квадратный корень из 6 плюс 3, конечно же, это 9, квадратный корень из 9 равен 3. С другой стороны, мы получим 6 минус 3, что также равно 3.

Две стороны работают . Итак, этот законно работает и решает проблему. Итак, у этого уравнения есть одно работающее решение, x равно 6. Это единственное работающее решение. X, равное 1, является посторонним корнем, потому что, несмотря на то, что мы правильно следовали алгебре, и хотя алгебра дала нам этот корень, этот корень на самом деле не работает в исходном уравнении.

Нам нужно выровнять обе стороны, чтобы отменить радикал, но само это действие может привести к появлению посторонних корней. Если мы получим квадратное число после возведения в квадрат, что часто встречается в тесте, алгебра приведет к двум корням. Иногда работают оба корня.

Иногда работает один корень и один посторонний. Иногда оба являются посторонними, и уравнение не имеет решения. Итак, вот проблема с практикой. Поставьте видео на паузу, а потом поговорим об этом. Хорошо.

Итак, у нас радикал с обеих сторон. Радикал равный радикалу. Так что, конечно, мы просто будем выравнивать обе стороны. Получаем 2x минус 2 равно x минус 4. Что ж, очень легко решить уравнение. И мы получаем x равно минус 2.

Хорошо. Отлично. Но что произойдет, если мы подставим это обратно в исходное уравнение? Когда мы подключаем это, это приводит к квадратному корню из отрицательного значения с обеих сторон. Таким образом, мы получили бы квадратный корень из минус 6. А квадратный корень из минус 6 — это что-то вне реальной системы счисления. Он не живет нигде на числовой прямой.

Так что мы не можем с этим посчитать. Вот только для наших целей это просто ошибка и это уравнение не имеет решения. Наконец, имейте в виду, что мы должны возводить в квадрат обе стороны только тогда, когда радикал сам по себе находится на одной стороне уравнения.

Если подкорень появляется с другими элементами с одной стороны, нам придется изолировать подкорень с одной стороны, прежде чем будет иметь смысл квадратировать обе стороны. Итак, вот проблема с практикой. Поставьте видео на паузу, а потом поговорим об этом. Итак, у нас нет радикала самого по себе.

Итак, самое первое, что нам нужно сделать, это вычесть 2 с обеих сторон. Таким образом, мы получаем радикал, 4 минус 3 х равно х минус 2. Теперь мы можем возвести в квадрат обе стороны. И, конечно же, мы получаем квадрат разности, квадрат этого двучлена. И это расширяется до х в квадрате минус 4 х плюс 4. Теперь мы собираемся вычесть 4 с обеих сторон и добавить 3х к обеим сторонам, и это приведет нас к х в квадрате минус х.

Очень легко это учесть. Это умножает на x, умноженное на x минус 1, и алгебра приводит нас к решениям: x равно 0 и x равно 1. Теперь нам нужно проверить эти ответы. Хорошо.

Итак, это те корни, которые нашла для нас алгебра. Прежде всего, проверьте, что x равно 0. Подставьте это к левой стороне, и мы получим 2 плюс корень 4, что равно 2 плюс 2, что равно 4. Подставьте его к правой стороне на 0 и, конечно же, 4 не равно 0. Так что этот не работает.

Значит, это посторонний корень. Теперь проверьте, что x равно 1. Плюс это в левую сторону, мы получаем 2 плюс 4 минус 3 умножить на 1, так что 4 минус 3. И, конечно же, это будет 1. Итак, это будет 2 плюс 1, что равно 3 , И, конечно же, это не равно 1.

Не равно x, равному 1, на другой стороне уравнения. Так что этот тоже не работает. Так что ни один из корней, которые дала нам алгебра, не работает. Так что это уравнение просто не имеет решения. Оба решения, которые давала алгебра, были посторонними корнями. Таким образом, чтобы отменить радикал в уравнении, нам нужно возвести в квадрат обе его части.

No related posts.