Кривые второго порядка
Содержание
Введение
1.Кривые второго порядка
1.1 Эллипс
1.2 Гипербола
1.3 Парабола
2.Теоремы, связанные с кривыми второго порядка
Литература
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
1. Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая
оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения: Илиλ2 − Iλ + D = 0.
Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
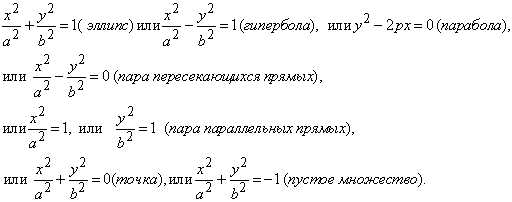
1.1 Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
1.2 Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
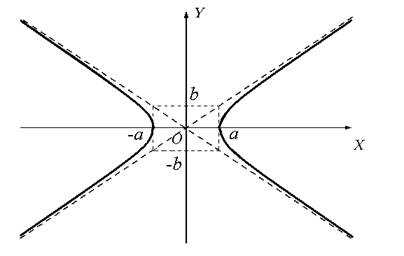
Рис.1
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
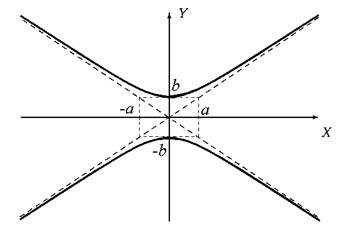
Рис.2
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
1.3 Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
y2 = 2 px
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
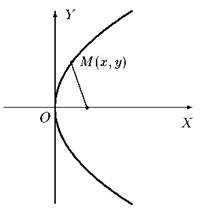
Рис.3
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
2. Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой.Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
7 Исследование кривых второго порядка
7.1 Цель работы
Определить вид кривых, найти их основные характеристики и сделать рисунки.
7.2 Теоретическое введение
I Классификация кривых второго порядка
Алгебраической кривой второго порядка называется кривая, уравнение которой в декартовой прямоугольной системе координат (ДПСК) можно представить в виде:
| (7.1) |
Одна и та же кривая в зависимости от расположения, относительно ДПСК будет, иметь разные уравнения. Оказывается, что для каждой кривой, определяемой уравнением (7.1), можно подобрать такую новую ДПСК ( повернутую), что ее уравнение примет вид:
Ax2 + By2 + Cx + Dy + E = 0; (A2 + B2 ≠ 0), | (7.2) |
т.е. уравнение не будет содержать произведение xy. В типовом расчете дается именно это уравнение (7.2), поэтому мы и будем его рассматривать. Вид кривой, определяемой уравнением (7.2), зависит от коэффициентов A, B, C, D, E поэтому проведем подробный анализ каждого из следующих случаев.
1. AB ≠ 0, т.е. A ≠ 0 и B ≠ 0 случай центральной кривой. Выделим полные квадраты: Таким образом (7.2) примет вид
(7.3) |
Положим α = –C / 2A, β = –D / 2B и тогда получим
A(x – α)2+B(y – β)2=H | (7.4) |
Перейдем теперь к новой ДПСК – X′O′Y′, которая получается из исходной ДПСК XOY параллельным переносом (соответствующие оси координат параллельны и сонаправлены). Начало ДПСК X′O′Y′ поместим в т. O′(α, β ). Тогда точка M, имеющая относительно ДПСК XOY координаты (Х,У) будет иметь относительно ДПСК X′O′Y′ координаты x’ = x – α и y’ = y – β, а уравнение (7.4) в ДПСК X′O′Y′ запишется
(7.5) |
(для удобства в дальнейшем вместо x’ и y’ будем писать x и y).
1.1 AB > 0 – эллиптический тип . a) A > 0, B > 0, H > 0. Положив перепишем (7.5) в виде
(7.6) |
В этом уравнении, не нарушая общности, можно считать a2 ≥ b2, в противном случае нужно просто ДПСК повернуть на 90°. Кривая, уравнение которой относительно некоторой ДПСК имеет вид называется эллипсом. Уравнение называется каноническим уравнением эллипса. b) A > 0, B > 0, H = 0. Положив a2 = 1 / A, b2 = 1 / B, получим . Этому уравнению удовлетворяют координаты единственной точки O’ (0,0). c) A > 0, B > 0, H < 0. Положив a2 = –
1.2 AB < 0 – гиперболический тип. a) A > 0, B < 0, H > 0. Положив a2 = H / A, b2 = –H / B, перепишем (7.5) в виде
(7.7) |
Кривая, уравнение которой относительно некоторой ДПСК имеет вид , называется гиперболой. Уравнение называется каноническим уравнением гиперболы. Замечание. Если A > 0, B < 0, H > 0, то (7.5) можно преобразовать к виду повернув затем ДПСК X′O′Y′ на 90°, мы получим уравнение вида , где x» = y’, y» = –x’. b) A > 0, B < 0, H = 0. Положив a2 = 1 / A, b2 = –1 / B, получим: . Разложим левую часть на множители: . Теперь хорошо видно, что этому уравнению удовлетворяют координаты точек двух прямых, проходящих через начало координат O’ (0,0): и . Поэтому говорят, что уравнение определяет вырожденную гиперболу. Итак, мы полностью выяснили, какие кривые могут получаться при AB ≠ 0 и переходим к случаю, когда AB = 0.
2 AB = 0 – параболический тип. 2.1 A = 0 (B ≠ 0), C ≠ 0. В этом случае (7.2) имеет вид: By2 + Cx + Dy + E = 0. Выделив полный квадрат, преобразуем это уравнение: . Положим, далее, , , , тогда уравнение перепишется в виде: (y – β )2 = 2p(x – α). Перейдя теперь, как и в случае 1 к новой ДПСК X ′O′Y′ получим: (y’ )2 = 2px’. Опустим для удобства штрихи:
Кривая, уравнение которой относительно некоторой ДПСК имеет вид y2 = 2px, называется параболой. Уравнение y2 = 2px называется каноническим уравнением параболы. Замечание. В уравнении (7.8), не нарушая общности, можно считать p > 0, в противном случае нужно повернуть ДПСК на 180°. Замечание. Случай B = 0, D ≠ 0, очевидно, сводится к предыдущему, если повернуть ДПСК на 90°. Наконец, чтобы полностью завершить анализ уравнения (7.2) нам осталось рассмотреть последние три случая.
2.2 A = 0 (B ≠ 0), C = 0. В этом случае уравнение (7.2) имеет вид By2 + Dy + E = 0. Выделив полный квадрат, преобразуем его к виду: . Положим , , получим, (y – β)2 = H, перейдя к ДПСК и опуская в уравнении штрихи, получим:
a) H > 0 Обозначим a2 = H тогда (7.9) примет вид:
Этому уравнению удовлетворяют координаты точек, лежащих на параллельных прямых y = a и y = –a(вырожденная парабола). b) H < 0 Обозначив a2 = –H, перепишем (7.9) в виде: y2 = –a2. Этому уравнению не удовлетворяют координаты ни одной точки, т.е. оно определяет пустое множество, которое условно называют парой мнимых параллельных прямых. c) H = 0 То есть (7.9) имеет вид
Этому уравнению удовлетворяют координаты точек оси абсцисс. Так как уравнение (7.11) есть “предельный” случай (7.10) (a2 → 0), то говорят, что уравнению y2 = 0 соответствует пара совпадающих параллельных прямых. Замечание. Случай B = 0 и D = 0 сводится к предыдущему поворотом осей на 90°. Таким образом, подобрав новую ДПСК, уравнение Ax2 + By2 + Cx + Dy + E = 0 можно привести к одному из следующих 9 видов (см. таблицу).
Классификация алгебраических кривых второго порядка | |||
Номер вида | Уравнение кривой | Название кривой | Рисунок кривой |
Эллиптический тип кривой (AB> 0) | |||
1 | (a>b> 0) | Эллипс | |
2 | Точка | ||
3 | Мнимый эллипс | ||
Гиперболический тип кривой (AB< 0) | |||
4 | Гипербола | ||
5 | Пара пересекающихся прямых (вырожденная гипербола) | ||
Параболический тип кривой (AB= 0) | |||
6 | y2= 2px(p> 0) | Парабола | |
7 | y2=b2 | Пара параллельных прямых (вырожденная парабола) | |
8 | y2= –b2 | Пара мнимых паралельных прямых | |
9 | y2= 0 | Пара совпадающих параллельных прямых | |
Уравнения 1-5 относятся к случаю центральной кривой, так как каждое из них описывает либо пустое множество, либо множество, имеющее единственный центр | |||
Наш анализ показывает, что из всех алгебраических кривых второго порядка интерес представляют только эллипс, гипербола и парабола (прямые мы рассматривали ранее). Эти кривые действительно обладают рядом замечательных свойств, которые используются в технике. Отметим важнейшие из них.
II ЭЛЛИПС | (a>b> 0) |
1. Эллипс имеет центр симметрии – начало координат O(0,0). 2. Эллипс имеет две оси симметрии – оси координат. 3. Точки пересечения эллипса с осями симметрии называются вершинами – A1(–a,c), A2(a,0), B1(0,–b), B2(0,b) (4 вершины). 4. Отрезок A1A2 называется большой осью эллипса, длина этой оси равна 2a; аналогично, отрезок B1 B2называется малой осью эллипса, длина малой оси 2b (2b < 2a). Отрезки OA1, OA2 – большие полуоси; OB1, OB2– малые полуоси, их длины соответственно равны a и b (a < b). Иногда слова “большая полуось”, “малая полуось”, “большая ось”, “малая ось” относятся не к отрезкам, а к их длинам, т.е. к числам a, b, 2a и 2bсоответственно. 5. Точки, лежащие на большой оси эллипса F1 (–C,0) и F2(C,0), где (0 < c < a) называютсяфокусами эллипса. Эти точки являются замечательными. Фокальное свойство эллипса: для любой точки M, лежащей на эллипсе, |F1M| + |F2M| = 2a, т.е. эллипс является множеством точек плоскости, для которых сумма расстояний до двух данных точек плоскости, фокусов, есть величина постоянная, равная 2a, и которая больше расстояния между фокусами (2a > 2c). 6. Эксцентриситетом эллипса называется число ε = c/a. Заметим, что эксцентриситет эллипса ε < 1. Это число характеризует форму эллипса: при ε = 0, a = b, т.е. эллипс становится окружностью, а чем ближе эксцентриситет к 1, тем больше эллипс отличается от окружности, т.е. эллипс становится более вытянутым. 7. Прямые: и перпендикулярные оси симметрии, соответствующей большой оси эллипса, называются директрисами. Заметим, что так как ε < 1, то директрисы лежат вне эллипса, за его вершинами A1и A2. Эти прямые являются также замечательными для эллипса. Директориальное свойство эллипса: для любой точки M, лежащей на эллипсе, , где ρ(M, L1) – расстояние от точки M до директрисы соответствующей фокусу F1(–c, 0), ρ(M, L2) – расстояние до директрисы , соответствующей фокусу F2(c, 0). То есть эллипс – множество точек плоскости, для каждой из которых расстояние до данной точки (фокуса), деленное на расстояние до данной прямой (директрисы), есть постоянная величина, которая меньше 1 (и равна эксцентриситету). Замечание. Директориальное и фокальное свойства являются определяющими для эллипса. Например, множество точек плоскости, для которых расстояние до данной точки (фокуса), деленное на расстояние до данной прямой (директрисы), есть постоянная величина, которая меньше 1, является эллипсом. 8. Оптическое свойство эллипса: если изготовить “зеркальную” нить в форме эллипса, то луч, идущий из одного фокуса, отразившись от эллипса, попадает в другой фокус, т.е. если в т. M, лежащей на эллипсе провести к нему касательную T, то углы между этой касательной и прямыми MF1 и MF2 будут равны (α = β). Ниже приводим рис. 7.1, на котором изображен эллипс и все его замечательные точки и прямые.
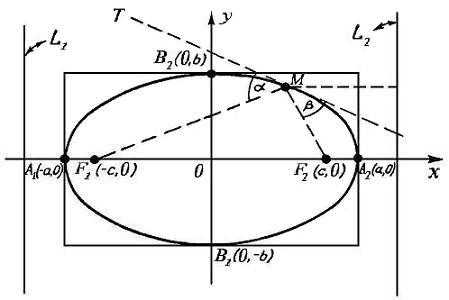 Рис.
7.1 Эллипс
Рис.
7.1 Эллипс
Замечание. Чтобы выяснить форму эллипса, следовало бы разрешить уравнение (7.6) относительно Y, средствами математического анализа исследовать функцию и построить ее график. Он совпадает с частью эллипса, лежащей в 1-й четверти, поэтому по симметрии можно достроить весь эллипс. Замечание. Отметим, что эллипс, в отличие от гиперболы и параболы, является ограниченной кривой, поэтому когда его рисуют, то, обычно, сначала рисуют “коробочку” – основной прямоугольник, который касается вершин эллипса.
III ГИПЕРБОЛА | (a> 0,b> 0) |
1. Гипербола имеет центр симметрии – начало координат т.O(0,0). 2. Гипербола имеет две оси симметрии – оси координат. 3. Точки пересечения с осями симметрии называются вершинами гиперболы. В отличие от эллипса гипербола имеет 2 вершины: A1(–a, 0) и A2(a, 0) – т.е. гипербола пересекает только одну ось симметрии. 4. Отрезок A1A2 называется действительной осью гиперболы, длина действительной оси равна 2a. Точки B1(0, –b) и B2(0, b) лежат на оси симметрии, которую гипербола не пересекает. Отрезок B1B2 называется мнимой осью гиперболы, длина мнимой оси равна 2b . Все сказанное далее в предыдущем разделе II п.4 для эллипса, касающееся полуосей и терминологии, относится и к гиперболе. 5. Точки, лежащие на продолжении действительной оси гиперболы F1(–C, 0) и F2(C, 0), где , называются фокусами гиперболы. Фокальное свойство гиперболы: для любой точки M, лежащей на гиперболе ||F1M| – |F2M|| = 2a, т.е. гипербола является множеством точек плоскости, для которых модуль разности расстояний до двух данных точек плоскости, фокусов, есть величина постоянная, равная 2a > 0. 6. Эксцентриситетом гиперболы называется число ε = C/a. Заметим, что эксцентриситет гиперболы ε > 1. 7. Прямые z1: x = – a/ε и z2: x = a/ε перпендикулярные действительной оси гиперболы, называютсядиректрисами. Директориальное свойство гиперболы дословно формулируется так же, как и для эллипса, только ε < 1, поэтому директрисы гиперболы лежат между ее вершинами. Замечание. Как и для эллипса, директориальное и фокальное свойства являются определяющими для гиперболы. 8. Гипербола, как и эллипс, обладает оптическим свойством: луч, идущий из фокуса F1 отразившись от гиперболы в т. M, лежащей на гиперболе, идет по прямой F2 M; т.е., если в т. M, лежащей на гиперболе, провести касательную T, то она будет биссектрисой угла между прямыми MF1 и MF2. 9. Гипербола имеет две асимптоты: и (у эллипса их нет и быть не может, так как эллипс ограниченная кривая).
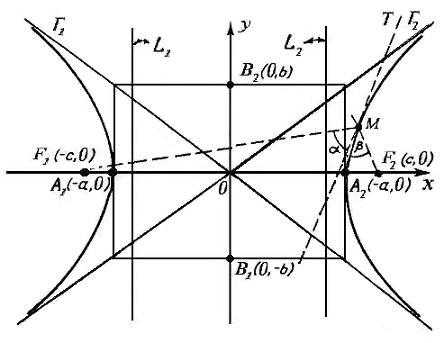 Рис.
7.2 Гипербола
Рис.
7.2 Гипербола
На рис. 7.2 изображена гипербола и все ее замечательные точки и прямые. Замечание. Чтобы выяснить форму гиперболы и найти ее асимптоты, следовало бы поступить так же, как и в случае эллипса. Замечание. При построении гиперболы, как и для эллипса, обычно сначала рисуют основной прямоугольник. Его центр – центр симметрии гиперболы, стороны параллельны осям гиперболы и касаются ее вершин, длины сторон равны 2a и 2b. Диагонали основного прямоугольника (продолжение) являются асимптотами гиперболы. В отличие от эллипса гипербола лежит вне основного прямоугольника.
IV ПАРАБОЛА | y2= 2px(p> 0) |
1. Парабола в отличие от эллипса и гиперболы, не имеет центра симметрии, т.е. не относится к центральным кривым. 2. Парабола имеет одну ось симметрии – ось абсцисс. 3. Точка пересечения параболы с осью симметрии называется вершиной – т. О(0,0), т.е. парабола имеет одну вершину. 4. Число p > 0 называется параметром параболы. 5. Точка , лежащая на оси симметрии параболы и отстоящая от ее вершины на p/2, называется фокусом параболы. 6. Прямая , перпендикулярная оси параболы и отстоящая от ее вершины на p/2, называетсядиректрисой параболы. Заметим, что фокус лежит “внутри” параболы, а директриса “вне” ее, т.е. фокус и директриса лежат по разные стороны от параболы, как и в случае эллипса и гиперболы. Директориальное свойство параболы: для любой точки M, лежащей на параболе, |FM| = ρ(M,L), т.е. |FM| /ρM(L) = 1 и можно считать, что эксцентриситет параболы ε = 1. Таким образом, парабола занимает промежуточное положение между эллипсом, у которого ε < 1, и гиперболой, у которой ε > 1. Замечание. Директориальное свойство является определяющим для параболы так же , как и для эллипса, и для гиперболы. 7. Оптическое свойство параболы: луч, идущий из фокуса, отразившись от параболы, идет параллельно оси параболы, т.е. параболическое зеркало дает параллельный пучок света, если источник поместить в фокус параболы. На рис. 7.3 изображена парабола с ее замечательными точками и прямыми.
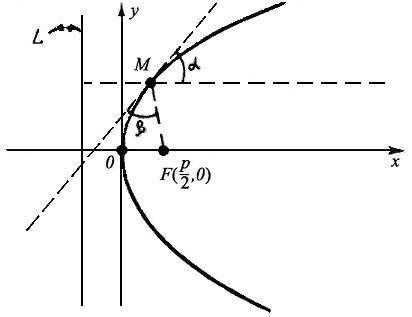 Рис.
7.3 Парабола
Рис.
7.3 Парабола
Замечание. Форма параболы хорошо известна из школьного курса, так как парабола является графиком квадратного трехчлена.
studfiles.net
Уравнения кривых второго порядка.
Определить тип каждого из уравнений, привести к каноническому виду; установить, какие геометрические образы они определяют и изобразить на чертеже. Найти координаты центра, полуоси, фокусы, эксцентриситет, уравнения асимптот и директрис.
Дано: уравнение второго порядка
.
Решение:
Сгруппируем
слагаемые, содержащие  и
дополним до полного квадрата:
;
;
;
вынесем за скобки коэффициент при
и
дополним до полного квадрата:
;
;
;
вынесем за скобки коэффициент при  :
.
Т.о. привели уравнение к виду
—
каноническое уравнение параболы с
вершиной в т.
:
.
Т.о. привели уравнение к виду
—
каноническое уравнение параболы с
вершиной в т. 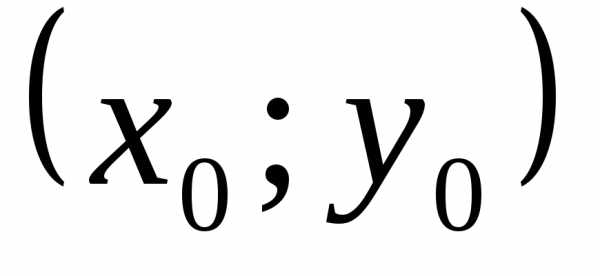 и осью симметрии параллельной
и осью симметрии параллельной 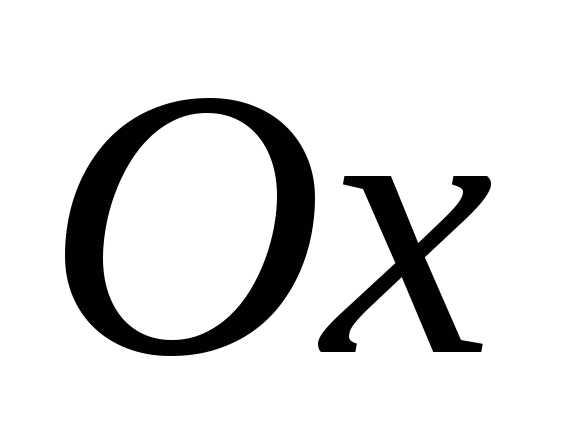 .
Следовательно, для нашего примера:
уравнение определяет параболу. Вершина в т.
.
Следовательно, для нашего примера:
уравнение определяет параболу. Вершина в т. 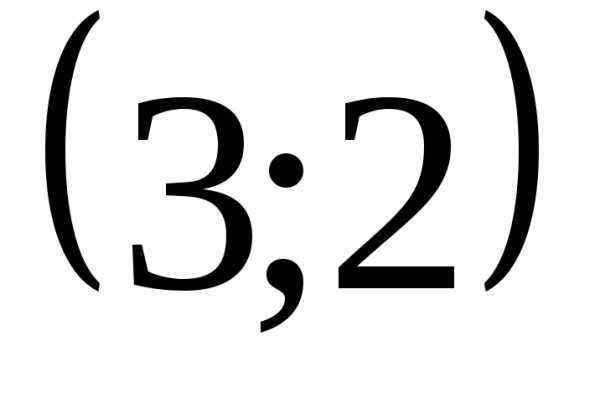 .
Параметр
.
Параметр 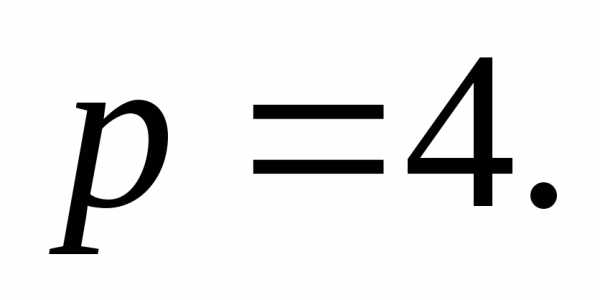 Ветви направлены вправо. Уравнение
директрисы для несмещенной параболы
Ветви направлены вправо. Уравнение
директрисы для несмещенной параболы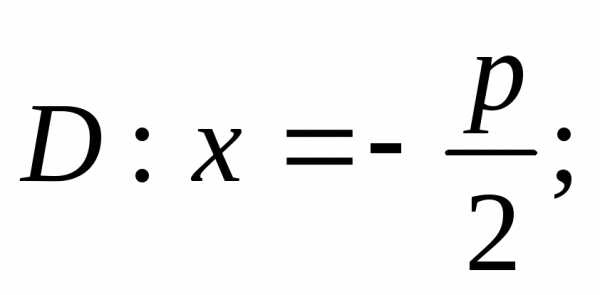 для смещенной
.
Фокус имеет координаты
.
для смещенной
.
Фокус имеет координаты
.
Построим график:
Дополнительные точки
| -2 | 6 | 0 | 4 |
| 5 | 5 | 3,5 | 3,5 |
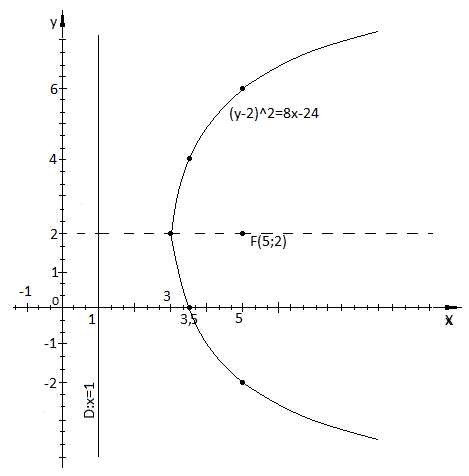
Рис.2.1 Парабола
Матричные уравнения.
Решить матричное уравнение: , (3.1)
где
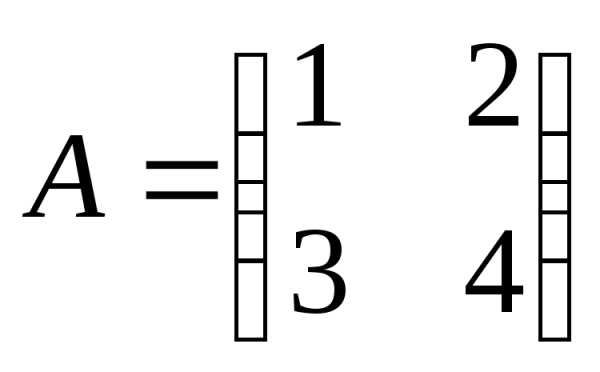 ;
;  ;
; 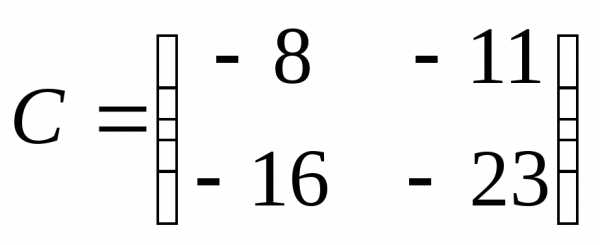 .
.
Решение.
Если
для матриц  и
и  существуют обратные матрицы
существуют обратные матрицы и
и 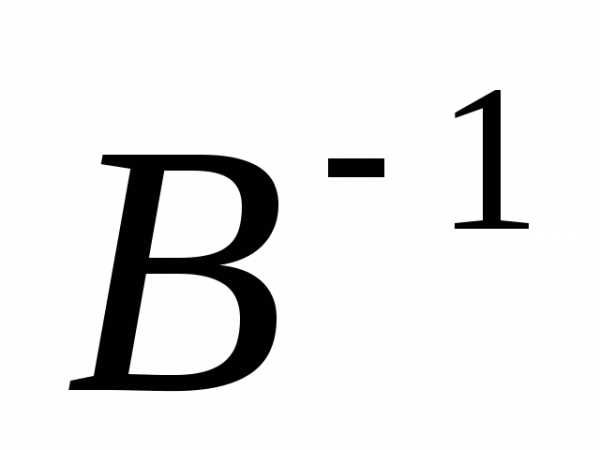 соответственно, умножим обе части
уравнения слева на
соответственно, умножим обе части
уравнения слева на 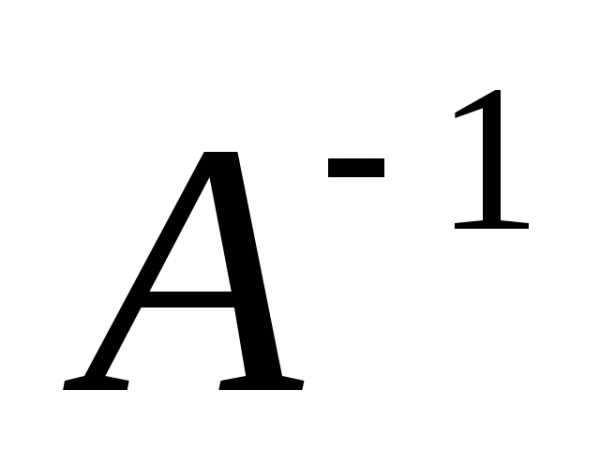 ,
справа на
,
справа на 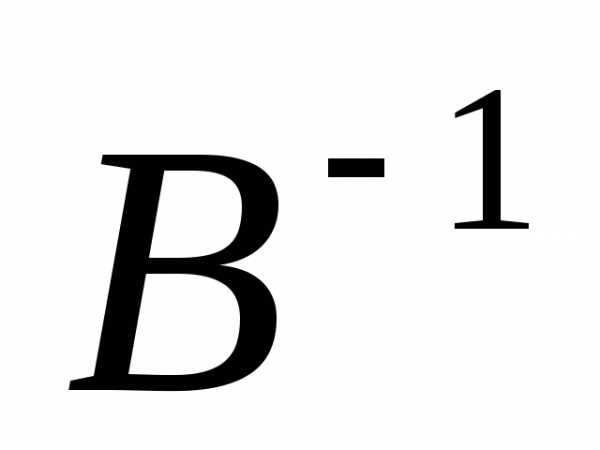 .
В результате получим:
.
В результате получим:
.
Учитывая, что
, ( —
единичная матрица) можно записать:
.
Так как
—
единичная матрица) можно записать:
.
Так как  — единичная матрица, окончательно имеем
уравнение:
— единичная матрица, окончательно имеем
уравнение:
(3.2)
где
матрица 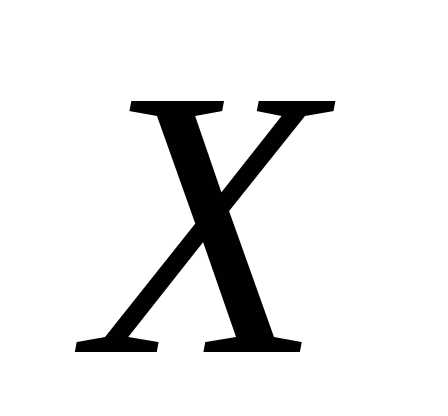 — решение уравнения (3.1).
— решение уравнения (3.1).
Если
же хотя бы одна из матриц  или
или  не имеет обратную, уравнение (3.1) не имеет
решения.
не имеет обратную, уравнение (3.1) не имеет
решения.
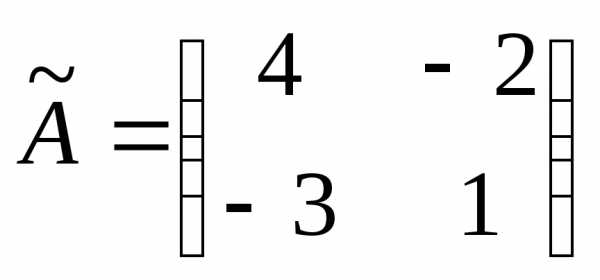
3.1. Для матрицы  найдем
найдем 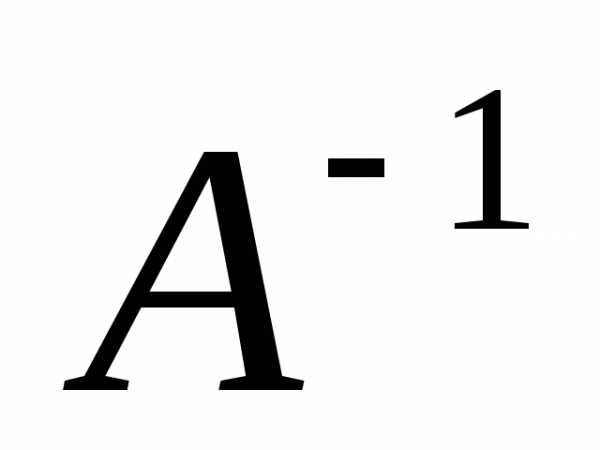 или
докажем, что она не существует.
или
докажем, что она не существует.
а) обратная матрица существует.
б) .
в) Найдем алгебраические дополнения для
матрицы  и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу  :
:
 .
.
г) Известно, что 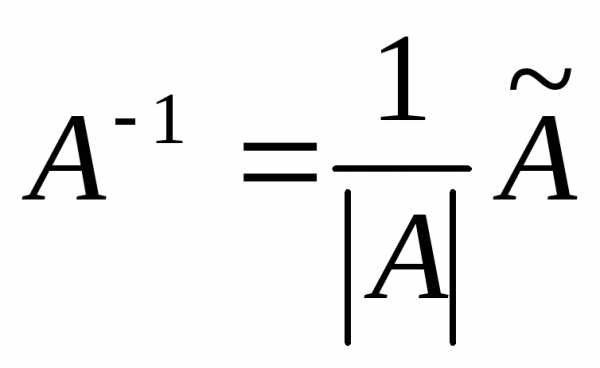 ;
тогда
;
тогда
 .
.
3.2. Для матрицы  найдем
найдем  или докажем, что она не существует.
или докажем, что она не существует.
а) обратная матрица существует.
б) .
в) Найдем алгебраические дополнения для
матрицы  и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу  :
:
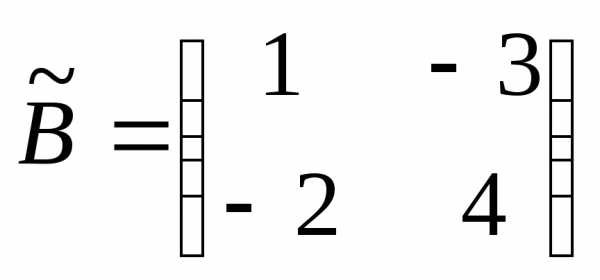 .
.
г) По формуле 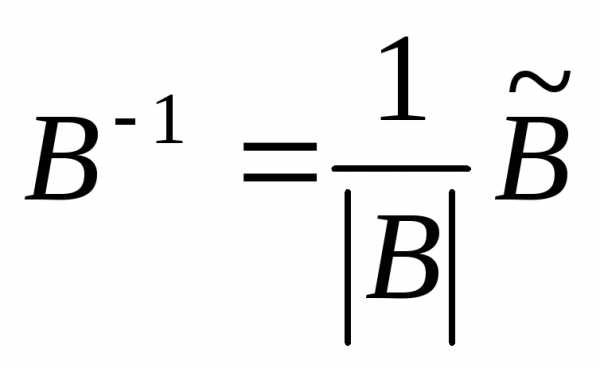 ;
;
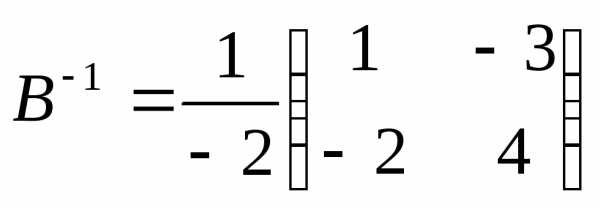 .
.
3.3. Найдем неизвестную матрицу  .
.
.
Ответ: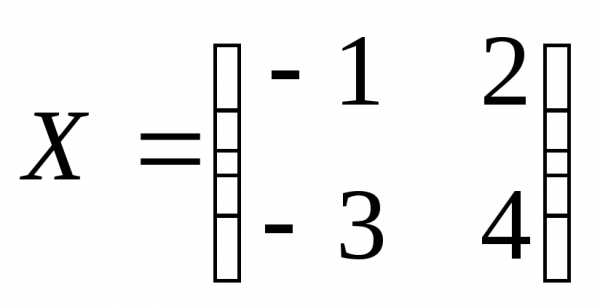 .
.
Решение слау.
Исследовать и решить систему линейных алгебраических уравнений, используя теорему Кронекера – Капелли.
Дана система уравнений:
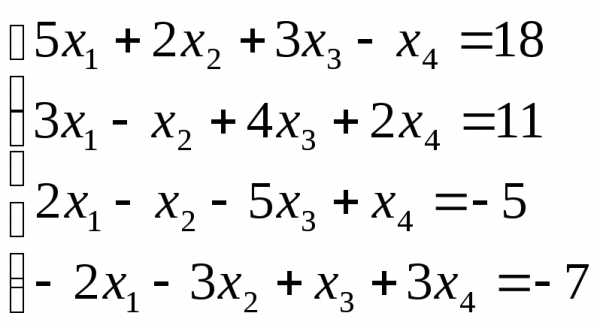
Решение. Решим систему уравнений методом Гаусса.
Прямой ход метода Гаусса.
Составим расширенную матрицу системы:
 .
.
Используя элементарные преобразования строк, приведем ее к ступенчатому виду:
4.1. Получим нули в первом столбце матрицы.
а) Элементы второй строки умножим на 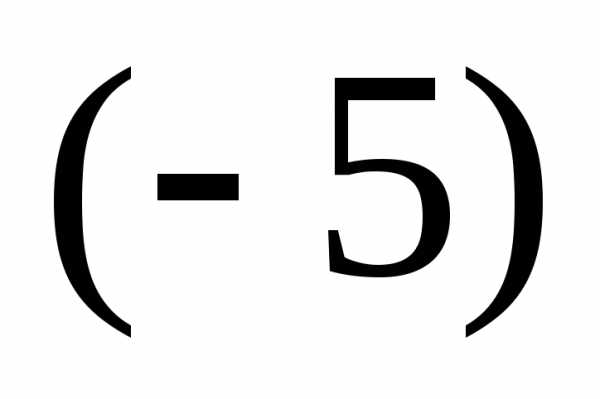 и прибавим к ним, умноженные на
и прибавим к ним, умноженные на  , элементы первой строки:
, элементы первой строки:
.
б) Элементы третьей строки умножим на  и прибавим к ним, умноженные на
и прибавим к ним, умноженные на  ,
элементы первой строки:
,
элементы первой строки:
.
в) Элементы четвертой строки умножим на  и прибавим к ним, умноженные на
и прибавим к ним, умноженные на  ,
элементы первой строки:
,
элементы первой строки:
.
4.2. Получим нули во втором столбце матрицы.
а) Элементы третьей строки умножим на 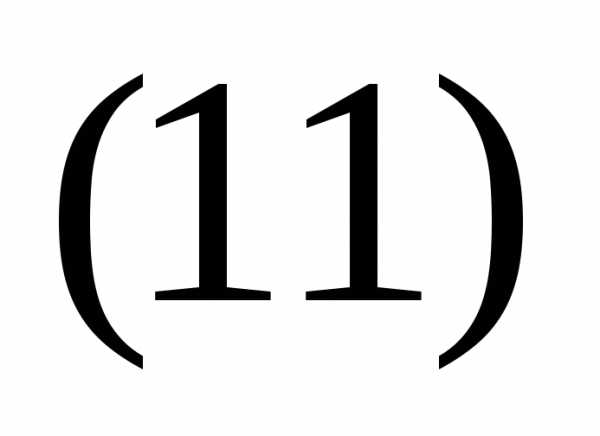 и прибавим к ним, умноженные на
и прибавим к ним, умноженные на  ,
элементы второй строки:
,
элементы второй строки:
.
б) К элементам четвертой строки прибавим элементы второй строки:
.
Матрица приведена к ступенчатому виду. На этом закончен прямой ход метода Гаусса.
Исследуем систему, используя теорему Кронекера – Капелли.
Теорема Кронекера – Капелли: система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
Ранг
матрицы ступенчатого вида равен
количеству ненулевых строк. Значит в
нашем случае ранг матрицы системы  равен рангу расширенной матрицы системы
равен рангу расширенной матрицы системы 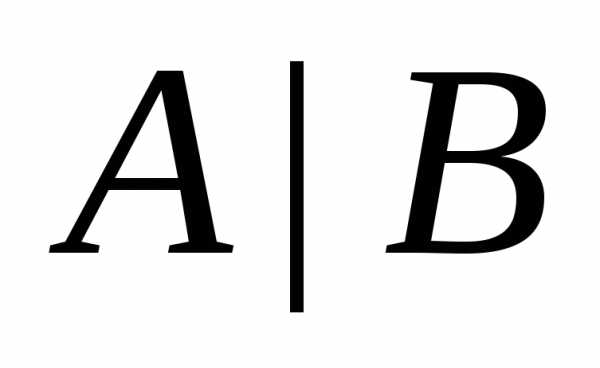 , а именно:
.
Следовательно система имеет решение.
, а именно:
.
Следовательно система имеет решение.
Т.к.
число неизвестных 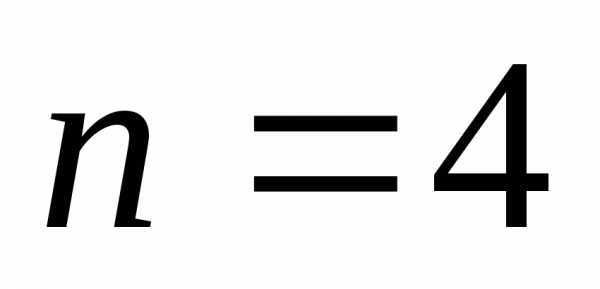 меньше числа линейно независимых
уравнений
меньше числа линейно независимых
уравнений 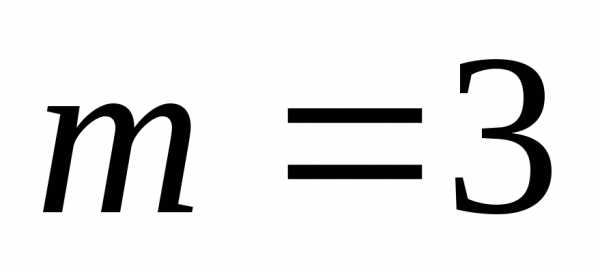 (числа ненулевых строк), система будет
иметь бесконечное множество решений.
Найдем общее решение данной системы
уравнений.
(числа ненулевых строк), система будет
иметь бесконечное множество решений.
Найдем общее решение данной системы
уравнений.
Обратный ход метода Гаусса:
Разобьем неизвестные на две группы: базисные (или основные) и свободные (или неосновные). Количество базисных неизвестных равно рангу матрицы. Базисные неизвестные находятся в строках и столбцах базисного минора.
Базисный
минор должен быть отличен от нуля и
иметь порядок равный рангу матрицы
системы. В качестве базисного минора
выберем минор 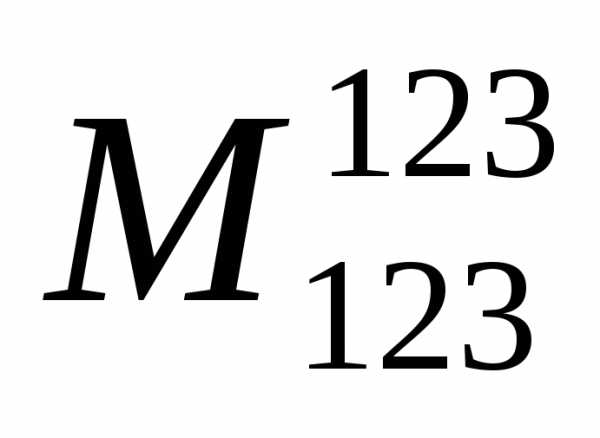 ,
т.е. определитель, состоящий из элементов
находящихся на пересечении 1-ой, 2-ой,
3-ей строк и 1-го, 2-го, 3-го столбцов. Т.о.
базисными неизвестными будем считать
,
т.е. определитель, состоящий из элементов
находящихся на пересечении 1-ой, 2-ой,
3-ей строк и 1-го, 2-го, 3-го столбцов. Т.о.
базисными неизвестными будем считать 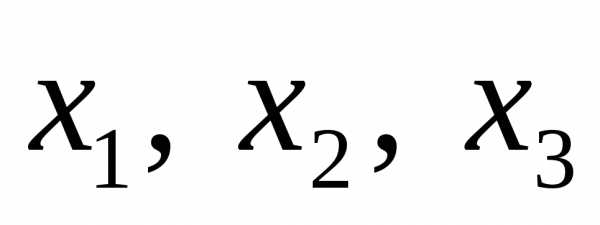 ;
свободными
;
свободными 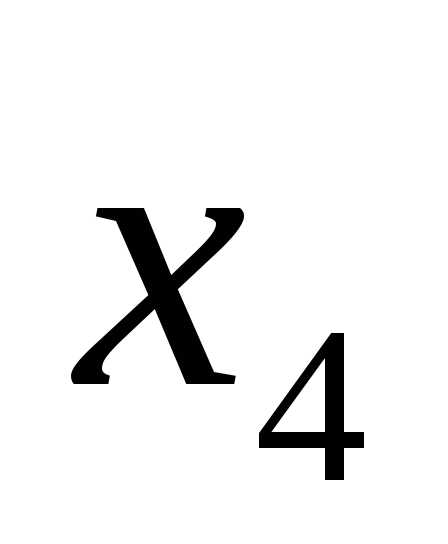 .
Пусть
.
Пусть 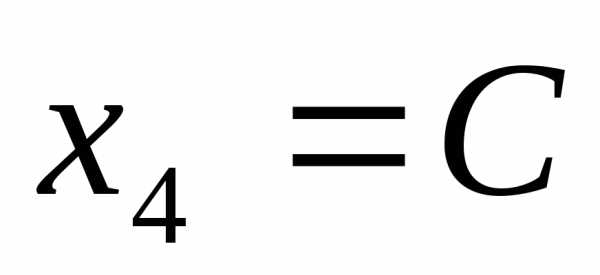 ,
где
,
где  —
произвольная постоянная.
—
произвольная постоянная.
Выразим
базисные переменные через  .
.
Отбросим нулевые строки и снова перейдем к системе уравнений:
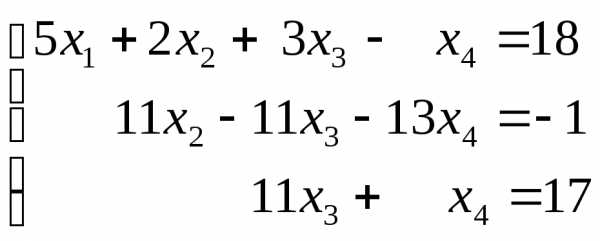 .
.
4.3.Из
третьего уравнения выразим 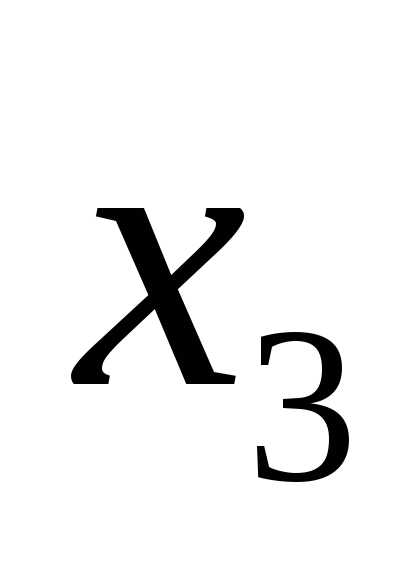 :
:
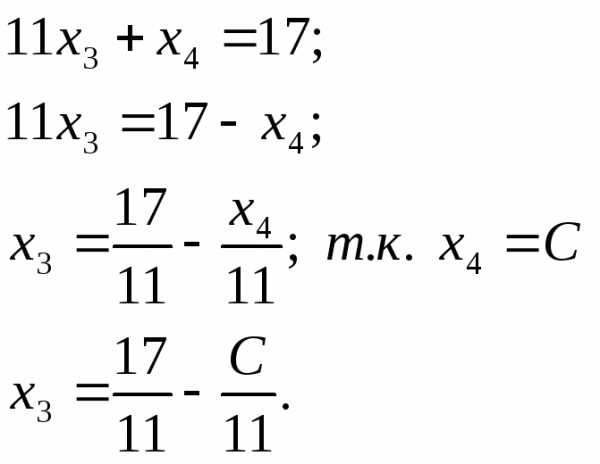
4.4. Подставим полученное во второе уравнение
и выразим 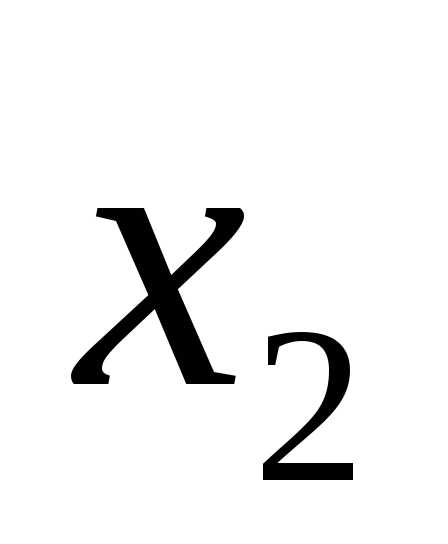 :
:
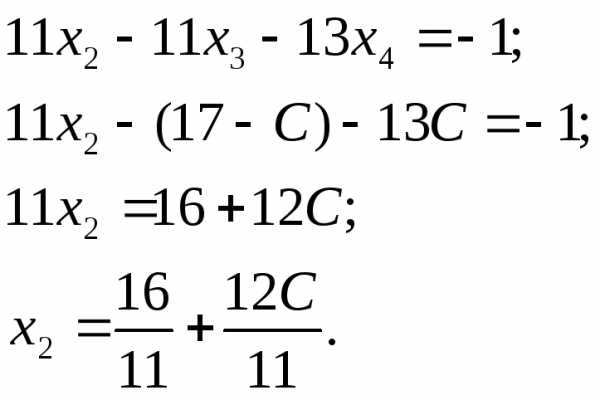
4.5. Подставим полученное в первое уравнение
и выразим 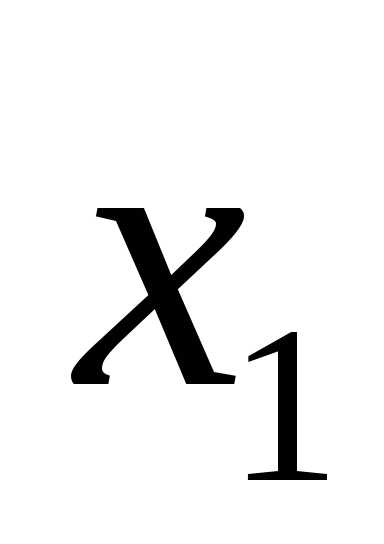 :
:
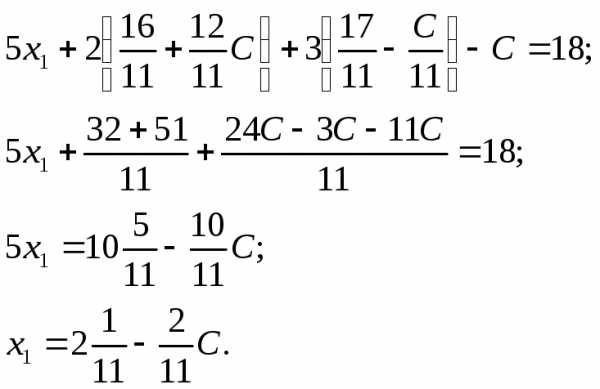
Закончен обратный ход метода Гаусса.
Запишем ответ: 1 способ. 2 способ.
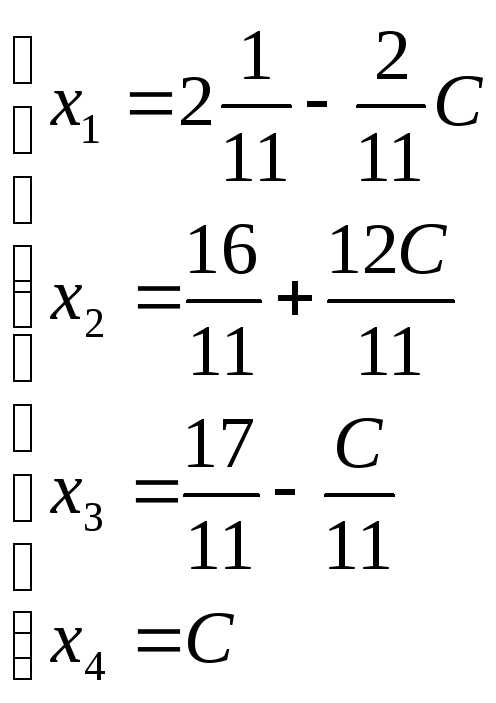 .
. 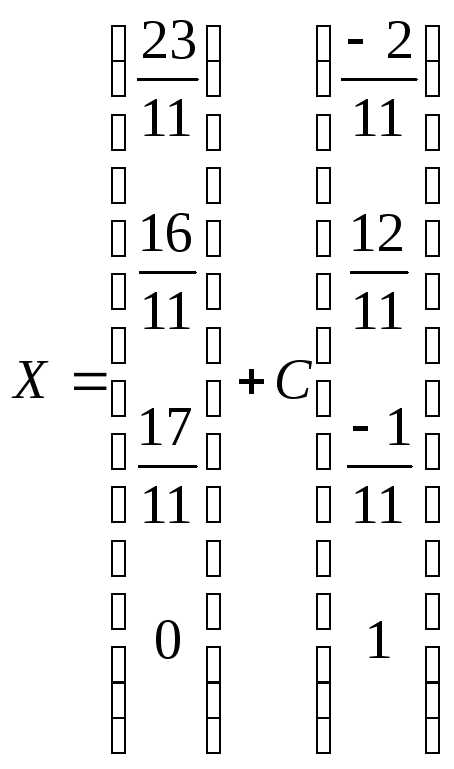 .
.
studfiles.net
Введение
ЛЕКЦИЯ
по учебной дисциплине
МАТЕМАТИКА
Тема № 2. Основы аналитической геометрии
Занятие. Линии (кривые) второго порядка
Знакомые вам из школьного курса математики эллипс, гипербола, парабола были известны греческим геометрам давно, более 2000 лет назад. Первое наиболее полное сочинение, посвященное этим кривым, принадлежит Апполонию и относится к III веку до нашего летоисчисления. Апполоний дал и название этим кривым. Сами эти линии греки первоначально получили как сечения прямого кругового конуса плоскостями, наклоненными под разными углами к его оси, поэтому эти кривые часто называют коническими сечениями.
Понятие линии (кривой) второго порядка
В этой лекции будут рассмотрены линии второго порядка.
Линия 2-го порядка – это плоская линия, декартовы прямоугольные координаты которой удовлетворяют алгебраическому уравнению второй степени, т. е. уравнению вида
где
т. е. хотя бы один из коэффициентов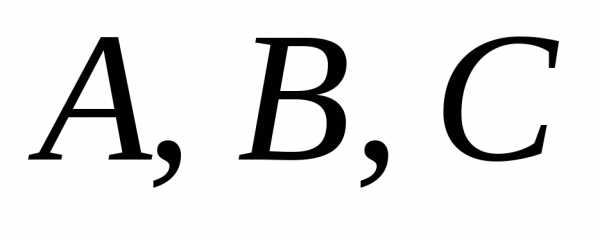 отличен от нуля.
отличен от нуля.
Наиболее интересными среди линий второго порядка являются эллипсы, гиперболы и параболы. Они часто встречаются как в самой математике, так и в её приложениях.
2. Эллипс
Каноническое уравнение эллипса
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через F1 и F2,, расстояние между ними через 2с, а сумму расстояний от произвольной точки эллипса до фокусов – через 2а (см. рис. 1). По определению 2а > 2с, т. е. а > с.

Рис. 1
Для вывода уравнения
эллипса выберем систему координат Оху так, чтобы фокусы F1 и F2 лежали на оси Ох, а начало координат совпадало с серединой
отрезка F1F2.
Тогда фокусы будут иметь следующие
координаты: 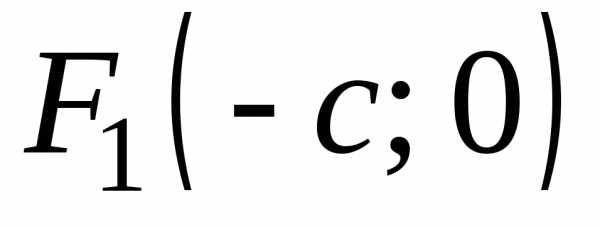 и
и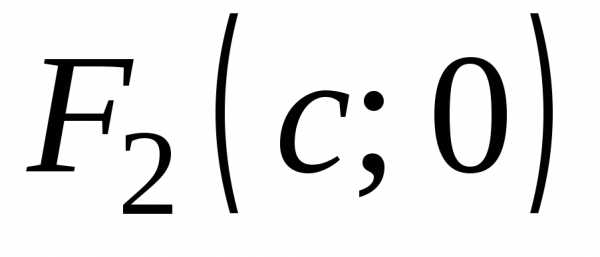 .
.
Пусть М(х; у) – произвольная точка эллипса. Тогда, согласно определению эллипса, MF1 + MF2, = 2а, т. е.
.(1)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (1) к более простому виду следующим образом:
Так как a > с, то а2 – с2 > 0. Положим
(2)
Тогда последнее уравнение примет вид или
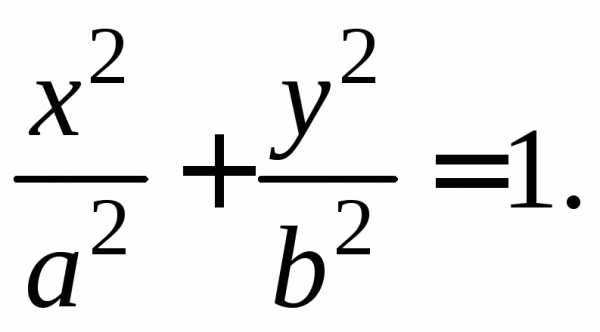 (3)
(3)
Можно доказать, что уравнение (3) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс – кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (3) содержит х и у только в четных степенях, поэтому если точка (х;у) принадлежит эллипсу, то ему также принадлежат точки (х; –у), (–х; у), (– х;– у). Отсюда следует, что эллипс симметричен относительно осей Ох и Оу, а также относительно точки 0(0; 0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив у = 0, находим две точки A1(a; 0) и A2 (– a; 0), в которых ось Ox пересекает эллипс (см. рис. 2). Положив в уравнении (3) х = 0, находим точки пересечения эллипса с осью Оу: В1(0; b) и В2{0;–b). Точки A1, A2, В1, B2 называются вершинами эллипса. Отрезки A1A2 и В1В2,, а также их длины 2а и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
3. Из уравнения (3)
следует, что каждое слагаемое в левой
части не превосходит единицы, т. е. имеют
место неравенства 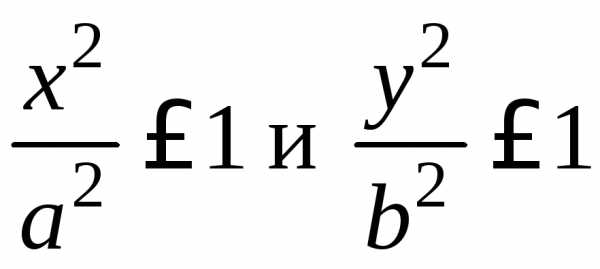 или.
Следовательно, все точки эллипса лежат
внутри прямоугольника, образованного
прямымих =
±а, у = ±b.
или.
Следовательно, все точки эллипса лежат
внутри прямоугольника, образованного
прямымих =
±а, у = ±b.
4. В уравнении (3)
сумма неотрицательных слагаемых 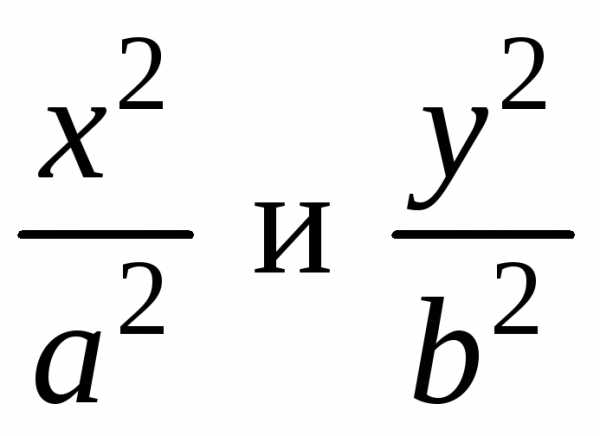 равна единице. Следовательно, при
возрастании одного слагаемого другое
будет уменьшаться, т. е. если |х | возрастает, то
равна единице. Следовательно, при
возрастании одного слагаемого другое
будет уменьшаться, т. е. если |х | возрастает, то  уменьшается и наоборот.
уменьшается и наоборот.
Рис. 2
Из сказанного следует, что эллипс имеет форму, изображенную на рис. 2 (овальная замкнутая кривая).
Форма эллипса
зависит от отношения 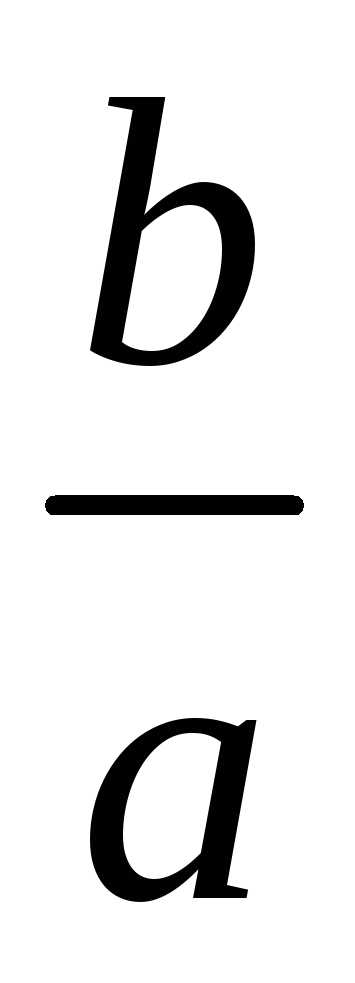 .
Приb = а эллипс превращается в окружность,
уравнение эллипса (3) принимает вид х2 + у2 = а2. В качестве характеристики формы эллипса
чаще пользуются отношением
.
Приb = а эллипс превращается в окружность,
уравнение эллипса (3) принимает вид х2 + у2 = а2. В качестве характеристики формы эллипса
чаще пользуются отношением 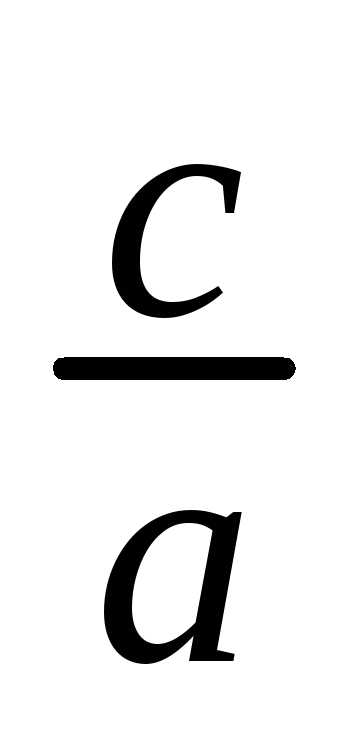 .
.
Отношение половины
расстояния между фокусами к большой
полуоси эллипса называется эксцентриситетом
эллипса и
обозначается буквой  («эпсилон»):
(«эпсилон»):
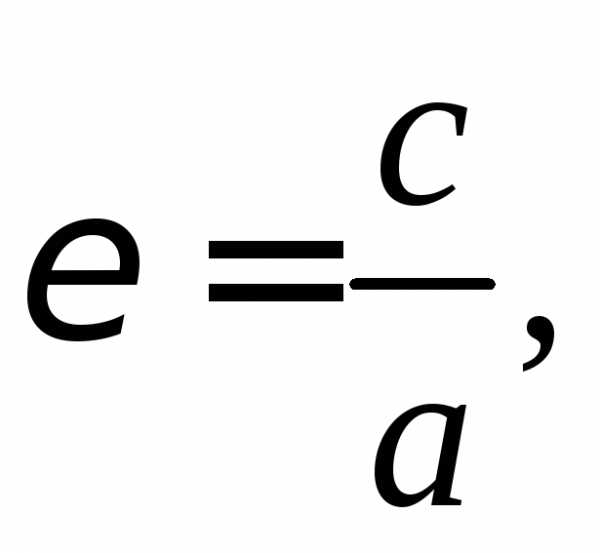 (4)
(4)
причем 0<  < 1, так как 0 < c < a.
С учетом равенства (2) формулу (4) можно
переписать в виде
< 1, так как 0 < c < a.
С учетом равенства (2) формулу (4) можно
переписать в виде
т. е.
Отсюда видно, что
чем меньше эксцентриситет эллипса, тем
эллипс будет менее сплющенным; если
положить  = 0, то эллипс превращается в окружность.
= 0, то эллипс превращается в окружность.
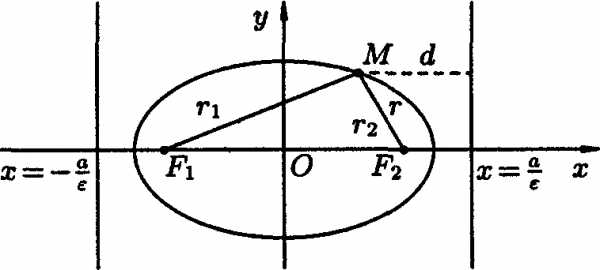
Рис. 3.
Пусть М(х;у) – произвольная точка эллипса с фокусами F1 и F1 (см. рис. 3). Длины отрезков F1M = r1 и F2M = r2 называются фокальными радиусами точки М. Очевидно,
.
Имеют место формулы
.
Прямые 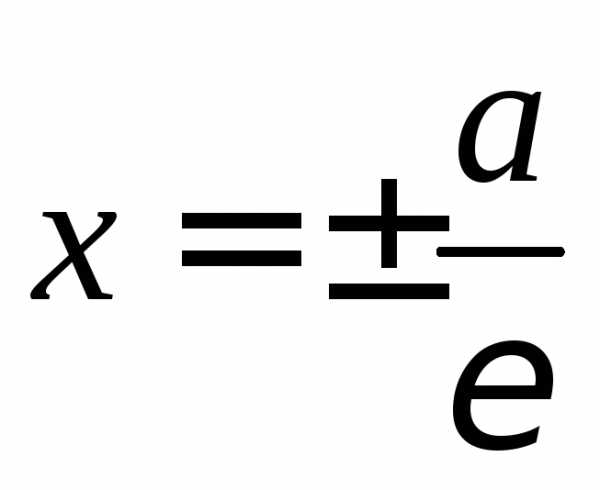 называются директрисами эллипса. Значение директрисы эллипса
выявляется следующим утверждением
называются директрисами эллипса. Значение директрисы эллипса
выявляется следующим утверждением
Теорема 1. Если r – расстояние от произвольной точки
эллипса до какого-нибудь фокуса, d – расстояние от этой же точки до
соответствующей этому фокусу директрисы,
то отношение 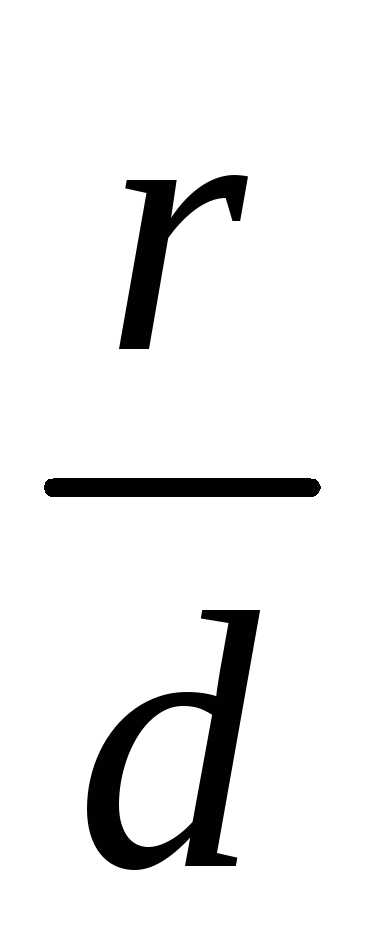 есть постоянная величина, равная
эксцентриситету эллипса:
есть постоянная величина, равная
эксцентриситету эллипса: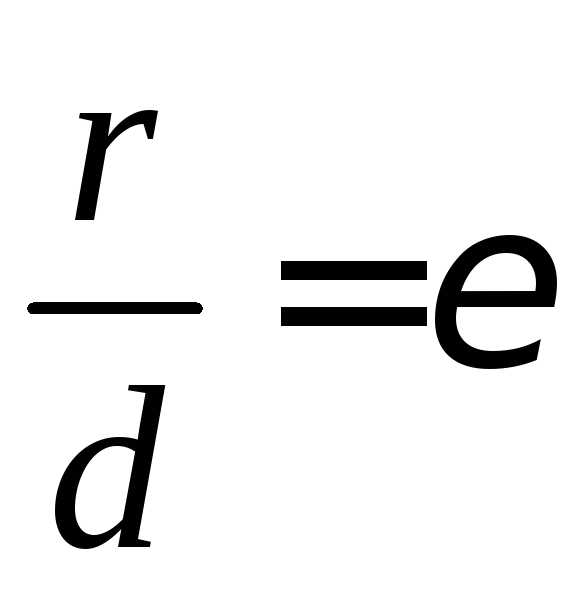 .
.
Из равенства (2) следует, что a > b. Если же a < b, то уравнение (3) определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а — на оси Ох. Фокусы такого эллипса находятся в точках F1(0; c) и F2(0; – с), где
studfiles.net
Уравнений кривых второго порядка — КиберПедия
■ Преобразование координат. Задача преобразования координат на плоскости состоит в том, чтобы, зная координаты любой точки плоскости М(х, у), найти координаты этой же точки в другой системе координат. Формулы, связывающие координаты точки М в «старой» и «новой» системах координат, называются формулами преобразования координат. При удачном выборе новой системы координат можно добиться, чтобы уравнение линии приняло наиболее простой канонический вид (что позволит исследовать свойства линии и облегчит ее построение).
1-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат , начало которой находится в точке (где а и b – координаты точки в старой системе координат), а новые оси и параллельны старым осям Ох и Оу (и одинаково с ними направлены). Тогда между координатами произвольной точки в этих двух системах координат имеется следующая зависимость:
(1)
Эти формулы позволяют выразить первоначальные координаты точки x, y через ее новые координаты и координаты нового начала в старой системе координат.
Если же требуются формулы обратного перехода, выражающие новые координаты через старые, то из (1) легко видеть, что
(2)
Пример 1. Даны координаты точки в системе хОу. Перенесем начало координат в точку , сохраняя направления осей. Найти новые координаты точки М.
Решение. Имеем , ; тогда по формулам (2) , .
Ответ: .
Пример 2. С помощью параллельного переноса осей координат (без изменения их направления) упростить уравнение линии .
Решение. Выделим в левой части уравнения полные квадраты:
или ,
откуда .
Воспользуемся формулами (2):
.
Отсюда видно, что если взять , , т.е. перенести начало координат в точку , то в новой системе координат уравнение примет вид , откуда видно, что исходное уравнение определяет гиперболу, действительная полуось которой , мнимая полуось , а центр находится в точке .
2-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат (с тем же самым началом О), которая получается при повороте осей координат на угол (рис. 6). Тогда имеют место соотношения
 . (3)
. (3)
Формулы обратного перехода имеют вид
. (4)
Пример 3. Дана точка . Найти ее координаты в системе координат , повернутой на угол 30° против часовой стрелки относительно исходной системы (без изменения начала координат).
Решение. Имеем , , . Тогда по формулам (4)
,
.
Ответ: .
Замечание. Можно объединить соотношения (1) и (3), получая формулы преобразования координат при параллельном переносе и повороте системы координат:
.
Тогда формулы обратного перехода будут иметь вид
.
■ Упрощение уравнений кривых второго порядка. Общее уравнение второй степени имеет вид
(5)
(где коэффициенты А, В, С не равны нулю одновременно).
Рассмотренные выше окружность, эллипс, гипербола и парабола имеют уравнения, которые являются частными случаями общего уравнения (5) (поэтому их называют кривыми второго порядка). Однако этому уравнению могут соответствовать и другие геометрические образы, иллюстрируемые следующими примерами.
Пример 4. Уравнение определяет пару пересекающихся прямых, т.к. его можно записать в виде , откуда получаем и .
Пример 5. Уравнению отвечает пара параллельных прямых и .
Пример 6. Уравнению , которое можно переписать в виде , отвечает одна прямая (или, как еще говорят, пара слившихся прямых).
Пример 7. Уравнению удовлетворяют только значения , , т.е. оно определяет одну точку («вырожденный эллипс»).
Пример 8.Уравнению не удовлетворяют никакие значения х и у, так что оно не определяет никакого геометрического образа («мнимый эллипс»).
Можно доказать, что все возможные случаи, которые могут встретиться при исследовании общего уравнения второй степени (5), исчерпываются либо кривыми второго порядка; либо ситуациями в Примерах 4 – 8.
Составим из коэффициентов уравнения два определителя:
и .
В зависимости от значений этих определителей уравнение (5) определяет следующий геометрический образ (см. таблицу):
Задача упрощения уравнения (5) состоит в том, чтобы при переходе к новой системе координат добиться устранения члена с произведением координат. Практически такой переход можно осуществить следующим образом.
1-й случай. Если , то геометрический образ имеет центр симметрии . Координаты центра находятся из системы уравнений
. (6)
После переноса начала координат в новый центр уравнение (5) в системе координат примет вид
. (7)
Далее повернем систему координат на угол , определяемый формулой (если , то угол поворота 45°). При этом координаты , заменяются на новые координаты , по формулам поворота:
(8)
Теперь последнее уравнение примет канонический вид
,
из которого легко распознать вид геометрического образа и расположение на плоскости.
2-й случай. Если , то отвечающий уравнению (5) геометрический образ не имеет определенного центра симметрии. При этом система уравнений (6) либо совсем не имеет решений, либо имеет бесконечно много решений. Тогда рекомендуется действовать иначе, чем в случае, когда .
Если повернуть оси координат на угол , определяемый как в предыдущем случае, старые координаты х, у выразятся через новые координаты , по формулам (3), произведение координат исчезнет, а уравнение (5) примет вид:
, или
.
Остается выделить полный квадрат, вид геометрического образа и его расположение на плоскости.
Замечание. В подробных курсах аналитической геометрии приводится ряд других приемов процедуры приведения общего уравнения кривой второго порядка к каноническому виду.
Пример 9. Выяснить, какую линию определяет уравнение и привести его к каноническому виду.
Решение. 1) Составим определители и (см. стр. ___):
, .
Так как , , то данная линия является эллипсом (см. таблицу на стр. ___).
2) Составим систему уравнений для нахождения координат центра эллипса :
,
откуда , .
3) Перенесем начало координат в центр (без поворота осей). Тогда в системе координат уравнение кривой примет вид (7):
.
4) Теперь повернем систему координат на угол (против часовой стрелки), так как здесь . При этом новые координаты , связаны с координатами , соотношениями (8):
,
.
Если преобразовать по этим формулам последнее уравнение, то, согласно общей теории, член с произведением координат исчезнет и мы получим или – каноническое уравнение эллипса с полуосями , , фокусы которог
 |
о расположены на оси (см. рис. 7).
Примеры уравнений кривых в полярных координатах
Уравнения некоторых кривых в полярных координатах выглядят значительно проще, чем в декартовой системе координат. Приведем примеры (для простоты на всех рисунках предполагается, что параметр а положителен).
cyberpedia.su
Классификация кривых второго порядка
Невырожденные кривые
Кривая второго порядка называется невырожденной, если Могут возникать следующие варианты:
- Невырожденная кривая второго порядка называется центральной, если
- эллипс — при условии D> 0 и ΔI< 0;
- частный случай эллипса — окружность — при условии I2 = 4D или a11 = a22,a12 = 0;
- мнимый эллипс (ни одной вещественной точки) — при условии ΔI> 0;
- гипербола — при условии D< 0;
- Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0
- парабола — при условии D = 0.
Вырожденные кривые
Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
- вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D> 0;
- пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D< 0;
- вырожденная парабола — при условии D = 0:
- пара вещественныхпараллельных прямых — при условии B< 0;
- одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;
- пара мнимыхпараллельных прямых (ни одной вещественной точки) — при условии B> 0.
Диаметры и центр кривой второго порядка
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:
Если выполняется условие то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают.
Координаты центра определяются системой уравнений:
Решая эту систему относительно x0 и y0, получим:
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
где — координаты относительно новой системы.
Главные оси и вершины кривой второго порядка
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.
Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям
где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой
Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.
Уравнения
Общее уравнение в матричном виде
Общее уравнение кривой можно записать в матричном виде
Канонический вид
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты и корни характеристического уравнения (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
Для центральной кривой в каноническом виде её центр находится в начале координат.
Через эксцентриситет
Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду
В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при кривая является окружностью, при — эллипсом, при — параболой, при — гиперболой.
Уравнение директрисы кривой выражается уравнением а координаты фокуса Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно
Если кривая второго порядка центральная (эллипс или гипербола), то прямая
является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы.
Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда).
Полярные координаты
Если взять в качестве полюса полярной системы координат фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
infopedia.su
27. Кривые второго порядка, их канонические уравнения
§ 27. Кривые второго порядка, их канонические уравнения
Это плоские кривые, которые неявно задаются уравнением второй степени относительно переменных Х и У. К ним относятся эллипс, гипербола и парабола. Эллиптическую орбиту имеет Земля и все планеты при движении вокруг Солнца, гиперболическую – гипотетический спутник, получивший скорость, большую второй космической (11,2 км/с). Обе эти линии имеют две замечательные точки F1 И F2, называемые фокусами. В рассмотренных примерах в одной из этих точек находится Солнце.
У эллипса любая точка М отстоит от фокусов на расстоянии R1 и R2 так, что их сумма постоянна R1 + R2 = 2А И больше, чем расстояние между фокусами . У гиперболы разность R1 и R2 постоянна , причем .
У параболы имеется один фокус и одна прямая линия, называемая директрисой; расстояние любой точки параболы до фокуса равно ее расстоянию до директрисы.
Эти свойства обычно используют в качестве определения соответствующей линии. Тогда для получения уравнения кривой выбирают каноническую систему координат: за ось ОХ принимают прямую F1F2, Соединяющую оба фокуса, а за начало координат О середину отрезка , ось ОY проходит перпендикулярно оси ОХ.
Для параболы ось ОХ проводят через фокус F Перпендикулярно директрисе, а за начало координат выбирают середину перпендикуляра, опущенного из фокуса на директрису, ось . В выбранных таким образом системах координат получаются самые простые уравнения кривых в неявной форме, и эти уравнения называются каноническими.
1. Каноническое уравнение эллипса , здесь .
Кривая имеет две оси симметрии ОХ и ОY и центр – начало координат. Она полностью помещается внутри прямоугольника, ограниченного линиями , , , . Точки (А,0), (–А,0), (0,B), (0,–B) называются вершинами. Форма эллипса зависит от соотношения А и С.
Рисунок 1.9
Отношение называется эксцентриситетом эллипса (и гиперболы). Чем больше , тем больше вытянут эллипс. При С=0 (фокусы слиплись, А=B, ) эллипс превращается в окружность .
2. Каноническое уравнение гиперболы , здесь .
А) б) | Г) в) | Рисунок 1.10 |
Кривая имеет две оси симметрии ОХ и ОY и центр – начало координат. Она пересекает только ось ОХ и имеет две вершины (А,0), (–А,0). Эта ось называется действительной, а вторая (ОY ) – мнимой. Вся гипербола расположена вне прямоугольника, ограниченного прямыми , . Диагонали этого прямоугольника расположены на асимптотах гиперболы , . График приведен на рис. 1.10 (а).
Уравнение определяет гиперболу с теми же асимптотами, но ее действительной осью является ось ОY, на ней располагаются фокусы, рис.1.10 (б). Обе эти гиперболы называются сопряженными. Если А=B, то гипербола называется равносторонней.
Эксцентриситет гиперболы больше 1. Эксцентриситет параболы принят равным 1 ().
Обратно пропорциональная зависимость описывает равностороннюю гиперболу , рис. 1.10 (в, г). В этом случае оси координат оказываются асимптотами гиперболы. Каноническая система координат такой гиперболы должна иметь оси, проходящие по биссектрисам координатных углов.
3. Каноническое уравнение параболы имеет вид , ее график приведен на рис. 1.11 (а).
Она имеет одну ось симметрии – ось ОХ, называемую фокальной и вершину – начало координат. Заменив Р на –Р, получим зеркально отображенную параболу, рис. 1.11 (б), а заменив Х на У, получим , частный вид квадратичной функции , рис. 1.11 (в).
а) б) в)
Рисунок 1.11
| < Предыдущая | Следующая > |
|---|
matica.org.ua


