Размещения с повторениями — 3 Августа 2015 — Примеры решений задач
Пусть имеется три элемента (n = 3): a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента (k = 2): ab, ac, ba, bc, ca, cb, aa, bb, cc (порядок важен!)
Общее число размещениями с повторениями определяется формулой:
или
Пример 1. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?
Решение. Данная задача есть задача на отыскание числа размещений с повторениями
.
Пример 2. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Пример 3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно .
Число всех букв, каждая из которых записывается двумя символами, равно .
Число всех букв, каждая из которых записывается тремя символами, равно .
Число всех букв, каждая из которых записывается четырьмя символами, равно .
Число всех букв, каждая из которых записывается пятью символами, равно .
Число всех указанных букв будет равно 62.
Задачи.
1. Сколькими способами можно разложить 12 различных деталей по 3 ящикам?
2. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ: .
3. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?
Ответ: .
4. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ: .
5. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?
Ответ: .
6. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа (повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?
Ответ: .
7. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно . б) Для трёх цифр аналогично получаем . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим чисел.
8. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: способов выбора кур. Точно так же есть способов выбора уток и способов выбора гусей. Всего способов.
www.reshim.su
Задачи на размещения с повторениями — КиберПедия
Пример 1. Множество Р={2,4,5}. Перечислите все размещения этого множества по 2 с повторениями.
Решение: <2,2>,<2,4>,<4,2>,<2,5>,<5,2>,<4,4>,<4,5>,<5,4>,<5,5>.
Мы можем проверить себя, вычислив число данных размещений, воспользовавшись формулой (3):
.
Число размещений, которое мы получили, равно 9.
Ответ. <2,2>,<2,4>,<4,2>,<2,5>,<5,2>,<4,4>,<4,5>,<5,4>,<5,5>.
Пример 2. Сколько пятизначных чисел мы можем получить из цифр 2,4,9?
Решение: Нам нужно получить пятизначные числа, тогда как даны 3 цифры, значит, мы будем вычислять число размещений с повторениями:
.
Ответ. 243 числа.
Пример 3. Сколько трехзначных чисел, кратных 5, можно составить из цифр 0,1,4,5,8 (цифры могут повторяться)? А кратных 2?
Решение: У нас есть 5 цифр и нужно составить трехзначные числа с повторяющимися цифрами, т.е. мы будем находить число размещений с повторениями, и чтобы число было кратно 5, его последней цифрой должен быть 0 или 5. Значит, мы воспользуемся правилом произведения: . Однако нам надо исключить числа, У которых на первом месте стоит 0. Тогда искомое число будет равно:
.
Мы могли посчитать это другим способом. Нам необходимо получить трехзначное число, кратное 5, т.е. на первое место мы можем поставить 1 из 4 цифр (все, кроме 0), на второе – 1 из 5 цифр и на третье – 1 из 2 цифр (0 или 5), т.е.:
.
Вычислим количество чисел, кратных 2. На первом месте у нас может стоять любая цифра, кроме 0, т.е. , на втором – любая из пяти цифр, т.е. , и на третьем месте может стоять 0,4 и 8, т.е. . Тогда искомое число мы можем вычислить следующим образом:
.
Ответ. 40 чисел, кратных 5; 60 чисел, кратных 2.
Пример 4. Сколько двузначных чисел можно составить из четных цифр, исключая 0.
Решение: {2,4,6,8}, n=4.
.
Ответ. 16 чисел.
Пример 5. В автобусе по маршруту №210 сидит 6 пассажиров. До конечной осталось 10 остановок. Сколькими способами пассажиры могут выходить из автобуса на каждой остановке, начиная с 10 с конца?
Решение: 6 пассажиров, т.е. n=6; осталось 10 остановок и конечная, т.е. в сумме 11, т.е. k=11. Распределим 6 пассажиров по 11 остановкам. Пассажиры могут выходить как по одному, так и все вместе, т.е. будем искать число размещений с повторениями:
.
Ответ. 177156 способами.
Пример 6. Сколькими способами можно разместить 4 кресла по трем комнатам дома, если каждая из комнат может вместить все 4?
.
Ответ. 81 способом.
Выводы к главе 2
Таким образом, существует много типов задач, сводящихся к нахождению числа размещений с повторениями и без повторений. В том числе могут встречаться задачи, где комбинируются числа размещений, сочетаний и перестановки. Необходимый уровень владения теоретическим материалом и практическими навыками в области решения комбинаторных задач существенно упрощает процесс поиска решений, так как зачастую существует очень много способов и подходов к решению одного и того же задания. Умение видеть простейший из них позволяет быстрее и эффективнее найти требуемое решение. Из чего можно сделать вывод, что должным образом изученная и рассмотренная теоретическая часть должна быть подкреплена соответствующими практическими навыками, что позволит быстрее и проще продвигаться в изучении и исследовании различных областей знаний, в том числе и математичеких.
ЗАКЛЮЧЕНИЕ
В ходе исследования темы «Размещения» были изучены и проанализированы найденные исторические сведения и теоретический материал, благодаря чему было выявлено, что комбинаторика формируется и развивается в течение уже очень долгого времени. Ее история насчитывает много веков. Хотя в качестве раздела науки она начала развиваться сравнительно недавно. Значительный вклад в ее развитие внесли известные ученые-математики, такие как Паскаль, Лейбниц, Бернулли, Эйлер и многие другие задолго до них, к примеру, в Древней Греции и Индии.
В ходе исследования теоретического материала и практических задач темы «Размещения» было выявлено, что комбинаторика имеет связи с различными областями математики, такими как алгебра, геометрия, теория вероятностей, а так же имеет широкий спектр применения в разных областях знаний (генетике, информатике, статистической физике).
Различные задачи на размещения в комбинаторике опираются как на абсолютно абстрактные ситуации, так и на вполне способные на существованию, что говорит о практической пользе науки.
К тому же, как уже говорилось ранее, комбинаторика достаточно популяризованная наука на данный момент. Так, к примеру, в книге Н. Я. Виленкина «Популярная комбинаторика» (1975 г.) [6] научно-популярным, доступным и понятным языком рассказывается история возникновения комбинаторики, ее основы, а также в книге представлены комбинаторные задачи. В целом ее можно считать очень понятным учебником по комбинаторике с подробной и интересной исторической справкой. На примере этой книги можно показать, что популяризация комбинаторики проходит достаточно успешно. Кроме того это наука действительно интересна не только для ученых, но и для людей не вовлеченных в науку тоже.
Таким образом, в ходе проведенного исследования и реализации всех поставленных мной целей этой работы было выявлено, что комбинаторика тесно связана со многими разделами математики, широко применяется в различных сферах знаний. А также она может применяться и для решения привычных нам задач, связанных с окружающим нас бытом.
Список литературы
1. http://hijos.ru/izuchenie-matematiki/algebra-10-klass/18-kombinatorika-razmeshheniya-perestanovki-sochetaniya/
2. Айгнер М. Комбинаторная теория. М.: Мир, 1982.
3. Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8.
4. Белешко Дмитрий Дискретная математика: алгоритмы.– СПб: Изд-во СПбНИУ ИТМО, 2004.
5. Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики. Киев: Ряданська школа, 1979.
6. Виленкин Н. Я. Популярная комбинаторика . — М.: Наука, 1975.
7. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. М.: Мир, 1998.
8. Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
9. Ерусалимский Я. М. Дискретная математика: теория, задачи, приложения. 10-е изд., перераб. и доп.– М.: Вузовская книга, 2009, 288 с.
10. История математики с дрвнейших времён до начала XIX столетия / Под ред. А.Н. Колмогорова, А.П. Юшкевича. М: Наука, 1970-1972. T.1-3.
11. Клейн Ф. Лекции о развитии математики в XIX столетии. М.: Наука, 1989.
12. Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
13. Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике . — Летняя школа «Современная математика». — Дубна, 2006.
14. Раизер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
15. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
16. Риордан Дж. Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
17. Романовский И.В. Дискретный анализ. — 3-е изд. — СПб: Невский Диалект; БХВ Петербург, 2003.
18. Рыбников К.А. Введение в комбинаторный анализ.– М.: Изд-во МГУ, 1985
19. Рыбников К.А. История математики. М.: МГУ, 1994.
20. Сачк пов В.Н Введение в Комбинаторные методы дискретной математики.– М.: Наука, 1982
21. Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2.
22. Стенли Р. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — С. 767. — ISBN 978-5-03-003476-8.
23. Степанов В. Элементы комбинаторики.– СПб., 2004.
24. Холл М. Комбинаторика.– М.: Мир, 1970
25. Яблонский С.В. Введениев дискретную математику: Учеб. Пособие для вузов.- 2-е изд., перераб. И доп.- М.: Наука, 1986. Гл. ред. Физ.-мат. аЛит.- 384 с..
cyberpedia.su
Решение комбинаторных задач Размещения перестановки сочетания Задача
Решение комбинаторных задач Размещения, перестановки, сочетания
Задача. Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг? Решение. Если бы они стояли на месте, то получилось бы Pn=P 7=7! = 5040 перестановок. Перестановки кругу n различных предметов можно расположить по (n-1)! cпособами Pn=(7 -1)! = 6!=720 перестановок.
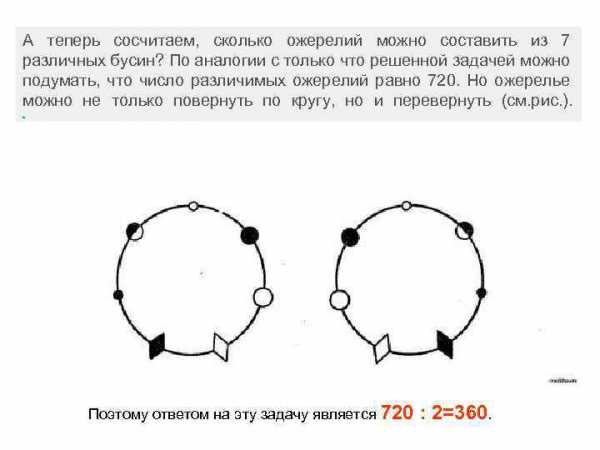А теперь сосчитаем, сколько ожерелий можно составить из 7 различных бусин? По аналогии с только что решенной задачей можно подумать, что число различимых ожерелий равно 720. Но ожерелье можно не только повернуть по кругу, но и перевернуть (см. рис. ). Поэтому ответом на эту задачу является 720 : 2=360.
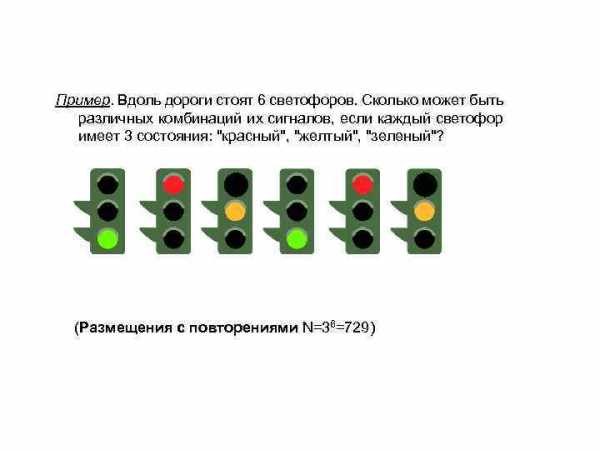Пример. Вдоль дороги стоят 6 светофоров. Сколько может быть различных комбинаций их сигналов, если каждый светофор имеет 3 состояния: «красный», «желтый», «зеленый»? (Размещения с повторениями N=36=729)
Пример. Из урны, в которой находятся 3 красных шара, 3 синих и 2 зеленых, вынимают шар, отмечают его цвет и возвращают в урну. Всего эта операция проводится 5 раз. Сколько существует вариантов вытягивания шаров? (Размещения с повторениями. Всего 3 цвета шаров, вытаскивают 5 раз N=35=243)
Пример. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, так, чтобы цифры в числе не повторялись? Перестановки без повторений Решение. Из данных четырех цифр можно составить Р = 3*3*2*1 перестановок. Числа, начинающиеся на нуль, не являются четырехзначными.
Пример. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись? Размещения без повторений Решение. 6!/(6 -4)!=3*4*5*6=360 = все возможные комбинации. 5!/(5 -3)!=3*4*5=60 – кол-во комбинаций, где 0 на 1 месте. Ответ: 360 -60=300
Пример. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски? Решение. Первая линия шахматной доски представляет собой 8 клеток, на которых и надо расположить эти 8 фигур. Различные варианты расположения будут отличаться только порядком фигур, значит, это будут перестановки с повторениями Р 8 (2, 2, 2). Получаем способов :
Сколькими способами можно выбрать к предметов из n? Например: а) одновременно вынимают две карты из колоды: C = 36! / (36 — 2)!2! = (36 ∙ 35) / 2 = 630; б) наугад зачеркивают 6 чисел из 49: C = 49! / (43! ∙ 6!) = 13 980 000; в) случайно отбирают трех человек из 25: C = 25! / (22! ∙ 3!) = 2 300.
1. Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев 2. Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой? 3. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов? 4. Сколько существует различных номеров автомашин? 5. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков? 6. Сколько есть шестизначных чисел, делящихся на 5? 7. Сколькими способами можно разложить 7 разных монет в три кармана? 8. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5? 9. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
present5.com
Комбинаторика
Реферат на тему:
Выполнил ученик 10 класса «В»
средней школы №53
Глухов Михаил Александрович
г. Набережные Челны
2002 г.
Содержание
Из истории комбинаторики
Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют «сочетания». В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге «Теория и практика арифметики» (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу.
Б. Паскаль в «Трактате об арифметическом треугольнике» и в «Трактате о числовых порядках» (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги «Ars conjectandi» (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в.
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
Правило суммы
Если конечные множества не пересекаются, то число элементов X U Y {или} равно сумме числа элементов множества X и числа элементов множества Y.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.
Примеры задач
Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: X=17, Y=13
По правилу суммы X U Y=17+13=30 тем.
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?
Решение: Так как денежно-вещевая лотерея в выборе не участвует, то всего 6+10=16 вариантов.
Правило произведения
Если элемент X можно выбрать k способами, а элемент Y-m способами то пару (X,Y) можно выбрать k*m способами.
То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.
Примеры задач
Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX , где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
Пересекающиеся множества
Но бывает, что множества X и Y пересекаются, тогда пользуются формулой
, где X и Y — множества, а — область пересечения. Примеры задач20 человекзнаютанглийскийи 10 — немецкий, изних 5 знаютианглийский, инемецкий. СколькоЧеловеквсего?
Ответ: 10+20-5=25 человек.
Также часто для наглядного решения задачи применяются круги Эйлера. Например:
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?Решение: Выразим условие этой задачи графически. Обозначим кругом тех, кто знает английский, другим кругом — тех, кто знает французский, и третьим кругом — тех, кто знают немецкий.
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.
Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек.По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Размещения без повторений.
Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?
Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.
Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов называется упорядоченное множество X, содержащее m элементов.
Количество всех размещений из n элементов по m обозначают
n! — n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n
n!=1*2*3*…*n 0!=1
Значит, ответ на вышепоставленную задачу будет
Задача
Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?
Решение : два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому:
Возможно 360 вариантов.
Перестановки без повторений
В случае n=m (см. размещения без повторений) из n элементов по m называется перестановкой множества x.
Количество всех перестановок из n элементов обозначают Pn.
Pn =n!
Действительно при n=m:
Примеры задач
Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?
Решение:
1) Найдем количество всех перестановок из этих цифр: P6 =6!=720
2) 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P5 =5!=120.
P6 -P5 =720-120=600
Квартет
Проказница Мартышка
Осел,
Козел,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
mirznanii.com
| Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. | Комбинаторика. Комбинаторика— специальный раздел математики, изучающий задачи составления тех или иных комбинаций из заданного множества элементов.
Размещения
Пусть имеется множество, содержащее т элементов. Сколькими способами можно составить подмножества из п элементов, то их число называется размещением из т элементов по п элементов (0 ≤ п ≤ т). Для подсчета числа всех размещений и обозначения этого числа применяется специальный символ (читается так: «число размещений из т элементов по п элементов»): Т.е., если в комбинации из т элементов по п важен и состав, и порядок следования, то это – размещение.
Пример. Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д? АБ АВ АГ АД БА БВ БГ БД ВА ВБ ВГ ВД ГА ГБ ГВ ГД ДА ДБ ДВ ДГ или = =20. Пример. Изучается 12 дисциплин. Сколькими способами можно составить расписание лекций, если в этот день должны быть три различные лекции? Различных вариантов составления расписания лекций, очевидно, столько, сколько существует трехэлементных упорядоченных подмножеств у 12-элементного множества. То есть число вариантов равно числу размещений из 12 элементов по 3. По формуле = , полагая в ней т=12, п=3, находим = . Пример. В группе 30 студентов. Сколькими способами могут быть выбраны староста и его заместитель?По условию задачи каждый студент может быть выбран старостой, то, следовательно, существует 30 вариантов выбора старосты. Его заместителем может стать любой из оставшихся 29 студентов. Таким образом, любой из 30 вариантов выбора старосты может осуществляться вместе с любым из 29 вариантов выбора его заместителя. Следовательно, существует 30 · 29 = 870 вариантов выбора. Или по формуле: = .
Если рассматривать число размещений, где будут учитываться комбинации с повторениями, то число таких размещений из т элементов по п в каждом подмножестве обозначают и вычисляют по следующей формуле: Т.е., если в размещениях из т элементов по п некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения называют размещениями с повторениями из т элементов по п. Пример. число размещений для предыдущего примера составит = 52 = 25 комбинаций (добавятся АА ББ ВВ ГГ ДД). Пример. Абонент забыл две последние цифры номера телефона и набирает их наудачу. Каково наибольшее число безуспешных попыток? В каждой из двух позиций может оказаться любая цифра от нуля до девяти. Следовательно, общее число возможных комбинаций составит 10 х 10 = 100. Одна из них будет верной. Из чего следует, количество безуспешных попыток будет равно: 100 — 1 = 99 или по формуле . Перестановки Перестановки являются частным случаем размещений, т. к. любая перестановка содержит все n элементов множества, а различные перестановки отличаются друг от друга только порядком элементов. Перестановкамииз п различных элементов называются все возможные последовательности этих п элементов. Число перестановок без повторений из п элементов обозначают символом Рnи подсчитывают так: Рn = n! = 1·2·… ·n . Т.е., если в комбинации из т элементов по п важен только порядок следования, то это – перестановка. Пример. Сколькими способами можно составить трехцветный флаг?Флаг представляет собой три сшитые полосы материала разного цвета. Следовательно, если в этой комбинации поменять цвета местами, то получим другой флаг, отличный от первого. Всего можно получить Р3 = 3! =1·2·3 = 6 различных флагов. Пример.Порядок выступления семи участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно? Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из семи элементов. Их число по формуле Р7= 7! = 1·2·3·4·5·6·7 = 5040. Перестановки с повторением: Пусть n1-число элементов 1-го типа, n2-число элементов 2-го типа, ………. nk -число элементов k-ro типа и Перестановками с повторением из п элементов к типов (к ≤ п) называются все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают символом и подсчитывают его так: . Пример.Перестановки элементов с повторениями из п = 3: а,а,b двух типов («а» повторяется п1= 2 раза, «b» повторяется п2= 1 раз), таковы: aab; aba; baa. Число перестановок равно 3. И согласно формуле получим такой же результат: Пример.У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? Решение. Имеем набор {я, я, г, г, г}. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!. Получаем в итоге Пример.Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?1) Найдем количество всех перестановок из этих цифр: P6=6!=7202) 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P5=5!=120. P6-P5=720-120=600
Сочетания Если имеется множество, состоящее из т элементов, и при этом рассматривается каждое его подмножество, содержащее n элементов, в котором нас интересует не порядок элементов в комбинации, а лишь ее состав, называется сочетанием из т элементов по п элементов (0≤ n ≤ т). Итак, сочетаниями из т элементов по п элементов называют всевозможные n подмножества, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число п сочетаний, которые можно составить из т элементов, обозначается символом (читается: «число сочетаний из т элементов по п), и вычисляется формуле: . Т.е., если в комбинации из т элементов по п неважен порядок следования, то это – сочетание.
Пример.Если в решении задачи (Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д?) убрать комбинации АА, ББ, ВВ, ГГ, ДД и комбинации с одними и теми же символами: АБ и БА, то получим число сочетаний из 5 элементов по 2: или АБ, АВ, АГ, АД, БВ, БГ, БД, ВГ, ВД, ГД. Пример.Всоревнованиях участвуют 10 команд. Сколько встреч проведено на этих соревнованиях? Встреч будет столько, сколько существует двухэлементных подмножеств у множества, содержащего 10 элементов, в результате получаем . Пример.Сколько команд по 5 человек можно составить из 12 человек? команд. Пример.В урне 10 белых шаров и 5 черных. · Сколькими способами можно вынуть наугад 3 белых шара? Число сочетаний из 10 по 3: способов. · Сколькими способами можно вынуть наугад 3 черных шара? Число сочетаний из 5 по 3: способов. · Сколькими способами можно вынуть наугад 2 белых и 1 черный шар? Число сочетаний из 10 по 2, умноженное на число сочетаний из 5 по 1: способов. · Сколькими способами можно вынуть наугад 1 белый и 2 черных шара? Число сочетаний из 10 по 1, умноженное на число сочетаний из 5 по 2: способов.
Если в сочетаниях из т элементов по п некоторые из элементов (или все) могут оказаться одинаковыми, то такие сочетания называют сочетаниями с повторениямииз т элементов по п инаходятся по формуле .
Пример.Если в решении задачи (Сколько различных комбинаций по 2 буквы можно составить из 5 разных букв: А,Б,В,Г,Д?) добавить комбинации АА, ББ, ВВ, ГГ, ДД, то получим число сочетаний из 5элементов по 2 с повторениями: АБ, АВ, АГ, АД, БВ, БГ, БД, ВГ, ВД, ГД, АА, ББ, ВВ, ГГ, ДД. Или ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Первоначальным понятием теории вероятностей является понятие «событие«. Оно считается основным, не подлежащим определению. События обозначаются заглавными латинскими буквами. Для определения вероятностей события сущ-ют различные подходы: · вер-ть м. рассматриваться в статистическом смысле (как относительная частота появления события при каком-то кол-ве испытаний). Отношение т/п числа т опытов, в которых событие А появилось, к общему числу п проведенных опытов называется частотой события А. При многократном повторении опыта частота события принимает значения, близкие к некоторому числу. Так, испытания, проведенные математиками в XVIII в. с бросанием однородной монеты, показали, что частота выпадения герба незначительно отличалась от числа 0,5.
Пример. Простейший опыт — подбрасывают монету. Выпадение герба или цифры, конечно, чисто случайное явление. Но при многократном подбрасывании обычной монеты можно заметить, что появление герба происходит примерно в половине случаев. Кто и когда впервые проделал опыт с монетой, неизвестно. Французский естествоиспытатель Ж. Л. Л. Бюффон (1707— 1788) в восемнадцатом столетии 4.040 раз подбрасывал монету — герб выпал 2048 раз. Математик К. Пирсон в начале нынешнего столетия подбрасывал ее 24.000 раз — герб выпал 12.012 раз. Лет 20 назад американские экспериментаторы повторили опыт. При 10.000 подбрасываний герб выпал 4.979 раз. Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону. Пример. Парадокс де Мере. В результате многократных наблюдений игры в кости француз де Мере подметил, что при одновременном бросании трех игральных костей более часто выпадает комбинация, дающая в сумме 11 очков, чем комбинация, дающая в сумме 12 очков, хотя — с его точки зрения — эти комбинации были равновероятны. Де Мере рассуждал следующим образом: 11 очков можно получить 6 способами 6-4-1, 6-3-2, 5-5-1, 5-4-2, 5-3-3, 4-4-3, и столькими же способами можно получить 12 очков 6-5-1, 6-4-2, 6-3-3, 5-5-2, 5-4-3, 4-4-4, а это означает равенство их вероятностей. Ошибка де Мере была указана знаменитым Паскалем, который заметил, что рассматриваемые де Мере исходы в данной задаче не являются равновероятными. Нужно учитывать не только выпадающие очки, но и то, на каких именно костях они выпали. Комбинации 6-4-1 соответствует один из шести исходов (6,4,1), (6,1,4), (4,6,1), (4,1,6), (1,6,4), (1,4,6), комбинация 5-5-1 выпадает лишь при трех исходах (5,5,1), (5,1,5) и (1,5,5),а комбинация 4-4-4 выпадает лишь при одном-единственном исходе (4,4,4). Итак. Событию «сумма выпавших очков равна 11» благоприятствуют ? 27 исходов, а событию «сумма выпавших очков равна 12» благоприятствуют лишь ? 25 исходов. Это и объясняет подмеченную де Мере тенденцию к более частому выпадению 11 очков. · геометрическая вер-ть. Здесь число всевозможных исходов бесконечно. Пример: вер-ть попадания точки в некоторую область, например, на острове (как отношение площадей). Пример: вер-ть обрыва провода на участке 30-35 км, если известно, что обрыв на 20-70км (как отнош. длин) · классический подход к определению вер-ти. Вероятностью случайного событияА называется отношение числа равновозможных событий, благоприятствующих этому событию, к числу всех равновозможных событий. Обозначается вероятность события А: р(А). Пример. Подбрасывают две игральные кости. Найти вероятность того, что на них в сумме выпадает шесть очков (событие А). При подбрасывании двух игральных костей общее число равновозможных элементарных исходов равно 6·6=36. Событию А благоприятствуют пять пар: (1; 5), (2; 4), (3; 3), (4; 2), (5; 1), т.е. т = 5. Следовательно, искомая вероятность р(А) = 5 / 36. Пример. Таня и Ваня хотели сидеть за праздничным столом рядом. Какова вероятность исполнения их желания, если среди их друзей принято места распределять путем жребия? Все могут усесться за стол 2·9! разными способами (Таня и Ваня, сидя рядом, считаются за 1 чел. и она могу меняться местами). Следовательно, Р = 2·9! / 10! = 1/5. Пример. В урне 5 белых и 7 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые (событие А)? Здесь число элементарных событий = 66. Число случаев, благоприятствующих событию А: ® Р(А) = . Пример.На каждой из 7 одинаковых карточек напечатана одна из следующих букв: а, г, к, и, н, р, с. Найти вероятность того, что на пяти взятых наугад и расположенных в ряд карточках можно будет прочитать слово «книга» (событие А). Общее число возможных элементарных исходов , а благоприятствует событию А лишь один, т. е. m = 1. Поэтому вероятность события равна: Р(А) = . Пример.В соревнованиях по бегу участвуют 20 перворазрядников и 5 мастеров спорта. На стартовую позицию наугад последовательно вызываются два участника. Найти вероятность того, что оба участника соревнований мастера спорта (событие А). Здесь число элементарных событий п Число случаев, благоприятствующих событию А Следовательно, вероятность равна: р(А) = 10/300 = 0,033 Пример.В урне 8 белых и 12 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди них будет 4 белых, а, следовательно, 2 — черных шара. Р(А) =
Классификация событий Достоверное— событие, которое при соблюдении некоторых условий произойдет обязательно. Например, после ночи обязательно будет утро. Невозможное — событие, которое при соблюдении некоторых условий не может произойти. Например, после зимы сразу не наступит лето. Неопределенное — событие, результат которого заранее не может быть предсказан. Совместимые: события А, и В называются совместимыми при данном испытании, если исход одного не исключает возможности появления другого. Например, появление облачности не исключает появления дождя. Несовместимые: события А и Вназываются несовместимыми, если появление одного из них исключает возможность появления другого. Например, из коробки, содержащей два яблока разного сорта, вытаскивается одно яблоко. Вероятность того, что оно окажется первого и второго сорта, — событие несовместимое. Зависимые: события А и Взависимы, если исход события А зависит от исхода события В. Случайные события являются зависимыми друг от друга, если вероятность появления одного из них зависит от появления или непоявления другого события. Например, вероятность появления дождя зависит от вероятности появления тучи. Независимые: события А и В независимы, если исход одного из них никак не влияет на возможность появления другого. Случайные события являются независимыми друг от друга, если вероятность появления одного из них не зависит от появления или непоявления другого события. Например, в урне п белых и т черных шаров. Из урны вынимают подряд два шара. Какова вероятность того, что оба шара белые, если первый извлеченный шар вновь возвращается в урну? События, что оба извлеченных шара белые, независимы.
Итак. Любому случайному событию А соответствует определенное число р(А), удовлетворяющее условию 0≤р(А) ≤ 1. Это число называется вероятностью события А.
|
megapredmet.ru
Перестановки с повторениями
Поиск ЛекцийПравило суммы
Если конечные множества не пересекаются, то число элементов X U Y {или} равно сумме числа элементов множества X и числа элементов множества Y.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.
Примеры задач
1. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: X = 17, Y = 13
По правилу суммы XUY = 17+13=30 тем.
2. Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?
Решение: Так как денежно-вещевая лотерея в выборе не участвует, то всего 6+10 = 16 вариантов.
Правило произведения
Если элемент X можно выбрать k способами, а элемент Y-m способами, то пару (X,Y) можно выбрать k*m способами.
То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10 = 50 способами.
Примеры задач
1. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3 = 36 вариантов переплета.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z — любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10 = 900 вариантов.
Размещения без повторений
1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?
Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.
Если X-множество, состоящие из n элементов, m?n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов называется упорядоченное множество X, содержащее m элементов.
Количество всех размещений из n элементов по m обозначают n! — n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа
n n! = 1*2*3*…*n 0! = 1
Значит, ответ на вышепоставленную задачу будет…
2. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?
Решение: два юноши не могут одновременно пригласить одну и ту же девушку.
И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому возможно 360 вариантов.
Перестановки без повторений
комбинаторика множество сумма повторение
В случае n = m (см. размещения без повторений) из n элементов по m называется перестановкой множества x.
Количество всех перестановок из n элементов обозначают Pn.
Pn = n!
Действительно при n = m.
Размещения и сочетания с повторениями
Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа — цифры.
Для таких задач при размещениях используется формула, а для сочетаний…
Примеры задач
1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?
Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три, а их число равно …
2. В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.
Решение: Покупка не зависит от того, в каком порядке укладывают купленные пирожные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта.
Следовательно, количество различных покупок равно числу сочетаний четырех видов пирожных по семь.
3. Обезьяну посадили за пишущую машинку с 45 клавишами, определить число попыток, необходимых для того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого «Анна Каренина», если строка содержит 52 знака и повторений не будет?
Решение: порядок букв имеет значение. Буквы могут повторяться.
Значит, всего есть … вариантов.
Перестановки с повторениями
n-количество всех элементов, n1, n2,…, nr — количество одинаковых элементов.
Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания: ab, ac, bc.
Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом Cnk и вычисляется по формуле:
Случайные события.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например если брошена монет она может упасть вверх гербом или вверх надписью. Поэтому событие ?при бросании монеты выпал герб? — случайное. Каждое случайное событие , в частности выпадение герба, есть следствие действия многих случайных причин (сила с которой брошена монета, форма монеты, вес и т.д.). Не возможно учесть влияние этих причин на результат, по сколку их число очень велико, по этому теория вероятностей не ставит перед собой задачу предсказать. Произойдет единичное событие или нет.
В дальнейшем, вместо того чтобы говорить ?совокупность условий S осуществлена?, будем говорить кратко ?произведено испытание?. Таким образом, события будет рассматривается как результат испытания.
.Классификация случайных событий.
Полной группой событий называются несколько событий таких что в результате опыта непременно должно произойти хотя бы одно из них.
События называют несовместными, если появление одного из них исключает появления других событий в одном и том же испытании.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Действия над случайными событиями и отношения между ними определяются по аналогии с действиями и отношениями в теории множеств.
Обозначаем А, если — элементарный исход события А; А В, если событие А влечет за собой В; А, В
Равенство (эквивалентность) событий: А = В, если А В и В А.
О: Суммой событий A и В называется их теоретико-множественное объединение, т.е. событие, состоящее из элементарных событий или В.
Произведением АВ (А В) событий А и В называется их теоретико-множественное пересечение, т.е. событие, состоящее из элементарных событий: А и В. Разностью событий Аи В называется их теоретико-множественная разность, т.е. событие, состоящее из элементарных событий но В. Противоположным событием для события A называется теоретико-множественное дополнение А до т.е. происходит тогда, когда А не происходит.
Свойства операций над событиями:
1. А+В=В+А, АВ=ВА – переместительное свойство
2. (А+В)?С=А?С+В?С, А?С+В=(А+В) ?(А+С) – распределительное свойство
3. (А+В)+С = А+(В+С), (АВ) ?С=А?(ВС) – сочетательное свойство
4. А+А=А, А?А=А
5. А+?=?, А?? = А
6. = ?, ?
7. А-В=А?
8. , — законы де Моргана.
2. Вероятность суммы событий..
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Определение. Противоположными называются два несовместных события, образующие полную группу.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Задачи на перестановки без повторений
Задача в общем виде: Дано конечное множество М различных элементов. Необходимо подсчитать число способов упорядочивания элементов данного множества.
Группа туристов за пять дней пребывания в Гагре может посетить Сухум, Альпийские луга, Каман, озеро Рица и экскурсию по ночной Гагре. Сколькими способами они могут сделать это?
Горзеленхоз закупило семь сортов цветов для озеленения города. Было решено оформлять клумбы в виде семи окружностей, имеющих один центр и разные радиусы. Сколько различных клумб можно сделать?
Веселые человечки построились в ряд: Незнайка, Знайка, Тобик, Винтик, Шпунтик, Кнопочка, Сиропчик, Цветик, Гунька, Ворчун, Пончик. Сколькими способами они могли это сделать?
Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо?
Сколько есть перестановок чисел 1, 2, 3, …, 9, в которых цифры 4 и 8 стоят на своих местах?
Двенадцати семиклассникам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
Сколько четных пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4 при условии, что каждая цифра входит в число только один раз?
Питер Пен и его друзья нашли сокровища семи морей. Для того, чтобы открыть сундук, им надо разложить в правильном порядке по кругу 7 драгоценных камней. Сколько может оказаться неудачных попыток?
Сколько существует способов размещения 5 мужчин и 5 женщин за круглым столом так, чтобы мужчины и женщины чередовались?
Сколько шестизначных чисел, не кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что каждая цифра входит в число только один раз?
Задача в общем виде: Дано конечное множество, содержащее т1 элементов одного типа, т2 элементов второго типа, …, тпэлементов п-го типа. Необходимо подсчитать число способов упорядочивания элементов данного множества.
Сколько имеется различных шестизначных чисел, у которых три цифры – 3, и три цифры – 6?
Для премии на математической олимпиаде выделено 8 экземпляров одной книги, 9 экземпляров второй и 13 экземпляров третей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Сколько «слов» можно получить, переставляя буквы слова «парабола», слова «метаморфоза»?
Сколькими способами можно расставить шахматные фигуры (короля, ферзя, две ладьи, двух слонов и двух коней) на первой горизонтали шахматной доски?
Вовочка нарисовал «свою» радугу, составленную из двух обычных (применяя по 2 цвета). Сколькими еще способами он мог это сделать?
Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
Сколько «слов» можно составить из пяти букв А и не более, чем из трех букв Б?
Сколько существует способов расстановки на полке 3-х книг одного вида, 5 – другого и 8 – третьего?
У Шалтая-Балтая на завтрак 2 коровы, 3 овцы, 5 кадок масла, 4 жареных цыпленка. Сколькими способами он может изменить последовательность приема пищи?
На новогоднем утреннике присутствуют 12 детей. У Снегурочки для конкурса есть 15 конфет «Маска», 12 конфет «Белочка» и 9 конфет «Орешек». Сколькими способами дети могут получить по 3 одинаковые конфеты? по 3 разные конфеты?
studfiles.net