Пример №1:
Решим уравнение:
\(\sqrt{3x} = 6\)
1. Возведем обе части уравнения в квадрат, при условии, что они неотрицательные.
\(\left\{ \begin{matrix} 3x \geq 0 \\ 6 \geq 0 \\ 3x = 36 \\ \end{matrix} \right.\ \)
2. Определить знак числа справа можно сразу, 6 – положительное число, а значит больше нуля. В первом неравенстве выразим «х», получим:
\(\left\{ \begin{matrix} x \geq 0 \\ 3x = 36 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x \geq 0 \\ x = 12 \\ \end{matrix} \right.\ \)
3. Система имеет решение при \(x = 12\). Запишем ответ.
Ответ: 12.
Если a < 0, то решений нет
Например, решим уравнение:
\(\sqrt{3x} = \ –6\)
1. Составим систему:
\(\left\{ \begin{matrix} 3x \geq 0 \\ –6 \geq 0 \\ 3x = 36 \\ \end{matrix} \right.\ \)
2. Второе неравенство не имеет смысла, поэтому вся система не имеет решений.
Ответ:
То, что мы с вами сейчас сделали будет верно для любого корня четной степени.
{n}\)
Пример №2:
Решим уравнение:
\(\sqrt[3]{3x} = \ –6\)
1. Видим корень нечетной степени – сразу возводим в эту степень обе части:
\(\sqrt[3]{3x} = \ –6\)
\(3x = \ –216\)
\(x = \ –72\)
2. Записываем ответ. Уравнение не имеет никаких ограничений.
Ответ: –72.
ВТОРОЙ ТИП ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ «КОРЕНЬ=КОРЕНЬ»:
\(\sqrt{f(x)} = \sqrt{g(x)}\)
Решение:
Если и слева и справа будет стоять корень алгоритм остается тот же: записываем ОДЗ и возводим обе части в квадрат.
\(\sqrt{f(x)} = \sqrt{g(x)} \Leftrightarrow \left\{ \begin{matrix} f(x) \geq 0 \\ g(x) \geq 0 \\ f(x) = g(x) \\ \end{matrix} \right.\ \)
Пример №3:
Решим уравнение:
\(\sqrt{–2x + 6} = \sqrt{15 + x}\)
1. Составим систему:
\(\left\{ \begin{matrix} –2x + 6 \geq 0 \\ 15 + x \geq 0 \\ –2x + 6 = 15 + x \\ \end{matrix} \right.\ \)
2.
{2}\ –\ 20x + 36 = 0 \\ \end{matrix} \right.\ \)
5. Решим квадратное уравнение через теорему Виета:
\(\left\lbrack \frac{x_{1} = 18}{x_{2} = 2} \right.\ \)
Только \(x = 2\) является уравнением системы. Это значение переменной и запишем в ответ.
Ответ: 2.
ПЯТЫЙ ВИД ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ «КОРЕНЬ – КОРЕНЬ = ЧИСЛО»:
\(\sqrt{f(x)}\ –\ \sqrt{g(x)} = a\)
Решение:
\(\sqrt{f(x)} = a + \sqrt{g(x)}\)
И решаем такое уравнение как четвертый вид «корень + корень = число».
Пример решения иррационального уравнения с двумя корнями
Нам нужно решить иррациональное уравнение (см. что такое иррациональное уравнение). В его записи присутствуют два корня и еще одно слагаемое помимо них. Такие иррациональные уравнения очень характерны, для их решения обычно используется метод возведения обеих частей уравнения в одну и ту же степень. Причем, для избавления от обоих радикалов к возведению обеих частей уравнения в степень придется прибегать два раза.
Напомним последовательность действий для решения иррациональных уравнений по методу возведения обеих частей в одну и ту же степень:
-
Во-первых, переходим к более простому уравнению, для чего циклически выполняем следующие три действия:
- Уединяем радикал.
- Возводим обе части полученного уравнения в одну и ту же натуральную степень.
- Упрощаем вид уравнения, полученного после возведения в степень.
- Во-вторых, решаем полученное уравнение.
- В-третьих, отсеиваем посторонние корни, если выше проводилось возведение в четную степень.
Начнем. Выполним тройку действий – уединение радикала, возведение в степень, упрощение вида – в первый раз.
Уединение радикала приводит нас к уравнению .
Так как степень уединенного корня равна двум, то возведем обе части уравнения во вторую степень: , что дальше позволит избавиться от уединенного радикала.
Теперь упростим вид полученного уравнения при помощи преобразования уравнений. В первую очередь, базируясь на определении корня, заменим выражение в левой части тождественно равным выражением x−6, и, учитывая формулу сокращенного умножения «квадрат разности», заменим выражение в правой части тождественно равными ему выражением . Имеем . Продолжим упрощать вид уравнения. Вновь оттолкнемся от определения корня для замены выражения тождественно равным ему выражением x+2, а числовое выражение 2
Очевидно, после первого прохода цикла мы освободились от одного корня, но остался еще один корень. Поэтому второй раз выполним указанную тройку действий – уединение радикала, возведение обеих частей уравнения в степень, упрощение выражения.
В уравнении уединять радикал не нужно, так как это уже сделано.
Для избавления от квадратного корня выполним возведение обеих частей уравнения в квадрат: .
Упрощаем вид полученного уравнения:
x+2=9,
x=7.
Второй этап – решение полученного уравнения – также можно считать завершенным, так как корень уравнения x=7 очевиден. Это число 7.
Остается третий этап решения – отсеивание посторонних корней. В нашем случае отсеивание обязательно, так как некоторые из проводимых выше преобразований могли привести к появлению посторонних корней. Действительно, мы дважды прибегали к возведению обеих частей уравнения в одну и ту же четную степень, а, как известно, такое преобразование может привести к появлению посторонних корней.
Также в цепочке преобразований был переход от уравнения к уравнению x+2=9, при котором расширилась ОДЗ, что тоже могло привести к появлению посторонних корней. Так что проведем отсеивание посторонних корней. Сделаем это через
Подстановка дала верное числовое равенство, значит, x=7 является искомым корнем.
На этом решение иррационального уравнения методом возведения обеих частей уравнения в одну и ту же степень завершено, оно потребовало двух возведений в степень для избавления от двух корней.
Приведем краткий вариант решения:
Алгебра — уравнения с радикалами
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Уравнения с радикалами
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.10: Уравнения с радикалами
Название этого раздела может немного ввести в заблуждение. Название, кажется, подразумевает, что мы будем рассматривать уравнения, в которых есть радикалы. Однако мы собираемся ограничиться уравнениями с квадратными корнями. Методы, которые мы собираемся применить здесь, можно использовать для решения уравнений с другими радикалами, однако работа обычно значительно сложнее, чем при работе с квадратными корнями. Поэтому в этом разделе мы будем работать только с квадратными корнями.
Прежде чем продолжить, следует также упомянуть, что в некоторых учебниках по алгебре вы найдете этот раздел с уравнениями, приводимыми к квадратичной форме.
Причина в том, что в большинстве случаев мы на самом деле приходим к решению квадратного уравнения. Однако подход существенно отличается, поэтому в этом курсе мы разделим две темы на разные разделы.
Обычно лучше всего посмотреть, как они работают, на примере.
Пример 1 Решить \(x = \sqrt {x + 6} \).
Показать решение
В этом уравнении основной проблемой является квадратный корень. Если бы этого не было, мы могли бы решить проблему. Весь процесс, который мы собираемся пройти здесь, настроен на устранение квадратного корня. Однако, как мы увидим, шаги, которые мы собираемся предпринять, на самом деле могут вызвать у нас проблемы. Итак, давайте посмотрим, как это все работает. 92} — x — 6 & = 0\\ \left( {x — 3} \right)\left( {x + 2} \right) & = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0,25 дюйма}\hspace{0,25 дюйма}x = 3,\,\,\,x = — 2\end{align*}\]
После возведения в квадрат обеих частей мы видим, что мы получаем факторизуемое квадратное уравнение, которое дает нам два решения \(x = 3\) и \(x = — 2\).
Теперь, без всякой видимой причины, давайте сделаем то, чего мы фактически не делали со времен раздела о решении линейных уравнений. Давайте проверим наши ответы. Помните также, что нам нужно проверить ответы в исходном уравнении! Это очень важно. 9? \sqrt { — 2 + 6} \\ — 2 & \ne \sqrt 4 = 2\hspace{0,25 дюйма}\hspace{0,25 дюйма}{\mbox{НЕ ОК}}\end{align*}\]
У нас проблема. Напомним, что квадратные корни ВСЕГДА положительны, поэтому \(x = — 2\) не работает в исходном уравнении. Одна из возможностей здесь заключается в том, что мы где-то допустили ошибку. Однако мы можем вернуться и посмотреть, и мы быстро увидим, что не ошиблись.
Итак, в чем дело? Помните, что нашим первым шагом в процессе решения было возведение обеих сторон в квадрат. Заметьте, что если мы подставим \(x = — 2\) в квадратное уравнение, которое мы решили, оно на самом деле будет его решением. Когда мы возвели в квадрат обе части уравнения, мы фактически изменили уравнение и в процессе ввели решение, которое не является решением исходного уравнения.
При таких проблемах жизненно важно проверить свои решения, так как это часто случается. В этом случае мы берем только те значения, которые являются фактическими решениями исходного уравнения.
Итак, исходное уравнение имело единственное решение \(x = 3\).
Теперь, как показал этот пример, мы должны быть очень осторожны при решении этих уравнений. Когда мы решим квадратное уравнение, мы получим два решения, и возможно, что оба из них, одно из этих или ни одно из этих значений не являются решениями исходного уравнения. Единственный способ узнать это проверить свои решения!
Давайте поработаем еще с парой примеров, которые немного сложнее.
Пример 2. Решите каждое из следующих уравнений.
- \(у + \sqrt {у — 4} = 4\)
- \(1 = t + \sqrt {2t — 3} \)
- \(\sqrt {5z + 6} — 2 = z\)
Показать все решения Скрыть все решения
a \(y + \sqrt {y — 4} = 4\) Показать решение
В этом случае давайте заметим, что если мы просто возведем в квадрат обе стороны, у нас будут проблемы.
92}\]
с \(a = y\) и \(b = \sqrt {y — 4} \). Вы должны быть в состоянии сделать это, потому что, хотя это, возможно, не сработало здесь, нам понадобится такая работа в следующем наборе задач.
В чем проблема? Хорошо помните, что смысл возведения в квадрат обеих сторон в первой задаче заключался в том, чтобы исключить квадратный корень. Мы этого не сделали. В задаче по-прежнему есть квадратный корень, и мы сделали оставшуюся часть задачи еще более беспорядочной. 92} — 9y + 20\\ 0 & = \left( {y — 5} \right)\left( {y — 4} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}y = 4 ,\,\,\,y = 5\end{align*}\]
Как и в первом примере, нам нужно убедиться и проверить оба этих решения. Опять же, убедитесь, что вы проверили исходное уравнение. Как только мы возведем в квадрат обе стороны, мы изменим задачу, и поэтому проверка здесь не принесет нам никакой пользы. На самом деле проверка там вполне может привести нас к неприятностям.
9? 4\\ 6 & \ne 4\hspace{0,25 дюйма}{\mbox{НЕ}}{\mbox{OK}}\end{align*}\] Итак, как и в первом примере, который мы рассмотрели, на самом деле существует единственное решение исходного уравнения \(y = 4\).
2} — z — 2\\ & 0 = \left( {z — 2 } \right)\left( {z + 1} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,z = — 1,\,\,\, \,z = 2\конец{выравнивание*}\]
9? 2\\ 4 — 2 & = 2\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]
Это тоже было решением.
Итак, в данном случае мы увидели пример, в котором оба возможных решения фактически также являются решениями исходного уравнения.
Итак, как мы видели в предыдущем наборе примеров, как только мы получим список возможных решений, от ни одного до всех, они могут быть решениями исходного уравнения. Не забывайте проверять свои ответы!
Хорошо, давайте поработаем еще с одним набором примеров, которые имеют дополнительную сложность. До сих пор все уравнения, которые мы рассматривали, содержали один квадратный корень. Однако в этих уравнениях может быть более одного квадратного корня. Следующий набор примеров предназначен для того, чтобы показать нам, как справляться с такого рода проблемами.
Пример 3. Решите каждое из следующих уравнений.
- \(\sqrt {2x — 1} — \sqrt {x — 4} = 2\)
- \(\sqrt {t + 7} + 2 = \sqrt {3 — t} \)
Показать все решения Скрыть все решения
Показать обсуждение
В обоих из них есть два квадратных корня в задаче. Однако мы будем работать с ними в основном таким же образом. Первый шаг состоит в том, чтобы получить один из квадратных корней в одной части уравнения, а затем возвести в квадрат обе части. На этом этапе процесс отличается, поэтому мы увидим, как двигаться дальше, как только мы достигнем его в первом примере. 92}\\ 2x — 1 & = 4 + 4\sqrt {x — 4} + x — 4\\ 2x — 1 & = 4\sqrt {x — 4} + x\end{align*}\]
Итак, у нас все еще есть квадратный корень в задаче, но нам удалось исключить один из них. Не только это, но и то, что у нас осталось, идентично примерам, с которыми мы работали в первой части этого раздела.
2} — 18x + 65 & = 0 \\ \left( {x — 13} \right)\left( {x — 5} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = 13,\,\,\ ,х = 5\конец{выравнивание*}\]
9? \sqrt 9 \\ 1 + 2 & = 3\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]
Похоже, в этом случае у нас есть единственное решение, \(t = — 6\).
Итак, когда в задаче больше одного квадратного корня, мы снова сталкиваемся с задачей проверки наших возможных решений. Вполне возможно, что все возможные решения, от нуля до всех, на самом деле будут решениями, и единственный способ узнать наверняка — проверить их в исходном уравнении.
10.7: Решение радикальных уравнений — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49983
Цели обучения
К концу этого раздела вы сможете: 9{2}−6n+8=0\).
Если вы пропустили эту проблему, просмотрите пример 6.45.
Решение подкоренных уравнений
В этом разделе мы будем решать уравнения, в которых подкоренное выражение содержит переменную. Уравнение этого типа называется радикальным уравнением .
Определение: подкоренное уравнение
Уравнение, в котором переменная стоит под корнем подкоренного выражения, называется подкоренным уравнением .
Как обычно, при решении этих уравнений то, что мы делаем с одной частью уравнения, мы должны делать и с другой его частью. Как только мы изолируем радикал, наша стратегия будет состоять в том, чтобы возвести обе части уравнения в степень индекса. Это устранит радикал. 9{п}=а\).
Пример \(\PageIndex{1}\) решения радикального уравнения
Решите: \(\sqrt{5 n-4}-9=0\).
Решение :
Шаг 1 : Выделите радикал на одной стороне уравнения. | Чтобы изолировать радикал, добавьте \(9\) к обеим сторонам. Упростить. | \(\ begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9{2}=а\). | \(\begin{выровнено} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{выровнено}\) |
| Шаг 4 : Проверьте ответ в исходном уравнении. | Проверьте ответ. \(\ begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}- 4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{? }{=} 0} \\ {9-9=0} \\ {0=0}\конец{массив}\) Решение: \(n=17\). |
Упражнение \(\PageIndex{1}\)
Решите: \(\sqrt{3 m+2}-5=0\).
- Ответить
\(м=\фракция{23}{3}\)
Упражнение \(\PageIndex{2}\)
Решите: \(\sqrt{10 z+1}-2=0\).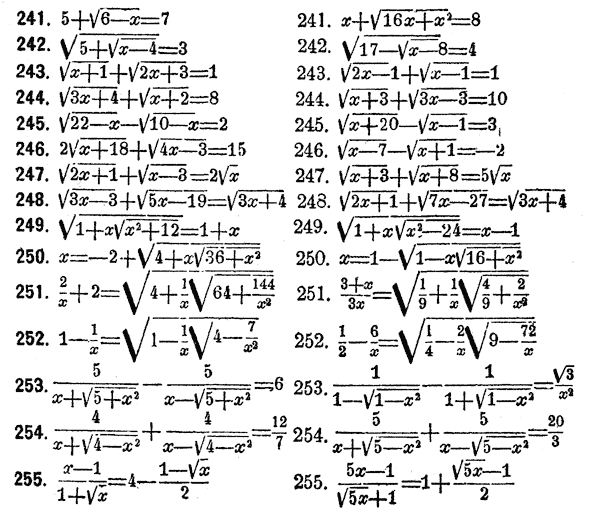
- Ответить
\(z=\frac{3}{10}\)
Решите радикальное уравнение с одним радикалом
- Изолируйте радикал с одной стороны уравнения.
- Возведите обе части уравнения в степень индекса.
- Решите новое уравнение.
- Проверьте ответ в исходном уравнении.
Когда мы используем радикальный знак, он указывает на главный или положительный корень. Если уравнение имеет радикал с четным индексом, равным отрицательному числу, то это уравнение не будет иметь решения.
Пример \(\PageIndex{2}\)
Решите: \(\sqrt{9 k-2}+1=0\).
Решение :
| Чтобы изолировать радикал, вычтите \(1\) с обеих сторон. | |
| Упрощение. |
6.2Поскольку квадратный корень равен отрицательному числу, уравнение не имеет решения.
Упражнение \(\PageIndex{3}\)
Решите: \(\sqrt{2 r-3}+5=0\).
- Ответить
нет решения
Упражнение \(\PageIndex{4}\)
Решите: \(\sqrt{7 s-3}+2=0\).
- Ответить
нет решения
Если одна часть уравнения с квадратным корнем является двучленом, мы используем образец произведения биномиальных квадратов, когда возводим его в квадрат. 9{2}}\end{array}\)
Не забудьте средний термин!
Пример \(\PageIndex{3}\)
Решить: \(\sqrt{p-1}+1=p\).
Решение :
| Чтобы изолировать радикал, вычтите \(1\) с обеих сторон. | |
Упрощение. | |
| Возведите в квадрат обе части уравнения. | |
| Упростите, используя образец произведения биномиальных квадратов справа. Затем решите новое уравнение. | |
| Это квадратное уравнение, поэтому с одной стороны получаем ноль. | |
| Фактор правой стороны. | |
| Использовать свойство нулевого продукта. | |
| Решите каждое уравнение. | |
| Проверьте ответы. | |
Решения: \(p=1, p=2\).
Упражнение \(\PageIndex{5}\)
Решите: \(\sqrt{x-2}+2=x\).
- Ответить
\(х=2, х=3\)
9{3}\)- Ответ
\(х=-6\)
- Ответ
\(х=-9\)
- Ответ
\(х=6\)
- Ответ
\(м=7\)
- Ответить
\(n=3\)
- Ответить
\(а=63\)
- Ответ
\(б=311\)
- Ответить
\(х=3\)
- Ответить
\(х=-\фракция{6}{5}\)
- Ответить
\(х=4\)
- Ответить
\(х=9\)
- Ответ
\(х=5\)
- Ответ
\(х=0 х=4\)
- Прочтите задачу и убедитесь, что все слова и идеи понятны.
При необходимости нарисуйте рисунок и подпишите его с помощью данной информации. - Определите , что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для ее представления.
- Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
- Решите уравнение , используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
- Ответить
\(9\) секунд
- Ответить
\(3,5\) секунд
- Ответить
\(42,7\) миль/ч
- Ответить
\(54,1\) миль/ч
- Решение радикального уравнения
- Изолируйте один из радикальных членов на одной стороне уравнения.
- Возведите обе части уравнения в степень индекса.
- Есть еще радикалы?
Если да, повторите Шаг 1 и Шаг 2 еще раз.
Если нет, решите новое уравнение. - Проверьте ответ в исходном уравнении.
- Стратегия решения проблем для приложений с формулами
- Прочитайте задачу и убедитесь, что все слова и идеи понятны. При необходимости нарисуйте рисунок и подпишите его с помощью данной информации.
- Определите, что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для ее представления.
- Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
- Падающие предметы
- На Земле, если объект падает с высоты \(h\) футов, время в секундах, необходимое для достижения земли, определяется по формуле \(t=\frac{\sqrt{h} {4}\).
- Следы заноса и скорость автомобиля
- Если длина следов заноса составляет \(d\) футов, то скорость \(s\) автомобиля до включения тормозов можно найти по формуле \(s=\sqrt{24d} \).
- радикальное уравнение
- Уравнение, в котором переменная стоит под корнем подкоренного выражения, называется подкоренным уравнением.
Упражнение \(\PageIndex{7}\)
Решить: \( \sqrt[3]{4 x-3}+8=5\)
Упражнение \(\PageIndex{8}\)
Решить: \(\sqrt[3]{6 x-10}+1=-3\)
Иногда уравнение может содержать рациональные показатели вместо радикала. Мы используем те же методы для решения уравнения, что и в случае, когда у нас есть радикал. Возведем каждую часть уравнения в степень знаменателя рационального показателя.
{m \cdot n}\), мы имеем, например, 9{4}\)
Иногда решение радикального уравнения приводит к двум алгебраическим решениям, но одно из них может быть посторонним решением !
Пример \(\PageIndex{6}\)
Решите: \(\sqrt{r+4}-r+2=0\).
Решение :
| \(\sqrt{r+4}-r+2=0\) | |
Фактор правой стороны. | \(0=r(r-5)\) |
| Использовать свойство нулевого продукта. | \(0=r \quad 0=r-5\) |
| Решите уравнение. | \(r=0 \квадратный r=5\) |
| Проверьте свой ответ. | |
| Решение: \(r=5\). | |
| \(r=0\) — экстравагантное решение. |
Упражнение \(\PageIndex{11}\)
Решить: \(\sqrt{m+9}-m+3=0\)
Упражнение \(\PageIndex{12}\)
Решите: \(\sqrt{n+1}-n+1=0\).
Когда перед корнем стоит коэффициент, мы должны возвести и его в степень индекса.
Пример \(\PageIndex{7}\)
Решите: \(3 \sqrt{3 x-5}-8=4\).
Решение :
| \(3 \sqrt{3 x-5}-8=4\) | |
| Изолируйте радикальный термин. | \(3 \sqrt{3 x-5}=12\) |
| Изолируйте радикал, разделив обе части на \(3\). 9{2}\) | |
| Упростите, затем решите новое уравнение. | \(3 х-5=16\) |
| \(3x=21\) | |
| Решите уравнение. | \(х=7\) |
| Проверьте ответ. | |
| Решение: \(x=7\). |
Упражнение \(\PageIndex{13}\)
Решите: \(2 \sqrt{4 a+4}-16=16\).
Упражнение \(\PageIndex{14}\)
Решить: \(3 \sqrt{2 b+3}-25=50\)
Решение радикального уравнения с двумя радикалами
Если радикальное уравнение имеет два радикала, мы начинаем с выделения одного из них.
Часто проще всего сначала выделить более сложный радикал. 9{3}\)
Упростите, затем решите новое уравнение.
\(\begin{align} 4 x-3 &=3 x+2 \\ x-3 &=2 \\ x &=5 \end{align}\)
Решение \(x=5 \).
Проверьте ответ.
Мы предоставляем вам показать, что \(5\) проверяет!
Упражнение \(\PageIndex{15}\)
Решите: \(\sqrt[3]{5 x-4}=\sqrt[3]{2 x+5}\).
Упражнение \(\PageIndex{16}\)
Решите: \(\sqrt[3]{7 x+1}=\sqrt[3]{2 x-5}\).
Иногда после возведения обеих частей уравнения в степень у нас все еще есть переменная внутри корня. Когда это происходит, мы повторяем Шаг 1 и Шаг 2 нашей процедуры. Мы изолируем радикал и снова возводим обе части уравнения в степень индекса.
Пример \(\PageIndex{9}\) как решить радикальное уравнение
Решите: \(\sqrt{m}+1=\sqrt{m+9}\).
Решение :
| Шаг 1 : Выделите один из радикальных членов на одной стороне уравнения. | Радикал справа изолирован. | \(\sqrt{м}+1=\sqrt{м+9}\) |
| Шаг 2 : Возведите обе части уравнения в степень индекса. | Подравниваем обе стороны. 9{2}\) | |
Шаг 3 : Есть еще радикалы? Если да, повторите Шаг 1 и Шаг 2 еще раз. Если нет, решите новое уравнение. | В уравнении все еще есть радикал. Итак, мы должны повторить предыдущие шаги. Выделите корневой термин. Здесь мы можем легко выделить радикал, разделив обе части на \(2\). 9{2} \\ m &=16 \end{выровнено}\) | |
Шаг 4 : Проверьте ответ в исходном уравнении. | \(\begin{align}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{? }{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{выровнено}\ ) Решение: \(m=16\). |
Упражнение \(\PageIndex{17}\)
Решите: \(3-\sqrt{x}=\sqrt{x-3}\).
Упражнение \(\PageIndex{18}\)
Решите: \(\sqrt{x}+2=\sqrt{x+16}\).
Здесь мы суммируем шаги. Мы скорректировали наши предыдущие шаги, чтобы включить в уравнение более одного радикала. Теперь эта процедура будет работать для любых радикальных уравнений. 9{2}\).
Пример \(\PageIndex{10}\)
Решите: \(\sqrt{q-2}+3=\sqrt{4 q+1}\).
Решение :
| Радикал справа изолирован. Подровняйте обе стороны. | |
| Упрощение. | |
| В уравнении все еще есть радикал, поэтому мы должны повторить предыдущие шаги. Изолировать радикал. | |
| Квадрат с обеих сторон. Разделение обеих частей на \(6\) не помогло бы. Не забудьте возвести в квадрат как \(6\), так и \(\sqrt{q-2}\). | |
| Упростите, затем решите новое уравнение. | |
| Распределить. | |
| Это квадратное уравнение, поэтому с одной стороны получаем ноль. | |
| Фактор правой стороны. | |
Использовать свойство нулевого продукта. | |
| Чеки оставляются вам. | Решения: \(q=6\) и \(q=2\). |
Упражнение \(\PageIndex{19}\)
Решить: \(\sqrt{x-1}+2=\sqrt{2 x+6}\)
Упражнение \(\PageIndex{20}\)
Решить: \(\sqrt{x}+2=\sqrt{3 x+4}\)
Использование радикалов в приложениях
По мере прохождения курсов в колледже вы столкнетесь с формулами, содержащими радикалы, во многих дисциплинах. Мы немного изменим нашу стратегию решения задач для приложений геометрии, чтобы получить план решения приложений с формулами из любой дисциплины.
Используйте стратегию решения проблем для приложений с формулами
При необходимости нарисуйте рисунок и подпишите его с помощью данной информации.Одно из применений радикалов связано с влиянием гравитации на падающие предметы. Формула позволяет определить, через какое время упавший предмет ударится о землю.
Определение: Падающие предметы
На Земле, если объект падает с высоты \(h\) футов, время в секундах, необходимое для достижения земли, определяется по формуле
\(t=\frac{\sqrt{ h}}{4}\)
Например, если объект падает с высоты \(64\) футов, мы можем найти время, необходимое для достижения земли, подставив \(h=64\) в формула.
| Извлеките квадратный корень из \(64\). | |
| Упростите дробь. |
Предмету, упавшему с высоты \(64\) футов, потребуется \(2\) секунды, чтобы достичь земли.
Пример \(\PageIndex{11}\)
Марисса уронила солнцезащитные очки с моста \(400\) футов над рекой. Используйте формулу \(t=\frac{\sqrt{h}}{4}\), чтобы найти, сколько секунд потребовалось солнцезащитным очкам, чтобы достичь реки.
Решение :
| Шаг 1 : Прочтите задачу. | |
| Шаг 2 : Определите что мы ищем. | Время, за которое солнечные очки достигают реки. |
| Шаг 3 : Назовите то, что мы ищем. | Пусть (t=\) время. |
| Шаг 4 : Переведите в уравнение, написав соответствующую формулу. Замените предоставленную информацию. | |
| Шаг 5 : Решите уравнение . | |
| Шаг 6 : Проверьте ответ в задаче и убедитесь, что он имеет смысл. | |
| \(5\) секунд кажется разумным отрезком времени? | Да. |
| Шаг 7 : Ответьте на уравнение. | Солнцезащитные очки доберутся до реки через \(5\) секунд. |
6.11Упражнение \(\PageIndex{21}\)
Вертолет сбросил спасательный пакет с высоты \(1296\) футов. Используйте формулу \(t=\frac{\sqrt{h}}{4}\), чтобы найти, сколько секунд потребовалось пакету, чтобы достичь земли.
Упражнение \(\PageIndex{22}\)
Мойщик окон уронил швабру с платформы \(196\) футов над тротуаром. Используйте формулу \(t=\frac{\sqrt{h}}{4}\), чтобы найти, сколько секунд потребовалось, чтобы швабра достигла тротуара.
Полицейские, расследующие автомобильные аварии, измеряют длину следов заноса на тротуаре. Затем они используют квадратные корни, чтобы определить скорость , в милях в час, автомобиль ехал до того, как затормозил.
Определение: следы заноса и скорость автомобиля
Если длина следов заноса составляет \(d\) футов, то скорость \(s\) автомобиля до включения тормозов можно найти по формуле используя формулу
\(s=\sqrt{24 d}\)
Пример \(\PageIndex{12}\)
После автомобильной аварии следы заноса одного автомобиля измерялись \(190\) футов.
Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
Решение :
| Шаг 1 : Прочтите задачу. | |
| Шаг 2 : Определите , что мы ищем. | Скорость автомобиля. |
| Шаг 3 : Имя то, что мы ищем. | Пусть \(s=\) скорость. |
| Шаг 4 : Переведите в уравнение, написав соответствующую формулу. Замените предоставленную информацию. | |
| Шаг 5 : Решите уравнение . | |
Округлить до \(1\) десятичного знака. | |
| Скорость автомобиля до торможения составляла \(67,5\) миль в час. |
Упражнение \(\PageIndex{23}\)
Исследователь ДТП измерил следы заноса автомобиля. Длина следов заноса составляла \(76\) футов. Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
Упражнение \(\PageIndex{24}\)
Следы заноса автомобиля, попавшего в аварию, были \(122\) футов в длину. Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость транспортного средства до включения тормозов. Округлите ответ до десятых.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения радикальных уравнений.
9{2}}\конец{массив}\)
Глоссарий
10.7: Solve Radical Equations распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.