решение тригонометрических уравнений 10 класс
Содержание
|
|
Ι. Решение простейших тригонометрических уравнений | 2– 7 |
ΙΙ. Общие методы решения тригонометрических уравнений |
|
1. Метод разложения на множители | 8 – 10 |
2. Метод введения новой переменной | 10 – 14 |
3. Функционально-графические методы | 15 – 17 |
ΙΙΙ. Решение комбинированных уравнений | 18 – 23 |
ΙV. | 24 – 25 |
V. Тесты для самостоятельного решения | 26 – 27 |
Литература | 28 |
Ι. Решение простейших тригонометрических уравнений
Все тригонометрические уравнения сводятся к простейшим. Поэтому особое внимание следует уделять решению простейших уравнений. Начинать нужно с самых простых.
К простейшим тригонометрическим уравнениям относятся уравнения вида:
Для каждого из простейших тригонометрических уравнений определены формулы, справедливость которых обосновывается с помощью тригонометрического круга и с учетом периодичности тригонометрических функций.
sinx=а, |а|>1, решений нет; sinx=0, x= πn, nєZ sinx =–1, x= –+2πn, nєZ; sinx =1, x=+2πn, nєZ; sinx=а, |а|<1, x= arcsinа +2πn, nєZ; x= π–arcsinа +2πn, nєZ. В последнем случае для сокращения записи используют формулу: x=(–1)narcsinа + πn, nєZ. | cos x=а, |а|>1,решений нет; cos x=0, x= –+πn, nєZ; cos x=–1, x= π +2πn, nєZ; cos x=1, x=2πn, nєZ; cos x=а, |а|<1, x= ± arccosа +2πn, nєZ. |
Решения уравнения tg x=а и ctg x=а записываются существенно проще:
x= arctgа +πn, nєZ и, соответственно, x= arcсtg
Пример 1. Решить уравнение sinx = .
Решение: так как <1, значит x=(–1)narcsin + πn, nєZ.
Ответ: (–1)narcsin + πn, nєZ.
Пример 2. Решить уравнение cos x =.
Решение: так как >1, значит уравнение не имеет решения.
Ответ: нет решения.
Пример 3.
Решить
уравнение tg x+ = 0.
Решение:
tg x+ = 0
tg x = –
x = arctg (–) + πn, nєZ
x = – arctg + πn, nєZ
x = –+2πn, nєZ;
Ответ: –+2πn, nєZ.
Пример 4. Решить уравнение 2cos x = –.
Решение:
2cos x = –
cos x = –
x= ± arccos (–)+2πn, nєZ
x= ±( π – arccos )+2πn, nєZ
x= ±( π – )+2πn, nєZ
x = ± + 2πn, nєZ
Ответ: ± + 2πn, nєZ.
Для отработки общих формул решения простейших уравнений можно предложить для устного решения задания такого вида.
Образуют ли арифметическую прогрессию расположенные в порядке возрастания положительные корни уравнения : sinx =0; cosx = 0,5; tg x=1.
На начальном этапе, пока не отработаны навыки использования общих формул решения простейших уравнений желательно прописывать эти формулы, чтобы учащиеся быстрее их запомнили.
Далее нужно
переходить к решению более сложных уравнений, которые чаще всего встречаются в
вариантах ЕГЭ в разделе А.
Пример 5. Решить уравнение cos = .
Решение: cos =
Это уравнение сводится к простейшему cos t = заменой t =, которую можно не прописывать.
= ± arccos +2πn, nєZ
= ± +2πn, nєZ
х = ± + 10πn, nєZ
Ответ: ± + 10πn, nєZ.
Пример 6. Решить уравнение: sin (2x–) = .
Решение: sin (2x–) =
2x–= (–1)narcsin + πn, nєZ
2x– = (–1)n + πn, nєZ
2x– = ++ 2πn, nєZ
2x– = –+ (2m + 1)π,mєZ
2x = + 2πn, nєZ
2x =π + 2πm, mєZ
x = + πn, nєZ
x = + πm, mєZ
Ответ: + πn, + πm, n,mєZ.
Так же нужно обратить внимание учащихся на то, что довольно часто исходное уравнение приводится к простейшему лишь после различных тождественных преобразований и применения формул тригонометрии.
Пример 7. Решить уравнение 4 sin3x cos 3x =1.
Решение: 4 sin3x cos 3x =1
2(2sin3x cos 3x) =1
2sin6x =1
sin6x =
6x = (–1)n+ πn, nєZ
x = (–1)n+ n, nєZ
Ответ: (–1)n+ n, nєZ.
Часто предлагается решить тригонометрическое уравнение на некотором промежутке. Целесообразно начинать решать такие уравнения до вывода общих формул решения простейших тригонометрических уравнений.
Рассмотрим примеры.
Пример 8. Найдите корни уравнения 2cosx = –1, принадлежащие промежутку [0;2π].
Решение:
2cosx = –1
cosx = –
Выбор значений x , которые принадлежат указанному промежутку можно выполнить различными способами.
Наиболее рационально это делать с помощью единичной окружности.
x1 = ; x2 = .
Ответ: ;.
В тестах часто требуется не просто найти корни, принадлежащие данному промежутку, а вычислить их сумму или разность; определить наибольший или наименьший корень; указать количество корней.
Пример 9. Найдите
сумму корней уравнения (cos 2 x –1)(2 sin – 1)
= 0, принадлежащих промежутку [–; π ).
Решение: x1 = 0; x2 = , x1 + x2 =
Ответ: .
Решите самостоятельно.
1. Найдите сумму корней уравнения 2sinx = –1 на указанном промежутке
2. Найдите количество корней уравнения 4cos 22х = 1 на указанном промежутке
3. Найдите сумму наименьшего положительного и наименьшего отрицательного корней уравнения sinx cos + sin cos х = на указанном промежутке
Уже при решение простейших тригонометрических уравнений полезно предлагать нестандартные уравнения.
Пример 10. Решить уравнение cos x2 = 1.
Можно дать это уравнение для самостоятельного решения.
Найдутся ученики, которые решат его в одну строчку:
х2 = 2πk, kЄZ
х = , kЄZ.
Целесообразно продемонстрировать это решение на доске и предложить ученикам найти допущенные ошибки.
В случае затруднений, чтобы внести полную ясность, решить для начала уравнение
х2 = a.
Его решение имеет вид х = ± при а0.
Если а <0, то уравнение не имеет решений. Значит решением исходного уравнения является х = ±, kЄZ, k0.
Ответ: ±, kЄZ, k0.
Пример 11. Решить уравнение sinsinx = 1.
Решение: sinsinx = 1.
sinx = +2πn, nєZ
Выражение |+2πn | > 1 при любых значениях n , nєZ.
Поэтому исходное уравнение не имеет решений.
Ответ: нет решений.
ΙΙ. Общие методы решения тригонометрических уравнений
1. Метод разложения на множители.
Этот метод заключается в том , что исходное уравнение сводится к уравнению вида
f (x)g(x)h(x) = 0, которое можно заменить совокупностью уравнений, каждое из которых сводится к простейшему.
Решив уравнения совокупности нужно взять только те решения, которые принадлежат области определения исходного уравнения, а остальные корни отбросить.
Пример 1.
Решить
уравнение sin4x = 3 cos2х.
Решение:
sin4x = 3 cos2х.
2 sin2x cos2х = 3 cos2х
Получив такое уравнение, ученики достаточно часто делают ошибку, «сократив» левую и правую части уравнения на cos2х. Некоторые из них при этом оговаривают, что cos2х 0,но одной оговорки здесь, увы, недостаточно. Необходимо ещё рассмотреть случай, когда cos2х = 0, и проверить, не являются ли значения х, удовлетворяющие этому равенству, корнями исходного уравнения. Разумеется, лучше всего не делить левую и правую части уравнения на cos2х, а разложить на множители
(2 sin2x – 3) cos2х = 0.
Полученное уравнение равносиьно совокупности двух уравнений
х = , nЄZ.
Первое уравнение решения не имеет, так как функция синус не может принимать значений по модулю больших единицы. К сожалению, не все ученики это понимают, а из тех, кто понимает, не всякий вспоминает вовремя.
Ответ: , nЄZ.
Пример 2. Решить уравнение sin2x = sin4x
Решение: некоторые учащиеся, встретив такое уравнение, решительно записывают
2х = 4х или 2х = 4х + 2πn, nЄZ, что приводит к
потере решений исходного уравнения.
Решение исходного уравнения состоит в переходе к уравнению sin2x – sin4x = 0
и последующем применении формулы для преобразования разности тригонометрических функций в произведение
2cos = 0
cos3x (–sinx) = 0
Ответ:
Пример 3. (ЕГЭ 2009г. Вариант 1, С2.).
Найдите все значения , при каждом из которых выражения
принимают равные значения.
Решение:
Ответ:
Пример 4. (ЕГЭ 2009г. Вариант 2, B7.).
Найдите наименьший корень уравнения
Решение:
Ответ:
2. Метод замены переменной.
В школьном курсе в основном рассматриваются уравнения, которые после введения нового неизвестного t = f(x),где f(x) – одна из основных тригонометрических функций, превращаются в квадратные либо рациональные уравнения с неизвестным t.
Пример 5. Решить уравнение cos2 πx + 4sinπx + 4 =0
Решение: 1 – sin 2 πx + 4sinπx + 4 =0
– sin 2 πx + 4sinπx + 5 =0
Заменим sin πx = t , -1
–t 2 + 4t +5 = 0
t 2 – 4t – 5 = 0
t1 = –1, t2 = 5
t2 не удовлетворяет условию -1
sin πx = –1
πx = –
х = –
Ответ: –
Решение однородных
тригонометрических уравнений.
Уравнение вида аsinx +bcosx =0, где а и b –некоторые числа, называются однородными уравнениями первой степени относительно sinx и cosx.
Уравнение вида аsin 2 x +bcos 2 x + с =0, где а,b,с – некоторые числа, называются однородными уравнениями второй степени относительно sinx и cosx.
Пример 6. Решить уравнение sinx – cosх = 0.
Решение: легко убедиться, что cosx = 0 не является корнем исходного уравнения.
В самом деле, если cosx = 0, то, в силу исходного уравнения, и sinx = 0, что противоречит основному тригонометрическому тождеству. Этот факт позволяет разделить левую и правую части уравнения на cosx.
Получим уравнение tg x = 1, откуда х =
Ответ:
Пример 7. Решить уравнение sin 2 x – 3sinx cosх + 2cos 2 x = 0.
Решение: поскольку cosx = 0 не является корнем tg x данного уравнения,
разделим левую и
правую части уравнения на cos 2 x.
В результате приходим к квадратному уравнению относительно tg2 x – 3 tg x + 2 = 0,
решив которое, получим
Ответ:
Введение вспомогательного аргумента.
Уравнение вида аcosx + b sinx = с, где а, b, с –некоторые числа, причем
называют линейными тригонометрическими уравнениями.
Для решения таких уравнений используют введение вспомогательного аргумента.
Так как а 2 + b2 >0, то можно разделить обе части уравнения на , получим
Введём в рассмотрение угол такой, что
Угол , удовлетворяющий этим двум условиям, принято называть дополнительным (или вспомогательным) аргументом. Для любых значений а и b такой угол существует, так как
Вообще, полезно напомнить учащимся, что любые числа p и g такие, что
p2 + g2 = 1 можно рассматривать как косинус и синус некоторого угла.
Теперь исходное уравнение можно записывать в виде
coscosx + sinsinx =
cos (x – ) =
Аналогично можно вводить вспомогательный угол такой, что:
Тогда исходное уравнение можно привести к виду
sincosx + cossinx =
sin (x +) =
Полезно также
обратить внимание учащихся, что умение преобразовывать выражения вида а cosx + b sinx может
понадобиться не только при решении уравнений, но и для построения оценок,
нахождения наибольших значений и т.
д.
Пример 8. Решить уравнение 3 sinx – 4cosх = 5.
Решение. 3 sinx – 4cosх = 5
==5
, cosx = ,
cos(x + ) = –1
x + = π + 2πn, nЄZ
x = – + π + 2πn, nЄZ
x = –arcsin+ π + 2πn, nЄZ
Ответ: –arcsin+ π + 2πn, nЄZ.
Пример 9. Решить уравнение 2cosх = 1– 2cos 2х –sin2x.
Решение. Воспользуемся формулой 2cos 2х – 1 = cos 2x,
получим 2cosх = – cos2х –sin2x.
Применим к правой части процедуру введения вспомогательного аргумента.
=
2cosх = – 2(cos2х +sin2x)
2cosх = – 2 (сos cos2х + sinsin2x), где
2cosх = – 2(cos2х – )
cosх + cos (2х – ) = 0
Последнее уравнение легко решить, преобразовав сумму косинусов в произведение:
2coscos
cos
Необходимо
обратить внимание учащихся на то, что в тригонометрических системах и
совокупностях при записи имеет смысл употреблять разные буквы, обозначающие
целые числа.
Ответ: .
Универсальная тригонометрическая подстановка.
Универсальная тригонометрическая подстановка позволяет перейти от синуса и косинуса аргумента х к тангенсу половинного аргумента:
sin , cos
При таком переходе возможна потеря решений, следует помнить, что (в этих точках tg не существует). Поэтому всякий раз, когда приходится пользоваться универсальной подстановкой, значения х = π + 2πn, nЄZ необходимо проверять отдельно, подставляя в исходное уравнение.
Пример 10. Решить уравнение sinx + cosх = –1.
Решение: = –1, заменим tg , получим
2t +1 – t2 = –1– t2
2t = – 2
t = – 1
tg
Подставим теперь в исходное уравнение значение и убедимся, что они действительно являются его решениями.
Ответ:
Уравнение вида
Уравнение вида где — многочлен, удобно решать при помощи введения новой переменной
Тогда можно получить выражение для произведения из формулы
Пример 11.
Решить
уравнение
Решение: введем новую переменную
Тогда
Следовательно, и исходное уравнение принимает вид
Для определения переменной получаем два уравнения
Для решения таких уравнений используют введение вспомогательного аргумента.
Ответ:
После завершения изучения рассмотренных методов, при наличии времени, рекомендуем провести урок-практикум – «Урок решения одного уравнения»
3. Функционально-графические методы
1) Использование свойств ограниченности функций, метод оценок.
Часто приходится иметь дело с уравнениями, имеющими вид f(x) = g(x), где f и g – некоторые функции, составленные с помощью тригонометрических выражений, такие, что можно исследовать области значений Е(f) и Е(g) и доказать, что эти области либо не пересекаются, либо имеют небольшое число общих точек. В таких случаях решения уравнения f(x) = g(x) следует искать среди таких x , которые удовлетворяют более простым уравнениям f(x) = a, g(x) = a , где а – такое действительное число, что
Пример 12.
Решить
уравнение .
Решение:
Ответ: нет решения.
Пример13. Решить уравнение .
Решение:
Ответ: нет решения.
Пример14. Решить уравнение .
Решение:
Ответ: .
Пример15. Решить уравнение
Решение:
Ответ:
Пример16. Решить уравнение
Решение.
Заметим, что сумма в левой части полученного уравнения может принимать значение 2, только если одновременно, т.е. наше уравнение равносильно системе уравнений
И должно выполняться равенство Поскольку
Ответ:
2) Использование графиков.
Суть метода использования графиков для решения уравнения f(x) = g(x) проста: нужно построить графики функций y = f(x) и y = g(x) и найти все точки их пересечения, абсциссы которых и будут являться корнями нашего исходного уравнения.
Пример 17.
Сколько
корней имеет уравнение:
Решение: в данном примере для решения уравнений используются свойства графиков функций.
Ответ: 1 решение.
Ответ: 1 решение.
Ответ: 7 решений.
ΙΙΙ. Решение комбинированных уравнений
Пример1. Решите уравнение
Решение:
Ответ: .
Пример 2. Решите уравнение
Решение:
Ответ:
Пример 3. Решите уравнение
Решение:
Решим первое уравнение системы с использованием универсальной тригонометрической подстановки:
С учетом неравенств системы имеем:
Ответ:
Пример 4.
Решите
уравнение
Решение:
Ответ:
Пример 5.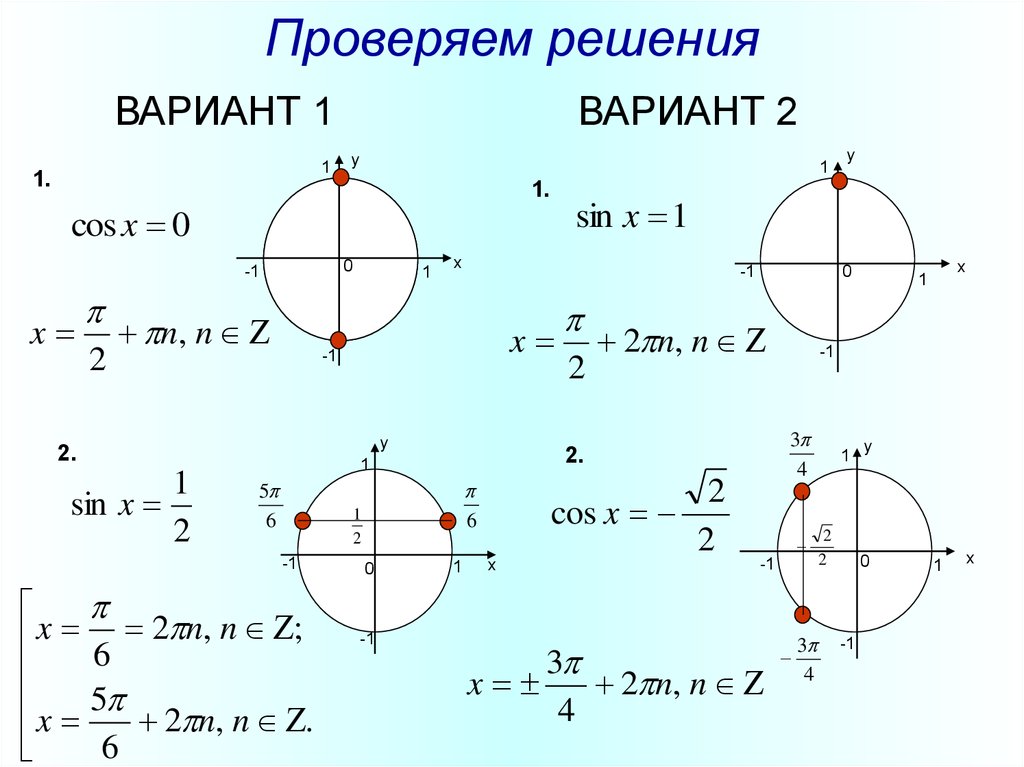
Решите
уравнение
Решение:
Ответ:
Пример 6. Решите уравнение
Решение:
Ответ:
Пример 7. Решите уравнение
Решение:
Ответ:
Пример 8. Решите уравнение
Решение: воспользуемся формулой понижения степени
Ответ:
Пример 9. Решите уравнение
Решение:
Решим полученное уравнение графически, для этого в одной системе координат построим графики функций
Ответ:
Пример 10. Решите уравнение
Решение: введем функцию тогда получим
Исследуем функцию на монотонность
Ответ:
Пример 11.
Решите
уравнение
Решение: данное уравнение равносильно системе
Ответ:
ΙV. Решение тригонометрических уравнений с параметром.
Пример1. Найти все значения параметра , при которых уравнение имеет решение.
Решение:
Пример 2. Найти все значения параметра , при которых уравнение имеет на отрезке ровно три корня.
Решение:
Пример 3. Решите уравнение.
Решение:
V. Тесты для самостоятельного решения
Данные тесты предназначены для проверки умений решения тригонометрических уравнений различными способами.
Вариант№1.
Вариант№2.
Вариант№3.
Вариант№4.
Литература
1. Алгебра и начала анализа: дидактические материалы для 10 класса / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.
2. Алгебра и начала анализа: дидактические материалы для 11 класса: базовый и профильные уровни / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.
3. Бурмистрова Н.В.,СтаростенковаН.Г.Математика.11класс. Подготовка к экзамену.
-Саратов: Лицей,2005.
4. Единый государственный экзамен: Математика: контрольные измерительные материалы: 2006-2007.-М.:Просвещение: СПб.: Просвещение,2007.
5. ЕГЭ-2009.Математика: Сдаём без проблем!/ О.А.Креславская, В.В.Крылов, В.И.Снегурова, В.Е.Ярмолюк.-М.:Эксмо.2008.
6. ЕГЭ. Репетитор. Математика.Эффективная методика./ Л.Д.Лаппо, А.В.Морозов, М.А.Попов.-М.:Издательство «Экзамен»,2007.
7.
Панчишкин А.А.. Шавгулидзе Е.Т. Тригонометрические
функции в задачах — М.
:Наука. Главная редакция физико – математической
литературы,1986.
8. Самое полное издание типовых вариантов реальных заданий ЕГЭ:2009:Математика /
авт.-сост. В.И.Ишина, В.В.Кочагин, Л.О.Денишева и др.-М.:АСТ: Астрель,2009.
9. Сборник заданий для подготовки и проведения письменного экзамена по математике
(курс А) и алгебре и началам анализа (курс В) за курс средней школы.11 класс/
Г.В,Дорофеев, Г.К.Муравин ,Е.А.Седова.-10-е изд.,стереотип.-М.:Дрофа,2007.
10. Тематические тесты. Математика. ЕГЭ-2009.Часть2.10-11 классы/ Под редакцией Ф.Ф.Лысенко. — Ростов-на-Дону:Легион,2008.
11. Макеева А.В.Карточки по тригонометрии.10-11 класс: Дидактический материал
для учителей. — Саратов:Лицей.2002.
12. Макарова Л.В. Уроки-практикумы в системе работы учителя. //Математика в школе,1998,№3.
13. Математика: интенсивный курс подготовки к экзамену.-4-е изд.испр. и доп.-М.:Рольф:Айрис-пресс,1999.
14. Математика: Тематическое планирование уроков подготовки к экзамену /
А.
В.Белошинстая.-М.:Издательство «Экзамен»,2007.
15. Шаммин В.М. Тематические тесты для подготовки к ЕГЭ по математике. Изд.3-е.-
Ростов н/Д: Феникс,2004.
Основные методы решения тригонометрических уравнений
iskakov20151 iskakov20151
- Математика
- 10 — 11 классы
ответ дан
Aslan2904 Aslan2904
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называетсятригонометрическим. Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида ( см. выше ) и решение полученного простейшего тригонометрического уравнения.
Существует семь основных методов решения тригонометрических уравнений. 1. Алгебраический метод. Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ). 2. Разложение на множители. Этот метод рассмотрим на примерах. П р и м е р 1. Решить уравнение: sin x + cos x = 1 . Р е ш е н и е . Перенесём все члены уравнения влево: sin x + cos x – 1 = 0 , преобразуем и разложим на множители выражение в левой части уравнения: П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1. Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 , sin x · cos x – sin 2 x = 0 , sin x · ( cos x – sin x ) = 0 , П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1.
Р е ш е н и е . cos 2x + cos 6x = 1 + cos 8x , 2 cos 4x cos 2x = 2 cos ² 4x , cos 4x · ( cos 2x – cos 4x ) = 0 , cos 4x · 2 sin 3x · sin x = 0 , 1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 , 3.Приведение к однородному уравнению. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо: а) перенести все его члены в левую часть; б) вынести все общие множители за скобки; в) приравнять все множители и скобки нулю; г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos ( или sin ) в старшей степени; д) решить полученное алгебраическое уравнение относительно tan .
П р и м е р . Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2. Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x , sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 , tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 , корни этого уравнения: y1 = -1, y2 = -3, отсюда 1) tan x = –1, 2) tan x = –3, 4. Переход к половинному углу. Рассмотрим этот метод на примере: П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7. Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) = = 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) , 2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 , tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 , .
. . . . . . . . .5. Введение вспомогательного угла. Рассмотрим уравнение вида: a sin x + b cos x = c , где a, b, c – коэффициенты; x – неизвестное.Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемыйвспомогательный угол ), и наше уравнение принимает вид: 6. Преобразование произведения в сумму. Здесь используются соответствующие формулы. П р и м е р . Решить уравнение: 2 sin 2x · sin 6x = cos 4x. Р е ш е н и е . Преобразуем левую часть в сумму: cos 4x – cos 8x = cos 4x , cos 8x = 0 , 8x = p / 2 + pk , x = p / 16 + pk / 8 . 7. Универсальная подстановка.
Рассмотрим этот метод на примере. П р и м е р . Решить уравнение: 3 sin x – 4 cos x = 3 .
Новые вопросы в Математика
Будь ласка памажіть срочна нада даю 25 балав! Скилькі буде 19-9+(8+3)=? пажалуств памажіть кантрольна работа!
Срочно помогите 7×2,(3)
УСЛОВИЕ ЗАДАЧИРешить в натуральных числах уравнение:a! + 5a + 13 = b²
ШВИДКО ДАМ 100 БАЛІВ
допоможіть дам 50 балів
Предыдущий
Следующий
Решение тригонометрических уравнений | Предварительное исчисление
Результаты обучения
- Решение уравнений, включающих одну тригонометрическую функцию.
- Решите тригонометрические уравнения с помощью калькулятора.
- Решите тригонометрические уравнения с факторингом.
- Решите тригонометрические уравнения, используя фундаментальные тождества.
- Решите тригонометрические уравнения с несколькими углами.
- Решите задачи на прямоугольный треугольник.
Решение линейных тригонометрических уравнений с помощью синуса и косинуса
Тригонометрические уравнения — это, как следует из названия, уравнения, включающие тригонометрические функции. Во многом подобно решению полиномиальных уравнений или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Часто мы будем решать тригонометрическое уравнение на заданном интервале. Однако столь же часто нас будут просить найти все возможные решения, а поскольку тригонометрические функции являются периодическими, решения повторяются в каждом периоде. Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым.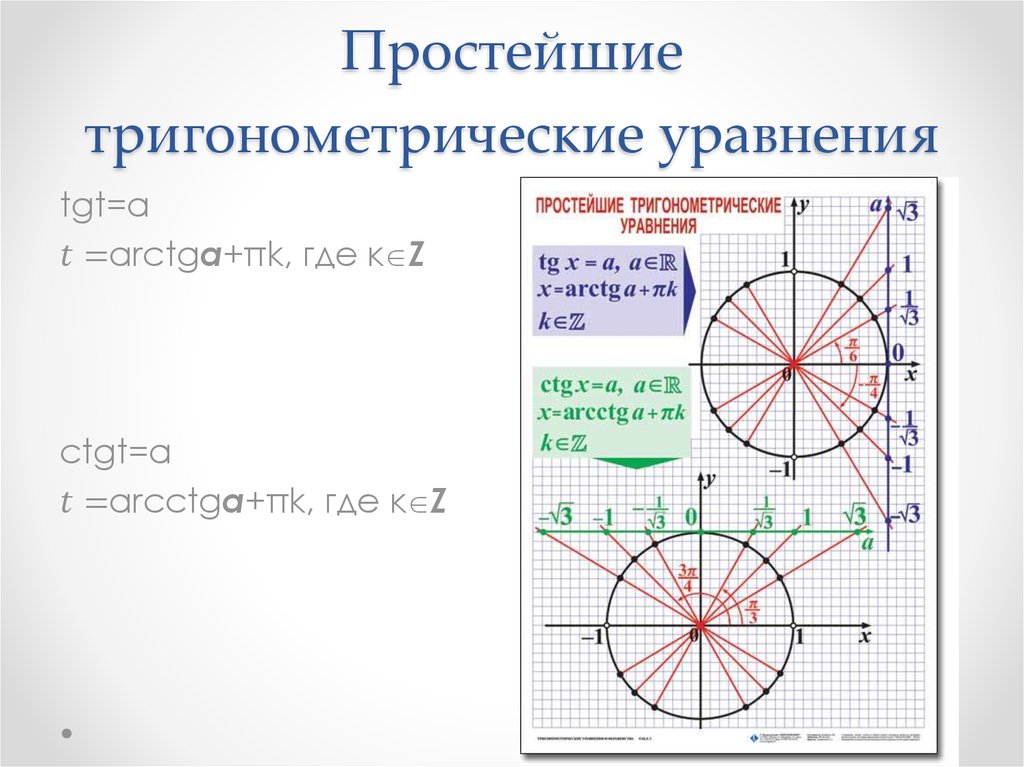
период функции синуса и функции косинуса равен [латекс]2\пи [/латекс]. Другими словами, через каждые [latex]2\pi [/latex] единицы значения y- повторяются. Если нам нужно найти все возможные решения, то мы должны добавить к исходному решению [латекс]2\pi k[/латекс], где [латекс]к[/латекс] — целое число. Вспомните правило, которое дает формат для определения всех возможных решений для функции, где период равен [латекс]2\пи :[/латекс]
[латекс]\sin \theta =\sin \left(\theta \pm 2k \пи \справа)[/латекс]
Аналогичные правила указывают все возможные решения для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Читаем уравнение слева направо, по горизонтали, как предложение. Мы ищем известные шаблоны, факторизуем, находим общие знаменатели и заменяем определенные выражения переменной, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1. Решение линейного тригонометрического уравнения с функцией косинуса
Найдите все возможные точные решения уравнения [latex]\cos \theta =\frac{1}{2}[/latex].
Показать решение
Пример 2. Решение линейного уравнения с функцией синуса
Найдите все возможные точные решения уравнения [latex]\sin t=\frac{1}{2}[/latex].
Показать решение
Как: Решите тригонометрическое уравнение с помощью алгебры.
- Ищите шаблон, который предполагает алгебраическое свойство, такое как разность квадратов или факторинговая возможность.
- Замените тригонометрическое выражение одной переменной, например [latex]x[/latex] или [latex]u[/latex].
- Решите уравнение так же, как решали бы алгебраическое уравнение.
- Замените тригонометрическое выражение на переменную в результирующих выражениях.
- Найдите угол.
Пример 3.
Решение тригонометрического уравнения в линейной формеТочное решение уравнения: [латекс]2\cos \theta -3=-5,0\le \theta <2\pi [/latex].
Показать решение
Попробуйте
Решите точно следующее линейное уравнение на интервале [латекс]\влево[0,2\пи \вправо):2\sin x+1=0[/латекс].
Показать решение
Попробуйте
Решение тригонометрических уравнений с помощью калькулятора
Не все функции можно решить точно, используя только единичную окружность. Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам нужно будет использовать калькулятор. Убедитесь, что он установлен в правильном режиме, либо в градусах, либо в радианах, в зависимости от критериев данной задачи.
Пример 4. Использование калькулятора для решения тригонометрического уравнения, содержащего синус радианы.
Показать решение
Пример 5.
Использование калькулятора для решения тригонометрического уравнения с секущейИспользуйте калькулятор для решения уравнения [латекс]\сек \тета =-4[/латекс], давая ответ в радианах.
Показать решение
Попробуйте
Решите [латекс]\cos\theta =-0,2[/латекс].
Показать решение
Попробуйте
Решение уравнений с одной тригонометрической функцией
Когда нам даются уравнения, включающие только одну из шести тригонометрических функций, их решения включают использование алгебраических методов и единичной окружности. Нам нужно сделать несколько соображений, когда уравнение включает тригонометрические функции, отличные от синуса и косинуса. Проблемы, связанные с обратными величинами основных тригонометрических функций, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса.
Во-первых, как мы знаем, период касательной равен [латекс]\пи [/латекс], а не [латекс]2\пи [/латекс]. Кроме того, областью определения тангенса являются все действительные числа, за исключением нечетных целых чисел, кратных [латекс]\фракция{\пи} {2}[/латекс], если, конечно, проблема не накладывает свои собственные ограничения на область определения. 9{2}\theta -1=0,0\le \theta <2\pi [/latex].
Показать решение
Пример 7. Решение тригонометрического уравнения с косекансом
Точно решить следующее уравнение: [latex]\csc \theta =-2,0\le \theta <4\pi [/latex].
Показать решение
Пример 8. Решение уравнения с касательной
Точно решить уравнение: [латекс]\танг\влево(\тета -\фракция{\пи }{2}\вправо)=1,0\le \theta <2 \пи[/латекс].
Показать решение
Попробуйте
Найдите все решения для [латекс]\tan x=\sqrt{3}[/латекс].
Показать решение
Попробуйте
Пример 9.
Найдите все решения уравнения, содержащего тангенсНайдите все точные решения уравнения [латекс]2\left(\tan x+3\right)=5+\tan x,0\ le x<2\pi [/латекс].
Показать решение
Решение тригонометрических уравнений в квадратной форме
Решение квадратного уравнения может быть более сложным, но опять же, мы можем использовать алгебру, как и для любого квадратного уравнения. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция является квадратом? Если представлена только одна функция и один из ее членов возведен в квадрат, подумайте о стандартной форме квадратного числа. Замените тригонометрическую функцию переменной, такой как [latex]x[/latex] или [latex]u[/latex]. Если подстановка делает уравнение похожим на квадратное уравнение, то мы можем использовать те же методы решения квадратного уравнения для решения тригонометрических уравнений.
9{2}\тета +\cos \тета =0[/латекс].
Показать решение
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, поскольку они упрощают решение уравнений. Помните, что методы, которые мы используем для решения, отличаются от методов проверки личности. Здесь применяются основные правила алгебры, в отличие от переписывания одной стороны тождества, чтобы она соответствовала другой стороне. В следующем примере мы используем два тождества для упрощения уравнения.
Пример 14. Использование тождеств для решения уравнения
Использование тождеств для точного решения тригонометрического уравнения на интервале [latex]0\le x<2\pi [/latex].
[латекс]\cos x\cos \left(2x\right)+\sin x\sin \left(2x\right)=\frac{\sqrt{3}}{2}[/latex]
Показать Решение
Пример 15.
Решение уравнения с использованием формулы двойного углаТочное решение уравнения с использованием формулы двойного угла: [латекс]\cos \left(2\theta \right)=\cos \theta [/latex] . 9{2}\theta ,0\le \theta <2\pi [/latex].
Показать решение
Попробуйте
Решение тригонометрических уравнений с кратными углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратные углы, например [латекс]\sin \left(2x\right)[/latex] или [латекс]\cos\left(3x\right)[/латекс]. Столкнувшись с этими уравнениями, вспомните, что [latex]y=\sin \left(2x\right)[/latex] — это горизонтальное сжатие с коэффициентом 2 функции [latex]y=\sin x[/ латекс]. На интервале [latex]2\pi [/latex] мы можем изобразить два периода [latex]y=\sin \left(2x\right)[/latex], а не один цикл [latex]y =\грех х[/латекс]. Это сжатие графика приводит нас к мысли, что 9 может быть в два раза больше.0023 x — перехваты или решения для [латекс]\sin \left(2x\right)=0[/латекс] по сравнению с [латекс]\sin x=0[/латекс].
Эта информация поможет нам решить уравнение.
Пример 17. Решение тригонометрического уравнения с несколькими углами
Решите точно: 2\пи \справа)[/латекс].
Показать решение
Решение задач с прямоугольными треугольниками
Теперь мы можем использовать все изученные нами методы для решения задач, включающих применение свойств прямоугольных треугольников и
{2}[/latex] и смоделируйте уравнение, соответствующее ситуации.
Пример 18. Использование теоремы Пифагора для моделирования уравнения
Используйте теорему Пифагора и свойства прямоугольных треугольников для моделирования уравнения, соответствующего задаче.
Необходимо заменить один из тросов, которыми колесо обозрения London Eye крепится к земле. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле — в 23 метрах от основания колеса обозрения. Приблизительно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)?
Рисунок 4
Показать решение
Пример 19: Использование теоремы Пифагора для моделирования абстрактной задачи
Правила техники безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы.
Найдите угол, под которым лестница любой длины образует землю, и высоту, на которой лестница касается стены.
Показать решение
- При решении линейных тригонометрических уравнений мы можем использовать алгебраические методы точно так же, как при решении алгебраических уравнений. Ищите шаблоны, такие как разность квадратов, квадратичная форма или выражение, которое хорошо поддается замене.
- Уравнения, содержащие одну тригонометрическую функцию, можно решить или проверить с помощью единичной окружности.
- Мы также можем решать тригонометрические уравнения с помощью графического калькулятора.
- Многие уравнения имеют квадратную форму. Мы можем использовать подстановку, чтобы сделать уравнение более простым, а затем использовать те же методы, которые мы используем для решения алгебраического квадратного уравнения: разложение на множители, формулу квадратного уравнения и т. д.
- Мы также можем использовать тождества для решения тригонометрического уравнения.
- Мы можем использовать подстановку для решения тригонометрического уравнения с несколькими углами, которое представляет собой сжатие стандартной тригонометрической функции. Нам нужно будет принять во внимание сжатие и убедиться, что мы нашли все решения на заданном интервале.
- Реальные сценарии можно моделировать и решать с помощью теоремы Пифагора и тригонометрических функций.
Тригонометрические уравнения: решение общих уравнений
Тождества и условные уравнения
Тригонометрические уравнения можно разбить на две категории: тождества и тождества. условные уравнения. Тождества верны для любого угла, тогда как условные уравнения верны только для определенных углов. Тождества могут быть протестировано, проверено и создано с использованием знания восьми фундаментальных тождества. Мы уже обсуждали эти процессы в «Тригонометрических тождествах». . Следующие разделы посвящены объясняя, как решать условные уравнения.
Условные уравнения
При решении условного уравнения действует общее правило: если имеется одно
решение, то существует бесконечное множество решений.
Эта странная правда
следует из того факта, что тригонометрические функции являются периодическими, повторяющимися
каждые 360 градусов или 2 Π радиан. Например, значения
тригонометрические функции на 10 градусов такие же, как и на 370 градусов
и 730 градусов. Форма любого ответа на условное уравнение: θ +2 nΠ , где θ — одно решение уравнения, а n — целое число.
более короткий и распространенный способ выразить решение условного уравнения:
чтобы включить все решения уравнения, которые попадают в границы
[0, 2 Π ), и опустить часть решения «+2 nΠ ». так как предполагается
как часть решения любого тригонометрического уравнения. Потому что множество
значения от 0 до 2 Π содержит домен для всех шести тригонометрических
функций, если нет решения уравнения между этими границами, то нет
решение существует.
Решения тригонометрических уравнений не следуют стандартной процедуре, но есть
есть ряд методов, которые могут помочь в поиске решения.
Эти
методы в основном те же, что и при решении алгебраических задач.
уравнениями, только теперь мы манипулируем тригонометрическими
функции: мы можем разложить выражение, чтобы получить другое, более понятное
выражения, мы можем умножать или делить на скаляр, мы можем возводить в квадрат или
извлечь квадратный корень из обеих частей уравнения и т. д. Кроме того, с помощью восьми
фундаментальные тождества, мы можем
заменить одни функции другими или разбить одну функцию на две
различные, такие как выражение тангенса с помощью синуса и косинуса. В проблемах
ниже мы увидим, насколько полезными могут быть некоторые из этих методов.
проблема1
| 2 cos( x ) — 1 = 0 |
| 2 cos( x ) = 1 |
| потому что ( х ) = |
| х = , |
В этой задаче мы нашли два решения в диапазоне [0, 2 Π ) : x = и x = .
Добавляя 2 nΠ к любому из этих
решений, где n — целое число, у нас может быть бесконечное количество решений.
проблема2
| sin( x ) = 2 cos 2 ( x ) — 1 |
| sin( x ) = 2(1 — sin 2 ( x )) — 1 |
| sin( x ) = 1 — 2 sin 2 ( x ) |
| 2 sin 2 ( x ) + sin( x ) — 1 = 0 |
| (sin( x ) + 1)(2 sin( x ) — 1) = 0 |
На данный момент, после факторизации, у нас есть два уравнения, с которыми нам нужно иметь дело.
отдельно. Сначала решим (sin( х ) + 1) = 0, и тогда решим
(2 грех( х ) — 1) = 0
проблема2а
| sin( x ) + 1 = 0 |
| sin( x ) = — 1 |
| х = |
| 2 sin( x ) — 1 = 0 |
| sin( x ) = |
| х = , |
Таким образом, для задачи у нас есть три решения: x = ,.