Признаки ⚠️ параллелограмма, свойства параллелограмма: определение с доказательством
Содержание:
- Свойства параллелограмма
- Признаки параллелограмма
Содержание
- Свойства параллелограмма
- Признаки параллелограмма
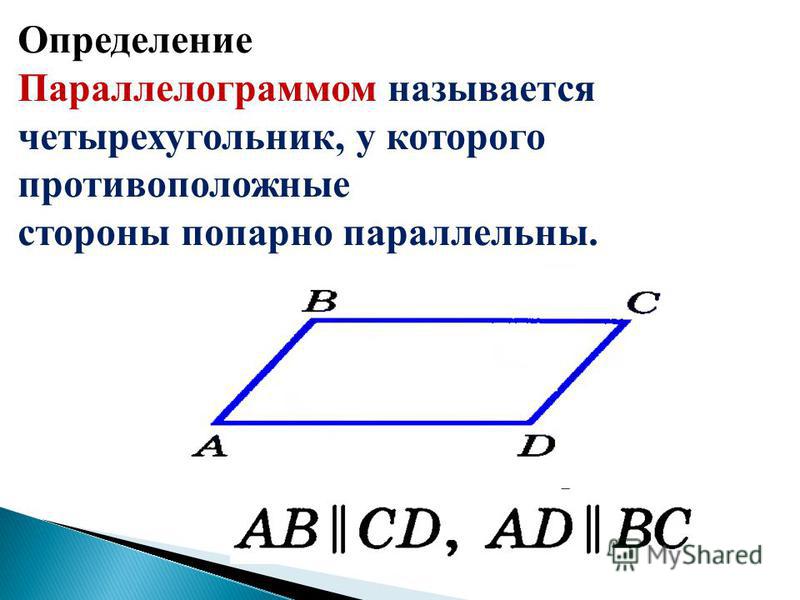
Определение
Параллелограмм в геометрии — это геометрическая фигура (прямоугольник), у которой противоположные стороны лежат на параллельных прямых.
Свойства параллелограмма
- В данной фигуре противоположные стороны и противоположные углы равны: AB=CD, BC=CD, BC=AD, ∠ABC=∠ADC, ∠BAD=∠BCD.
- Прилежащие к любой стороне углы в сумме дают 180º.
- Его диагонали делятся пополам точкой пересечения: AO=OC, OD=OB.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC2+BD2=2AB2+2BC2.
- Его диагонали делят его на два равных треугольника.
Признаки параллелограмма
Сформулируем основные ПП и обоснуем их.
Теорема
Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник будет считаться параллелограммом.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.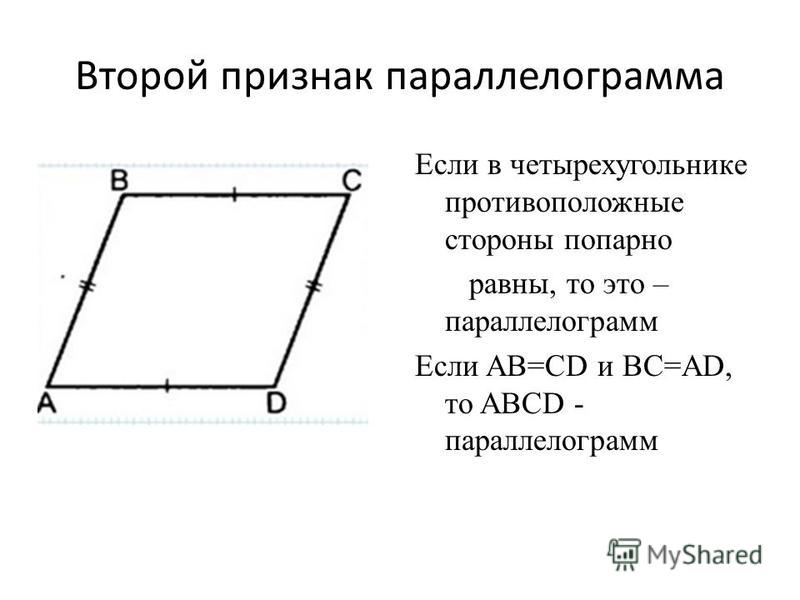
Доказательство
Рассмотрим четырехугольник MNOP.
MN и OP — параллельные стороны. Кроме того, OP=MN. NP — диагональ, которая делит рассматриваемую фигуру на два одинаковых треугольника: MNP и ONP. Эти треугольники приравниваются по двум сторонам и углу между ними (так как есть общая сторона NP, MN=OP изначально, а ∠1=∠2, потому что это накрест лежащие углы при секущей NP).
Из этого следует, что ∠3=∠4. Они же являются накрест лежащими при пересечении NO и MP секущей NP. Соответственно, NO и MP параллельны друг другу.
Получаем, что в четырехугольнике MNOP противоположные стороны лежат на параллельных прямых. Тогда данная фигура есть параллелограмм.
Теорема
Если в четырехугольнике попарно равны противоположные стороны, то данный четырехугольник будет считаться параллелограммом.
Доказательство
Доказажем эту теорему. Возьмем четырехугольник KLMN.
LN — диагональ. Она делит данную геометрическую фигуру на два идентичных треугольника: KLN и MLN.
Она делит данную геометрическую фигуру на два идентичных треугольника: KLN и MLN.
Данные фигуры равны между собой по трем сторонам (так как есть общая сторона LN, а KL=MN и LM=KN изначально).
Из этого делаем вывод, что ∠1=∠2.
Из этого следует, что KL параллельна MN.
А так как KL=MN и KL параллельна MN, то по первому признаку параллелограмма KLMN будет считаться параллелограммом.
Теорема
Если в четырехугольнике пересекаются диагонали и точкой пересечения делятся пополам, то этот четырехугольник будет параллелограммом.
Доказательство
Возьмем четырехугольник MNOP. Проведем MO и NP — две диагонали, пересекающиеся в точке A и делящиеся ей пополам.
ΔMAN и ΔOAP равны по первому признаку равенства (так как MA=AO, NA=AP изначально, ∠MAN=∠OAP, потому что это вертикальные углы).
Следовательно, MN=OP и ∠1=∠2. Из данного выражения получаем, что MN параллельна OP.
Тогда имеем, что в четырехугольнике MNOP стороны MN и OP равны и параллельны. Делаем вывод, что по первому признаку MNOP будет считаться параллелограммом.
Делаем вывод, что по первому признаку MNOP будет считаться параллелограммом.
Насколько полезной была для вас статья?
Рейтинг: 3.33 (Голосов: 3)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Методическая разработка интегрированного урока геометрия+информатика по теме «Параллелограмм и его свойства»
Цель: открытие учащимися свойств параллелограмма в ходе эксперимента при работе в виртуальной среде «Живая математика»; применение свойств параллелограмма в ходе решения задач.
Оборудование:
- компьютер учителя;
- нетбуки для учащихся;
- мультимедийный проектор, экран;
- документ-камера,
- тетради на печатной основе по геометрии для 8 класса (у каждого учащегося).
Структура урока:
- Организационный момент.
- Постановка цели урока.

- Актуализация знаний учащихся в ходе проверки домашней работы.
- Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно).
- Изучение нового материала, экспериментальная работа.
- Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.
- Постановка домашнего задания.
- Подведение итогов урока.
Ход урока
1. Организационный момент
Проверяется подготовленность классного помещения и готовность учащихся к уроку.
2. Постановка целей урока
Данный урок является уроком изучения нового материала по теме «Параллелограмм и его свойства». На уроке в ходе исследовательской работы в виртуальной среде «Живая математика» учащиеся экспериментально выводят свойства параллелограмма. А также приобретают практические навыки применения знаний по теме в стандартных условиях в ходе решения задач в рабочих тетрадях на печатной основе.
3. Актуализация знаний учащихся в ходе проверки домашней работы
Решение задач домашней работы проверяется с помощью документ-камеры.
4. Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно)
Учащиеся решают устно задачи на готовых чертежах (чертежи заранее заготовлены на доске).
Работа проводится с целью подготовки к изучению нового материала. Учащимся дается 1-2 минуты на обдумывание задачи, а затем заслушиваются различные варианты решений, обсуждается, какое из решений наиболее верное, рациональное.
Задачи
- Дано: АВ || CD, BC || AD (рисунок 1)
Доказать: ВС = АD, - Дано АВ || CD, AB = CD (рисунок 2)
Доказать: О – середина AC и BD.
5. Изучение нового материала, экспериментальная работа
Учащиеся работают с нетбуками в виртуальной среде «Живая математика».
- Вводится понятие параллелограмма.

- Исследовательская работа в виртуальной среде «Живая математика», в ходе которой учащиеся экспериментально выводят свойства параллелограмма. Они производят измерения отрезков и углов с помощью инструментария программы «Живая математика». Учащиеся сопровождают решение каждой задачи анализом того, насколько формулируемые ими положения выдерживают вариации исходных элементов чертежей, полученных из исходных, с помощью команды Анимация.
- Первый этап: учащиеся измеряют стороны фигуры с помощью выбора вкладки Измерения горизонтального меню.
- Второй этап: воспользовавшись командой Анимация (меню Вид) учащиеся наблюдают, анализируют и делают выводы, каким образом меняются измеренные ими величины. Учитель контролирует правильность умозаключений и формулировок свойств параллелограмма, предложенных учащимися.
- Далее учащиеся работают в виртуальной среде «Живая математика», следуя четко инструкции, записанной справа на каждом слайде презентации в программе под руководством учителя (выполняя первый и второй этапы).
 Смотри Приложение 1.
Смотри Приложение 1.
6. Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.
Задачи № 8, 9, 10 учащиеся решают самостоятельно, затем один из учащихся читает свое решение, остальные проверяют свое решение, исправляют ошибки отвечающего.
Задача № 8
В параллелограмме ABCD найдите: а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64 см; б) углы, если
Решение.
а) По свойству параллелограмма АВ = CD, ВС = АD и . По условию РABCD = 64 см, следовательно, 2 (АВ + ВС) = 64 см, откуда АВ + ВС = 32 см, но ВС на 8 см больше АВ, поэтому АВ + АВ + 8 см = 32 см, откуда АВ = 12 см, ВС = 12 см + 8 см = 20 см.
б) По условию , а так как , то
Задача № 9
В параллелограмме АВСD диагональ АС, равная 24 см, образует со стороной АD угол в 30о, о – точка пересечения диагоналей АС и ВD, .
Решение.
Диагонали параллелограмма точкой пересечения делятся пополам, поэтому АО = ОС = 12 см. Треугольник AOE – прямоугольный с гипотенузой АО и острым углом А, равным 30°. Поэтому катет ОЕ, лежащий против угла в 30о, равен ½ АО, т.е. ОЕ = ½ * 12 см = 6 см.
Ответ: 6 см.
Задача №10.
Биссектриса угла АВ параллелограмма АВСD пересекает сторону ВС в точке Р, причем ВР = РС. Найдите стороны параллелограмма, если его периметр равен 54 см.
Решение.
- , так как луч АР – биссектриса угла А, , так как эти углы накрест лежащие при пересечении параллельных прямых AD и ВС секущей АР. Следовательно, .
- Треугольник АВР – равнобедренный, так как его углы 1 и 3 равны, поэтому АВ = ВР.
- По условию ВР = РС, следовательно, ВС = 2 * ВР = 2 * АВ.

Итак, Р ABCD = 2(АВ + 2 * АВ) = 6 * АВ.
Так как периметр параллелограмма равен 54 см, то 6 * АВ = 54 см, откуда АВ = 9 см и ВС = 18 см.
Ответ: АВ = DC = 9 см.
ВС = AD = 18 см.
7. Постановка домашнего задания
Домашнее задание находится на столах учащихся на листах с напечатанными на них готовыми чертежами (смотри Приложение 2).
8. Подведение итогов урока
Учитель: «Итак, изучением какой темы мы с вами занимались на сегодняшнем уроке? А чем конкретно мы занимались, и что нам дал этот урок?»
Сообщаются оценки учащимся, отвечавшим на уроке.
1. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия 7-9: учебник для общеобразоват. учреждений.- М.: Просвещение, 2014.
2. Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс. – М.: ВАКО, 2014.
3. Атанасян Л.С., Бутузов В.Ф.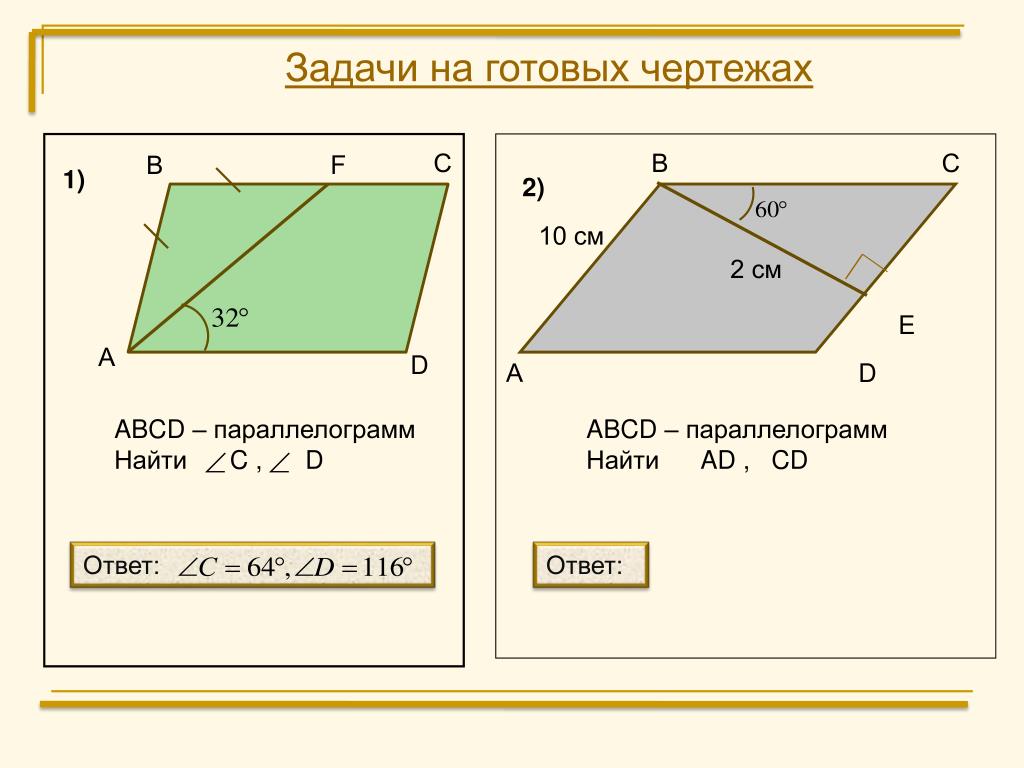 и др. Геометрия. Рабочая тетрадь для 8 класса общеобразовательных учреждений. – М.: Просвещение, 2014.
и др. Геометрия. Рабочая тетрадь для 8 класса общеобразовательных учреждений. – М.: Просвещение, 2014.
4. Учебно-методический комплект «Живая математика». — М.: KEY CURRICULUM PRESS. Научный руководитель проекта Г.Б. Шабат.
5. Рабинович Е.М. Задачи и упражнения на готовых чертежах 7-9 класс. – М.: Илекса.
Рисунок— Как нарисовать параллелограмм в виде фигуры в iOS?
Я должен получить следующий результат:
Как видите, он содержит список параллелограммов (не прямоугольных) с меткой внутри него. Кроме того, он может быть динамическим, что означает, что я могу использовать stackview. Прежде всего, нарисуем наш параллелограмм вида view:
class ParallelogramView: UIView {
переопределить инициализацию (кадр: CGRect) {
super.init(кадр: кадр)
фоновый цвет = .clear
}
переопределить функцию рисования (_ rect: CGRect) {
супер.рисовать(прямо)
пусть путь = UIBezierPath()
/// начнем с этой точки
path.move (к: CGPoint (x: 8, y: 0))
/// рисуем горизонтальную верхнюю линию, пока не сможем
path. addLine (к: CGPoint (x: rect.maxX, y: 0))
/// рисуем вниз, но немного влево
path.addLine(к: CGPoint(x: rect.maxX - 16, y: rect.maxY))
/// рисуем справа налево
path.addLine (к: CGPoint (x: 0, y: rect.maxY))
/// соединяем все
путь.закрыть()
/// просто для пробы заливки каким-нибудь цветом. Я не знаю, как это изменить позже :(
UIColor.red.setFill()
путь.заполнить()
}
}
addLine (к: CGPoint (x: rect.maxX, y: 0))
/// рисуем вниз, но немного влево
path.addLine(к: CGPoint(x: rect.maxX - 16, y: rect.maxY))
/// рисуем справа налево
path.addLine (к: CGPoint (x: 0, y: rect.maxY))
/// соединяем все
путь.закрыть()
/// просто для пробы заливки каким-нибудь цветом. Я не знаю, как это изменить позже :(
UIColor.red.setFill()
путь.заполнить()
}
}
Весь код закомментирован. После этого давайте определим LabelView , который содержит наш параллелограмм с меткой внутри него.
класс LabelView: UIView {
/// вывод текста
ленивая метка переменной: UILabel = {
пусть метка = UILabel()
метка.numberOfLines = 0
label.translatesAutoresizingMaskIntoConstraints = false
ярлык возврата
}()
/// наш параллелограммView
ленивый var plView: ParallelogramView = {
пусть trView = ParallelogramView()
trView.translatesAutoresizingMaskIntoConstraints = false
вернуть trView
}()
переопределить инициализацию (кадр: CGRect) {
super. init(кадр: кадр)
/// добавление метки к параллелограмму
plView.addSubview (метка)
addSubview (plView)
NSLayoutConstraint.активировать([
plView.leadingAnchor.constraint(equalTo: leadingAnchor),
plView.trailingAnchor.constraint(equalTo: trailingAnchor),
plView.bottomAnchor.constraint(equalTo: bottomAnchor),
plView.topAnchor.constraint(equalTo: topAnchor),
label.leadingAnchor.constraint (equalTo: plView.leadingAnchor, константа: 16),
label.trailingAnchor.constraint(equalTo: plView.trailingAnchor, константа: -16),
label.bottomAnchor.constraint(equalTo: plView.bottomAnchor),
label.topAnchor.constraint(equalTo: plView.topAnchor)
])
}
init(кадр: кадр)
/// добавление метки к параллелограмму
plView.addSubview (метка)
addSubview (plView)
NSLayoutConstraint.активировать([
plView.leadingAnchor.constraint(equalTo: leadingAnchor),
plView.trailingAnchor.constraint(equalTo: trailingAnchor),
plView.bottomAnchor.constraint(equalTo: bottomAnchor),
plView.topAnchor.constraint(equalTo: topAnchor),
label.leadingAnchor.constraint (equalTo: plView.leadingAnchor, константа: 16),
label.trailingAnchor.constraint(equalTo: plView.trailingAnchor, константа: -16),
label.bottomAnchor.constraint(equalTo: plView.bottomAnchor),
label.topAnchor.constraint(equalTo: plView.topAnchor)
])
}
}
Хорошо. Наш вид готов. Теперь мы должны добавить его в горизонтальное представление стека с заливкой выравнивания.
для элемента в ["Текст", "Текст", "Текст"] {
пусть labelView = LabelView()
labelView. label.text = элемент
stackView.addArrangedSubview (labelView)
}
label.text = элемент
stackView.addArrangedSubview (labelView)
}
Вот что у нас получилось.
Это не похоже на желаемый результат, потому что у него есть рациональные проблемы. Как я понял, рамка каждого вида в iOS прямоугольная и изменить ее нельзя. Даже интервал моего стека равен 0, у меня все еще есть интервал (на самом деле его нет), потому что вид все равно прямоугольный. Итак, как добиться результата, как на скриншоте? Что я делаю не так?
Инструменты четырехугольника содержат обычный прямоугольник, прямоугольник с углами, параллелограмм, ромб, два способа рисования набора, трапецию, прямоугольники со скругленными углами и инструмент растрового изображения.
Щелчок правой кнопкой мыши на одной из сторон прямоугольника позволит вам добавить метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины.
Доступные параметры для прямоугольников
$высота $ширина $периметр $область
Видео — Рисование квадратов
Инструмент «Прямоугольник под углом» очень похож на обычный прямоугольник с той лишь разницей, как он определен. Угловые прямоугольники определяются путем рисования одной из сторон (которая может быть под любым углом) и их перемещения к третьей точке, которая определяет высоту прямоугольника. Третья точка не обязательно должна быть на прямоугольнике.
Щелчок правой кнопкой мыши на одной из сторон прямоугольника позволит вам добавить метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины.
Доступные параметры для прямоугольников
$высота $ширина $периметр $область
Инструмент «Параллелограмм» упрощает рисование параллелограммов. Первая линия может быть любой длины и направления. Третья точка определяет параллелограмм.
Щелчок правой кнопкой мыши на одной из сторон параллелограмма позволит вам добавить метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины.
Инструмент «Ромб» позволяет быстро и легко нарисовать ромб.
Два инструмента для воздушных змеев позволяют рисовать воздушных змеев двумя немного разными способами.
При использовании первого инструмента для воздушных змеев первая нарисованная линия является одной из сторон воздушного змея. Третья точка определяет кайт.
При использовании второго инструмента воздушного змея первая линия определяет большую ось воздушного змея.
Щелчок правой кнопкой мыши на одной из сторон воздушного змея позволит вам добавить метки в середине линии.
Инструмент «Трапеция» позволяет быстро нарисовать трапецию. Щелчок правой кнопкой мыши на одной из сторон трапеции позволит вам добавить метки и текст к середине ребер, в том числе возможность автоматически отмечать параллельные стороны.
Инструмент «Прямоугольник со скругленными углами» рисует незакрашенные прямоугольники со скругленными углами. |



 Смотри Приложение 1.
Смотри Приложение 1.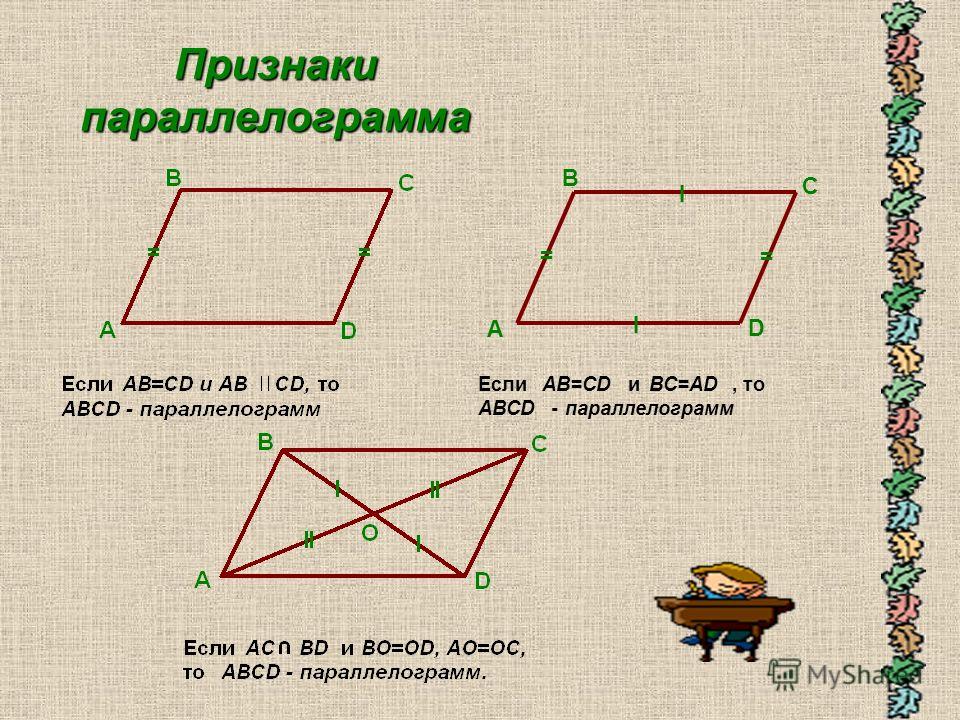
 addLine (к: CGPoint (x: rect.maxX, y: 0))
/// рисуем вниз, но немного влево
path.addLine(к: CGPoint(x: rect.maxX - 16, y: rect.maxY))
/// рисуем справа налево
path.addLine (к: CGPoint (x: 0, y: rect.maxY))
/// соединяем все
путь.закрыть()
/// просто для пробы заливки каким-нибудь цветом. Я не знаю, как это изменить позже :(
UIColor.red.setFill()
путь.заполнить()
}
}
addLine (к: CGPoint (x: rect.maxX, y: 0))
/// рисуем вниз, но немного влево
path.addLine(к: CGPoint(x: rect.maxX - 16, y: rect.maxY))
/// рисуем справа налево
path.addLine (к: CGPoint (x: 0, y: rect.maxY))
/// соединяем все
путь.закрыть()
/// просто для пробы заливки каким-нибудь цветом. Я не знаю, как это изменить позже :(
UIColor.red.setFill()
путь.заполнить()
}
}
 init(кадр: кадр)
/// добавление метки к параллелограмму
plView.addSubview (метка)
addSubview (plView)
NSLayoutConstraint.активировать([
plView.leadingAnchor.constraint(equalTo: leadingAnchor),
plView.trailingAnchor.constraint(equalTo: trailingAnchor),
plView.bottomAnchor.constraint(equalTo: bottomAnchor),
plView.topAnchor.constraint(equalTo: topAnchor),
label.leadingAnchor.constraint (equalTo: plView.leadingAnchor, константа: 16),
label.trailingAnchor.constraint(equalTo: plView.trailingAnchor, константа: -16),
label.bottomAnchor.constraint(equalTo: plView.bottomAnchor),
label.topAnchor.constraint(equalTo: plView.topAnchor)
])
}
init(кадр: кадр)
/// добавление метки к параллелограмму
plView.addSubview (метка)
addSubview (plView)
NSLayoutConstraint.активировать([
plView.leadingAnchor.constraint(equalTo: leadingAnchor),
plView.trailingAnchor.constraint(equalTo: trailingAnchor),
plView.bottomAnchor.constraint(equalTo: bottomAnchor),
plView.topAnchor.constraint(equalTo: topAnchor),
label.leadingAnchor.constraint (equalTo: plView.leadingAnchor, константа: 16),
label.trailingAnchor.constraint(equalTo: plView.trailingAnchor, константа: -16),
label.bottomAnchor.constraint(equalTo: plView.bottomAnchor),
label.topAnchor.constraint(equalTo: plView.topAnchor)
])
}
 label.text = элемент
stackView.addArrangedSubview (labelView)
}
label.text = элемент
stackView.addArrangedSubview (labelView)
}
 Вы также можете указать прямоугольнику разделить себя на столбцы и строки.
Вы также можете указать прямоугольнику разделить себя на столбцы и строки. Вы также можете указать прямоугольнику разделить себя на столбцы и строки.
Вы также можете указать прямоугольнику разделить себя на столбцы и строки.
