Условие перпендикулярности двух векторов: Условие перпендикулярности двух векторов

alexxlab / / Разное

Необходимое и достаточное условие перпендикулярности двух векторов — Студопедия

Поделись  

Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.

Определение.

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( радиан).

Теорема.

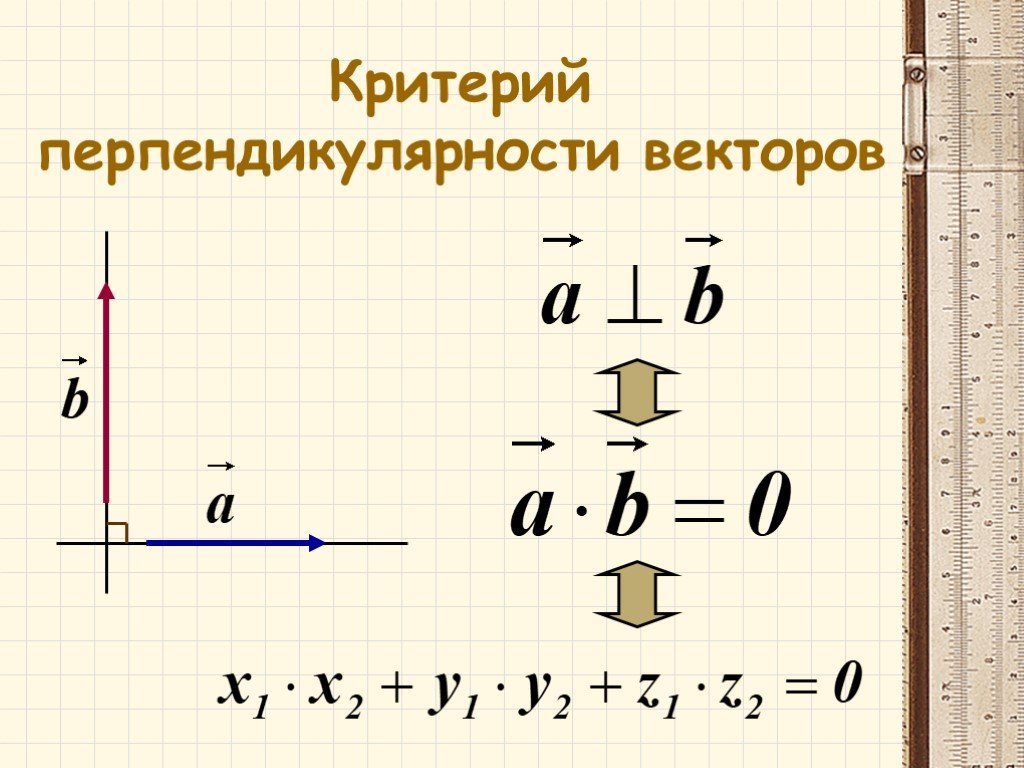
Для перпендикулярности двух ненулевых векторов и необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .

Доказательство.

Пусть векторы и перпендикулярны. Докажем выполнение равенства .

По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы и перпендикулярны, то угол между ними равен девяноста градусам, следовательно, , что и требовалось доказать.

Переходим ко второй части доказательства.

Теперь считаем, что . Докажем, что векторы и перпендикулярны.

Так как векторы и ненулевые, то из равенства следует, что . Таким образом, косинус угла между векторами и равен нулю, следовательно, угол равен , что указывает на перпендикулярность векторов и .

Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.

Как же выглядит условие перпендикулярности двух векторов в координатной форме?

В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами и на плоскости справедливо равенство , а для двух векторов и в пространстве . Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид на плоскости, а в трехмерном пространстве .

Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.

Пример.

Перпендикулярны ли векторы .

Решение.

Вычислим их скалярное произведение по координатам .

Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.

Ответ:

да, векторы перпендикулярны.

Пример.

Перпендикулярны ли векторы и , где — координатные векторы прямоугольной системы координат в трехмерном пространстве.

Решение.

Векторы и имеют соответственно координаты и (при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:

Так как , то векторы и не перпендикулярны.

Ответ:

нет, не перпендикулярны.

Пример.

Найдите значение , при котором векторы и перпендикулярны.

Решение.

Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме

Ответ:

векторы перпендикулярны при .

В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.

Пример.

Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы и перпендикулярны.

Решение.

Если векторы и перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство . Проверим его справедливость: .

Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы и перпендикулярны.



Решение задач с помощью векторной алгебры. Условие коллинеарности, условие перпендикулярности, условие компланарности векторов

©dereksiz.org 2022
әкімшілігінің қараңыз

ТЕМА 2. Векторная алгебра.

  1. Линейные действия над векторами (сложение, вычитание, умножение на число).

  2. Нелинейные действия с векторами (скалярное произведение, векторное произведение, смешанное произведение).

  3. Решение задач с помощью векторной алгебры. Условие коллинеарности, условие перпендикулярности, условие компланарности векторов.

СПИСОК ЛИТЕРАТУРЫ


  1. Бугров Я.С. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский.-М. : Наука, 1980.-175 с.

  2. Клетеник Д.В. Сборник задач по аналитической геометрии / Д. В. Клетеник. — М. — Наука, 1975. — 239 с.

  3. Привалов И.И. Аналитическая геометрия / И. И. Привалов. — М.: Гос. изд-во физ. — мат. лит-ры, 1961. — 229 с.

  4. Данко П. Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А. Г. Попов. — М. : Высшая математика, 1974. — 415 с.

Решение типового варианта контрольной работы.
Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где

Решение:

1. Вычислим проекции векторов на оси координат:

2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:

не коллинеарны.
Задание 2: Перпендикулярны ли векторы ?

Решение: Два вектора перпендикулярны , если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:, где вычислим скалярное произведение:

векторы не перпендикулярны.

Задание 3: Компланарны ли векторы ?

Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , гдевычислим смешанное произведение векторов:

векторы не компланарны.
Задание 4: При каком значении векторы где , перпендикулярны?

Решение:

1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора

Итак: векторы и перпендикулярны при и при
Задание 5:

Даны точки:

Найти:


  1. пр;

  2. ;

  3. ;

  4. орт вектора ;

  5. ;

  6. ;



Решение:

1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр где скалярное произведение векторов вычисляется по формуле: где и длина вектора: итак ,в нашем случае, формула принимает вид:для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

на основании формулы, выше написанной, получим :

пр;
2. Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:

;

Итак:

3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:

Итак

4. Направление вектора определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину орт вектора .

Итак: орт вектора

5. Скалярное произведение векторов вычисляем по формуле:

(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :

Итак:

6. Векторное произведение векторов вычисляется по формуле:

, где

Находим проекции векторов на оси координат:

Итак:

7. Смешанное произведение векторов вычисляется по формуле:

, где Итак:
Задание 6: Даны координаты вершин пирамиды:

Вычислить:


  1. объем пирамиды;

  2. длину ребра ;

  3. площадь грани ;

Решение:

1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем

параллелипипеда, построенного на векторах как на ребрах равен:

Найдем проекции соответствующих векторов на оси координат:

Тогда объем пирамиды равен:

Вычислим объем по указанной формуле:

;

2. Длина ребра

; (смотри пункт 5,3)

3. Площадь грани вычисляется по формуле:

так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат:

;

Контрольная работа
Задания для индивидуальной контрольной работы
Задание 1: Коллинеарны ли векторы и, разложенные по векторам и?
Задание 2: Перпендикулярны ли векторы и ?
Задание 3: Компланарны ли векторы ?
Задание 4: При каком значении векторы и перпендикулярны?
Задание 5: Даны координаты точек . Вычислить:

1) пр;

2) ;

3) ;

4) орт вектора ;

5) ;

6) ;

7) ;


Задание 6: Даны координаты вершин пирамиды . Вычислить:

1) объем пирамиды;

2) длину ребра ;

3) площадь грани ;


Варианты для индивидуальной контрольной работы.

Вариант 1


1.1

3.1

2.1

4.1

5.1

6.1

Вариант 2


1.2

2.2

3.2

4.2

5.2

6.2


Вариант 3
1.3

2.3

3.3

4.3

5.3

6.3


Вариант 4
1.4

2.4

3.4

4.4

5.4

6.4


Вариант 5
1.5

2.5

3.5

4.5

5.5

6.5

Вариант 6


1.6

2.6

3.6

4.6

5.6

6.6


Вариант 7
1.7

2.7

3.7

4.7

5.7

6.7


Вариант 8
1.8

2.8

3.8

4.8

5.8

6.8


Вариант 9
1. 9

2.9

3.9

4.9

5.9

6.9


Вариант 10
1.10

2.10

3.10

4.10

5.10

6.10

Вариант 11
1.11

2.11

3.11

4.11

5.11

6.11


Вариант 12
1.12

2.12

3.12

4.12

5.12

6.12


Вариант 13
1.13

2.13

3.13

4.13

5.13

6.13

Вариант 14
1.14

2.14

3.14

4.14

5.14

6.14


Вариант 15
1.15

2.15

3.15

4.15

5..15

6.15


Вариант 16
1.16

2.16

3.16

4.16

5.16

6.16


Вариант 17
1.17

2.17

3.17

4.17

5.17

6.17

Вариант 18


1.18

2.18

3.18

4.18

5.18

6.18


Вариант 19
1.19

2.19

3.19

4.19

5.19

6.19


Вариант 20
1. 20

2.20

3.20

4.20

5.20

6.20


Вариант 21
1.21

2.21

3.21

4.21

5.21

6.21

Вариант 22
1.22

2.22

3.22

4.22

5.22

6.22


Вариант 23
1.23

2.23

3.23

4.23

5.23

6.23


Вариант 24
1.24

2.24

3.24

4.24

5.24

6.24


Вариант 25
1.25

2.25

3.25

4.25

5.25

6.25

Вариант 26


1.26

2.26

3.26

4.26

5.26

6.26


Вариант 27
1.27

2.27

3.27

4.27

5.27

6.27


Вариант 28
1.28

2.28

3.28

4.28

5.28

6.28


Вариант 29
1.29

2.29

3.29

4.29

5.29

6.29

Вариант 30
1.30

2.30

3.30

4.30

5.30

6.30

Каталог: files -> file -> Resurs matematika
file -> Относно: Информация за внос в Общността на отпадъци
file -> Алматы облысы Кербұлақ ауданы Сарыөзек ауыл округінің әкімі Бекежанов Бақберген Сейтжанұлының ауыл тұрғындарының алдында 2014 жылғы бір жылдық атқарған жұмыстары туралы есебі бойынша жинақталған құжаттар Сарыөзек ауылы


жүктеу/скачать 0. 8 Mb.


Достарыңызбен бөлісу:

линейная алгебра — какие векторы перпендикулярны друг другу?

Задавать вопрос

спросил

Изменено 3 года, 5 месяцев назад

Просмотрено 211 тысяч раз

$\begingroup$ 9\circ$? Но как я узнаю, есть ли там перпендикуляр?

  • линейная алгебра
  • векторные пространства

$\endgroup$

2

$\begingroup$

Если скалярное произведение двух векторов равно $0$, они ортогональны; другими словами, они перпендикулярны.

Скалярное произведение двух векторов $\vec u, \vec v$ определяется как $\vec{u}\cdot\vec{v} = |\vec{u}||\vec{v}|\cos (\theta)$, поэтому $$\vec u \cdot \vec v = 0 \подразумевает \cos \theta = 0 \подразумевает \theta = \pi/2 \;\;(9п\: a_i b_i.$

$\endgroup$

0

$\begingroup$

Это числовой ответ, так как поясняющие ответы уже были даны.

$\vec a = (1,-2,3)$ и $\vec b=(5,4,1)$ перпендикулярны (ортогональны)

$\vec b = (5,4,1)$ и $\vec c=(1,0,-5)$ также перпендикулярны.

Почему?

$$\vec a\cdot \vec b=\begin{bmatrix}1\\-2\\3\end{bmatrix}\cdot\begin{bmatrix}5\\4\\1\end{bmatrix} =1\cdot 5-2\cdot 4+3\cdot 1=5-8+3=0$$

$$\vec b\cdot \vec c=\begin{bmatrix}5\\4\\1\end{bmatrix}\cdot\begin{bmatrix}1\\0\\-5\end{bmatrix} =5\cdot 1+4\cdot 0+1\cdot -5=5-0-5=0$$

Это потому, что их скалярные произведения равны нулю.

$\endgroup$

1

$\begingroup$

Два вектора перпендикулярны, если угол между ними равен $\frac{\pi}{2}$, т. е. скалярное произведение равно $0$. Это следует из того, что для двух векторов $\vec{v}, \vec{w}$ имеем $\vec{v}\cdot\vec{w} = |\vec{v}||\vec{ w}|\cos(\theta)$, где $\theta$ — угол между $\vec{v}$ и $\vec{w}$. 9{\circ}$.

$\endgroup$

Когда два вектора перпендикулярны, их векторное произведение равно нулю?

Ответить

Проверено

157,8 тыс.+ просмотров

Подсказка: Сначала определим термины вектор, векторное произведение и перпендикуляр и решим данную задачу дальше.
Вектор имеет величину и направление, где величина также известна как размер.
Длина линии или стрелки показывает величину, а точки стрелки ($\overrightarrow a $) — направление.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *