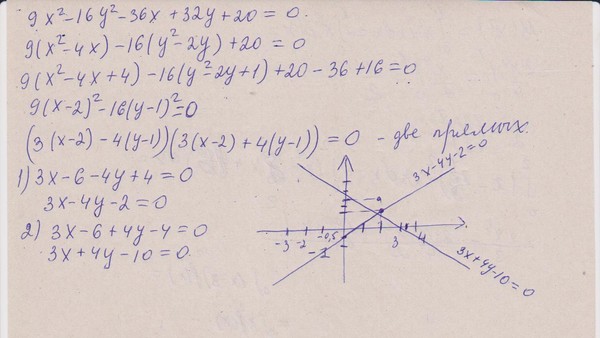Установить какая линия определяется уравнением: Какая линия определяется уравнением : Геометрия

Установить , какая линия определяется уравнением , нарисовать ее.Подробно, пожалуйста) — вопрос №2209768 — Учеба и наука

Лучший ответ по мнению автора

19. 11.16 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. (2x-5)-9)

Пользуйтесь нашим приложением

Лекция линии на плоскости и их уравнения. Какое уравнение называется уравнением данной линии? Приведите пример Какую линию на плоскости описывает уравнение

Цель: Рассмотреть понятие линии на плоскости, привести примеры. Основываясь на определение линии, ввести понятие уравнения прямой на плоскости. Рассмотреть виды прямой, привести примеры и способы задания прямой. Закрепить умение переводить уравнение прямой из общего вида в уравнение прямой «в отрезках», с угловым коэффициентом.

1. Уравнение линии на плоскости.
2. Уравнение прямой на плоскости. Виды уравнений.
3. Способы задания прямой.

1. Пусть х и у – две произвольные переменные.

Определение : Соотношение вида F(x,y)=0 называется уравнением , если оно справедливо не для всяких пар чисел х и у.

Пример : 2х + 7у – 1 = 0 , х 2 + y 2 – 25 = 0.

Если равенство F(x,y)=0 выполняется для любых х, у, то, следовательно, F(x,y) = 0 – тождество.

Пример: (х + у) 2 — х 2 — 2ху — у 2 = 0

Говорят, что числа х 0 и у 0 удовлетворяют уравнению , если при их подстановке в это уравнение оно обращается в верное равенство.

Важнейшим понятием аналитической геометрии является понятие уравнения линии.

Определение : Уравнением данной линии называется уравнение F(x,y)=0, которому удовлетворяют координаты всех точек, лежащих на этой линии, и не удовлетворяют координаты никакой из точек, не лежащих на этой линии.

Линия, определяемая уравнением y = f(x), называется графиком функции f(x). Переменные х и у – называются текущими координатами, т. к. являются координатами переменной точки.

Несколько примеров определения линий.

1) х – у = 0 => х = у. Это уравнение определяет прямую:

2) х 2 — у 2 = 0 => (х-у)(х+у) = 0 => точки должны удовлетворять либо уравнению х — у = 0, либо уравнению х + у = 0, что соответствует на плоскости паре пересекающихся прямых, являющихся биссектрисами координатных углов:

3) х 2 + у 2 = 0.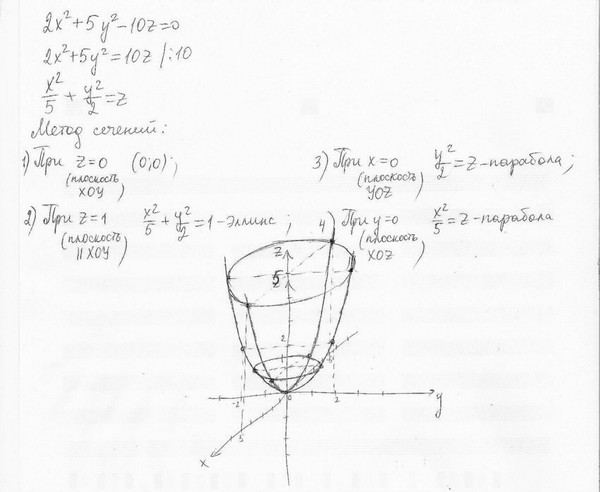 Этому уравнению удовлетворяет только одна точка О(0,0).

2. Определение: Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А 2 + В 2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат

А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох

В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу

В = С = 0, А ¹ 0 – прямая совпадает с осью Оу

А = С = 0, В ¹ 0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких–либо заданных начальных условий.

Уравнение прямой с угловым коэффициентом.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом k .

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С ¹ 0, то, разделив на –С, получим: или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем , то получим

xcosj + ysinj — p = 0 –нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы m×С

р – длина перпендикуляра, опущенного из начала координат на прямую, а j — угол, образованный этим перпендикуляром с положительным направлением оси Ох.

3. Уравнение прямой по точке и угловому коэффициенту.

Пусть угловой коэффициент прямой равен k, прямая проходит через точку М(х 0 , у 0). Тогда уравнение прямой находится по формуле: у – у 0 = k(x – x 0)

Уравнение прямой, проходящей через две точки.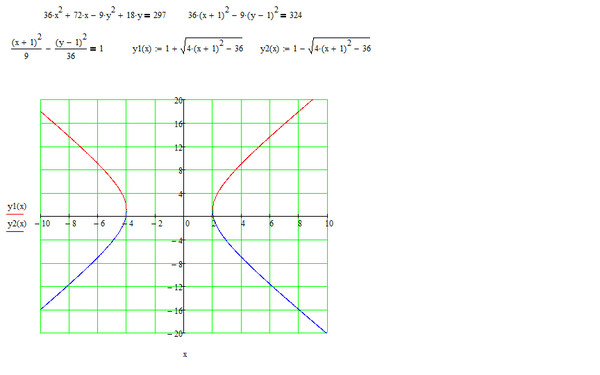

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M 2 (x 2, y 2 , z 2), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:

если х 1 ¹ х 2 и х = х 1 , еслих 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой.

Решение уравнения

Иллюстрация графического метода нахождения корней уравнения

Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).

При подстановке другого корня получается неправильное утверждение:

.

Таким образом, второй корень нужно отбросить, как посторонний.

Виды уравнений

Различают алгебраические , параметрические , трансцендентные , функциональные , дифференциальные и другие виды уравнений.

Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.

К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение , квадратное уравнение , кубическое уравнение и уравнение четвёртой степени . Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.

Уравнение, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.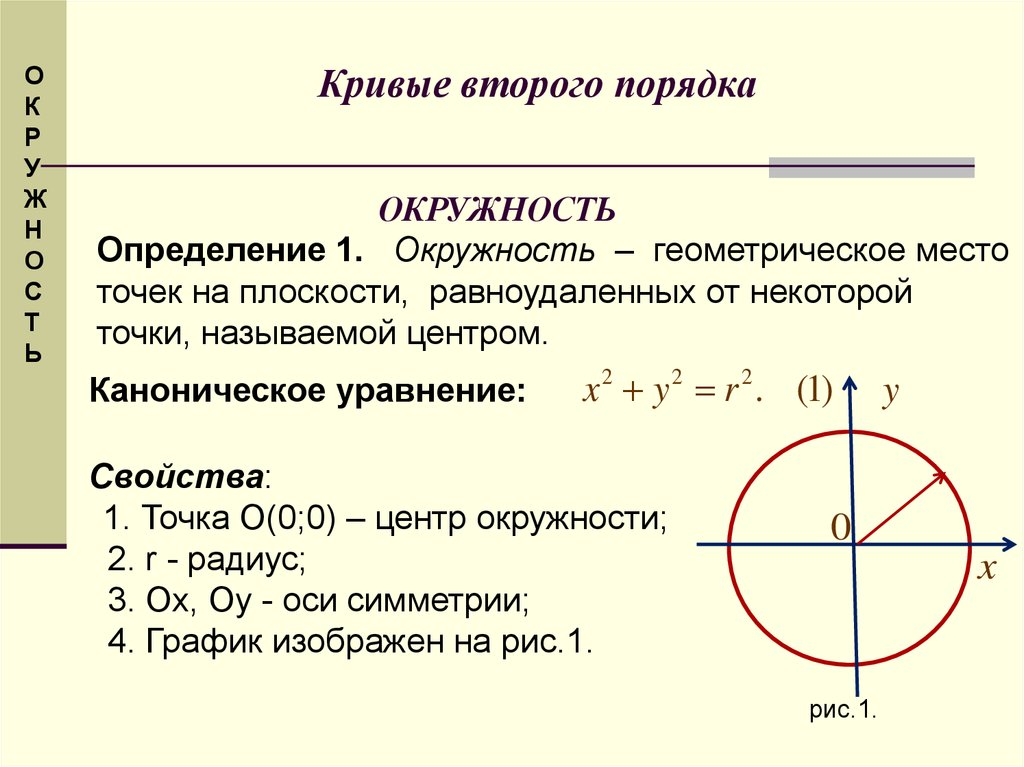

В общем случае, когда аналитического решения найти не удается, применяют численные методы . Численные методы не дают точного решения, а только позволяют сузить интервал , в котором лежит корень, до определенного заранее заданного значения.

Примеры уравнений

См. также

Литература

• Бекаревич, А. Б. Уравнения в школьном курсе математики / А. Б. Бекаревич. — М., 1968.
• Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.
• Каплан Я. В. Рівняння. — Киев: Радянська школа, 1968.
• Уравнение — статья из Большой советской энциклопедии
• Уравнения // Энциклопедия Кольера. — Открытое общество. 2000.
• Уравнение // Энциклопедия Кругосвет
• Уравнение // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977-1985.

Ссылки

• EqWorld — Мир математических уравнений — содержит обширную информацию о математических уравнениях и системах уравнений.

Wikimedia Foundation . 2010 .

Синонимы :

Антонимы :

• Хаджимба, Рауль Джумкович
• ЕС ЭВМ

Смотреть что такое «Уравнение» в других словарях:

УРАВНЕНИЕ — (1) математическая запись задачи о разыскании таких значений аргументов (см. (2)), при которых значения двух данных (см.) равны. Аргументы, от которых зависят эти функции, называют неизвестными, а значения неизвестных, при которых значения… … Большая политехническая энциклопедия

УРАВНЕНИЕ — УРАВНЕНИЕ, уравнения, ср. 1. Действие по гл. уравнять уравнивать и состояние по гл. уравняться уравниваться. Уравнение в правах. Уравнение времени (перевод истинного солнечного времени в среднее солнечное время, принятое в общежитии и в науке;… … Толковый словарь Ушакова

УРАВНЕНИЕ — (equation) Требование того, чтобы математическое выражение принимало определенное значение. Например, квадратное уравнение записывается в виде: ах2+bх+с=0. Решением является такие значения х, при котором данное уравнение становится тождеством. В… … Экономический словарь

УРАВНЕНИЕ — математическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются неизвестными, а значения неизвестных, при которых значения функций равны,… … Большой Энциклопедический словарь

УРАВНЕНИЕ — УРАВНЕНИЕ, два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными. Решить уравнение значит найти все значения неизвестных, при которых оно обращается в тождество, или установить … Современная энциклопедия

Если указано правило, согласно которому с каждой точкой М плоскости (или какой-нибудь части плоскости) сопоставляется некоторое число u, то говорят, что на плоскости (или на части плоскости) «задана функция точки»; задание функции символически выражается равенством вида u=f(M). 2–16. Определить выражение этой функции в новой системе координат, если координатные оси повернуты на угол –45 градусов.

Параметрические уравнения линии

Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:

x=φ(t), y=ψ(t) (1)

При изменении t величины х и у будут, вообще говоря, меняться, следовательно, точка М будет перемещаться. Равенства (1) называются параметрическими уравнениями линии , которая является траекторией точки М; аргумент t носит название параметра. Если из равенств (1) можно исключить параметр t, то получим уравнение траектории точки М в виде

Равенство вида F(x, у) = 0 называется уравнением с двумя переменными х, у, если оно справедливо не для всяких пар чисел х, у. Говорят, что два числа х = x 0 , у = y 0 удовлетворяют некоторому уравнению вида F(x, y) = 0, если при подстановке этих чисел вместо переменных х и у в уравнение его левая часть обращается в нуль.

Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.

В дальнейшем вместо выражения «дано уравнение линии F(x, у) = 0» мы часто будем говорить короче: дана линия F(x, у) = 0.

Если даны уравнения двух линий F(x, у)= 0 и Ф(x, у) = 0, то совместное решение системы

F(x,y) = 0, Ф(х, у) = 0

дает все точки их пересечения. Точнее, каждая пара чисел, являющаяся совместным решением этой системы, определяет одну из точек пересечения,

157. Даны точки *) M 1 (2; -2), М 2 (2; 2), M 3 (2; — 1), M 4 (3; -3), M 5 (5; -5), М 6 (3; -2). Установить, какие из данных точек лежат на линии, определенной уравнением х + y = 0, и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)

158. На линии, определенной уравнением х 2 + у 2 = 25, найти точки, абсциссы которых равны следующим числам: 1) 0, 2) -3, 3) 5, 4) 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5) 3, 6) -5, 7) -8. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)

159. Установить, какие линии определяются следующими уравнениями (построить их на чертеже): 1)x — у = 0; 2) х + у = 0; 3) x — 2 = 0; 4)x + 3 = 0; 5) y — 5 = 0; 6) у + 2 = 0; 7) х = 0; 8) у = 0; 9) х 2 — хy = 0; 10) ху + у 2 = 0; 11) х 2 — у 2 = 0; 12) ху = 0; 13) у 2 — 9 = 0; 14) х 2 — 8x + 15 = 0; 15) у 2 + by + 4 = 0; 16) х 2 у — 7ху + 10y = 0; 17) у — |х|; 18) х — |у|; 19) y + |x| = 0; 20) x + |у| = 0; 21) у = |х — 1|; 22) y = |x + 2|; 23) х 2 + у 2 = 16; 24) (х — 2) 2 + {у- 1) 2 = 16; 25 (x + 5) 2 + (у-1) 2 = 9; 26) (x — 1) 2 + y 2 = 4; 27) x 2 + (y + 3) 2 = 1; 28) (x — 3) 2 + y 2 = 0; 29) x 2 + 2y 2 = 0; 30) 2x 2 + 3y 2 + 5 = 0; 31) (x — 2) 2 + (y + 3) 2 + 1 = 0.

160. Даны линии: l)x + y = 0; 2)х — у = 0; 3)x 2 + у 2 — 36 = 0; 4) х 2 + у 2 — 2х + у = 0; 5) х 2 + у 2 + 4х — 6у — 1 = 0. Определить, какие из них проходят через начало координат.

161. Даны линии: 1) х 2 + у 2 = 49; 2) {х — 3) 2 + (у + 4) 2 = 25; 3) (х + 6) 2 + (y — З) 2 = 25; 4) (х + 5) 2 + (y — 4) 2 = 9; 5) х 2 + у 2 — 12x + 16у — 0; 6) х 2 + у 2 — 2x + 8y + 7 = 0; 7) х 2 + у 2 — 6х + 4у + 12 = 0. Найти точки их пересечения: а) с осью Ох; б) с осью Оу.

162. Найти точки пересечения двух линий:

1) х 2 + у 2 — 8; х — у =0;

2) х 2 + у 2 — 16х + 4у + 18 = 0; х + у = 0;

3) х 2 + у 2 — 2х + 4у — 3 = 0; х 2 + у 2 = 25;

4) х 2 + у 2 — 8y + 10у + 40 = 0; х 2 + у 2 = 4.

163. В полярной системе координат даны точки M 1 (l; π/3),M 2 (2; 0).М 3 (2; π/4), М 4 (√3; π/6) и M 5 (1; 2/3π). Установить, какие из этих точек лежат на линии, определенной в полярных координатах уравнением р = 2cosΘ, и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже. )

164. На линии, определенной уравнением p = 3/cosΘ найти точки, полярные углы которых равны следующим числам: а) π/3 , б) — π/3, в) 0, г) π/6. Какая линия определена данным уравнением? (Построить ее на чертеже.)

165. На линии, определенной уравнением p = 1/sinΘ, найти точки, полярные радиусьмкоторых равны следующим числам: а) 1 6) 2, в) √2 . Какая линия определена данным уравнением? (Построить ее на чертеже.)

166. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже): 1) р = 5; 2) Θ = π/2; 3) Θ = — π/4; 4) р cosΘ = 2; 5) p sinΘ = 1; 6.) p = 6cosΘ; 7) р = 10 sinΘ; 8) sinΘ = 1/2; 9) sinp = 1/2.

167. Построить на черТёЖе следующие спйралй Архимеда: 1) р = 20; 2) р = 50; 3) p = Θ/π; 4) р = -Θ/π.

168. Построить на чертеже следующие гиперболиче-ские спирали: 1) p = 1/Θ; 2) p = 5/Θ; 3) р = π/Θ; 4) р= — π/Θ

169. Построить на чертеже следующие логарифми-ческие спирали: 1) р = 2 Θ ; 2) p = (1/2) Θ .

170. Определить длины отрезков, на которые рассе-кает спираль Архимеда р = 3Θ луч, выходящий из полюса и наклоненный к полярной оси под углом Θ = π/6. Сделать чертеж.

171. На спирали Архимеда р = 5/πΘ взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С. Сделать чертеж.

172. На гиперболической спирали P = 6/Θ найти точку Р, полярный радиус которой равен 12. Сделать чертеж.

173. На логарифмической спирали р = 3 Θ найти точку P, полярный радиус которой равен 81. Сделать чертеж.

Уравнением линии на плоскости XOY называется уравнение, которому удовлетворяют координаты x и y каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. В общем случае уравнение линии может быть записано в виде 0), (yx. F или)(xfy

Пусть задана прямая, пересекающая ось у в точке В (0, в) и образующая с осью х угол α Выберем на прямой произвольную точку М(х, у).

x y M N

Координаты точки N (x , в).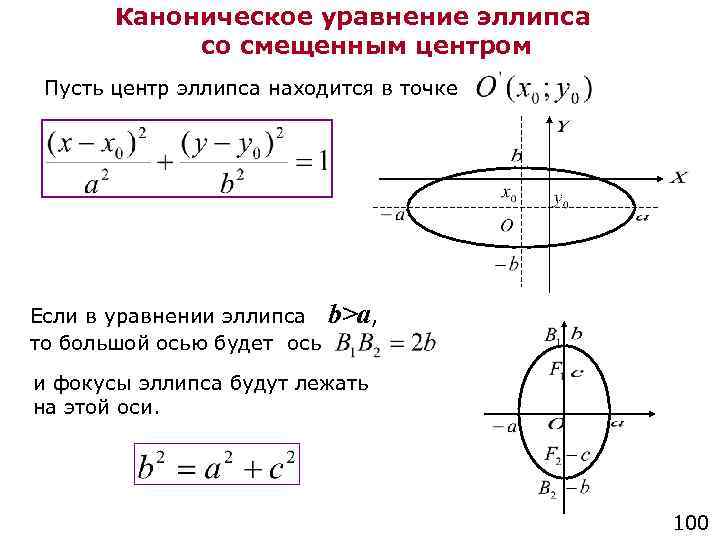 Из треугольника BMN: k – угловой коэффициент прямой. k x by NB MN tg bkxy

Рассмотрим частные случаи: — уравнение прямой, проходящей через начало координат. 10 bkxy 2 bytg 00 — уравнение прямой, параллельной оси х.

т. е. у вертикальной прямой нет углового коэффициента. 3 22 tg — не существует Уравнение прямой, параллельной оси у, в этом случае имеет вид ax где а – отрезок, отсекаемый прямой на оси х.

Пусть задана прямая, проходящая через заданную точку2 и образующая с осью х угол α), (111 yx. M

Т. к. точка М 1 лежит на прямой, ее координаты должны удовлетворять уравнению (1): Вычитаем это уравнение из уравнения (1): bkxy 11)(11 xxkyy

Если в этом уравнении угловой коэффициент не определен, то оно задает пучок прямых, проходящих через данную точку, кроме прямой, параллельной оси у, не имеющей углового коэффициента. xy

Пусть задана прямая, проходящая через две точки: Запишем уравнение пучка прямых, проходящих через точку М 1:), (111 yx. M), (222 yx. M)(11 xxkyy

Т. к. точка М 2 лежит на данной прямой, подставим ее координаты в уравнение пучка прямых:)(1212 xxkyy 12 12 xx yy k Подставляем k в уравнение пучка прямых. Тем самым мы выделяем из этого пучка прямую, проходящую через две данные точки:

1 12 12 1 xx xx yy yy или 12 1 xx xx yy yy

РЕШЕНИЕ. Подставляем координаты точек в уравнение прямой, проходящей через две точки. 53 5 42 4 xy)5(8 6 4 xy 4 1 4 3 xy

Пусть задана прямая, отсекающая на осях координат отрезки, равные а и в. Это значит, что она проходит через точки)0, (a. A), 0(b. B Найдем уравнение этой прямой.

xy 0 ab

Подставим координаты точек А и В в уравнение прямой, проходящей через две точки (3): a ax b y 00 0 a ax b y 1 ax b y 1 b y a x

ПРИМЕР. Составить уравнение прямой, проходящей через точку А(2, -1) если она отсекает от положительной полуоси у отрезок, вдвое больший, чем на положительной полуоси х.

РЕШЕНИЕ. По условию задачи, ab 2 Подставляем в уравнение (4): 1 2 a y a x Точка А(2, -1) лежит на этой прямой, следовательно ее координаты удовлетворяют этому уравнению: 1 2 12 aa 1 2 41 a 23 a 1 35. 1 yx

Рассмотрим уравнение: Рассмотрим частные случаи этого уравнения и покажем, что при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, это уравнение есть уравнение прямой на плоскости. 0 CBy. Ax

Тогда уравнение (5) можно представить в виде: Тогда получаем уравнение (1): Обозначим: 10 B B C x B A y k B A b B C bkxy

Тогда уравнение имеет вид: Получаем уравнение: — уравнение прямой, проходящей через начало координат. 2000 CAB x B A y 3 000 CAB BC y — уравнение прямой, параллельной оси х.

Тогда уравнение имеет вид: Получаем уравнение: — уравнение оси х. 40 y 5 000 CAB — уравнение прямой, параллельной оси у. 000 CAB A C x

Тогда уравнение имеет вид: — уравнение оси у. 60 x 000 CAB Таким образом, при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, уравнение (5) есть уравнение прямой на плоскости. Это

1.3: Определение уравнения прямой

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

40109

• Рупиндер Секон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе вы научитесь:

• Находить уравнение прямой, если известны точка и наклон.
• Найдите уравнение прямой, если даны две точки.

Необходимые навыки

Прежде чем начать, пройдите этот обязательный тест.

1. Упростите каждое выражение:

a. \(3(2x-5)\)

б. \(-7(4x-2)\)

Нажмите здесь, чтобы проверить свой ответ

а. \(6x-15\)

б. \(-28x+14\)

Если вы пропустили какую-либо часть этой проблемы, просмотрите здесь . (Обратите внимание, что это откроет другой учебник в новом окне.)

 

2. Найдите наклон линии, содержащей точки (1, 4) и (5, -2).

Нажмите здесь, чтобы проверить свой ответ

\(-\dfrac{3}{2}\)

Если вы пропустили эту проблему, просмотреть Раздел 1.2 . (Обратите внимание, что это откроется в новом окне.)

 

3. Найдите наклон линии, содержащей точки (-2, 5) и (10, -4).

Нажмите здесь, чтобы проверить свой ответ

\(-\dfrac{3}{4}\)

Если вы пропустили эту проблему, просмотрите Раздел 1.2 . (Обратите внимание, что это откроется в новом окне.)

До сих пор нам давали уравнение прямой и просили дать информацию о нем. Например, нас просили найти точки на прямой, найти ее наклон и даже найти точки пересечения. Теперь мы собираемся повернуть процесс вспять. То есть нам будут заданы либо две точки, либо точка и наклон прямой, и нас попросят найти ее уравнение.

Уравнение прямой может быть записано в трех формах: форма наклон-отрезок , форма точка-наклон, или стандартная форма . Мы обсудим каждый из них в этом разделе.

Линия полностью определяется двумя точками или точкой и наклоном. Информация, которую нам дают о конкретной линии, повлияет на то, какую форму уравнения наиболее удобно использовать. Как только мы узнаем какую-либо форму уравнения прямой, легко переформулировать уравнение в других формах, если это необходимо.

ФОРМА ПЕРЕСЕЧЕНИЯ НАКЛОНА ЛИНИИ: \(y = mx + b\)

В предыдущем разделе мы узнали, что уравнение линии, у которой наклон = \(m\) и \(y\)-отрезок = \(b\) равно \[y=mx+b.\] Это называется формой пересечения наклона линии и является наиболее часто используемой формой.

Пример \(\PageIndex{1}\)

Найдите уравнение прямой, у которой наклон равен 5, а точка пересечения \(y\) равна 3.

Решение

Поскольку наклон равен \(m = 5\), а \(y\)-перехват равен \(b = 3\), уравнение имеет вид \(y = 5x + 3\).

Пример \(\PageIndex{2}\)

Найдите уравнение прямой, проходящей через точку (\(2, 7\)) и имеющей наклон \(3\).

Решение

Поскольку \(m = 3\), уравнение в частных производных имеет вид \(y = 3x + b\).

Теперь \(b\) можно определить, подставив точку (\(2, 7\)) в уравнение \(y = 3x + b\).

\begin{align}
&7=3(2)+b \nonumber \\
&b=1 \nonumber
\end{aligned}

Таким образом, уравнение \(y = 3x + 1\).

Пример \(\PageIndex{3}\)

Найдите уравнение прямой, проходящей через точки (-1, 2) и (1, 8).

Решение

Сначала нам нужно найти наклон линии, содержащей эти точки. Помните, что если (\(x_1\), \(y_1\)) и (\(x_2\), \(y_2\)) две разные точки на линии, наклон линии равен

\[ \text{наклон}=m=\frac{y_2-y_1}{x_2-x_1} \label{наклон}\nonumber\]

\(m=\frac{8-2}{1-(-1)} =\frac{6}{2}=3\). Таким образом, уравнение в частных производных имеет вид \(y = 3x + b\).

Мы можем использовать любую из двух точек (-1, 2) или (1, 8), чтобы найти \(b\). Подстановка (-1, 2) дает

\begin{align}
&2=3(-1)+b \nonumber \\
&5=b \nonumber
\end{aligned}

Итак, уравнение \(y = 3х+5\).

Пример \(\PageIndex{4}\)

Найдите уравнение прямой, которое имеет точку пересечения \(x\) 3 и точку пересечения \(y\) 4.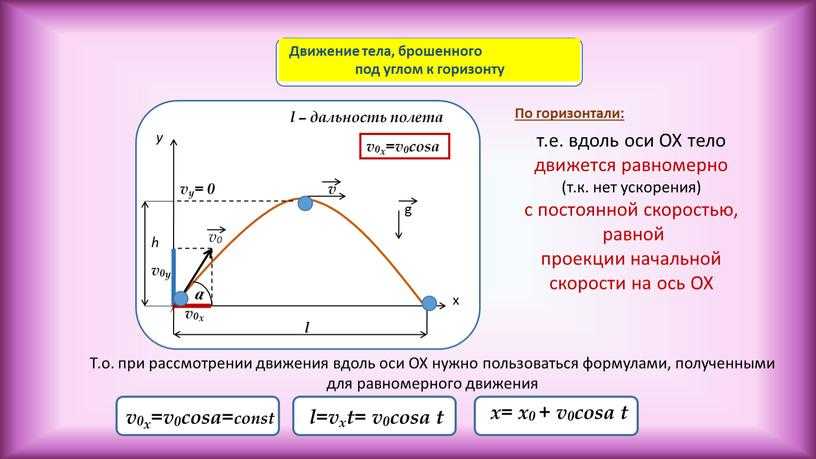

Решение

\( x\)-intercept = 3 и \(y\)-intercept = 4 соответствуют точкам (3, 0) и (0, 4) соответственно.

\[ m=\frac{4-0}{0-3} = -\frac{4}{3} \nonumber \]

Нам говорят, что \(y\)-отрезок равен 4; таким образом, \(b\) = 4

Следовательно, уравнение имеет вид \(y = -\frac{4}{3} x + 4\).

ФОРМА ТОЧКА-НАКЛОН ЛИНИИ: \(y — y_1 = m(x — x_1)\)

Форма точка-наклон полезна, когда мы знаем две точки на линии и хотим найти уравнение линии.

Определение уклона приводит нас к формуле точка-уклон. Используя две точки (\(x_1\), \(y_1\)) и любые другие (\(x,y\)), наклон равен \(\frac{y-y_1}{x-x_1}= m\) .

Умножение обеих сторон на (\(x-x_1\)) дает форму точка-наклон: \(y — y_1 = m(x — x_1)\).

Линия с уклоном м , содержащая определенную точку (\(x_1, y_1)\), может быть выражена в виде \[y — y_1 = m(x — x_1).\]

Пример \(\ PageIndex{5}\)

Найдите форму точка-наклон уравнения линии, приведенной в примере \(\PageIndex{2}\).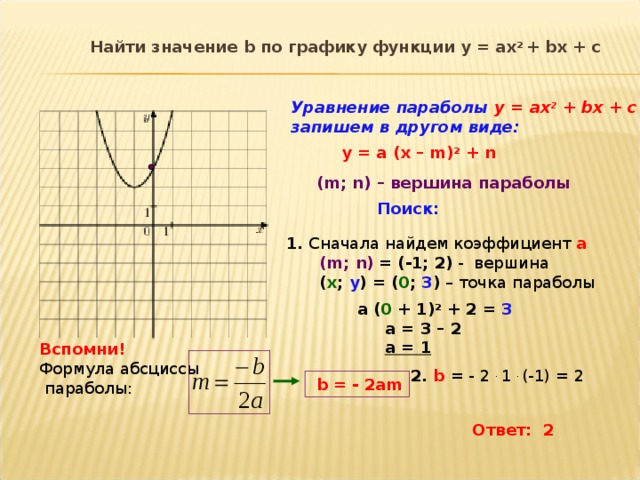 (Найдите уравнение прямой, проходящей через точку (\(2, 7\)) и имеющей наклон \(3\).) Покажите, что две формы уравнений эквивалентны.

Решение

Подставляя точку \((x_1,y_1) = (2,7)\) и \(m= 3\) в формулу угла наклона, получаем

\[\mathbf{y — y_1 = m(x — x_1)} \nonumber \]

\[y — 7 = 3(x — 2) \nonumber \]

Мы можем показать, что формы эквивалентны, решив это уравнение относительно \(y \).

\[y — 7 = 3(x — 2) \nonumber \]

\[y — 7 = 3x — 6 \nonumber \]

\[y = 3x + 1 \nonumber \]

Это форма уравнения с пересечением наклона, которую мы нашли в примере \(\PageIndex{2}\).

Пример \(\PageIndex{6}\)

Найдите форму точки-наклона уравнения линии, которая имеет наклон \(\frac{1}{2}\) и проходит через точку (12,4 ). Затем запишите уравнение в форме пересечения наклона.

Решение

Подставив точку \((x_1,y_1) = (12,4)\) и \(m= \frac{1}{2}\) в формулу точка-наклон, получим

\[\mathbf{y — y_1 = m(x — x_1)} \nonumber \]

\[y — 4 = \frac{1}{2}(x — 12) \nonumber \]

\[ y — 4 = \frac{1}{2}x — 6 \nonumber \]

\[y = \frac{1}{2}x — 2 \nonumber \]

СТАНДАРТНАЯ ФОРМА ЛИНИИ: \(Ax + By = C\)

Другая полезная форма уравнения прямой является стандартной формой.

Если мы знаем уравнение линии в форме точка-наклон, \(y — y_1 = m(x — x_1)\), или если мы знаем уравнение линии в форме точки и точки пересечения \(y = mx + b\), мы можем упростить формулу, чтобы все члены для переменных \(x\) и \(y\) находились на одной стороне уравнения, а константа — на другой стороне уравнения.

Результат называется стандартной формой строки: \[\mathbf{Ax + By = C}.\]

Мы всегда должны иметь возможность преобразовать одну форму уравнения в другую. Например, если нам дана линия в форме наклона-пересечения, мы должны быть в состоянии выразить ее в стандартной форме, и наоборот.

Пример \(\PageIndex{7}\)

Запишите уравнение \(y = -\frac{2}{3}x + 3\) в стандартной форме.

Решение

Умножив обе части уравнения на 3, мы получим

\begin{aligned}
&3y = -2x + 9 \\
&2x + 3y = 9 \quad \text { Standard Form }
\end{align}

Пример \(\PageIndex{8}\)

Запишите уравнение \(3x — 4y = 10\) в форме пересечения наклона.

Решение

Решая \(y\), получаем

\begin{aligned}
&-4y = -3x + 10 \\
&y = \frac{3}{4}x — \frac {5}{2} \quad \text {Стандартная форма}
\end{aligned}

Пример \(\PageIndex{9}\)

С помощью формулы точка-наклон найдите стандартную форму уравнения прямой, проходящей через точку (2, 3) и имеющей наклон \(-3/5\).

Решение: 3 = — 3/5(x — 2) \nonumber \]

Умножение обеих сторон на 5 дает нам

\begin{align}
&5(y-3)=-3(x-2)\\
&5 y-15=-3 x+6\\
&3 x+5 y=21 \quad \text { Стандартная форма }
\end{aligned}

Пример \(\PageIndex{10}\)

Найдите стандартную форму линии, проходящей через точки (1, -2) и (4, 0).

Решение

Сначала находим наклон: \(m = \frac{0-(-2)}{4-1} = \frac{2}{3}\)

Затем точка- форма наклона: \(y — (-2) = \frac{2}{3}(x -1)\)

Умножение обеих сторон на 3 дает нам

\begin{align}&3(y+2)=2(x-1) \\
&3 y+6=2 x-2\\
&-2 x+3 y=-8\\
&2 x -3 y=8 \quad \text{ Стандартная форма } \end{aligned}

Наконец, мы узнаем очень быстрый и простой способ записи уравнения прямой в стандартной форме. Но сначала мы должны научиться находить наклон линии в стандартной форме путем проверки.

Находя \(y\), можно легко показать, что наклон линии \(Ax + By = C\) равен \(-A/B\).
Читатель должен убедиться в этом.

Пример \(\PageIndex{11}\)

Найдите наклон следующих линий путем проверки.

1. \(3x-5y=10\)
2. \(2x+7y=20\)
3. \(4x-3y=8\)

Решение

1. \(A=3\), \(B=-5\), следовательно, \(m=\frac{3}{-5}=\frac{3}{5}\ )
2. \(A=2\), \(B=7\), следовательно, \(m=-\frac{2}{7}\)
3. \(m=\frac{4}{-3}=\frac{4}{3}\)

Теперь, когда мы знаем, как найти наклон линии в стандартной форме путем проверки, наша работа по нахождению уравнения линии будет легкой.

Пример \(\PageIndex{12}\)

Найдите уравнение прямой, проходящей через (2, 3) и имеющей наклон — 4/5.

Решение

Поскольку наклон прямой равен -4/5, мы знаем, что левая часть уравнения равна \(4x + 5y\), а уравнение в частных производных будет

\[4x + 5y = c \nonumber\]

Конечно, \(c\) можно легко найти, подставив \(x\) и \(y\).

\begin{align}
&4(2)+5(3)=c\\
&23=c
\end{aligned}

Искомое уравнение:

\[4x + 5y = 23. \nonumber\]

Если вы будете использовать этот метод достаточно часто, то сможете решить эти задачи очень быстро.

Мы суммируем формы для уравнений линии ниже:

Уклон Форма пересечения: \(\mathbf{y = mx + b}\),
где \(m\) = уклон, \(b\) = \(y\)-перехват

Форма наклона точки: \(\mathbf{y — y_1 = m(x — x_1)}\),
, где \(m\) = уклон, \((x_1, y_1)\) — точка на прямой

Стандартная форма: \(\mathbf{Ax + By = C}\)

Горизонтальная линия: \(\mathbf{y = b}\)
где \(b\) = \(y\ )-перехват

Вертикальная линия: \(\mathbf{x = a}\)
где \(a\) = \(x\)-перехват

---

Эта страница под названием 1.3: Определение уравнения линии распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Рупиндер Сехон и Роберта Блум

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. точка-наклон
   2. точечно-наклонная форма
   3. Форма пересечения наклона
   4. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
   5. источник[1]-math-37807
   6. источник[2]-math-37807
   7. стандартная форма

Уравнение прямой — Формула, поиск

Уравнение прямой представляет собой алгебраическую форму представления набора точек, которые вместе образуют линию в системе координат. Многочисленные точки, которые вместе образуют линию на оси координат, представлены как (x, y), а отношение между x и y образует алгебраическое уравнение, которое называется уравнением линии. Используя уравнение любой прямой, мы можем найти, лежит ли данная точка на прямой или нет.

Уравнение прямой представляет собой линейное уравнение со степенью один. Давайте узнаем больше о различных формах уравнения линии и о том, как найти уравнение линии.

1.	Что такое уравнение линии?
2.	Стандартная форма уравнения линии
3.	Уравнение прямой Формула
4.	Как найти уравнение прямой?
5.	Часто задаваемые вопросы по уравнению линии

Что такое уравнение линии?

Уравнение линии является линейным по переменным x и y, которые представляют отношение между координатами каждой точки (x, y) на линии. т. е. уравнению прямой удовлетворяют все ее точки.

Уравнение прямой можно составить с помощью наклона прямой и точки на прямой. Давайте узнаем больше о наклоне линии и необходимой точке на линии, чтобы лучше понять формирование уравнения линии. Наклон линии представляет собой наклон линии с положительной осью x и выражается целым числом, дробью или тангенсом угла, который она образует с положительной осью x. Точка относится к точке с координатой x и координатой y

Общая форма уравнения прямой с наклоном m и проходящей через точку (x ₁ , y ₁ ) имеет вид: y — y ₁ = m(x — x ₁ ). Далее, это уравнение может быть решено и упрощено до стандартной формы/формы пересечения наклона/формы пересечения уравнения прямой.

Стандартная форма уравнения линии

Стандартная форма уравнения прямой: ax + by + c = 0. Здесь a, b — коэффициенты, x, y — переменные, а c — постоянный член. Это уравнение первой степени с переменными x и y. Значения x и y представляют собой координаты точки на линии, представленной на координатной плоскости. В процессе написания этой стандартной формы уравнения прямой необходимо соблюдать следующие простые правила.

• Сначала записывается член x, затем член y и, наконец, записывается постоянный член.
• Коэффициенты и постоянные значения не должны быть записаны в виде дробей или десятичных знаков и должны быть записаны как целые числа.
• Значение ‘a’, коэффициент x всегда записывается как положительное целое число.

Уравнение прямой в стандартной форме: ax + by + c = 0
где,

• а, b — коэффициенты
• x, y переменные
• c — константа

Ниже представлены пять различных форм уравнений линии. Все это можно преобразовать и представить в стандартной форме.

Уравнение прямой Формула

Существует около пяти основных различных формул записи уравнения линии на основе известных параметров линии. Эти различные формулы, используемые для нахождения и представления уравнения линии, приведены ниже:0032

• Форма уклона точки: (y — y ₁ ) = m(x — x ₁ )
• Двухточечная форма: (y -y ₁ ) = [(y ₂ — y ₁ ) / (x ₂ — x ₁ )] (x — x _{1 0)2 )}
• Форма точки пересечения наклона: y = mx + c
• Форма перехвата: x/a + y/b = 1
• Нормальная форма: x cos θ + y sin θ = p

Давайте попробуем понять больше о каждой из этих форм уравнения линии.

Точечная форма наклона уравнения линии

Точечно-наклонная форма уравнения линии требует точки на линии и наклона линии. Если (x ₁ , y ₁ ) является точкой на линии, а наклон линии равен m, то уравнение линии в форме точка-наклон:

(y — y ₁ ) = m(x — x ₁ )

Здесь m = наклон линии, а линия может иметь положительный наклон, отрицательный наклон или нулевой наклон.

Двухточечная форма уравнения линии

Двухточечная форма уравнения прямой является расширением формы точечно-наклонной уравнения прямой. В точечно-наклонной форме уравнения прямой наклон m = (y ₂ — y ₁ )/(x ₂ — x ₁ ) подставляется в двухточечную форму уравнения уравнение линии. Уравнение линии из двух точек (x ₁ , y ₁ ) и (x ₂ , y ₂ ) задается в двухточечной форме следующим образом.

(г-г ₁ ) = [(y ₂ — y ₁ ) / (x ₂ — x ₁ )] (x — x ₁ )

016 9 Откос1 Форма пересечения Форма пересечения наклона линии: y = mx + c. Здесь m — наклон линии, а «c» — точка пересечения линии по оси y. Эта линия пересекает ось у в точке (0, с), а с — расстояние этой точки по оси у от начала координат. Форма уравнения линии с пересечением наклона важна и имеет большое применение в различных областях математики и техники.

y = mx + c

Форма точки пересечения линии

Уравнение линии в форме точки пересечения формируется с точкой пересечения x «a» и точкой пересечения y «b». Линия пересекает ось x в точке (a, 0) и ось y в точке (0, b), а a, b являются соответствующими расстояниями этих точек от начала координат. Далее эти две точки можно подставить в двухточечную форму уравнения прямой и упростить, чтобы получить эту форму пересечения уравнения прямой. Уравнение линии в форме точки пересечения:

x/a + y/b = 1

Уравнение прямой с использованием нормальной формы

Нормальная форма уравнения прямой основана на перпендикуляре, проведенном к прямой из начала координат. Прямая, перпендикулярная данной прямой и проходящая через начало координат, называется нормалью. Здесь параметры длины нормали «p» и угла, образуемого нормалью «θ» с положительной осью x, полезны для формирования уравнения линии. Нормальная форма уравнения прямой выглядит следующим образом:

x cos θ + y sin θ = p

☛ Также проверьте: Далее, помимо определенных выше форм уравнения прямой, мы также можем использовать калькулятор уравнения прямой, чтобы удобно было найти уравнение линии быстрыми и легкими шагами. Кроме того, чтобы использовать это уравнение линейного калькулятора, нам нужно указать значения наклона m и точки пересечения с осью c, чтобы получить ответ уравнения линии в форме наклона и точки пересечения и в стандартной форме.

Как найти уравнение прямой?

Для нахождения уравнения линии мы можем применить формулы для любой из форм, объясненных выше, в зависимости от известных нам данных. Шаги, которые можно выполнить для различных случаев на основе известных параметров и формы, приведены ниже:

• Шаг 1: Запишите предоставленные данные, наклон линии как «м» и координаты заданной точки ( у) по форме (х _н , у _н ).
• Шаг 2: Примените требуемую формулу в зависимости от заданных параметров,
  (i) Для нахождения уравнения линии с учетом ее наклона или градиента и точки пересечения на оси Y используйте форму пересечения наклона.
  (ii) Чтобы найти уравнение линии, зная ее наклон и координаты одной точки, лежащей на линии, используйте форму точка-наклон.
  (iii) Для нахождения уравнения прямой по координатам двух лежащих на ней точек используйте двухточечную форму.
  (iv) Чтобы написать уравнение, учитывая точки пересечения по осям x и y, используйте форму пересечения.
• Шаг 3: Переставьте члены, чтобы выразить уравнение прямой в стандартной форме.

Примечание: Альтернативный метод для случаев (ii), (iii) и (iv) может состоять в том, чтобы сначала вычислить наклон, применяя формулу наклона с использованием заданных данных, а затем, наконец, применяя формулу пересечения наклона.

Уравнение горизонтальной и вертикальной прямой

Нам не нужны никакие из приведенных выше формул, чтобы найти уравнение горизонтальной/вертикальной прямой.

• Уравнение горизонтальной линии (линии, параллельной оси x) находится с помощью общего уравнения: y = b , где b — координата y любой точки, лежащей на прямой.
• Аналогично, уравнение вертикальной линии (прямой, параллельной оси y) может быть задано как: x = a , где a — координата x любой точки, лежащей на данной прямой.

Используя те же правила, можно увидеть, что уравнение оси x равно y = 0, а уравнение оси y равно x = 0.

☛ Связанные темы:

• Координатная плоскость
• Уравнение окружности
• Декартова форма
• Уравнение плоскости

Важные примечания по уравнению прямой:

• Уравнение оси X: y = 0, а уравнение оси Y: x = 0.
• Уравнение прямой, параллельной оси x, имеет вид y = b, где она пересекает ось y в точке (0, b).
• Уравнение прямой, параллельной оси y, имеет вид x = a, где она пересекает ось x в точке (a, 0).
• Уравнение прямой, параллельной ax + by + c = 0, равно ax + by + k = 0.
• Уравнение прямой, перпендикулярной оси ax + by + c = 0, есть bx — ay + k = 0.

 

Примеры уравнения прямой

1. Пример 1: Выведите уравнение прямой в нормальной форме.

   Решение:

   Пусть длина нормали равна P, и она наклонена под углом θ к положительной оси x.

   Проекция нормали на оси x и y равна Pcosθ и Psinθ соответственно.

   Координаты точки P (Pcosθ, Psinθ).
   

   Наклон нормали равен tanθ, а наклон требуемой линии, перпендикулярной нормали, равен -1/tanθ

   Теперь у нас есть точка (Pcosθ, Psinθ) и требуемый наклон m = -1 /Tanθ для формирования уравнения линии.

   (y — Psinθ) = -1/tanθ. (x — Pcosθ)

   (y — Psinθ) = -1/sinθ/cosθ. (х — Pcosθ)

   (y — Psinθ) = -cosθ/sinθ. (x — Pcosθ)

   sinθ(y — Psinθ) = -cosθ. (x — PCOSθ)

   YSINθ — PSIN ² θ = -xcosθ + PCOS ² θ

   XCOSθ + YSINθ = PSIN ² θ + PCOS ² θ

   θ + PCOS ² θ
   θ + PCOS ² θ

13913913913 θ + PCOS ² vin 9082 . 2 θ + cos ² θ)

xcosθ + ysinθ = P

☛Также проверьте: Уравнение прямой Рабочие листы

Ответ: уравнение нормальной прямой.

2. Пример 2: Найдите уравнение прямой, у которой точка пересечения по оси x равна 5 единицам, а точка пересечения по оси y равна 4 единицам. Кроме того, представьте это уравнение в стандартной форме.

   Решение:

   Заданная точка пересечения по оси x равна a = 5, а y = 4.

   Применяя это в форме точки пересечения к уравнению прямой x/a + y/b = 1, мы получаем уравнение прямой следующим образом.

   x/5 + y/4 = 1

   Далее нам нужно преобразовать это уравнение в стандартный вид.

   х/5 + у/4 = 1

   (4х + 5у)/20 = 1

   4х + 5у = ​​20

   4х + 5у — 20 = 0

   Ответ: уравнение линии: 4x + 5y = 20,

3. Пример 3: Найдите наклон и точку пересечения y линии с помощью уравнения 3x — 4y + 7 = 0.

   Решение:

   Данное уравнение линии 3x — 4y + 7 = 0

   Чтобы найти точку пересечения по оси Y и наклон из уравнения прямой, нам нужно преобразовать это уравнение в форму точки пересечения с наклоном.

   3x — 4y + 7 = 0

   3x + 7 = 4y

   4y = 3x + 7

   y = 3x/4 + 7/4 y = mx + c мы имеем наклон m = 3/4, а точка пересечения с осью y c = 7/4.

   Ответ: Наклон m = 3/4, точка пересечения с осью y c = 7/4.

перейти к слайдуперейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по уравнению прямой

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по уравнению прямой

Что такое уравнение линии в координатной геометрии?

Уравнение прямой представляет собой единое представление множества точек на прямой. Общая форма уравнения линии имеет вид ax + by + c = 0, и любая точка на линии удовлетворяет этому уравнению. В большинстве случаев уравнение линии с наклоном m и точкой (x ₁ , у ₁ ) на нем находится по формуле y — y ₁ = m × (x — x ₁ ).

Что такое процесс написания уравнений линий?

Для написания уравнений линий сначала запишите известную информацию о них. Обычно в задачах дается некоторая информация, такая как наклон, точки на нем, точки пересечения, угол между линией и осью x и т. д. Затем мы можем использовать одну из формул уравнения линии, упомянутых на странице выше.

Каково уравнение прямой, параллельной оси X?

Уравнение прямой, параллельной оси x, имеет форму y = b, которая пересекает ось y в точке (0, b). Примером может служить уравнение прямой y = 5, которая параллельна оси x и пересекает ось y в точке (0,5). Кроме того, такие точки, как (2, 5), (-3, 5) и т. д., лежат на этой линии y = 5, так как их координата y равна 5.

Что такое уравнение линии в форме пересечения наклона ?

Уравнение прямой с пересечением наклона имеет вид y = mx + c, где m — наклон линии, а c — точка пересечения линии с осью y.

• Наклон этой линии ‘m’ представляет собой числовое значение, которое указывает наклон линии, а также равно тангенсу угла, который линия образует с положительной осью x.
• Точка пересечения оси y ‘c’ представляет собой расстояние от точки на оси y, где эта линия пересекает ось y от начала координат.

Каково уравнение прямой, проходящей через две точки?

Уравнение прямой в двухточечной форме: (y — y ₁ ) = (y ₂ — у ₁ )/(х ₂ — х ₁ ) . (х — х ₁ ). Здесь (y ₂ — y ₁ )/(x ₂ — x ₁ ) — наклон линии, и эта линия проходит через две точки (x ₁ , y ₁ ) , и (х ₂ , у ₂ ). Эта двухточечная форма является интерпретацией формы точка-наклон.

Что такое уравнение линии в стандартной форме?

Стандартная форма уравнения прямой: ax + by + c = 0. Здесь a, b — коэффициенты, x, y — переменные, а c — постоянный член. Любая упорядоченная пара (x, y), лежащая на прямой, удовлетворяет этому уравнению.

Что представляет собой уравнение прямой, перпендикулярной другой прямой?

Уравнение линии, проведенной перпендикулярно прямой ax + by + c = 0, есть bx — ay + c = 0. Давайте разберемся с этим на быстром примере. Уравнение прямой, перпендикулярной прямой 4x + 3y + 7 = 0, равно 3x — 4y + k = 0. Здесь k — постоянная, и ее значение можно получить, подставив в это уравнение любую точку этой прямой.

Как найти уравнение наклона прямой?

Наклон линейного уравнения: ax + by + c = 0 is — a/b. Кроме того, данное уравнение линии может быть преобразовано из стандартной формы в форму пересечения наклона, а коэффициент x будет наклоном линии. В качестве примера мы можем получить наклон линии, имеющей уравнение линии 4x — 5y + 11 = 0, используя формулу для получения наклона как -(4/-5) = 4/5.

Как найти уравнение прямой с одной точкой?

Уравнение прямой с одной заданной точкой (x ₁ , y ₁ ) равно (y — y ₁ ) = m(x — x ₁ ). Здесь m — наклон линии. Далее это уравнение можно окончательно решить и представить в стандартной форме в виде ax + by + c = 0. Найдем уравнение прямой, проходящей через точку (2, 1) и имеющей наклон 3. Искомое уравнение линии с использованием этой одноточечной формы (y — 1) = 3 (x — 2), что при упрощении дает окончательное уравнение в стандартной форме как 3x — y — 5 = 0

Как найти уравнение прямой, параллельной прямой?

Уравнение прямой, параллельной данной прямой, будет таким же, но постоянный член будет другим. Уравнение прямой, параллельной прямой ax + by + c = 0, будет ax + by + k = 0. Здесь k — постоянный член, который можно получить, подставив любую точку, лежащую на прямой, в уравнение линия. Пример: Уравнение прямой, параллельной прямой 5x + 6y + 11 = 0, равно 5x + 6y + k = 0,

Как найти уравнение линии, если наклон не определен?

Линия, наклон которой не определен, является либо осью Y, либо линией, параллельной оси Y. Следовательно, уравнение линии, наклон которой не определен, имеет вид x = a, и она пересекает ось x в точке (a, 0).