Узнать длину окружности по диаметру онлайн калькулятор: Онлайн калькулятор. Длина окружности. Периметр круга

Онлайн калькулятор: Длина стороны правильного многоугольника

РаботаИнженерные

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

Определение длины стороны правильного многоугольника по радиусу описанной окружности

Радиус описанной окружности

Число сторон

Число сторон правильного многоугольника

Точность вычисления

Знаков после запятой: 2

Длина стороны правильного многоугольника

 

P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?

Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла.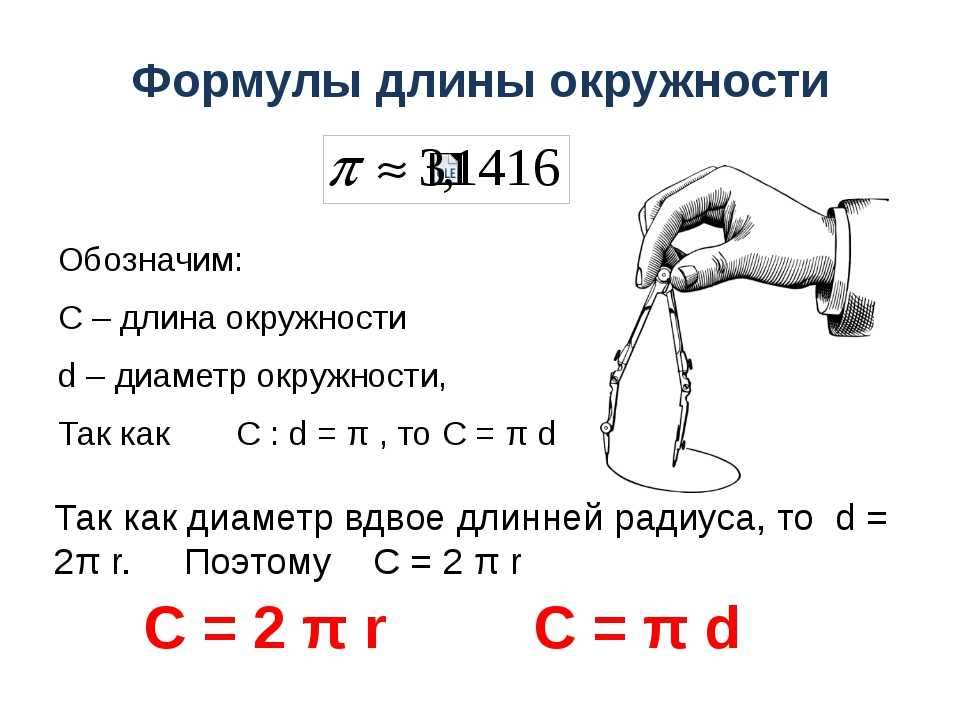 Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

Радиус вписанной окружности

Число сторон

Число сторон правильного многоугольника

Точность вычисления

Знаков после запятой: 2

Длина стороны правильного многоугольника

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Правильный многоугольник. Описанная и вписанная окружность
• • Определение параметров правильного многоугольника по радиусам вписанной и описанной окружности
• • Треугольник. Вписанная окружность
• • Треугольник. Описанная окружность
• • Площадь правильного многоугольника
• • Раздел: Инженерные ( 100 калькуляторов )

 вписанная окружность Инженерные многоугольники описанная окружность

 PLANETCALC, Длина стороны правильного многоугольника

Timur2020-11-03 14:19:27

Длина окружности.

Онлайн калькулятор.

1. Длина окружности по радиусу
2. Длина окружности по диаметру
3. Длина окружности по площади
4. Длина окружности по стороне вписанного квадрата
5. Длина окружности по стороне описанного квадрата
6. Длина окружности по стороне вписанного правильного треугольника
7. Длина окружности по стороне описанного правильного треугольника
8. Длина окружности по стороне вписанного правильного многоугольника
9. Длина окружности по стороне описанного правильного многоугольника

Длина окружности по радиусу

Введите радиус

Формула длины окружности по радиусу

P=2πR

Где R — радиус окружности, π=3.1415926536

Длина окружности по диаметру

Введите диаметр

Формула длины окружности по диаметру

P=πd

Где d — диаметр окружности, π=3.1415926536

Длина окружности по площади

Введите площадь

Формула длины окружности по площади

Из формулы площади окружности выразим радиус R

Подставим радиус R в формулу длины окружности через радиус

Где S — площадь окружности, π=3. 1415926536

Длина окружности по стороне вписанного квадрата

Введите сторону a

Формула длины окружности по стороне вписанного квадрата

По теореме пифагора

Подставим диаметр d в формулу длины окружности через диаметр

Где a — сторона квадрата, π=3.1415926536

Длина окружности по стороне описанного квадрата

Введите сторону a

Формула длины окружности по стороне описанного квадрата

Т.к. диаметр равен стороне описанного около окружности квадрата

P=πd=πa

Где a — сторона описанного около окружности квадрата, π=3.1415926536

Длина окружности по стороне вписанного правильного треугольника

Введите сторону a

Формула длины окружности по стороне вписанного в неё правильного треугольника

Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.

Из этого следует что нам нужно найти радиус окружности, а он будет равен 2/3 от медианы(высоты) BD.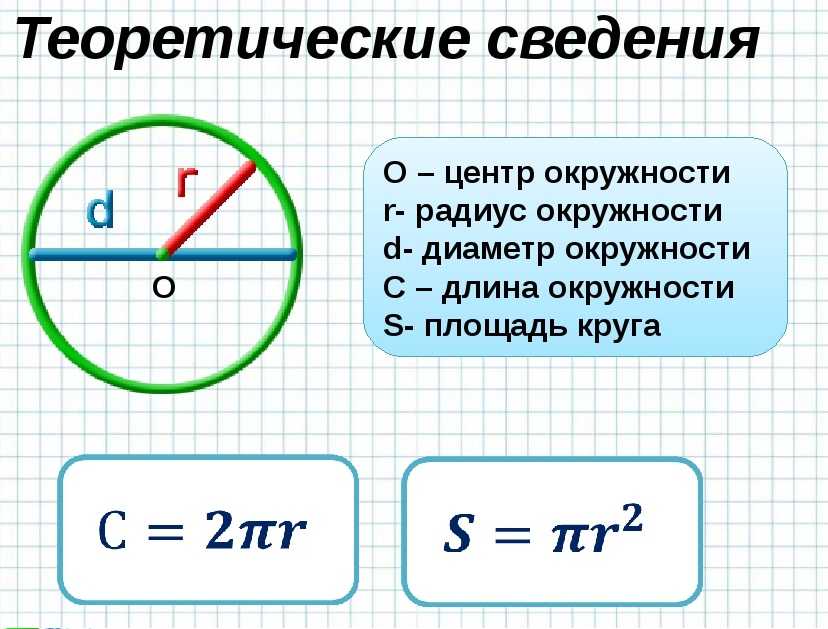

По теореме Пифагора найдём BD.

Подставим полученный радиус в формулу окружности по радиусу

Где a — сторона правильного треугольника, π=3.1415926536

Длина окружности по стороне описанного правильного треугольника

Введите сторону a

Формула длины окружности по стороне описанного правильного треугольника

Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.

Из этого следует что нам нужно найти радиус окружности, а он будет равен 1/3 от медианы(высоты) BD т.е. OD.

По теореме Пифагора найдём BD.

Подставим полученный радиус в формулу окружности по радиусу

Где a — сторона правильного треугольника, π=3.1415926536

Длина окружности по стороне вписанного правильного многоугольника

Введите сторону многоугольника

Введите количество вершин многоугольника

Формула длины окружности по стороне вписанного правильного многоугольника

Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Т.к. они одинаковые обозначим их за x. Т.к. вершины лежат на окружности то длина этих отрезков и будет радиусом окружности.

В итоге у нас получится равнобедренный треугольник ACO с двумя равными сторонами AO и CO.

Проведём высоту OB

Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.

y=180/n

AB=a/2

Из прямоугольного треугольника ABO следует

Выразим x

Т.к. x=R

Где a — сторона правильного многоугольника, π=3.1415926536, n — количество вершин многоугольника

Длина окружности по стороне описанного правильного многоугольника

Введите сторону многоугольника

Введите количество вершин многоугольника

Формула длины окружности по стороне описанного правильного многоугольника

Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Получится равнобедренный треугольник ACO. С вершины O треугольника проведём высоту. Которая разделит сторону AC пополам в точке B.

Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.

y=180/n

AB=a/2

Из прямоугольного треугольника ABO следует

Выразим x

Т.к. x=R

Где a — сторона правильного многоугольника, π=3.1415926536, n — количество вершин многоугольника

Найти окружность с помощью калькулятора диаметра

Калькулятор окружности

решение….

Помогите, поделившись: чтобы поделиться этим ответом, скопируйте и вставьте эту ссылку в электронное письмо, текст или социальные сети.

сообщить об этом объявлении

Параметры круга

Как использовать онлайн-калькулятор круга

Вы можете использовать наш онлайн-калькулятор для круга, чтобы найти различные параметры, такие как площадь, окружность/периметр, диаметр, радиус для любого заданного круга

Для каждого расчета вам потребуется ввести базовый параметр в зависимости от выбранного вами расчета. Используйте раскрывающийся список, чтобы выбрать тип расчета, например, Вычислить площадь из диаметра

После того, как вы ввели базовый параметр, например, радиус, окружность, площадь или диаметр, нажмите кнопку расчета, чтобы вычислить

Часто используемые символы и их значение

• r = радиус
• d = диаметр
• С = окружность
• А = область
• π = пи = 3,1415926535898
• √ = квадратный корень

Калькулятор площади круга с радиусом

Окружностью называется фигура, ограниченная гладкой кривой, все точки которой находятся на равном расстоянии от центральной точки (центра окружности).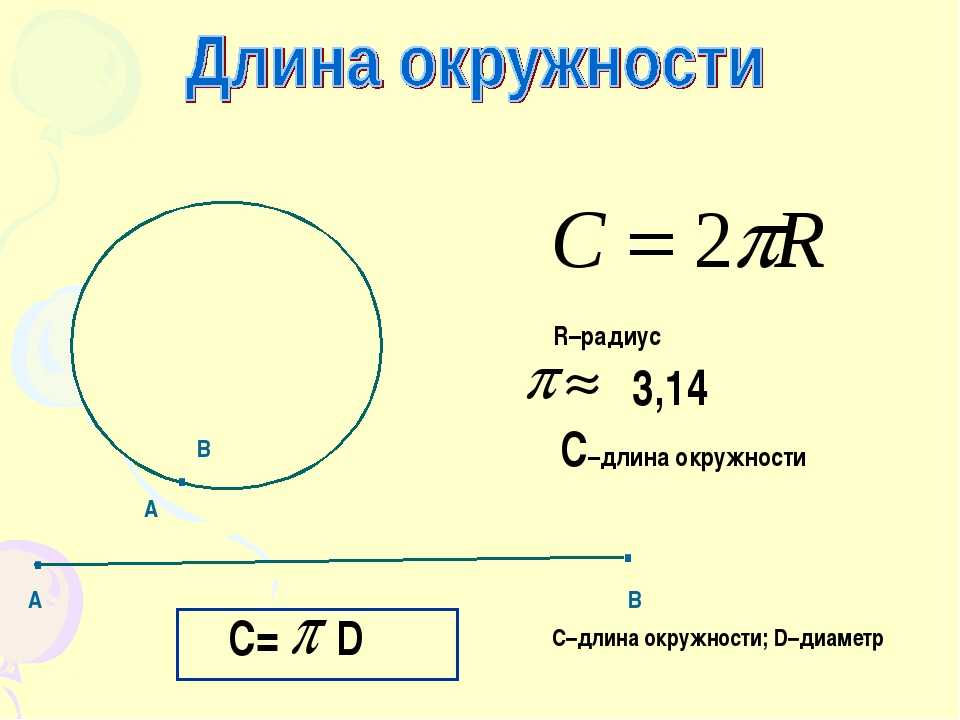 Площадь круга — это мера единичных квадратов, которые могут поместиться внутри фигуры. Чтобы вычислить площадь круга, мы используем формулу площади круга, используя радиус или диаметр. 92

Где \pi — константа приближения, равная приблизительно 3,14159265359

Калькулятор расчета площади круга по формуле радиуса

Этот калькулятор поможет вам найти площадь любого заданного круга, используя его радиус. Таким образом, с помощью радиуса можно легко вычислить площадь, длину окружности или диаметр круга. Чтобы вычислить площадь круга с заданным радиусом, просто введите радиус, в поле ввода выберите единицы измерения и нажмите кнопку расчета, чтобы вычислить площадь.

Калькулятор площади круга в квадратных футах

В то время как большинство онлайн-калькуляторов работают с метрическими единицами измерения, такими как см и м, наш решатель площади круга позволяет вам выбрать предпочтительные единицы измерения. Вы можете найти площадь круга, используя футы, ярды, метры, дюймы и т.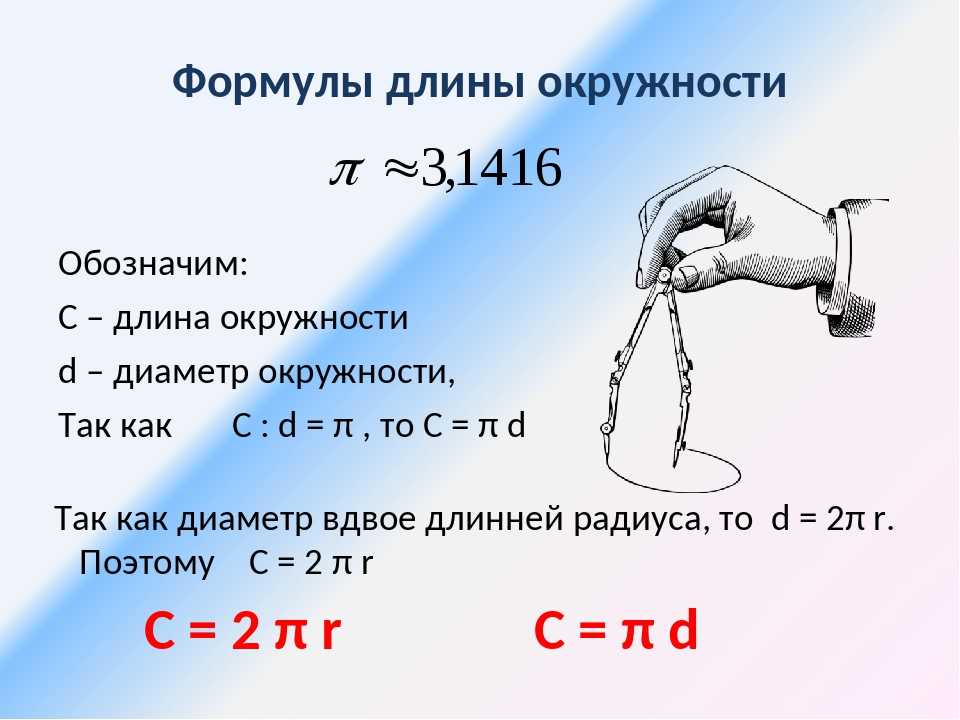

2 92

Калькулятор площади круга по диаметру

Для любого заданного круга легко вычислить его площадь по диаметру или радиусу. Все, что требуется, это подставить заданные параметры в формулу. При нахождении площади круга по диаметру могут возникать ошибки, приводящие к неправильному ответу. Чтобы избежать всего этого, просто используйте калькулятор площади круга, используя диаметр

Найдите площадь круга по окружности

92}{2 \раз \пи}

Найдите площадь с помощью калькулятора длины окружности

Зная длину окружности, легко вычислить ее площадь с помощью онлайн-калькулятора площади. Окружность сначала используется для нахождения диаметра круга, который затем применяется для нахождения радиуса. С радиусом круга вы можете легко найти площадь или окружность данного круга.

Нахождение длины окружности с помощью калькулятора радиуса

Наш калькулятор позволяет вычислить длину окружности любого заданного круга по его радиусу. Зная радиус круга, мы можем найти его длину окружности по формуле

C= 2pir, где r= радиус окружности и C= длина окружности.

Вычислить длину окружности по радиусу

Этот онлайн-калькулятор использует формулу длины окружности для нахождения периметра любой заданной окружности. Чтобы продолжить, просто введите значение радиуса в соответствующее поле ввода, выберите предпочтительные единицы измерения и нажмите кнопку расчета для расчета. 92 Таким образом, r = \sqrt {\frac{A}{\pi}} И C= \sqrt ({A}{\pi}) d = 2 \times \sqrt( \frac {A}{\pi})

Калькулятор преобразования длины окружности в площадь

Для любой заданной окружности наш калькулятор позволяет вычислить длину окружности по заданной площади. Для любой заданной площади мы можем легко найти длину окружности, используя формулу периметра круга.

Окружность (периметр) круга с калькулятором

Окружность (периметр) круга с калькулятором — Math Open Reference

Открытая математическая ссылка

Главная Контакт О Тематический указатель

Расстояние вокруг края круга.

Также «периферия», «периметр».

Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер круга. Окружность показана синим цветом. Обратите внимание на изменение радиуса, и длина окружности рассчитывается для этого радиуса.

Иногда вы видите слово «окружность» для обозначения изогнутой линии, которая проходит по кругу. В других случаях это означает длину этой линии, например, «окружность составляет 2,11 см».

Также иногда используется слово «периметр», хотя обычно это относится к расстоянию вокруг полигонов. фигуры, составленные из отрезков прямых.

Если вы знаете радиус

Учитывая радиус окружности, длину окружности можно рассчитать по формуле где:
R  радиус окружности
π  пи, примерно 3,142

См. Также Вывод формулы длины окружности.

Если вы знаете диаметр

Если известен диаметр окружности, длину окружности можно найти по формуле
, где:
D  – диаметр окружности
  π  – число Пи, примерно 3,142.

См. Также Вывод формулы длины окружности.

Если вы знаете район

Если известна площадь круга, длину окружности можно найти по формуле
, где:
A — площадь круга
π — число Пи, примерно 3,142.

См. Также Вывод формулы длины окружности.

Калькулятор

Радиус		прозрачный
Диаметр		прозрачный
Зона		прозрачный
Окружность		прозрачный

Используйте калькулятор выше, чтобы рассчитать свойства круга.

Введите любое отдельное значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.