Метод Жордана-Гаусса
Определение 1
Метод Жордана-Гаусса – это метод решения линейных уравнений путём полного исключения неизвестных. Данный метод является модификацией метода Гаусса, только в случае метода Жордана-Гаусса элементарные преобразования проводятся дальше.
История возникновения метода
Исторически метод Гаусса возник достаточно давно. Решение систем уравнений подобным способом было изложено ещё в древнем китайском математическом трактате под названием “Математика в девяти книгах”, представляющим собой разрозненное собрание решений различных прикладных математических задач.
Некоторые главы этого трактата датируются 150 г. до н.э.
В Европе же первым, кто занимался изучением этого метода, был Исаак Ньютон. Учёный изучил много книг по алгебре того времени и обнаружил, что ни в одной из них не предложено решений систем уравнений со множеством переменных, после чего он предложил свой способ решения.
Его работа на эту тему была опубликована в 1707 г., в это время Ньютон уже больше не работал в Кембридже. После этого в течение века метод появился во многих книгах и учебниках по алгебре.
В 1810 году известный немецкий учёный и математик К. Ф. Гаусс опубликовал свои дополнения к этому методу вместе с другими своими работами по линейной алгебре, после чего метод с получением верхней треугольной матрицы стал широко известен под его именем.
Затем в в конце XIX века геодезист и математик Жордан разработал на основе метода Гаусса свой усовершенствованный вариант с получением диагональной матрицы.
Примечательно, что он сделал это практически одновременно с другим учёным, тем не менее, в названии усовершенствованного метода отразилось только имя геодезиста Жордана.
Практическое применение метода Жордана-Гаусса
Метод Жордана и Гаусса используется для решения систем линейных уравнений, а также для получения обратных матриц и нахождения ранга матрицы. Также этот метод весьма полезен и часто применяем для решения технических задач со множеством неизвестных.
Для решения получаемых на основе технических задач систем уравнений выделяют наибольшие по модулю переменные для уменьшения ошибки погрешности, а затем производят поочередное удаление лишних переменных из строчек матрицы.
Для решения технических задач методом Жордана-Гаусса также используются реализации на различных языках программирования, они позволяют получать более точные значения переменных.
Объяснение сущности метода Жордана-Гаусса
Обычно матрица, полученная с помощью метода Жордана-Гаусса выглядит как диагональ с единицами, вот например:
$A = \begin{array}{ccc|c} 1& 0 &0 &a_1 \\ 0& 1 &0 &a_2 \\ 0 & 0 & 1 &a_3 \end{array}$
Разница между методом Гаусса и методом Жордана-Гаусса состоит в том, что в случае метода Гаусса необходимо привести только нижнюю часть матрицы к нулям, тогда как в случае метода Жордана-Гаусса в каждой строчке матрицы остаётся лишь один коэффициент при переменной.
С помощью метода Гаусса можно найти базисное и общее решение системы уравнений, также как и с помощью метода Жордана-Гаусса.
Базисное решение системы уравнений – это решение, при котором все свободные переменные равны нулю.
Общее решение системы уравнений – это решение, при котором основные переменные выражаются через свободные переменные.
Также методом Жордана-Гаусса производят получение обратных матриц.
Получение обратной матрицы методом Жордана-Гаусса
Обратная матрица – это такая матрица, при умножении на которую из исходной матрицы получается единичная матрица. Обратные матрицы существуют только для квадратных и невырожденных матриц.
Сущность метода нахождения обратной матрицы состоит в том, чтобы записать рядом исходную матрицу и единичную, и затем, производить элементарные преобразования по методу Жордана-Гаусса одновременно к двум матрицам.
В результате мы получим диагональную единичную матрицу из исходной, а рядом с ней будет её обратная матрица, полученная из единичной матрицы.
Исходная матрица:
$\begin{array}{cc} 1& 2 \\ 3 & 4 \\ \end{array}$
Запишем рядом единичную матрицу и исходную:
$ \begin{array}{cc|cc} 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end{array}$
Теперь к нижней строчке прибавляем верхнюю строчку, умноженную на $-3$:
$ \begin{array}{cc|cc} 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end{array}$
Прибавляем к верхней строчке нижнюю:
$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end{array}$
Делим вторую строку на $-2$:
$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end{array}$
Обратной исходной будет следующая матрица:
$\begin{array}{cc} -2& 1 \\ 3/2 & -1/2 \\ \end{array}$
Чтобы решить СЛАУ методом Жордана-Гаусса, к матрице возможно применить те же элементарные преобразования, что и в случае решения методом Гаусса, а именно:
- умножение любой строчки на константу, отличную от нуля;
- вычитание или сложение двух любых строчек;
- перестановка любых двух строчек местами;
- удаление строчек, состоящих из одних нулей;
- удаление лишних строк, пропорциональных друг другу.
Соответственно, чтобы решить систему линейных уравнений методом Гаусса-Жордана, необходимо выполнить ряд преобразований над получающейся после применения метода Гаусса матрицей.
Общий алгоритм решения системы уравнений методом Жордана-Гаусса
- Выбирают строчку, в которой первый элемент имеет ненулевое значение максимально приближенное к единице и ставят её на место первой строки. Такой элемент называют также “разрешающим”
- Приводят значение верхней левой ячейки к $1$ посредством деления или умножения всей верхней строки.
- Из оставшихся строчек вычитают верхнюю строчку, помноженную на коэффициент, стоящий на первом месте в строчке, над которой ведутся преобразования.
- Далее тоже самое проделывают необходимое количество раз с целью получения треугольной матрицы, в которой все элементы ниже главной диагонали, проходящей слева направо сверху вниз, равны нулю. Последовательность действий, описанных выше, называется прямым ходом преобразования матрицы.
- После получения треугольной матрицы затем вычитают последнюю строку из предпоследней, помножив последнюю строку на элемент из предпоследней. На данном этапе в последней и предпоследней строке остаётся по одному коэффициенту. Эту операцию повторяют пока не дойдут до верха матрицы, получив диагональную матрицу. Эти действия носят название обратного хода преобразования матрицы.
Пример 1
Задача. Решить систему линейных уравнений методом Гаусса-Жордана
$\begin{cases} 3x_1 + 2x_2 – 5x_3 = -1 \\ 2x_1 – x_2 + 3x_3 = 13 \\ x_1 + 2x_2 – x_3 = 9 \end{cases}$
Теперь запишем эту систему в виде расширенной матрицы:
$ \begin{array}{ccc|c} 3& 2 & -5 & -1\\ 2 & -1& 3 & 13 \\ 1 & 2 & -1 & 9 \\ \end{array}$
Путём элементарных преобразований методом Гаусса получим следующую матрицу:
$ \begin{array}{ccc|c} 1& 2 & -1 & 9\\ 0 & 1& -1 & 1 \\ 0 & 0& 1 & 4 \\ \end{array}$
Теперь начнём использовать обратный ход и преобразуем эту матрицу чтобы получить диагональ из единиц.
Сначала к средней и верхней строчкам необходимо добавить последнюю строчку, получается:
$ \begin{array}{ccc|c} 1& 2 & 0 & 13\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$
А теперь к верхней строчке прибавим среднюю, умноженную на $-2$:
$ \begin{array}{ccc|c} 1& 0 & 0 & 3\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$
Получаем следующую систему:
$\begin{cases} x_1 = 3 \\ x_2 = 5 \\ x_3 = 4 \end{cases}$
Пример 2
Решить систему линейных уравнений методом Жордана-Гаусса:
$\begin{cases} x_1 – 8x_2 + x_3 — 9x_4 = 6 \\ x_1 – 4x_2 – x_3 — 5x_4 = 2 \\ -3x_1 + 2x_2 + 8x_3 + 5x_4 = 4 \\ 5x_1 + 2x_2 + 2x_3 + 3x_4 = 12 \end{cases}$
Сначала запишем систему в матричном виде:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ -1 & -4& -1 & -5 & 2 \\ -3 & 2 & 8 & 5 & 4 \\ 5& 2 & 2 & 3 & 12 \\ \end{array}$
Затем преобразуем до треугольной:
К самой верхней строчке прибавляем вторую строчку, домноженную на $-1$. К третьей строчке прибавляем утроенную самую верхнюю строчку, затем к последней строчке прибавляем самую верхнюю, помноженную на $-5$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 4& -2 & 4 & -4 \\ 0 & -22 & 11 & -22 & 22 \\ 0& 42 & -3 & 48 & -18 \\ \end{array}$
Теперь вторую строчку необходимо поделить на $2$, третью строчку на на $11$, а самую нижнюю строку делим на 3:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0 & -2 & 1 & -2 & 2 \\ 0& 14 & -1 & 16 & -6 \\ \end{array}$
Удаляем третью строчку, так как она пропорциональна со второй. А к последней строке прибавляем вторую, предварительно домноженную на $-7$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 6 & 2 & 8 \\ \end{array}$
Теперь сокращаем последнюю строчку с $2$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
В полученной матрице количество строк и столбцов неодинаково, а значит, она имеет бесконечное множество решений. Продолжаем дальнейшее преобразование системы, для этого необходимо в третьем столбце получить числа с равным модулем, поэтому сначала верхнюю строку умножаем на $-3$, а среднюю на $3$:
$ \begin{array}{cccc|c} -3& 24 & -3 & 27 & -18 \\ 0 & 6& -3 & 6 & -6 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Складываем поочередно первую строчку с третьей, а затем вторую с третьей:
$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & 6 & 0 & 7 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Домножаем вторую строчку на $-4$ чтобы получить одинаковые по модулю числа во втором столбце нашей матрицы:
$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Складываем верхнюю строчку со второй:
$ \begin{array}{cccc|c} -3& 0 & 0 & 0 & -6 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Теперь необходимо разделить верхнюю строчку на $-3$, среднюю строчку на $-24$, а последнюю строчку нужно разделить на 3:
$ \begin{array}{cccc|c} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 7/6 & -1/3 \\ 0& 0 & 1 & 1/3 & 4/3 \\ \end{array}$
Если переписать в виде системы, получим следующее:
$\begin{cases} x_1 = 2 \\ x_2 + \frac{7}{6}x_4 = -\frac{1}{3} \\ x_3 + \frac{1}{3}x_4 = \frac{4}{3} \\ \end{cases}$
А теперь просто выражаем базисные переменные:
$\begin{cases} x_1 = 2 \\ x_2 = -\frac{7}{6}x_4 — \frac{1}{3} \\ x_3 = -\frac{1}{3}x_4 + \frac{4}{3} \\ \end{cases}$
Данная система является общим решением уравнения.
spravochnick.ru
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)
Пример 2.
Запишем систему в виде:
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
-2 | 4 | -4 | -2 | -2 | 1 | 1 |
-1 | 1 | 0 | -1 | 1 | 1 | -2 |
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | -1 | 2 | -2 | 0 | 3 | 2 |
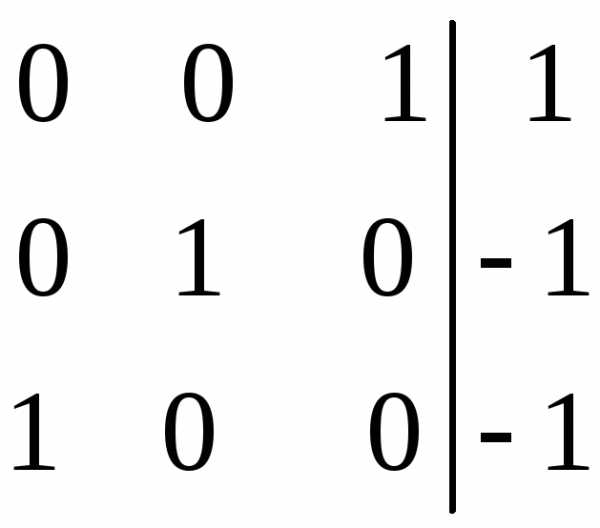
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | -1 | -3 | 1 | -2 | 2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | 0 | -8 | 2 | -1 | 6 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | 0 | 8 | -10.75 | -7.75 |
0 | 1 | 0 | 0 | 10 | -11 | -12 |
0 | 0 | 1 | 0 | 6 | -5.25 | -7.25 |
0 | 0 | 0 | 1 | 1 | -1.25 | -2.25 |
Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.
www.matem96.ru
3. Метод Жордана—Гаусса
Применяется для решения как неоднородных, так и однородных систем с произвольным числом уравнений m и произвольным числом неизвестных n. С помощью элементарных преобразований строк расширенной матрицы системы (АВ) исходную систему (4) преобразуют в равносильную, которая позволяет решить вопрос о совместности системы, и, если она совместна, записать её решение. Преобразования проводятся по следующей схеме, которая называется схемой Жордановых исключений:
1) выбираем любой элемент матрицы А, отличный от нуля. Он называется разрешающим элементом. Пусть это ars, тогда r-я строка называется разрешающей строкой, а s-й столбец называется разрешающим столбцом;
2) элементы разрешающей строки (r-й) оставляем без изменения;
3) элементы разрешающего столбца (s-го), кроме разрешающего элемента ars, заменяем нулями;
4) остальные элементы матрицы (АВ) пересчитываем по формуле:
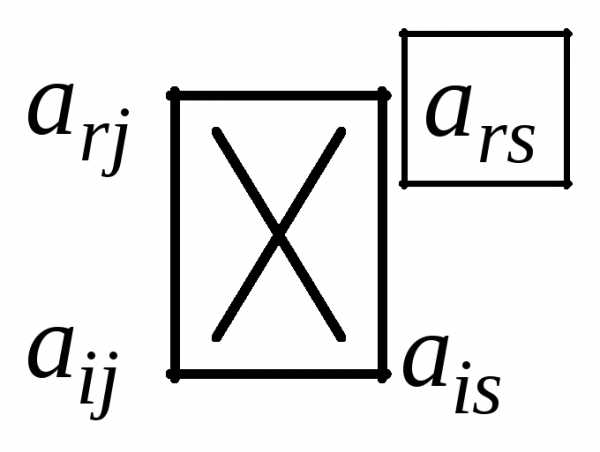
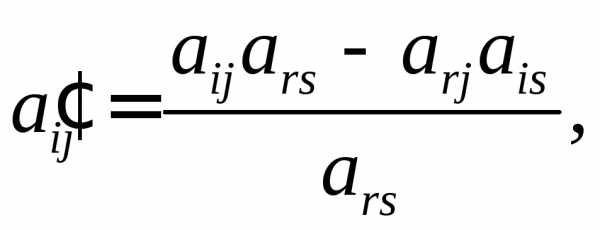
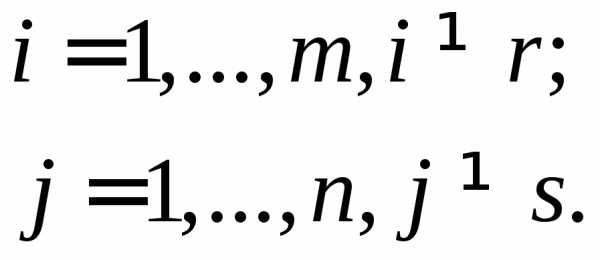 (7)
(7)
По этому же правилу
преобразуются и элементы столбца В,
кроме br.
В результате матрица (АВ)
преобразуется в эквивалентную матрицу
А, в которой снова выбираем разрешающий
элемент. Это любой элемент 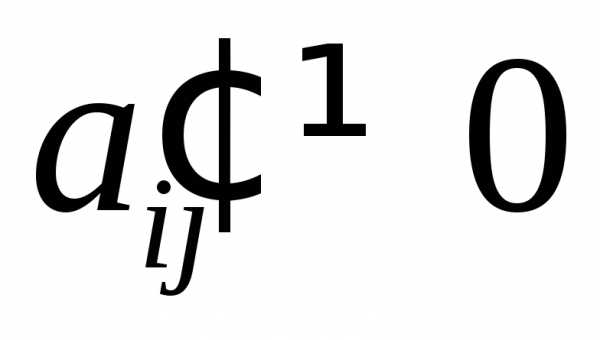 матрицыА
и расположенный в строке и столбце,
которые ещё не были разрешающими. Схему
преобразований 1—4 повторяем до тех
пор, пока все строки (или столбцы) матрицы А не будут использованы как разрешающие.
матрицыА
и расположенный в строке и столбце,
которые ещё не были разрешающими. Схему
преобразований 1—4 повторяем до тех
пор, пока все строки (или столбцы) матрицы А не будут использованы как разрешающие.
Если при преобразованиях появляется строка, полностью состоящая из нулей, то её можно отбросить.
Если при преобразованиях появляется строка, соответствующая противоречивому уравнению вида:
0·х1+
0·х2 + … + 0·хn = bi,
где 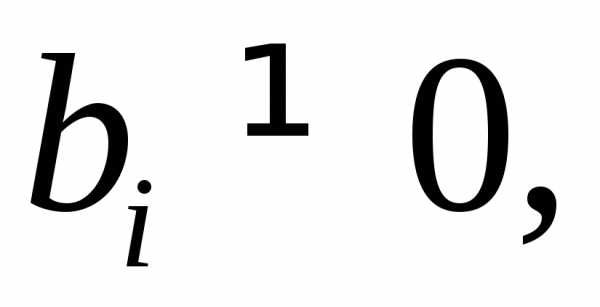
то процесс преобразований на этом прекращают, так как система уравнений несовместна.
Пример 2. Дана система уравнений А·Х = В, где
Решить систему тремя методами:
а) по формулам Крамера;
б) матричным методом;
в) методом Жордана—Гаусса.
Решение. Согласно условиям задания имеем:
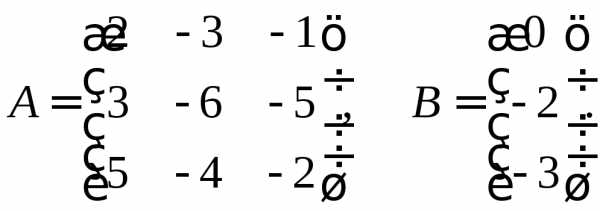
Систему линейных алгебраических уравнений А·Х = В запишем в координатной форме:
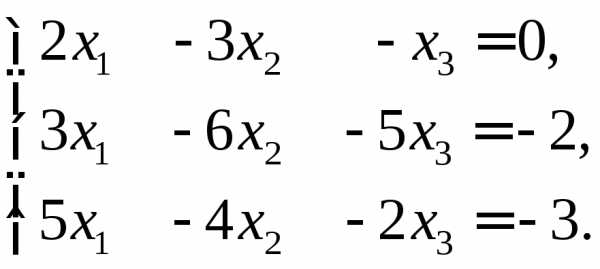
а) Решим систему по формулам Крамера.
Найдём определитель системы, используя формулы (2) и (1):
Так как 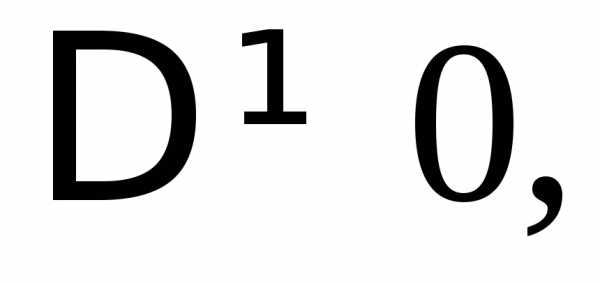 система имеет единственное решение,
которое находим по формулам Крамера
(5):
система имеет единственное решение,
которое находим по формулам Крамера
(5):
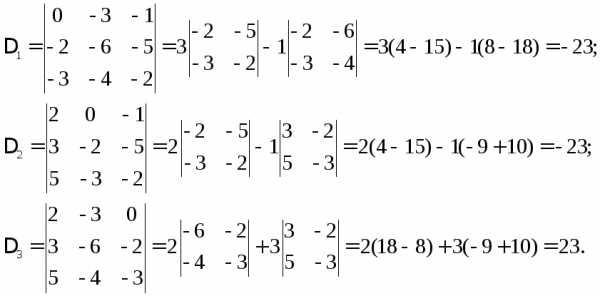
Итак,
Сделаем проверку, подставив найденные значения х1, х2, х3 в исходную систему, и убедимся, что все три уравнения данной системы обращаются в тождества:
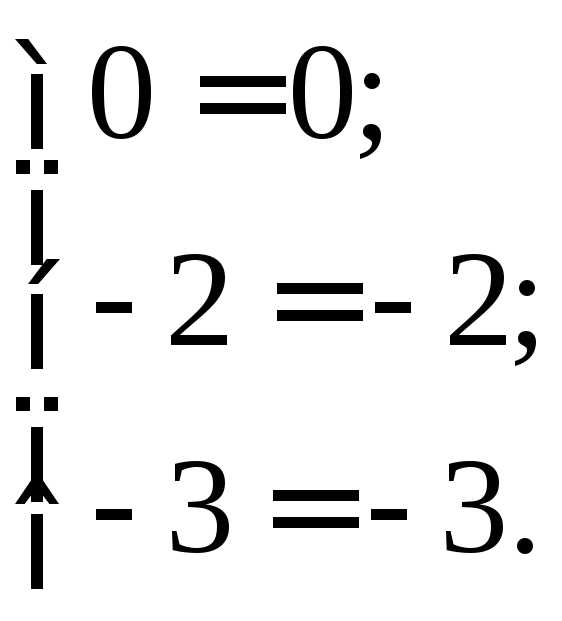
Ответ: х1 =–1, х2 = –1, х3 =1.
б) Решим систему матричным методом.
Из пункта а) следовательно, матрица системы имеет обратнуюА–1, которую найдём по формуле (3).
Для этого вычислим алгебраические дополнения:
Получим А–1 по формуле (3):
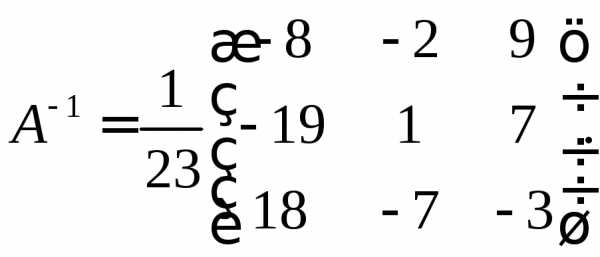
По формуле (6) имеем
Ответ: х1 = –1, х2 = –1, х3 = 1.
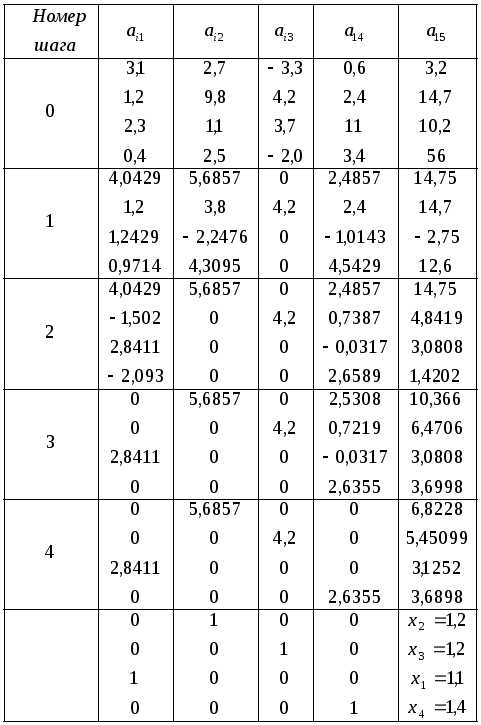
в) Решим систему методом Жордана—Гаусса.
Преобразования расширенной матрицы системы оформим в виде таблицы (см. табл.).
А/В | | Примечания |
|
| Умножим первую строку на –1 |
|
| Разрешающий элемент а13=1. Оставляем разрешающую строку (первую) без изменений. Все элементы разрешающего столбца (третьего), кроме а13, заменяем нулями. Остальные элементы преобразуем по формуле (7) |
|
| Разрешающий элемент а31=1. Оставляем разрешающую строку (третью) без изменений. Все элементы разрешающего столбца (первого), кроме а31, заменяем нулями. Остальные элементы преобразуем по формуле (7) |
|
| Умножим вторую строку на 1/23 |
|
| Разрешающий элемент а22 = 1. Оставляем разрешающую строку (вторую) без изменений. Все элементы разрешающего столбца (второго), кроме а22, заменяем нулями. Остальные элементы преобразуем по формуле (7) |
|
|
В последнем (четвертом) столбце матрицы АВ получено решение системы, соответствующее неизвестным в тех столбцах, в которых элементы равны единице, а именно: х1 = –1, х2 = –1, х3 = 1. Отметим, что решения системы, полученные в пунктах а), б) и в), как и следовало ожидать, совпадают.
Ответ: х1 = –1, х2 = –1, х3 = 1.
studfiles.net
Метод Гаусса-Жордана_методичка
Березнёва Т. Д.
Тема 7
«СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
МЕТОД ГАУССА – ЖОРДАНА.»
(Учебная дисциплина “Введение в линейную алгебру и аналитическую геометрию”)
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
МЕТОД ГАУССА – ЖОРДАНА.
Основные понятия
Уравнение с n переменными называется линейным, если все переменные (x1,x2, …xn) входят в него в степени 1. Общий вид такого уравнения формально записывается следующим образом:
a1x1 + a2x2 + … ajxj + … anxn = b, (*)
или

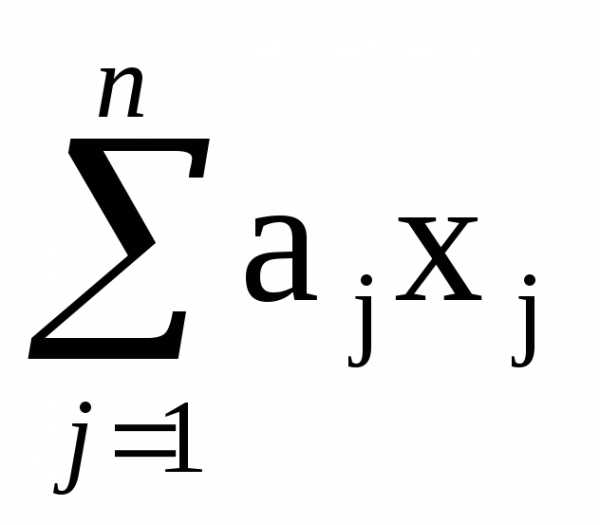 =b.
=b.
Величины aj, j = 1,…,n, и b являются известными (заданными). Величины aj называются коэффициентами при переменных (при неизвестных), а b — свободным членом.
Решением линейного
уравнения (*) называется упорядоченный набор (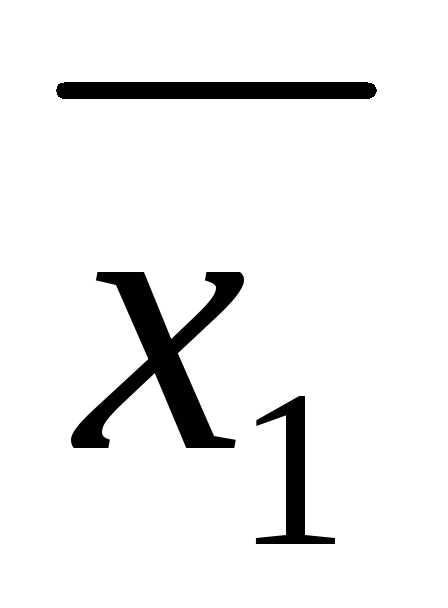 ,
,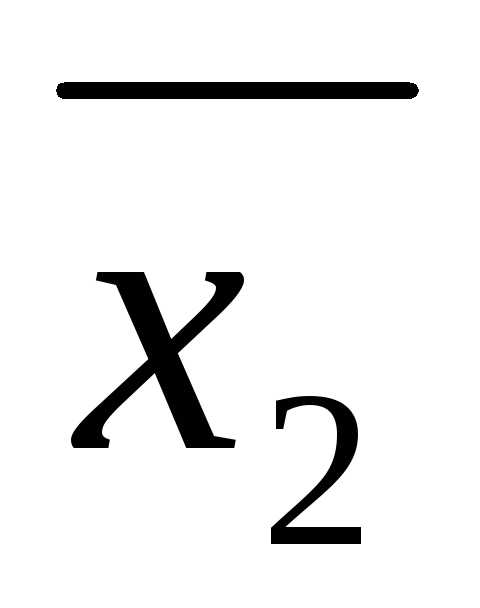 ,…,
,…,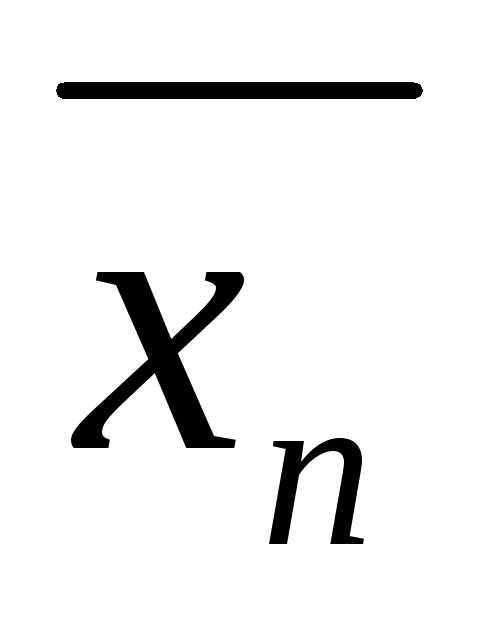 )
значений переменных, который при
подстановке в уравнение (т.е. при замене xjна
)
значений переменных, который при
подстановке в уравнение (т.е. при замене xjна 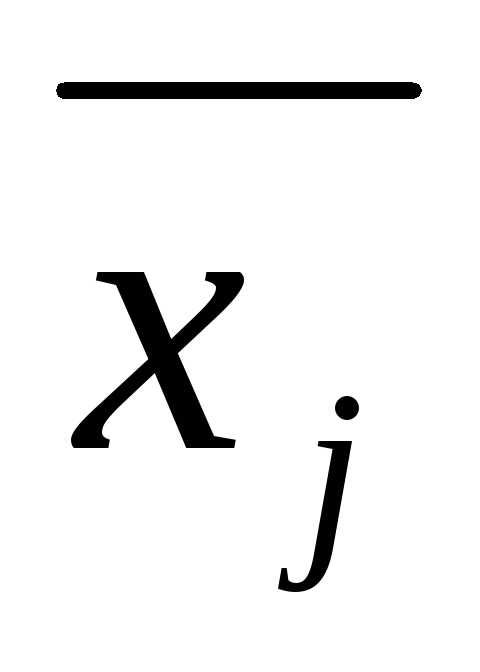 при всехj от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.
при всехj от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.
Рассмотрим одновременно m уравнений вида (*), т.е. систему m линейных алгебраических уравнений с n переменными. Пусть каждое i — е уравнение, i = 1,2,…,m, задается коэффициентами при переменных ai1, ai2, …, ain и свободным членом bi, т.е. имеет вид
ai1x1 + ai2 x2 + … + aij xj + … + ain xn = bi.
Тогда в общем виде система m линейных алгебраических уравнений с n переменными может быть записана в виде:
a11x1 + a12 x2 + … + a1j xj + … + a1n xn = b1
a21x1 + a22 x2 + … + a2j xj + … + a2n xn = b2
………………………………………………………………………………
ai1x1 + ai2 x2 + … + aij xj + … + ain xn = bi (1)
…………………………………………………
am1x1 + am2 x2 + … + amj xj + … + amn xn = bm
или, что то же самое,
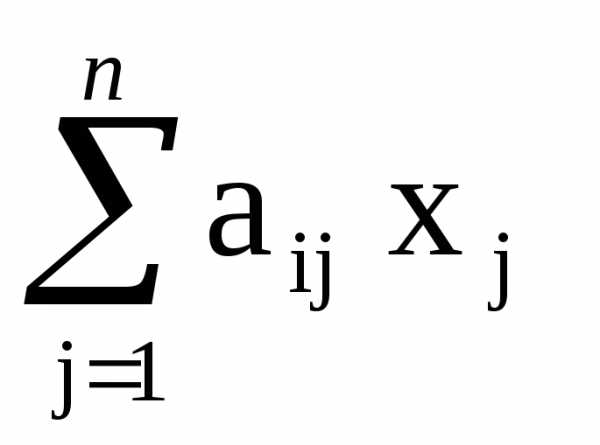 =bi, i = 1,…,m.
=bi, i = 1,…,m.
Если все свободные члены равны нулю, то система (1) называется однородной, т.е. имеет вид
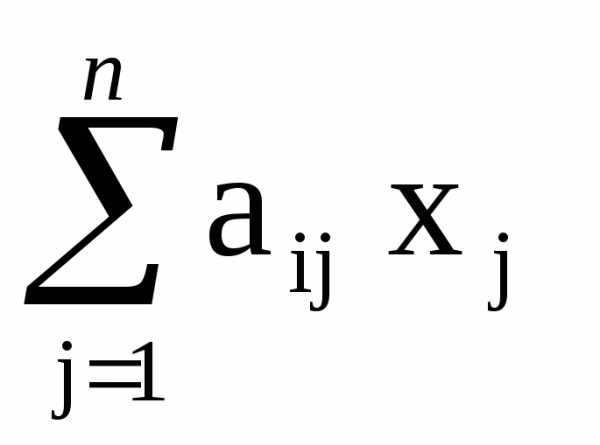 =
0,i = 1,…,m, (10)
=
0,i = 1,…,m, (10)
в противном случае — неоднородной. Система (10) является частным случает общей системы (1).
Решением системы
уравнений (1) называется упорядоченный набор ( ,
, ,…,
,…,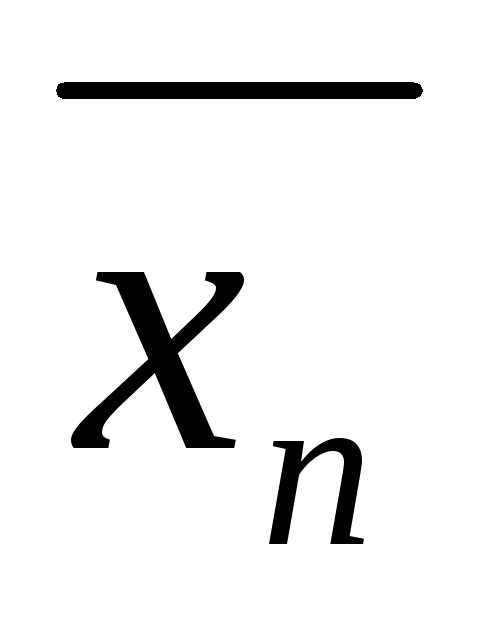 )
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xjна
)
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xjна 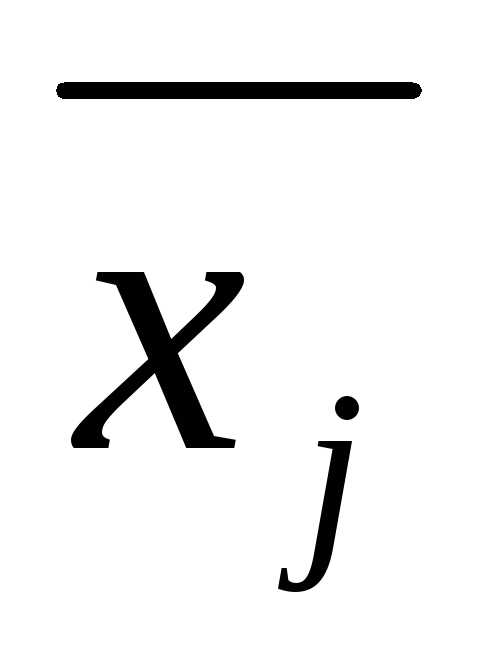 , j
= 1,…,n) все эти уравнения обращает в тождества,
т.е.
, j
= 1,…,n) все эти уравнения обращает в тождества,
т.е. 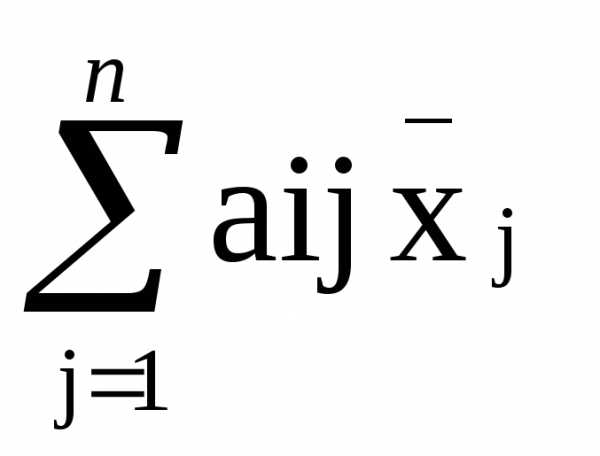 =bi при всех i
= 1,…,m.
=bi при всех i
= 1,…,m.
Система уравнений (1) называется совместной, если у нее существует хотя бы одно решение. В противном случае система называется несовместной.
Совокупность всех
решений системы уравнений (1) мы будем
называть множеством
ее решений и обозначать Xb(X0,
если система однородная). Если система
несовместна, то Xb =  .
.
Основная задача теории систем линейных алгебраических уравнений состоит в том, чтобы выяснить, совместна ли система (1), и, если совместна, то описать множество всех её решений. Существуют методы анализа таких систем, которые позволяют описывать множество всех решений в случае совместных систем или убеждаться в несовместности в противном случае. Одним из таких универсальных методов является метод последовательного полного исключения неизвестных, или метод Гаусса — Жордана, который мы будем подробно изучать.
Прежде, чем переходить к описанию метода Гаусса — Жордана, приведем ряд полезных для дальнейшего определений и утверждений.
Две системы уравнений называются эквивалентными, если они имеют одно и то же множество решений. Другими словами, каждое решение одной системы является решением другой, и наоборот. Все несовместные системы считаются эквивалентными между собой.
Из определений эквивалентности и множества решений систем вида (1) сразу же вытекает справедливость следующих утверждений, которые мы сформулируем в виде теоремы.
Теорема 1. Если в системе
(1) имеется уравнение с номером k,
1 k
k  m,
такое, что akj = 0
m,
такое, что akj = 0  j,
то
j,
то
если соответствующий свободный член bk
 0,
то система (1) несовместна;
0,
то система (1) несовместна;если соответствующий свободный член bk = 0, то k — е уравнение можно отбросить и получить систему из (m – 1) — го уравнения с n переменными, эквивалентную исходной.
Справедливость утверждений теоремы становится очевидной, если заметить, что k – е уравнение имеет вид
0x1 + 0 x2 + … + 0 xj + … + 0 xn = bk.
Теорема 2. Если к одному уравнению системы (1) прибавить другое уравнение этой же системы, умноженное на любое число, то получится система уравнений, эквивалентная исходной системе.
Доказательство. Умножим, например, второе уравнение
системы (1) на некоторое число  и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид
и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид
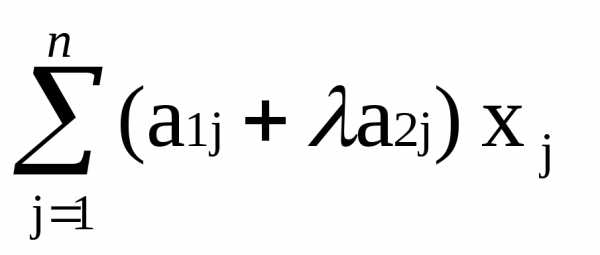 = b1 +
= b1 +  b2.
b2.
Очевидно, если
какой-нибудь набор (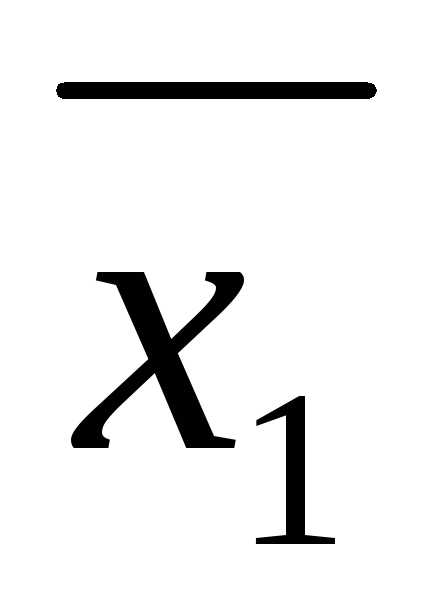 ,
,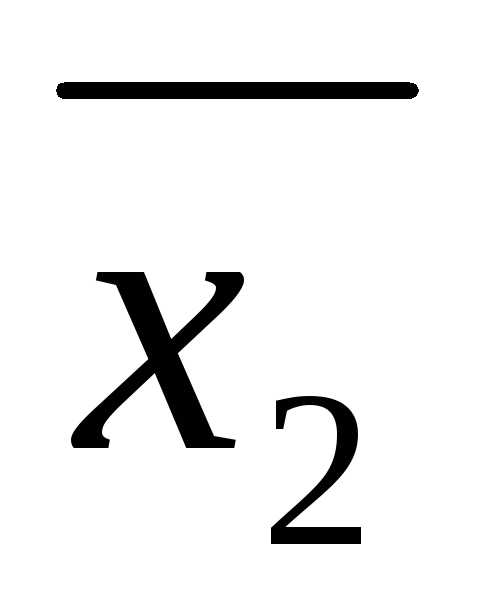 ,…,
,…,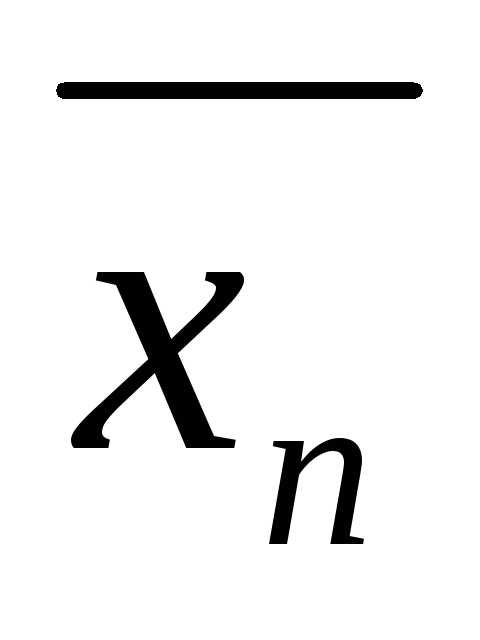 )
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (-
)
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (- ).
).
Точно также доказывается и следующее утверждение.
Теорема 2’. Умножение произвольного уравнения системы (1) на любое число, отличное от нуля, переводит систему (1) в эквивалентную ей систему уравнений.
Теоремы 2 и 2’ дают два вида преобразований, которым подвергалась система (1), оставаясь эквивалентной:
а) умножение (или деление) произвольного уравнения системы (1) на любое число, отличное от нуля;
б) прибавление (или вычитание) к одному уравнению другого, умноженного на некоторое число.
Такие преобразования а) и б) называются элементарными преобразованиями системы уравнений (1).
Если к системе уравнений (1) несколько раз применить элементарные преобразования, то полученная в результате система, очевидно, также будет эквивалентна первоначальной.
Систему уравнений (1) можно записать в табличной форме:
x1 | x2 | xj | xn | b | ||
a11 | a12 | … | a1j | … | a1n | b1 |
a21 | a22 | … | a2j | … | a2n | b2 |
… | … | … | … | … | … | … |
ai1 | ai2 | … | aij | … | ain | bi |
… | … | … | … | … | … | … |
am1 | am2 | … | amj | … | amn | bm |
(2)
Прямоугольная
таблица чисел, составленная из
коэффициентов aij при неизвестных системы (1), называется матрицей системы (1) и обозначается A
(в ней m
строк и n
столбцов), столбец свободных членов
обозначается b.
Прямоугольная таблица, составленная
из коэффициентов aij при неизвестных и из столбца свободных
членов b
системы (1), называется расширенной
матрицей системы
(1) и обозначается  (в нейm
строк и (n+1)
столбцов), т.е
(в нейm
строк и (n+1)
столбцов), т.е  = (A,
b).
В i
– ой строке матрицы
= (A,
b).
В i
– ой строке матрицы  содержатся всеизвестные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1).
содержатся всеизвестные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1).
Числа aij называются элементами матрицы А. Элемент aij находится в i — ой строке и в j — м столбце матрицы А. Принято говорить, что элемент aij находится на пересечении i — ой строки и j — го столбца матрицы А. Если все элементы строки (столбца) матрицы А (кроме одного) равны нулю, а ненулевой элемент равен единице, то такая строка (столбец) называется единичной (единичным).
Элементарным преобразованиям системы (1) соответствуют следующие элементарные преобразования таблицы (2):
а) умножение (или деление) всех элементов произвольной строки таблицы (2) на любое число, отличное от нуля,
б) прибавление (или вычитание) к одной строке (поэлементно) другой строки, умноженной на некоторое число.
В результате любого элементарного преобразования получается новая таблица, в которой вместо той строки, к которой прибавляли (или умножали на любое число, отличное от нуля), пишется новая строка, а остальные строки (в том числе и та, которую прибавляли) пишутся без изменения. Новая таблица соответствует системе уравнений, эквивалентной исходной системе.
Применяя элементарные преобразования можно таблицу (2) и соответственно систему (1) упростить так, что решить исходную систему становится просто. На этом и основан предлагаемый метод.
Метод последовательного полного исключения неизвестных
(Метод Гаусса — Жордана)
Метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана, является универсальным методом анализа любых (заранее неизвестно, каких — совместных или несовместных) систем линейных алгебраических уравнений. Он позволяет решать совместные системы или убеждаться в несовместности несовместных систем.
Отметим принципиальное отличие предлагаемого метода решения систем линейных алгебраических уравнений от метода решения, скажем, стандартного квадратного уравнения. Оно решается с помощью хорошо известных формул, в которых неизвестные выражаются через коэффициенты уравнения. В случае общих систем линейных алгебраических уравнений мы таких формул не имеем и используем для отыскания решения метод итераций, или итеративный метод, или итерационный метод. Такие методы задают не формулы, а последовательность действий.
Метод Гаусса — Жордана представляет собой последовательную реализацию ряда однотипных больших шагов (или итераций). Это конкретный итерационный метод — один из многих методов итераций, предложенных для решения систем линейных алгебраических уравнений вида (1). Он состоит из начального этапа, основного этапа и заключительного этапа. Основной этап содержит повторяющиеся итерации – наборы однотипных действий.
Пусть задана конкретная система линейных алгебраических уравнений (1). Это значит, что известны n, m, aij, bi, i = 1,…,m; j = 1,…,n. Опишем предлагаемый метод решения этой системы.
Начальный этап включает в себя построение таблицы I(0) вида (2) и выбор в ней ведущего элемента – любого ненулевого коэффициента при переменных из таблицы (2). Столбец и строка, на пересечении которых стоит ведущий элемент, называются ведущими. (Пусть выбран элемент ai0j0. Тогда i0 – ая строка ведущая, j0— й столбец ведущий.) Переходим к основному этапу. Заметим, что часто ведущий элемент называют разрешающим.
Основной этап состоит из повторяющихся однотипных итераций с номерами k = 1, 2,…. Опишем подробно итерации метода Гаусса — Жордана.
К началу каждой итерации известна некоторая таблица I вида (2), в ней выбран ведущий (разрешающий) элемент и, соответственно, ведущий столбец и ведущая строка. Кроме того, имеется информация о том, какие строки и столбцы уже были ведущими. (Так, например, после начального этапа, т.е. на итерации 1 известны I(0), ведущий (разрешающий) элемент ai0j0 и i0 – ая строка ведущая, j0— ой столбец ведущий.)
Итерация(с номером k) состоит из следующих действий.
Преобразование ведущего столбца (т.е. столбца, содержащего ведущий элемент) в единичный с 1 на месте ведущего элемента путем последовательного поэлементного вычитания ведущей строки (т.е. строки, содержащей ведущий элемент), умноженной на некоторые числа, из остальных строк таблицы. Сама ведущая строка преобразуется путем поэлементного деления ее на ведущий элемент.
Выписывается новая таблица I(k), (k — номер итерации), в которой все столбцы, которые были когда-либо ведущими, – единичные.
Проверяется, можно ли в таблице I(k) выбрать новый ведущий (разрешающий) элемент. По определению это любой ненулевой элемент, который стоит на пересечении строки и столбца, которые еще не были ведущими.
Если такой выбор возможен, то столбец и строка, на пересечении которых стоит ведущий (разрешающий) элемент, называются ведущими. Затем итерация повторяется с новой таблицей I(k), т.е. действия 1 – 3 повторяются с новой таблицей I(k). При этом строится новая таблица I(k+1).
Если нельзя выбрать новый ведущий элемент, то переходим к заключительному этапу.
Заключительный этап. Пусть проделано r итераций, получена таблица I(r), состоящая из матрицы коэффициентов при переменных A(r) и столбца свободных членов b(r) , и в ней нельзя выбрать новый ведущий элемент, т.е. метод остановился. Заметим, что метод обязательно остановится за конечное число шагов, т.к. r не может быть больше min{m,n}.
Каковы варианты остановки метода? Что значит «нельзя выбрать новый ведущий элемент»? Это значит, что после r – ой итерации в матрице A(r) новой системы, эквивалентной системе (1), либо
а) все строки A(r) были ведущими, т.е. в каждой строке стоит одна и ровно одна единица, которая не стоит больше не в какой другой строке,
либо
б) остались строки в A(r) , состоящие только из нулей.
Рассмотрим эти варианты.
а) В этом случае r
= m,
m  n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде
n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде
x1 | x2 | xr | xr+1 | xn | b | ||
1 | 0 | … | 0 | a(r)1,r+1 | … | a(r)1n | b(r)1 |
0 | 1 | … | 0 | a(r)2,r+1 | … | a(r)2n | b(r)2 |
… | … | … | … | … | … | … | … |
0 | 0 | … | 0 | a(r)i,r+1 | … | a(r)in | b(r)i |
… | … | … | … | … | … | … | … |
0 | 0 | … | 1 | a(r)m,r+1 | … | a(r)mn | b(r)m |
(3)
Подчеркнем, что в таблице (3) каждая переменная с номером i, не превосходящим r, встречается только в одной строке. Таблица (3) соответствует системе линейных уравнений вида
x1 + 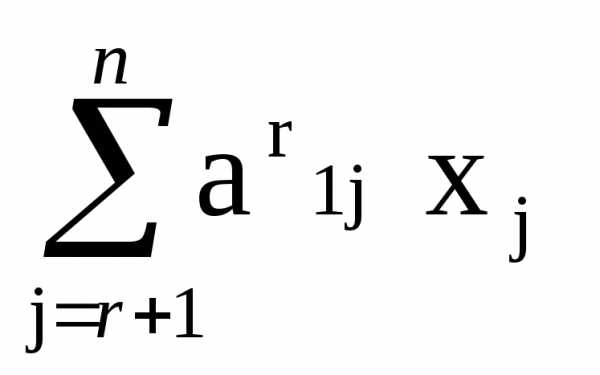 =b(r)1 ,
=b(r)1 ,
x2 + 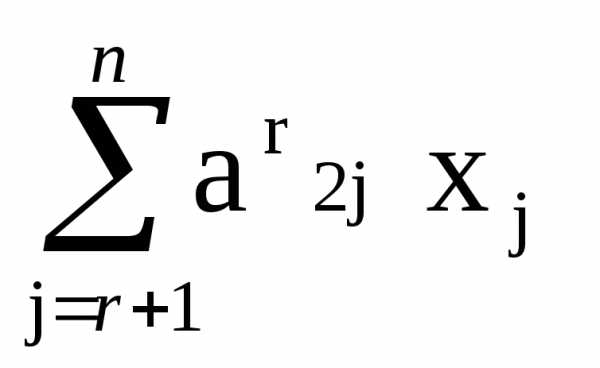 =b(r)2 ,
=b(r)2 ,
………………………, (4)
xr+ 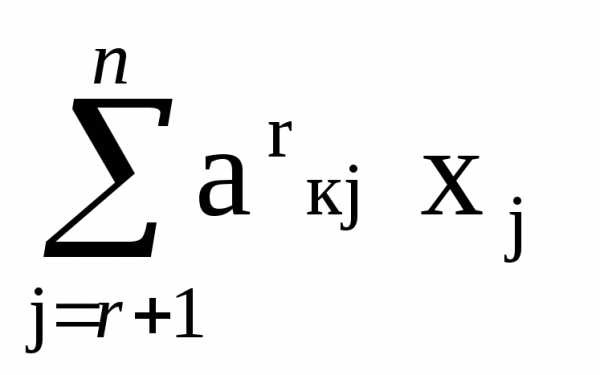 =b(r)r ,
=b(r)r ,
в которой каждая переменная с номером i, не превосходящим r, однозначно выражается через переменные xr+1 , … ,xn, коэффициенты матрицы a(r)ij , j = r+1,…,n, и свободный член b(r)i, представленные в таблице (3). На переменные xr+1 , … ,xn не накладываются никакие ограничения, т.е. они могут принимать любые значения. Отсюда произвольное решение системы, описываемой таблицей (3), или, что то же самое, произвольное решение системы (4), или, что то же самое, произвольное решение системы (1) имеет вид
xi = b(r)i — 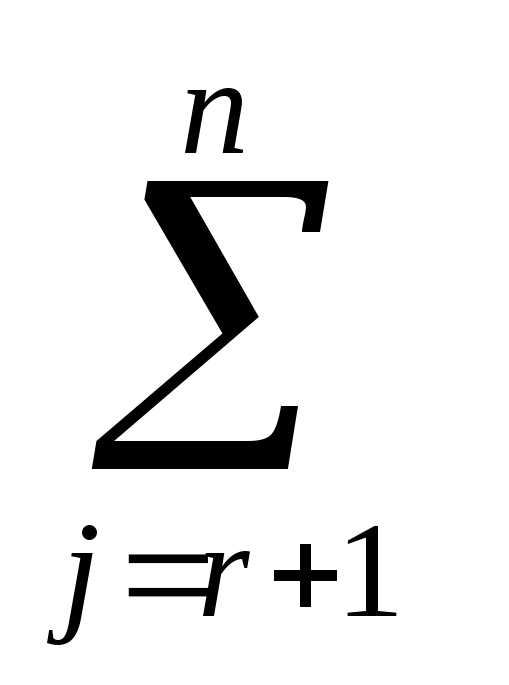 a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5)
a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5)
Тогда множество решений системы (1) можно записать как
Xb = {x=(x1 , … ,xn)
: xi = b(r)i — 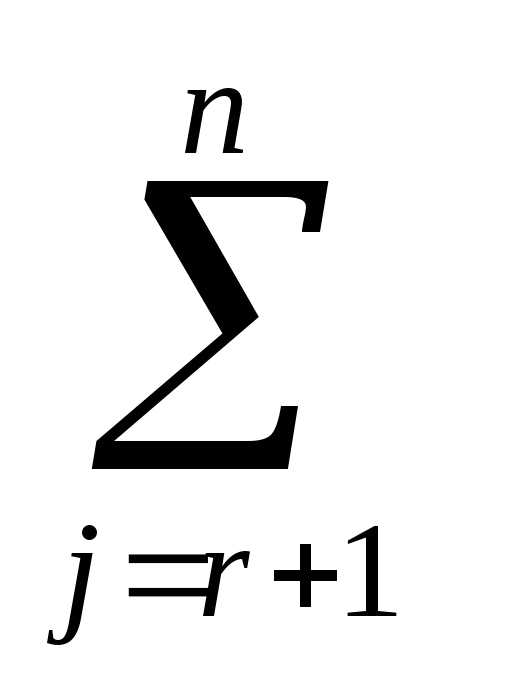 a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
б) В этом случае r < m, и существует хотя бы одна строка k, k > r, (предполагаем, что сделана перестановка строк и столбцов такая же, как в пункте а)) такая, что a(r)kj= 0 при всех j. Тогда, если соответствующий свободный член b(r)kне равен 0, то k — е уравнение не имеет решения, и, следовательно, вся система не имеет решения, т.е. система (1) несовместна.
Если же соответствующий b(r)kравен 0, то k — ое уравнение является лишним и его можно отбросить. Отбросив все такие уравнения, получим, что система (1) эквивалентна системе из r уравнений с n переменными, которая через r шагов записывается с помощью таблицы вида (3), в которой все строки были ведущими. Таким образом, мы пришли к рассмотренному выше случаю а) и можем выписать решение вида (5).
Метод Гаусса – Жордана описан полностью. За конечное число итераций система линейных алгебраических уравнений будет решена (если она совместна) или будет очевидно, что она несовместна (если она действительно несовместна).
Переменные, соответствующие ведущим (разрешающим) элементам, или стоящие в ведущих столбцах, принято называть базисными, а остальные переменные — свободными.
Обратим внимание на следующее.
1) Когда мы начинаем решать систему методом Гаусса — Жордана, мы можем не знать, совместна эта система или нет. Метод Гаусса — Жордана за конечное число итераций r даст ответ на этот вопрос. В случае совместной системы на основании последней таблицы выписывается общее решение исходной системы. В этом случае число базисных переменных обязательно равно номеру r последней итерации, т.е. числу выполненных итераций. Число r всегда не превосходит min{m,n}, где m — число уравнений системы, а n — число переменных системы. Если r < n, то (n – r) равно числу свободных переменных.
2) При записи общего решения не нужно перенумеровывать переменные, как это делалось для простоты понимания при описании Заключительного этапа. Это сделано для более ясного понимания.
3) При решении системы (1) методом Гаусса — Жордана базисными переменными будут только переменные, соответствующие столбцам, которые на каких-то итерациях выступали в роли ведущих, и наоборот, если на какой-то итерации столбец выступал в качестве ведущего, соответствующая ему переменная обязательно будет в числе базисных.
4) Если общее решение системы (1) содержит хотя бы одну свободную переменную, то эта система имеет бесконечно много частных решений, если же свободных переменных нет, то система имеет единственное решение, которое совпадает с общим решением.
5) Ведущие элементы могут быть выбраны на каждой итерации различным способом. Важно только то, что это ненулевые коэффициенты, стоящие на пересечении строки и столбца, которые до этого не были ведущими. Различный выбор ведущих элементов может дать различные записи множества решений. Однако, само множество решений при любой записи одно и то же.
Поясним работу метода на примерах.
Пример I. Решить следующую систему линейных алгебраических уравнений
2 x1 – 3 x2 + 3 x3 + 5 x4 = -1,
3 x1 + 4 x2 — 2 x3 + 6 x4 = 2, (6)
5 x1 – 4 x2 + 6 x3 + 10 x4 = 2
методом последовательного полного исключения неизвестных (методом Гаусса — Жордана).
Начальный этап. Сначала выпишем систему уравнений (6) в более удобной форме — в виде таблицы I(0).
x1 | x2 | x3 | x4 | b | |
I(0) | 2 | -3 | 3 | 5 | -1 |
3 | 4 | -2 | 6 | 2 | |
5 | -4 | 6 | 10 | 2 |
studfiles.net
1.Решение систем линейных уравнений методом гаусса – жордана
1.1. Основные понятия
Система m линейных уравнений с n неизвестными имеет следующий вид:
Здесь хj ( j=1, n ) – переменные ( или неизвестные) системы, аij ( i =1,m; j = 1,n ) – коэффициенты при переменных, вi ( i =1,m ) – свободные члены.
Решением системы ( І.І) называется всякий набор значений переменных х1, х2, …, хn, при котором все уравнения превращаются в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае.
Например, система
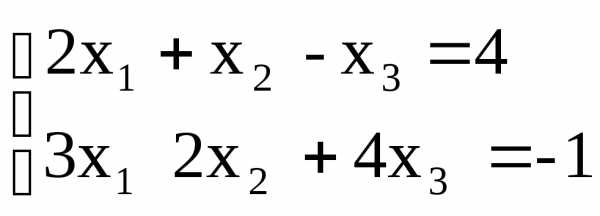
совместна, так как она имеет, в частности, такое решение:
х1 =
1; х2 =
2; х3 = 0 .
Система же 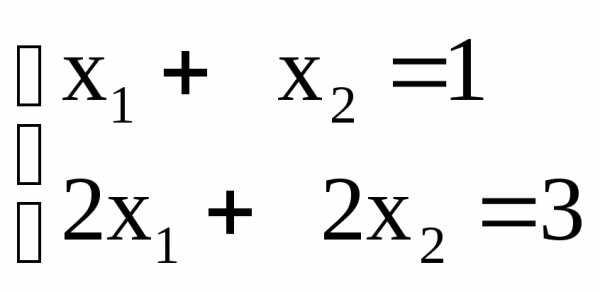
несовместна.
Две системы линейных уравнений называются равносильными, если каждое решение одной из них является решением другой, и наоборот. Если какое-либо уравнение системы умножить на постоянный множитель λ ≠ 0 , то получится система уравнений, равносильная исходной. Аналогично, если к какому-либо уравнению системы прибавить другое уравнение системы, то получится система, равносильная исходной.
Наконец если, в системе есть уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = 0, то такое уравнение можно убрать, получив систему, равносильную исходной.
1.2. Приведение системы линейных уравнений к жордановой форме
Процесс отыскания решения системы линейных уравнений начинается с того, что система приводится к жордановой форме.
Определение. Жордановой формой системы (I.I) называется система линейных уравнений, обладающая следующими свойствами:
а) она равносильна системе (I.I)
б) в каждом уравнении жордановой формы есть такая переменная, которая входит в это уравнение с коэффициентом 1, а в остальные уравнения — с коэффициентом 0.
Так, если системе (I.I) равносильна следующая система линейных уравнений:
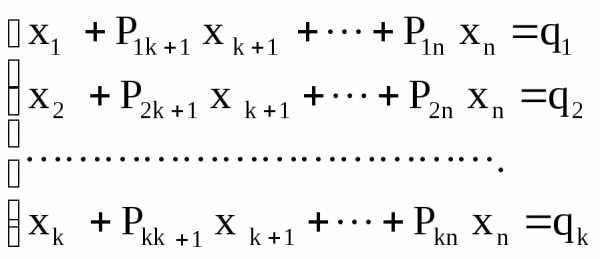 (1.2)
(1.2)
то (І.2) есть жорданова форма для (I.I). При этом переменные х1, х2,… ,хк называются базисными, остальные переменные хк+1,…, хn называются свободными. Жорданова форма всегда является совместной системой линейных уравнений. Действительно, система (І.2) имеет следующее решение:
(І.3)
Так как система (І.2) равносильна системе ( І.І ) , то (І.3) является решением системы (І.І).
Таким образом, если для системы линейных уравнений ( І.І ) существует жорданова форма, то ( І.І ) – совместная система. Несовместная система жордановой формы не имеет.
Покажем, что любую совместную систему можно привести к жордановой форме. Это достигается методом Гаусса-Жордана, который состоит в следующем.
Рассмотрим первое уравнение системы (І.І). Выберем в нем переменную, коэффициент при которой отличен от нуля. Предположим, что а11 ≠ 0. Поделим уравнение на а11.
Получим уравнение
х1+ а12х2 + … + а1nхn = в1 (І.4)
Будем переменную х1 делать базисной в жордановой форме. Для этого ее нужно исключить из остальных уравнений системы. Чтобы исключить х1 из второго уравнения, умножим уравнение (І.4) на -а21 и сложим со вторым уравнением. Затем исключим х1 из третьего уравнения, для чего уравнение (І.4) умножим на –а31 и сложим с третьим уравнением. Аналогично переменная х1 исключается из остальных уравнений. Таким образом, взяв в качестве «ведущего» первое уравнение и проведя серию «жордановых исключений», мы получим равносильную (I.I) систему уравнений, в которой x1 входит в первое уравнение с коэффициентом 1 , а в остальные уравнения — с коэффициентом 0.
После этого выбираем в качестве ведущего второе уравнение полученной системы. В этом уравнении берем коэффициент, отличный от нуля (пусть это коэффициент при х2), делим уравнение на этот коэффициент и затем исключаем х2 из всех остальных уравнений (в том числе и из первого). Затем в качестве ведущего выбираем третье уравнение и т.д.
Если на некотором шаге возникнет уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = 0 (І.5)
то удаляем его из системы. Если же возникнет уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = b ≠ 0, то это свидетельствует о несовместности исходной системы ( І.І), а несовместная система к жордановой форме не приводится.
Таким образом, метод Гаусса-Жордана совместную систему линейных уравнений приводит к жордановой форме, а в случае несовместности системы обнаруживает несовместность.
Ясно,
что в жордановой
форме число уравнений не может быть
больше числа уравнений в исходной
системе. Так, если система (1.2) является
жордановой формой для системы (I.I),
то 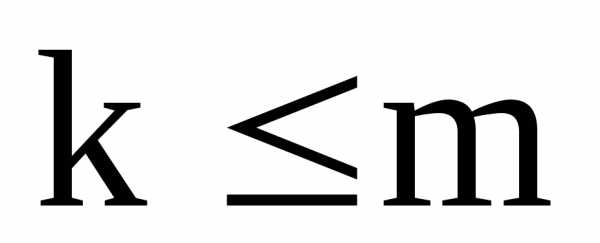 ,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).
,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).
Очевидно, одна и та же система может иметь много различных жордановых форм.
Пример. Привести к жордановой форме
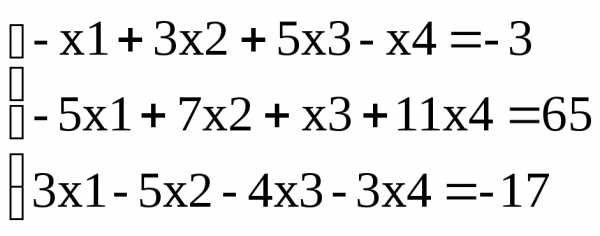
Выберем в качестве ведущего первое уравнение, а в качестве базисной переменной — переменную х1. Поделим первое уравнение на (-1) (коэффициент при х1), получим:

Умножим это уравнение на (+5) и прибавим ко второму уравнению, затем умножим его на (-3) и прибавим к третьему уравнению.
Получим систему:
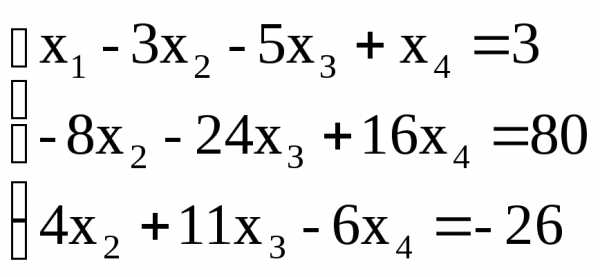
Теперь
сделаем ведущим второе уравнение, а
базисной переменной — переменную 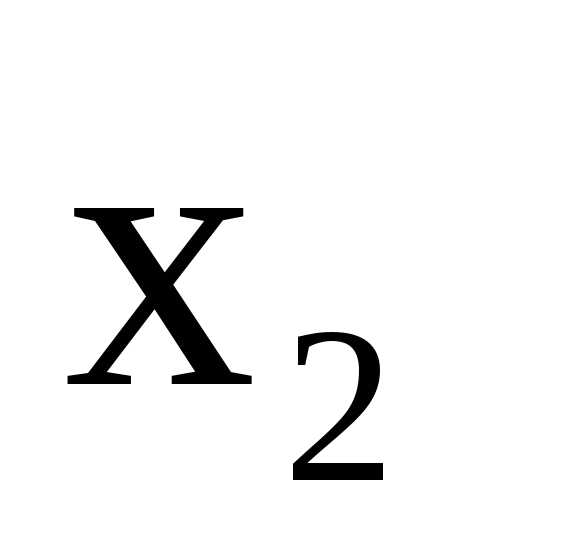 .
Поделив второе уравнение на (-8) и исключив
.
Поделив второе уравнение на (-8) и исключив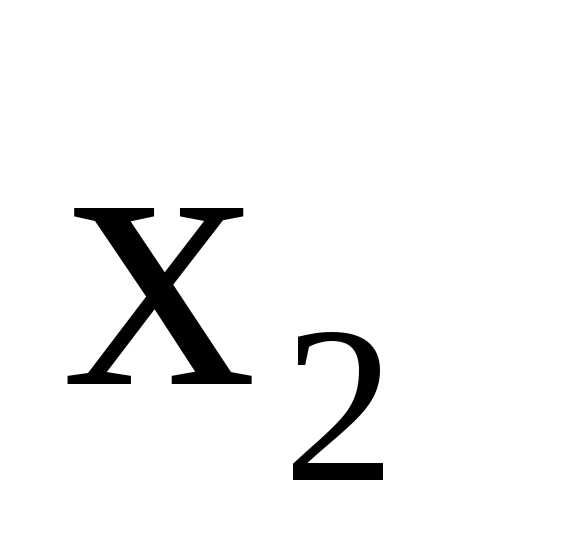 из
первого и третьего уравнений, получим
систему:
из
первого и третьего уравнений, получим
систему:
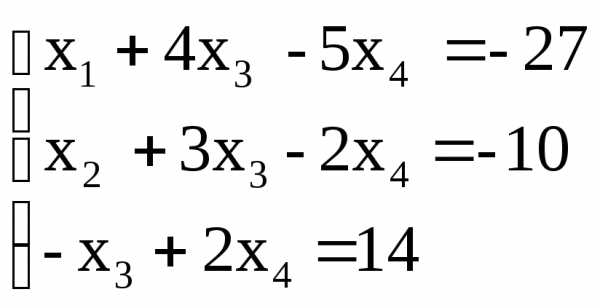
Наконец,
в третьем уравнении выбираем в качестве
базисной переменную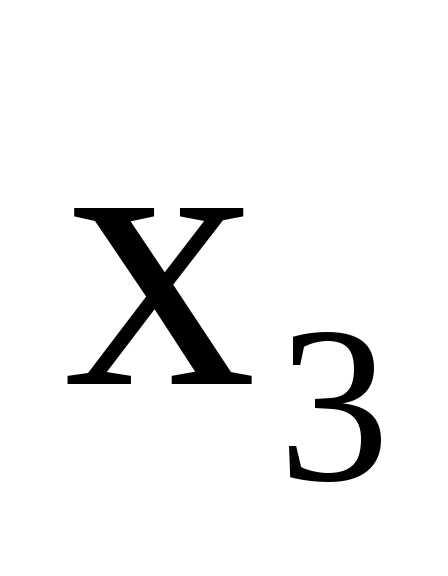 .
Поделим это уравнение на (-1) и исключим
.
Поделим это уравнение на (-1) и исключим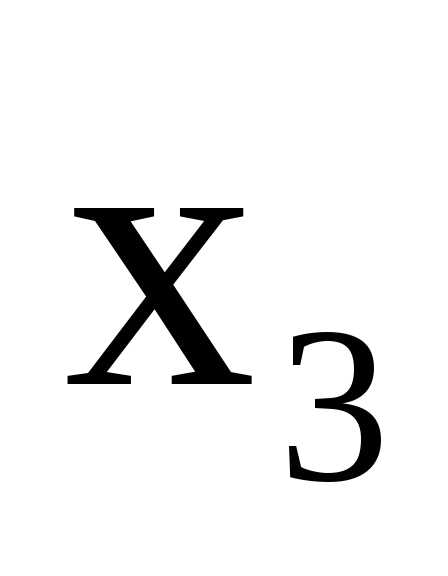 из остальных уравнений. Получим жорданову
форму:
из остальных уравнений. Получим жорданову
форму:
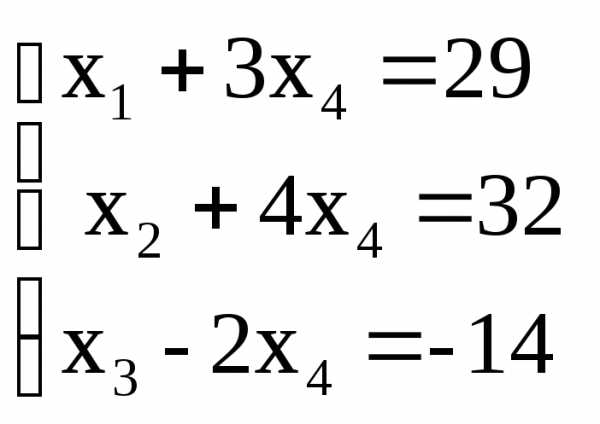
Переменные
являются
базисными, переменная —
свободной.
—
свободной.
studfiles.net
Метод Гаусса-Жордана (единичная матрица) (метод полного исключения)
Схема Гаусса-Жордана или метод полного исключения, заключается в одновременном исключении (Жордановом исключении) какого либо переменного из всех уравнений системы, кроме одного. Его удобно реализовать на ЭВМ, учитывая ограниченность на их памяти, так как схема вычислений не требует выполнения обратного хода.
На первом шаге
этого метода выберем ведущий элемент 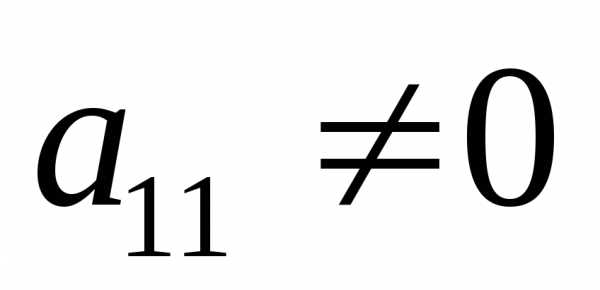 (перестановкой уравнений системы можно
добиться того, что
(перестановкой уравнений системы можно
добиться того, что будет наибольшим по модулю коэффициентом
при
будет наибольшим по модулю коэффициентом
при ).
Разделим первое уравнение системы на
).
Разделим первое уравнение системы на ,
во всех остальных уравнениях исключим
,
во всех остальных уравнениях исключим ,
то есть сведем расширенную матрицы
системы к виду
,
то есть сведем расширенную матрицы
системы к виду
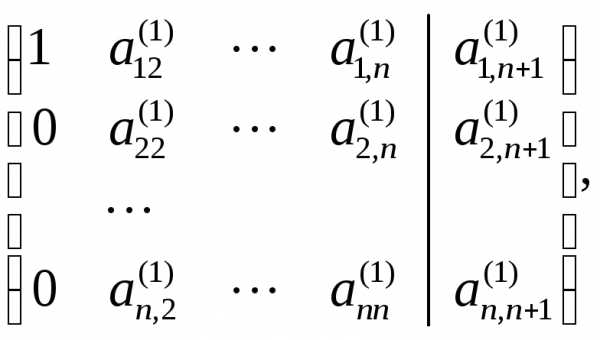
где
во втором шаге
выберем ведущий элемент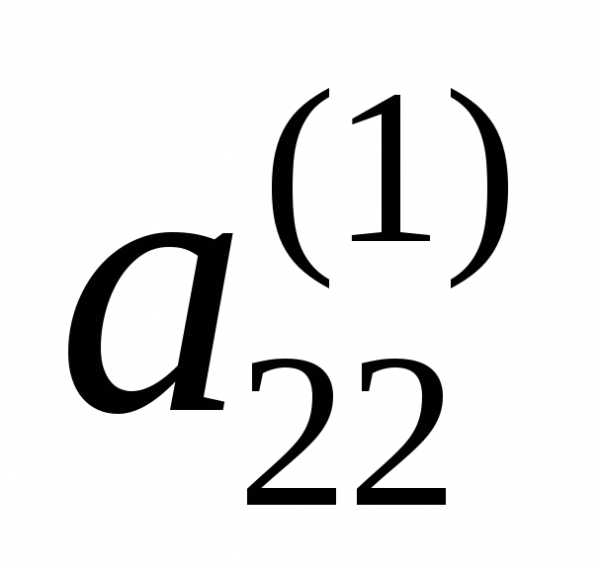 (можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на
(можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на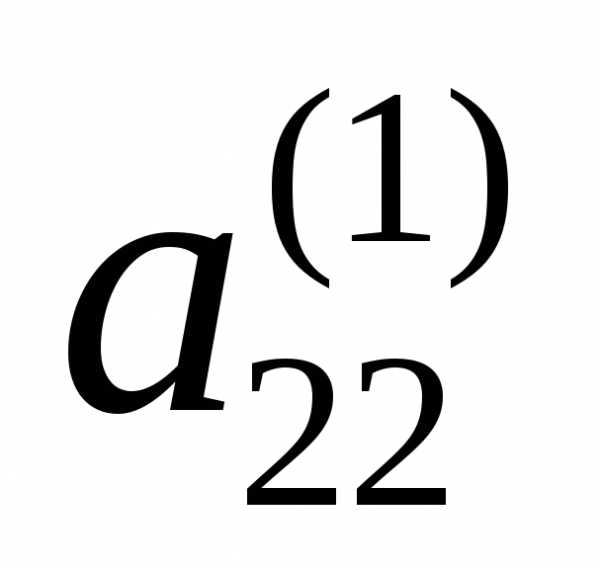 ,
исключим
,
исключим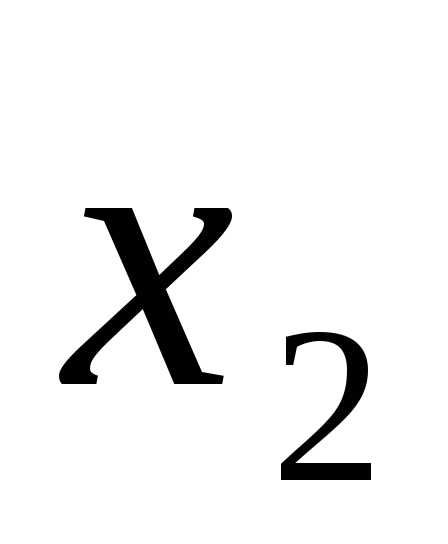 из всех уравнений кроме второго.
из всех уравнений кроме второго.

где
После n шагов получим матрицу

и численное значение неизвестных
Контроль вычислений можно осуществлять также, как и в схеме единственного деления, используя контрольные суммы.
Вычисление определителя и обратной матрицы метода Гаусса
В прямом ходе метода Гаусса над элементами матрицы А производятся элементарные преобразования, которые не изменяют определитель матрицы, кроме операции деления на ведущий элемент. Матрица преобразуется к треугольному виду с единичными диагональными элементами, ее определитель равен единице. Если в прямом ходе строки матрицы не переставляются то знак определителя не изменяется. Таким образом определитель не вырожденной матрицы системы равен произведению ведущих элементов в прямом ходе исключения Гаусса
.
Для его вычисления прямой ход метода Гаусса , как и при решении системы, только без преобразований вектора b. При решении линейной системы определитель можно вычислить попутно.
Если применяется
метод исключения с выбором главного
элемента, то в (13) необходимо добавить
множитель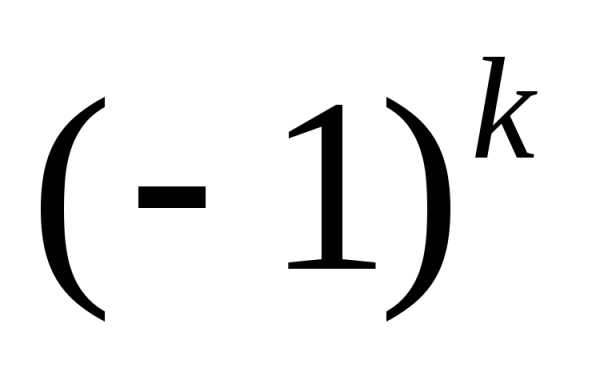 ,
гдек – количество перестановок строк и
столбцов.
,
гдек – количество перестановок строк и
столбцов.
Все вычислительные схемы метода Гаусса позволяют осуществлять одновременное решение систем линейных уравнений с различными правыми частямиПри этом количество вычислений увеличивается на преобразование новых столбцов правых частей, что дает значительную экономию времени счета.
В частности если
вместо столбцов 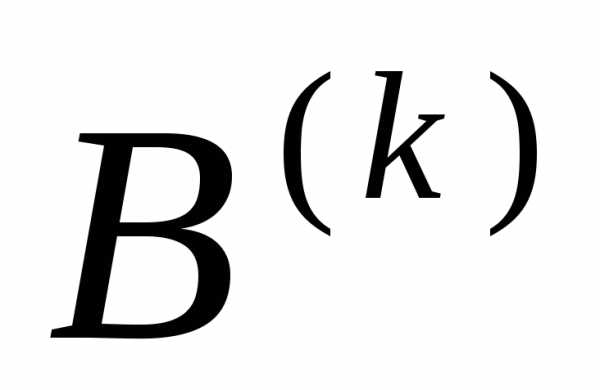 выбирать столбцы единичной матрицы
порядкаn:
выбирать столбцы единичной матрицы
порядкаn:
(1 на к-ом
месте, остальные элементы – нули), к=1.2
, …, n, то
решение 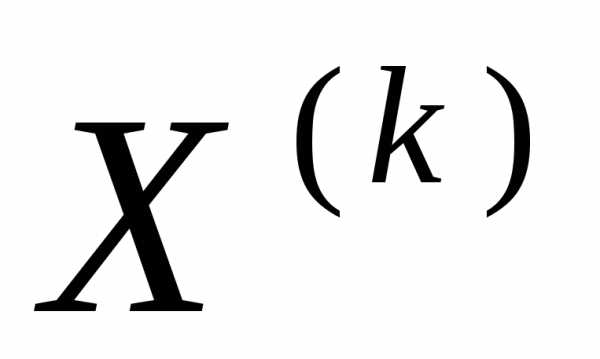 системыбудетк-м
столбцом обратной матрицы
системыбудетк-м
столбцом обратной матрицы 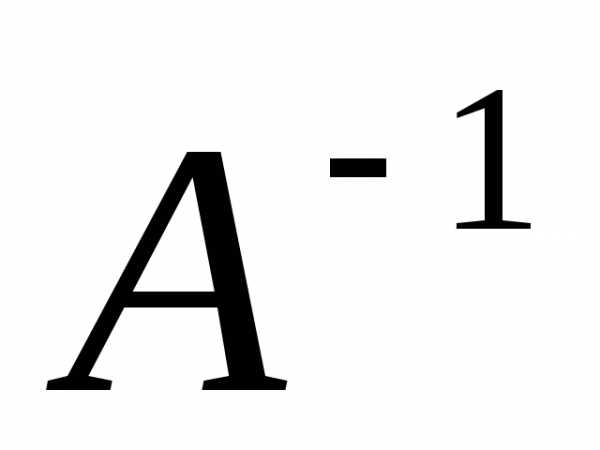 .
.
Таким образом для вычисления обратной матрицы требуется решить одновременно n систем уравнений с n неизвестными. Проводим последовательные исключения неизвестных в расширенной матрице
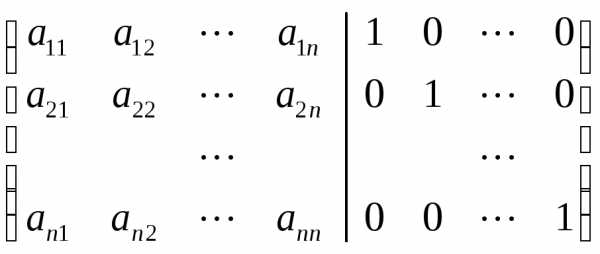 ~после n шагов
~после n шагов
~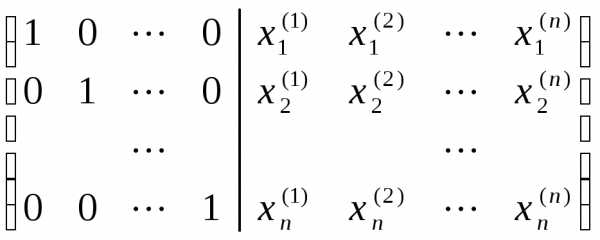 .
.
Справа получим элементы обратной матрицы
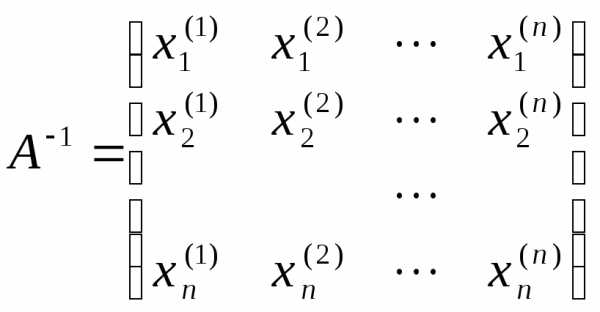 .
.
Пример. Решить систему
методом Жордана-Гаусса.
Ответ,,.
Пример. Решить методом Гаусса-Жордана с выбором главного элемента системы
Ответ
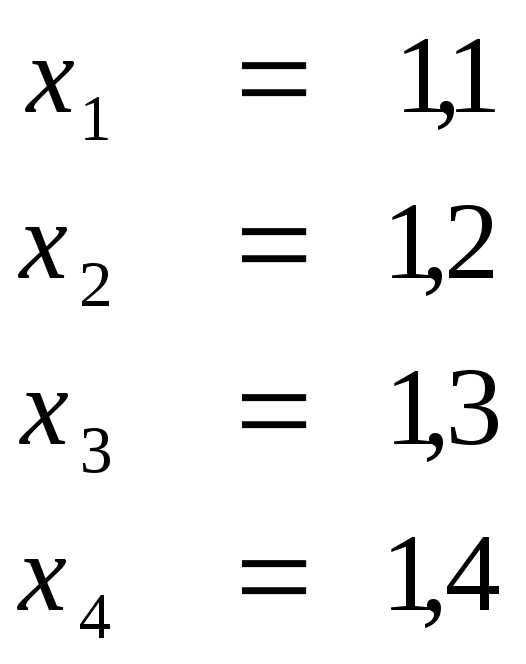 .
.
Определитель равен .
Метод прогонки
Большинство технических задач сводится к решению систем линейных алгебраических уравнений, в которых матрицы содержат много нулевых элементов, а ненулевые элементы расположены по специальной структуре, например, ленточные квазитреуголные матрицы.
Задачи построения интерполяционных сплайнов, разностные методы решения краевых задач для дифференциальных уравнений сходится к решению системы алгебраических уравнений с трехдиагональной матрицей А. В матрице А все элементы не лежащие на главной диагонали и двух соседних диагоналях равны нулю. Такие системы можно записать
Выбор наибольшего элемента при исключении неизвестных методом Гаусса в таких системах делать нельзя, поскольку перестановка строк разрушает структуру матрицы. Наиболее часто к решению систем с трехдиагональной матрицей применяют метод прогонки, который является частным случаем метода Гаусса.
Прямой ход метода
прогонки заключается в исключении
элементов 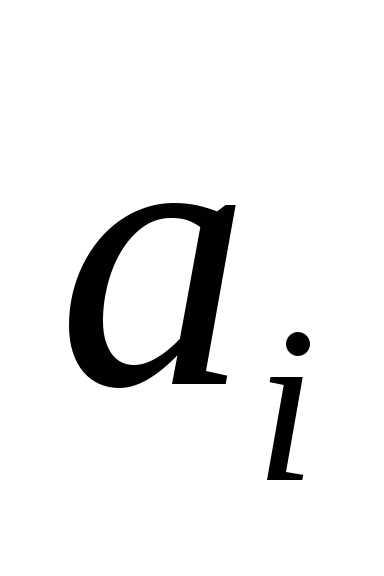 в системе (25). Так как
в системе (25). Так как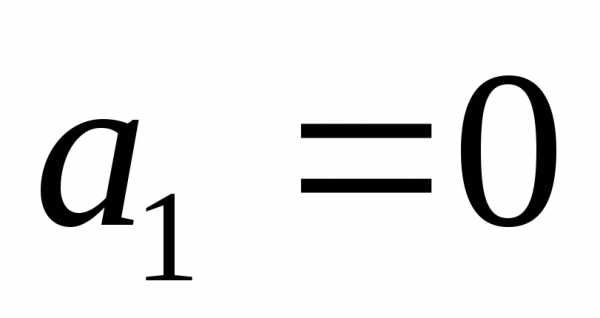 ,
то первое уравнение системы имеет вид
,
то первое уравнение системы имеет вид
.
Выразим  через
через :
: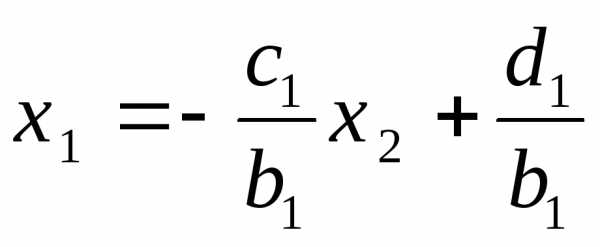 и подставим во второе уравнение системы,
получим уравнение связывающее
и подставим во второе уравнение системы,
получим уравнение связывающее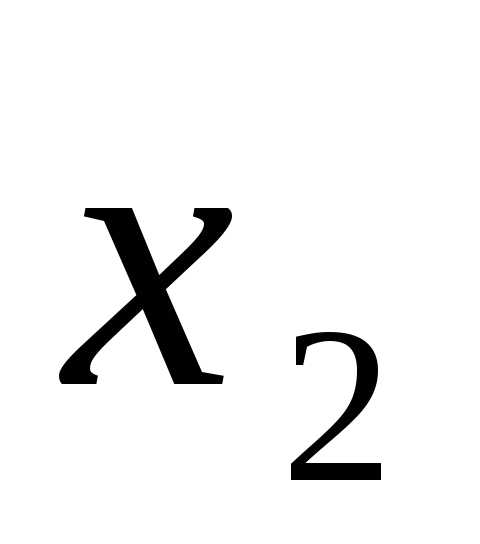 и
и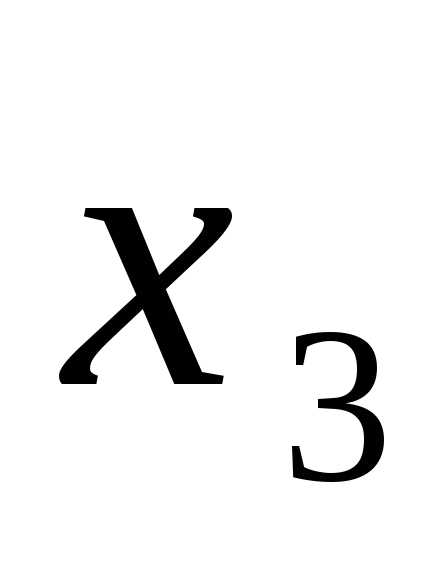 и так далее. Пусть уже получено соотношение
и так далее. Пусть уже получено соотношение
Понизим в (26) индекс
на единицу и подставим значение 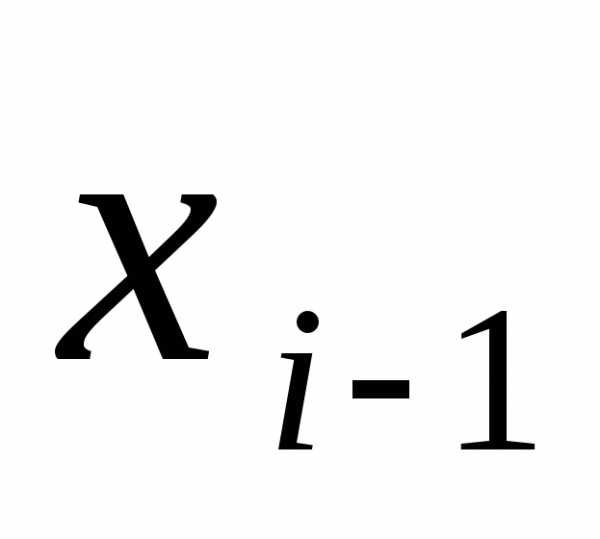 вi-е
уравнение системы (25)
вi-е
уравнение системы (25)
.
Отсюда
.
Сравнивая это
выражение с (26) получим рекуррентные
формулы для вычисления  в прямом ходе:
в прямом ходе:
.
Учитывая, что , полагаем. Обратный ход осуществляется по (26).
Почти во всех задачах, приводящих к решению системы (25) с трехдиагональной матрицей, обеспечивается условие преобладания диагональных элементов .
Это обеспечивает существование единичного решения и достаточно хорошую устойчивость метода прогонки относительно
studfiles.net
Решение системы линейных уравнений методом Гаусса-Жордана
метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.
Алгоритм метода Гаусса
- На основании системы линейных уравнений составляем расширенную матрицу системы;
- Приводим матрицу к «треугольному» виду;
- Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
- В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через
переменные которые могут принимать произвольные значения;
Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.
Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:
Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.
На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:
- Рассматриваем строку i(начиная с первой). Если, элемент aii равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a11 отличен от нуля — переходим к следующему шагу;
- Для каждой строки j, ниже i-й находим значение коэффициента Kj=aji/aii;
- Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: ajkнов.=ajk-Kj*aik;
После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A- В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пaii, которое и будет являтся определителем;
Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
Комментарий к шагу 3 Метода Гаусса. Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k столбцов с сохранением их порядка. Если номера столбцов, в которых расположен минор M, совпадают с номерами строк, то этот минор называется главным. Каждая матрица A порядка n имеет
(Ckn)2 миноров k-го порядка. Минорами 1-го порядка являются сами элементы матрицы A.
Основываясь на сравнении полученных значений рангов для основной и расширенной матрицы можно сделать следующие выводы о разрешимости системы:
- если ранг основной системы равен рангу расширенной и равен числу уравнений системы (rangA=rangA’=n), то система совместна и имеет единственное решение;
- если ранг основной системы равен рангу расширенной, но меньше числа уравнений в системе (rangA=rangA’
- если ранг основной системы меньше ранга расширенной (rangA
uchimatchast.ru

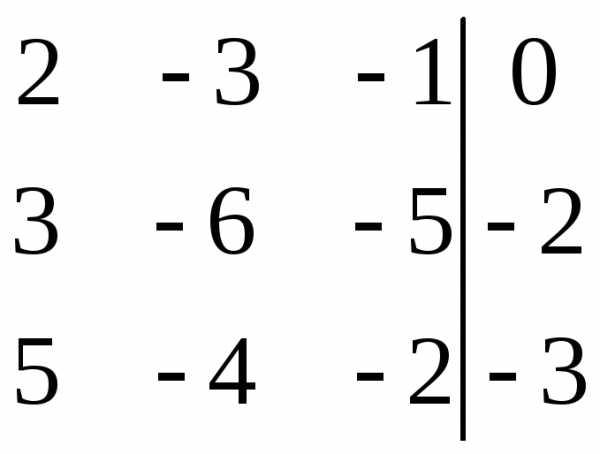
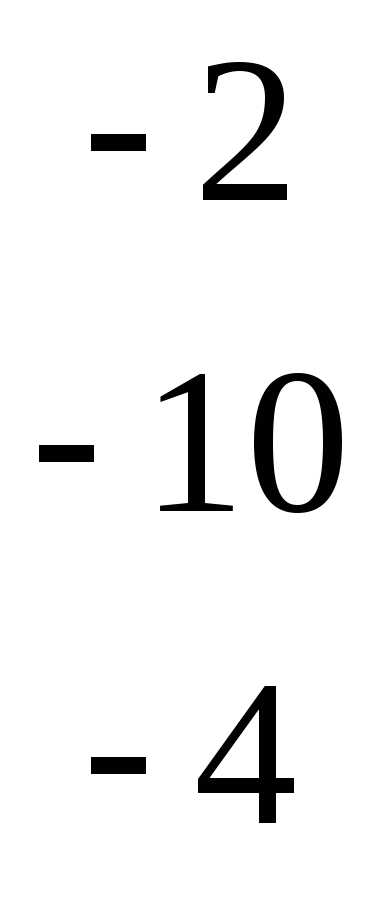
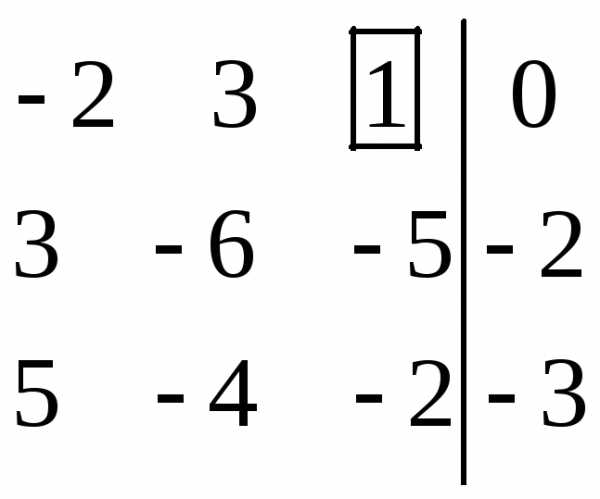
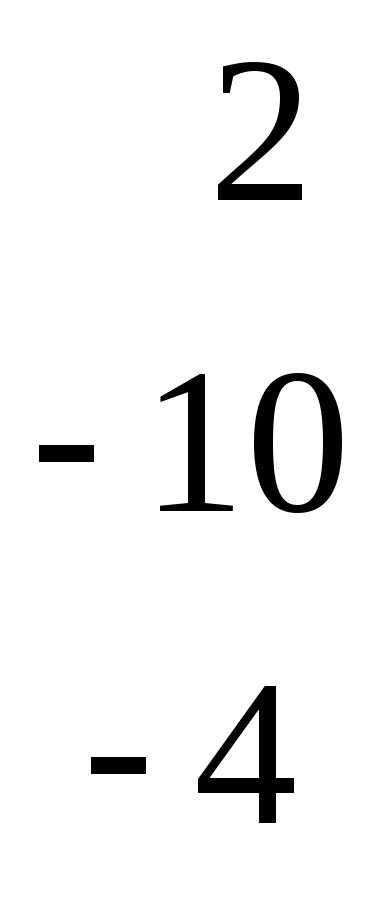
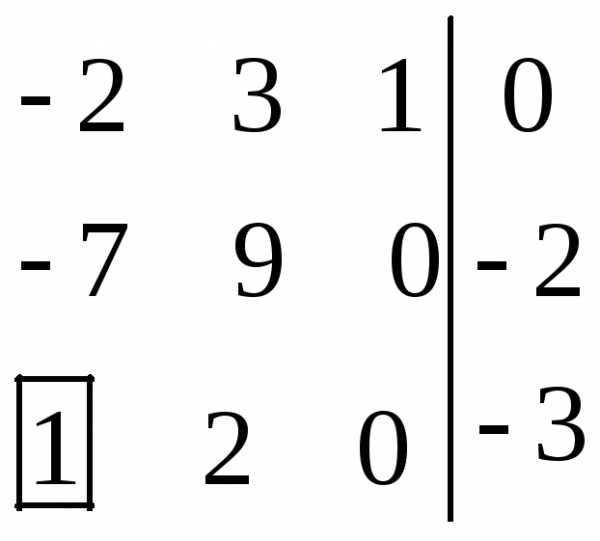
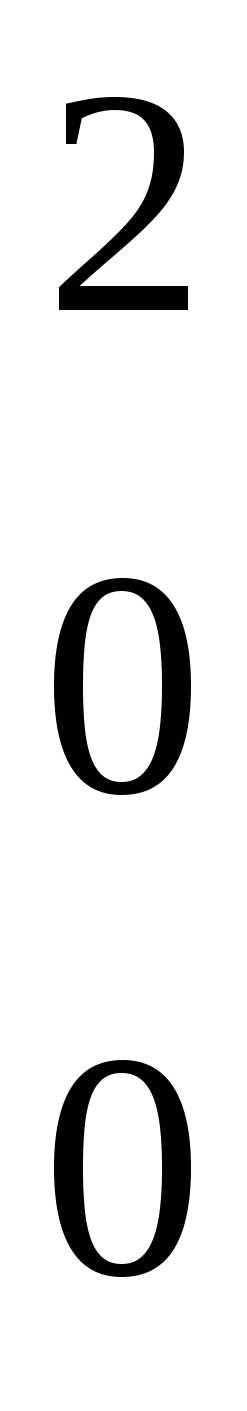
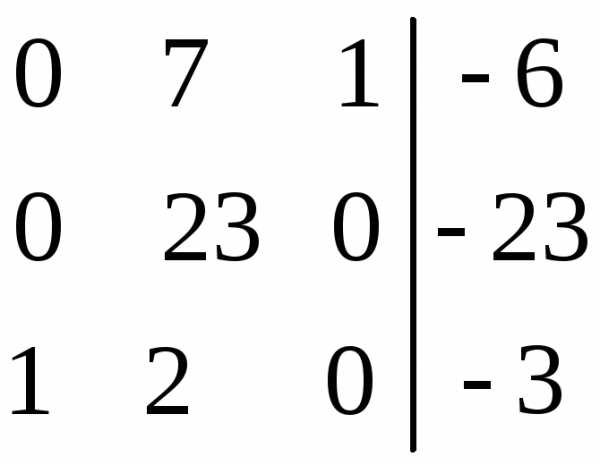
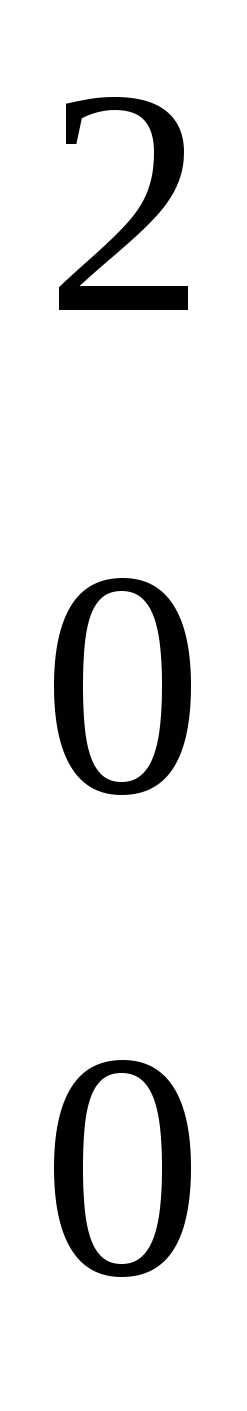
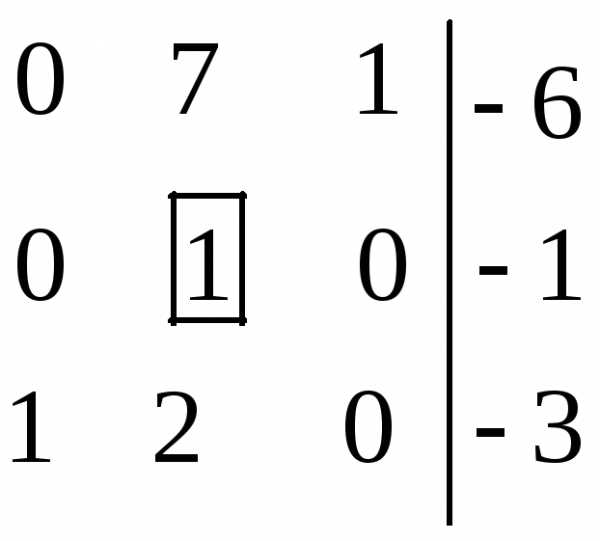
 0,
то система (1) несовместна;
0,
то система (1) несовместна;