В дроби числитель и знаменатель дроби: Числитель и знаменатель обыкновенной дроби

Обыкновенные дроби и действия с ними — что это, определение и ответ

Доля – это часть от целого.

Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).

Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)

Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.

Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.

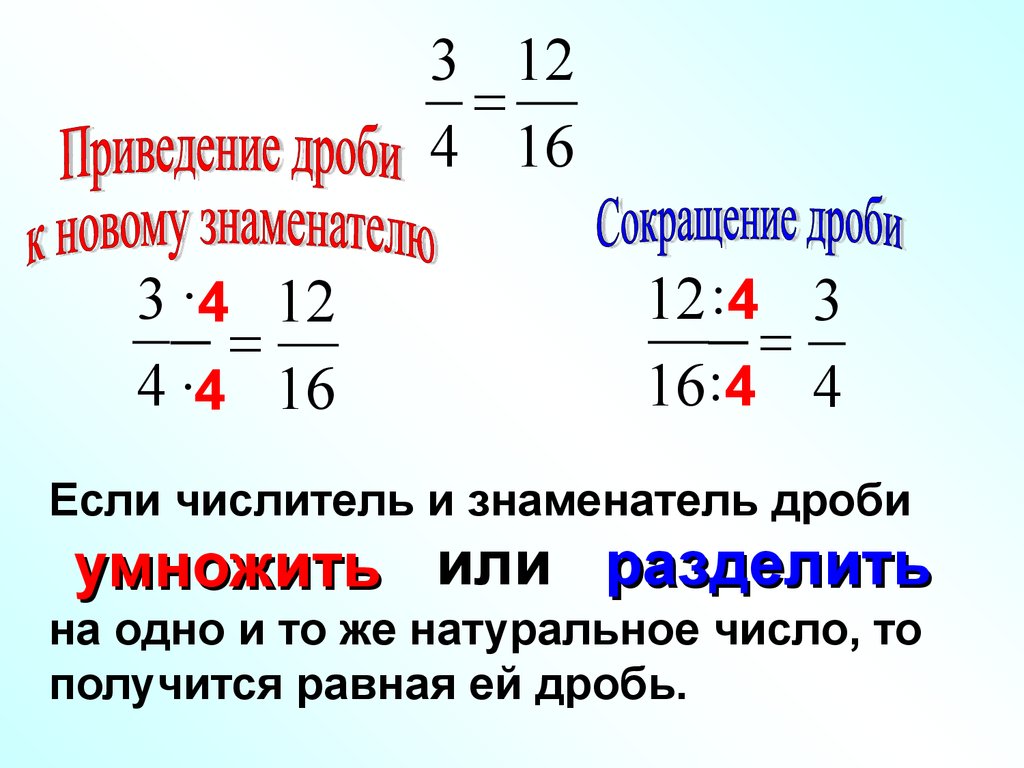
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:

Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).

Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.

Например:

\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)

\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)

\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:

1. Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.

\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)

Например:

\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)

\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)

2. Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:

\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)

Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.

Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.

АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:

1. Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.

2. Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.

3. Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

4. Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.

Например:

\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:

1. Обратные числа:

Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:

\(\frac{a}{1} = a : 1 = a\)

Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).

Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.

2. Умножение дробей:

Представим умножение дроби на число как сумму дробей:

\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)

Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:

\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)

3. Деление дробей:

Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.

Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:

\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)

Таким же образом делят дроби на дроби:

\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)

Основное свойство алгебраической дроби (продолжение) 8 класс онлайн-подготовка на Ростелеком Лицей

Приведение к общему знаменателю дробей с численными знаменателями

 

Вспомним основные понятия, упомянутые в предыдущих уроках, которые пригодятся нам сегодня.

 

Определение. Рациональная (алгебраическая) дробь – дробное выражение вида , где  многочлены.  – числитель,   – знаменатель.

Основное свойство алгебраической дроби – и числитель и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля.

Рассмотрим примеры.

Пример 1. Привести дроби  и  к общему знаменателю.

Решение. Т.к. общим знаменателем дроби является , то и приведем эти обе дроби к знаменателю 12. Для этого знаменатель и числитель первой дроби умножим на 2, а первую дробь оставим без изменения.

.

Ответ.  и .

Пример 2. Привести дроби  и  к общему знаменателю.

Решение.  — это и будет общий знаменатель дробей. Чтобы его получить, числитель и знаменатель первой дроби умножим на 3, а второй дроби на 2.

; .

Ответ. и .

Как мы видим, в указанных примерах для приведения дробей к общему знаменателю необходимо было их умножить на определенные числа, их удобно называть дополнительные множители.

Определение.Дополнительный множитель – результат деления общего знаменателя на знаменатель соответствующей дроби. В школе обычно учат писать их над числителями соответствующих дробей, отделяя от них своеобразными «палочками» (см. рис. 1), это действительно удобно, и позволяет не забывать, на что следует домножить числитель дроби.

    

Рис. 1.

Далее мы уже рассмотрим примеры, когда в качестве дополнительных множителей будут выступать и числа, а буквенные выражения.

 

Приведение к общему знаменателю дробей с буквенными знаменателями

 

 

Пример 3. Привести дроби  и  к общему знаменателю.

 

Решение. Знаменатель первой дроби  делится на знаменатель второй дроби , т.е. уже сам по себе является общим знаменателем для дробей. Следовательно, первую дробь мы оставим без изменений, а для второй дроби дополнительным множителем будет .

.

Ответ. и .

Пример 4. Привести дроби  и  к общему знаменателю.

Решение. Т.к. у знаменателей дробей нет общих множителей, то для нахождения общего знаменателя их следует просто перемножить. В таком случае дополнительным множителем для первой дроби будет знаменатель второй дроби, аналогично для второй дроби.

; .

Ответ. и .

На данном примере мы вспомнили удобное правило для нахождения общего знаменателя для дробей со знаменателями, не имеющими общих делителей. Это правило, как работало для случая обыкновенных дробей, так же работает для алгебраических и является универсальным для всех случаев нахождения общего знаменателя, даже, если у знаменателей есть общие делители. Просто в таком случае, применяя это правило, мы найдем не наименьший общий делитель, что не так оптимально для решения. Изобразить это правило нахождения общего знаменателя удобно с помощью рисунка 2.

  

Рис. 2.

Пример. 5. Привести дроби  и  к общему знаменателю.

Решение. Задача полностью аналогична предыдущей, только в качестве дополнительно множителя для первой дроби выступает уже многочлен , поэтому поступаем таким же образом.

; .

Ответ.  и.

Перейдем теперь к примерам, в которых для нахождения общего знаменателя необходимо будет знаменатели дробей раскладывать на множители.

Пример 6. Привести дроби  и  к общему знаменателю.

Решение. Рассматривая предыдущие примеры, мы могли убедиться в том, что для нахождения общего знаменателя у дробей удобно видеть на какие множители их знаменатели можно разложить. Если процедура разложения не проведена еще в условии задачи, то необходимо ее провести при решении. Это поможет нам находить дополнительные множители для дробей.

В нашем случае видно, что можно разложить на множители (вынести общий множитель) знаменатель второй дроби:

 . Мы провели сокращение и уже получили знаменатель такой же, как и у первой дроби. Следовательно, задача уже решена.

 

Ответ. и .

Как мы видим, для нахождения общего знаменателя полезны простейшие действия, такие как разложение на множители, сокращение и все остальные арифметические действия, кстати, тоже. Т.е. до проведения дополнительных процедур по приведению дробей к общему знаменателю следует их сначала просто упростить, если это возможно.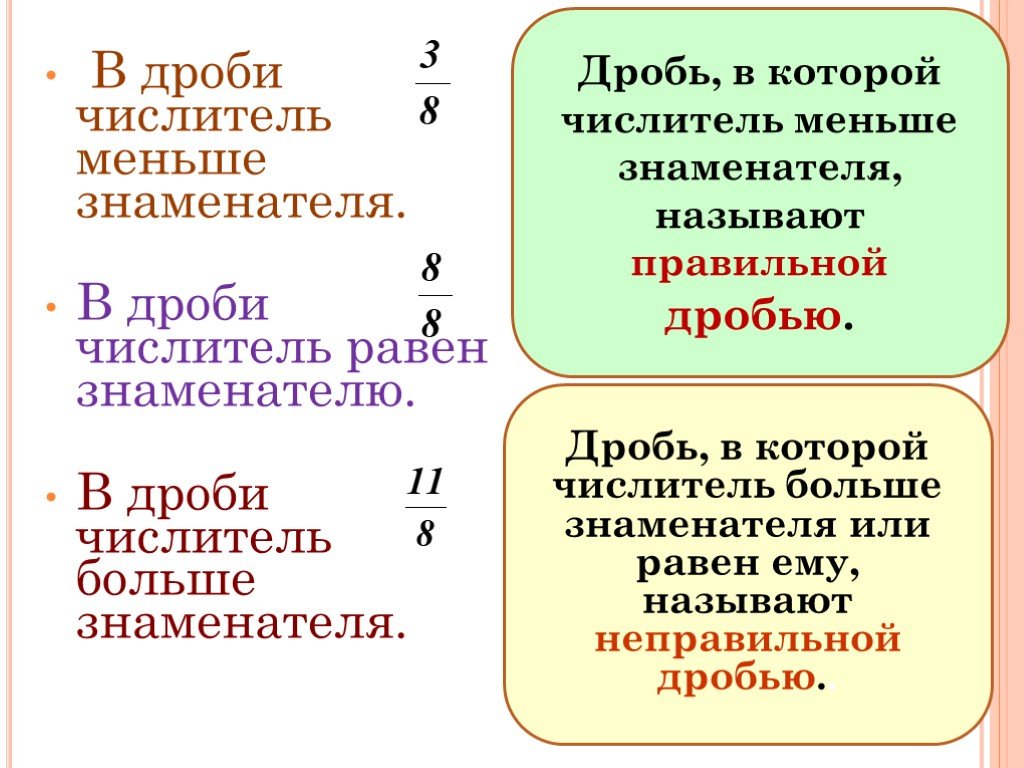

 

Приведение к общему знаменателю трех дробей с использованием разложения на множители

 

 

Рассмотрим теперь аналогичные примеры, но уже с тремя дробями.

 

Пример. 7. Привести дроби ,  и  к общему знаменателю.

Решение. У знаменателей каждой из дробей присутствует численный коэффициент, наименьшим общим кратным для чисел 2, 4 и 6 является число 12. Буквенные множители знаменателей, в свою очередь, являются делителями выражения . Следовательно, наименьшим общим знаменателем дробей будет . Дополнительные множители для числителей дробей находим, как и ранее: для первой дроби , для второй  , для третьей .

; ; .

Ответ.,  и .

Пример 8. Привести дроби ,  и  к общему знаменателю.

Решение. Знаменатель первой дроби можно разложить на множители . Мы видим, что он уже содержит в себе знаменатели двух других дробей в виде множителей, следовательно, для первой дроби знаменатель менять не нужно, а для двух других найдем дополнительные множители: вторая дробь , третья дробь .

; .

Ответ. ,  и .

Пример 9. Привести дроби ,  и  к общему знаменателю.

Решение. Очевидно, что основной частью метода приведения к общему знаменателю здесь будет разложение на множители для дальнейшего поиска дополнительным множителей. Разложим первый знаменатель методом группировки множителей:

.

Второй и третий знаменатели раскладываются с вынесением общего множителя, причем, проделаем это таким образом, чтобы получить в качестве множителей выражения соответствующие множителям первого знаменателя, чтобы проще находить затем дополнительные множители.

; .

Общий знаменатель дробей должен содержать все различные множители, которые мы нашли, т.е. будет равен:

Дополнительные множители: первая дробь , вторая дробь , третья дробь .

; ; .

Ответ. ,  и .

 

 

Пример на вычитание дробей с одинаковым знаменателем

 

 

Основное внимание на уроке мы уделили сложным случаям нахождения общих знаменателей у дробей. В дальнейшем это умение пригодится для проведения простейших операций с дробями, таких как сложение и вычитание. Рассмотрим один такой пример.

 

Пример 10. Найдите значение выражения  при .

Решение. В подобных примерах подстановка числового значения в исходное выражение не является рациональной, сначала следует проделать все возможные операции в буквенном виде, т.е. упростить выражение, а уже затем подставлять числа. В данном случае необходимо вычесть дроби, они уже с одинаковыми знаменателями, поэтому поступаем, как и в случае обыкновенных дробей.

Сокращение дроби на множитель  мы имеем полное право проводить, т.к. значение подставляемой в дальнейшем переменной не входит в область недопустимых значений (см. урок №1). Недопустимым значением переменной в данном случае является: .

Ответ:  .

На следующих уроках мы более подробно рассмотрим технику сложения и вычитания алгебраических дробей и убедимся, что она аналогична методам работы с обыкновенными дробями.

 

Список рекомендованной литературы.

1. Башмаков М.И. Алгебра 8 класс. М.: Просвещение. 2004 г.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
3. Никольский С.М., Потапом М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет.

1. Интернет портал «ru.onlinemschool.com» (Источник)
2. Интернет портал «www.berdov.com» (Источник)

 

Рекомендованное домашнее задание.

1. № 48 (в-и), 202, 203. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
2. Привести к общему знаменателю дроби   и  .
3. Привести к общему знаменателю дроби    и  .
4. Привести к общему знаменателю дроби  ,    и  .

 

Числитель и знаменатель — определение, разница, дробь, примеры

Числитель и знаменатель — это части дробей, разделенные горизонтальной чертой, известной как винкулум. Числитель – это верхняя часть дроби, а знаменатель – нижняя часть дроби. Когда мы представляем числитель и знаменатель в операции деления, мы рассматриваем числитель как делимое, а знаменатель как делитель. Давайте подробно прочитаем о различных параметрах, связанных с числителем и знаменателем.

1.	Что такое числитель и знаменатель?
2.	Разница между числителем и знаменателем
3.	Числитель и знаменатель дроби
4.	Числитель и знаменатель в делении
5.	Часто задаваемые вопросы о числителе и знаменателе

Что такое числитель и знаменатель?

В числителе указано общее количество выбранных равных частей. Принимая во внимание, что знаменатель указывает общее количество равных частей. Рассмотрим пример, приведенный ниже. Круглое колесо разделено на 6 равных частей. Эту ситуацию можно представить в виде дроби 5/6, числитель 5 представляет собой количество равных заштрихованных частей, вынутых из набора 6 равных частей, а знаменатель 6 представляет, что 6 равных частей составляют целое целое.

Разница между числителем и знаменателем

Разница между числителем и знаменателем показана ниже в таблице.

Числитель	Знаменатель
Член над винкулумом дроби называется числителем. Он показывает количество частей, которые у нас есть из целого.	Член дроби под винкулумом называется знаменателем. Он показывает общее количество частей, которые у нас есть в целом.
Если значение числителя равно нулю, то полное значение дроби равно нулю.	Знаменатель никогда не может быть равен нулю, потому что нулевые части никогда не могут составить целое.
Если числитель больше или равен знаменателю, дробь называется неправильной.	Когда знаменатель > числитель, дробь является правильной дробью.
Числитель действует как делимое.	Знаменатель действует как делитель.
Например, 13/3, здесь 13 — числитель.	Например, 13/3, здесь 3 — знаменатель

Числитель и знаменатель дроби

Как мы знаем, числитель и знаменатель — две отдельные части дроби. Дробь обычно представляется в виде «X/Y», где «X» — числитель, а «Y» — знаменатель.

Давайте лучше поймем это, взглянув на решенный пример.

Пример: Определите числитель и знаменатель следующих дробей.

а) 7/9 б) 10/23 в) 15/4

Решение:

а) В данной дроби 7/9 в числителе 7, а в знаменателе 9.
б) В данной дроби 10/23 числитель 10, а знаменатель 23.
в) В данной дроби 15/4 числитель 15, а знаменатель 4.

Числитель и знаменатель в делении

Когда мы записываем любой член дроби в виде x/y, он обычно представляется как x ÷ y. Проще говоря, это означает, что нам нужно разделить числитель (x) на знаменатель (y), чтобы упростить его.

Например, представить 3 ÷ 6 в виде дроби и определить числитель и знаменатель после упрощения. 3 ÷ 6 можно представить как 3/6. При дальнейшем упрощении получается 1/2. В дроби 1/2 1 — числитель, а 2 — числитель.

☛Темы, связанные с числителем и знаменателем

Ознакомьтесь с еще несколькими интересными статьями, тесно связанными с числителем и знаменателем.

• Расстановка дробей по порядку
• Рационализация знаменателя
• Фракции-формула
• Калькулятор подобных дробей
• Калькулятор числителя и знаменателя

 

Примеры числителя и знаменателя

1. Пример 1: Питер заказал чесночный хлеб в ресторане. Каждый кусок хлеба представляет собой часть целого. Хлеб делится на 7 равных ломтиков. Он съел два кусочка. Представьте ситуацию в виде дроби и определите числитель и знаменатель дроби.

   Решение:

   Общее количество ломтиков хлеба = 7
   Общее количество съеденных ломтиков = 2
   Доля хлеба, которую он съел 2/7
   Здесь 7 — это число, обозначающее общее количество ломтиков хлеба, а 2 — числитель, представляющий порцию, которую он съел.

2. Пример 2: Чему равна сумма числителей и сумма знаменателей первой и второй дроби: 1/3, 7/5.

   Решение:

   Чтобы найти сумму дробей, давайте сначала найдем числитель и знаменатель в обеих дробях.
   Числитель первой дроби 1/3 равен 1, а знаменатель равен 3.
   Числитель второй дроби 7/5 равен 7, а знаменатель равен 5.
   Сумма числителей = 1 + 7 = 8.
   Сумма знаменателей = 3 + 5 = 8

   Следовательно, сумма числителей и сумма знаменателей обеих дробей равны 8, 8 соответственно.

3. Пример 3: В классе 27 учеников, из них 13 девочек. Представьте количество мальчиков и количество девочек в числителе и знаменателе.

   Решение:

   Число девочек в классе равно 13.
   Количество мальчиков в классе (27 — 13 = 14)
   Дробь, представляющая количество мальчиков в классе = 14/27
   Дробь, представляющая количество девочек в классе = 13/27

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические задачи на числитель и знаменатель

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о числителе и знаменателе

Что означают числитель и знаменатель?

Числитель и знаменатель — две части, образующие дроби. Другими словами, они являются частью дробей. Наибольшее число в дроби всегда считается числителем. Он показывает количество деталей, которые у нас есть. Нижнее число в дроби считается знаменателем. Он показывает общее количество частей, на которые что-либо делится. Например, в дроби 8/7 8 — числитель, а 7 — знаменатель.

Как отличить числитель и знаменатель дроби?

Дробь представляется в виде «x/y», где «x» — числитель, а «y» — знаменатель. Числитель представляет собой общее количество учитываемых частей. Принимая во внимание, что знаменатель представляет собой общее количество равных частей в дроби. Наибольшее число в дроби всегда считается числителем. Нижнее число в дроби считается знаменателем.

Как запомнить числитель и знаменатель?

Существуют различные способы и приемы для запоминания числителей и знаменателей. Самый простой способ запомнить это — понять расположение чисел в дробях. Мы должны помнить, что числитель всегда будет располагаться в верхней части дроби, а числовое значение знаменателя всегда будет располагаться внизу.

Как разделить числитель и знаменатель?

Когда числитель и знаменатель представлены в виде p/q, это означает p ÷ q. Здесь «p» действует как числитель, а «q» — как знаменатель. Например, 7/2 означает 7 ÷ 2, здесь числитель 7 делится на знаменатель 2. При делении будем читать 7 (числитель как делимое) и 2 (знаменатель как делитель).

Как называется линия между числителем и знаменателем?

Линия между числителем и знаменателем называется Vinculum или чертой дроби. Например, 7/6 здесь числитель 7 и знаменатель 6 разделены чертой.

Определите числитель и знаменатель дроби 18/7?

В данной дроби 18/7 числитель 28 равен 18, а знаменатель 7.

Что такое числитель и знаменатель следующих дробей? 7/3 и 9/7

В дроби 7/3 7 — числитель, а 3 — знаменатель. В дроби 9/7 9 — числитель, а 7 — знаменатель.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы числителя и знаменателя

Числитель и знаменатель: определение, разность

Числовой термин, который символизирует одну часть, разделенную на равные части, является дробью в математике. Делимые величины можно представить, разделив значения горизонтальной линией. Чтобы знать, что такое числитель и знаменатель? Прочтите последующие пояснения. Число, расположенное над ним, называется числителем, а число, расположенное ниже, называется знаменателем.

Горизонтальная линия, отделяющая числитель от знаменателя, называется винкулумом. Эта горизонтальная линия также используется для обозначения операций деления. Однако дробь несколько отличается. Несмотря на то, что операции деления также имеют числитель и знаменатель, числитель рассматривается как делимое, а знаменатель — как делитель.

Проще говоря, дробь представляет собой часть вещи в целом. Например, если плитку шоколада разделить на десять равных частей, то каждая часть шоколада будет представлена ​​как 1/10. Это представление показывает нам стоимость одного кусочка шоколада как части всей плитки шоколада.

Дроби — это удобный способ распределения чисел. Следовательно, делая расчет быстрее. С другой стороны, дроби также представлены десятичными значениями. Тем не менее, дроби выглядят проще и понятнее. Но что такое числитель и знаменатель?

Хороший способ определить дробь — найти горизонтальную линию, разделяющую числитель и знаменатель. Эта горизонтальная линия дает понять, что значение, расположенное над ней, является числителем, а значение, расположенное под ней, является знаменателем.

В числителе указано общее количество взятых частей, а в знаменателе — все части в целом.

Например, если ⅖ — дробь, то

2 — числитель, а 5 — знаменатель.

Типы дробей

В зависимости от числового значения числителя и знаменателя дроби могут быть двух видов.

•  Неправильные дроби
•  Правильные дроби 

Неправильные дроби – в дроби этого типа числитель имеет большее значение, чем знаменатель. При решении смешанных дробей получаются неправильные дроби.

Например- 7/2, 11/5, 7¾ и так далее.

Правильные дроби – в правильных дробях числитель меньше знаменателя. Такие дроби называются правильными, потому что они легко делятся.

Например – 3/8, 2/9, 6/7 и так далее.

Что такое числитель?

В дроби два числовых значения разделены горизонтальной чертой. В этом представлении дроби числитель — это значение, расположенное над этой горизонтальной линией.

Числитель показывает части, взятые из общей суммы частей. Другими словами, числитель делится на знаменатель, чтобы упростить дробь.

Числитель может представлять выбранные или удаленные части из общего числа элементов. Например, если квадрат разрезать на четыре равные части и одну из них удалить, то долю оставшихся частей квадрата можно представить как ¾.

C общие примеры числителя

Фракция

Numerator

7/11

7

(2 + 5)/ 14

(2 + 5)

14 0008

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

2Q/

(2 + 5)

140008

2 3C

2Q

3C

8/(18 — 4)

8

(18 — 4)

7/6

7

6

90087. знаменатель?

Числовое значение, расположенное под горизонтальной чертой, называется знаменателем. Значение знаменателя представляет общее число, на которое делится объект.

В то время как числитель показывает выбранные части, знаменатель показывает все части. Например, если в пицце всего 6 ломтиков, и кто-то съел один, то дробь, представляющая оставшиеся ломтики пиццы, выражается как 5/6. Здесь 6 — это знаменатель, представляющий общее количество кусочков пиццы. 12/50008 5 11/3 3 2/10 10 3x/2y 2y 2m + n/5 5 p – q/7 7

Почему числители и знаменатели важны для изучения математики?

Числитель и знаменатель образуют дробь. И дробь важна для понимания отношений между разными значениями. Дробное представление числовых значений помогает понять природу и взаимодействие числовых значений.

Дроби применимы не только в учебе, но и в реальной жизни. Значения числителя и знаменателя помогают понять природу дроби. Зная значения числителя и знаменателя, можно понять общий вывод дробного значения.

Дроби помогают разделить время, материю, пищу и другие физические и нефизические сущности.

Может ли числитель быть равен 0?

Вы можете увидеть дробь, в которой числитель равен 0. Это особый случай, когда результирующее значение дроби также становится 0, когда числитель равен 0.

Это также означает, что независимо от значения знаменателя, результирующее упрощение дроби будет равно 0, если числитель равен 0.

Каким будет значение дроби, если знаменатель равен 0?

Вообще говоря, знаменатель никогда не должен быть равен 0. Это потому, что знаменатель представляет общее количество вещей, и когда это общее число равно 0, дроби не существует.

Другими словами, дроби, знаменатель которых равен 0, называются неопределенными.

В чем разница между числителем и знаменателем дроби?

Несмотря на то, что числитель и знаменатель являются частями одной и той же дроби, они имеют разное значение.

Обратитесь к таблице ниже, чтобы понять разницу между числителем и знаменателем.

Числитель	Знаменатель
Значение, помещенное над горизонтальной чертой в дроби, называется числителем. Оно означает количество частей, вынесенных из целого.	Числовое значение под центром дроби называется знаменателем. Он представляет собой общее количество равных частей в целом.
Если числовое значение числителя равно нулю, то результирующее значение полной дроби также равно нулю.	Значение знаменателя никогда не может быть равно нулю. Это потому, что ноль частей чего-то никогда не может составить целое.
Если значение числителя больше или равно значению знаменателя, то дробь называется неправильной.	Дробь является правильной дробью, если знаменатель больше числителя.
Числитель дроби также выступает в роли делимого.	Знаменатель дроби также действует как делитель.
Например, 11/3, здесь 11 — числитель.	Например, 11/3, здесь 3 — знаменатель.

Какое значение может иметь знаменатель дроби?

Знаменатель стоит внизу дроби. Это означает, что его значение, безусловно, может повлиять на итоговое значение всей дроби.

Не у всех дробей знаменатель имеет большее значение, чем числитель. И в зависимости от значения знаменателя; дроби могут быть двух типов –

• Правильная дробь
•  Неправильная дробь

Чтобы понять приведенные выше типы дробей, можно взглянуть на приведенные ниже примеры.

1. 15/23 – Это правильная дробь. Это потому, что знаменатель имеет большее значение, чем числитель. Здесь 15 обозначает значение числителя, а 23 указывает значение знаменателя.
2. 3/8 — правильная дробь. Большее числовое значение знаменателя делает эту дробь правильной дробью. Здесь 3 — числитель, а 8 — знаменатель.
3. 13/7- Это неправильная дробь. Это потому, что значение знаменателя меньше, чем значение числителя. Здесь 13 — числитель, а 7 — знаменатель.
4. 6/5- Это неправильная дробь. Значение знаменателя равно 5, что меньше значения числителя, равного 6.

Некоторые примеры правильных дробей

В правильных дробях значение числителя всегда меньше значения знаменателя. Такие дроби обычно легко решить.

Примеры правильных дробей: 7/11, 3/7, 2/6, 23/47 и т. д.

S Некоторые примеры неправильных дробей

Неправильными дробями называются дроби, в которых значение числителя всегда больше значения знаменателя. Это сложные виды дробей, которые образуются путем упрощения смешанных дробей.