Задачи по маркетингу. Часть 26 (конкуренция)
Задача №12 (задача о модели отраслевой конкуренции М.Портера)
Провести анализ угольной отрасли на основе использования модели отраслевой конкуренции М. Портера.
Решение задачи:
Угольная промышленность – это мощный многофункциональный производственный комплекс со значительными объемами производства, сложными внутренними и внешними связями, специфическими условиями работы предприятий и трудящихся. Однако, в последние годы определились противоречия между чрезвычайно важным значением угольной отрасли и техническим, а также экономическим состоянием, в котором она находится. В настоящее время угольная отрасль переживает спад. Анализ ключевых статистических показателей, в частности, объемов добычи угля, производительности труда рабочих очистных забоев, производственных мощностей шахт, объемов проведения горных выработок на 1000 т добываемого угля подтверждает, что угольная промышленность относится к группе отраслей, переживающих спад.
Для идентификации и анализа благоприятных возможностей и опасностей, с которыми может встретиться предприятие в отрасли, используется модель Портера, включающая следующие пять сил:
- Риск входа потенциальных конкурентов создает опасность прибыльности предприятия. Барьером к включению в рыночный механизм для основного звена производства – угледобывающих предприятий является их убыточность. Предприятие, где расходы на производство превышают возможный доход, в рыночной среде как самостоятельный хозяйствующий субъект, существовать не может. Рыночная среда его уничтожит посредством механизмов банкротства и ликвидации. Это объективный процесс, но ему нужно придать управляемость. Существует определенная угроза появления так называемых «копанок», однако они находятся вне закона, с ними постоянно ведется борьба, а если даже не учитывать эти обстоятельства, то конкурировать с шахтами по объему добычи они не могут. Исходя из этого, риск появления новых конкурентов для угольного предприятия практически сведен к нулю.

- Соперничество существующих в отрасли предприятий. Подавляющее большинство предприятий, работающих в отрасли, являются государственными. План переработки угольной продукции каждого конкретного угледобывающего предприятия утверждается на год в соответствии с проектом программы экономического развития, разработанным в соответствии со стратегией предприятия. В результате конкуренция между предприятиями в угольной отрасли практически отсутствует.
- Возможность покупателей «торговаться» представляет угрозу давления на цены из-за потребностей в лучшем качестве или сервисе. Покупателями угольной продукции являются металлургические заводы и теплоэлектростанции. Цены на уголь устанавливает государство. При этом эти цены гораздо ниже себестоимости. И рассматривая именно эту конкурентную силу, следует оценивать вероятность предоставления угольному предприятию дотаций, а не способность покупателей торговаться.
- Давление со стороны поставщиков заключается в их угрозе поднять цены, вынуждая предприятия снизить количество поставляемой продукции, а, следовательно, и прибыль.
 Этот фактор, на мой взгляд, самый существенный. Поставщики горюче-смазочных материалов, взрывчатых веществ, крепежных элементов весьма часто поднимают цены.
Этот фактор, на мой взгляд, самый существенный. Поставщики горюче-смазочных материалов, взрывчатых веществ, крепежных элементов весьма часто поднимают цены. - Угроза появления заменяющих продуктов. Проблему для руководства угольных предприятий представляет контроль изменений интересов потребителей. Эти изменения касаются, например, развития атомной энергетики, рынка топливной энергетики, увеличения количества газовых котельных и так далее.
|
|
25.
 1: Системы координат — Физика LibreTexts
1: Системы координат — Физика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19563
- Howard Martin пересмотрено Аланом Нг
- University of Wisconsin-Madison
Системы координат используются для описания положения объекта в пространстве. Система координат — это искусственный математический инструмент, который мы строим для описания положения реального объекта.
Одномерные системы координат
Самая простая для построения система координат — та, которую мы можем использовать для описания местоположения объектов в одномерном пространстве. Например, мы можем захотеть описать местоположение поезда на прямом участке пути, идущем в направлении восток-запад.
Мы можем описать положение поезда, указав, как далеко он находится от железнодорожной станции (отправной точки), используя одно действительное число, скажем, \(x\). Если поезд находится в точке \(x=0\), то мы знаем, что он находится на станции Кингстон. Если объект не находится в начале координат, то нам нужно указать, с какой стороны (на востоке или западе в нашем примере с поездом) от начала координат находится объект. Мы делаем это, выбирая направление для нашей одномерной координаты \(x\). Например, мы можем выбрать, чтобы восточная сторона дорожки соответствовала положительным значениям \(x\), а западная сторона дорожки соответствовала отрицательным значениям \(x\). Таким образом, чтобы полностью задать одномерную систему координат, нам нужно выбрать:
- место отправления.

- направление увеличения координаты \(x\).
- единиц, в которых мы хотим выразить \(х\).
В одном измерении обычно используется переменная \(x\) для определения положения вдоль «\(x\)-оси». Ось \(х\) — это наша система координат в одном измерении, и мы представляем ее, рисуя линию со стрелкой в направлении увеличения \(х\) и указываем, где находится начало координат (как на рис. А1.1.1).
Рисунок A1.1.1 : Одномерная система координат, описывающая положение поезда. Железнодорожная станция Кингстона является отправной точкой, а восточная сторона пути соответствует положительным значениям \(x\). Поезд находится в позиции \(x_{1}\).2D системы координат
Рисунок A1.1.2 : Пример декартовой системы координат и точки \(P\) с координатами \((x_{p}, y_{p})\). Чтобы описать положение объекта в двух измерениях (например, шарик, катящийся по столу), нам нужно указать два числа. Самый простой способ сделать это — определить две оси, \(x\) и \(y\), начало и направление которых мы должны определить. На рисунке A1.1.2 показан пример такой системы координат. Хотя в этом нет необходимости, мы выбрали оси \(x\) и \(y\), перпендикулярные друг другу. Начало системы координат находится там, где пересекаются две оси. Можно выбрать любые два направления для осей (при условии, что они не параллельны). Однако выбор осей, которые перпендикулярны (декартова система координат), обычно является наиболее удобным.
На рисунке A1.1.2 показан пример такой системы координат. Хотя в этом нет необходимости, мы выбрали оси \(x\) и \(y\), перпендикулярные друг другу. Начало системы координат находится там, где пересекаются две оси. Можно выбрать любые два направления для осей (при условии, что они не параллельны). Однако выбор осей, которые перпендикулярны (декартова система координат), обычно является наиболее удобным.
Чтобы полностью описать положение объекта, мы должны указать его положение по осям \(x\) и \(y\). Например, точка \(P\) на рисунке A1.1.2 имеет две координаты , \(x_p\) и \(y_p\), которые определяют ее положение. Координата \(x\) находится путем проведения через \(P\) линии, параллельной оси \(y\) и задаваемой пересечением этой линии с осью \(x\). Координата \(y\) находится путем проведения линии через точку \(P\), которая параллельна оси \(x\) и задается пересечением этой линии с осью \(y\).
Упражнение \(\PageIndex{1}\)
На рисунке A1.1.3 показана неортогональная система координат (где оси \(x\) и \(y\) не перпендикулярны). Какое значение на рисунке правильно указывает координату \(y\) точки \(P\)?
Какое значение на рисунке правильно указывает координату \(y\) точки \(P\)?
- \(у_1\)
- \(у_2\)
- \(у_3\)
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Наиболее распространенным выбором системы координат в двух измерениях является декартова система координат, которую мы только что описали, где оси \(x\) и \(y\) перпендикулярны и имеют общее начало, как показано на рисунке A1. 1.2. Когда это применимо, по соглашению мы обычно выбираем ось \(y\), чтобы она соответствовала вертикальному направлению.
Другим распространенным выбором является «полярная» система координат, где положение объекта определяется расстоянием до начала координат \(r\) и углом \(\theta\) относительно заданного направления , как показано на рисунке A1. 1.4. Часто наряду с декартовой системой определяется полярная система координат, так что \(r\) — это расстояние до начала декартовой системы, а \(\theta\) — угол относительно оси \(x\). . 92}\\ \tan(\theta) &= \frac{y}{x}\end{aligned}\] Полярные координаты часто используются для описания движения объекта, движущегося по окружности, так как это означает, что только один координат (\(\theta\)) меняется со временем (если начало системы координат выбрано так, чтобы оно совпадало с центром окружности).
1.4. Часто наряду с декартовой системой определяется полярная система координат, так что \(r\) — это расстояние до начала декартовой системы, а \(\theta\) — угол относительно оси \(x\). . 92}\\ \tan(\theta) &= \frac{y}{x}\end{aligned}\] Полярные координаты часто используются для описания движения объекта, движущегося по окружности, так как это означает, что только один координат (\(\theta\)) меняется со временем (если начало системы координат выбрано так, чтобы оно совпадало с центром окружности).
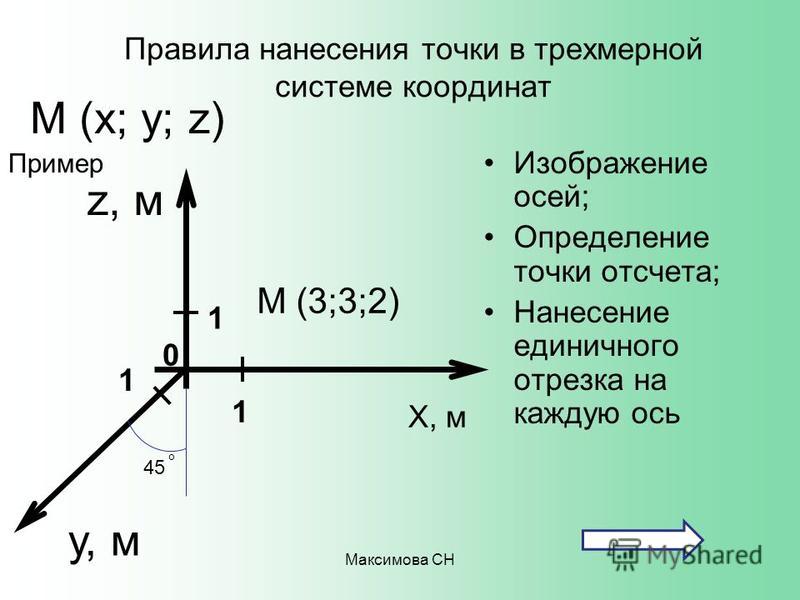
Трехмерные системы координат
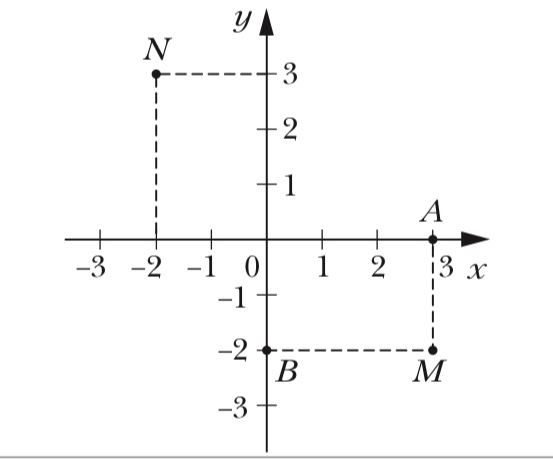
В трех измерениях нам нужно указать три числа, чтобы описать положение объекта (например, птицы, летящей в воздухе). В трехмерной декартовой системе координат мы просто добавляем третью ось \(z\), которая взаимно перпендикулярна как \(x\), так и \(y\). Затем положение объекта можно указать с помощью трех координат: \(x\), \(y\) и \(z\). По соглашению мы используем ось \(z\) как вертикальное направление в трех измерениях.
В трех измерениях распространены две дополнительные системы координат: «цилиндрическая» и «сферическая» координаты.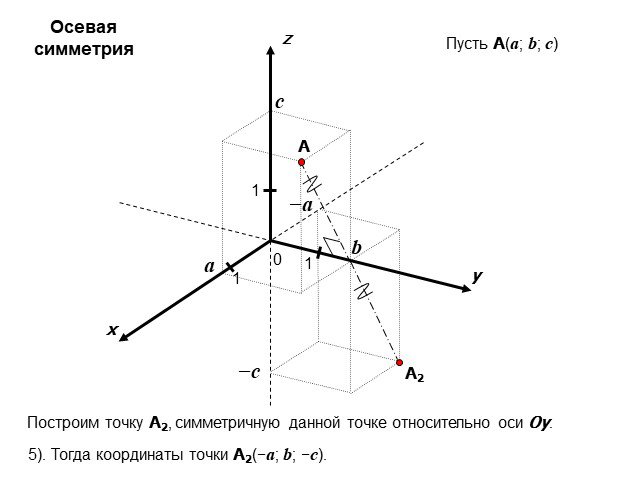 Все три системы показаны на рисунке A1.1.5 в сочетании с декартовой системой.
Все три системы показаны на рисунке A1.1.5 в сочетании с декартовой системой.
Цилиндрические координаты можно рассматривать как расширение полярных координат. Мы сохраняем ту же декартову координату \(z\), чтобы указать высоту над плоскостью \(xy\), однако мы используем азимутальный угол , \(\phi\) и радиус, \(\rho\), для описания положения проекции точки на плоскость \(xy\). \(\phi\) — угол между осью \(x\) и линией от начала координат до проекции точки на плоскость \(xy\), а \(\rho\) — расстояние между точкой и ось \(z\). Таким образом, цилиндрические координаты очень похожи на полярную систему координат, введенную в двух измерениях, за исключением добавления координаты \(z\). Цилиндрические координаты полезны для описания ситуаций с азимутальной симметрией, таких как движение по поверхности цилиндра. Например, рассмотрим точку \(P\) на рисунке A1.1.6. Точка \(P\) расположена на расстоянии \(\rho\) от оси \(z\), так как расположена на поверхности цилиндра (круглый конец цилиндра имеет радиус \(\rho\ )). Точка \(P\) — это высота \(z\) над плоскостью \(xy\), а прямая из оси \(z\) в точку \(P\) образует угол \(\phi\) с осью \(х\). 92}\\ \tan(\phi) &= \frac{y}{x}\\ z&=z\end{aligned}\] В сферических координатах точка \(P\) описывается радиусом, \ (r\), полярный угол \(\theta\) и азимутальный угол , \(\phi\). Радиус — это расстояние между точкой и началом координат. Полярный угол — это угол с осью \(z\), который составляет линия от начала координат до точки. Азимутальный угол определяется так же, как и в полярных координатах. Обратите внимание, что значение \(\phi\) должно быть между \(0\) и \(2\pi\), тогда как значение \(\theta\) должно быть между \(0\) и \(\ Пи\).
Например, рассмотрим точку \(P\) на рисунке A1.1.6. Точка \(P\) расположена на расстоянии \(\rho\) от оси \(z\), так как расположена на поверхности цилиндра (круглый конец цилиндра имеет радиус \(\rho\ )). Точка \(P\) — это высота \(z\) над плоскостью \(xy\), а прямая из оси \(z\) в точку \(P\) образует угол \(\phi\) с осью \(х\). 92}\\ \tan(\phi) &= \frac{y}{x}\\ z&=z\end{aligned}\] В сферических координатах точка \(P\) описывается радиусом, \ (r\), полярный угол \(\theta\) и азимутальный угол , \(\phi\). Радиус — это расстояние между точкой и началом координат. Полярный угол — это угол с осью \(z\), который составляет линия от начала координат до точки. Азимутальный угол определяется так же, как и в полярных координатах. Обратите внимание, что значение \(\phi\) должно быть между \(0\) и \(2\pi\), тогда как значение \(\theta\) должно быть между \(0\) и \(\ Пи\).
Сферические координаты полезны для описания ситуаций, имеющих сферическую симметрию, например, человека, идущего по поверхности Земли, поскольку радиальная координата не изменится. 2}}\\ \tan(\phi) &= \frac{y}{x}\\\ конец {выровнено}\]
2}}\\ \tan(\phi) &= \frac{y}{x}\\\ конец {выровнено}\]
Эта страница под названием 25.1: Системы координат распространяется по лицензии CC BY-SA, ее автор, ремикширование и/или куратор — Говард Мартин, редакция Алана Нг.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Райан Мартин и др.
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
- Теги

Что такое оси X и Y? Определение, факты, пример графика и тест
Ось в математике определяется как линия, которая используется для выполнения или отметки измерений. Оси x и y являются двумя важными линиями координатной плоскости. Ось X — это горизонтальная числовая линия, а ось Y — вертикальная числовая линия. Эти две оси пересекаются перпендикулярно, образуя координатную плоскость. Ось x также называется абсциссой, а ось y — ординатой.
Любая точка на координатной плоскости может быть расположена или представлена с помощью этих двух осей в виде упорядоченной пары вида ( х, у ). Здесь x представляет положение точки относительно оси x, а y представляет положение точки относительно оси y.
Начало координат находится в месте пересечения двух осей и записывается как (0,0).
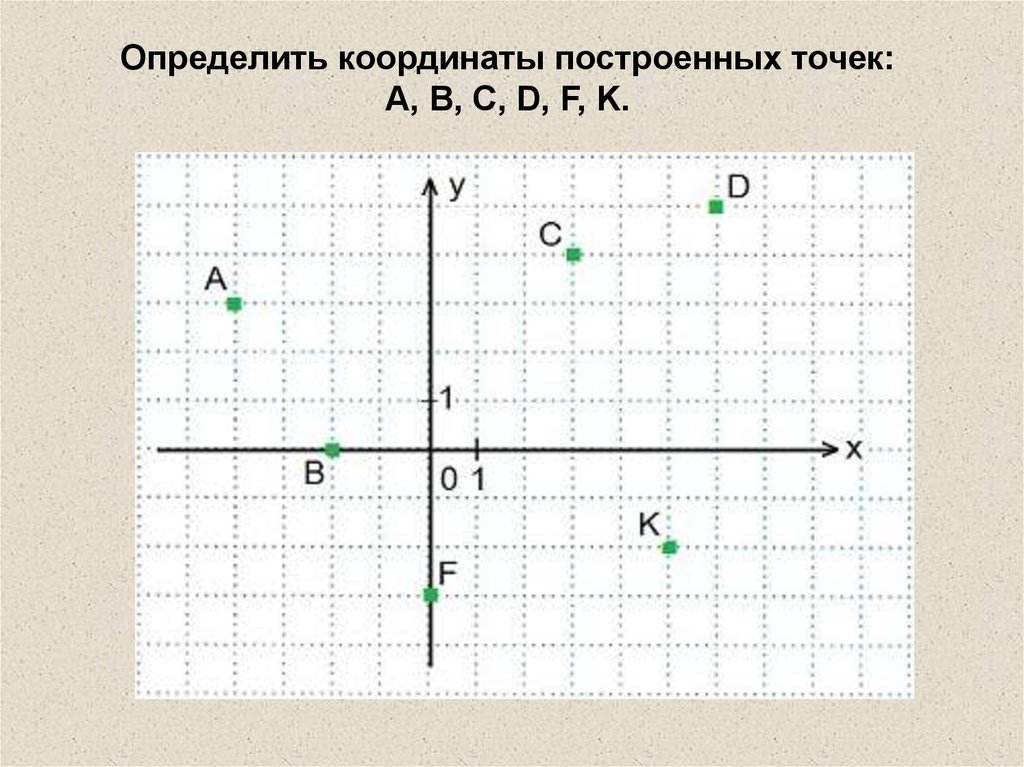
Нанесение точек на оси X и Y
Давайте узнаем, как наносить точки на график с помощью осей X и Y.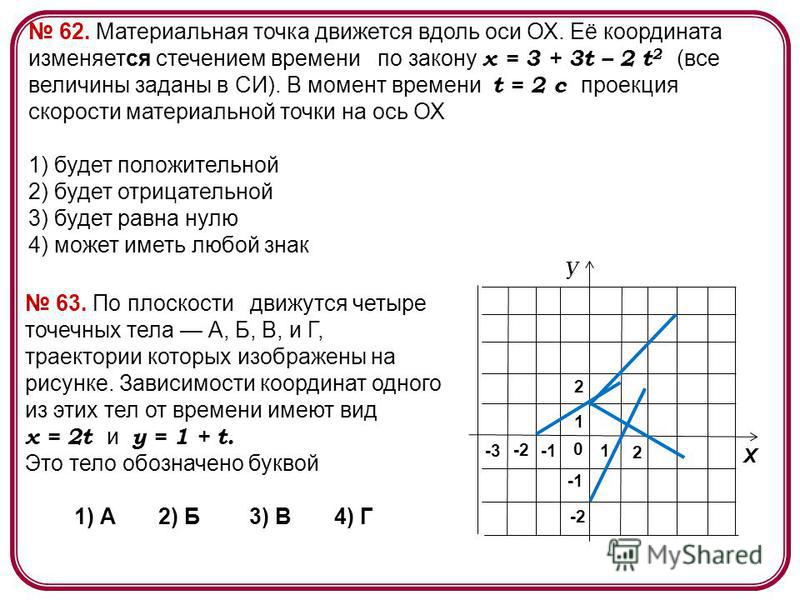
Например: Попробуем нарисовать точку B(3,4) на графике.
Здесь координата x точки B равна 3. Итак, мы начнем с начала координат и переместимся на 3 единицы вправо по оси x.
Теперь координата y B(3,4) равна 4, поэтому мы поднимемся на 4 позиции вверх от этой точки.
Итак, мы начертили нашу точку B(3,4) на графике с помощью осей.
Связанные игры
Представление линейного уравнения по осям X и Y
Чтобы понять, как представить линейное уравнение на графике с использованием осей X и Y,
, давайте рассмотрим линейное уравнение, y = x + 1.
Теперь давайте построим таблицу для представления соответствующих значений y для различных значений x и создадим их упорядоченные пары:
| x | y | Ordered pair |
| 0 | 1 | (0,1) |
| 1 | 2 | (1,2) |
| 2 | 3 | (2,3) |
| 3 | 4 | (3,4).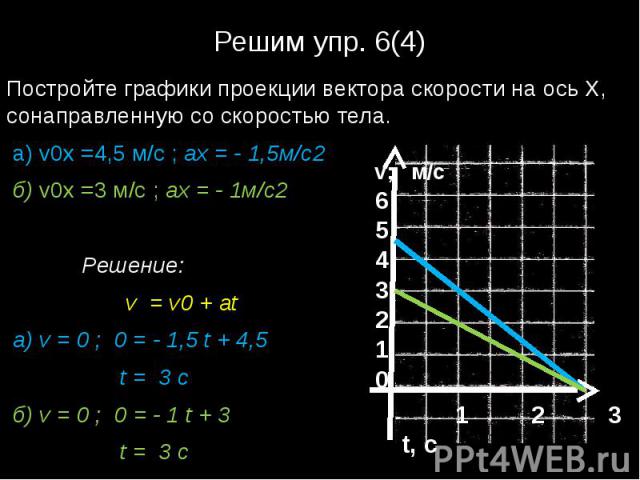 В качестве последнего шага мы соединим эти точки, чтобы сформировать прямую линию, которая будет представлением уравнения y = x + 1, Связанные рабочие листыРешенные вопросы Вопрос 1: Какие из следующих точек лежат на оси x? (0, 1) (4, 0) (7, 7) (−5, 0) (−4, 4) (0, −5) (8, 0) (6, 0) Ответ: Поскольку координаты, лежащие на оси x, имеют координату y, равную нулю (0), следующие точки будут лежать на оси x: (4, 0) (−5, 0) (8, 0) (6 , 0) Вопрос 2: На график нужно нанести две разные точки. Если заданы точки (3,2) и (2,3), нанесите эти две точки на оси X и Y. Кроме того, найдите точку, где прямая, проходящая через эти точки, пересекает ось x. Ответ: Для (3,2), как мы видим, точка с координатой x равна 3, а точка с координатой y равна 2. Аналогичным образом мы можем построить точку (2,3). Теперь мы можем соединить обе точки прямой линией, когда обе точки нанесены на график. Вопрос 3: Для линейного уравнения y = 2x + 6 найдите точку, в которой прямая пересекает ось y на графике. Ответ: По оси y координата x точки равна 0. Следовательно, мы можем найти точку пересечения оси y и y = 2x + 6, просто приравняв значение x к 0 и найдя значение у. y = 2(0)+6 = 0 + 6 = 6. Таким образом, прямая линия уравнения y = 2x + 6 пересекает ось y в точке (0,6). Практические задачи1 Как называется ось X?Ордината Абсцисса Аппликат Ничего из вышеперечисленного Правильный ответ: Абсцисса 2 Как правильно изобразить точку на графике?(координата X, координата X) (координата Y, координата X) (координата Y, координата Y) (координата X, координата Y) Правильный ответ: (координата X, координата Y) 3 Как исходная точка представлена на графике?(0,0) (0,x) (y,0) (x,y) Правильный ответ: (0,0) 4 Точка (0,5) будет лежать наОсь X Ось Y Начало Ничего из вышеперечисленного Правильный ответ: Ось Y Часто задаваемые вопросыПочему важны оси X и Y? Ось X и Y необходимы для графического представления данных. Эти оси составляют координатную плоскость. Данные расположены в координатах в соответствии с их расстоянием от осей X и Y. Графическое представление помогает в решении сложных уравнений. Как формируется координатная плоскость? Координатная плоскость — это двумерная плоскость, образованная пересечением двух числовых линий. |

 Этот фактор, на мой взгляд, самый существенный. Поставщики горюче-смазочных материалов, взрывчатых веществ, крепежных элементов весьма часто поднимают цены.
Этот фактор, на мой взгляд, самый существенный. Поставщики горюче-смазочных материалов, взрывчатых веществ, крепежных элементов весьма часто поднимают цены.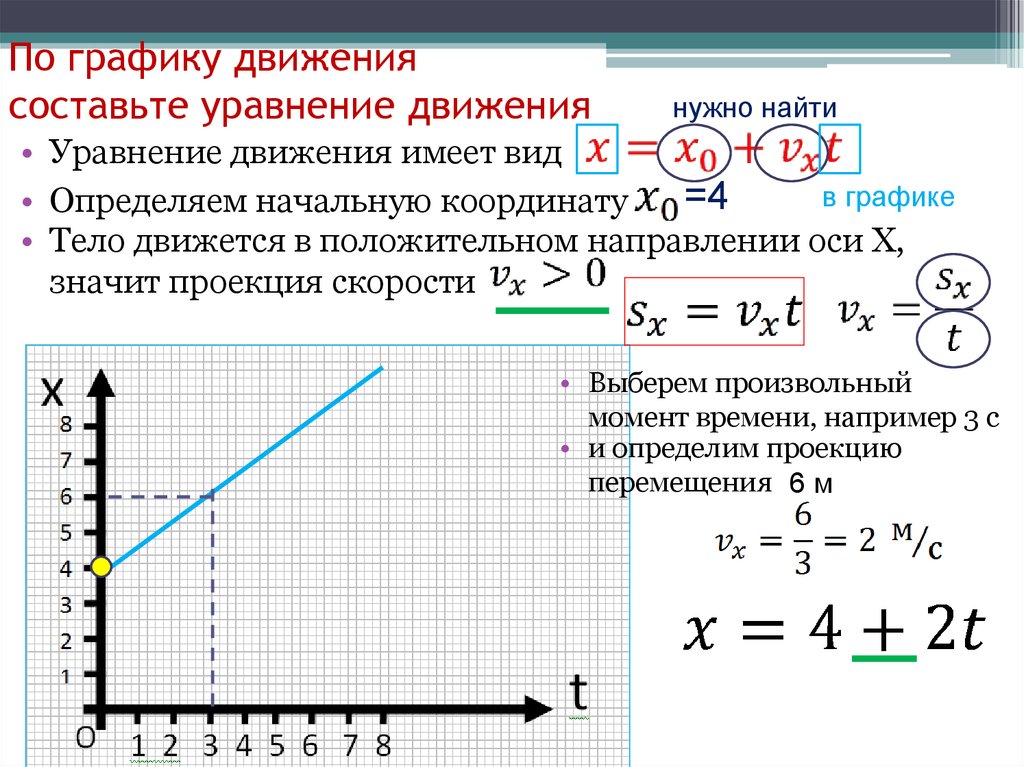
 Продлив прямую, мы видим, что эта линия пересекает ось x в точке (5,0).
Продлив прямую, мы видим, что эта линия пересекает ось x в точке (5,0).