В опыте юнга отверстия освещались монохроматическим светом: №1580. В опыте Юнга отверстия освещались монохроматическим светом длиной волны 600 нм. Расстояние между отверстиями 1 мм, расстояние от отверстий до экрана 3 м. Найдите положение первых трех светлых полос.

Примеры решения задач

Задача 1. В опыте Юнга отверстия освещались монохроматическим светом с длиной волны м. Расстояние между отверстиямиd = 1мм, расстояние от отверстия до экрана L = 3 м. Найти положение трех первых светлых и темных полос на экране; доказать, что полосы имеют одинаковую ширину.

Дано:

м

мм = м

L = 3 м

Решение

Источники S₁ и S₂ (отверстия) должны находиться на одном фронте волны, идущей от источника S, тогда они будут когерентны.

Лучи, приходящие в точку 0 имеют одинаковые фазы, так как их разность хода равна нулю. Лучи, приходящие в точку М имеют разность хода .

По условию задачи поэтому из подобия треугольников можно записать

, откуда .

Усиление освещенности (максимум) будет при условии, что в разности хода интерферирующих лучей уложится четное число полуволн, т.

е.

,

тогда

.

при

м,

при

м,

при

м.

Темные полосы (минимум) будут при условии

;

где

м;

м;

м.

Таким образом, на экране получается чередование светлых и темных полос, симметричных относительно центральной светлой полосы.

Находим ширину полосы:

;

;

м.

Ширина полосы не зависит от номера, т.е. все полосы одинаковой ширины.

Задача 2.

Во сколько раз увеличится расстояние между светлыми соседними полосами на экране в опыте Юнга, если зеленый светофильтр заменить красным (м)?

Решение Ширина полосы (см.

Задачу 1)

;

;

Дано:

м

м

— ?

.

Ответ: красные полосы шире зеленых в 1,3 раза.

Вопрос. Описать вид интерферирующей картины, если отверстия в опыте Юнга освещать белым светом?

Ответ: центральная полоса будет белая, так как разность хода интерферирующих лучей, приходящих в точку 0, равна нулю для всех длин волн; остальные максимумы спектральные, расположенные симметрично относительно центрального. Так как расстояние от точки 0 зависит от длины волны , то спектр каждого порядка (m = ±1, ±2, …) начинается с фиолетового цвета и заканчивается красным .

Задача 3. В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка, вследствие чего светлая нулевая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной).

Луч падает на пластинку перпендикулярно. Показатель преломления пластинки . Длина волны светам. Какова толщина пластинки?

Дано:

м

d — ?

Решение

Стеклянная пластинка толщиной d, поставленная на пути второго луча, изменит оптическую длину пути этого луча. Теперь оптическая длина пути складывается из оптической длины пути луча в воздухе ()n_возд= = l₂ – d и оптической длины пути в самой пластинке nd, т.е. .

Оптическая разность хода лучей

,

по условию задачи тогда

Если интерферирующие лучи усиливают друг друга, то должно выполняться условие

.

Приравнивая, получаем

.

Откуда

м.

Ответ: м.

Задача 5. На толстую стеклянную пластинку, покрытую очень тонкой пленкой (n = 1,4) падает нормально параллельный пучок лучей монохроматического света (м). Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину пленки.

Дано:

м

d — ?

StudyPort.Ru — Интерференция света

Страница 1 из 2

41. Определите длину отрезка l₁, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l₂ = 5 мм в стекле. Показатель преломления стекла n = 1,5.

 

42. Два параллельных световых пучка, отстоящих друг от друга на расстоянии d = 5 см, падают на кварцевую призму (n = 1,49) с преломляющим углом α = 25° . Определите оптическую разность хода d этих пучков на выходе их из призмы.

43. В опыте Юнга расстояние между щелями d = 1 мм, а расстояние l от щелей до экрана равно 3 м. Определите: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны λ = 0,5 мкм.

44. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определите длину волны желтого света.

45. Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ = 0,6 мкм). Определите расстояние l от щелей до экрана, если ширина Δх интерференционных полос равна 1,2 мм.

46. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определите угловое расстояние между соседними светлыми полосами, если третья световая полоса на экране отстоит от центра интерференционной картины на 4,5 мм.

47. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n = 1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны λ = 0,5 мкм. Определите толщину пластинки.

48. Определите, во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалом Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм).

49. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равно a = 30 см и b = 1,5 м. Бипризма стеклянная (n = 1,5) с преломляющим углом ν = 20′. Определите длину волны света, если ширина интерференционных полос Δx = 0,65 мм.

50. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равно a = 48 см и b = 6 м. Бипризма стеклянная (n = l,5) с преломляющим углом ν = 10′. Определите максимальное число полос, наблюдаемых на экране, если λ = 600 нм.

51. На плоскопараллельную пленку с показателем преломления n = 1,33 под углом i = 45° падает параллельный пучок белого света. Определите, при какой наименьшей толщине пленки зеркально отраженный свет наиболее сильно окрасится в желтый цвет (λ = 0,6 мкм).

52. На стеклянный клин (n = 1,5) нормально падает монохроматический свет (λ = 698 нм). Определите угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм.

53. На стеклянный клин (n = 1,5) нормально падает монохроматический свет. Угол клина равен 4′. Определите длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.

54. На тонкую мыльную пленку (n = 1,33) под углом i = 30° падает монохроматический свет с длиной волны λ = 0,6 мкм. Определите угол между поверхностями пленки, если расстояние b между интерференционными полосами в отраженном свете равно 4 мм.

55. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами Δx₁ = 0,4 мм. Определите расстояние Δx₂ между интерференционными полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33.

56. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определите длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.

57. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,55 мкм, падающим нормально. Определите толщину воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой в том месте, где в отраженном свете наблюдается четвертое темное кольцо.

58. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,6 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определите показатель преломления жидкости, если радиус второго светлого кольца r = 1,8 мм.

59. Плосковыпуклая линза с показателем преломления n = 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете (λ = 0,6 мкм) равен 0,9 мм. Определите фокусное расстояние линзы.

60. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света.

61. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определите показатель преломления жидкости.

 

Свет | Определение, свойства, физика, характеристики, типы и факты

видимый спектр света

Смотреть все СМИ

Ключевые люди:

Исаак Ньютон Альберт Эйнштейн Джеймс Клерк Максвелл Птолемей Роджер Бэкон

Похожие темы:

цвет Солнечный лучик фотон интенсивность света скорость света

Просмотреть весь связанный контент →

Популярные вопросы

Что такое свет в физике?

Свет — это электромагнитное излучение, воспринимаемое человеческим глазом. Электромагнитное излучение возникает в чрезвычайно широком диапазоне длин волн, от гамма-лучей с длиной волны менее примерно 1 × 10 ⁻¹¹ метров до радиоволн, измеряемых в метрах.

Какова скорость света?

Скорость света в вакууме является фундаментальной физической константой, и в настоящее время принято значение 29.9 792 458 метров в секунду, или около 186 282 миль в секунду.

Что такое радуга?

Радуга образуется при преломлении солнечного света сферическими каплями воды в атмосфере; два преломления и одно отражение в сочетании с хроматической дисперсией воды создают первичные цветовые дуги.

Почему свет важен для жизни на Земле?

Свет является основным инструментом восприятия мира и взаимодействия с ним для многих организмов. Солнечный свет согревает Землю, определяет глобальные погодные условия и запускает поддерживающий жизнь процесс фотосинтеза; около 10 ²² джоулей солнечной лучистой энергии достигает Земли каждый день. Взаимодействие света с материей также помогло сформировать структуру Вселенной.

Каково отношение цвета к свету?

В физике цвет ассоциируется именно с электромагнитным излучением определенного диапазона длин волн, видимым человеческому глазу. Излучение таких длин волн составляет часть электромагнитного спектра, известную как видимый спектр, т. е. свет.

Сводка

Прочтите краткий обзор этой темы

свет , электромагнитное излучение, воспринимаемое человеческим глазом. Электромагнитное излучение возникает в чрезвычайно широком диапазоне длин волн, от гамма-лучей с длиной волны менее примерно 1 × 10 ⁻¹¹ метров до радиоволн, измеряемых в метрах. В этом широком спектре длины волн, видимые человеку, занимают очень узкую полосу, от примерно 700 нанометров (нм; миллиардных долей метра) для красного света до примерно 400 нм для фиолетового света. Области спектра, примыкающие к видимому диапазону, часто также называют световыми, инфракрасными с одной стороны и ультрафиолетовыми с другой. Скорость света в вакууме — фундаментальная физическая константа, принятое в настоящее время значение которой равно ровно 299 792 458 метров в секунду, или около 186 282 миль в секунду.

Нет однозначного ответа на вопрос «Что такое свет?» удовлетворяет множеству контекстов, в которых свет воспринимается, исследуется и используется. Физик интересуется физическими свойствами света, художник — эстетической оценкой визуального мира. Благодаря зрению свет является основным инструментом восприятия мира и общения в нем. Солнечный свет согревает Землю, определяет глобальные погодные условия и запускает поддерживающий жизнь процесс фотосинтеза. В самом большом масштабе взаимодействие света с материей помогло сформировать структуру Вселенной. Действительно, свет дает окно во Вселенную, от космологических до атомных масштабов. Почти вся информация об остальной Вселенной достигает Земли в виде электромагнитного излучения.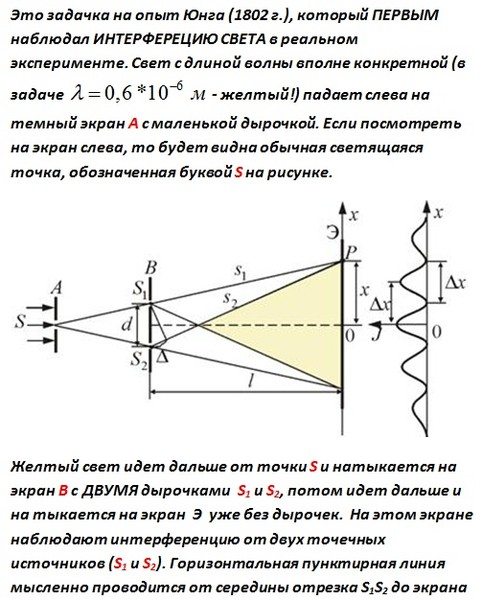

Интерпретируя это излучение, астрономы могут заглянуть в самые ранние эпохи Вселенной, измерить общее расширение Вселенной и определить химический состав звезд и межзвездной среды. Подобно тому, как изобретение телескопа значительно расширило возможности исследования Вселенной, так и изобретение микроскопа открыло сложный мир клетки. Анализ частот света, испускаемого и поглощаемого атомами, явился основным толчком к развитию квантовой механики. Атомная и молекулярная спектроскопия по-прежнему остается основным инструментом для исследования структуры вещества, обеспечивая сверхчувствительные тесты атомных и молекулярных моделей и способствуя изучению фундаментальных фотохимических реакций.

Свет передает пространственную и временную информацию. Это свойство лежит в основе областей оптики и оптических коммуникаций, а также множества связанных с ними технологий, как зрелых, так и развивающихся. Технологические приложения, основанные на манипулировании светом, включают лазеры, голографию и волоконно-оптические телекоммуникационные системы.

В большинстве повседневных обстоятельств свойства света можно вывести из теории классического электромагнетизма, в которой свет описывается как связанные электрические и магнитные поля, распространяющиеся в пространстве в виде бегущей волны. Однако эта волновая теория, разработанная в середине 19 в.го века недостаточно для объяснения свойств света при очень низкой интенсивности. На этом уровне квантовая теория необходима для объяснения характеристик света и взаимодействия света с атомами и молекулами. В своей простейшей форме квантовая теория описывает свет как состоящий из дискретных пакетов энергии, называемых фотонами. Однако ни классическая волновая модель, ни классическая модель частиц не описывают свет правильно; свет имеет двойственную природу, которая раскрывается только в квантовой механике. Этот удивительный корпускулярно-волновой дуализм характерен для всех первичных составляющих природы (например, электроны имеют как корпускулярный, так и волновой аспекты). С середины 20-го века физики считали законченной более полную теорию света, известную как квантовая электродинамика (КЭД).

КЭД объединяет идеи классического электромагнетизма, квантовой механики и специальной теории относительности.

Britannica Quiz

27 правильных или неверных вопросов из самых сложных научных викторин Britannica

В этой статье основное внимание уделяется физическим характеристикам света и теоретическим моделям, описывающим природу света. Его основные темы включают введение в основы геометрической оптики, классические электромагнитные волны и эффекты интерференции, связанные с этими волнами, а также основные идеи квантовой теории света. Более подробные и технические презентации этих тем можно найти в статьях «Оптика, электромагнитное излучение, квантовая механика и квантовая электродинамика». См. также относительность для получения подробной информации о том, как рассмотрение скорости света, измеренной в различных системах отсчета, сыграло решающую роль в развитии специальной теории относительности Альберта Эйнштейна в 1905 году. world

Хотя есть явные свидетельства того, что ряд ранних цивилизаций использовали простые оптические инструменты, такие как плоские и криволинейные зеркала и выпуклые линзы, древнегреческим философам обычно приписывают первые формальные рассуждения о природе света. Концептуальное препятствие, заключающееся в том, чтобы отличить человеческое восприятие визуальных эффектов от физической природы света, препятствовало развитию теорий света. В этих ранних исследованиях преобладало созерцание механизма зрения. Пифагор ( с. 500 г. до н.э.) предположил, что зрение вызывается визуальными лучами, исходящими из глаза и поражающими объекты, тогда как Эмпедокл ( г. ок. 450 г. до н.э.), по-видимому, разработал модель зрения, в которой свет излучался как объектами, так и глазом. Эпикур ( г. ок. г. 300 г. до н.э.) считал, что свет излучается другими источниками, помимо глаза, и что зрение возникает, когда свет отражается от объектов и попадает в глаз. Евклид ( г. ок. г. 300 г. до н.э.) в своей книге Оптика представил закон отражения и обсудил распространение световых лучей по прямым линиям. Птолемей ( с. 100 н.э.) предпринял одно из первых количественных исследований преломления света при переходе из одной прозрачной среды в другую, сведя в таблицу пары углов падения и пропускания для комбинаций нескольких сред.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

С упадком греко-римского царства научный прогресс переместился в исламский мир. В частности, аль-Махмун, седьмой аббасидский халиф Багдада, основал Дом Мудрости (Байт аль-Хикма) в 830 г. н.э. для перевода, изучения и улучшения эллинистических научных и философских трудов. Среди первых ученых были аль-Хорезми и аль-Кинди. Известный как «философ арабов», аль-Кинди расширил концепцию прямолинейно распространяющихся световых лучей и обсудил механизм зрения. К 1000 г. от пифагорейской модели света отказались, и возникла лучевая модель, содержащая основные концептуальные элементы того, что сейчас известно как геометрическая оптика. В частности, Ибн аль-Хайтам (латинизированный как Альхазен) в Китаб аль-маназир ( ок. 1038; «Оптика») правильно приписал зрение пассивному восприятию световых лучей, отраженных от предметов, а не активному излучению световых лучей глазами. Он также изучал математические свойства отражения света от сферических и параболических зеркал и нарисовал подробные изображения оптических компонентов человеческого глаза. Работа Ибн аль-Хайтама была переведена на латынь в 13 веке и оказала побудительное влияние на францисканского монаха и естествоиспытателя Роджера Бэкона. Бэкон изучал распространение света через простые линзы и считается одним из первых, кто описал использование линз для коррекции зрения.

3.2: Двухщелевая интерференция Юнга — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4499

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснять явление интерференции
• Определение конструктивной и деструктивной интерференции для двойной щели

Голландский физик Кристиан Гюйгенс (1629–1695) думал, что свет — это волна, а Исаак Ньютон — нет. Ньютон считал, что существуют и другие объяснения цвета, а также наблюдаемых в то время эффектов интерференции и дифракции. Благодаря огромной репутации Ньютона его точка зрения в целом возобладала; тот факт, что принцип Гюйгенса работал, не считался прямым доказательством того, что свет является волной. Признание волнового характера света произошло много лет спустя, в 1801 г., когда английский физик и врач Томас Янг (1773–1829) продемонстрировал оптическую интерференцию в своем теперь уже классическом эксперименте с двумя щелями.

Если бы было не один, а два источника волн, волны можно было бы интерферировать, как в случае с волнами на воде (рис. \(\PageIndex{1}\)). Если свет представляет собой электромагнитную волну, то при соответствующих обстоятельствах он должен проявлять интерференционные эффекты. В эксперименте Янга солнечный свет пропускался через отверстие в доске. Выходящий луч попал в два отверстия на второй доске. Затем свет, исходящий из двух отверстий, падал на экран, где наблюдалась картина из ярких и темных пятен. Этот узор, называемый полосами, можно объяснить только интерференцией, волновым явлением.

Рисунок \(\PageIndex{1}\): Фотография интерференционной картины, создаваемой круговыми водными волнами в резервуаре с пульсацией. Два тонких плунжера синхронно вибрируют вверх и вниз на поверхности воды. Круговые водяные волны создаются и исходят от каждого плунжера.

Мы можем проанализировать двухщелевую интерференцию с помощью рисунка \(\PageIndex{2}\), на котором изображен аппарат, аналогичный аппарату Юнга. Свет от монохроматического источника падает на щель \(S_0\). Свет, исходящий из \(S_0\), падает на две другие щели \(S_1\) и \(S_2\), которые равноудалены от \(S_0\). Шаблон интерференционные полосы на экране создаются светом, исходящим от \(S_1\) и \(S_2\). Предполагается, что все щели настолько узкие, что их можно считать вторичными точечными источниками вейвлетов Гюйгенса («Природа света»). Щели \(S_1\) и \(S_2\) находятся на расстоянии d друг от друга (\(d≤1\,мм\)), а расстояние между экраном и щелями равно D(≈1м), т. е. намного больше, чем d.

Рисунок \(\PageIndex{2}\): Эксперимент по интерференции с двумя щелями с использованием монохроматического света и узких щелей. На экране наблюдаются полосы, создаваемые интерферирующими вейвлетами Гюйгенса от щелей \(S_1\) и \(S_2\).

Поскольку \(S_0\) считается точечным источником монохроматического света, вторичные вейвлеты Гюйгенса, выходящие из \(S_1\) и \(S_2\), всегда поддерживают постоянную разность фаз (в данном случае ноль, потому что \(S_1\ ) и \(S_2\) равноудалены от \(S_0\)) и имеют одинаковую частоту. Тогда говорят, что источники \(S_1\) и \(S_2\) когерентны. Под когерентными волнами мы подразумеваем, что волны находятся в фазе или имеют определенное фазовое соотношение. Термин «некогерентный» означает, что волны имеют случайные фазовые соотношения, что имело бы место, если бы \(S_1\) и \(S_2\) освещались двумя независимыми источниками света, а не одним источником \(S_0\). Два независимых источника света (которые могут быть двумя отдельными областями внутри одной лампы или Солнца) обычно не излучают свет в унисон, то есть не когерентно. Кроме того, поскольку \(S_1\) и \(S_2\) находятся на одинаковом расстоянии от \(S_0\), амплитуды двух вейвлетов Гюйгенса равны.

Янг использовал солнечный свет, где каждая длина волны образует свой собственный рисунок, что затрудняет видимость эффекта. В следующем обсуждении мы проиллюстрируем эксперимент с двумя щелями с монохроматическим светом (один λ), чтобы прояснить эффект. На рисунке \(\PageIndex{3}\) показана чистая конструктивная и деструктивная интерференция двух волн с одинаковой длиной волны и амплитудой.

Рисунок \(\PageIndex{3}\): Амплитуды волн складываются. (а) Чистая конструктивная интерференция получается, когда одинаковые волны находятся в фазе. (б) Чистая деструктивная интерференция возникает, когда идентичные волны точно не совпадают по фазе или сдвинуты на половину длины волны.

Когда свет проходит через узкие щели, щели действуют как источники когерентных волн, а свет распространяется в виде полукруглых волн, как показано на рисунке \(\PageIndex{1a}\). Чистая конструктивная интерференция возникает там, где волны располагаются от гребня к гребню или от впадины к впадине. Чистая деструктивная интерференция происходит там, где они находятся от гребня к впадине. Свет должен падать на экран и рассеиваться в наших глазах, чтобы мы могли видеть узор. Аналогичная картина для волн на воде показана на рисунке \(\PageIndex{1}\). Обратите внимание, что области конструктивной и деструктивной интерференции выходят из щелей под определенными углами к исходному лучу. Эти углы зависят от длины волны и расстояния между щелями, как мы увидим ниже.

Рисунок \(\PageIndex{4}\): Двойные щели создают два когерентных источника интерферирующих волн. (а) Свет распространяется (дифрагирует) от каждой щели, потому что щели узкие. Эти волны перекрываются и интерферируют конструктивно (светлые линии) и деструктивно (темные области). Мы можем видеть это, только если свет падает на экран и рассеивается в наших глазах. б) Когда свет, прошедший через двойные щели, падает на экран, мы видим такую ​​картину.

Чтобы понять интерференционную картину с двумя щелями, рассмотрим, как две волны проходят от щелей к экрану (рис. \(\PageIndex{5}\)). Каждая щель находится на разном расстоянии от заданной точки на экране. Таким образом, на каждый путь укладывается разное количество длин волн. Волны выходят из щелей в фазе (гребень к гребню), но они могут закончиться не в фазе (гребень к впадине) на экране, если пути различаются по длине на половину длины волны, создавая деструктивные помехи. Если пути различаются на целую длину волны, то волны приходят на экран синфазно (гребень к гребню), конструктивно интерферируя. В более общем случае, если разность длин пути \(\Delta l\) между двумя волнами составляет любое полуцелое число длин волн [(1/2)λ, (3/2)λ, (5/2)λ и т. д. .], то происходит деструктивная интерференция. Точно так же, если разность длин пути составляет любое целое число длин волн (λ, 2λ, 3λ и т. д.), возникает конструктивная интерференция. Эти условия могут быть выражены в виде уравнений:

\[\underbrace{\Delta l = m \lambda}_{\text{конструктивная интерференция}} \nonumber \]

для \(m = 0, \, ±1, \, ±2, \, ±3…\)

\[\underbrace{\Delta l = \left(m + \frac{1}{2}\right)\lambda}_{\text{деструктивная интерференция}} \nonumber \]

для \(m = 0, \, ±1, \, ±2, \, ±3…\)

Рисунок \(\PageIndex{5}\): Волны следуют разными путями от щелей до общей точки P на экране.