Вектор на плоскости: Векторы на плоскости и в пространстве: основные определения

Векторы на плоскости и в пространстве: основные определения

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Определение 1

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.

Нулевой вектор

Определение 2

Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Определение 3

Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектораAB→ принято обозначать так AB→.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

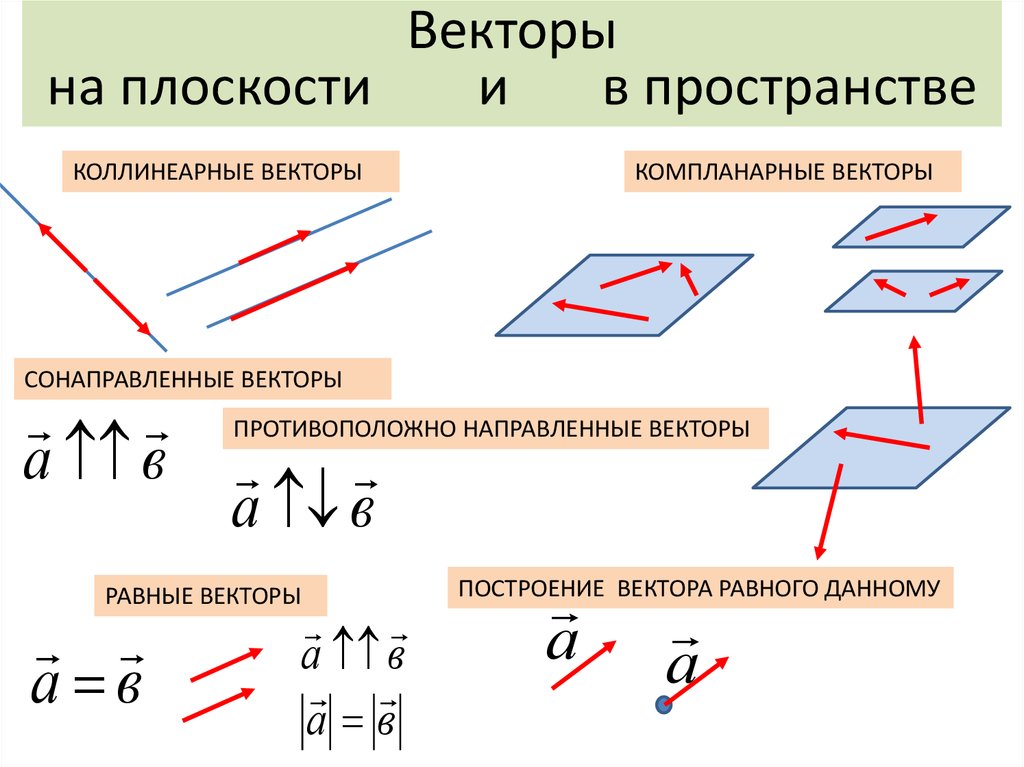
Коллинеарность векторов

Определение 4

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Определение 5

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.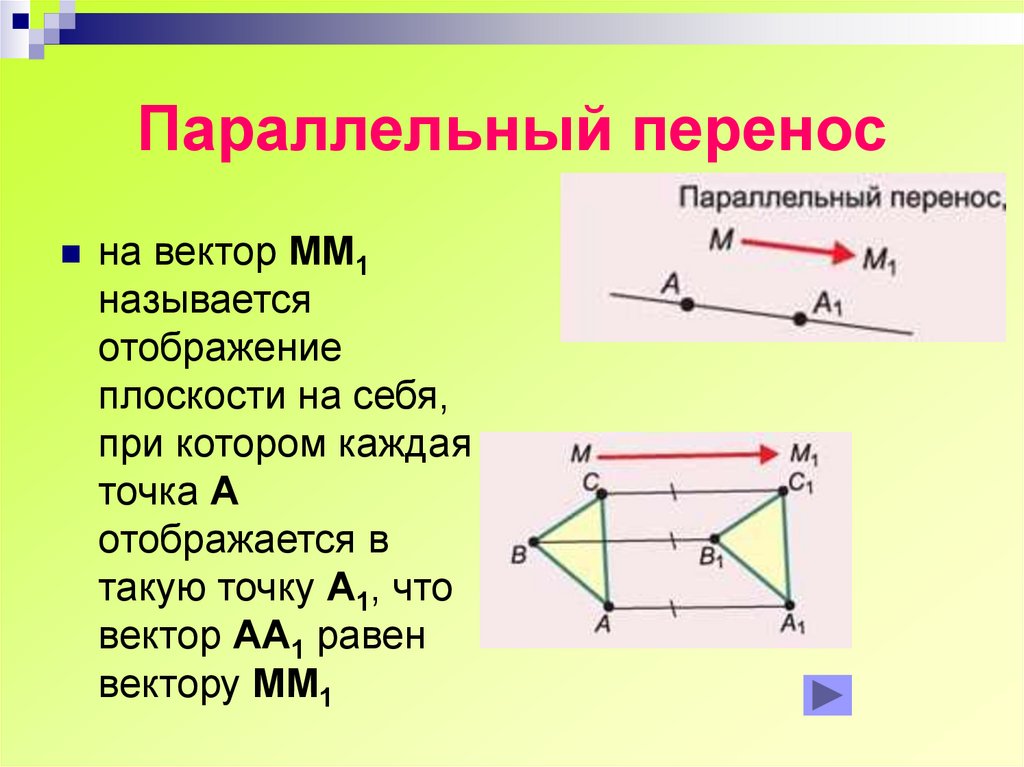

Направление векторов

Определение 6

Сонаправленными векторами называют два коллинеарных вектора a→ и b→, у которых направления совпадают, такие векторы обозначаются так a→↑↑b→.

Определение 7

Противоположно направленными векторами называются два коллинеарных вектора a→ и b→, у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a→↑↓b→.

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Определение 8

Равными

называются сонаправленные вектора, у которых длины равны.

Определение 9

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a→ и b→. Отложим от некоторой точки O плоскости или пространства векторы OA→=a→ и OB→=b→. Лучи OA и OB образуют угол ∠AOB=φ.

Углы между векторами

Определение 9

Угол φ=∠AOB называется углом между векторами a→=OA→ и b→=OB→.

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Определение 10

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π2 радиан).

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Координаты вектора в ДСК

Следующая статья

Длина вектора

• Векторное произведение
• Векторное пространство
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Длина вектора
• Все темы по математике

• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Дистанционный экзамен

Заказать такую же работу

Основы информационных технологий в строительстве

Заказать такую же работу

Дистанционный экзамен по ИНЖЕНЕРНОЙ ГРАФИКЕ

Заказать такую же работу

Теория функций комплексного переменного Операционное исчисление

• Вид работы:

  Контрольная работа

• Выполнена:

  20 июня 2022 г.

• Стоимость:

  1 600 руб

Заказать такую же работу

математика вокруг нас

• Вид работы:

  Домашняя работа

• Выполнена:

  30 марта 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

монтажная привязка оборудования горячего цеха кафе на мест

• Вид работы:

  Чертёж

• Выполнена:

  18 февраля 2022 г.

• Стоимость:

  3 200 руб

Заказать такую же работу

Смотреть все работы по теоретической механике

Векторы на плоскости и в пространстве: основные определения

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Определение 1

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.

Нулевой вектор

Определение 2

Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Определение 3

Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектораAB→ принято обозначать так AB→.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Определение 4

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Определение 5

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Определение 6

Сонаправленными векторами называют два коллинеарных вектора a→ и b→, у которых направления совпадают, такие векторы обозначаются так a→↑↑b→.

Определение 7

Противоположно направленными векторами называются два коллинеарных вектора a→ и b→, у которых направления не совпадают, т.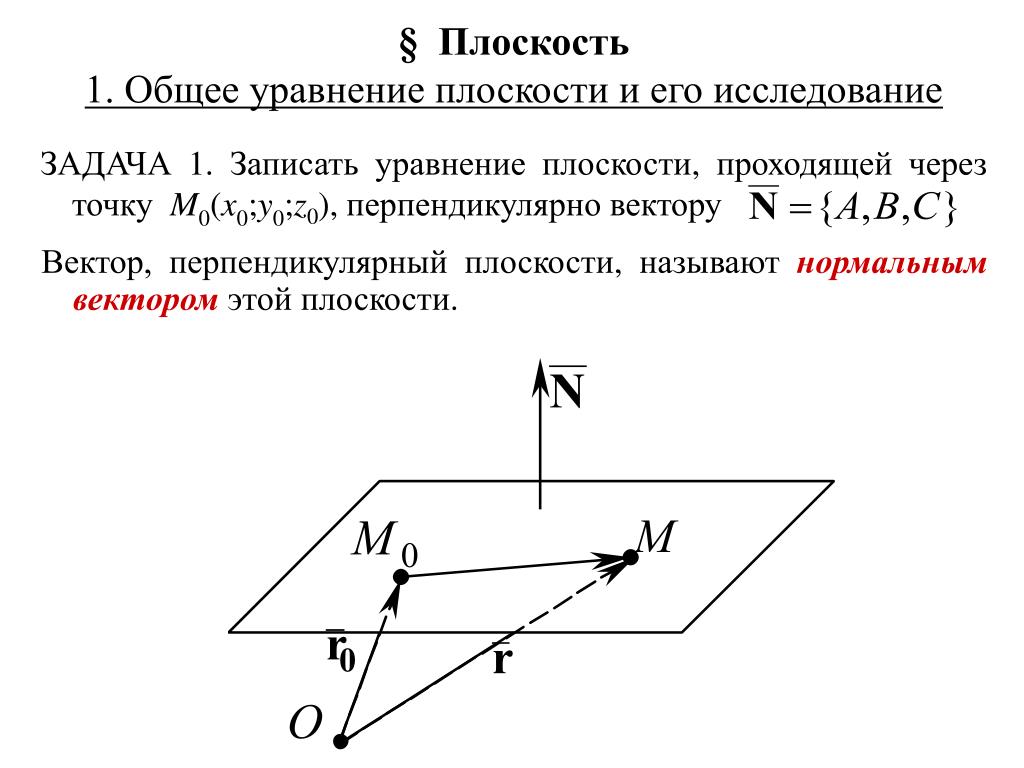 е. являются противоположными, такие векторы обозначаются следующим образом a→↑↓b→.

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Определение 8

Равными называются сонаправленные вектора, у которых длины равны.

Определение 9

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a→ и b→. Отложим от некоторой точки O плоскости или пространства векторы OA→=a→ и OB→=b→. Лучи OA и OB образуют угол ∠AOB=φ.

Углы между векторами

Определение 9

Угол φ=∠AOB называется углом между векторами a→=OA→ и b→=OB→.

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Определение 10

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π2 радиан).

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Координаты вектора в ДСК

Следующая статья

Длина вектора

• Векторное произведение
• Векторное пространство
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Длина вектора
• Все темы по математике

• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Дистанционный экзамен

Заказать такую же работу

Основы информационных технологий в строительстве

Заказать такую же работу

Дистанционный экзамен по ИНЖЕНЕРНОЙ ГРАФИКЕ

Заказать такую же работу

Теория функций комплексного переменного Операционное исчисление

• Вид работы:

  Контрольная работа

• Выполнена:

  20 июня 2022 г.

• Стоимость:

  1 600 руб

Заказать такую же работу

математика вокруг нас

• Вид работы:

  Домашняя работа

• Выполнена:

  30 марта 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

монтажная привязка оборудования горячего цеха кафе на мест

• Вид работы:

  Чертёж

• Выполнена:

  18 февраля 2022 г.

• Стоимость:

  3 200 руб

Заказать такую же работу

Смотреть все работы по теоретической механике

Объяснение урока: Уравнение плоскости: вектор, скаляр и общие формы

В этом объяснении мы узнаем, как найти вектор, скаляр (стандартный или компонентный) и общий (Декартовы или нормальные) формы уравнения плоскости с заданным вектором нормали и точкой на нем.

Давайте сначала рассмотрим уравнение линии в декартовой форме и перепишем его в векторной форме в двух измерениях, ℝ, так как ситуация будет аналогична для плоскости в трех измерениях, ℝ.

Напомним, что общая форма уравнения прямой в двух измерениях имеет вид 𝑎𝑥+𝑏𝑦+𝑐=0.

Это также можно записать в виде 𝑦=𝑚𝑥+𝑑, где 𝑚 — градиент, а 𝑑 — это 𝑦-перехват, который мы можем определить, зная две точки на прямой. Если (𝑥,𝑦) — точка, лежащая на прямой, мы можем определить 𝑐 из общая форма как 𝑐=−(𝑎𝑥+𝑏𝑦); таким образом, уравнение прямой можно записать в виде 𝑎𝑥+𝑏𝑦−(𝑎𝑥+𝑏𝑦)=0𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)=0,

Уравнение прямой также может быть реализовано как скалярное произведение двух векторов как (𝑎,𝑏)⋅(𝑥−𝑥,𝑦−𝑦)=0(𝑎,𝑏)⋅((𝑥,𝑦)−(𝑥,𝑦))=0.

Теперь, если мы определим векторы положения, ⃑𝑟=(𝑥,𝑦),⃑𝑟=(𝑥,𝑦), то уравнение прямой можно записать в векторной форме как ⃑𝑛⋅⃑𝑟−⃑𝑟=0⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝑟, где ⃑𝑛=(𝑎,𝑏) называется нормальным вектором прямой и ⃑𝑟−⃑𝑟 полностью ляжет на прямую. Свойство скалярного произведения утверждает, что два вектора перпендикулярны друг другу, если их скалярное произведение равно нулю.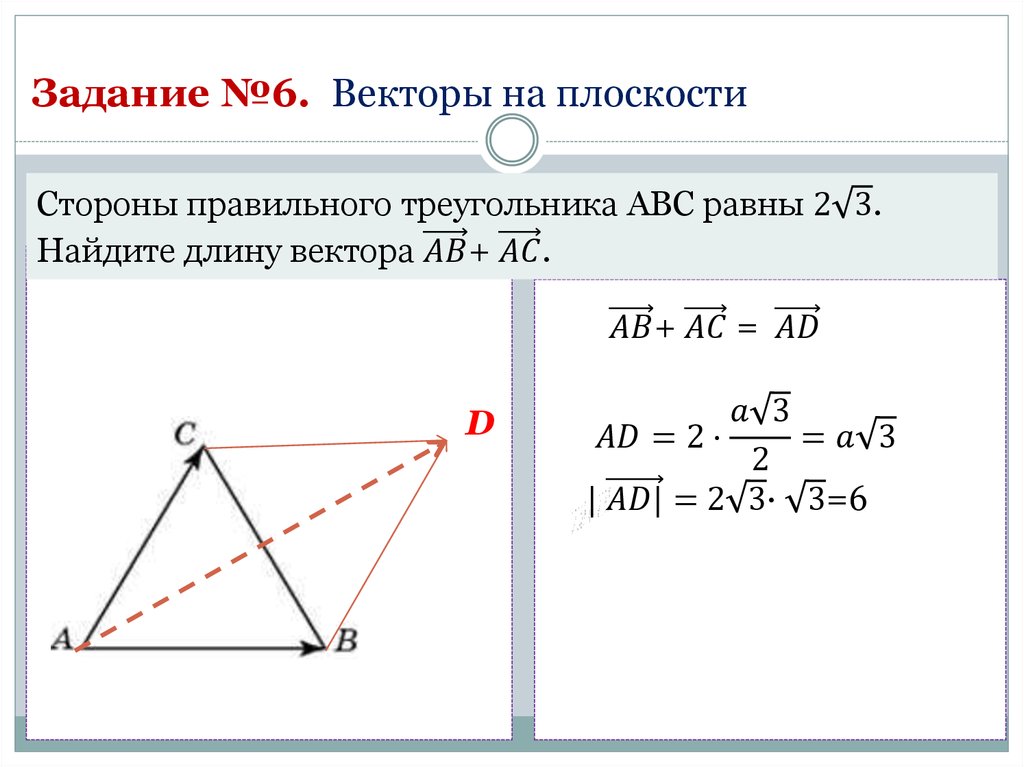 Это уравнение прямой в векторная форма показывает, что вектор нормали ⃑𝑛 и вектор ⃑𝑟−⃑𝑟 перпендикулярны друг другу по этому свойству.

Вектор нормали ⃑𝑛 к прямой или плоскости — это вектор, перпендикулярный к прямой или плоскости. Другими словами, вектор нормали перпендикулярен любому вектору ⃑𝑣, параллельному линия или плоскость, и мы имеем ⃑𝑛⋅⃑𝑣=0, по свойству скалярного произведения.

Подобно уравнению прямой в двух измерениях, уравнение плоскости в трех измерениях может быть представлено в терминах нормального вектора на плоскости. Мы можем представить уравнение плоскости следующим образом.

Определение: Общая форма уравнения плоскости

Общая форма уравнения плоскости в ℝ: 𝑎𝑥+𝑏𝑦+𝑐𝑧+𝑑=0, где 𝑎, 𝑏 и 𝑐 — компоненты вектора нормали ⃑𝑛=(𝑎,𝑏,𝑐), который перпендикулярен плоскости или любой вектор, параллельный плоскости.

Если (𝑥,𝑦,𝑧) — точка, лежащая на плоскости, то 𝑑=−(𝑎𝑥+𝑏𝑦+𝑐𝑧) и мы можем записать уравнение плоскости как 𝑎𝑥+𝑏𝑦+𝑐𝑧−(𝑎𝑥+𝑏𝑦+𝑐𝑧)=0. 

Это можно переставить, чтобы получить уравнение плоскости в скалярной форме.

Определение: скалярная форма уравнения плоскости

Скалярная форма уравнения плоскости в ℝ, содержащая точку (𝑥,𝑦,𝑧) это 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0, где 𝑎, 𝑏 и 𝑐 — компоненты вектора нормали ⃑𝑛=(𝑎,𝑏,𝑐), который перпендикулярен плоскости или любой вектор, параллельный плоскости.

Теперь рассмотрим пример, где мы определяем уравнение плоскости в таком виде из нормального вектор и заданную точку, лежащую на плоскости.

Пример 1. Нахождение уравнения плоскости по точке и ее вектору нормали

Приведите уравнение плоскости с вектором нормали (10,8,3) содержащий точку (10,5,5).

Ответ

В этом примере мы хотим определить уравнение плоскости, используя одну точку на плоскости и задан вектор нормали к плоскости.

Напомним, что скалярная форма уравнения плоскости с вектором нормали ⃑𝑛=(𝑎,𝑏,𝑐), содержащим точку (𝑥,𝑦,𝑧), имеет вид 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0,

Таким образом, подставляя значения для заданного вектора нормали (10,8,3) и точки (10,5,5), имеем 10(𝑥-10)+8(𝑦-5)+3(𝑧-5)=010𝑥-100+8𝑦-40+3𝑧-15=010𝑥+8𝑦+3𝑧-155=0.

Таким образом, общий вид уравнения плоскости с вектором нормали (10,8,3) содержащий точку (10,5,5), есть 10𝑥+8𝑦+3𝑧−155=0.

Если даны точка, лежащая на плоскости (𝑥,𝑦,𝑧), и два непараллельных вектора, ⃑𝑣 и ⃑𝑣, которые параллельны плоскости, то мы можем определите нормаль к плоскости из этих двух векторов. Поскольку оба вектора параллельны плоскости, вектор нормали должны быть перпендикулярны как ⃑𝑣, так и ⃑𝑣. Напомним, что перекрестное произведение двух векторов дает вектор, перпендикулярный обоим векторам. Мы можем использовать это свойство креста продукт для вычисления вектора нормали к плоскости, который приводит к вектору нормали ⃑𝑛=⃑𝑣×⃑𝑣.

В следующем примере мы определим уравнение плоскости, сначала найдя вектор нормали плоскости из двух вектора, параллельные ему.

Пример 2. Нахождение общего уравнения плоскости, проходящей через данную точку и параллельно двум заданным векторам

Найдите общее уравнение плоскости, проходящей через точку (5,1,−1) и параллельной к двум векторам (9,7,−8) и (−2,2,−1).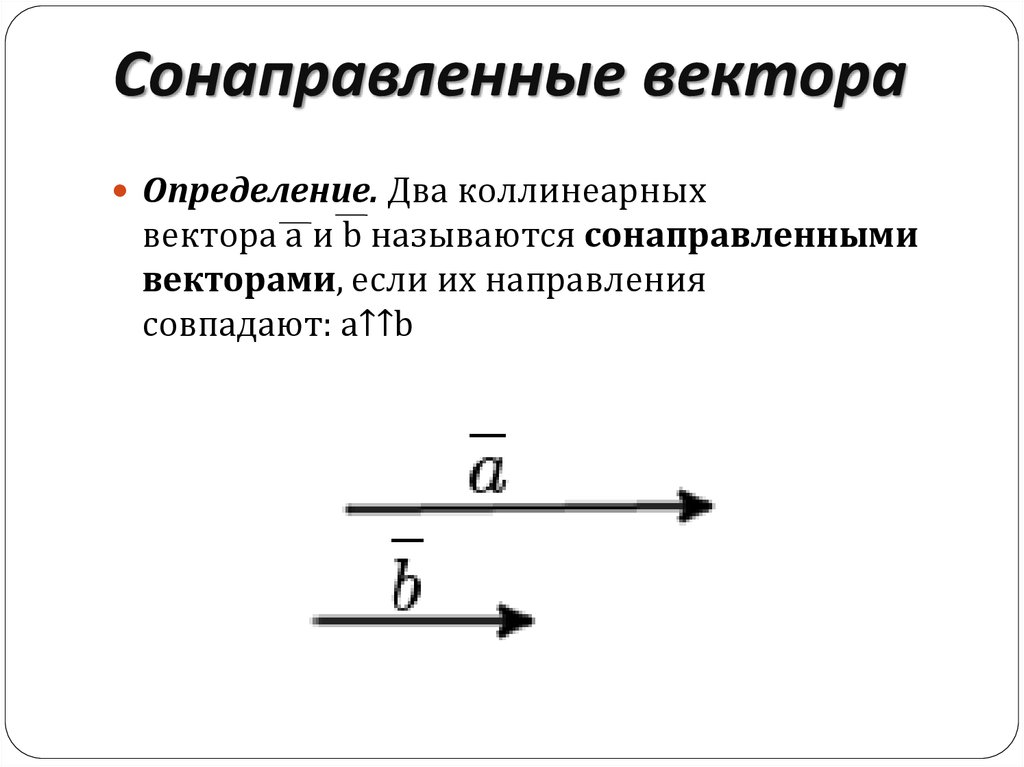

Ответ

В этом примере мы хотим определить уравнение плоскости, которая проходит через точку и параллельна двум заданным векторам.

Напомним, что скалярная форма уравнения плоскости с вектором нормали ⃑𝑛=(𝑎,𝑏,𝑐), содержащим точку (𝑥,𝑦,𝑧), имеет вид 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0,

Нам нужно определить нормаль ⃑𝑛 к плоскости, которая является вектором, перпендикулярным обеим (9,7,−8) и (−2,2,−1), так как они параллельны к самолету. Мы можем найти вектор нормали, взяв векторное произведение между этими векторами: ⃑𝑛=(9,7,−8)×(−2,2,−1)=||||⃑𝑖⃑𝑗⃑𝑘97−8−22−1||||=||7−82−1||⃑𝑖−|| 9−8−2−1||⃑𝑗+||97−22||⃑𝑘=(7×(−1)−(−8)×2)⃑𝑖−(9×(−1)−(−8)×( −2))⃑𝑗+(9×2−7×(−2))⃑𝑘=9⃑𝑖+25⃑𝑗+32⃑𝑘=(9,25,32).

Используя вектор нормали (9,25,32) и точку на плоскости (5,1,−1), имеем 9(𝑥−5)+25(𝑦−1)+32(𝑧+1)=09𝑥−45+25𝑦−25+32𝑧+32=09𝑥+25𝑦+32𝑧−38=0.

Таким образом, общее уравнение плоскости, проходящей через точку (5,1,−1) и параллелен двум векторам (9,7,−8) и (−2,2,−1) равно 9𝑥+25𝑦+32𝑧−38=0.

Если плоскость содержит три точки (𝑥,𝑦,𝑧), (𝑥,𝑦,𝑧), и (𝑥,𝑦,𝑧), то мы можем определить уравнение плоскости. Подставив эти точки в скалярную форму уравнения плоскости получаем 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0,𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0,  подобно тому, как мы можем определить уравнение прямой с двумя заданными точками. Однако это не стандартный способ определения уравнение плоскости. Вместо этого мы определим вектор нормали, заметив, что разность векторов положения любого две точки на плоскости — это вектор, параллельный плоскости; мы еще вернемся к этому при рассмотрении векторной формы уравнения самолета.

Если обозначить векторы положения трех неколлинеарных точек как и ⃑𝑟=(𝑥,𝑦,𝑧), то можно получить два вектора, параллельных плоскости путем вычитания пар этих векторов положения как ⃑𝑣=⃑𝑟−⃑𝑟=(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧),⃑𝑣=⃑𝑟−⃑𝑟=(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧). 

Фактически, мы можем сделать это с любыми парами и в любом порядке; например, другой выбор может быть ⃑𝑣=⃑𝑟−⃑𝑟,⃑𝑣=⃑𝑟−⃑𝑟. 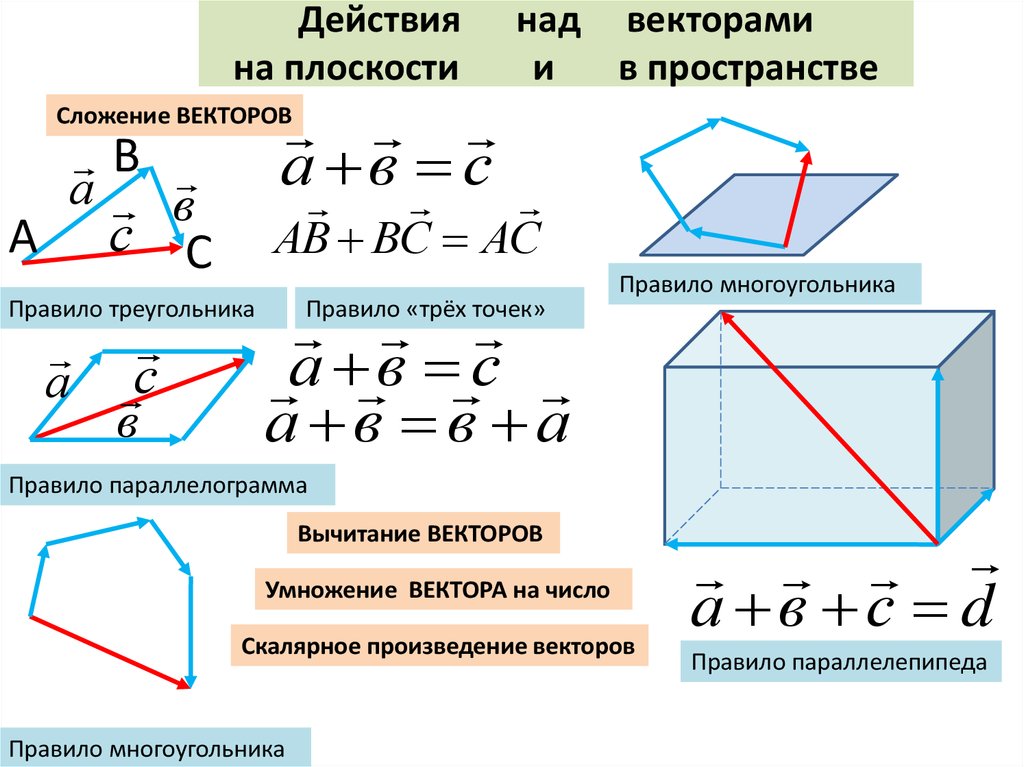

В любом случае вектор нормали можно определить из векторного произведения этих двух векторов: ⃑𝑛=⃑𝑣×⃑𝑣.

Теперь рассмотрим пример, где мы используем эту форму вместе с информацией о трех точках, лежащих на плоскости, чтобы определить уравнение.

Пример 3. Нахождение общего уравнения плоскости, проходящей через три неколлинеарные точки

Запишите в нормальной форме уравнение плоскости (1,0,3), (1,2,−1), и (6,1,6).

Ответ

В этом примере мы хотим определить уравнение плоскости по трем заданным точкам, лежащим на плоскости.

Напомним, что уравнение плоскости с вектором нормали ⃑𝑛=(𝑎,𝑏,𝑐) содержащий точку (𝑥,𝑦,𝑧), является 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0.

Сначала определим вектор нормали к плоскости. Мы можем получить два вектора на плоскости, вычитая положение векторы пар точек на плоскости: ⃑𝑣=(1,0,3)−(1,2,−1)=(0,−2,4),⃑𝑣=(1,0,3)−(6,1,6)=(−5, −1,−3).

Мы можем найти вектор нормали, взяв векторное произведение между этими векторами: ⃑𝑛=⃑𝑣×⃑𝑣=(0,−2,4)×(−5,−1,−3)=||||⃑𝑖⃑𝑗⃑𝑘0−24−5−1−3||||=||−24−1 −3||⃑𝑖−||04−5−3||⃑𝑗+||0−2−5−1||⃑𝑘=((−2)×(−3)−4×(−1))⃑𝑖− (0×(−3)−4×(−5))⃑𝑗+(0×(−1)−(−2)×(−5))⃑𝑘=10⃑𝑖−20⃑𝑗−10⃑𝑘=(10,−20,− 10). 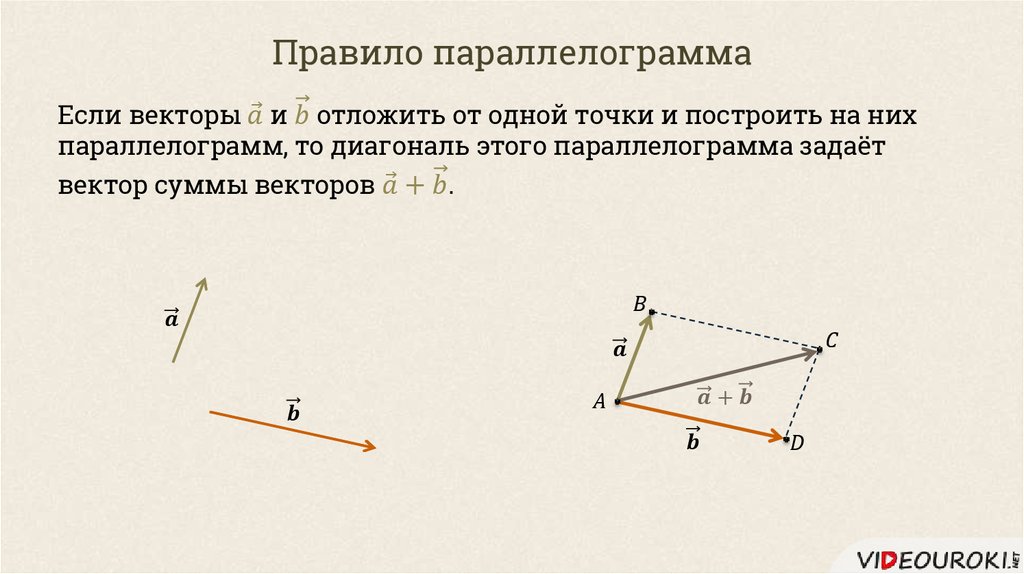

Используя вектор нормали (10,−20,−10) и любую из заданных точек, которые лежат на плоскости, например, (1,0,3), уравнение плоскости принимает вид 10(𝑥-1)-20(𝑦-0)-10(𝑧-3)=010𝑥-10-20𝑦-10𝑧+30=010𝑥-20𝑦-10𝑧+20=0.

Таким образом, разделив на 10, получим уравнение плоскости в общем виде в виде 𝑥−2𝑦−𝑧+2=0.

Скалярное уравнение плоскости также может быть реализовано как скалярное произведение двух векторов как (𝑎,𝑏,𝑐)⋅(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧)=0(𝑎,𝑏,𝑐)⋅((𝑥,𝑦,𝑧)−(𝑥,𝑦,𝑧))=0 .

Теперь пусть 𝑃=(𝑥,𝑦,𝑧) — точка на плоскости и 𝑃=(𝑥,𝑦,𝑧) любая точка на плоскости, представленная векторами положения ⃑𝑟 и ⃑𝑟 соответственно, то есть ⃑𝑟=(𝑥,𝑦,𝑧) и ⃑𝑟=(𝑥,𝑦,𝑧), и пусть ⃑𝑛=(𝑎,𝑏,𝑐) — вектор нормали к плоскости.

Уравнение плоскости в векторной форме можно записать в виде ⃑𝑛⋅⃑𝑟−⃑𝑟=0.

Вектор ⃑𝑛 перпендикулярен плоскости, а значит, перпендикулярен вектору разность векторов положения любых двух точек на плоскости. Это имеет смысл, поскольку по построению ⃑𝑟−⃑𝑟 всегда будет полностью лежать на плоскости, и скалярное произведение этого вектор с вектором нормали равен нулю, что означает, что они перпендикулярны.

Это уравнение плоскости можно преобразовать, чтобы получить векторную форму уравнения плоскости.

Определение: векторная форма уравнения плоскости

Векторная форма уравнения плоскости в ℝ ⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝑟, где ⃑𝑟 — вектор положения любой точки, лежащей на плоскости и ⃑𝑛 — вектор нормали, перпендикулярный плоскости, или любой вектор, параллельный плоскости.

Теперь давайте рассмотрим два примера, где мы определяем уравнение плоскостей в векторной форме из заданных нормальные векторы и точки, лежащие на плоскости.

Пример 4. Нахождение векторной формы уравнения плоскости по заданному векторному уравнению нормали (2,6,6).

Ответ

В этом примере мы хотим определить уравнение плоскости в векторной форме, используя точку, лежащую на плоскости и заданному вектору нормали.

Напомним, что векторное уравнение плоскости можно записать в виде ⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝑟, где ⃑𝑛 — вектор нормали к плоскости, а ⃑𝑟 вектор положения точки, лежащей на плоскости.

Уравнение плоскости с вектором нормали ⃑𝑛=(1,1,1) который содержит точку (2,6,6) с вектором положения ⃑𝑟=(2,6,6), является (1,1,1)⋅⃑𝑟=(1,1,1)⋅(2,6,6)=1×2+1×6+1×6=14.

Таким образом, векторная форма уравнения плоскости имеет вид (1,1,1)⋅⃑𝑟=14.

Теперь давайте рассмотрим пример, где мы преобразуем уравнение плоскости из общего вида в векторный вид.

Пример 5: Нахождение векторной формы уравнения плоскости

Уравнение плоскости имеет общий вид 5𝑥+6𝑦+9𝑧−28=0. Какова его векторная форма?

Ответ

В этом примере мы хотим определить уравнение плоскости в векторной форме, используя данное уравнение плоскости в общем виде.

Напомним, что общая форма уравнения плоскости в ℝ имеет вид 𝑎𝑥+𝑏𝑦+𝑐𝑧+𝑑=0, где 𝑎, 𝑏 и 𝑐 — компоненты вектора нормали ⃑𝑛=(𝑎,𝑏,𝑐), который перпендикулярен плоскости или любому вектору параллельно плоскости. Векторное уравнение плоскости можно записать в виде ⃑𝑛⋅⃑𝑟=−𝑑.

Из заданного уравнения плоскости 5𝑥+6𝑦+9𝑧−28=0 мы можем определить вектор нормали как ⃑𝑛=(5,6,9) и 𝑑=-28. Векторное уравнение плоскость можно записать как (5,6,9)⋅⃑𝑟=28.

Уравнение прямой в ℝ в векторной форме имеет вид ⃑𝑟=⃑𝑟+𝑡⃑𝑣,𝑡∈ℝ,линия где ⃑𝑟=(𝑥,𝑦,𝑧) — вектор положения точки 𝑃=(𝑥,𝑦,𝑧) на прямой и ⃑𝑣=(𝑎,𝑏,𝑐) — вектор, параллельный прямой.

Если у нас есть плоскость, содержащая две пересекающиеся прямые линии с векторными уравнениями ⃑𝑟=⃑𝑎+𝑡⃑𝑣,⃑𝑟=⃑𝑎+𝑡⃑𝑣, тогда мы можем определить точку, лежащую на плоскости, из любого из этих уравнений. Для простоты мы можем заменить 𝑡=0 в первом уравнении, дающем вектор положения точки, лежащей на первой прямой, и, следовательно, самолет как ⃑𝑎.

Для определения вектора нормали к плоскости заметим, что векторы ⃑𝑣 и ⃑𝑣 параллельно линиям ⃑𝑟 и ⃑𝑟 оба параллельны плоскости.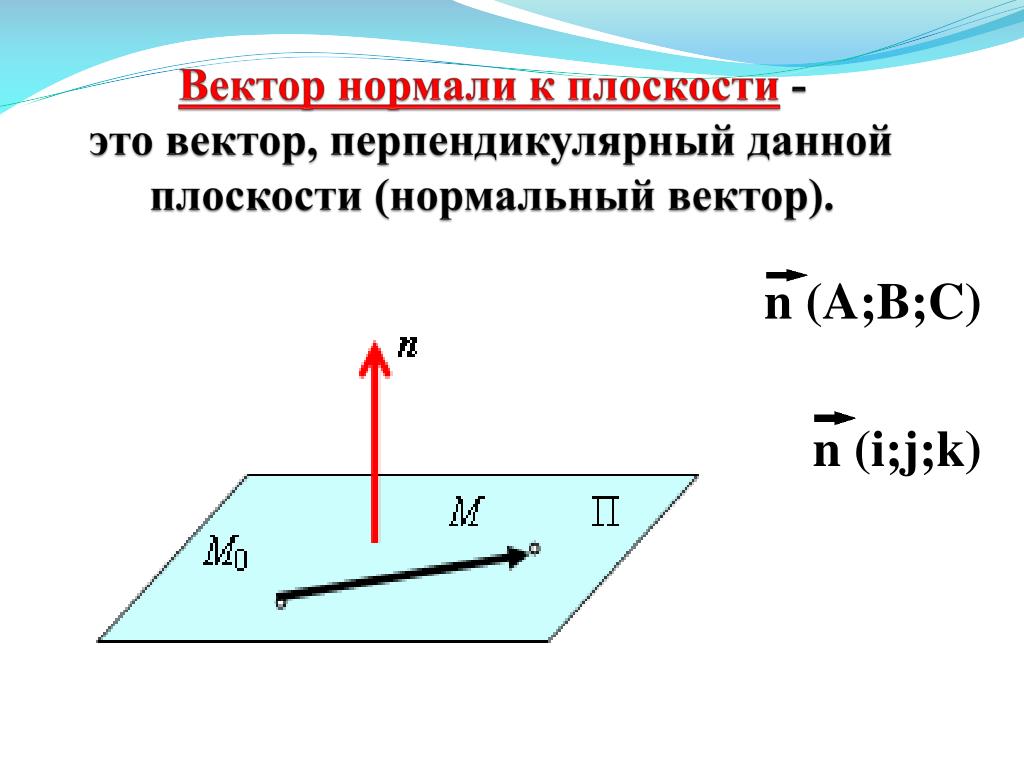 Следовательно, нам нужно определить вектор, перпендикулярный как ⃑𝑣, так и ⃑𝑣, чтобы определить нормаль. Пока так как ⃑𝑣 и ⃑𝑣 не параллельны, мы можем получить нормальный вектор на плоскость, взяв векторное произведение двух векторов: ⃑𝑛=⃑𝑣×⃑𝑣.

Собрав их вместе, уравнение плоскости можно записать в виде ⃑𝑣×⃑𝑣⋅⃑𝑟=⃑𝑣×⃑𝑣⋅⃑𝑎.

В нашем последнем примере мы определим уравнение плоскости в векторной форме из векторных уравнений двух прямых линии, лежащие на плоскости.

Пример 6. Нахождение векторного уравнения плоскости, содержащей две прямые, по их векторным уравнениям

Найдите векторную форму уравнения плоскости, содержащей две прямые 3⃑𝑗+4⃑𝑘 и ⃑𝑟=−⃑𝑖−2⃑𝑗−3⃑𝑘+𝑡−⃑𝑖−2⃑𝑗−4⃑𝑘.

Ответ

В этом примере мы хотим определить уравнение плоскости, содержащей две прямые линии, уравнения которых задан в векторной форме.

Векторная форма уравнения плоскости может быть записана как ⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝑟, где ⃑𝑛 — вектор нормали к плоскости, а ⃑𝑟 — положение вектор точки, лежащей на плоскости.

Для простоты начнем с записи векторных уравнений прямых в виде ⃑𝑟=(1,−1,−3)+𝑡(3,3,4),⃑𝑟=(−1,−2,−3)+𝑡(−1,−2,−4).

Заметим, что из векторных уравнений прямых вектор (3,3,4) параллелен первой прямой, а (−1,−2,−4) параллелен второй, что означает оба параллельны плоскости. Таким образом, чтобы определить вектор нормали ⃑𝑛 к плоскости, нам нужно найти вектор, который перпендикулярен как (−1,−2,−4), так и (3,3,4). Мы можем сделать это, взяв векторное произведение: ⃑𝑛=(−1,−2,−4)×(3,3,4)=||||⃑𝑖⃑𝑗⃑𝑘−1−2−4334||||=||−2−434||⃑𝑖−||− 1−434||⃑𝑗+||−1−233||⃑𝑘=(−2×4+4×3)⃑𝑖−(−1×4+4×3)⃑𝑗+(−1×3+2×3 )⃑𝑘=4⃑𝑖−8⃑𝑗+3⃑𝑘=(4,−8,3).

Мы можем определить вектор положения ⃑𝑟 для точки на плоскости из любого уравнения линии, так как обе линии содержатся на плоскости. Для простоты мы можем заменить 𝑡=0 в первое уравнение для определения вектора положения точки как ⃑𝑟=(1,−1,−3).

Подставляя вектор нормали (4,−8,3) и вектор положения точки на плоскости (1,−1,−3), имеем (4,−8,3)⋅⃑𝑟=(4,−8,3)⋅(1,−1,−3)=4×1+(−8)×(−1)+3×(−3) =3.

Таким образом, уравнение плоскости, содержащей две прямые ⃑𝑟 и ⃑𝑟 в векторной форме (4,−8,3)⋅⃑𝑟=3.

Ключевые моменты

• Общая форма уравнения плоскости в ℝ: 𝑎𝑥+𝑏𝑦+𝑐𝑧+𝑑=0.
• Если (𝑥,𝑦,𝑧) — точка, лежащая на плоскости, то 𝑑=−(𝑎𝑥+𝑏𝑦+𝑐𝑧), и мы можем записать точечно-нормальную или скалярную форму уравнение плоскости как 𝑎(𝑥−𝑥)+𝑏(𝑦−𝑦)+𝑐(𝑧−𝑧)=0, где 𝑎, 𝑏 и 𝑐 — компоненты вектора нормали ⃑𝑛=(𝑎,𝑏,𝑐), который перпендикулярен плоскости или любому вектору параллельно плоскости.
• Если даны точка на плоскости (𝑥,𝑦,𝑧) и два ненулевых и непараллельных вектора ⃑𝑣 и ⃑𝑣, которые параллельны плоскости, мы можем определить вектор нормали из векторного произведения: ⃑𝑛=⃑𝑣×⃑𝑣.
• Уравнение плоскости в векторной форме можно записать как ⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝑟, с ⃑𝑟=(𝑥,𝑦,𝑧) и ⃑𝑟 как вектор положения точки, лежащей на плоскости.

Формирование плоскостей — Math Insight 93$), плоскость определяется однозначно, если мы также указываем вектор нормали $\vc{n}$ (т.е. вектор, перпендикулярный самолет).

Следующий апплет иллюстрирует этот факт. Вы можете экспериментировать с заменой точки $P$ и вектора нормали $\vc{n}$ и посмотрим, как самолет меняется.

Загрузка апплета

Плоскость из точки и вектора нормали. Вы можете изменить точку $\color{red}{P}$ (красного цвета) и вектор нормали $\color{green}{\vc{n}}$ (зеленого цвета), перетаскивая цветные шарики. Перетаскивание мыши в другое место вращает всю фигуру.

Дополнительная информация об апплете.

Обратите внимание, что плоскости не важна длина $\vc{n}$, только его направление. На самом деле, если вы замените $\vc{n}$ на точку в в противоположном направлении, вы все равно получите тот же самолет обратно. Конечно, изменение $P$ на любую другую точку на плоскости не изменит самолет же.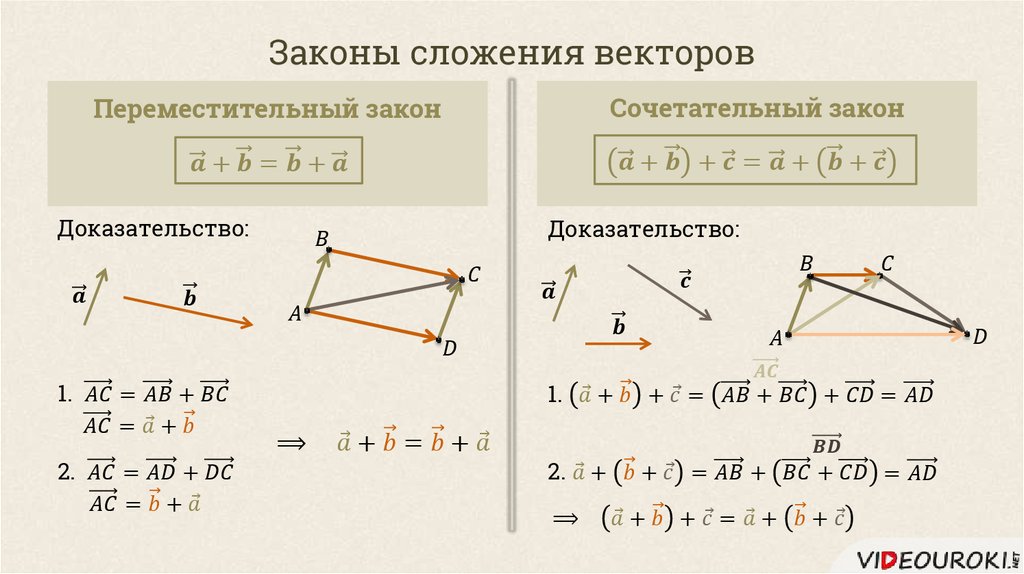 (На самом деле плоскость должна простираться до бесконечности во всех направлениях, поэтому смещение ее из стороны в сторону фактически не изменит плоскость.)

Из этих свойств мы можем вывести уравнение плоскости. Позволять $\vc{a}$ — вектор, представляющий точку $P$ (т. е. вектор от начала до $P$). Пусть $\vc{x}=(x,y,z)$ — вектор, представляющий другую точку $Q$ на плоскости. Поскольку мы знаем, что $Q$ находится в плоскости, можете ли вы придумать какое-либо условие для вектора из $P$ в $Q$, т. е. вектора $\vc{x} — \vc{a}$? В приведенном ниже апплете посмотрите, можете ли вы вывести связь между вектором $\vc{x} — \vc{a}$ и вектором $\vc{n}$.

Загрузка апплета

Плоскость из точки и вектора нормали с дополнительной точкой на плоскости. В дополнение к точке $\color{red}{P}$ (выделено красным) и вектору нормали $\color{green}{\vc{n}}$ (выделено зеленым), определяющим плоскость, есть еще один точка $Q$ (желтая), которая должна лежать на плоскости. Вектор от $P$ до $Q$ показан голубым цветом.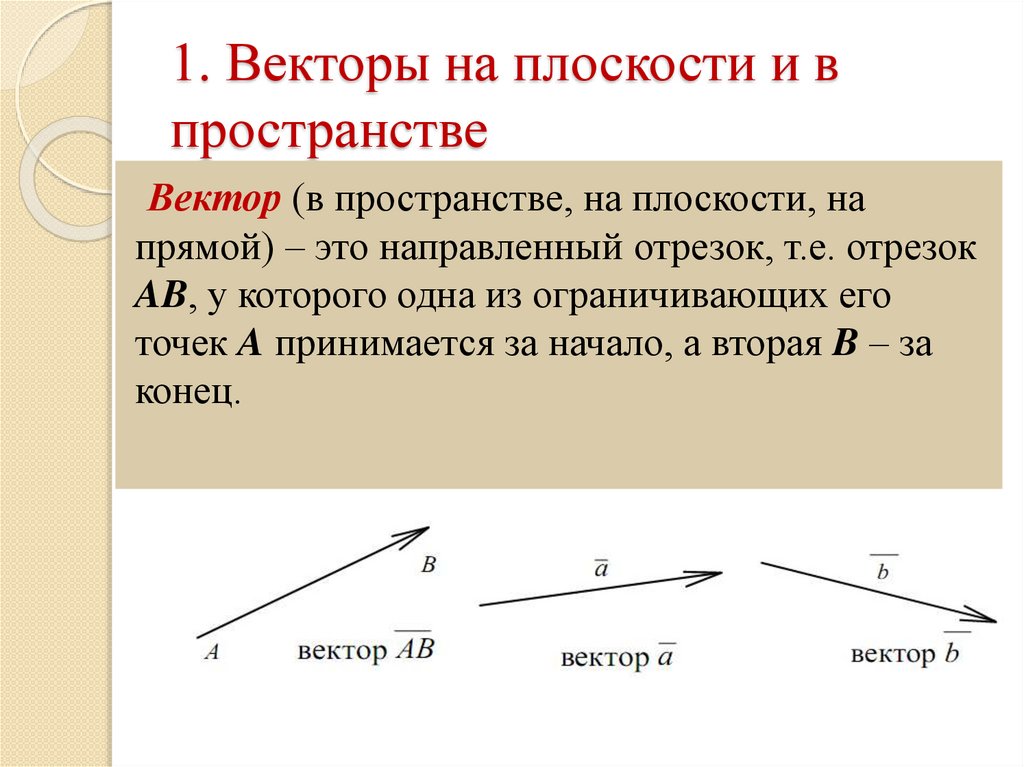 Вы можете перемещать точки $P$ и $Q$ и вектор $\vc{n}$, перетаскивая их мышью. Перетаскивание мыши в другое место вращает всю фигуру.

Дополнительная информация об апплете.

Если точка, представленная $\vc{x}$, находится в плоскости, вектор $\vc{x}-\vc{a}$ должен быть параллелен плоскости, следовательно, перпендикулярно вектору нормали $\vc{n}$. Два вектора перпендикулярны, если их скалярное произведение равно нулю. Делаем вывод, что для любого точка, представленная $\vc{x}$, которая находится на плоскости, следующие должно выполняться уравнение: \начать{выравнивать*} \vc{n} \cdot (\vc{x}-\vc{a})=0. \конец{выравнивание*} Это уравнение для плоскости, перпендикулярной $\vc{n}$, которая идет через точку, представленную $\vc{a}$.

Плоскость определяется тремя точками

Мы только что определили, что для записи уравнения плоскости нам нужно точка $P$ на плоскости и вектор нормали $\vc{n}$. Но большинство из нас знает, что три точки определяют плоскость (при условии, что они не коллинеарны, т.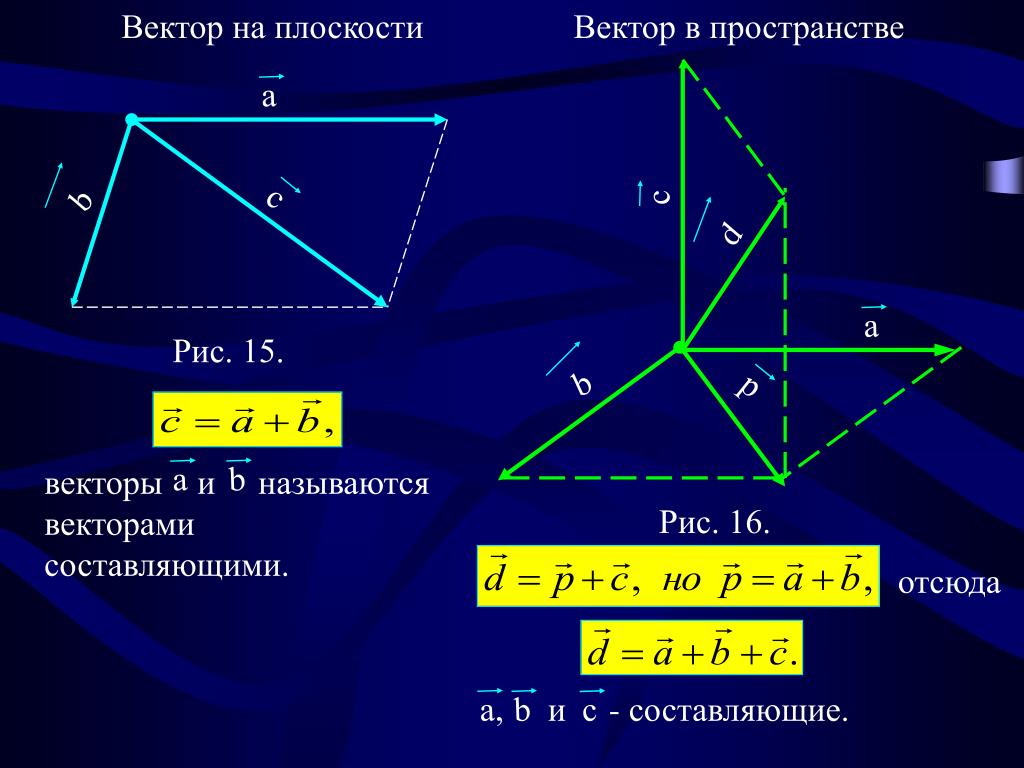 е. лежат на одной прямой). Вот самолет определяется тремя такими точками.

Загрузка апплета

Плоскость определяется по трем точкам. Плоскость определяется точками $\color{red}{P}$ (выделено красным), $\color{green}{Q}$ (выделено зеленым) и $\color{blue}{R}$ ( синего цвета), который можно перемещать, перетаскивая мышью. Векторы от $\color{red}{P}$ до $\color{green}{Q}$ и $\color{blue}{R}$ рисуются соответствующими цветами. Вектор нормали (голубой) представляет собой перекрестное произведение зеленого и синего векторов.

Дополнительная информация об апплете.

Поскольку плоскость задается точкой (скажем, $\color{red}{P}$) и нормальной вектор, каким-то образом добавление двух точек (скажем, $\color{green}{Q}$ и $\color{blue}{R}$ должен определять вектор нормали. Следуя приведенной выше логике, вектор нормали должен быть перпендикулярен вектору из $\color{red}{P}$ в $\color{green}{Q}$ и вектору из $\color{red}{P}$ в $\color{синий}{R}$. Один из способов получить вектор, перпендикулярный двум векторам, равен их векторному произведению.