Проверьте векторы AB BD и CE компланарные. Бесплатный доступ к решению задач
Проверьте векторы AB BD и CE компланарные.docЗарегистрируйся в два клика и получи неограниченный доступ к материалам, а также промокод на новый заказ в Автор24. Это бесплатно.
Условие
Проверьте, векторы AB, BD и CE компланарные?
Ответ
вектора не компланарны так, как их смешанное произведение не равно нулю.
Решение
AB1;1;2 BD0;-3;0 CE-3;-1;0 Найдем смешанное произведение векторов AB∙BD×CE=1120-30-3-10=0+0+0-18+0+0=-18 Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Зарегистрируйся, чтобы продолжить изучение работы
и получи доступ ко всей экосистеме Автор24
Больше решений задач по высшей математике:
Все Решенные задачи по высшей математике
Закажи решение задач
Наш проект является банком работ по всем школьным и студенческим предметам. Если вы не хотите
тратить
время на написание работ по ненужным предметам или ищете шаблон для своей работы —
он есть у нас.
Если вы не хотите
тратить
время на написание работ по ненужным предметам или ищете шаблон для своей работы —
он есть у нас.
Не нашел ответ на свой вопрос?
Опиши, с чем тебе нужна помощь. Эксперты Автор24 бесплатно ответят тебе в течение часа
Выбери предметАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАгрохимия и агропочвоведениеАктерское мастерствоАнализ хозяйственной деятельностиАнглийский языкАнтикризисное управлениеАрхеологияАрхитектура и строительствоАстрономияБазы данныхБанковское делоБезопасность жизнедеятельностиБиблиотечно-информационная деятельностьБизнес-планированиеБиологияБиотехнологияБухгалтерский учет и аудитВетеринарияВнешнеэкономическая деятельностьВодные биоресурсы и аквакультураВоенное делоВоспроизводство и переработка лесных ресурсовВысшая математикаГеографияГеодезияГеологияГеометрияГидравликаГидрометеорологияГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиДетали машинДизайнДокументоведение и архивоведениеЕстествознаниеЖелезнодорожный транспортЖурналистикаЗемлеустройство и кадастрИздательское делоИнвестицииИнженерные сети и оборудованиеИнновационный менеджментИнформатикаИнформационная безопасностьИнформационные технологииИскусствоИсторияКартография и геоинформатикаКитайский языкКонфликтологияКраеведениеКредитКриминалистикаКулинарияКультурологияЛитератураЛогикаЛогистикаМаркетингМатериаловедениеМашиностроениеМедицинаМеждународные отношенияМеждународные рынкиМенеджментМенеджмент организацииМеталлургияМетрологияМеханикаМикро-, макроэкономикаМикропроцессорная техникаМорская техникаМузыкаНалогиНаноинженерияНачертательная геометрияНемецкий языкНефтегазовое делоОрганизационное развитиеПарикмахерское искусствоПедагогикаПожарная безопасностьПолиграфияПолитологияПочвоведениеПраво и юриспруденцияПриборостроение и оптотехникаПриродообустройство и водопользованиеПрограммированиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментПроцессы и аппаратыПсихологияРабота на компьютереРадиофизикаРежиссураРеклама и PRРелигияРусский языкРынок ценных бумагСадоводствоСварка и сварочное производствоСвязи с общественностьюСельское и рыбное хозяйствоСервисСопротивление материаловСоциальная работаСоциологияСтандартизацияСтатистикаСтрановедениеСтратегический менеджментСтрахованиеТаможенное делоТеатроведениеТекстильная промышленностьТелевидениеТеоретическая механикаТеория вероятностейТеория игрТеория машин и механизмовТеория управленияТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТовароведениеТорговое делоТранспортные средстваТуризмУправление качествомУправление персоналомУправление проектамиФармацияФизикаФизическая культураФилософияФинансовый менеджментФинансыФранцузский языкХимияХирургияХолодильная техникаЦенообразование и оценка бизнесаЧертежиЧерчениеЭкологияЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЭтикаЯдерная энергетика и теплофизикаЯдерные физика и технологииЯзыки (переводы)Языкознание и филологияEVIEWSSPSSSTATAДругоеТвой вопрос отправлен
Скоро мы пришлем ответ экпертов Автор24 тебе на почту
Помощь эксперта
Нужна помощь по теме или написание схожей работы?
Свяжись напрямую с автором и обсуди заказ.
4.7
Shyrochka30
Высшая математика 545 заказов
Отправить письмо схожим авторам, которые сейчас на сайте
Регистрация прошла успешно!
Теперь вам доступен полный фрагмент работы, а также
открыт доступ ко всем сервисам
экосистемы
Введи почту
Зарегистрируйся через почту и получи неограниченный доступ к материалам. Это бесплатно.
Читать тексты на сайте можно без ограничений. Однако для копирования и использования работ нужно зарегистрироваться в экосистеме Автор24. Это бесплатно.Понятие вектора в пространстве — презентация онлайн
1.
 Векторы в пространстве
Векторы в пространстве2. Понятие вектора в пространстве
Вектор(направленный отрезок) –отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0
3. Коллинеарные векторы
Два ненулевых вектора называются коллинеарными,если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы
4. Равные векторы
Равные векторы — сонаправленные векторы,длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.
5. Противоположные векторы
Противоположные векторы – противоположнонаправленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.
6. Признак коллинеарности
Если существует такое число k при которомвыполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.

вектор k a b, если k 0
вектор k a b, если k 0
7. Действия с векторами
• Сложение• Вычитание
• Умножение вектора на число
8. Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
9. Правило треугольника
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C
10. Правило треугольника
Ba
А
a b
b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC
11. Правило параллелограмма
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4.
 диагональ параллелограмма сумма векторов
диагональ параллелограмма сумма векторовB
a
a
b
А
с
b
с a b
C
12. Правило многоугольника
Сумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE
13. Пример
B1A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0
14. Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d
15. Свойства
B1A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелеп ипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда
16. Вычитание
Разностью векторов a и b называется такойвектор, сумма которого с вектором
равна
b
вектору .
a
17. Вычитание
Для вычитания одного вектора из другого необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C
18. Умножение вектора на число
Произведением ненулевог о вектора a на число kназывается такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3
19. Свойства
Для любыхвект оровa и b и любыхчисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон
20. Определение компланарных векторов
Компланарные векторы – векторы, приоткладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.

Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)
21. О компланарных векторах
Любые два вектора всегда компланарны.α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb
22. Признак компланарности
Если вектор c можно разложить по векторама и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.
23. Задачи на компланарность
1)Компланарны ли векторы:
а) a, b, 2a, 3b;
б) a, b, a b, a b ?
2.) Известно, что векторы , и компланарны.
Компланарны ли векторы:
a b c
а)
б) a, 2b, 3c;
a b, a 2c, 2b 3c ?
24. Решение
а )векторы a и 2a коллинеарн ы,векторы b и 3b коллинеарн ы,
значит векторы a, b, 2a и 3b компланарн ы
б )векторы a, b и a b компланарн ы,
векторы a, b и a b компланарн ы,
значит векторы a, b, a b и a b компланарн ы
25.
 Решениеa) если векторы a , 2b , 3c компланарн ы,
Решениеa) если векторы a , 2b , 3c компланарн ы,то существуют такие х и у,что
a xb y c
проверяем существуют ли такие т и п,что
a m 2b n 3c
имеем :
x
2m x m
2
y
3n y n
3
m и п определяют ся единственным образом,
значит векторы компланарн ы
26. Решение
б)если векторы a b , a 2c , 2b 3cкомпланарн ы, то существуют такие х и у,что
a b x( a 2c ) y(2b 3c )
a b x a 2xc 2yb 3y c
a(1 x) b(1 2y) c( 2x 3y) 0
1 x 0 x 1
1
1 2y 0
y
3y 2x 0
2
1
a b a 2c (2b 3c )
2
искомые х и у существуют,
значит векторы компланарн ы
27. Разложение вектора
• По двум неколлинеарным векторам• По трем некомпланарным векторам
28. Разложение вектора по двум неколлинеарным векторам
Теорема.Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
29. Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в видеp xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .

Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
30. Доказательство теоремы
Сс
P
pB
b P2
O
P1
aA
Доказательство :
О произвольн ая точка
Дано :
abc
некомпланр ные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.
31. Базисные задачи
32. Вектор, проведенный в середину отрезка,
равен полусумме векторов, проведенных из той жеточки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство
33. Доказательство
СA
B
O
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.
 т.д.
т.д.2
34. Вектор, соединяющий середины двух отрезков,
равен полусумме векторов, соединяющих их концы.С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство
35. Доказательство
СN
D
B
M
A
Доказатель ство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2
36. Вектор, проведенный в точку пересечения диагоналей параллелограмма,
равен одной четверти суммы векторов, проведенныхиз этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство
37. Доказательство
OB
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.
 ò.ä.
ò.ä.4
38. Задача 1. Разложение векторов
Разложите вектор по a, b и c :D
N точка пересечения
медиан ABC
a
A
а)
б) DB
в) CB
г) DC
DN
Решение
b
B
N
c
C
39. Решение
а) DB b aб) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2
40. Задача 2. Сложение и вычитание
Упростите выражения:а)
б)
в)
г)
д)
е)
CM MK
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD
Решение
41. Решение
а) CM MK CKб) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK
Глава 30. Линейные операции над векторами
Суммой
двух векторов
и
называется вектор, который идет из начала
вектора
в конец вектора
при условии, что
вектор
приложен к концу вектора
(правильно треугольника). Построение суммы
изображено на рис. 1.
Построение суммы
изображено на рис. 1.
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы и приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала и (рис. 2). Отсюда сразу следует, что .
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов , , , ).
Разность
двух векторов
и
называется вектор, который в сумме с вектором
составляет вектор
. Если два вектора
и
приведены к общему началу, то разность их
есть вектор, идущий из конца
(«вычитаемого») к
концу
(«уменьшаемого»). Два вектора равной
длины, лежащие на одной прямой и направленные в
противоположные стороны, называются взаимно
обратными: если один из них обозначен символом
,
то другой обозначается символом
. Легко видеть,
что
. Таким образом, построение разности
равносильно прибавлению к «уменьшаемому»
вектора, обратного «вычитаемого».
Легко видеть,
что
. Таким образом, построение разности
равносильно прибавлению к «уменьшаемому»
вектора, обратного «вычитаемого».
Произведение (или также ) вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа ; он параллелен вектору или лежит с ним на одной прямой и направлен так же, как вектор , если — число положительное, и противоположно вектору , если — число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:
2). При умножении вектора на число его проекция умножается на то же число:
.
, ,
то
,
и
.
Если , то для любого числа
.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
, ,
является пропорциональность их координат:
.
Тройка векторов , , называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
1). Вектор лежит на оси Ох, вектор — на оси Оу, вектор — на оси Oz;
2). Каждый из векторов , , направлен по своей оси в положительную сторону;
3). Векторы , , единичные, то есть , , .
Каким бы ни был вектор , он всегда может быть разложен по базису , , , то есть может быть представлен в виде
;
коэффициенты этого разложения
являются координатами вектора
(то есть X, Y, Z суть проекции вектора
на координатные оси).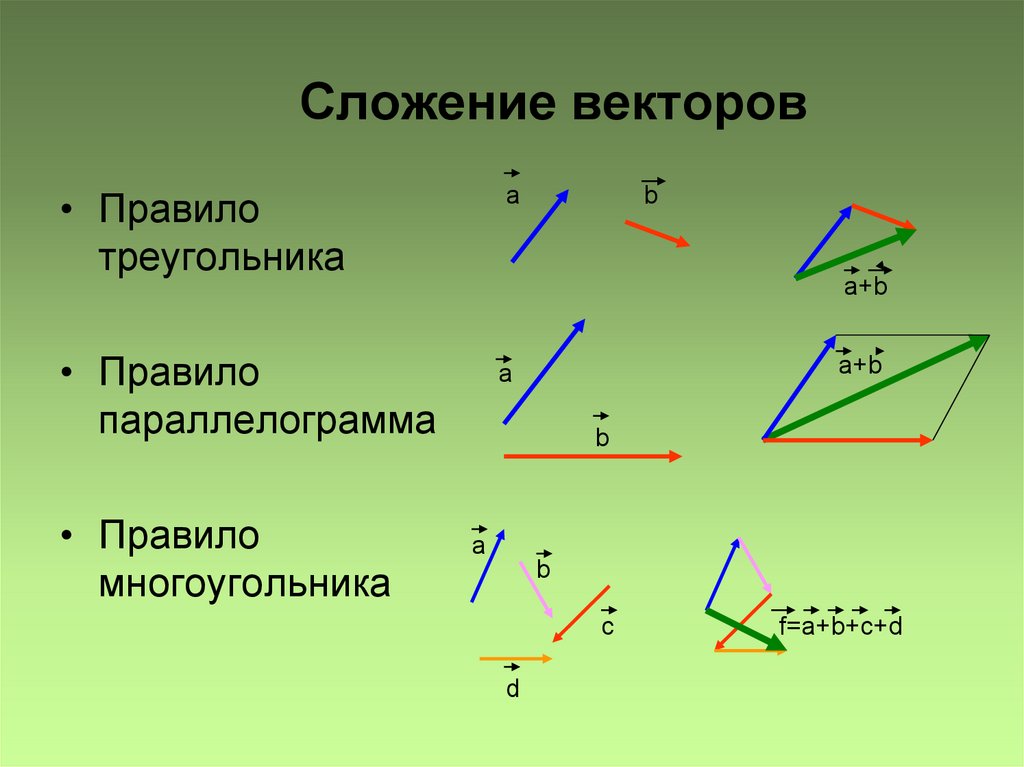
| 761 | По данным векторам и построить каждый из следующих векторов: 1). , 2). , 3). , 4). . | |
| 762 | Даны =13, =19 и =24. Вычислить . | |
| 763 | Даны =11, =23 и =30. Определить . | |
| 764 | Векторы и взаимно перпендикулярны, причем =5, =12. Определить и . | |
| 765 | Векторы и образуют
угол =600, причем=5 и =8. Определить и . Определить и . | |
| 766 | Векторы и образуют угол =1200, причем =3 и =5. Определить и . | |
| 767 | Какому условию должны удовлетворять векторы и , чтобы имели место следующие соотношения: | |
| 767.1 | ; | |
| 767.2 | ; | |
| 767.3 | . | |
| 768 | Какому условию
должны удовлетворять векторы и , чтобы
вектор делил пополам угол между векторами и . | |
| 769 | По данным векторам и построить каждый из следующих векторов: | |
| 769.1 | ; | |
| 769.2 | ; | |
| 769.3 | ; | |
| 769.4 | . | |
| 770 | В треугольнике АВС вектор и вектор . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы , построить также векторы: | |
770. 1 1 | ; | |
| 770.2 | ; | |
| 770.3 | ; | |
| 770.4 | ; | |
| 770.5 | ; | |
| 770.6 | . | |
| 771 | Точка О является центром масс треугольника АВС. Доказать, что . | |
| 772 | В правильном
пятиугольнике ABCDE заданы векторы, совпадающие с
его ребрами: , , , , . Построить векторы: Построить векторы: | |
| 772.1 | ; | |
| 772.2 | ; | |
| 772.3 | . | |
| 773 | В параллелепипеде ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с его ребрами: , , . Построить каждый из следующих векторов: | |
| 773.1 | ; | |
| 773.2 | ; | |
773. 3 3 | ; | |
| 773.4 | ; | |
| 773.5 | . | |
| 774 | Три силы , , , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей , если известно, что =2Н, =10Н, =11Н. | |
| 775 | Даны два вектора ={3; -2; 6}, ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов: | |
| 775.1 | ; | |
775. 2 2 | ; | |
| 775.3 | ; | |
| 775.4 | ; | |
| 775.5 | ; | |
| 775.6 | . | |
| 776 | Проверить коллинеарность векторов ={2; -1; 3} и ={-6; 3; -9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 777 | Определить, при
каких значениях , векторы и коллинеарны. | |
| 778 | Проверить, что четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат вершинами трапеции. | |
| 779 | Даны точки A(-1; 5; -10}, B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы и коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 780 | Найти орт вектора ={6; -2; -3}. | |
| 781 | Найти орт вектора ={3; 4; -12}. | |
| 782 | Определить модули
суммы и разности векторов ={3; -5; 8} и ={-1;
1; -4}.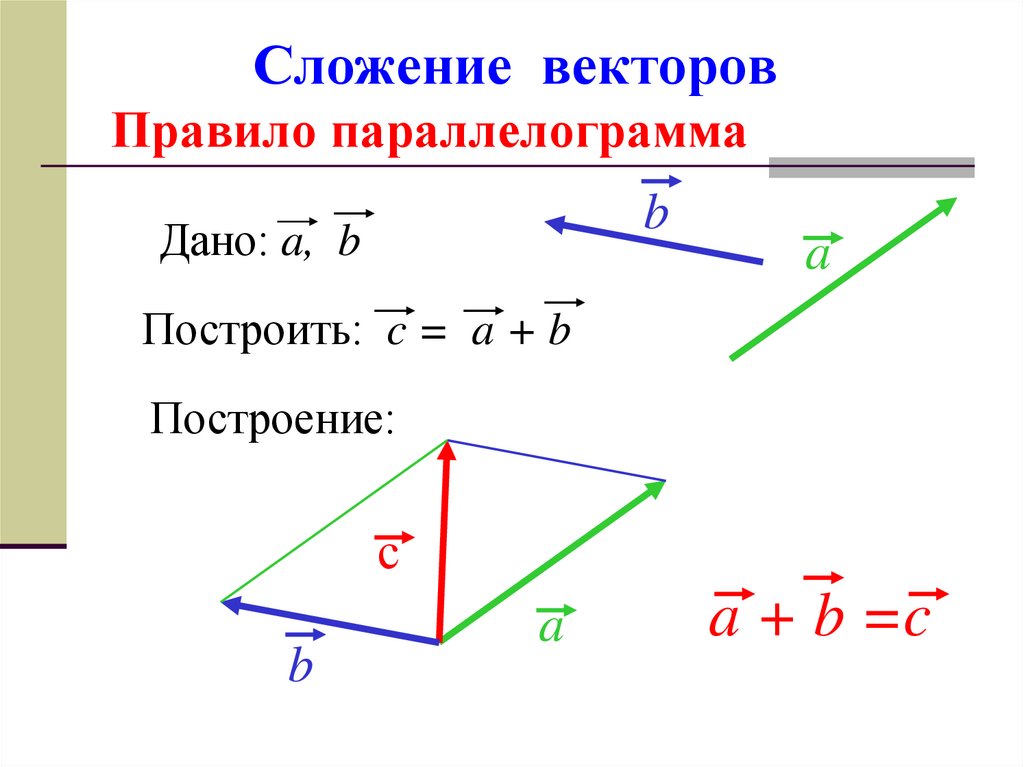 | |
| 783 | Дано разложение вектора по базису , , : . Определить разложение по этому же базису вектора , параллельного вектору и противоположного с ним направления, при условии, что =75. | |
| 784 | Два вектора ={2; -3; 6} и ={-1; 2; -2} приложены к одной точке. Определить координаты вектора направленного по биссектрисе угла между векторами и , при условии, что . | |
| 785 | Векторы ={2; 6; -4} и ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. | |
| 786 | Доказать, что если и
— какие угодно неколлинеарные
векторы, то всякий вектор, лежащих в их плоскости,
может быть представлен в виде . Доказать,
что числа и однозначно определяются векторами , и . Доказать,
что числа и однозначно определяются векторами , и . | |
| 787 | На плоскостиданы два вектора ={2; -3}, ={1; 2}. Найи разложение вектора ={9; 4} по базису , . | |
| 788 | На плоскости даны три вектора ={3; -2}, ={-2; 1}, ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других. | |
| 789 | Даны три вектора ={3; -1}, ={1; -2}, ={-1; 7}. Определить разложение вектора по базису , . | |
| 790 | Принимая в качестве
базиса векторы и , совпадающие
со сторонами треугольника АВС, опреедлить
разложение векторов, приложенных в вершинах
треугольника и совпадающие с его медианами. | |
| 791 | На плоскости даны етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить разложение векторов , , и , принимая в качестве базиса векторы и . | |
| 792 | Доказать, что если , , — какие угодно некомпланарные векторы, то всякий вектор пространства может быть представлен в виде . Доказать, что числа , , однознчно определяются векторами , , , . (Представление вектора в виде называется разложением его по базису , , . Числа , , называются коэффициентами этого разложения. | |
| 793 | Даны три вектора ={3; -2; 1}, ={-1; 1; -2}, ={2; 1; -3}. Найти разложение вектора ={11; -6; 5} по базису , , . | |
| 794 | Даны четыре вектора ={2; 1; 0}, ={1; -2; 2}, ={2; 2; -1}, ={3; 7; -7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных. |
векторов, графическое представление векторов, величина вектора, направление вектора
Векторы могут быть графически представлены направленными отрезками. Длина выбирается в соответствии с некоторым масштабом, чтобы представлять величину вектора , а направление направленного отрезка представляет направление вектора . Например, если мы допустим, что 1 см соответствует 5 км/ч, то северо-западный ветер со скоростью 15 км/ч будет представлен отрезком направленной линии длиной 3 см, как показано на рисунке слева.
Вектор на плоскости является направленным отрезком прямой. Два вектора эквивалентны , если они имеют одинаковую величину и направление .
Рассмотрим вектор, проведенный из точки A в точку B. Точка A называется начальной точкой вектора, а точка B называется конечной точкой . Символическое обозначение этого вектора (читай «вектор AB»). Векторы также обозначаются полужирными буквами, такими как u, v и w. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Таким образом, они представляют эквивалентно векторам; то есть
В контексте векторов мы используем = для обозначения эквивалентности.
Длина или величина выражается как ||. Чтобы определить, эквивалентны ли векторы, мы находим их величины и направления.
Пример 1 Векторы u, и w показаны на рисунке ниже. Покажите, что u = = w.
Решение Сначала найдем длину каждого вектора, используя формулу расстояния:
|у| = √[2 — (-1)] 2 + (4 — 3) 2 = √9 + 1 = √10,
|| = √[0 — (-3)] 2 + [0 — (-1)] 2 = √9 + 1 = √10,
|w| = √(4 — 1) 2 + [-1 — (-2)] 2 = √9 + 1 = √10.
Таким образом,
|u| = | = |ш|.
Векторы u, , и w идут в одном направлении, поэтому мы проверяем их наклоны. Если линии, на которых они находятся, имеют одинаковый наклон, векторы имеют одинаковое направление. Мы вычисляем наклоны:
. Так как u, и w имеют одинаковую величину и одно и то же направление,
ты = = ш.
Имейте в виду, что для эквивалентности векторов требуется только одна и та же величина и одно и то же направление, а не одно и то же местоположение. На рисунках слева каждая из первых трех пар векторов не эквивалентна. Четвертый набор векторов является примером эквивалентности.
Предположим, человек делает 4 шага на восток, а затем 3 шага на север. Затем он или она будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор длиной 4 единицы и направленный вправо представляет 4 шага на восток, а вектор длиной 3 единицы и направленный вверх представляет 3 шага на север. Сумма двух векторов представляет собой вектор с 5 шагами по величине и в указанном направлении.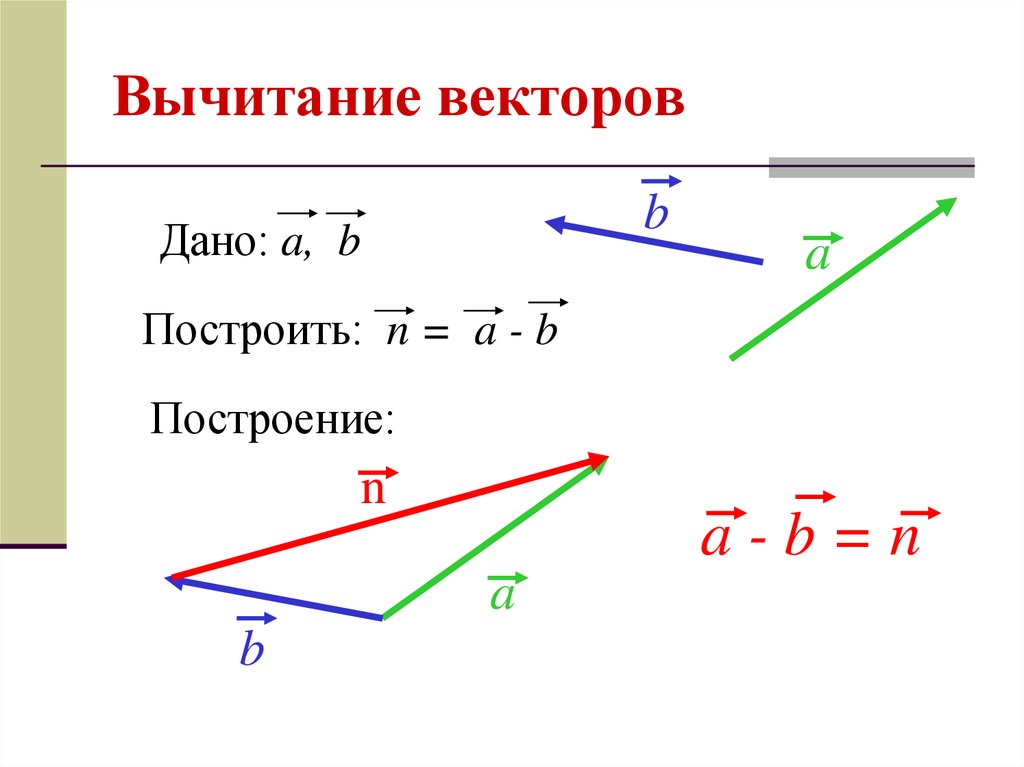 Сумма также называется равнодействующей двух векторов.
Сумма также называется равнодействующей двух векторов.
В общем, два ненулевых вектора u и v можно сложить геометрически, поместив начальную точку v в конечную точку u, а затем найдя вектор, который имеет ту же начальную точку, что и u, и ту же конечную точку, что и v, как показано на следующем рисунке.
Сумма представляет собой вектор, представленный направленным отрезком прямой от начальной точки A элемента u до конечной точки C элемента v. То есть, если u = и v = , то
и + v = + =
Мы также можем описать сложение векторов, сложив начальные точки векторов вместе, завершив параллелограмм и найдя диагональ параллелограмма. (См. рисунок слева внизу.) Это описание сложения иногда называют законом параллелограмма векторного сложения. Сложение векторов коммутативно. Как показано на рисунке справа ниже, u + v и v + u представлены одним и тем же направленным отрезком линии.
Если две силы F 1 и F 2 действуют на объект, то комбинированный эффект является суммой или равнодействующей F 1 + F 2 отдельных сил.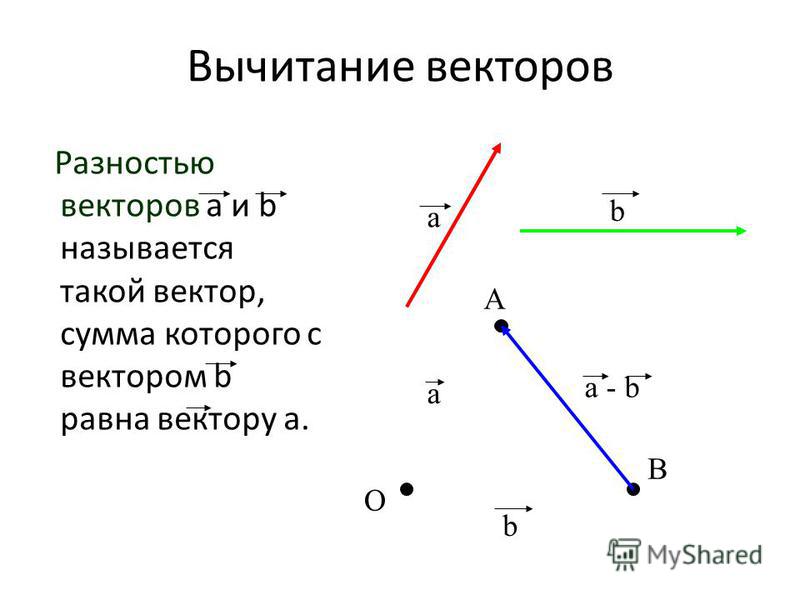
Пример 2 Силы в 15 ньютонов и 25 ньютонов действуют на объект под прямым углом друг к другу. Найдите их сумму или равнодействующую, определяя величину равнодействующей и угол, который она образует с большей силой.
Решение Мы делаем рисунок — на этот раз прямоугольник — используя v или для представления результата. Чтобы найти величину, воспользуемся теоремой Пифагора:
|в| 2 = 15 2 + 25 2 Здесь |v| обозначает длину или величину v.
|v| = √15 2 + 25 2
|v| ≈ 29,2.
Чтобы найти направление, заметим, что, поскольку треугольник OAB прямоугольный,
tanθ = 15/25 = 0,6.
С помощью калькулятора находим θ, угол, который образует равнодействующая с большей силой:
θ = tan — 1 (0,6) ≈ 31°
равнодействующая имеет величину 29,2 и составляет угол 31° с большей силой.
Пилоты должны корректировать направление своего полета при боковом ветре. И ветер, и скорость самолета можно описать векторами.
И ветер, и скорость самолета можно описать векторами.
Пример 3 Скорость и направление полета самолета. Самолет движется по азимуту 100° со скоростью 190 км/ч при скорости ветра 48 км/ч с направления 220°. Найдите путевую скорость самолета и направление его следа или курса относительно земли.
Решение Сначала делаем чертеж. Ветер представлен, а вектор скорости самолета — . Результирующий вектор скорости равен v, сумме двух векторов. Угол θ между v и называется угол сноса .
Обратите внимание, что мера COA = 100° — 40° = 60°. Таким образом, мера CBA также равна 60° (противоположные углы параллелограмма равны). Поскольку сумма всех углов параллелограмма равна 360°, а COB и OAB имеют одинаковую меру, каждый из них должен быть равен 120°. По закону косинусов в OAB имеем
|v| 2 = 48 2 + 190 2 — 2.48.190.cos120°
|v| 2 = 47 524
|v| = 218
Таким образом, |v| составляет 218 км/ч.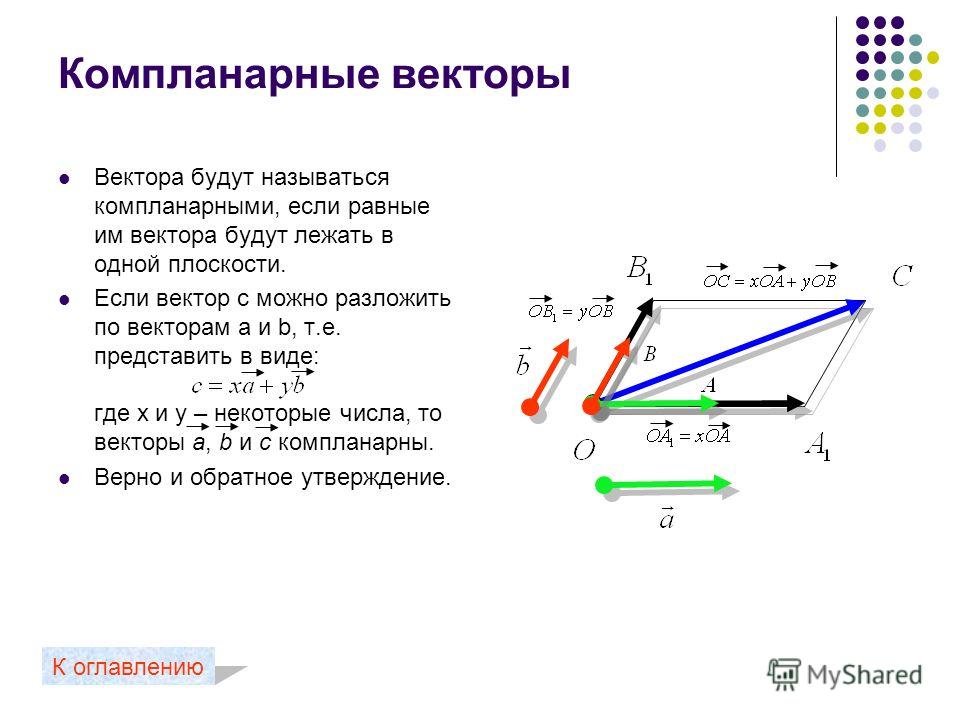 Закон синусов в том же треугольнике,
Закон синусов в том же треугольнике,
48 /sinθ = 218 /sin 120 ° ,
или
sinθ = 48.sin120 ° /218 ≈ 0,1907
θ ≈ 1120 ≈ 1120 лове120 ° /218 ≈ 0,1907
≈ ≈ 118. °
Таким образом, θ = 11° с точностью до градуса. Путевая скорость самолета составляет 218 км/ч, а его траектория — в направлении 100° — 11°, или 89°.
Имея вектор w, мы можем захотеть найти два других вектора u и v, сумма которых равна w. Векторы u и v называются компоненты w и процесс их нахождения называется разложением или представлением вектора в его компоненты вектора.
Когда мы разрешаем вектор, мы обычно ищем перпендикулярные компоненты. Чаще всего один компонент будет параллелен оси x, а другой — оси y. По этой причине их часто называют горизонтальными и вертикальными компонентами вектора. На рисунке ниже вектор w = представлен как сумма u = и v = .
Горизонтальная составляющая w равна u, а вертикальная составляющая равна v.
Пример 4 Вектор w имеет величину 130 и наклонен к горизонту под углом 40°. Разложите вектор на горизонтальную и вертикальную составляющие.
Решение Сначала мы нарисуем горизонтальные и вертикальные векторы u и v, сумма которых равна w.
Из ABC находим |u| и |v| используя определения функций косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84,
Таким образом, горизонтальный компонент w равен 100 вправо, а вертикальный компонент w равен 84 вверх.
Сложение компонентов (т. е. аналитический метод сложения векторов)
Ранее в этом уроке мы узнали, что векторы, ориентированные под прямым углом друг к другу, можно сложить, используя теорему Пифагора. Например, два вектора смещения с величиной и направлением 11 км, север и 11 км, восток можно сложить вместе, чтобы получить результирующий вектор, направленный как на север, так и на восток. Когда два вектора складываются «голова к хвосту», как показано ниже, в результате получается гипотенуза прямоугольного треугольника. Стороны прямоугольного треугольника имеют длины 11 км и 11 км. Результант можно определить с помощью теоремы Пифагора; его величина составляет 15,6 км. Решение показано под диаграммой.
Когда два вектора складываются «голова к хвосту», как показано ниже, в результате получается гипотенуза прямоугольного треугольника. Стороны прямоугольного треугольника имеют длины 11 км и 11 км. Результант можно определить с помощью теоремы Пифагора; его величина составляет 15,6 км. Решение показано под диаграммой.
Этот пифагорейский подход полезен для сложения любых двух векторов, направленных под прямым углом друг к другу. У прямоугольного треугольника две стороны плюс гипотенуза; поэтому теорема Пифагора идеально подходит для сложения двух прямоугольных векторов. Но есть пределы полезности теоремы Пифагора при решении задач сложения векторов. Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой. Так что на первый взгляд может показаться, что нельзя использовать теорему Пифагора для определения равнодействующей при сложении трех или четырех векторов.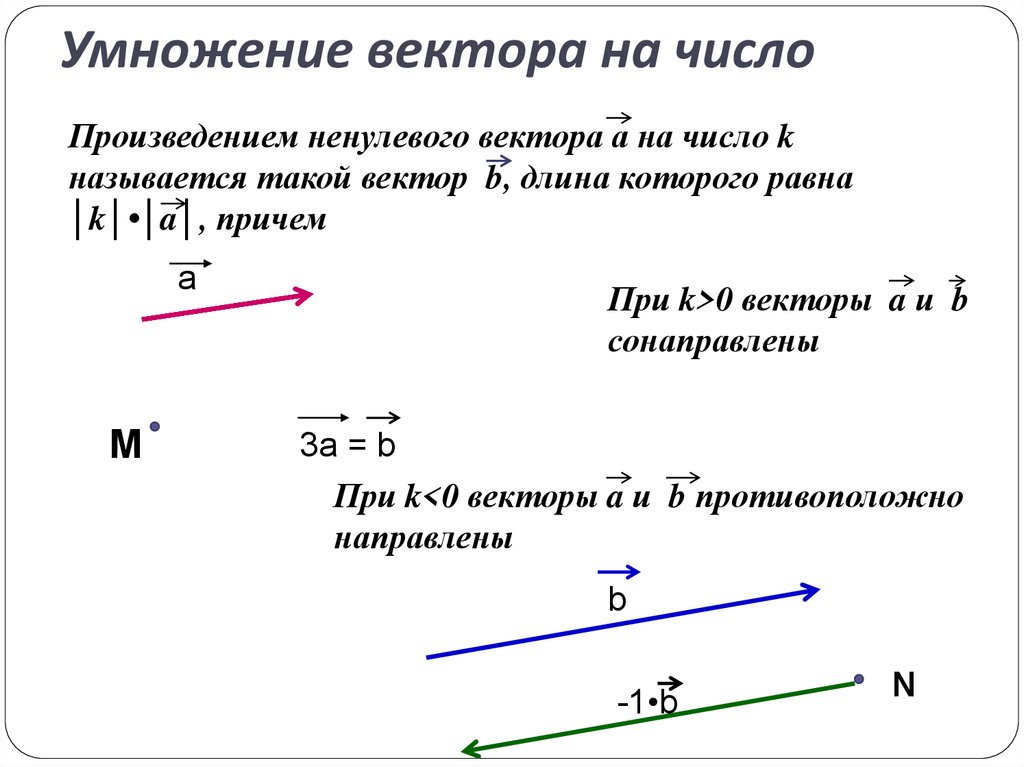 Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу, например, при добавлении вектора севера и вектора востока. Но что делать, если два складываемых вектора не находятся под прямым углом друг к другу? Есть ли способ использовать математику для надежного определения результата для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию компонентов вектора (обсуждавшуюся ранее) и принципы разрешения векторов (обсуждавшиеся ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу, например, при добавлении вектора севера и вектора востока. Но что делать, если два складываемых вектора не находятся под прямым углом друг к другу? Есть ли способ использовать математику для надежного определения результата для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию компонентов вектора (обсуждавшуюся ранее) и принципы разрешения векторов (обсуждавшиеся ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
Сложение трех или более прямоугольных векторов
В качестве первого примера рассмотрим следующую задачу сложения векторов:
Пример 1:
Студент проезжает на своей машине 6,0 км на север, затем поворачивает направо и 6,0 км на восток.Наконец, студент поворачивает налево и проезжает еще 2,0 км на север. Какова величина общего перемещения студента?
Как и любая задача в физике, успешное решение начинается с выработки мысленной картины ситуации. Построение диаграммы, подобной приведенной ниже, часто оказывается полезным в процессе визуализации.
Если эти три вектора сложить вместе по принципу «голова к хвосту», в результате получится вектор, который простирается от конца первого вектора (6,0 км, север, показано красным) до стрелки третьего вектора. (2,0 км, север, показано зеленым цветом). Диаграмма сложения векторов головы к хвосту показана ниже.
Как видно на диаграмме, результирующий вектор (нарисованный черным цветом) не является гипотенузой любого прямоугольного треугольника — по крайней мере, ни одного очевидного прямоугольного треугольника. Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ: Да! Для этого необходимо изменить порядок добавления трех векторов.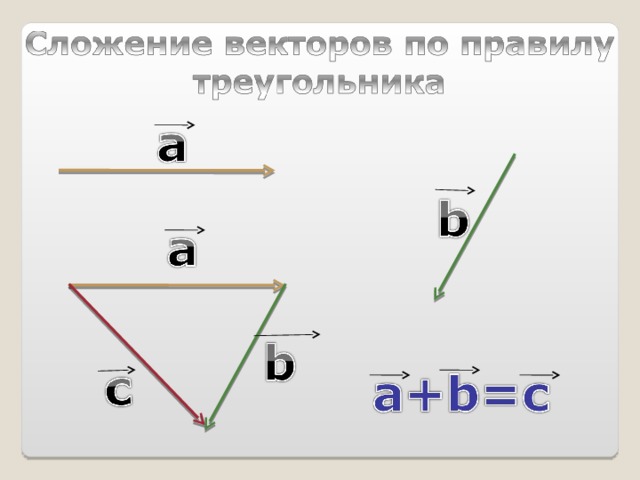 Векторы выше были нарисованы в том порядке, в котором они были заданы. Студент поехал на север, затем на восток и снова на север. Но если сложить три вектора в порядке 6,0 км, N + 2,0 км, N + 6,0 км, E, то диаграмма будет выглядеть так:
Векторы выше были нарисованы в том порядке, в котором они были заданы. Студент поехал на север, затем на восток и снова на север. Но если сложить три вектора в порядке 6,0 км, N + 2,0 км, N + 6,0 км, E, то диаграмма будет выглядеть так:
После изменения порядка сложения трех векторов результирующий вектор теперь является гипотенузой прямоугольного треугольника. Длины перпендикулярных сторон прямоугольного треугольника равны 8,0 м, север (6,0 км + 2,0 км) и 6,0 км, восток. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (8,0 км) 2 + (6,0 км) 2
R 2 = 64,0 км 2 + 36,0 км 2
R 2 = 100,0 км 2
R = SQRT (100,0 км2)
R = 10,0 км
(SQRT указывает квадратный корень)
На приведенной выше первой диаграмме сложения векторов три вектора были добавлены в том порядке, в котором они управляются. На второй диаграмме добавления векторов (сразу выше) порядок добавления векторов был изменен. Изменение порядка не повлияло на размер результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Добавление векторов A + B + C дает тот же результат, что и сложение векторов B + A + C или даже C + B + A . Пока все три вектора включены с их заданной величиной и направлением, результат будет одним и тем же. Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример задачи. Чтобы дополнительно проиллюстрировать стратегию, давайте рассмотрим ситуацию с добавлением векторов, описанную в примере 2 ниже.
На второй диаграмме добавления векторов (сразу выше) порядок добавления векторов был изменен. Изменение порядка не повлияло на размер результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Добавление векторов A + B + C дает тот же результат, что и сложение векторов B + A + C или даже C + B + A . Пока все три вектора включены с их заданной величиной и направлением, результат будет одним и тем же. Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример задачи. Чтобы дополнительно проиллюстрировать стратегию, давайте рассмотрим ситуацию с добавлением векторов, описанную в примере 2 ниже.
Пример 2:
Мак и Тош проводят лабораторную работу Vector Walk Lab . Начав у дверей своего кабинета физики, они проходят 2,0 метра на юг. Они поворачивают направо и проходят 16,0 метров на запад.Они снова поворачивают направо и проходят 24 метра на север. Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения?
Графическое представление заданной проблемы поможет визуализировать происходящее. На приведенной ниже диаграмме показано такое представление.
Когда эти четыре вектора складываются вместе в прямом направлении, в результате получается вектор, который простирается от конца первого вектора (2,0 м, юг, показано красным) до наконечника четвертого вектора (36,0 м, Запад, показан зеленым). Диаграмма сложения векторов головы к хвосту показана ниже.
Результирующий вектор (нарисованный черным и помеченный R ) на приведенной выше диаграмме сложения векторов не является гипотенузой какого-либо сразу очевидного прямоугольного треугольника. Но, изменив порядок сложения этих четырех векторов, можно заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника. Например, сложив векторы в следующем порядке: 2,0 м, S + 24,0 м, N + 16,0 м, W + 36,0 м. W, равнодействующая станет гипотенузой прямоугольного треугольника. Это показано на диаграмме сложения векторов ниже.
Например, сложив векторы в следующем порядке: 2,0 м, S + 24,0 м, N + 16,0 м, W + 36,0 м. W, равнодействующая станет гипотенузой прямоугольного треугольника. Это показано на диаграмме сложения векторов ниже.
После перестановки векторов результирующая теперь является гипотенузой прямоугольного треугольника, имеющего две перпендикулярные стороны с длинами 22,0 м, север и 52,0 м, запад. 22,0 м, северная сторона является результатом сложения 2,0 м, юга и 24,0 м, северной стороны. 52,0 м, западная сторона – результат 16,0 м, западной и 36,0 м, западной стороны, сложенных вместе. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (22,0 м) 2 + (52,0 м) 2
R 2 = 484,0 м 2 + 2704,0 м 2
R 2 = 3188,0 м 2
R = SQRT (3188,0 м2 2 )
R = 56,5 м
(SQRT указывает квадратный корень)
Как видно из этих двух примеров, результат сложения трех или более прямоугольных векторов можно легко определить с помощью теоремы Пифагора.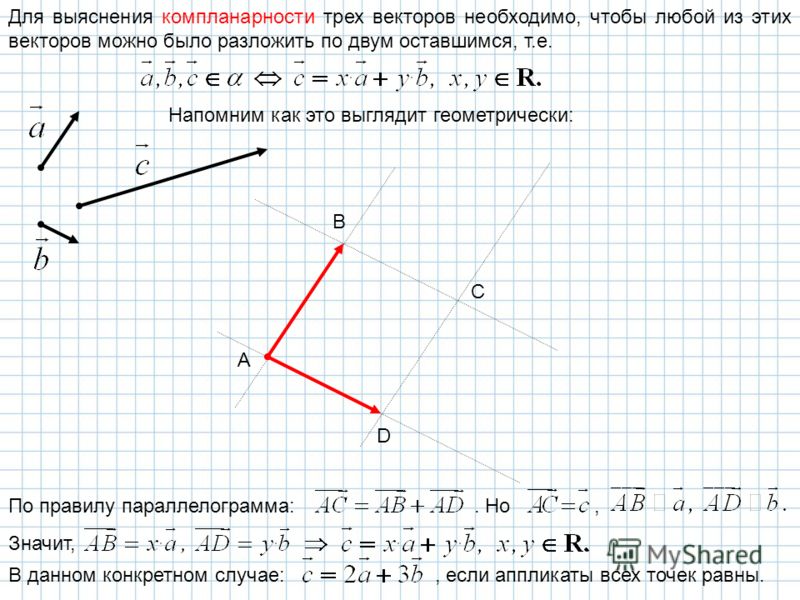 Это включает в себя добавление векторов в другом порядке.
Это включает в себя добавление векторов в другом порядке.
SOH CAH TOA и направление векторов
Приведенное выше обсуждение объясняет метод определения величины равнодействующей для трех или более перпендикулярных векторов. Тема направления была проигнорирована в обсуждении. Теперь обратим внимание на способ определения направления результирующего вектора. В качестве беглого обзора вспомним, что ранее в этом уроке было введено соглашение для выражения направления вектора. Конвенция известна как движение против часовой стрелки от восточной конвенции, часто сокращенно обозначаемое как 9.0004 Конвенция CCW . Используя это соглашение, направление вектора часто выражается как угол поворота вектора против часовой стрелки вокруг его хвоста на строго на восток.
Чтобы начать наше обсуждение, вернемся к Примеру 1 выше, где мы попытались добавить три вектора: 6,0 км, N + 6,0 км, E + 2,0 км, N.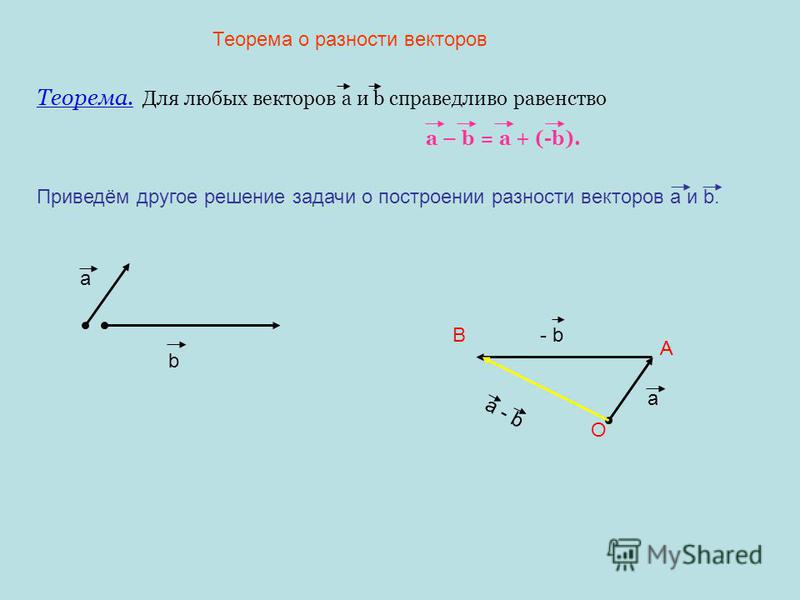 В решении порядок сложения трех векторов переставили так, чтобы получился прямоугольный треугольник, а полученная гипотенуза треугольника. Треугольник перерисовывается справа. Обратите внимание, что угол в левом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью. Theta (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке, — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA помогает запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тета (Θ) и знаем длину стороны, противоположной тета (Θ) — 6,0 км — и длину стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже.
В решении порядок сложения трех векторов переставили так, чтобы получился прямоугольный треугольник, а полученная гипотенуза треугольника. Треугольник перерисовывается справа. Обратите внимание, что угол в левом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью. Theta (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке, — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA помогает запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тета (Θ) и знаем длину стороны, противоположной тета (Θ) — 6,0 км — и длину стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже.
Касательная(Θ) = Противоположная/Смежная
Тангенс(Θ) = 6,0/8,0
Тангенс(Θ) = 0,75
Θ = тангенс -1 (0,75)
Θ = 36,869 …°
Θ =37°
Проблема не решена после того, как вычислено значение тета (Θ). Эта угловая мера теперь должна использоваться для указания направления. Один из способов сделать это — просто указать, что направление равнодействующей — 37 ° к востоку от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Поскольку угол, который равнодействующая образует с востоком, является дополнением угла, который она образует с севером, мы могли бы выразить направление как 53° против часовой стрелки.
Эта угловая мера теперь должна использоваться для указания направления. Один из способов сделать это — просто указать, что направление равнодействующей — 37 ° к востоку от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Поскольку угол, который равнодействующая образует с востоком, является дополнением угла, который она образует с севером, мы могли бы выразить направление как 53° против часовой стрелки.
Теперь мы рассмотрим Пример 2 в качестве второго примера того, как использовать SOH CAH TOA для определения направления равнодействующей. В Примере 2 мы пытались определить величину 2,0 м. S + 16,0 м, W + 24,0 м, N + 36,0 м, W. Решение заключалось в переупорядочении сложения таким образом, чтобы результирующая была гипотенузой прямоугольного треугольника с известными сторонами. Прямоугольный треугольник показан ниже. Результат рисуется черным цветом. Еще раз обратите внимание, что угол в правом нижнем углу треугольника помечен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью.
Тета (Θ) представляет собой угол, который вектор образует с северной осью.
Theta (Θ) можно рассчитать с помощью функции тангенса. В этой задаче мы хотим определить угловую меру тета (Θ) и знаем длину стороны, противоположной тета (Θ) — 52,0 м — и длину стороны, прилегающей к углу тета (Θ) — 22,0 м. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже.
Касательная(Θ) = Противоположная/Смежная
Тангенс(Θ) = 52,0/22,0
Тангенс(Θ) = 2,3636 …
Θ = тангенс -1 (2,3636 …)
Θ = 67,067 …°
Θ =67,1°
Проблема не решена после того, как вычислено значение тета (Θ). Эта угловая мера теперь должна использоваться для указания направления. Один из способов сделать это — просто указать, что направление равнодействующей — 67,1 ° к западу от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Северная ось повернута на 90 ° против часовой стрелки с востока, и этот вектор составляет дополнительные 67,1 ° против часовой стрелки после севера. Таким образом, направление против часовой стрелки равно 157,1° против часовой стрелки.
Один из способов сделать это — просто указать, что направление равнодействующей — 67,1 ° к западу от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Северная ось повернута на 90 ° против часовой стрелки с востока, и этот вектор составляет дополнительные 67,1 ° против часовой стрелки после севера. Таким образом, направление против часовой стрелки равно 157,1° против часовой стрелки.
Подводя итог, можно сказать, что направление вектора можно определить так же, как и всегда, — найдя угол поворота против часовой стрелки строго на восток. Поскольку равнодействующая является гипотенузой прямоугольного треугольника, это можно сделать, сначала найдя угол, который образует равнодействующая с одной из ближайших осей треугольника. После этого требуется немного подумать, чтобы связать угол с направлением.
Добавление неперпендикулярных векторов
Теперь мы рассмотрим ситуации, в которых два (или более) складываемых вектора не находятся под прямым углом друг к другу. Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольного треугольника. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразоваться в другие векторы, образующие прямоугольный треугольник. Хитрость включает в себя понятие компонента вектора и процесс разрешения вектора.
Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольного треугольника. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразоваться в другие векторы, образующие прямоугольный треугольник. Хитрость включает в себя понятие компонента вектора и процесс разрешения вектора.
Компонент вектора описывает действие вектора в заданном направлении. Любой вектор под углом состоит из двух компонентов; один направлен горизонтально, а другой направлен вертикально. Например, северо-западный вектор имеет северную составляющую и западную составляющую. Вместе эффект этих двух компонентов равен общему эффекту вектора под углом . В качестве примера рассмотрим самолет, который летит на северо-запад из аэропорта Чикаго О’Хара в направлении границы с Канадой. Вектор северо-западного смещения плоскости имеет две составляющие — северную и западную. При суммировании эти две составляющие равны общему смещению на северо-запад. Это показано на диаграмме ниже.
При суммировании эти две составляющие равны общему смещению на северо-запад. Это показано на диаграмме ниже.
Северо-западный вектор имеет северную и западную компоненты, которые представлены как A x и A y . Можно сказать, что
А = А х + А у
Поэтому всякий раз, когда мы думаем о северо-западном векторе, мы можем думать вместо двух векторов — северного и западного. Два компонента A x + A y можно заменить на один вектор А в проблеме.
Теперь предположим, что ваша задача заключается в сложении вместе двух неперпендикулярных векторов. Назовем векторы A и B . Вектор A — это вектор с неприятным углом , который не является ни горизонтальным, ни вертикальным. А вектор B — красивый, вежливый вектор, направленный горизонтально. Ситуация показана ниже.
А вектор B — красивый, вежливый вектор, направленный горизонтально. Ситуация показана ниже.
Конечно противный вектор А состоит из двух компонентов — А х и А у . Эти два компонента вместе равны вектору A . То есть А = А х + А у .
А так как это верно, то можно сказать, что А + В = А х + А у + В .
Итак, задача А+В превратилась в задачу, в которой все векторы лежат под прямым углом друг к другу. Nasty был заменен на nice , и это должно порадовать любого студента-физика. Поскольку все векторы расположены под прямым углом друг к другу, их сложение приводит к равнодействующей, которая находится в гипотенузе прямоугольного треугольника. Затем можно использовать теорему Пифагора для определения величины равнодействующей.
Затем можно использовать теорему Пифагора для определения величины равнодействующей.
Чтобы увидеть, как этот процесс работает с реальной задачей сложения векторов, рассмотрим пример 3, показанный ниже.
Пример 3:
Макс играет полузащитника футбольной команды Юга. Во время одной из игр в прошлую пятницу вечером против New Greer Academy он сделал следующие движения после того, как мяч был снэпован на третьем дауне. Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и пробежал по полю расстояние 4,8 метра в направлении 240° против часовой стрелки с востока (30° з.д. и ю.ш.), прежде чем, наконец, выбить ветер из широкого ресивера Нью Грир. Определите величину и направление общего смещения Макса.
Как обычно, решение начинается с диаграммы добавляемых векторов.
Для облегчения обсуждения три вектора были помечены как векторы A , B и C . Результатом является векторная сумма этих трех векторов; диаграмма сложения векторов головы к хвосту показывает, что результирующая направлена на юго-запад. Из трех добавленных векторов вектор C явно является неприятным вектором . Его направление не строго на юг и не строго на запад. Решение включает в себя разложение этого вектора на его компоненты.
Процесс разрешения векторов обсуждался ранее в этом уроке. Этот процесс включает в себя использование величины, функций синуса и косинуса для определения x- и y-компонент вектора. Вектор C образует угол 30° с южным направлением. Нарисовав прямоугольный треугольник с горизонтальными и вертикальными катетами и С в качестве гипотенузы, можно определить компоненты вектора С. Это показано на диаграмме ниже. Сторона, прилегающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C и . Таким образом, для определения C y используется функция косинуса. Сторона, противоположная углу 30°, является горизонтальной стороной; горизонтальная сторона представляет горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения южной составляющей, поскольку южная составляющая примыкает к углу 30°. Функция синуса используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30°. Работа представлена ниже.
Таким образом, для определения C y используется функция косинуса. Сторона, противоположная углу 30°, является горизонтальной стороной; горизонтальная сторона представляет горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения южной составляющей, поскольку южная составляющая примыкает к углу 30°. Функция синуса используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30°. Работа представлена ниже.
Теперь наша задача сложения векторов была преобразована из сложения двух хороших векторов и одного неприятного вектора в сложение четырех хороших векторов.
Поскольку все векторы ориентированы вдоль обычных осей север-юг и восток-запад, их можно сложить в любом порядке, чтобы получить прямоугольный треугольник, гипотенуза которого является равнодействующей. Такая схема показана ниже.
Такая схема показана ниже.
Перпендикулярные стороны треугольника имеют длину 4,6 метра и 6,756 метра. Длина горизонтальной стороны (4,6 м) определялась суммированием значений В (2,2 м) и С x (2,4 м). Длина вертикальной стороны (6,756… м) определялась путем сложения значений А (2,6 м) и С и (4,156… м). Результирующую величину (R) теперь можно определить с помощью теоремы Пифагора.
R 2 = (6,756… м) 2 + (4,6 м) 2
R 2 = 45,655… м 2 + 21,16 м 2
R 2 = 66,815… м 2
R = SQRT(66,815… m 2 )
R = 8,174 … м
R = ~8,2 м
Направление равнодействующей можно определить, найдя угол, который образует равнодействующая с вектором север-юг или восток-запад. На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов. Этот угол тета представляет собой угол, который равнодействующая образует с западом. Его значение можно определить с помощью функции тангенса. Функция тангенса (как и в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. То есть,
Этот угол тета представляет собой угол, который равнодействующая образует с западом. Его значение можно определить с помощью функции тангенса. Функция тангенса (как и в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. То есть,
тангенс(Θ) = (6,756… м)/(4,6 м) = 1,46889…
Используя функцию арктангенса, можно определить угол тета (Θ). На большинстве калькуляторов для этого используются кнопки 2nd-Tangent.
Θ = тангенс -1 (1,46889…) = 55,7536… °
Θ = ~56°
Этот угол 56° представляет собой угол между результирующим вектором (нарисованным черным выше) и направлением на запад. Это делает направление 56 ° к югу от запада. Направление равнодействующей, основанное на условном направлении против часовой стрелки от востока (CCW), можно определить, добавив 180 ° к 56 °. Таким образом, направление против часовой стрелки составляет 236°.
В примере 4 представлен последний пример того, как совместить разрешение векторов с добавлением векторов для добавления трех или более неперпендикулярных векторов. Поскольку этот пример включает в себя три особенно неприятных вектора , таблица будет использоваться для организации информации о величине и направлении компонентов. Использование таблицы — мудрая идея, когда проблемы усложняются.
Поскольку этот пример включает в себя три особенно неприятных вектора , таблица будет использоваться для организации информации о величине и направлении компонентов. Использование таблицы — мудрая идея, когда проблемы усложняются.
Пример 4:
Кэмерон Пер (друзья зовут его Кэм) и Бакстер Натюр в походе. Начиная с домашней базы, они совершают следующие движения.A: 2,65 км, 140° против часовой стрелки
Определить величину и направление их общего смещения.
B: 4,77 км, 252° против часовой стрелки
C: 3,18 км, 332° против часовой стрелки
Визуальное представление ситуации показано ниже.
Чтобы определить результат, три отдельных вектора разлагаются на горизонтальную и вертикальную составляющие. Информация об углах каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а перпендикулярные стороны ориентированы вдоль осей восток-запад и север-юг. Это показано на диаграмме ниже.
Это показано на диаграмме ниже.
Тригонометрические функции — синус, косинус и тангенс — затем используются для определения величины горизонтальной и вертикальной составляющей каждого вектора. Работа показана и организована в таблице ниже.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| А 2,65 км 140° против часовой стрелки | (2,65 км)•cos(40°) = 2,030… км, Запад | (2,65 км)•sin(40°) = 1,703… км, север |
| Б 4,77 км 252° против часовой стрелки | (4,77 км)•sin(18°) = 1,474… км, запад | (4,77 км)•cos(18°) = 4,536… км, юг |
| С 3,18 км 332° против часовой стрелки | (3,18 км)•cos(28°) = 2,808… км, Восток | (3,18 км)•sin(28°) = 1,493… км, Юг |
| Сумма А+В+С | 0,696 км, Запад | 4,326 км, Юг |
Последняя строка приведенной выше таблицы представляет собой сумму всех компонентов Восток-Запад и сумму всех компонентов Север-Юг.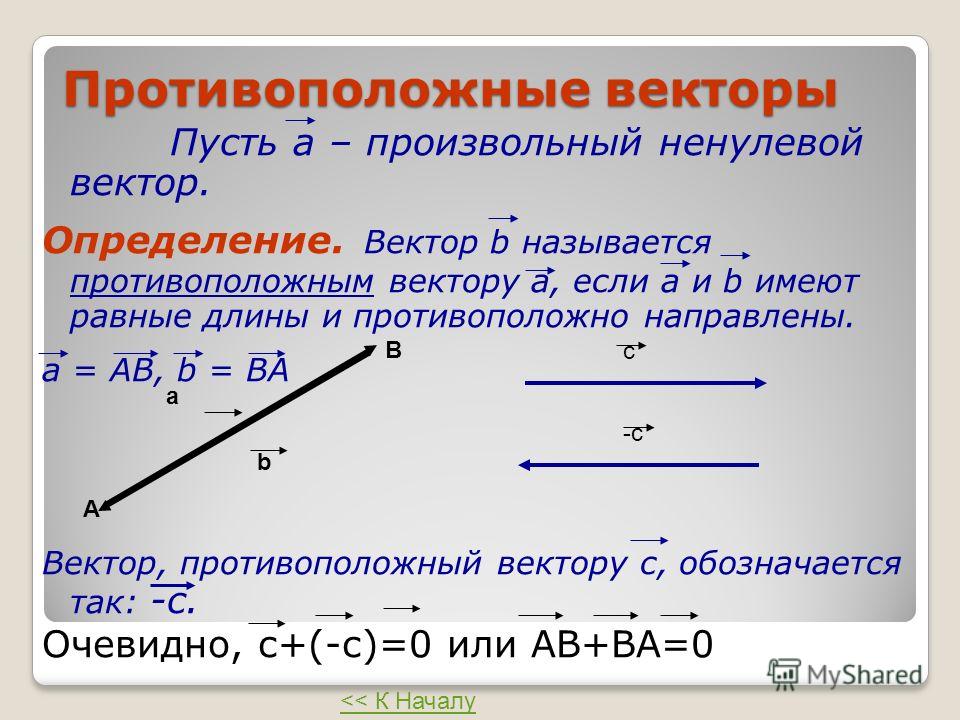 Результат состоит из этих двух компонентов. Результирующая определяется путем сложения этих двух компонентов, чтобы сформировать прямоугольный треугольник с гипотенузой, равной равнодействующей. Обычно это включает сложение всех горизонтальных компонентов для определения общей длины горизонтальной стороны прямоугольного треугольника… и сложение всех вертикальных компонентов для определения общей длины вертикальной стороны прямоугольного треугольника. Это делается в приведенной выше таблице простым добавлением еще одной строки в таблицу для векторной суммы всех компонентов. При сложении восточно-западных компонентов всех отдельных векторов необходимо учитывать, что восточный компонент и западный компонент складываются вместе как 9.0003 положительный и отрицательный . Некоторые студенты предпочитают думать об этом как о вычитании, а не о сложении. На самом деле это сложение — сложение векторов противоположного направления. Точно так же северный и южный компоненты также будут складываться как положительных и отрицательных .
Результат состоит из этих двух компонентов. Результирующая определяется путем сложения этих двух компонентов, чтобы сформировать прямоугольный треугольник с гипотенузой, равной равнодействующей. Обычно это включает сложение всех горизонтальных компонентов для определения общей длины горизонтальной стороны прямоугольного треугольника… и сложение всех вертикальных компонентов для определения общей длины вертикальной стороны прямоугольного треугольника. Это делается в приведенной выше таблице простым добавлением еще одной строки в таблицу для векторной суммы всех компонентов. При сложении восточно-западных компонентов всех отдельных векторов необходимо учитывать, что восточный компонент и западный компонент складываются вместе как 9.0003 положительный и отрицательный . Некоторые студенты предпочитают думать об этом как о вычитании, а не о сложении. На самом деле это сложение — сложение векторов противоположного направления. Точно так же северный и южный компоненты также будут складываться как положительных и отрицательных . Как только нижняя строка точно определена, величину равнодействующей можно определить с помощью теоремы Пифагора.
Как только нижняя строка точно определена, величину равнодействующей можно определить с помощью теоремы Пифагора.
Р 2 = (0,696 км) 2 + (4,326 км) 2
R 2 = 0,484 км 2 + 18,714 км 2
R 2 = 19,199 км 2
R = SQRT (19,199 км 2 )
R = ~4,38 км
Направление результирующего смещения можно определить, построив итоговый треугольник из составляющих равнодействующей. Компоненты равнодействующей представляют собой просто сумму компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который образует результирующая с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:
Тангенс(Θ) = противоположный/примыкающий
Тангенс (Θ) = (4,326 км)/(0,696 км)
Тангенс (Θ) = 6,216
Θ = тангенс -1 (6,216)
Θ = 80,9°
Эта угловая мера представляет собой угол поворота вектора к югу от строгого запада.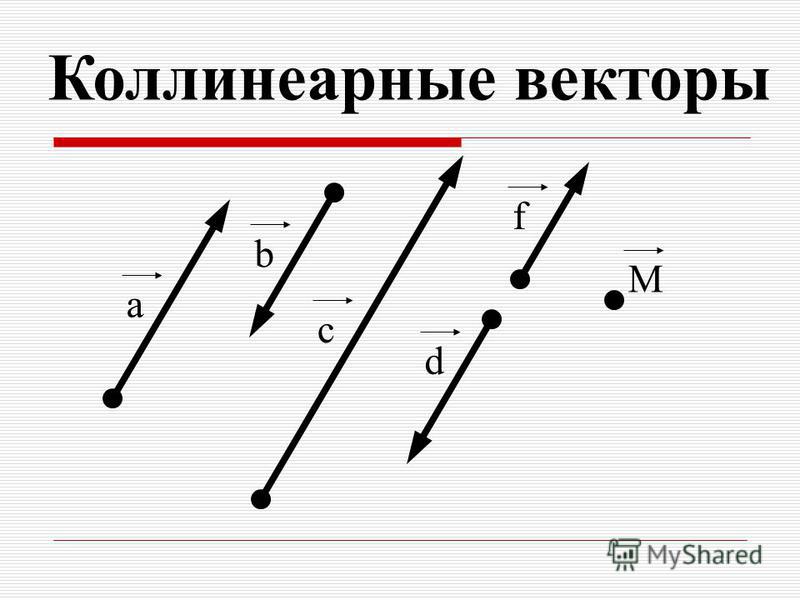 Это будет сформулировано как 80,9 ° к югу от запада. Поскольку запад составляет 180 ° против часовой стрелки от востока, направление также может быть выражено против часовой стрелки (CCW) от востока как 260,9 °.
Это будет сформулировано как 80,9 ° к югу от запада. Поскольку запад составляет 180 ° против часовой стрелки от востока, направление также может быть выражено против часовой стрелки (CCW) от востока как 260,9 °.
Таким образом, результатом нашего анализа является то, что общее перемещение составляет 4,38 км с направлением 260,9° (против часовой стрелки).
Вопросы, которые были рассмотрены на этой странице:
- Как можно сложить три или более перпендикулярных вектора, чтобы получить равнодействующую?
- Как можно сложить два или более неперпендикулярных вектора, чтобы получить результат?
Для обоих вопросов мы обнаружили, что любые два, три или более вектора могут быть преобразованы или переставлены так, что они складываются вместе, образуя прямоугольный треугольник с гипотенузой, являющейся равнодействующей. После формирования прямоугольного треугольника можно использовать теорему Пифагора и SOH CAH TOA для вычисления равнодействующей.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей интерактивной игры «Назовите этот вектор», интерактивной игры «Добавление вектора» или интерактивной игры «Угадай вектор». Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Посетите: Назовите этот вектор | Добавление вектора | Игра «Угадай вектор»
Поэкспериментируйте с виджетом ниже, а затем попробуйте решить задачи из раздела «Проверка понимания», чтобы проверить свои навыки добавления векторов с помощью компонентов.
Виджет ниже вычисляет сумму трех векторов, если известны x- и y-компоненты. Используйте виджет, чтобы потренироваться и проверить проблему.
Рассмотрим диаграмму ниже. На сетке представлены девять уникальных помеченных мест. Каждый квадрат на сетке представляет собой площадь 20 х 20 м. Вправо по сетке находится в восточном направлении и вверх по сетке в северном направлении. Используйте сетку, отвечая на следующие несколько вопросов.
1. Предположим, что человек начинает с позиции А и идет к позиции Е, а затем к позиции G. Заполните приведенную ниже таблицу, указав компоненты восток-запад и север-юг отдельных этапов ходьбы, а также компоненты пути. результирующее смещение. Сделайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от А до Е | ||
| В-Г | ||
| Результат от А до G |
Величина результата: _________________________
Направление результата: _________________________
2. Используя ту же сетку, повторите измерения для прохождения от точки C к точке B и к точке F. Выполните измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещение.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| С до В | ||
| от B до F | ||
| Результат С до Ж |
Величина результата: _________________________
Направление результата: _________________________
3. Наконец, используйте ту же сетку, чтобы повторить измерения для прогулки от точки I к точке B, к точке G и к точке H. Выполните измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA для определения магнитуды и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от I до Б | ||
| от B до G | ||
| G-H | ||
| Результат от I до Н |
Величина результата: _________________________
Направление результата: _________________________
4. Во время своего недавнего похода в продуктовый магазин Клэр де Иль прошла 28 м до конца прохода. Затем она повернула направо и прошла 12 м по концевому проходу. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг не являются фокусом.)
Затем она повернула направо и прошла 12 м по концевому проходу. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг не являются фокусом.)
5. В последнем матче прошлогоднего регулярного сезона команда South играла в New Greer Academy за титул чемпиона конференции. В последнем розыгрыше игры звездный квотербек Эйвери сделал рывок из схватки и отскочил назад (на север) на 8,0 ярда. Затем он пробежал боком (на запад) из кармана на 12,0 ярдов, прежде чем, наконец, бросить пас на 34,0 ярда прямо по полю (на юг) Кендаллу для победного в игре тачдауна. Определить величину и направление перемещения мяча.
6. Миа Андер выходит из парадной двери своего дома и идет по пути, показанному на схеме справа (не в масштабе). Прогулка состоит из четырех этапов со следующими величинами:
А = 46 м
В = 142 м
С = 78 м
Д = 89 м
Определите величину и направление результирующего смещения Мии. Рассмотрите возможность использования таблицы для организации ваших вычислений.
Рассмотрите возможность использования таблицы для организации ваших вычислений.
Следующий раздел:
Перейти к следующему уроку:
Перекрестное произведение двух векторов
При изучении математики, физики или техники бывают ситуации, когда нам требуется вычислить перекрестное произведение двух векторов. Его можно использовать в механике, например, для нахождения крутящего момента , приложенного силой, или в области компьютерной графики для вычисления нормали к поверхности для многоугольника (т. е. вектора, перпендикулярного поверхности многоугольник). Перекрестное произведение является результатом перемножения векторов вместе и дает третий вектор, равный 9.1031 перпендикулярно (т.е. под прямым углом или ортогонально ) к обоим исходным векторам. Таким образом, векторное произведение не имеет смысла в двумерной среде.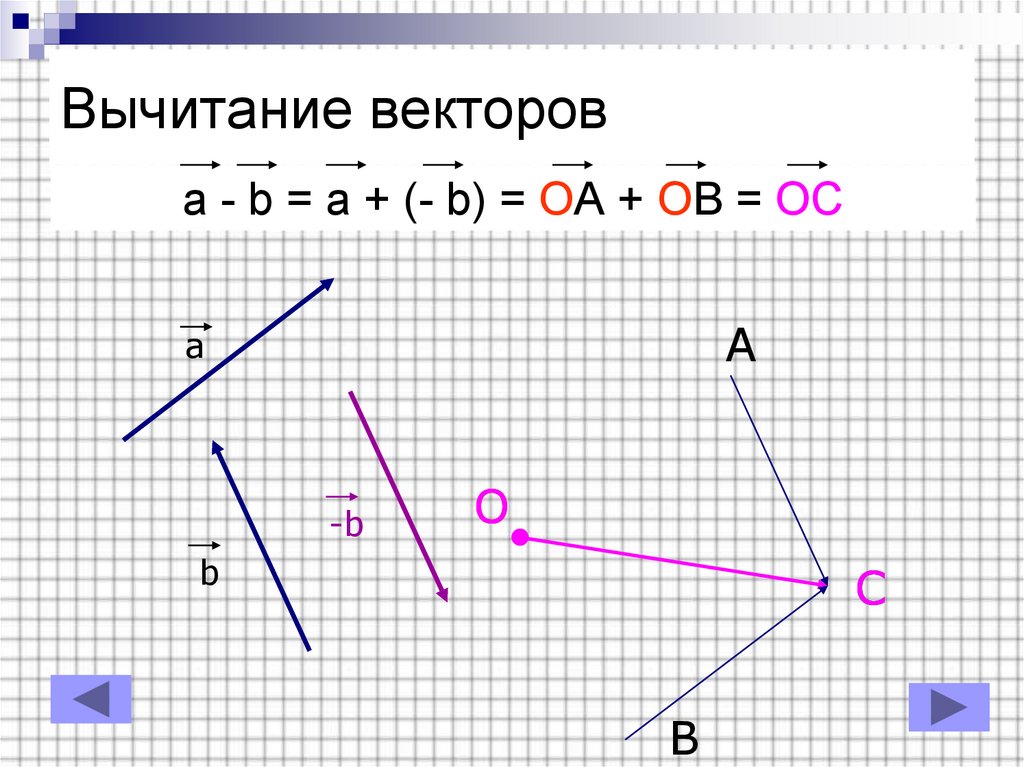 Фактически, это имеет смысл только в трехмерной среде или в семимерной среде (мы ограничимся обсуждением векторного произведения в трехмерной среде). Рассмотрим приведенную ниже иллюстрацию, на которой показаны два отдельных вектора в трехмерном пространстве.
Фактически, это имеет смысл только в трехмерной среде или в семимерной среде (мы ограничимся обсуждением векторного произведения в трехмерной среде). Рассмотрим приведенную ниже иллюстрацию, на которой показаны два отдельных вектора в трехмерном пространстве.
Два вектора в трехмерном пространстве
Трехмерные векторы AB → и CD → имеют фиксированные точки начала координат (т. е. они фактически являются векторами положения), и не существует единой плоскости, в которой они оба лежат. Мы, конечно, можем переместить один из векторов так, чтобы два вектора располагались хвост к хвосту, и в этом случае будет существовать одна (а только одна ) плоскость, общая для обоих векторов. Мы будем перемещать вектор AB → так, чтобы его хвост совпадал с хвостом вектора CD →. На приведенном ниже рисунке снова показаны два вектора, на этот раз с общей исходной точкой.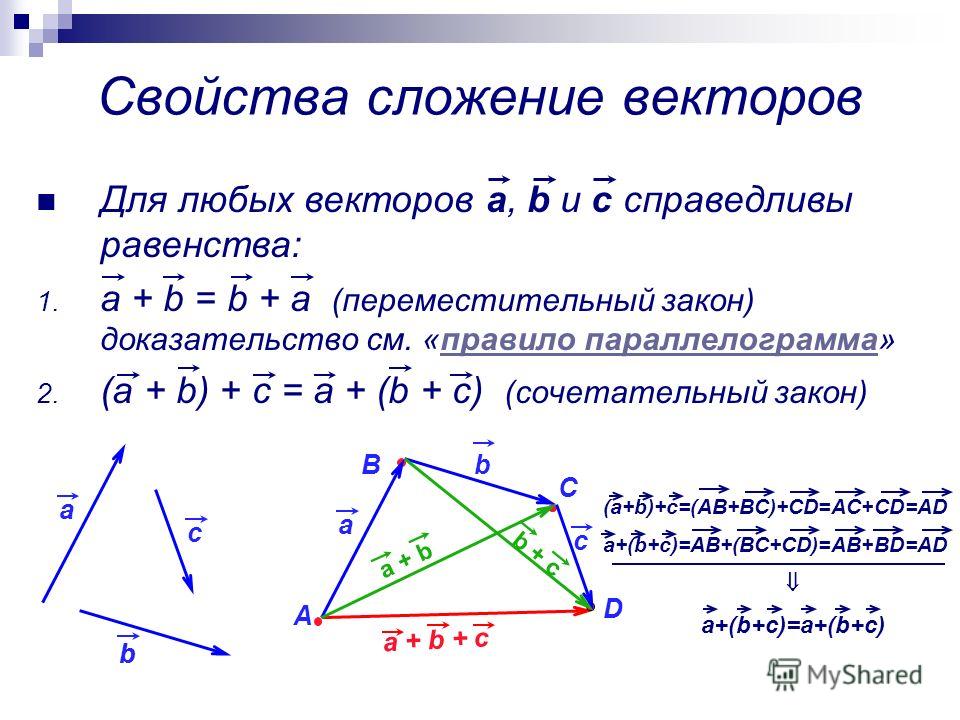 Сетка (которая лежит в плоскости x — y ) и метки точек были удалены для ясности.
Сетка (которая лежит в плоскости x — y ) и метки точек были удалены для ясности.
Векторы теперь хвост к хвосту
Что нас действительно интересует здесь, так это x , y и z компоненты векторов, а не x , y и z координаты их конечных точек. Нахождение значений компонентов x , y и z является простой задачей, если мы знаем координаты x , y и y и z начальной и конечной точек для каждого вектора. найти компонент x вектора, например, это вычесть x координаты его начальной точки относительно конечной точки. Когда у нас есть значения компонентов для каждого вектора, мы можем просто рассматривать их как свободные векторы, которые имеют общую точку начала координат и, следовательно, лежат в одной плоскости. На следующем рисунке мы показываем только значения компонентов и полностью удаляем оси x , y и z .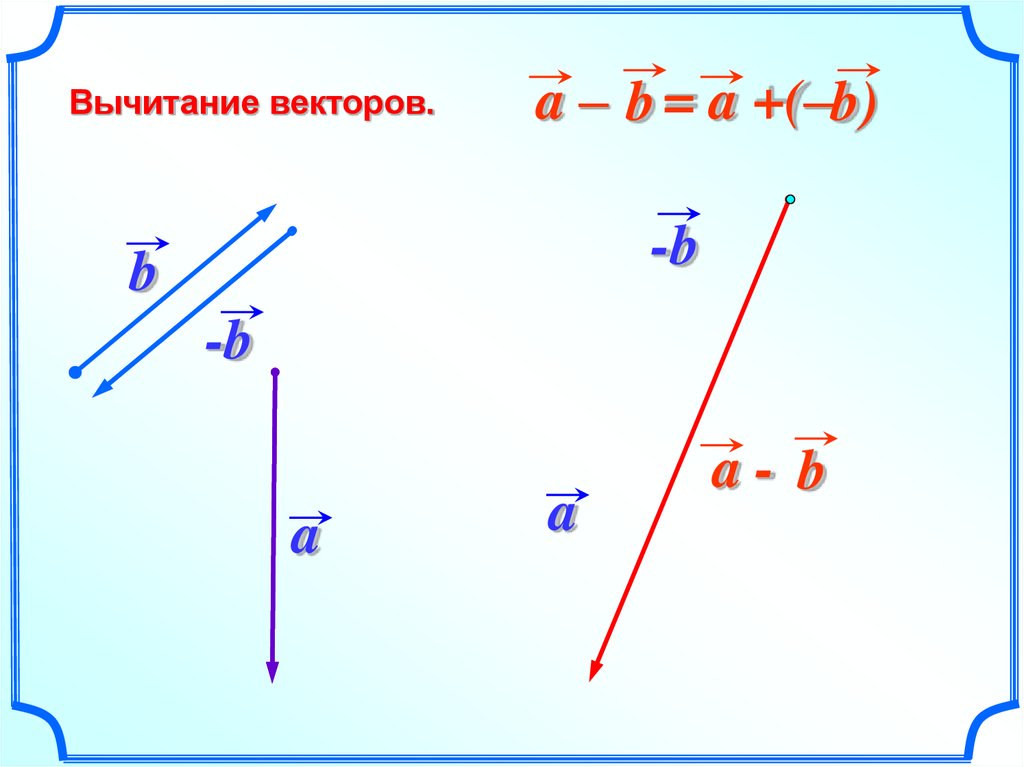
Значения компонентов для векторов , и б
Выше мы сказали, что векторное произведение двух векторов — это новый вектор, который перпендикулярен обоим исходным векторам, но это оставляет нас с вопросом. Есть два направления, которые перпендикулярны обоим векторам. Какой из них является правильным направлением? Ответ на этот вопрос обычно зависит от ориентации используемой системы координат. Предположим для целей этого обсуждения, что мы имеем дело с правая система координат (конечно, существуют и другие возможности, но мы постараемся сделать все относительно простым). Затем можно применить правило правой руки (проиллюстрированное ниже) для определения направления, в котором указывает вектор векторного произведения. Обратите внимание, что перекрестное произведение векторов a и b записывается как a x b .
Применение правила правой руки
Как видно из рисунка, если первый и второй пальцы правой руки расположены более или менее под прямым углом друг к другу, а большой палец более или менее под прямым углом к обоим пальцам, то указательный палец указывает примерно на в направлении вектора a , безымянный палец в направлении вектора b и большой палец в направлении a × b (т. е. вектор векторного произведения). Обратите внимание, что угол между векторами a и b могут быть любым углом между ноль и сто восемьдесят градусов. Ниже на графике показаны векторы a и b вместе с вектором перекрестного произведения, который мы обозначили вектором c . Обратите внимание, поскольку мы имеем дело с трехмерной средой, это всего лишь одна из возможных точек зрения. Имейте в виду, однако, что вектор c находится в под прямым углом к обоим векторам a и вектор b .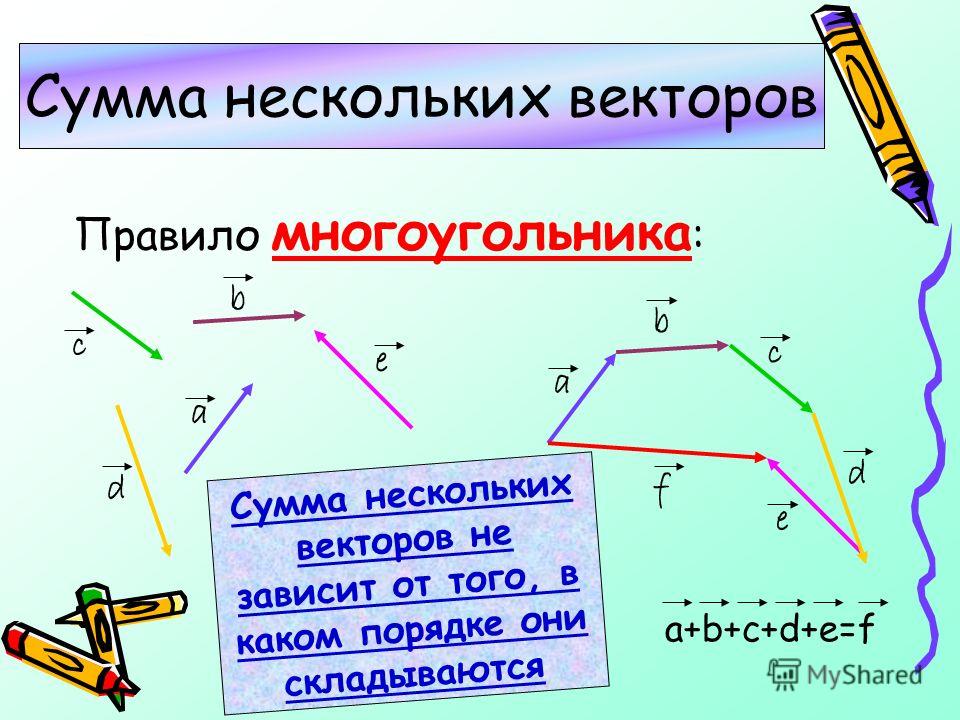
Векторы a и b с их векторным произведением, вектор c
Вопрос, который вы, вероятно, должны задать себе в этот момент, заключается в том, как мы пришли к компонентам x , y и z для вектора c , показанного на иллюстрации? Ну и не вдаваясь в пространные объяснения, находим x , y and z components of vector c (i.e. the cross product vector) by using the x , y and z components of vectors a and b as follows :
C x = A y B Z — A Z
6 A Z 6 B A 6 B A 6 A 6 A 6 A 6. (-1) = -1
(-1) = -1C y = A Z B x — A 95 — A 495 — . )(-2) = 4
c z = a x b y — a y b x = (1 )(-1) — (1)(2) = -3
Заметим, что поскольку вектор c перпендикулярен плоскости, в которой лежат оба вектора a и b , отсюда следует, что если векторы a и b оба лежат в плоскости x — y , их компонент z будет равен нулю. Следовательно, компоненты x и y вектора c также будут равны нулю (т. е. вектор c будет параллелен оси z ).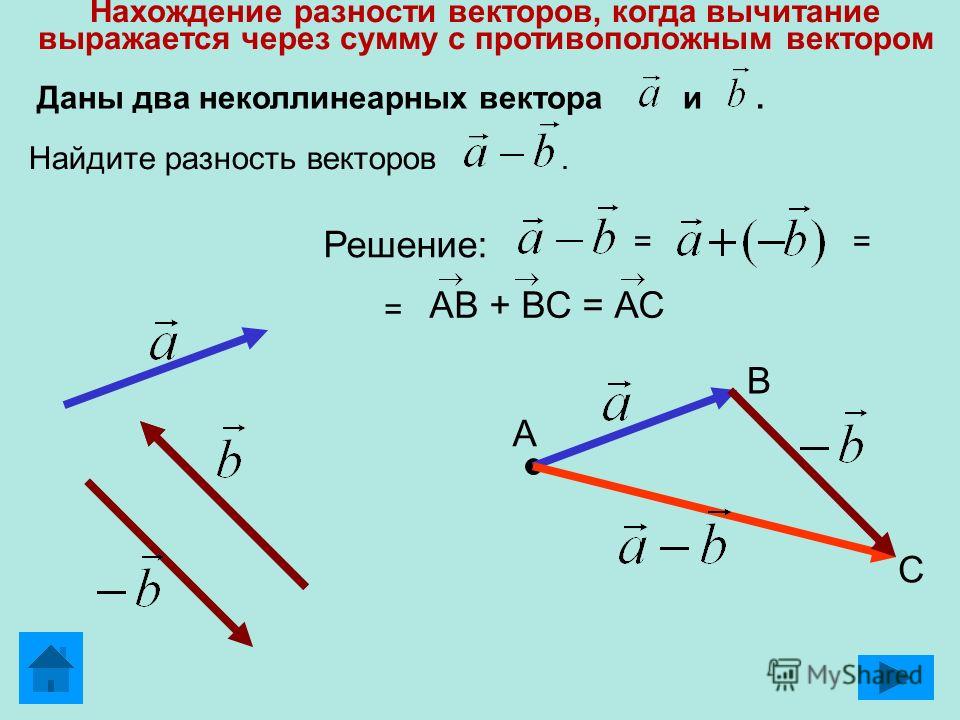 Заметим также, что если любой вектор a или b является нулевым вектором , или если векторы a и b параллельны , их векторное произведение также будет нулевым вектором. Пока векторы a и b не лежат в плоскости, определяемой любыми двумя из трех осей ( x , y и z ), тогда все компоненты вектор c будет ненулевым.
Заметим также, что если любой вектор a или b является нулевым вектором , или если векторы a и b параллельны , их векторное произведение также будет нулевым вектором. Пока векторы a и b не лежат в плоскости, определяемой любыми двумя из трех осей ( x , y и z ), тогда все компоненты вектор c будет ненулевым.
Мы также можем выразить перекрестное произведение двух векторов в матричной форме. Мы делаем это, сначала создавая 9Матрица 1031 три на три , содержащая компоненты x , y и z векторов a и b . Первая строка матрицы должна состоять из ортонормированных векторов x , y и z . Ортонормированный вектор — это единичный вектор (т. е. он имеет величину один ), который имеет только один ненулевой компонент. Чтобы проиллюстрировать, что это означает, ортонормированные векторы x , y и z могут быть представлены с использованием следующих матриц столбцов:
Чтобы проиллюстрировать, что это означает, ортонормированные векторы x , y и z могут быть представлены с использованием следующих матриц столбцов:
| x = | 1 | ||
| 0 | |||
| 0 |
| y = | 0 | ||
| 1 | |||
| 0 |
| z = | 0 | ||
| 0 | |||
| 1 |
Матрица три на три представлена ниже. Векторы x , y и z по существу используются как своего рода заполнители для представления значения на единицу в каждом столбце первой строки матрицы. В некоторых представлениях вы можете увидеть разные символы, используемые для представления ортонормированных векторов (например, i , j и k ), и символы могут отображаться с символом вставки («^») над ними, чтобы обозначить тот факт, что они являются ортонормированными векторами. Вторая и третья строки содержат x , y и z значения компонентов векторов a и b соответственно.
Вторая и третья строки содержат x , y и z значения компонентов векторов a и b соответственно.
| x | y | z | ||
| a x | a y | a z | ||
| б х | б у | б г |
 Обратите внимание, что определитель матрицы записывается в том же формате, что и исходная матрица, но вместо скобок столбцы заключены в вертикальные черточки.
Обратите внимание, что определитель матрицы записывается в том же формате, что и исходная матрица, но вместо скобок столбцы заключены в вертикальные черточки.| c = a × b = | x | y | z | = x | a y | a z | — y | a x | a z | + z | a x | a y | |||||||||||||||||||||||||||||||||||||||||||||||
| a x | a y | a z | b y | b z | b x | b z | b x | b y | |||||||||||||||||||||||||||||||||||||||||||||||||||
| b x | б г | б г | 4 Подставляя фактические значения, получаем: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c = a × b = | x | y | z | = x | 1 | 1 | — y | 1 | 1 | + z | 1 | 1 | ||||||||
| 1 | 1 | 1 | -1 | -2 | 2 | -2 | 2 | -1 | ||||||||||||
| 2 | -1 | -2 | ||||||||||||||||||
c = a × b = x ((1)(-2) — (-1)(1)) — y ((1)(-2) — (2)(1 )) + z ((1)(-1) — (2)(1))
c = — x + 4 y — 3 z
Это дает нам компоненты вектора x , y и z для вектора векторного произведения напрямую:
c = (-1, 4, -3)
Обратите внимание, что величина величины вектора c (вектор векторного произведения) фактически совпадает с площадью параллелограмма, для которого векторы a и b обеспечивают смежные стороны, как показано ниже.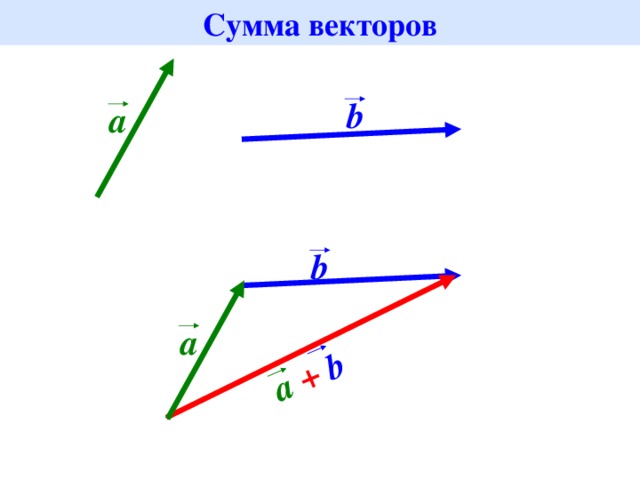
Векторы a и b могут представлять собой смежные стороны параллелограмма
Площадь параллелограмма получается путем умножения длины основания параллелограмма на его высоту. В приведенном выше примере мы предположили, что вектор b будет основанием параллелограмма. Высота параллелограмма получается путем умножения длины любой из сторон, прилегающих к основанию, на синус любого из его внутренних углов. В приведенном выше примере мы использовали вектор a и синус угла θ . Площадь параллелограмма, построенного с использованием векторов a и b , и, следовательно, величина вектора c , определяется выражением:
| с | = | a × b | = | и || б | грех ( θ )
Конечно, нам нужно получить значения угла θ (угол между векторами a и b ) и величины векторов a и b , прежде чем мы сможем выполнить это вычисление.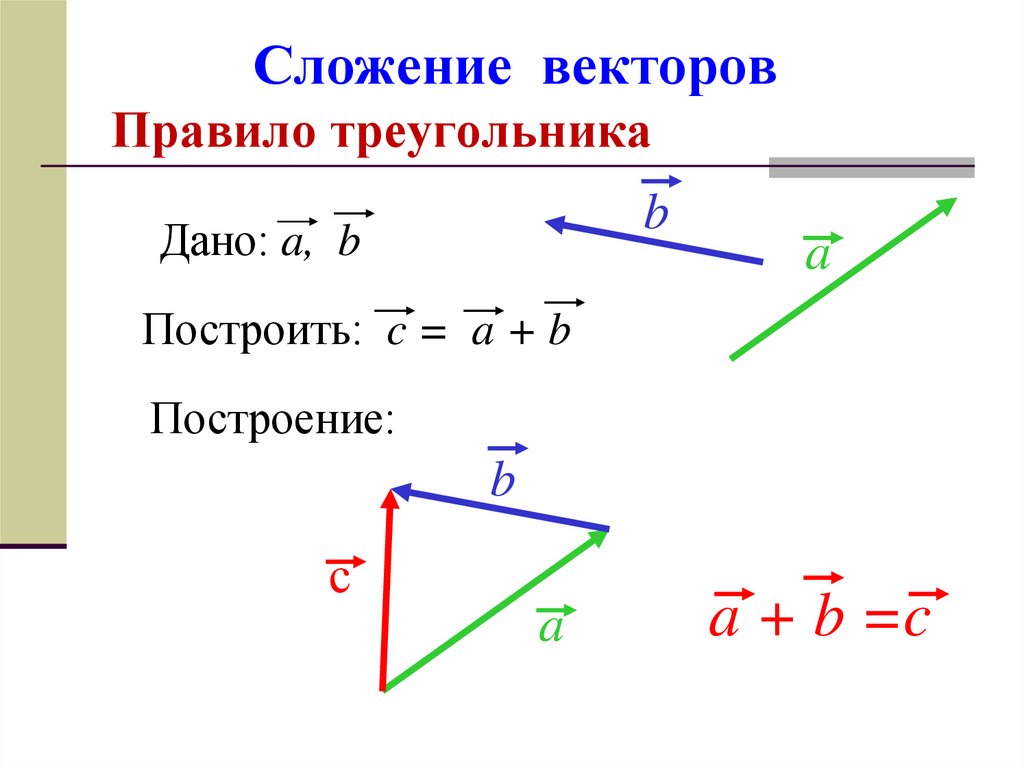 Когда у вас есть эти значения, вам не нужно понимать, как работает функция тригонометрического синуса, чтобы получить верный ответ, но вы можете do нужно знать, как правильно пользоваться кнопкой sine на калькуляторе.
Когда у вас есть эти значения, вам не нужно понимать, как работает функция тригонометрического синуса, чтобы получить верный ответ, но вы можете do нужно знать, как правильно пользоваться кнопкой sine на калькуляторе.
Есть еще одна вещь, о которой нужно знать, прежде чем мы двинемся дальше: в отличие от скалярного произведения двух векторов, перекрестное произведение не коммутативно . Другими словами, a × b дает результат, отличный от b × a . На самом деле векторное произведение b × a имеет точно такие же величина как векторное произведение a × b , но указывает в противоположном направлении ( b × a = -( a × b )).
Перекрестное произведение b × a указывает направление, противоположное a × b
На данный момент мы имеем дело с несколькими неизвестными. Мы не знаем величины векторов a и b , у нас нет значения угла θ (который будет минимальным углом, на который необходимо повернуть один из векторов, чтобы он указывал в том же направлении, что и другой вектор), и мы не знаем x , y и z компоненты единичного вектора n . Как найти эти недостающие значения? Мы начнем с нахождения величин (т.е. длин) векторов a и b , что относительно просто:
Мы не знаем величины векторов a и b , у нас нет значения угла θ (который будет минимальным углом, на который необходимо повернуть один из векторов, чтобы он указывал в том же направлении, что и другой вектор), и мы не знаем x , y и z компоненты единичного вектора n . Как найти эти недостающие значения? Мы начнем с нахождения величин (т.е. длин) векторов a и b , что относительно просто:
| и | = √ A x 2 + A Y 2 + A Z + A Z A .
| б | = √ b x 2 + b y 2 + b z 2 = √4 + 1 + 4 = √9 = 3
Чтобы найти угол θ , мы можем использовать скалярное произведение векторов a и b (если вы не знакомы с скалярным произведением двух векторов, посмотрите соответствующую страницу в этом разделе).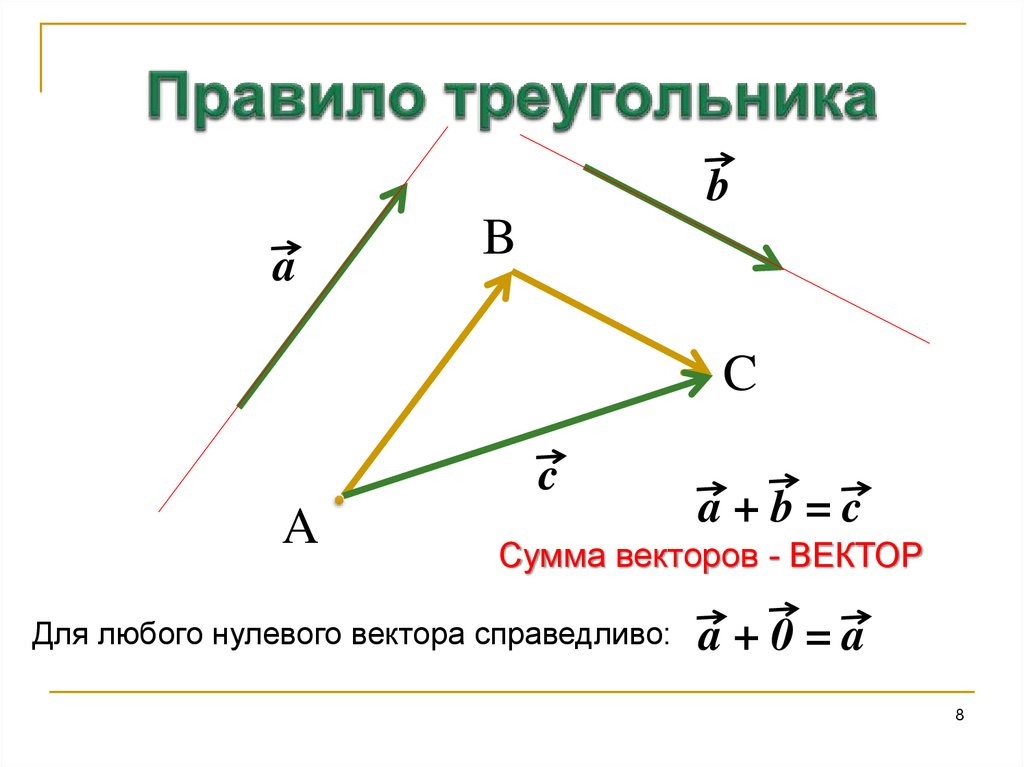 Мы можем найти скалярное произведение векторов a и b , используя уже имеющуюся информацию, следующим образом:
Мы можем найти скалярное произведение векторов a и b , используя уже имеющуюся информацию, следующим образом:
и · b = a x b x + a y b y + a z b z = ((1)(2)) + ((1)(-1) + (1)(-2)) = 2 — 1 — 2 = -1
Поскольку уравнение косинуса для скалярного произведения a и b :
a · b = | и || б | потому что ( θ )
мы можем изменить это уравнение, чтобы найти θ :
| θ = cos -1 | a · b | ||
Подставляя фактические значения, получаем:
| θ = cos -1 | -1 | = cos -1 (-0. 192) = 101.10° 192) = 101.10° |
| 1.732 × 3 |
Обратите внимание, что знак скалярного произведения важен. Если вы ошибетесь, вы получите дополнение угла θ (т.е. разница между θ и сто восемьдесят градусов ), а не θ .
Остается только найти компоненты x , y и z единичного вектора n . Принимая во внимание, что у нас уже есть компоненты x , y и z вектора c , это довольно просто. Единичный вектор по определению имеет длину в одну единицу, поэтому общая длина вектора c сообщит нам скалярное значение, на которое нужно умножить единичный вектор n , чтобы получить вектор 9.1031 с . Поэтому мы можем разделить компоненты x , y и z вектора c на его длину, чтобы получить компоненты x , y и z единичного вектора n. Чтобы найти длину вектора c , мы можем использовать следующий расчет:
Чтобы найти длину вектора c , мы можем использовать следующий расчет:
| с | = √ c x 2 + c y 2 + c z 2 = √1 + 16 + 9 = √26 = 5.099
Затем компоненты единичного вектора n находятся следующим образом:
n x = -1 ÷ 5.099 = -0.196
n y = 4 ÷ 5.099 = 0.784
n z = -3 ÷ 5.099 = -0,588
У нас уже есть альтернативное уравнение для величины вектора c (см. выше):
| с | = | a × b | = | и || б | грех ( θ )
Поскольку направление вектора c задается единичным вектором n , мы можем получить альтернативное уравнение для вектора c (то есть вектора векторного произведения), просто включив член n :
c = a × b = | и || б | грех ( θ ) п
Если мы теперь подставим фактические значения в наше уравнение, мы сможем получить тот же набор компонентов вектора для вектора c , как мы получили из нашего первоначального расчета с использованием компонентов x , y и z векторов a и b :
C = 1,732 × 3 × SIN (78,93 °) N = 5,099 N
C = 5,099 × (-0,196, 0,784, -0,588) = (-0,99, 3.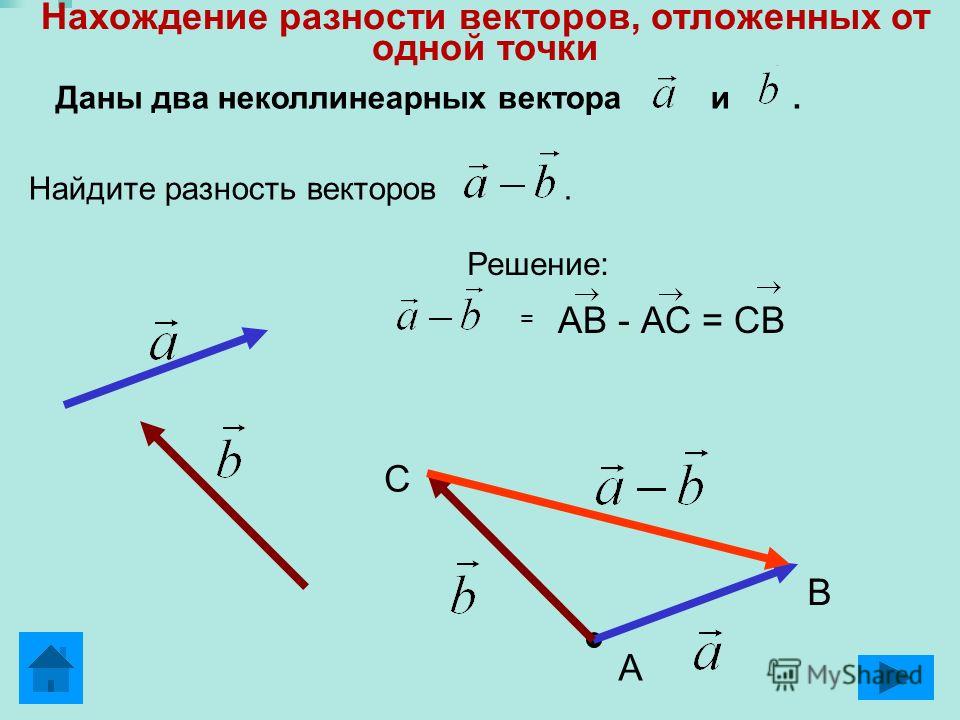 998, -2,998, -2,998, -2,998, -2,998, 0,784, -0,588).
998, -2,998, -2,998, -2,998, -2,998, 0,784, -0,588).
Итак, векторное произведение векторов a и b в форме вектора-строки (-0,999, 3,998, -1,998). Округлив эти числа в большую сторону, мы получим (-1, 4, -2). Это компоненты вектора c x , c y и c z , к которым мы пришли ранее. Обратите внимание, что поскольку n является единичным вектором (т. е. его величина равна одной единице), его единственной целью в уравнении является определение направления вектора векторного произведения. Это должно быть любое из двух направлений, перпендикулярных обоим векторам a и вектор b были выбраны с использованием правила правой руки . Очевидно, чтобы использовать это уравнение для получения вектора c , нам нужно знать величины векторов a и b , значение угла θ и значения x , y и z компоненты вектора n .

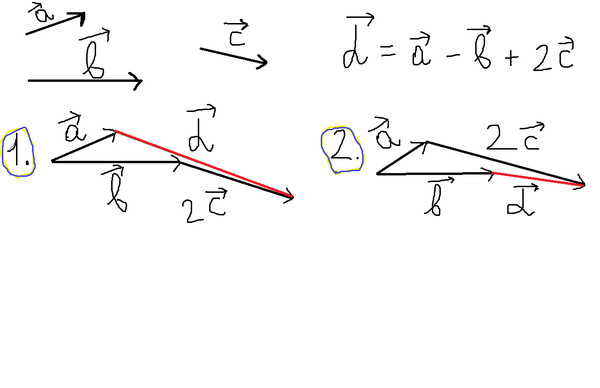 Наконец, студент поворачивает налево и проезжает еще 2,0 км на север. Какова величина общего перемещения студента?
Наконец, студент поворачивает налево и проезжает еще 2,0 км на север. Какова величина общего перемещения студента?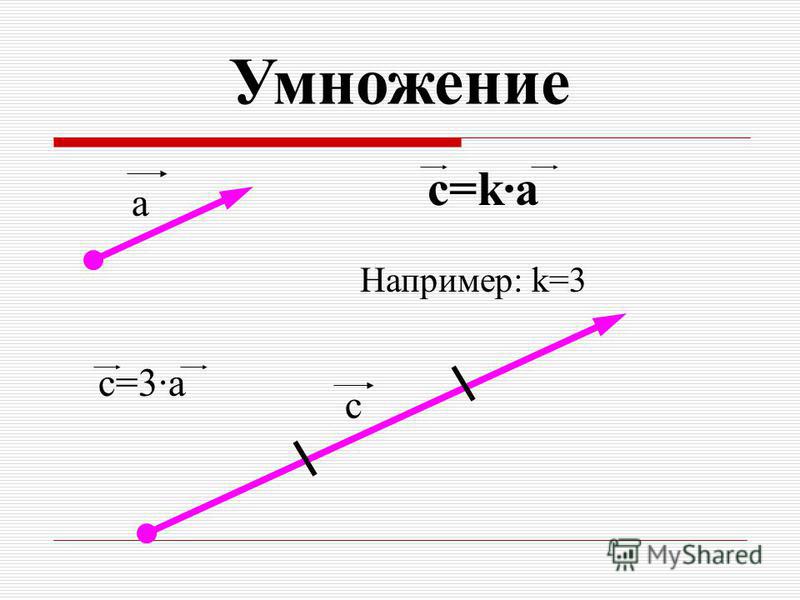 Они снова поворачивают направо и проходят 24 метра на север. Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения?
Они снова поворачивают направо и проходят 24 метра на север. Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения?