Описание алгоритма
Или же R унитарное кольцо и и B квадратные матрицы размера п , коэффициенты которого являются элементами набора , лежащим в основе R . Для простоты мы рассматриваем случай, когда n является степенью двойки. Мы всегда можем свести себя к этому случаю, возможно добавив столбцы и строки нулей. Алгоритм Штрассен может вычислить матричный продукт C .
Три матрицы A , B и C разделены на матрицы блоками одинакового размера:
- Взнак равно[В1,1В1,2В2,1В2,2] , Bзнак равно[B1,1B1,2B2,1B2,2] , ПРОТИВзнак равно[ПРОТИВ1,1ПРОТИВ1,2ПРОТИВ2,1ПРОТИВ2,2]{\ displaystyle \ mathbf {A} = {\ begin {bmatrix} \ mathbf {A} _ {1,1} & \ mathbf {A} _ {1,2} \\\ mathbf {A} _ {2,1 } & \ mathbf {A} _ {2,2} \ end {bmatrix}} {\ mbox {,}} \ mathbf {B} = {\ begin {bmatrix} \ mathbf {B} _ {1,1} & \ mathbf {B} _ {1,2} \\\ mathbf {B} _ {2,1} & \ mathbf {B} _ {2,2} \ end {bmatrix}} {\ mbox {,}} \ mathbf {C} = {\ begin {bmatrix} \ mathbf {C} _ {1,1} & \ mathbf {C} _ {1,2} \\\ mathbf {C} _ {2,1} & \ mathbf {C} _ {2,2} \ end {bmatrix}}}
или же
- Вя,j,Bя,j,ПРОТИВя,j∈Fнет/2×Fнет/2.
 {n / 2}.}
{n / 2}.}
Тогда у нас есть
- ПРОТИВ1,1знак равноВ1,1B1,1+В1,2B2,1{\ displaystyle \ mathbf {C} _ {1,1} = \ mathbf {A} _ {1,1} \ mathbf {B} _ {1,1} + \ mathbf {A} _ {1,2} \ mathbf {B} _ {2,1}}
- ПРОТИВ1,2знак равноВ1,1B1,2+В1,2B2,2{\ displaystyle \ mathbf {C} _ {1,2} = \ mathbf {A} _ {1,1} \ mathbf {B} _ {1,2} + \ mathbf {A} _ {1,2} \ mathbf {B} _ {2,2}}
- ПРОТИВ2,1знак равноВ2,1B1,1+В2,2B2,1{\ displaystyle \ mathbf {C} _ {2,1} = \ mathbf {A} _ {2,1} \ mathbf {B} _ {1,1} + \ mathbf {A} _ {2,2} \ mathbf {B} _ {2,1}}
- ПРОТИВ2,2знак равноВ2,1B1,2+В2,2B2,2{\ displaystyle \ mathbf {C} _ {2,2} = \ mathbf {A} _ {2,1} \ mathbf {B} _ {1,2} + \ mathbf {A} _ {2,2} \ mathbf {B} _ {2,2}}
Этот метод требует 8 умножений матриц для вычисления C i, j , как в классическом произведении.
Сила алгоритма Штрассена заключается в наборе из семи новых матриц M i, которые будут использоваться для выражения C i, j всего с 7 умножениями вместо 8:
- M1знак равно(В1,1+В2,2)(B1,1+B2,2){\ displaystyle \ mathbf {M} _ {1}: = (\ mathbf {A} _ {1,1} + \ mathbf {A} _ {2,2}) (\ mathbf {B} _ {1,1 } + \ mathbf {B} _ {2,2})}
- M2знак равно(В2,1+В2,2)B1,1{\ Displaystyle \ mathbf {M} _ {2}: = (\ mathbf {A} _ {2,1} + \ mathbf {A} _ {2,2}) \ mathbf {B} _ {1,1} }
- M3знак равноВ1,1(B1,2-B2,2){\ displaystyle \ mathbf {M} _ {3}: = \ mathbf {A} _ {1,1} (\ mathbf {B} _ {1,2} — \ mathbf {B} _ {2,2}) }
- M4знак равноВ2,2(B2,1-B1,1){\ displaystyle \ mathbf {M} _ {4}: = \ mathbf {A} _ {2,2} (\ mathbf {B} _ {2,1} — \ mathbf {B} _ {1,1}) }
- M5знак равно(В1,1+В1,2)B2,2{\ Displaystyle \ mathbf {M} _ {5}: = (\ mathbf {A} _ {1,1} + \ mathbf {A} _ {1,2}) \ mathbf {B} _ {2,2} }
- M6знак равно(В2,1-В1,1)(B1,1+B1,2){\ displaystyle \ mathbf {M} _ {6}: = (\ mathbf {A} _ {2,1} — \ mathbf {A} _ {1,1}) (\ mathbf {B} _ {1,1 } + \ mathbf {B} _ {1,2})}
- M7знак равно(В1,2-В2,2)(B2,1+B2,2){\ Displaystyle \ mathbf {M} _ {7}: = (\ mathbf {A} _ {1,2} — \ mathbf {A} _ {2,2}) (\ mathbf {B} _ {2,1 } + \ mathbf {B} _ {2,2})}
Тогда C i, j выражаются как
- ПРОТИВ1,1знак равноM1+M4-M5+M7{\ displaystyle \ mathbf {C} _ {1,1} = \ mathbf {M} _ {1} + \ mathbf {M} _ {4} — \ mathbf {M} _ {5} + \ mathbf {M} _ {7}}
- ПРОТИВ1,2знак равноM3+M5{\ Displaystyle \ mathbf {C} _ {1,2} = \ mathbf {M} _ {3} + \ mathbf {M} _ {5}}
- ПРОТИВ2,1знак равноM2+M4{\ Displaystyle \ mathbf {C} _ {2,1} = \ mathbf {M} _ {2} + \ mathbf {M} _ {4}}
- ПРОТИВ2,2знак равноM1-M2+M3+M6{\ displaystyle \ mathbf {C} _ {2,2} = \ mathbf {M} _ {1} — \ mathbf {M} _ {2} + \ mathbf {M} _ {3} + \ mathbf {M} _ {6}}
Процесс повторяется рекурсивно до тех пор, пока матрицы A и B не станут «маленькими». (Де) Фолькер Штрассен, « Исключение Гаусса не оптимально » , Numerische Mathematik , vol. 13,, стр. 354-356.
(Де) Фолькер Штрассен, « Исключение Гаусса не оптимально » , Numerische Mathematik , vol. 13,, стр. 354-356.
 112 .
112 .Библиография
(ru) Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Штайн , Введение в алгоритмы , MIT Press и McGraw-Hill ,, 2- е изд. [ деталь издания ], гл. 31, раздел 31.2 (« Алгоритм Штрассена для умножения матриц »), с. 739-745 .
Внешние ссылки
- (en) Эрик В. Вайстейн , « Формулы Штрассена » , на сайте MathWorld.
- (ru) Анализ алгоритма Штрассена с использованием Maple
- Жерар Сукахет, алгоритм В.
 Штрассена для быстрого умножения матриц
Штрассена для быстрого умножения матриц
Умножение | |||||
|---|---|---|---|---|---|
| |||||
| Характеристики |
| ||||
| Примеры |
| ||||
| Алгоритмы умножения |
| ||||
| Алгоритмы верификации |
| ||||
<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Алгоритм умножения матриц
| Нерешенная проблема в информатике: Какой алгоритм умножения матриц самый быстрый? (больше нерешенных проблем в информатике) |
Потому что матричное умножение такая центральная операция во многих численные алгоритмы, много работы было вложено в создание алгоритмы матричного умножения эффективный. Применение матричного умножения в вычислительных задачах можно найти во многих областях, включая научные вычисления и распознавание образов и в, казалось бы, не связанных между собой задачах, таких как подсчет путей через график.[1] Для умножения матриц на различных типах оборудования было разработано множество различных алгоритмов, включая параллельно и распределен системы, в которых вычислительная работа распределяется между несколькими процессорами (возможно, по сети).
Непосредственное применение математического определения умножения матриц дает алгоритм, который занимает время в порядке п3 умножить два п × п матрицы (Θ (п3) в нотация большой O ).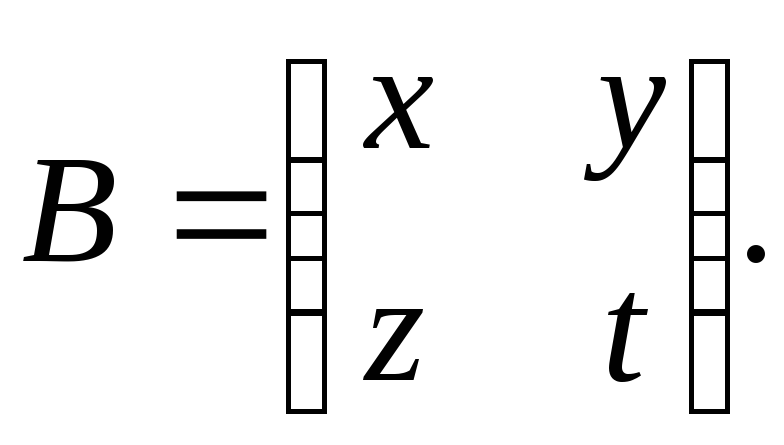 Лучшие асимптотические оценки времени, необходимого для умножения матриц, были известны со времен работы Штрассена в 1960-х годах, но до сих пор неизвестно, каково оптимальное время (т.е. сложность проблемы является).
Лучшие асимптотические оценки времени, необходимого для умножения матриц, были известны со времен работы Штрассена в 1960-х годах, но до сих пор неизвестно, каково оптимальное время (т.е. сложность проблемы является).
Содержание
- 1 Итерационный алгоритм
- 1.1 Поведение кеша
- 2 Алгоритм разделяй и властвуй
- 2.1 Неквадратные матрицы
- 2.2 Поведение кеша
- 3 Субкубические алгоритмы
- 4 Параллельные и распределенные алгоритмы
- 4.1 Параллелизм с общей памятью
- 4.2 Распределенные алгоритмы предотвращения общения
- 4.3 Алгоритмы для сеток
- 5 Смотрите также
- 6 использованная литература
- 7 дальнейшее чтение
Итерационный алгоритм
В определение умножения матриц это если C = AB для п × м матрица А и м × п матрица B, тогда C является п × п матрица с записями
- cяj=∑k=1маяkбkj{displaystyle c_ {ij} = sum _ {k = 1} ^ {m} a_ {ik} b_ {kj}}.

Исходя из этого, можно построить простой алгоритм, который перебирает индексы я с 1 по п и j с 1 по п, вычисляя указанное выше, используя вложенный цикл:
- Вход: матрицы А и B
- Позволять C быть новой матрицей подходящего размера
- Для я от 1 до п:
- Для j от 1 до п:
- Позволять сумма = 0
- Для k от 1 до м:
- Набор сумма ← сумма + Аik × BкДж
- Набор Cij ← сумма
- Для j от 1 до п:
- Вернуть C
Этот алгоритм занимает время Θ (nmp) (в асимптотическая запись ).[1] Обычное упрощение с целью анализ алгоритмов предполагает, что все входные данные представляют собой квадратные матрицы размера п × п, в этом случае время работы Θ (п3), т.е. кубический по размеру измерения.[2]
Поведение кеша
Иллюстрация порядка строк и столбцов
Три цикла в итеративном умножении матриц можно произвольно менять местами без влияния на правильность или асимптотическое время выполнения. Однако порядок может существенно повлиять на практические характеристики из-за шаблоны доступа к памяти и тайник использование алгоритма;[1]какой порядок лучше, также зависит от того, хранятся ли матрицы в рядовой порядок, порядок столбцов или их сочетание.
Однако порядок может существенно повлиять на практические характеристики из-за шаблоны доступа к памяти и тайник использование алгоритма;[1]какой порядок лучше, также зависит от того, хранятся ли матрицы в рядовой порядок, порядок столбцов или их сочетание.
В частности, в идеализированном случае полностью ассоциативный кеш состоящий из M байты и б байтов на строку кэша (т.е. M/б строки кэша), приведенный выше алгоритм не является оптимальным для А и B хранятся в строчном порядке. Когда п > M/б, каждая итерация внутреннего цикла (одновременное прохождение строки А и столбец B) вызывает промах в кэше при доступе к элементу B. Это означает, что алгоритм требует Θ (п3) кеш промахивается в худшем случае. По состоянию на 2010 г., скорость памяти по сравнению со скоростью процессоров такова, что промахи в кэше, а не фактические вычисления, доминируют во времени работы для значительных матриц.[3]
Оптимальный вариант итерационного алгоритма для А и B в строчном макете — это выложенный плиткой версия, где матрица неявно разделена на квадратные плитки размером √M от √M:[3][4]
- Вход: матрицы А и B
- Позволять C быть новой матрицей подходящего размера
- Выберите размер плитки Т = Θ (√M)
- Для я от 1 до п в шагах от Т:
- Для J от 1 до п в шагах от Т:
- Для K от 1 до м в шагах от Т:
- Умножить Ая:я+Т, K:K+Т и BK:K+Т, J:J+Т в Cя:я+Т, J:J+Т, это:
- Для я от я к мин (я + Т, п):
- Для j от J к мин (J + Т, п):
- Позволять сумма = 0
- Для k от K к мин (K + Т, м):
- Набор сумма ← сумма + Аik × BкДж
- Набор Cij ← Cij + сумма
- Для j от J к мин (J + Т, п):
- Для K от 1 до м в шагах от Т:
- Для J от 1 до п в шагах от Т:
- Вернуть C
В идеализированной модели кэша этот алгоритм требует только Θ (п3/б √M) промахи в кэше; делитель б √M составляет несколько порядков на современных машинах, так что фактические вычисления преобладают над временем выполнения, а не промахами в кэше. [3]
[3]
Алгоритм разделяй и властвуй
Альтернативой итерационному алгоритму является разделяй и властвуй алгоритм для матричного умножения. Это зависит от блочное разбиение
- C=(C11C12C21C22),А=(А11А12А21А22),B=(B11B12B21B22){displaystyle C = {egin {pmatrix} C_ {11} & C_ {12} C_ {21} & C_ {22} end {pmatrix}} ,, A = {egin {pmatrix} A_ {11} & A_ {12} A_ {21} & A_ {22} end {pmatrix}} ,, B = {egin {pmatrix} B_ {11} & B_ {12} B_ {21} & B_ {22} end {pmatrix}}},
который работает для всех квадратных матриц, размерность которых равна степени двойки, т.е. 2п × 2п для некоторых п. Матричный продукт теперь
- (C11C12C21C22)=(А11А12А21А22)(B11B12B21B22)=(А11B11+А12B21А11B12+А12B22А21B11+А22B21А21B12+А22B22){displaystyle {egin {pmatrix} C_ {11} & C_ {12} C_ {21} & C_ {22} end {pmatrix}} = {egin {pmatrix} A_ {11} & A_ {12} A_ {21} & A_ {22} end {pmatrix}} {egin {pmatrix} B_ {11} & B_ {12} B_ {21} & B_ {22} end {pmatrix}} = {egin {pmatrix} A_ {11} B_ {11 } + A_ {12} B_ {21} & A_ {11} B_ {12} + A_ {12} B_ {22} A_ {21} B_ {11} + A_ {22} B_ {21} & A_ {21} B_ {12} + A_ {22} B_ {22} end {pmatrix}}}
который состоит из восьми умножений пар подматриц с последующим этапом сложения. {2})},
{2})},
учет восьми рекурсивных вызовов матриц размера п/2 и Θ (п2) для поэлементного суммирования четырех пар полученных матриц. Применение основная теорема для повторений «разделяй и властвуй» показывает эту рекурсию, чтобы получить решение Θ (п3), так же, как итерационный алгоритм.[2]
Неквадратные матрицы
Вариант этого алгоритма, который работает для матриц произвольной формы и быстрее на практике[3] разбивает матрицы на две вместо четырех подматриц следующим образом.[5]Разделение матрицы теперь означает разделение ее на две части равного размера или как можно более близких к равным размерам в случае нечетных размеров.
- Входы: матрицы А размера п × м, B размера м × п.
- Базовый случай: если Максимум(п, м, п) ниже некоторого порога, используйте развернутый версия итерационного алгоритма.
- Рекурсивные случаи:
- Если Максимум(п, м, п) = п, Трещина А горизонтально:
- C=(А1А2)B=(А1BА2B){displaystyle C = {egin {pmatrix} A_ {1} A_ {2} end {pmatrix}} {B} = {egin {pmatrix} A_ {1} B A_ {2} Bend {pmatrix}}}
- Иначе, если Максимум(п, м, п) = п, Трещина B вертикально:
- C=А(B1B2)=(АB1АB2){displaystyle C = A {egin {pmatrix} B_ {1} & B_ {2} end {pmatrix}} = {egin {pmatrix} AB_ {1} & AB_ {2} end {pmatrix}}}
- В противном случае, Максимум(п, м, п) = м.
 Трещина А вертикально и B горизонтально:
Трещина А вертикально и B горизонтально:
- В противном случае, Максимум(п, м, п) = м.
- C=(А1А2)(B1B2)=А1B1+А2B2{displaystyle C = {egin {pmatrix} A_ {1} & A_ {2} end {pmatrix}} {egin {pmatrix} B_ {1} B_ {2} end {pmatrix}} = A_ {1} B_ {1} + A_ {2} B_ {2}}
Поведение кеша
Частота промахов в кэше рекурсивного умножения матриц такая же, как у выложенный плиткой итерационная версия, но в отличие от этого алгоритма рекурсивный алгоритм не обращающий внимания на тайник:[5] нет параметра настройки, необходимого для получения оптимальной производительности кеша, и он хорошо себя ведет в мультипрограммирование среда, в которой размеры кэша фактически динамичны из-за того, что другие процессы занимают кеш-пространство.[3](Простой итерационный алгоритм также не учитывает кеш, но на практике он намного медленнее, если макет матрицы не адаптирован к алгоритму.)
Количество промахов в кэше, вызванных этим алгоритмом на машине с M строки идеального кэша, каждая размером б байтов, ограничено[5]:13
- Θ(м+п+п+мп+пп+мпб+мппбM){displaystyle Theta left (m + n + p + {frac {mn + np + mp} {b}} + {frac {mnp} {b {sqrt {M}}}} ight)}
Субкубические алгоритмы
Низший ω такое, что умножение матриц, как известно, О(пω), построенный против времени. {2.807})}. Алгоритм Штрассена более сложен, и числовая стабильность уменьшается по сравнению с наивным алгоритмом,[6]но это быстрее в случаях, когда п > 100 или так[1] и присутствует в нескольких библиотеках, таких как BLAS.[7] Это очень полезно для больших матриц в точных областях, таких как конечные поля, где числовая стабильность не является проблемой.
{2.807})}. Алгоритм Штрассена более сложен, и числовая стабильность уменьшается по сравнению с наивным алгоритмом,[6]но это быстрее в случаях, когда п > 100 или так[1] и присутствует в нескольких библиотеках, таких как BLAS.[7] Это очень полезно для больших матриц в точных областях, таких как конечные поля, где числовая стабильность не является проблемой.
Электрический ток О(пk) алгоритм с наименьшим известным показателем k является обобщением Алгоритм Копперсмита – Винограда имеющая асимптотическую сложность О(п2.3728639), автор Франсуа Ле Галль.[8] Алгоритм Ле Галля и алгоритм Копперсмита – Винограда, на котором он основан, похожи на алгоритм Штрассена: изобретен способ умножения двух k × k-матрицы с числом меньше k3 умножения, и этот метод применяется рекурсивно. Однако постоянный коэффициент, скрытый Обозначение Big O настолько велик, что эти алгоритмы имеют смысл только для матриц, которые слишком велики для обработки на современных компьютерах. [9][10]
[9][10]
Поскольку любой алгоритм умножения двух п × п-матрицы должны обрабатывать все 2п2 элементов, существует асимптотическая нижняя оценка Ω (п2) операции. Раз доказал нижнюю оценку Ω (п2 журнал(п)) для арифметических схем с ограниченными коэффициентами над действительными или комплексными числами.[11]
Кон и другие. использовать такие методы, как алгоритмы Штрассена и Копперсмита – Винограда, в совершенно ином теоретико-групповой контекста, используя тройки подмножеств конечных групп, которые удовлетворяют свойству дизъюнктности, называемому свойство тройного продукта (TPP). Они показывают, что если семьи венки из Абелевы группы с симметричными группами реализуют семейства троек подмножеств с одновременной версией TPP, тогда существуют алгоритмы умножения матриц с существенно квадратичной сложностью.[12][13] Большинство исследователей считают, что это действительно так. [10] Однако Алон, Шпилка и Крис Уманс недавно показали, что некоторые из этих гипотез, предполагающих быстрое матричное умножение, несовместимы с другой правдоподобной гипотезой, догадка подсолнечника.[14]
[10] Однако Алон, Шпилка и Крис Уманс недавно показали, что некоторые из этих гипотез, предполагающих быстрое матричное умножение, несовместимы с другой правдоподобной гипотезой, догадка подсолнечника.[14]
Алгоритм Фрейвальдса это простой Алгоритм Монте-Карло что, учитывая матрицы А, B и C, проверяет в Θ (п2) время, если AB = C.
Параллельные и распределенные алгоритмы
Параллелизм с общей памятью
В разделяй и властвуй алгоритм набросал ранее может быть распараллеленный двумя способами для мультипроцессоры с общей памятью. Они основаны на том факте, что восемь рекурсивных матричных умножений в
- (А11B11+А12B21А11B12+А12B22А21B11+А22B21А21B12+А22B22){displaystyle {egin {pmatrix} A_ {11} B_ {11} + A_ {12} B_ {21} & A_ {11} B_ {12} + A_ {12} B_ {22} A_ {21} B_ {11}) + A_ {22} B_ {21} и A_ {21} B_ {12} + A_ {22} B_ {22} end {pmatrix}}}
могут выполняться независимо друг от друга, как и четыре суммирования (хотя алгоритм должен «соединить» умножения перед выполнением суммирования). Используя полный параллелизм задачи, можно получить алгоритм, который может быть выражен в виде вилка – стиль соединения псевдокод:[15]
Используя полный параллелизм задачи, можно получить алгоритм, который может быть выражен в виде вилка – стиль соединения псевдокод:[15]
Процедура умножить (C, А, B):
- Базовый случай: если п = 1, набор c11 ← а11 × б11 (или умножьте небольшую блочную матрицу).
- В противном случае выделите место для новой матрицы Т формы п × п, тогда:
- Раздел А в А11, А12, А21, А22.
- Раздел B в B11, B12, B21, B22.
- Раздел C в C11, C12, C21, C22.
- Раздел Т в Т11, Т12, Т21, Т22.
- Параллельное исполнение:
- Вилка умножить (C11, А11, B11).

- Вилка умножить (C12, А11, B12).
- Вилка умножить (C21, А21, B11).
- Вилка умножить (C22, А21, B12).
- Вилка умножить (Т11, А12, B21).
- Вилка умножить (Т12, А12, B22).
- Вилка умножить (Т21, А22, B21).
- Вилка умножить (Т22, А22, B22).
- Вилка умножить (C11, А11, B11).
- Присоединиться (дождитесь завершения параллельных вилок).
- Добавить(C, Т).
- Освободить Т.
Процедура Добавить(C, Т) добавляет Т в C, поэлементно:
- Базовый случай: если п = 1, набор c11 ← c11 + т11 (или сделайте короткий цикл, возможно, развернутый).

- В противном случае:
- Раздел C в C11, C12, C21, C22.
- Раздел Т в Т11, Т12, Т21, Т22.
- В параллели:
- Вилка Добавить(C11, Т11).
- Вилка Добавить(C12, Т12).
- Вилка Добавить(C21, Т21).
- Вилка Добавить(C22, Т22).
- Присоединиться.
Вот, вилка — ключевое слово, которое сигнализирует, что вычисление может выполняться параллельно с остальной частью вызова функции, а присоединиться ожидает завершения всех ранее «разветвленных» вычислений. раздел достигает своей цели только манипуляциями с указателями.
Этот алгоритм имеет длина критического пути из Θ (журнал2п) шагов, то есть на идеальной машине с бесконечным количеством процессоров требуется столько времени; следовательно, он имеет максимально возможное ускорение из Θ (п3/журнал2п) на любом реальном компьютере. Алгоритм непрактичен из-за затрат на связь, связанных с перемещением данных во временную матрицу и из нее. Т, но в более практичном варианте достигается Θ (п2) ускорение без использования временной матрицы.[15]
Алгоритм непрактичен из-за затрат на связь, связанных с перемещением данных во временную матрицу и из нее. Т, но в более практичном варианте достигается Θ (п2) ускорение без использования временной матрицы.[15]
Блочное умножение матриц. В 2D-алгоритме каждый процессор отвечает за одну подматрицу C. В 3D-алгоритме каждая пара подматриц из А и B то, что умножается, назначается одному процессору.
Распределенные алгоритмы предотвращения общения
В современных архитектурах с иерархической памятью стоимость загрузки и хранения элементов матрицы ввода имеет тенденцию преобладать над затратами на арифметику. На одной машине это объем данных, передаваемых между ОЗУ и кешем, тогда как на многоузловой машине с распределенной памятью это объем, передаваемый между узлами; в любом случае это называется пропускная способность связи. Наивный алгоритм, использующий три вложенных цикла, использует Ω (п3) пропускная способность связи.
Алгоритм Кэннона, также известный как 2D алгоритм, это алгоритм предотвращения общения который разбивает каждую входную матрицу на блочную матрицу, элементы которой являются подматрицами размера √M/3 от √M/3, где M это размер быстрой памяти.[16] Затем наивный алгоритм используется над блочными матрицами, вычисляя продукты подматриц полностью в быстрой памяти. Это снижает пропускную способность связи до О(п3/√M), что является асимптотически оптимальным (для алгоритмов, выполняющих Ω (п3) вычисление).[17][18]
В распределенной среде с п процессоры расположены в √п от √п 2D-сетка, одна подматрица результата может быть назначена каждому процессору, и произведение может быть вычислено с каждым процессором, передающим О(п2/√п) слов, что является асимптотически оптимальным при условии, что каждый узел хранит минимум О(п2/п) элементы. [18] Это можно улучшить с помощью 3D алгоритм, который объединяет процессоры в трехмерную кубическую сетку, назначая каждое произведение двух входных подматриц одному процессору. Затем подматрицы результатов генерируются путем сокращения по каждой строке.[19] Этот алгоритм передает О(п2/п2/3) слов на процессор, что является асимптотически оптимальным.[18] Однако это требует репликации каждого элемента входной матрицы. п1/3 раз, и поэтому требуется фактор п1/3 больше памяти, чем необходимо для хранения входных данных. Этот алгоритм можно комбинировать со Strassen для дальнейшего сокращения времени выполнения.[19] Алгоритмы «2.5D» обеспечивают постоянный компромисс между использованием памяти и пропускной способностью связи.[20] В современных распределенных вычислительных средах, таких как Уменьшение карты, разработаны специализированные алгоритмы умножения.
[18] Это можно улучшить с помощью 3D алгоритм, который объединяет процессоры в трехмерную кубическую сетку, назначая каждое произведение двух входных подматриц одному процессору. Затем подматрицы результатов генерируются путем сокращения по каждой строке.[19] Этот алгоритм передает О(п2/п2/3) слов на процессор, что является асимптотически оптимальным.[18] Однако это требует репликации каждого элемента входной матрицы. п1/3 раз, и поэтому требуется фактор п1/3 больше памяти, чем необходимо для хранения входных данных. Этот алгоритм можно комбинировать со Strassen для дальнейшего сокращения времени выполнения.[19] Алгоритмы «2.5D» обеспечивают постоянный компромисс между использованием памяти и пропускной способностью связи.[20] В современных распределенных вычислительных средах, таких как Уменьшение карты, разработаны специализированные алгоритмы умножения. [21]
[21]
Алгоритмы для сеток
Умножение матриц выполнено за 2n-1 шагов для двух матриц размера n × n на перекрестной сетке.
Существует множество алгоритмов умножения на сетки. Для умножения двух п×п на стандартной двумерной сетке с использованием 2D Алгоритм Кэннона, можно завершить умножение на 3п-2 шага, хотя при повторных вычислениях это число уменьшается вдвое.[22] Стандартный массив неэффективен, потому что данные из двух матриц не поступают одновременно, и он должен быть дополнен нулями.
Результат будет еще быстрее на двухслойной сетке с перекрестной связью, где всего 2пТребуется -1 шаг.[23] Производительность улучшается еще больше для повторных вычислений, что приводит к 100% эффективности.[24] Сетчатый массив с перекрестными связями можно рассматривать как частный случай неплоской (то есть многослойной) структуры обработки.[25]
Смотрите также
- Вычислительная сложность математических операций
- Алгоритм CYK, алгоритм §Valiant
- Умножение матричной цепочки
- Умножение разреженной матрицы на вектор
использованная литература
- ^ а б c d Скиена, Стивен (2008).
 Как, S (1988). «Многослойные массивные вычисления». Информационные науки. 45 (3): 347–365. CiteSeerX 10.1.1.90.4753. Дои:10.1016/0020-0255(88)90010-2.
Как, S (1988). «Многослойные массивные вычисления». Информационные науки. 45 (3): 347–365. CiteSeerX 10.1.1.90.4753. Дои:10.1016/0020-0255(88)90010-2.
дальнейшее чтение
- Буттари, Альфредо; Лангу, Жюльен; Курзак, Якуб; Донгарра, Джек (2009). «Класс параллельных мозаичных алгоритмов линейной алгебры для многоядерных архитектур». Параллельные вычисления. 35: 38–53. arXiv:0709.1272. Дои:10.1016 / j.parco.2008.10.002. S2CID 955.
- Гото, Казушигэ; ван де Гейн, Роберт А. (2008). «Анатомия высокопроизводительного матричного умножения». Транзакции ACM на математическом ПО. 34 (3): 1–25. CiteSeerX 10.1.1.140.3583. Дои:10.1145/1356052.1356053. S2CID 9359223.
- Van Zee, Field G .; ван де Гейн, Роберт А. (2015). «BLIS: структура для быстрого создания экземпляра функциональности BLAS». Транзакции ACM на математическом ПО. 41 (3): 1–33. Дои:10.1145/2764454. S2CID 1242360.

- Как оптимизировать GEMM
Алгоритм Штрассена
Алгоритм Штрассена.
Содержание
1 | Вступление и постановка задачи | 2 |
2 | Алгоритм Штрассена | 2 |
3 | Умножение матриц по определению, встроенная функция |
|
| matmul и оптимизация | 4 |
4 | Реализация алгоритма | 8 |
1
1Вступление и постановка задачи
Одна из главных задач данной работы — реализовать алгоритм Штрассена. Это рекурсивный алгоритм для умножения матриц, который позволяет значительно ускорить процесс умножения. Надо заметить, что данный алгоритм эффективен только для матриц достаточно большого размера. Определить размер матриц, с которого имеет смысл начинать умножать по алгоритму Штрассена, можно экспериментальным путем.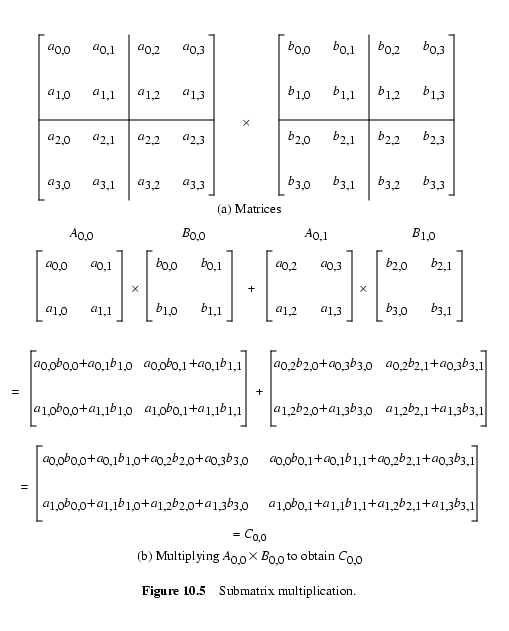 Кроме того, я уже упоминала, что алгоритм является рекурсивным. В нерекурсивной ветви алгоритма используется «простое»умножение матриц, т.е. умножение по определению. Сделать нерекурсивную ветвь наиболее эффективной и организовать выход из рекурсии в нужный момент — еще одна задача моей работы.
Кроме того, я уже упоминала, что алгоритм является рекурсивным. В нерекурсивной ветви алгоритма используется «простое»умножение матриц, т.е. умножение по определению. Сделать нерекурсивную ветвь наиболее эффективной и организовать выход из рекурсии в нужный момент — еще одна задача моей работы.
Итак, наметим цели работы:
Реализовать алгоритм Штрассена;
Экспериментально найти размер матрицы, для которого следует переходить на умножение по алгоритму;
Организовать выход из рекурсии в нужный момент;
Сделать не рекурсивную ветвь наиболее эффективной.
2Алгоритм Штрассена
Самая затратная по времени операция — умножение. Т.е. чтобы ускорить процесс, нужно сократить их число. Штрассен придумал алгоритм [1, 2, 3], который позволяет избежать одного умножения. Замечательно, что формулы не требуют коммутативности сложения, т.е. они приминимы и для матриц, что позволяет применять алгоритм рекурсивно.
Алгоритм работает с квадратными матрицами размера 2n.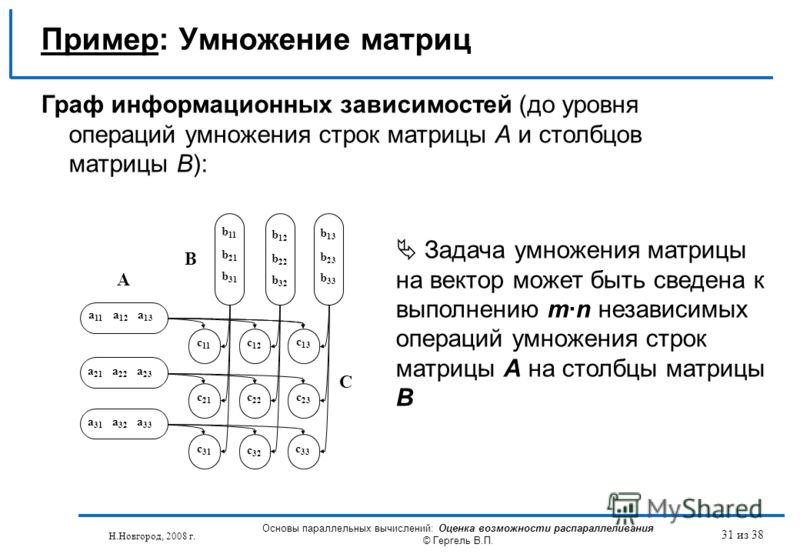 Заметим, что для умножения матриц такого размера требуется 23n умножений. Если же матрицы не квадратные, то можно расширить их до нужного размера, заполнив недостающие строки и столбцы нулями. Допустим, есть две матрицы A и B размера 2n, которые требуется перемножить: C = AB. Разобьем каждую матрицу на четыре подматрицы:
Заметим, что для умножения матриц такого размера требуется 23n умножений. Если же матрицы не квадратные, то можно расширить их до нужного размера, заполнив недостающие строки и столбцы нулями. Допустим, есть две матрицы A и B размера 2n, которые требуется перемножить: C = AB. Разобьем каждую матрицу на четыре подматрицы:
A2;1 | A2;2 | B2;1 | B2;2 | = | C2;1 | C2;2 |
|
A1;1 | A1;2 | B1;1 | B1;2 |
| C1;1 | C1;2 |
|
2
Тогда матрицы Ai;j и Bi;j имеют размер 2n 1. А элементы матрицы можно вычислить следующим образом:
C1;1 = A1;1B1;1 + A1;2B2;1
C1;2 = A1;1B1;2 + A1;2B2;2
C2;1 = A2;1B1;1 + A2;2B2;1
C2;2 = A2;1B1;2 + A2;2B2;2
Но в этом случае мы не уменьшили количество умножений, т. к. каждое уравнение требует двух умножений матриц размера 2n 1. А на каждом шаге рекурсии умножений получится восемь.
к. каждое уравнение требует двух умножений матриц размера 2n 1. А на каждом шаге рекурсии умножений получится восемь.
Штрассен ввел семь новых элементов, которые вычисляются с помощью одного умножения, а матрица C получается из них сложением или вычитанием. Определим эти семь элементов:
M1 = (A1;1 + A2;2)(B1;1 + B2;2)
M2 = (A2;1 + A2;2)B1;1
M3 = A1;1(B1;2 B2;2)
M4 = A2;2(B2;1 B1;1)
M5 = (A1;1 + A1;2)B2;2
M6 = (A2;1 A1;1)(B1;1 + B1;2)
M7 = (A1;2 A2;2)(B2;1 + B2;2)
Элементы матрицы C вычисляются по формулам:
C1;1 = M1 + M4 M5 + M7
C1;2 = M3 + M5
C2;1 = M2 + M4
C2;2 = M1 M2 + M3 + M6
Теперь на каждом этапе рекурсии требуется выполнять только семь умножений вместо восьми. Предполагается, что итерационный процесс продолжается 2n раз, до тех пор, пока матрицы Ci;j не выродятся в числа. Заметим, что для маленьких матриц алгоритм теряет свою эффективность. Также этот алгоритм не имеет большой устойчивости [3], т. е. для вещественных матриц, в случае, если нужна очень высокая точность, не
е. для вещественных матриц, в случае, если нужна очень высокая точность, не
3
стоит умножать по Штрассену. Этот существенный минус легко объяснить большим количесвом сложений и вычитаний. Но для целочисленных матриц, конечно, проблемы не возникает.
Рекурсивный алгоритм Штрассена умножает две матрицы за время (n2:81) [1], тогда как простое умножение справляется с этой задачей за (n3). Для матриц большого размера(начиная примерно с 2000) эта разница существенна.
3Умножение матриц по определению, встроенная функция matmul и оптимизация
В этом разделе пойдет речь об умножении матриц без помощи алгоритма Штрассена. Прежде чем приступать непосредственно к алгоритму, нужно выяснить, нельзя ли ускорить процесс умножения с помощью других возможностей фортрана. Также в фортране есть специальная встроенная функция matmul, которая возвращает результат умножения двух матриц. Каким образом эта функция производит умножение, неизвестно. Попробуем написать код для умножения матриц по опредлению. Пусть A и B — умножаемые матрицы, а C — их произведение.
Пусть A и B — умножаемые матрицы, а C — их произведение.
do i = 1, N
do j = 1, N C (i , j) = 0
do k = 1, N
C(i , j) = C(i , j) + A(i , k )* B(k , j)
end do
end do
end do
Назовем такой вариант def mul. Посмотрим, как быстро умножает матрицы matmul и как медленно происходит умножение по определению. В первой строке таблицы указан размер умножаемых матриц, во второй — время, за которое умножает matmul, а втретьей — время умножения по определению. Время указано в секундах, т.о. матрицы размера 2048 умножаются в первом случае — за 13 секунд, а во втором — за 15 минут!
| size | 128 | 256 | 512 | 1024 | 2048 |
| matmul | 4.00000019E-03 | 2.00009998E-02 | 0.21601403 | 1.7041068 | 13.596855 |
| def mul | 2. | 0.28801799 | 6.7804241 | 98.874176 | 900.42432 |
Откуда возникает такая разница? В фортране обращение к элементам массива происходит по столбцам [4]. Т.е., к примеру, чтобы обратиться к первому элементу пятого столбца, компилятор сначала просчитает все впереди стоящие элементы по столбцам. Значит, имеет смысл попробовать переписать умножение так, чтобы индекс столбца менялся быстрее,
4
чем индекс строки. Для этого надо поменять внешний и внутренний циклы местами, а средний оставить на месте:
do k = 1, N
do j = 1, N
do i = 1, N
C(i , j) = C(i , j) + A(i , k )* B(k , j)
end do
end do
end do
Теперь к предыдущей таблице добавим результат получившейся программы, назовем ее def mul tr.
| size | 128 | 256 | 512 | 1024 | 2048 |
| matul | 4. | 2.00009998E-02 | 0.21601403 | 1.7041068 | 13.596855 |
| def mul tr | 4.00019996E-02 | 0.26401600 | 2.1721358 | 17.385088 | 138.56866 |
| def mul | 2.80019976E-02 | 0.28801799 | 6.7804241 | 98.874176 | 900.42432 |
Нетрудно догадаться, что транпонировав одну из матриц, можно перемножать только столбцы, что еще сократит время умножения. Для транспонирования можно воспользоваться встроенной функцией transpose. Далее можно избавившись от одного цикла. Это позволяет сделать возможным описание сечений (в данном случае — столбцов) и использование встроенной функции сложения массивов sum. Тогда умножение двух матриц приобретёт вид:
A = transpose (A) do i = 1, N
do j = 1, N
C(j , i) = sum (A(: , j )* B(: , i ))
end do
end do
Посмотрим, на что способен такой вариант(его название — two loops mul):
| size | 128 | 256 | 512 | 1024 | 2048 |
| matmul | 4. | 2.00009998E-02 | 0.21601403 | 1.7041068 | 13.596855 |
| two loops mul | 8.00000131E-03 | 5.60030043E-02 | 0.49202991 | 3.6642284 | 29.393829 |
| def mul tr | 4.00019996E-02 | 0.26401600 | 2.1721358 | 17.385088 | 138.56866 |
| def mul | 2.80019976E-02 | 0.28801799 | 6.7804241 | 98.874176 | 900.42432 |
Очевидно, что последний вариант — самый быстрый из рассмотренных, но он уступает matmul. Для наглядности ниже представлен график.
5
Чтобы усовершенствовать наш метод, нужно обратить внимание на компилятор. Что вообще такое компилятор? Это программа, которая переводит текст с языка программирования высокого уровня(в данном случае на Фортране) на язык машинного уровня. Компилятор позволяет осуществить связь между тем, что пишет программист, и процессором компьютера. Я пользуюсь компилятором GF ortran из GNU Compiler Collection, который позволяет оптимизировать компиляцию[5]. Существует несколько уровней оптимизации: O1; O2; O3; Ofast. Каждый имеет свои особенности, которые я не буду подробно описывать. Для умножения матриц и алгоритма Штрассена лучше всего подходит уровень Ofast, т.к. он включает в себя наибольшее количество опций и является самым быстрым. Также можно использовать опцииmarch = native и mtune = native [6], которые генерируют код для указанной архитектуры процессора. На место native компилятор сам ставит значение, соответствующее данному процессору.
Компилятор позволяет осуществить связь между тем, что пишет программист, и процессором компьютера. Я пользуюсь компилятором GF ortran из GNU Compiler Collection, который позволяет оптимизировать компиляцию[5]. Существует несколько уровней оптимизации: O1; O2; O3; Ofast. Каждый имеет свои особенности, которые я не буду подробно описывать. Для умножения матриц и алгоритма Штрассена лучше всего подходит уровень Ofast, т.к. он включает в себя наибольшее количество опций и является самым быстрым. Также можно использовать опцииmarch = native и mtune = native [6], которые генерируют код для указанной архитектуры процессора. На место native компилятор сам ставит значение, соответствующее данному процессору.
До этого момента я использовала стандартную компиляцию:
gfortran -o test_mul test_mul . f90
А теперь при компиляции добавлю вышеописанные опции. Тогда компиляция будет выглядеть так:
gfortran -o test_mul — Ofast — mtune = native — march = native test_mul . f90
6
Посмотрим, как изменятся результаты:
| size | 128 | 256 | 512 | 1024 | 2048 |
| two loops mul | 0. | 8.00000131E-03 | 9.20059681E-02 | 0.69604301 | 5.7083435 |
| def mul tr | 0.0000000 | 1.20010078E-02 | 0.16401005 | 1.2800789 | 9.8126221 |
| matmul | 4.00000019E-03 | 2.40010004E-02 | 0.21201299 | 1.6761041 | 13.372837 |
| def mul | 1.20009994E-02 | 8.80059898E-02 | 1.9721229 | 22.437403 | 220.77379 |
7
Matmul занял на этот раз третье место, и время его работы почти не изменилось. Это объясняется тем, что эта встроенная функция уже скомпилирована, а вот написанные мной программы — нет, и на них опции компиляции влияют очень сильно. Теперь первое место в таблице занимает умножение с двумя циклами, второе место досталось умножению по столбцам, а умножение по определению занимает почётное последнее место.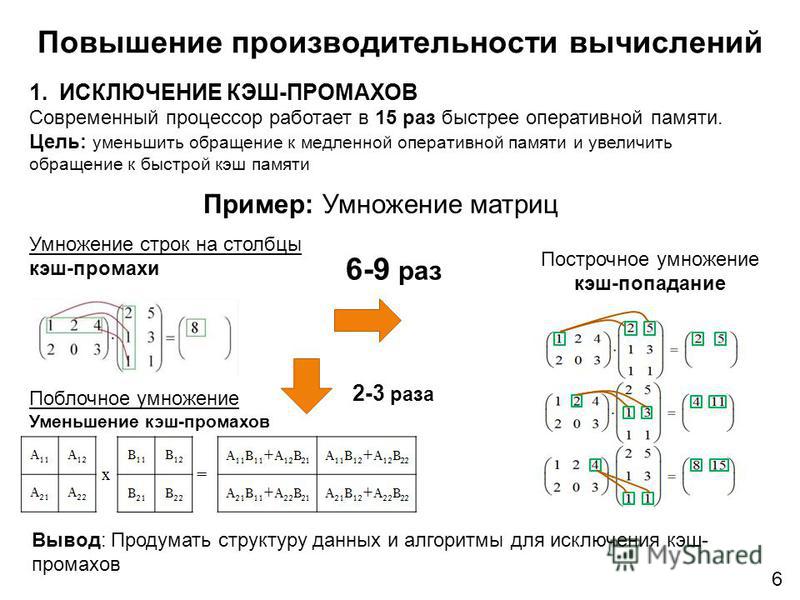 Последние результаты показывают, что преуспеть можно и без алгоритма Штрассена, а лишь используя знания о том, как устроен язык программирования. Опции компилятора Ofast; mtune = native; march = native сыграли решающую роль в оптимизации, что говорит о том, насколько важно собирать программу под конкретный процессор. В дальнейшем я всегда буду использовать эти три опции. Самое быстрое умножение с двумя циклами лучше всего подойдет для нерекурсивной ветви алгоритма Штрассена, так что часть задачи уже решена.
Последние результаты показывают, что преуспеть можно и без алгоритма Штрассена, а лишь используя знания о том, как устроен язык программирования. Опции компилятора Ofast; mtune = native; march = native сыграли решающую роль в оптимизации, что говорит о том, насколько важно собирать программу под конкретный процессор. В дальнейшем я всегда буду использовать эти три опции. Самое быстрое умножение с двумя циклами лучше всего подойдет для нерекурсивной ветви алгоритма Штрассена, так что часть задачи уже решена.
4Реализация алгоритма
В ходе своей работы я придумала несколько вариантов реализации алгоритма Штрассена. Хотя эти варианты очень похожи, каждый их них имеет свои преимущества и недостатки. Так как алгоритм работает только с квадратными матрицами, размер которых два в натуральной степени, то
8
все остальные матрицы нужно пополнить до нужного размера нулевыми строками и столбцами. Как это будет реализовано непосредственно на языке программирования, не имеет значения. После совершения этой операции мы можем иметь дело с матрицами любого размера. Написать рекурсивную подпрограмму, выполняющую алгоритм Штрассена, не очень сложно: для этого надо просто воспроизвести все то, что описано в соответствующем разделе, на языке программирования. Пусть есть две матрицы A и B, заполненные случайными числами, которые требуется перемножить, и пусть эти матрицы уже имеет размер 2n, а матрица C — результат умножения. В ходе алгоритма потребуется семь новых элементов M1 M7, которые будут вычисляться рекурсивно. Пока оставим вопрос о том, начиная с какого номера лучше выходить из рекурсии, будем умножать по алгоритму, пока матрица не станет размера 8 8.
После совершения этой операции мы можем иметь дело с матрицами любого размера. Написать рекурсивную подпрограмму, выполняющую алгоритм Штрассена, не очень сложно: для этого надо просто воспроизвести все то, что описано в соответствующем разделе, на языке программирования. Пусть есть две матрицы A и B, заполненные случайными числами, которые требуется перемножить, и пусть эти матрицы уже имеет размер 2n, а матрица C — результат умножения. В ходе алгоритма потребуется семь новых элементов M1 M7, которые будут вычисляться рекурсивно. Пока оставим вопрос о том, начиная с какого номера лучше выходить из рекурсии, будем умножать по алгоритму, пока матрица не станет размера 8 8.
9
recursive function strassen (A , B , | N) | result (C) | ||
real C(N , N), AT (N , | N) |
|
| |
integer , intent ( in ) :: N |
|
| ||
integer P , i , j , | k |
|
|
|
real , intent ( in ) | :: A(N , N), B(N , | N) |
| |
real , dimension (: ,:) , allocatable :: A11 , A12 | , | A21 , | A22 |
| ||||
real , | dimension (: ,:) , | allocatable :: | B11 , | B12 | , | B21 , | B22 |
|
real , | dimension (: ,:) , | allocatable :: | M1 , | M2 , | M3 , M4 , | M5 | , M6 , M7 | |
if (N == 8) then |
|
AT = transpose (A) |
|
do i = 1, N |
|
do j | = 1, N |
| C(j , i) = sum ( AT (: , j )* B(: , i )) |
end | do |
end do |
|
return |
|
end if |
|
P=N /2
allocate ( A11 (P ,P), A12 (P ,P), A21 (P ,P), A22 (P ,P )) allocate ( B11 (P ,P), B12 (P ,P), B21 (P ,P), B22 (P ,P ))
A11 | = | A | (1:P , 1: P) |
A12 | = | A | (1:P , P +1: N) |
A21 | = | A | (P +1:N , 1: P) |
A22 | = | A | (P +1:N , P +1: N) |
B11 | = | B | (1:P , 1: P) |
B12 | = | B | (1:P , P +1: N) |
B21 | = | B | (P +1:N , 1: P) |
B22 | = | B | (P +1:N , P +1: N) |
allocate ( M1 (P ,P), M2 (P ,P), M3 (P ,P), M4 (P ,P )) allocate ( M5 (P ,P), M6 (P ,P), M7 (P ,P ))
M1 | = | strassen ( A11 + A22 , B11 + B22 , P) | |||||
M2 | = | strassen ( A21 + A22 , B11 , P) | |||||
M3 | = | strassen (A11 , B12 | — B22 , P) | ||||
M4 | = | strassen (A22 , B21 | — B11 , P) | ||||
M5 | = | strassen ( A11 | + | A12 , | B22 , | P) | |
M6 | = | strassen ( A21 | — | A11 , | B11 | + B12 , P) | |
M7 | = | strassen ( A12 | — | A22 , | B21 | + B22 , P) | |
deallocate (A11 , A12 , A21 , A22 , B11 , B12 , B21 , B22 )
C | (1:P , | 1: P) = M1 | + | M4 | — M5 + M7 | |
C | (1:P , | P +1: N) | = | M3 | + | M5 |
C | (P +1:N , 1: P) | = | M2 | + | M4 | |
C (P +1:N , P +1: N) = M1 — M2 | + M3 + M6 |
deallocate (M1 , M2 , M3 , M4 , | M5 , M6 , M7 ) |
end function |
|
Разберем тут же еще один вариант. Этот вариант не предполагает объявления семи матриц M1 M7, и тогда четыре блока матрицы C можно найти следующим образом:
Этот вариант не предполагает объявления семи матриц M1 M7, и тогда четыре блока матрицы C можно найти следующим образом:
10
(2.81)).Вскоре после объявления результата Штрассена С. Виноград нашел способ умножить матрицы 2 X 2, используя 7 умножений и 15 добавления/удаления. Это наблюдение улучшает константу, но делает не меняет асимптотического времени вычислений. Впоследствии Виноград показал, что 7 умножений и 15 сложений/вычитаний оптимальны для матрицы 2 X 2 умножение. Его подход основан на следующих уравнениях.
[ А11 А12
]
[ В11 В12
]
[ С11 С12 ]
Пусть А =
[
] и B =
[
] и С =
[
] = А*В.
[ А21
А22]
[ В21 В22
]
[ С21 С22 ]
S1 = A21 + A22, T1 = B12 – B11
S2 = S1 – A11, T2 = B22 – T1
S3 = A11 – A21, T3 = B22 – B12
S4 = A12 – S2, T4 = B21 – T2
Р1 = А11*В11
Р2 = А12*В21
Р3 = С1*Т1
Р4 = С2*Т2
Р5 = С3*Т3
Р6= С4*В22
Р7 = А22*Т4
 Постройте количество операций различных алгоритмов.
Вычислите отношение количества операций, используемых вариантом Винограда
по сравнению с алгоритмом Штрассена, когда k стремится к бесконечности.
Постройте количество операций различных алгоритмов.
Вычислите отношение количества операций, используемых вариантом Винограда
по сравнению с алгоритмом Штрассена, когда k стремится к бесконечности. k — 1,9к.
k — 1,9к.Алгоритм Штрассена для умножения матриц: моделирование, анализ и реализация Стивен
- Идентификатор корпуса: 8734043
title={Алгоритм Штрассена для умножения матриц: моделирование, анализ и реализация, Стивен},
автор = {- Гус и Ледерман, Элейн и М. и Джейкобсон Дж},
год = {1996}
} - -.
 Huss, LedermanElaine, JacobsonJ
Huss, LedermanElaine, JacobsonJ - Опубликовано в 1996 г.
- Информатика
В этой статье мы сообщаем о разработке эффективной и портативной реализации алгоритма умножения матриц Штрассена для матриц произвольного размера. Наша реализация предназначена для использования вместо DGEMM, процедуры умножения матриц BLAS уровня 3. Наш код разработан таким образом, чтобы обеспечить эффективную производительность для всех размеров и форм матриц, а дополнительная память, необходимая для временных переменных, была сведена к минимуму. Замена DGEMM нашей процедурой должна обеспечить значимость…
Реализация алгоритма Штрассена для умножения матриц
Реализация предназначена для использования вместо DGEMM, процедуры умножения матриц BLAS уровня 3, и подтверждает, что алгоритм Штрассена применим для матриц реалистичного размера.
2356-5608 Эффективные рекурсивные реализации операций линейной алгебры
- Р.
 Махфуди, Сэми Ачур, З. Махджуб
Махфуди, Сэми Ачур, З. Махджуб Информатика
- 2014
- 0082 В этой статье разработаны рекурсивные алгоритмы D&C для решения четырех основных задач линейной алгебры, а именно: умножение матриц (MM), решение системы треугольных матриц, LU-факторизация, решение системы плотных матриц и алгоритм Штрассена.
Adaptive Winograd’s matrix multiplications
- P. D’Alberto, A. Nicolau
Computer Science
TOMS
- 2009
This work presents a novel, hybrid, and adaptive recursive Strassen-Winograd’s matrix multiplication ( MM), который использует автоматически настраиваемое программное обеспечение линейной алгебры (ATLAS) или GotoBLAS и представляет экспериментальные доказательства, основанные на установленных методологиях, найденных в литературе, что алгоритм для семейства матриц так же точен, как и классические алгоритмы.
Основа для практического параллельного быстрого умножения матриц
Показано, что новые алгоритмы быстрого умножения матриц могут значительно превзойти реализации поставщиками классического алгоритма и быстрого алгоритма Штрассена для задач небольшого размера и формы, и что лучший выбор быстрого алгоритма зависит от только от размера матриц, но и от формы.

Матричное умножение по методу Штрассена, подходящее для возведения в квадрат и более мощных вычислений
- Марко Бодрато
Информатика, математика
ISSAC
- 2010
Новый многовариантный вариант метода Штрассена для матричного умножения, который может сохранить, по крайней мере, не хуже, чем уже известные простые операции с матрицами. либо для цепных изделий, либо для возведения в квадрат, и может оказаться оптимальным для этих задач.
Фреймворк для высокопроизводительного умножения матриц на основе иерархических абстракций, алгоритмов и оптимизированных низкоуровневых ядер
В этой статье сделано несколько усовершенствований алгоритмов, включая осциллирующий итерационный алгоритм для умножения матриц и переменный критерий отсечения рекурсии для алгоритма Штрассена, а также необходимость стандартизации интерфейсов ядра линейной алгебры, отличных от BLAS, для написания портативных высокопроизводительных код выставлен.

Планирование алгоритма умножения матриц Штрассена-Винограда с эффективным использованием памяти
- Брис Бойер, Ж. Дюма, Клеман Перне, В. Чжоу
Информатика
ISSAC ’09
- 2009
Мы предлагаем несколько новых графиков для алгоритма умножения матриц Штрассена-Винограда. Умножение матриц на графических процессорах
В этой работе представлены эффективные реализации алгоритма Штрассена, а также варианта Винограда относительно кода sgemm в CUBLAS 3.0 с одинарной точностью и целочисленным графическим процессором при умножении матриц 16384×16384.
Смешанные параллельные реализации шага верхнего уровня алгоритмов Штрассена и Винограда для умножения матриц
В этой статье представлены параллельные реализации верхнего уровня алгоритмов Штрассена и Винограда для умножения матриц, которые используют смешанный параллелизм, т. е. одновременное использование данных и …
Плотная линейная алгебра над простыми полями размером в слово: пакеты FFLAS и FFPACK
- Дж.
 Дюма, Паскаль Джорджи, Клеман Перне
Дюма, Паскаль Джорджи, Клеман Перне Информатика, математика
TOMS
- 2008
В этой статье рассматриваются высокопроизводительные реализации основных подпрограмм линейной алгебры над простыми полями размером слова: особенно умножение матриц, с целью предоставить точную альтернативу числовой библиотеке BLAS. .
ПОКАЗАНЫ 1-10 ИЗ 27 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
Использование быстрого матричного умножения на уровне 3 BLAS
- Н. Хайэм
Информатика
TOMS
- 1990
Алгоритм для операций BLAS3, который асимптотически быстрее, чем обычный метод умножения для матриц, теперь распознается методом Фастсена, основанным на Страссене быть практически полезным методом, когда размеры матрицы превышают примерно 100.
Сверхскоростное умножение матриц на Cray-2
- D.
 Bailey
Bailey Business
- 1988
В этой статье описывается, как умножение матриц может быть выполнено еще быстрее, в два раза выше, чем указано выше, за счет использования алгоритма умножения матриц Штрассена для уменьшения количества выполняемых операций с плавающей запятой и использования локальная память на Cray-2, чтобы избежать потери производительности из-за конфликта банков памяти.
Быстрое умножение прямоугольных матриц и QR-разложение
- П. Найт
Математика
- 1995
Гауссовая ликвидация не является оптимальной
- V. Strassen
Математика
- 1969 9007
- J.
 Demmel, N. Higham
Demmel, N. Higham Информатика
TOMS
- 1992
- Р. Брента
Информатика
- 1970
- J. Hopcroft, L. R. Kerr
Математика, компьютерная наука
SWAT
- 1969
- М. Лам, Э. Ротберг, М. Э. Вольф
Информатика
ASPLOS IV
- 1991
T.. Ниже мы дадим алгоритм, который вычисляет коэффициенты произведения двух квадратных матриц A и B порядка n из коэффициентов A и B с tess больше 4 . 7 n l°g7 arithmetical…
Устойчивость блочных алгоритмов с быстрым уровнем 3 BLAS
Исследована численная устойчивость блочных алгоритмов в новой библиотеке программ линейной алгебры LAPACK и показано, что эти алгоритмы имеют обратную ошибку анализы, в которых обратные границы ошибки соизмеримы с границами ошибки для базового уровня 3 BLAS (BLAS3).
GEMMW: портативный уровень 3 BLAS Виноград Вариант алгоритма матричного умножения Штрассена
В этой работе пересматривается вариант Винограда алгоритма Штрассена и предлагается переносимое решение, основанное на интерфейсе BLAS уровня 3, которое обеспечивает некоторое облегчение при перемножении огромных хорошо обусловленных матриц.
Алгоритмы умножения матриц
Алгоритмы Штрассена и Винограда для умножения матриц исследуются и сравниваются с нормальными алгоритмами умножения матриц.
 что масштабирование необходимо для численной точности с использованием метода Винорада.
что масштабирование необходимо для численной точности с использованием метода Винорада.Некоторые методы доказывания определенных простых программ оптимальные
. разработаны наборы простых выражений и разработана модификация алгоритма Штрассена для умножения матриц размера n × p на матрицы размера p × q, устанавливающая, что умножение матриц с элементами из коммутативного кольца требует меньшего количества умножений, чем с элементами с некоммутативными элементами.
Производительность кеша и оптимизация заблокированных алгоритмов
7 чувствительны к шагу доступа к данным и размеру блоков и могут вызывать большие различия в производительности машины для разных размеров матриц.

LAPACK: Портативная библиотека линейной алгебры для высокопроизводительных компьютеров
Целью проекта LAPACK является разработка и внедрение переносимой библиотеки линейной алгебры для эффективного использования на различных высокопроизводительных компьютерах, основанной на широко используемых пакетах LINPACK и EISPACK, но расширяющей их функциональность несколькими способами.
Открытие новых алгоритмов с помощью AlphaTensor
Первое расширение AlphaZero для математики открывает новые возможности для исследований
Алгоритмы помогали математикам выполнять фундаментальные операции на протяжении тысячелетий. Древние египтяне создали алгоритм умножения двух чисел без использования таблицы умножения, а греческий математик Евклид описал алгоритм вычисления наибольшего общего делителя, который используется до сих пор.
Во времена Золотого века ислама персидский математик Мухаммад ибн Муса аль-Хорезми разработал новые алгоритмы для решения линейных и квадратных уравнений.
 На самом деле, имя аль-Хорезми, переведенное на латынь как Алгоритми , привело к появлению термина «алгоритм». Но, несмотря на знакомство с алгоритмами сегодня, которые используются во всем обществе от школьной алгебры до передовых научных исследований, процесс открытия новых алгоритмов невероятно сложен и является примером удивительных мыслительных способностей человеческого разума.
На самом деле, имя аль-Хорезми, переведенное на латынь как Алгоритми , привело к появлению термина «алгоритм». Но, несмотря на знакомство с алгоритмами сегодня, которые используются во всем обществе от школьной алгебры до передовых научных исследований, процесс открытия новых алгоритмов невероятно сложен и является примером удивительных мыслительных способностей человеческого разума.В нашей статье, опубликованной сегодня в журналах Nature , , мы представляем AlphaTensor , первую систему искусственного интеллекта (ИИ) для обнаружения новых, эффективных и доказуемо правильных алгоритмов для фундаментальных задач, таких как умножение матриц. Это проливает свет на 50-летний открытый вопрос в математике о поиске самого быстрого способа умножения двух матриц.
Этот документ является ступенькой в миссии DeepMind по развитию науки и раскрытию самых фундаментальных проблем с использованием ИИ. Наша система AlphaTensor основана на AlphaZero, агенте, который продемонстрировал сверхчеловеческую производительность в настольных играх, таких как шахматы, го и сёги, и эта работа впервые показывает путь AlphaZero от игр до решения нерешенных математических задач.

Умножение матриц
Умножение матриц — одна из простейших операций в алгебре, которую обычно преподают на уроках математики в средней школе. Но за пределами классной комнаты эта скромная математическая операция имеет огромное влияние в современном цифровом мире и повсеместно используется в современных вычислениях.
Пример процесса умножения двух матриц 3×3.Эта операция используется для обработки изображений на смартфонах, распознавания речевых команд, создания графики для компьютерных игр, запуска симуляций для прогнозирования погоды, сжатия данных и видео для публикации в Интернете и многого другого. Компании по всему миру тратят много времени и денег на разработку вычислительного оборудования для эффективного умножения матриц. Таким образом, даже незначительные улучшения эффективности матричного умножения могут иметь широкое значение.
На протяжении веков математики считали, что стандартный алгоритм умножения матриц является наилучшим с точки зрения эффективности.
Стандартный алгоритм по сравнению с алгоритмом Штрассена, который использует на одно скалярное умножение меньше (7 вместо 8) для умножения матриц 2×2. Умножения имеют гораздо большее значение, чем сложения для общей эффективности. Но в 1969 году немецкий математик Фолькер Штрассен шокировал математическое сообщество, показав, что существуют более совершенные алгоритмы.
Но в 1969 году немецкий математик Фолькер Штрассен шокировал математическое сообщество, показав, что существуют более совершенные алгоритмы.Изучая очень маленькие матрицы (размер 2×2), он обнаружил оригинальный способ объединения элементов матриц для получения более быстрого алгоритма. Несмотря на десятилетия исследований, последовавших за прорывом Штрассена, более масштабные версии этой проблемы остались нерешенными — вплоть до того, что неизвестно, насколько эффективно можно перемножать две матрицы размером всего 3×3.
В нашей статье мы рассмотрели, как современные методы искусственного интеллекта могут способствовать автоматическому обнаружению новых алгоритмов умножения матриц. Основываясь на прогрессе человеческой интуиции, AlphaTensor открыл алгоритмы, которые более эффективны, чем современные, для многих размеров матриц.
 Наши алгоритмы, разработанные искусственным интеллектом, превосходят алгоритмы, разработанные человеком, что является важным шагом вперед в области алгоритмических открытий.
Наши алгоритмы, разработанные искусственным интеллектом, превосходят алгоритмы, разработанные человеком, что является важным шагом вперед в области алгоритмических открытий.Процесс и прогресс автоматизации алгоритмического обнаружения
Во-первых, мы преобразовали проблему поиска эффективных алгоритмов для умножения матриц в игру для одного игрока. В этой игре доска представляет собой трехмерный тензор (массив чисел), отражающий, насколько далек от правильного текущий алгоритм. С помощью набора разрешенных ходов, соответствующих инструкциям алгоритма, игрок пытается изменить тензор и обнулить его элементы. Когда игроку удается это сделать, это приводит к доказуемо правильному алгоритму умножения матриц для любой пары матриц, а его эффективность определяется количеством шагов, предпринятых для обнуления тензора.
Эта игра невероятно сложна — количество возможных алгоритмов для рассмотрения намного превышает количество атомов во Вселенной, даже для небольших случаев матричного умножения.
 По сравнению с игрой в го, которая десятилетиями оставалась проблемой для ИИ, количество возможных ходов на каждом шаге нашей игры на 30 порядков больше (выше 10 33 для одной из рассматриваемых нами настроек).
По сравнению с игрой в го, которая десятилетиями оставалась проблемой для ИИ, количество возможных ходов на каждом шаге нашей игры на 30 порядков больше (выше 10 33 для одной из рассматриваемых нами настроек).По сути, чтобы хорошо играть в эту игру, нужно найти мельчайшую иголку в гигантском стоге сена возможностей. Чтобы решить проблемы этой области, которая значительно отличается от традиционных игр, мы разработали несколько важных компонентов, включая новую архитектуру нейронной сети, которая включает в себя индуктивные смещения для конкретных задач, процедуру для создания полезных синтетических данных и рецепт использования симметрии проблема.
Затем мы обучили агента AlphaTensor, используя обучение с подкреплением, играть в игру, начав без каких-либо знаний о существующих алгоритмах умножения матриц. Благодаря обучению AlphaTensor со временем постепенно совершенствуется, заново открывая исторические алгоритмы быстрого умножения матриц, такие как алгоритм Штрассена, в конечном итоге превосходя область человеческой интуиции и открывая алгоритмы быстрее, чем были известны ранее.
Однопользовательская игра от AlphaTensor, цель которой — найти правильный алгоритм умножения матриц. Состояние игры представляет собой кубический массив чисел (показанный серым цветом для 0, синим для 1 и зеленым для -1), представляющим оставшуюся работу, которую необходимо выполнить.
Например, если традиционный алгоритм, которому обучают в школе, умножает матрицу 4×5 на 5×5, используя 100 умножений, и это число было уменьшено до 80 благодаря человеческой изобретательности, AlphaTensor нашел алгоритмы, которые выполняют ту же операцию, используя всего 76 умножений.
Алгоритм, обнаруженный AlphaTensor, использует 76 умножений, что является улучшением по сравнению с современными алгоритмами.Помимо этого примера, алгоритм AlphaTensor улучшает двухуровневый алгоритм Штрассена в конечном поле впервые с момента его открытия 50 лет назад. Эти алгоритмы умножения малых матриц можно использовать в качестве примитивов для умножения гораздо больших матриц произвольного размера.
Кроме того, AlphaTensor также обнаруживает разнообразный набор алгоритмов с самой современной сложностью — до тысяч алгоритмов умножения матриц для каждого размера, показывая, что пространство алгоритмов умножения матриц богаче, чем считалось ранее.

Алгоритмы в этом богатом пространстве имеют разные математические и практические свойства. Используя это разнообразие, мы адаптировали AlphaTensor специально для поиска алгоритмов, которые быстро работают на данном оборудовании, таком как графический процессор Nvidia V100 и Google TPU v2. Эти алгоритмы умножают большие матрицы на 10-20% быстрее, чем обычно используемые алгоритмы на том же оборудовании, что демонстрирует гибкость AlphaTensor в оптимизации произвольных целей.
AlphaTensor с целью, соответствующей времени выполнения алгоритма. Когда обнаруживается правильный алгоритм умножения матриц, он тестируется на целевом оборудовании, а затем передается обратно в AlphaTensor, чтобы изучить более эффективные алгоритмы на целевом оборудовании.Изучение влияния на будущие исследования и приложения
С математической точки зрения наши результаты могут направить дальнейшие исследования в области теории сложности, целью которых является определение самых быстрых алгоритмов для решения вычислительных задач.
 Исследуя пространство возможных алгоритмов более эффективно, чем предыдущие подходы, AlphaTensor помогает лучше понять богатство алгоритмов умножения матриц. Понимание этого пространства может открыть новые результаты для определения асимптотической сложности матричного умножения, одной из самых фундаментальных открытых проблем в информатике.
Исследуя пространство возможных алгоритмов более эффективно, чем предыдущие подходы, AlphaTensor помогает лучше понять богатство алгоритмов умножения матриц. Понимание этого пространства может открыть новые результаты для определения асимптотической сложности матричного умножения, одной из самых фундаментальных открытых проблем в информатике.Поскольку умножение матриц является ключевым компонентом во многих вычислительных задачах, охватывающих компьютерную графику, цифровую связь, обучение нейронных сетей и научные вычисления, алгоритмы, открытые AlphaTensor, могут сделать вычисления в этих областях значительно более эффективными. Гибкость AlphaTensor для рассмотрения любых целей может также стимулировать появление новых приложений для разработки алгоритмов, которые оптимизируют такие показатели, как потребление энергии и числовая стабильность, помогая предотвратить лавинообразное увеличение небольших ошибок округления в процессе работы алгоритма.
Хотя здесь мы сосредоточились на конкретной проблеме матричного умножения, мы надеемся, что наша статья вдохновит других на использование ИИ для руководства алгоритмическими открытиями для других фундаментальных вычислительных задач.
 Наше исследование также показывает, что AlphaZero — это мощный алгоритм, который может быть расширен далеко за пределы области традиционных игр для решения открытых математических задач. Опираясь на наши исследования, мы надеемся стимулировать большую работу — применение ИИ, чтобы помочь обществу решить некоторые из наиболее важных проблем в математике и других науках.
Наше исследование также показывает, что AlphaZero — это мощный алгоритм, который может быть расширен далеко за пределы области традиционных игр для решения открытых математических задач. Опираясь на наши исследования, мы надеемся стимулировать большую работу — применение ИИ, чтобы помочь обществу решить некоторые из наиболее важных проблем в математике и других науках.Примечания
Дополнительную информацию можно найти в репозитории AlphaTensor на GitHub.
Благодарности: Франциско Р. Руис, Томас Хьюберт, Александр Новиков, Алекс Гонт за отзывы о публикации в блоге. Sean Carlson, Arielle Bier, Gabriella Pearl, Katie McAtackney, Max Barnett за помощь с текстом и рисунками. Эта работа была выполнена командой с участием Альхуссейна Фаузи, Матея Балога, Айи Хуанга, Томаса Хуберта, Бернардино Ромера-Паредеса, Мохаммадамина Барекатаина, Франсиско Руиса, Александра Новикова, Джулиана Шриттвизера, Гжегожа Свирща, Дэвида Сильвера, Демиса Хассабиса и Пушмита.


 {n / 2}.}
{n / 2}.}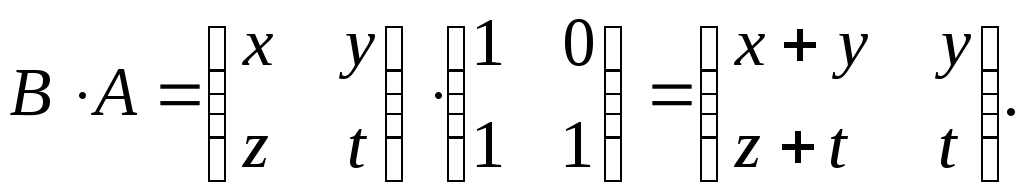 Штрассена для быстрого умножения матриц
Штрассена для быстрого умножения матриц
 Трещина А вертикально и B горизонтально:
Трещина А вертикально и B горизонтально:
 Как, S (1988). «Многослойные массивные вычисления». Информационные науки. 45 (3): 347–365. CiteSeerX 10.1.1.90.4753. Дои:10.1016/0020-0255(88)90010-2.
Как, S (1988). «Многослойные массивные вычисления». Информационные науки. 45 (3): 347–365. CiteSeerX 10.1.1.90.4753. Дои:10.1016/0020-0255(88)90010-2.
 80019976E-02
80019976E-02 00000019E-03
00000019E-03 00000019E-03
00000019E-03 0000000
0000000 Huss, LedermanElaine, JacobsonJ
Huss, LedermanElaine, JacobsonJ Махфуди, Сэми Ачур, З. Махджуб
Махфуди, Сэми Ачур, З. Махджуб

 Дюма, Паскаль Джорджи, Клеман Перне
Дюма, Паскаль Джорджи, Клеман Перне Bailey
Bailey Demmel, N. Higham
Demmel, N. Higham что масштабирование необходимо для численной точности с использованием метода Винорада.
что масштабирование необходимо для численной точности с использованием метода Винорада.
 На самом деле, имя аль-Хорезми, переведенное на латынь как Алгоритми , привело к появлению термина «алгоритм». Но, несмотря на знакомство с алгоритмами сегодня, которые используются во всем обществе от школьной алгебры до передовых научных исследований, процесс открытия новых алгоритмов невероятно сложен и является примером удивительных мыслительных способностей человеческого разума.
На самом деле, имя аль-Хорезми, переведенное на латынь как Алгоритми , привело к появлению термина «алгоритм». Но, несмотря на знакомство с алгоритмами сегодня, которые используются во всем обществе от школьной алгебры до передовых научных исследований, процесс открытия новых алгоритмов невероятно сложен и является примером удивительных мыслительных способностей человеческого разума.
 Но в 1969 году немецкий математик Фолькер Штрассен шокировал математическое сообщество, показав, что существуют более совершенные алгоритмы.
Но в 1969 году немецкий математик Фолькер Штрассен шокировал математическое сообщество, показав, что существуют более совершенные алгоритмы. Наши алгоритмы, разработанные искусственным интеллектом, превосходят алгоритмы, разработанные человеком, что является важным шагом вперед в области алгоритмических открытий.
Наши алгоритмы, разработанные искусственным интеллектом, превосходят алгоритмы, разработанные человеком, что является важным шагом вперед в области алгоритмических открытий.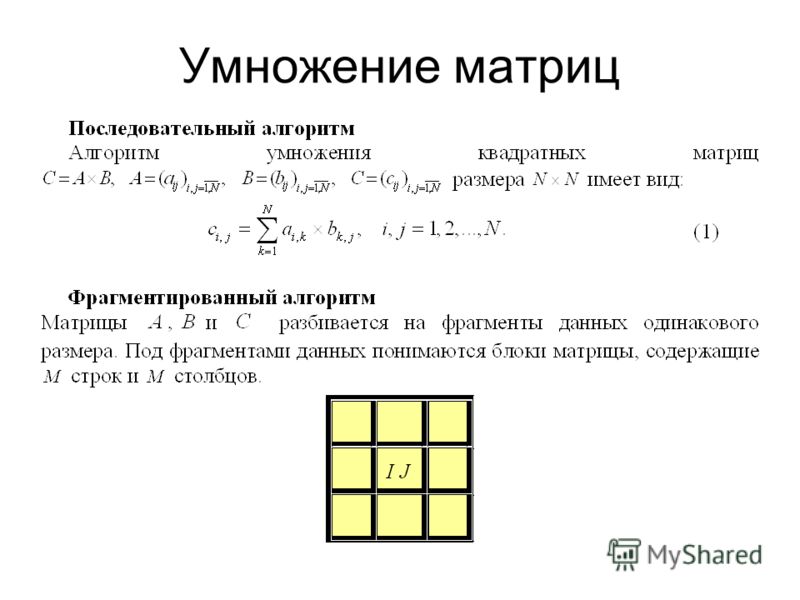 По сравнению с игрой в го, которая десятилетиями оставалась проблемой для ИИ, количество возможных ходов на каждом шаге нашей игры на 30 порядков больше (выше 10 33 для одной из рассматриваемых нами настроек).
По сравнению с игрой в го, которая десятилетиями оставалась проблемой для ИИ, количество возможных ходов на каждом шаге нашей игры на 30 порядков больше (выше 10 33 для одной из рассматриваемых нами настроек).

 Исследуя пространство возможных алгоритмов более эффективно, чем предыдущие подходы, AlphaTensor помогает лучше понять богатство алгоритмов умножения матриц. Понимание этого пространства может открыть новые результаты для определения асимптотической сложности матричного умножения, одной из самых фундаментальных открытых проблем в информатике.
Исследуя пространство возможных алгоритмов более эффективно, чем предыдущие подходы, AlphaTensor помогает лучше понять богатство алгоритмов умножения матриц. Понимание этого пространства может открыть новые результаты для определения асимптотической сложности матричного умножения, одной из самых фундаментальных открытых проблем в информатике. Наше исследование также показывает, что AlphaZero — это мощный алгоритм, который может быть расширен далеко за пределы области традиционных игр для решения открытых математических задач. Опираясь на наши исследования, мы надеемся стимулировать большую работу — применение ИИ, чтобы помочь обществу решить некоторые из наиболее важных проблем в математике и других науках.
Наше исследование также показывает, что AlphaZero — это мощный алгоритм, который может быть расширен далеко за пределы области традиционных игр для решения открытых математических задач. Опираясь на наши исследования, мы надеемся стимулировать большую работу — применение ИИ, чтобы помочь обществу решить некоторые из наиболее важных проблем в математике и других науках.