Буквенные выражения примеры: Что такое буквенное выражение? — ответ на Uchi.ru

Содержание

Числовые и буквенные выражения. Порядок действий.

теория по математике 🎲 алгебраические выражения

Что такое числовое выражение?

Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.

Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.

256 : 2 + 315×5
(181 – 19)×6 – 121:11
13,5 + 16 – 11
12² – 14×8,5

Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.

Важно!

Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей

ступени.

Порядок действий в выражении, не содержащем скобки

Порядок действий без скобок

При наличии действий одной ступени их выполняют по порядку слева направо.
При наличии действий разных ступеней – выполнение начинается с высшей ступени (то есть с третьей).

Пример №2.

890 – 567 + 2340 – 124

в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:

890 – 567 = 323
323 + 2340=2663
2663 – 124=2539

Пример №3.

1260:20×3,7:10

в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:

1260:20=63
63 3,7=233,1
233,1:10=23,31

Пример №4.

560:2 + 16² – 3×76,2

здесь присутствуют действия всех ступеней.

Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:

16²=256
560:2=280
3 76,2=228,6
280+256=536
536 – 228,6=307,4

Порядок действий в выражении, содержащем скобки

Порядок действий со скобками

Если числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.

Пример №5.

(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125

здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):

67,92:2=33,96
3245+33,96=3278,96
126×2=252
321:3=107
252-107=145

Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):

3278,96×3=9836,88
9836,88+145=9981,88
9981,88 – 125=9856,88

Буквенные выражения.

Числовое значение буквенного выражения. Какие выражения называют буквенными?

Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.

Пример №6. Примеры буквенных выражений:

5х + 6у
18 + a + b
12с – 11
m + n
(x + n) – 11m

Числовое значение буквенного выражения

Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.

Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х

их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17.

Таким образом, числовое значение буквенного выражения с + х равно 23,17.

Пример №8. Найдем значение выражения 11х +(с – d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.

Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.

Задание OM2001 Найти значение выражения 41a – 11b + 15, если 4a−9b+39a−4b+3..=5

Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:

4a−9b+39a−4b+3..=5

5(9а – 4b + 3)=4a – 9b+3

Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные): 45a – 20b +15 =4a – 9b+3 45a – 20b – 4a + 9b=3 – 15 Приведем подобные слагаемые: 41a – 11b = – 12 Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби: 41a – 11b + 15= – 12 + 15=3.

Видим, что значение нашего выражения получилось равным 3.Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1301o

Найдите значение выражения: (x + 5)

2 — x (x- 10) при x = — 1/20

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5)² – x (x – 10) = x² + 2 • 5 • x + 25 – x²+ 10x

Затем приведем подобные слагаемые:

x² + 2 • 5 • x + 25 – x²+ 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24

Ответ: 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0703o

На координатной прямо отмечены числа a и b:

Какое из приведенных утверждений для этих чисел неверно:

ab²<0
a — b > 0
a + b < 0
ab < 0

Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b < 0, так как расположено слева. К тому же, b значительно более удалено от ноля, а значит больше по модулю.

Для удобства, исходя из вышеизложенных рассуждений, примем a = 1, а b = -2.

Теперь подставим значения в данные неравенства:

ab²<0

1 • (-2)² = 4 > 0

Значит, утверждение неверно.

a — b > 0

1 — (-2) = 3 > 0

Утверждение верно.

a + b < 0

1 + (-2) = -1 < 0

Утверждение верно.

ab < 0

1 • (-2) = -2 < 0

Утверждение верно.

Следовательно, правильный ответ первый.

Ответ: ab²

pазбирался: Даниил Романович | обсудить разбор | оценить

Алла Василевская | Просмотров: 5.4k | Оценить:

Найди а в выражении. Значение числового, буквенного выражения и выражения с переменными

При изучении темы числовые, буквенные выражения и выражения с переменными необходимо уделить внимание понятию значение выражения . В этой статье мы ответим на вопрос, что такое значение числового выражения, и что называют значением буквенного выражения и выражения с переменными при выбранных значениях переменных. Для разъяснения этих определений приведем примеры.

Навигация по странице.

Что называют значением числового выражения?

Знакомство с числовыми выражениями начинается чуть ли не с первых уроков математики в школе. Практически сразу вводится и понятие «значение числового выражения». Его относят к выражениям, составленным из чисел, соединенных знаками арифметических действий (+, −, ·, :). Дадим соответствующее определение.

Определение.

Значение числового выражения – это число, которое получается после выполнения всех действий в исходном числовом выражении.

Для примера рассмотрим числовое выражение 1+2 . Выполнив , получаем число 3 , оно и является значением числового выражения 1+2 .

Часто в словосочетании «значение числового выражения» слово «числового» опускают, и говорят просто «значение выражения», так как все равно понятно, о значении какого выражения идет речь.

Данное выше определение значения выражения распространяется и на числовые выражения более сложного вида, которые изучаются в старших классах. Здесь нужно заметить, что можно столкнуться с числовыми выражениями, указать значения которых нет возможности. Это связано с тем, что в некоторых выражениях невозможно выполнить записанные действия. Например, поэтому мы не можем указать значение выражения 3:(2−2) . Подобные числовые выражения называют

выражениями, не имеющими смысла .

Часто на практике интерес представляет не столько числовое выражение, как его значение. То есть, встает задача, заключающаяся в определении значения данного выражения. При этом обычно говорят, что нужно найти значение выражения . В указанной статье подробно разобран процесс нахождения значения числовых выражений различного вида, и рассмотрена масса примеров с детальными описаниями решений.

Значение буквенного выражения и выражения с переменными

Помимо числовых выражений изучают буквенные выражения, то есть выражения, в записи которых вместе с числами присутствует одна или несколько букв. Буквы в буквенном выражении могут обозначать различные числа, и если буквы заменить этими числами, то буквенное выражение станет числовым.

Определение.

Числа, которыми заменяют буквы в буквенном выражении, называют значениями этих букв , а значение полученного при этом числового выражения называют значением буквенного выражения при данных значениях букв .

Итак, для буквенных выражений говорят не просто о значении буквенного выражения, а о значении буквенного выражения при данных (заданных, указанных и т.п.) значениях букв.

Приведем пример. Возьмем буквенное выражение 2·a+b . Пусть заданы значения букв a и b , например, a=1 и b=6 . Заменив буквы в исходном выражении их значениями, получим числовое выражение вида 2·1+6 , его значение равно 8 . Таким образом, число 8 есть значение буквенного выражения 2·a+b при заданных значениях букв a=1 и b=6 . Если бы были даны другие значения букв, то мы бы получили значение буквенного выражения для этих значений букв. Например, при a=5 и b=1 имеем значение 2·5+1=11 .

В старших классах при изучении алгебры буквам в буквенных выражениях позволяют принимать различные значения, такие буквы называют переменными, а буквенные выражения – выражениями с переменными. Для этих выражений вводится понятие значения выражения с переменными при выбранных значениях переменных. Разберемся, что это такое.

Определение.

Значением выражения с переменными при выбранных значениях переменных называется значение числового выражения, которое получается после подстановки выбранных значений переменных в исходное выражение.

Поясним озвученное определение на примере. Рассмотрим выражение с переменными x и y вида 3·x·y+y . Возьмем x=2 и y=4 , подставим эти значения переменных в исходное выражение, получаем числовое выражение 3·2·4+4 . Вычислим значение этого выражения: 3·2·4+4=24+4=28 . Найденное значение 28 является значением исходного выражения с переменными 3·x·y+y при выбранных значениях переменных x=2 и y=4 .

Если выбрать другие значения переменных, например, x=5 и y=0 , то этим выбранным значениям переменных будет соответствовать значение выражения с переменными, равное 3·5·0+0=0 .

Можно отметить, что иногда для различных выбранных значений переменных могут получаться равные значения выражения. К примеру, для x=9 и y=1 значение выражения 3·x·y+y равно 28 (так как 3·9·1+1=27+1=28 ), а выше мы показали, что такое же значение это выражение с переменными имеет при x=2 и y=4 .

Значения переменных можно выбирать из соответствующих им областей допустимых значений . В противном случае при подстановке в исходное выражение значений этих переменных получится числовое выражение, не имеющее смысла. К примеру, если выбрать x=0 , и подставить это значение в выражение 1/x , то получится числовое выражение 1/0 , которое не имеет смысла, так как деление на нуль не определено.

Остается лишь добавить, что существуют выражения с переменными, значения которых не зависят от значений входящих в них переменных. Например, значение выражения с переменной x вида 2+x−x не зависит от значения этой переменной, оно равно 2 при любом выбранном значении переменной x из области ее допустимых значений, которая в данном случае является множеством всех действительных чисел.

Список литературы.

Математика : учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.

Формула

Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции ). Этим арифметическим действиям соответствуют знаки арифметических действий:

+ (читаем «плюс «) — знак операции сложения,

— (читаем «минус «) — знак операции вычитания,

∙ (читаем «умножить «) — знак операции умножения,

: (читаем «разделить «) — знак операции деления.

Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 — (3 + 20 ∙ 15) является числовым выражением.

Результат выполнения действий над числами в числовом выражении называется значением числового выражения . Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.

Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением . В этой записи могут присутствовать скобки. Например, запись a + b — 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными .

Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.

Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла» . Например, буквенное выражение a — b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!

В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.

Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла) , т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное b: 0 не определено.

Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой . Например, если стороны семиугольника равны a, b, c, d, e, f, g , то формула (буквенное выражение) для вычисления его периметра p имеет вид:

p = a + b + c + d + e + f + g

При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.

При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.

Блок 1. Словарь

Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.

Операции: сложение, вычитание, умножение, деление.

2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «: » (разделить).

3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.

4.Результат выполнения действий над числами в числовом выражении.

5. Знак, стоящий перед значением числового выражения.

6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).

7. Общее название букв в буквенном выражении.

8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.

9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.

10. Числовое выражение, значение которого для натуральных чисел может быть найдено.

11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.

12. Алфавит, малые буквы которого используются для записи буквенных выражений.

Блок 2. Установите соответствие

Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…

Блок 3. Фасетный тест. Числовые и буквенные выражения

Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.

Дан треугольник со сторонами c, d, m, выраженными в см
Дан четырехугольник со сторонами b, c, d, m , выраженными в м
Скорость автомобиля в км/ч равна b, время движения в часах равно d
Расстояние, которое преодолел турист за m часов, составляет с км
Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
Сумма двух чисел больше второго числа на 15
Разность меньше уменьшаемого на 7
Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест. В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
m = 8, n = 10, k = 5
m = 6, n = 8, k = 15
t = 121, x = 1458

Значение данного выражения
Буквенное выражение для периметра имеет вид
Периметр, выраженный в сантиметрах
Формула пути s, пройденного автомобилем
Формула скорости v, движения туриста
Формула времени t, движения туриста
Путь, пройденный автомобилем в километрах
Скорость туриста в километрах в час
Время движения туриста в часах
Первое число равно…
Вычитаемое равно….
Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
Буквенное выражение для возраста Кати
Возраст Кати
Координата точки В, если координата точки С равна t
Координата точки D, если координата точки С равна t
Координата точки А, если координата точки С равна t
Длина отрезка BD на числовом луче
Длина отрезка CА на числовом луче
Длина отрезка DА на числовом луче

Числовым выражением является запись чисел в совокупности с арифметическими операциями и скобками. Когда в выражении совместно с числами используются переменные и все выражение составлено со смыслом, то его называют алгебраическим (буквенным) выражением. Если в выражении присутствуют прямые, производные, обратные и другие тригонометрические функции, тогда выражение называют тригонометрическим. Большое количество примеров и задач с применением различных выражений детально изложено в школьном курсе математики.

Основное что нужно помнить:

1. Значением числового выражения будет являться число, полученное при выполнении арифметических действий в этом выражении. Главное последовательно выполнять арифметические действия. Для простоты всей операции, действия можно пронумеровать. Если выражение содержит скобки, то первым делом выполняем действие соответствующее знаку в скобках. Возведение в степень будет следующим этапом. Дальше по приоритету выполняем умножение либо деление и только в самом конце сложение и вычитание.

А теперь найдем значение числового выражения 5+20*(60-45). Для начала «избавляемся» от скобок. Выполняя действие, получим 60-45=15. Теперь мы имеем 5+20*15. Следующее действие умножение 20*15=300. И последним действием будет сложение, выполняем его и получаем конечный результат 5+300=305.

2. При известном угле? Работая с тригонометрическими выражениями, потребуются знания основных тригонометрических формул, которые помогут упростить выражение. Найдем значение выражения cos 12? cos 18?- sin 12? sin 18?. Чтобы упростить данное выражение воспользуемся формулой cos (? +?) = cos? cos? — sin? sin?, тогда получим cos 12? cos 18?- sin 12? sin 18?= cos(12? +18?)= cos30? =v3?2.

3. Выражения с переменными. Нужно помнить, что значение алгебраического выражения напрямую зависит от переменной. Переменные можно обозначать буквами греческого либо латинского алфавита. Когда мы имеем заданные параметры алгебраического выражения, для начала его нужно упростить. После этого необходимо подставить заданные переменные и произвести арифметические операции. В итоге при заданных переменных мы получим число, которое и будет являться значением алгебраического выражения. Рассмотрим такой пример, где нужно найти значение выражения 3(a+y)+2(3a+2y) при a=4 и y=5. Упростим это выражение и получим 3a+3y+6a+4y=9a+7y. Теперь необходимо подставить значение переменных и вычислить, полученный результат и будет являться значением выражения. Итак, мы имеем 9a+7y при a=4 и y=5 получим 36+35=71. Обратите внимание на то, что алгебраические выражения не всегда имеют смысл. Например, такое выражение 15:(b-4) имеет смысл при любом b кроме b =4.

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Yandex.RTB R-A-339285-1

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.

Если в выражении есть только числа и арифметические знаки » + » , » · » , » — » , » ÷ » , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.

Пример 1. Значение числового выражения

Пусть нужно найти значения выражения 14 — 2 · 15 ÷ 6 — 3 .

Выполним сначала умножение и деление. Получаем:

14 — 2 · 15 ÷ 6 — 3 = 14 — 30 ÷ 6 — 3 = 14 — 5 — 3 .

Теперь проводим вычитание и получаем окончательный результат:

14 — 5 — 3 = 9 — 3 = 6 .

Пример 2. Значение числового выражения

Вычислим: 0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 .

Сначала выполняем преобразование дробей, деление и умножение:

0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 — (- 14) + 2 3 ÷ 11 4 · 11 12

1 2 — (- 14) + 2 3 ÷ 11 4 · 11 12 = 1 2 — (- 14) + 2 3 · 4 11 · 11 12 = 1 2 — (- 14) + 2 9 .

Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:

1 2 — (- 14) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .

Искомое значение найдено.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Пример 3. Значение числового выражения

Найдем значение выражения 0 , 5 · (0 , 76 — 0 , 06) .

В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.

0 , 5 · (0 , 76 — 0 , 06) = 0 , 5 · 0 , 7 = 0 , 35 .

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

Пример 4. Значение числового выражения

Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 .

Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.

1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4

1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .

В нахождении значений выражений со скобками главное — соблюдать последовательность действий.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Пример 5. Значение числового выражения

Вычислим значение выражения с корнями — 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .

Сначала вычисляем подкоренные выражения.

2 · 3 — 1 + 60 ÷ 4 3 = — 6 — 1 + 15 3 = 8 3 = 2

2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .

Теперь можно вычислить значение всего выражения.

2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Пример 6. Значение числового выражения

Сколько будет 3 + 1 3 — 1 — 1

Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.

3 + 1 3 — 1 = 3 — 1 .

Таким образом:

3 + 1 3 — 1 — 1 = 3 — 1 — 1 = 1 .

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Пример 7. Значение числового выражения

Найдем значение выражения 2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 .

Начинаем вычислять по порядку.

2 3 · 4 — 10 = 2 12 — 10 = 2 2 = 4

16 · 1 — 1 2 3 , 5 — 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .

Осталось только провести операцию сложение и узнать значение выражения:

2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 = 4 + 2 = 6 .

Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.

Пример 8. Значение числового выражения

Вычислим значение следующего выражения: 2 — 2 5 · 4 5 — 1 + 3 1 3 6 .

Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.

2 — 2 5 · 4 5 — 1 + 3 1 3 6 = 2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6

2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6 = 2 — 2 5 · 2 2 · 5 — 2 + 3 2 = 2 2 · 5 — 2 — 2 5 + 3 2

2 2 · 5 — 2 — 2 5 + 3 2 = 2 — 2 + 3 = 1 4 + 3 = 3 1 4

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Пример 9. Значение числового выражения

Найдем значение выражения, содержащего дроби: 3 , 2 2 — 3 · 7 — 2 · 3 6 ÷ 1 + 2 + 3 9 — 6 ÷ 2 .

Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.

3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6

7 — 2 · 3 6 = 7 — 6 6 = 1 6

1 + 2 + 3 9 — 6 ÷ 2 = 1 + 2 + 3 9 — 3 = 6 6 = 1 .

Перепишем наше выражение и вычислим его значение:

1 , 6 — 3 · 1 6 ÷ 1 = 1 , 6 — 0 , 5 ÷ 1 = 1 , 1

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Пример 10. Значение числового выражения

Вычислим выражение 2 5 — 1 — 2 5 — 7 4 — 3 .

Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.

2 5 — 1 = 2 5 + 1 5 — 1 5 + 1 = 2 5 + 1 5 — 1 = 2 5 + 2 4

Исходное выражение принимает вид:

2 5 — 1 — 2 5 — 7 4 — 3 = 2 5 + 2 4 — 2 5 — 7 4 — 3 .

Вычислим значение этого выражения:

2 5 + 2 4 — 2 5 — 7 4 — 3 = 2 5 + 2 — 2 5 + 7 4 — 3 = 9 4 — 3 = — 3 4 .

Выражения с логарифмами

Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .

Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 — 6 ÷ 3 5 2 + 2 + 7 . Имеем:

log 5 — 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Пример 11. Значение числового выражения

Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .

log 2 log 2 256 = log 2 8 = 3 .

По свойству логарифмов:

log 6 2 + log 6 3 = log 6 (2 · 3) = log 6 6 = 1 .

Вновь применяя свойства логарифмов, для последней дроби в выражении получим:

log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 — log 5 27 = — log 27 729 = — log 27 27 2 = — 2 .

Теперь можно переходить к вычислению значения исходного выражения.

log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + — 2 = 2 .

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Пример 12. Значение числового выражения

Найдите значение выражения: t g 2 4 π 3 — sin — 5 π 2 + cosπ .

Сначала вычисляем значения тригонометрических функций, входящих в выражение.

sin — 5 π 2 = — 1

Подставляем значения в выражение и вычисляем его значение:

t g 2 4 π 3 — sin — 5 π 2 + cosπ = 3 2 — (- 1) + (- 1) = 3 + 1 — 1 = 3 .

Значение выражения найдено.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Пример 13. Значение числового выражения

Нужно найти значение выражения cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 .

Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.

cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 = cos 2 π 8 cos 5 π 36 + π 9 — 1 = cos π 4 cos π 4 — 1 = 1 — 1 = 0 .

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Как найти значение выражения

Корни, степени, логарифмы и т.д. заменяются их значениями.
Выполняются действия в скобках.
Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.

Разберем пример.

Пример 14. Значение числового выражения

Вычислим, чему равно значение выражения — 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .

Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?

Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.

Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.

π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π

Теперь можно узнать значение синуса:

sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .

Вычисляем значение подкоренного выражения:

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .

Со знаменателем дроби все проще:

Теперь мы можем записать значение всей дроби:

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .

С учетом этого, запишем все выражение:

1 + 1 + 3 9 = — 1 + 1 + 3 3 = — 1 + 1 + 27 = 27 .

Окончательный результат:

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 — 3 , 789 ln e 2 — 56 + 8 — 3 , 789 ln e 2 также равно нулю.

Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.

Например, возьмем выражение 2 3 — 1 5 + 3 · 289 · 3 4 3 · 2 3 — 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.

Нахождение значений выражений с переменными

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Пример 15. Значение выражения с переменными

Вычислить значение выражения 0 , 5 x — y при заданных x = 2 , 4 и y = 5 .

Подставляем значения переменных в выражение и вычисляем:

0 , 5 x — y = 0 , 5 · 2 , 4 — 5 = 1 , 2 — 5 = — 3 , 8 .

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Например, выражение х + 3 — х, очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.

Еще один пример. Значение выражения x x равно единице для всех положительных иксов.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Вы, как родители, в процессе обучения своего ребенка, не раз столкнетесь с необходимостью помощи в решении домашних задач по математике, алгебре и геометрии. И одно из базовых умений, которое необходимо усвоить — как найти значение выражения. Многие заходят в тупик, ведь сколько лет прошло с того момента, как мы учились в 3-5 классах? Многое уже забылось, а что-то не училось. Сами правила математических действий — просты и вы легко их вспомните. Начнем с самых основ, что такое математическое выражение.

Определение выражения

Математическое выражение — совокупность чисел, знаков действий (=, +,-, *, /), скобок, переменных. Кратко — это формула, значение которой нужно будет найти. Такие формулы как раз встречаются в курсе математики еще со школы, а потом преследуют и студентов, которые выбрали для себя специальности, связанные с точными науками. Математические выражения разделяются на тригонометрические, алгебраические и так далее, не будем забегать в самые «дебри».

Делайте любые вычисления сначала на черновике, а после переписывайте в рабочую тетрадь. Таким образом вы избежите лишних перечеркиваний и грязи;
Пересчитайте общее количество математических действий, которые нужно будет выполнить в выражении. Обратите внимание, что согласно правилам, вначале выполняются действия в скобках, потом деление и умножение и в самом конце вычитание и сложение. Рекомендуем выделить все действия карандашом и поставить цифры над действиями в порядке очередности их выполнения. В этом случае и вам и ребенку будет легче сориентироваться;
Начинайте производить расчеты строго придерживаясь порядка выполнения действий. Пусть ребенок, если расчет простой, старается выполнять его в уме, если же это сложно, то ставьте карандашом цифру, соответствующую порядковому номеру выражения и выполняйте вычисление в письменном виде под формулой;
Как правило, найти значение простого выражения не составляет труда, если все расчеты выполнены в соответствии с правилами и правильным порядком. Большинство сталкиваются с проблемой именно на данном этапе нахождения значения выражения, потому будьте внимательны и не допускайте ошибок;
Запрещайте калькулятор. Сами математические формулы и задачи в жизни вашему ребенка может и не пригодятся, но не в этом цель изучения предмета. Главное — развитие логическое мышления. Если пользоваться калькуляторами, то смысл всего будет потерян;
Ваша задача как родителя — не решать за ребенка задачи, а помогать ему в этом, направлять. Пусть он сам производит все вычисления, а вы следите за тем, чтобы он не допускал ошибок, объясняйте, почему нужно делать так, а не иначе.
После того, как ответ на выражение найден, запишите его после знака «=»;
Откройте последнюю страницу учебника по математике. Обычно, там есть ответы под каждое упражнение в книге. Не мешает свериться, верно ли все посчитано.

Найти значение выражения — с одной стороны, простая процедура, главное вспомнить основные правила, которые мы проходили в школьном курсе математики.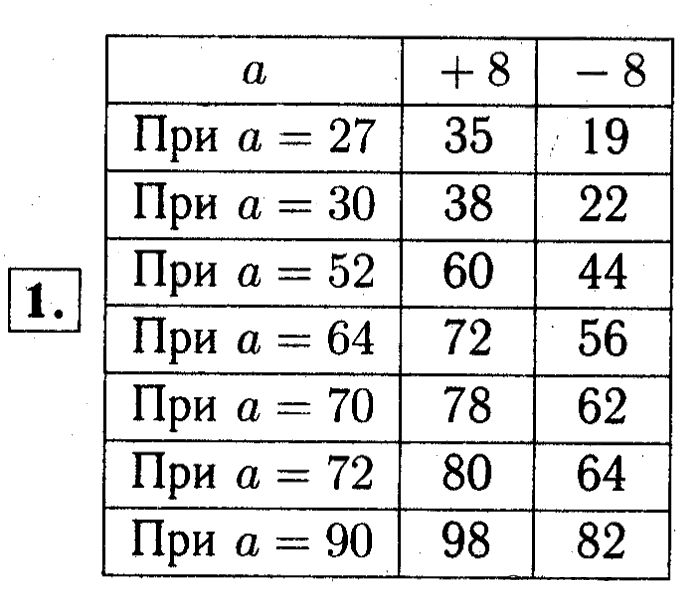 Однако, с другой стороны, когда вам нужно помочь малышу справиться с формулами и решением задач, вопрос осложняется. Ведь вы теперь не ученик, а учитель и на ваших плечах лежит воспитание будущего Эйнштейна.

Надеемся, что наша статья помогла вам найти ответ на вопрос, как найти значение выражения, и вы с легкостью раскусите любую формулу!

Числа от 1 до 100. Буквенные выражения. Математика 3 класс.

Задачи для 3 класса

Математические диктанты
Комбинаторные задачи
Нестандартные задачи
Множество и его элементы
Способы задания множеств
Пустое множество
Диаграмма Венна
Диаграмма Венна. Часть 2
Подмножество
Множество. Задачи
Скорость, время, расстояние

Числа от 1 до 100

Сложение и вычитание
Буквенные выражения
Единицы длины

Контрольные работы

Умножение и деление

Итоговая контрольная работа

Контрольная работа 1

Контрольная работа 2

Контрольная работа 3

Контрольная работа 1

Контрольная работа 2

Контрольная работа 1

Контрольная работа 1

Контрольная работа 2

Тесты. 3 класс.

Тесты по математике 3 класс
Табличное умножение и деление чисел
Особые случаи умножения и деления

Примеры, уравнения

Примеры
Уравнения
Кроссворды

Задание 1.

Прочитай выражения с + 6, с — 6 и найди их значения, если с = 10, с = 7.

Решение:
1) с + 6 (при с = 10) 10 + 6 = 16

2) с + 6 (при с = 7) 7 + 6 = 13

3) с — 6 (при с = 10) 10 — 6 = 4

4) с — 6 (при с = 7) 7 — 6 = 1

Задание 2

а = 27,
а = 30,
а = 53,
а = 65,
а = 72.

Решение:
1) 80 — а (при а = 27) 80 — 27 = 53

1) 80 — а (при а = 30) 80 — 30 = 50

1) 80 — а (при а = 53) 80 — 53 = 27

1) 80 — а (при а = 65) 80 — 65 = 15

1) 80 — а (при а = 72) 80 — 72 = 8

1) 4 + а (при а = 27) 4 + 27 = 31

1) 4 + а (при а = 30) 4 + 30 = 34

1) 4 + а (при а = 53) 4 + 53 = 57

1) 4 + а (при а = 65) 4 + 65 = 69

1) 4 + а (при а = 72) 4 + 72 = 76

Задание 3

1) с = 6,
2) с = 4,
3) с = 5,
4) с = 7,
5) с = 8;
6) m = 12,
7) m = 9,
8) m = 24,
9) m = 18,
10) m = 30

Решение:
1) с • 3 (при с = 6) 6 • 3 = 18

2) с • 3 (при с = 4) 4 • 3 = 12,

3) с • 3 (при с = 5) 5 • 3 = 15,

4) с • 3 (при с = 7) 7 • 3 = 21,

5) с • 3 (при с = 8) 8 • 3 = 24;

6) m : 3 (при m = 12) 12 : 3 = 4,

7) m : 3 (при m = 9) 9 : 3 = 3,

8) m : 3 (при m = 24) 24 : 3 = 8,

9) m : 3 (при m = 18) 18 : 3 = 6,

10) m : 3 (при m = 30) m : 3 = 5

Задание 4

1) а = 12 и b = 18,
2) а = 48 и b = 22,
3) а = 62 и b = 38,
4) а = 35 и b = 55,
5) а = 0 и b = 10;
6) с = 100 и d = 77,
7) с = 80 и d = 25,
8) с = 60 и d = 30,
9) с = 40 и d = 16,
10) с = 20 и d = 5;
11) m = 72 и n = 9,
12) m = 12 и n = 2,
13) m = 24 и n = 3,
14) m = 30 и n = 5,
15) m = 48 и n = 6;
16) х = 8 и у = 5,
17) х = 10 и у = 7,
18) х = 6 и у = 7,
19) х = 4 и у = 7,
20) х = 3 и у = 9.

Решение:
1) а + b (при а = 12 и b = 18) 12 + 18 = 30,

2) а + b (при а = 48 и b = 22) 48 + 22 = 70,

3) а + b (при а = 62 и b = 38) 62 + 38 = 100,

4) а + b (при а = 35 и b = 55) 35 + 55 = 90,

5) а + b (при а = 0 и b = 10) 0 + 10 = 10;

6) с — d (при с = 100 и d = 77) 100 — 77 = 23,

7) с — d (при с = 80 и d = 25) 80 — 25 = 55,

8) с — d (при с = 60 и d = 30) 60 — 30 = 30,

9) с — d (при с = 40 и d = 16) 40 — 16 = 24,

10) с — d (при с = 20 и d = 5) 20 — 5 = 15;

11) m : n (при m = 72 и n = 9) 72 : 9 = 8,

12) m : n (при m = 12 и n = 2) 12 : 2 = 6,

13) m : n (при m = 24 и n = 3) 24 : 3 = 8,

14) m : n (при m = 30 и n = 5) 30 : 5 = 6,

15) m : n (при m = 48 и n = 6) 48 : 6 = 8;

16) х • у (при х = 8 и у = 5) 8 • 5 = 40,

17) х • у (при х = 10 и у = 7) 10 • 7 = 70,

18) х • у (при х = 6 и у = 7) 6 • 7 = 42,

19) х • у (при х = 4 и у = 7) 4 • 7 = 28,

20) х • у (при х = 3 и у = 9) 3 • 9 = 27.

Задание 5

х = 13 и у = 60,
х = 20 и у = 55,
х = 20 и у = 80,
х = 7 и у = 22,
х = 45 и у = 55,
х — 30 и у = 65.

Решение:
х + у (при х = 13 и у = 60) 13 + 60 = 73,

х + у (при х = 20 и у = 55) 20 + 55 = 75,

х + у (при х = 20 и у = 80) 20 + 80,

х + у (при х = 7 и у = 22), 7 + 22

х + у (при х = 45 и у = 55), 45 + 55

х + у (при х — 30 и у = 65) 30 + 65.

у — х (при х = 13 и у = 60) 60 — 13 = 47

у — х (при х = 20 и у = 55) 55 — 20 = 35

у — х (при х = 20 и у = 80) 80 — 20 = 60

у — х (при х = 7 и у = 22) 22 — 7 = 15

у — х (при х = 45 и у = 55) 55 — 45 = 10

у — х (при х — 30 и у = 65) 65 — 30 = 35

Простые задачи

Задачи на умножение

Задачи на деление по содержанию и на равные части

Задачи на увеличение и уменьшение числа в несколько раз

Задачи на кратное сравнение

Задачи на приведение к единице

Задачи на цену количество стоимость

Составные задачи

Задачи на нахождение суммы

Задачи на нахождение уменьшаемого, вычитаемого, разности

Задачи на разностное и кратное сравнение

Задачи на деление суммы на число и числа на сумму

Задачи на цену, количество, стоимость

Задачи на разностное и кратное сравнение

Задачи на нахождение суммы двух произведений

Задачи на нахождение неизвестного слагаемого

Задачи на цену, количество, стоимость

Буквальное значение и буквальный перевод

Крейга Шривса

Эта страница содержит.

Тест для печати и отправки
Почему важны «буквальное значение» и «буквально»
Ключевые моменты

Что означают «буквальное значение» и «буквально»?

Термин «буквальное значение» говорит нам о том, что все слова находятся в строгом соответствии с их первоначальными значениями.

Многие слова (например, уйти ) имеют буквальное значение ( уйти ) и переносное ( умереть ). Применять буквальное значение означает брать слова в их самом основном смысле, т. е. не в их переносном смысле или в каком-либо дополнительном значении.

Простые примеры буквального значения

Комик умер на сцене.
Мы все будем в одной лодке.

Я выбросил предложение.

Другие примеры буквального значения

Буквальное значение слова контрастирует с любым переносным значением. (Помните, что образный язык — это использование слов в необычной или образной манере.)

Джону удалось убежать от волков.

Буквальное значение слова также контрастирует с любым дополнительным значением (т. Е. Не исходным значением).

Можно поиграть на улице, бабушка?
Можно, дорогой, но нельзя.

может

означает способность

может

, может

. иметь разрешение на

Подробнее о банка и май .

Что означает «буквально»?

Слово «буквально» раньше означало буквально или в смысле 9.0022 или ровно . Он использовался, чтобы подчеркнуть, что окружающие слова не использовались образно (например, метафорически).

Джон буквально сложил все яйца в одну корзину.

(В прошлом слово буквально могло быть оправдано только в том случае, если Джон клал все яйца в корзину.)

Однако в настоящее время «буквально» регулярно используется для выделения (т. Е. В качестве усилителя). Таким образом, приведенный выше пример следует понимать примерно так:

Джон действительно сложил все яйца в одну корзину [не распределил риски].

Почему важны «буквальное значение» и «буквально»

Вот два заслуживающих внимания вопроса, связанных с «буквальным значением»:

(Выпуск 1) Старайтесь использовать слова в их буквальном значении (т. е. избегайте фигурального языка), когда пишете для международной аудитории.

Не носители любого языка часто не понимают небуквальных или дополнительных значений слов. Поэтому, если вы пишете для аудитории, для которой английский язык не является родным, вам следует настроить свою дикцию (то есть выбор слов) на буквальное значение. Это может быть непросто.

Джанет бросили на растерзание волкам.

(Очевидно, что Джанет не бросили на растерзание настоящим волкам. Ее принесли в жертву. Ну, на самом деле ее не принесли в жертву. Ее бросили, чтобы причинить вред. Ну, физически ее не бросили.)

Вот признание. Я не могу найти определение , чтобы бросить на съедение , в котором все слова используются в их буквальном значении. Так что избежать переносных значений и дополнительных смыслов будет сложно.

Вот подсказка: вы не стремитесь к тексту с буквальным значением. Вы просто ищете альтернативы любым небуквальным терминам, которые могут помешать пониманию не носителем языка. Говоря «Джанет была принесена в жертву» (хотя принесено в жертву не используется в буквальном смысле) было бы безопасно.

(Выпуск 2) Имейте в виду, что в наши дни «буквально» буквально не означает буквально.

В настоящее время наречие буквально не всегда означает в буквальном значении . Часто используется просто как усилитель.

Она буквально горела во время лекции.

(Это означает, что она отлично выступила. На самом деле она не горела, несмотря на использование буквально .)
Я буквально умер, когда объявили мое имя.
(Это просто означает «Я был очень смущен».)

Современное использование буквально в качестве усилителя хорошо отражено в следующей цитате:

Использование «буквально» в переносном смысле буквально распространяется как лесной пожар. (Журналист Адам Льюис, The Guardian)

Ключевые моменты

Тест для печати

Help Us Improve Grammar Monster

Вы не согласны с чем-то на этой странице?
Вы заметили опечатку?

Найдите нас быстрее!

При использовании поисковой системы (например, Google, Bing) вы найдете Grammar Monster быстрее, если добавите #gm к своему поисковому запросу.

Следующий урок >

См. также

Что такое эвфемизм?Что такое образный язык? Что такое фигура речи?Что такое гипербола?Что такое идиома?Что такое метафора?Что такое олицетворение?Что такое сравнение?Словарь грамматических терминов

URL-адрес страницы

Техническая помощь

Загрузить последнее приложение для проверки грамматики

Приложение Grammarly поможет:

(1) Как избежать орфографических ошибок
(2) Исправление грамматических ошибок
(3) Поиск лучших слов

(Это бесплатное расширение для браузера работает с веб-почтой, социальными сетями и текстовыми приложениями, а также с онлайн-формами и документами Microsoft Office, такими как Word и Teams. )

Следующий урок >

Буквальные и небуквальные значения слов и идиом

Создано 23 июня 2016 г. пользователем пользовательMs. Алекс Элрингтон
Часть 1: Описание урока
Заголовок
Буквальные и небуквальные значения слов и идиом
Аннотация
На этом уроке учащиеся будут различать буквальное и небуквальное значение устного и письменного содержания в различных контекстах. Урок предназначен для взрослых, изучающих английский язык и продемонстрировавших уровень чтения 3-4 классов или B-C. Учащиеся продемонстрируют понимание идиом, используя контекстные подсказки в предложениях, чтобы помочь понять значения идиом, рисуя идиомы без использования слов или букв, давая письменные советы, используя идиомы, и создавая поздравительные открытки.
Аудитория учащихся/основные пользователи
Преподаватели и студенты
Использование в образовательных целях
Учебный план/Инструкция
Оценка, мини-урок, профессиональное развитие, домашняя школа, неформальное образование
Уровень
Образование для взрослых
Класс
CCRS Уровень B (3): Базовая грамотность
CCRS Уровень C (4): Базовая грамотность
Домен
Английский язык Искусство/грамотность
Раздел 4
Язык
Стандартный
L3. 5a;L4.5b
CCRS Якорь 5: Продемонстрировать понимание образного языка, отношений слов и нюансов в значениях.
Продемонстрировать понимание отношений слов и нюансов в значениях слов.
а. Различать буквальное и небуквальное значение слов и фраз в контексте (например, предпринять шаги).
б. Знать и объяснять значение распространенных идиом.
Язык
Английский
Тип материала
Учебный материал
Стратегии преподавания и обучения
Оценки
Изображения
Цели обучения
Цель этого урока для учащегося начального базового образования:
расшифровать буквальное и небуквальное значение идиом
Ключевые слова
Дизайнеры для обучения
Обучение взрослых
Образное значение
Образный язык
Идиома
Время, необходимое для урока
30 минут
Предыдущие знания
Уровень чтения не ниже 3-го класса
Начальный базовый уровень образования, уровень владения английским языком
Необходимые ресурсы
Рабочий лист по изучению идиом (распечатайте набор для класса) и ключ ответа
Карточки соответствия идиом (распечатайте один набор для каждых двух учащихся)
Образец и шаблон поздравительной открытки (распечатайте шаблон для каждого «продвинутого» ученика )
Ручки/карандаши
8,5 X 11 дюймов картон или плотная бумага (набор для печати)
Мелки, цветные карандаши или маркеры
Ведро, лист бумаги и одна пара ножниц, чашка молока, простыни (по желанию)
Компьютер, проектор и Интернет (дополнительно)
Раздаточный материал
Загрузить: IDIOM MATCHING CARDS_2. pdfЗагрузить: PracticingIdiomsWorksheet_1.pdfЗагрузить: Шаблон поздравительной открытки_1.pdfЗагрузить: PracticingIdioms_AnswerKey (1).pdf
Автор урока и лицензия
Автор: г-жа Алекс Элрингтон
Лицензия: лицензия Creative Commons CC BY 4.0
Часть 2: Урок
Цель обучения
К концу этого урока взрослые учащиеся должны уметь:
интерпретировать идиомы, используя контекстные подсказки в предложениях с точностью 70 %
рисовать идиомы без использования слов или букв со 100% точностью
составлять письменные подсказки, используя идиомы с точностью 70%
сделать поздравительную открытку, используя идиому со 100% точностью
Тема урока
ELA/Чтение/Грамотность
Резюме контекста
Часто учащиеся знают, что означает отдельное слово; однако, как только слово соединяется с другими словами для создания фраз или предложений, он / она изо всех сил пытается понять смысл. Он/она может понимать слова «летать» и «воздушный змей», но может счесть фразу «О, давай, запускай воздушного змея» озадачивающей. На этом уроке учащиеся будут различать буквальное и небуквальное значение понятий в разных контекстах. Учащиеся продемонстрируют понимание идиом, используя контекстные подсказки в предложениях, чтобы помочь расшифровать значения идиом, рисуя идиомы без использования слов или букв, давая письменные советы, используя идиомы, и создавая поздравительную открытку.
Актуальность для практики
В каждой культуре существует множество поговорок или советов, описывающих особенности повседневной жизни. Без знания и понимания этих выражений или идиом изучающие английский язык (ELL) часто оказываются в невыгодном положении. Например, неграмотный взрослый ELL может знать, что означает «гвоздь» или «головка», но он/она может не знать, что «ударить гвоздь по его головке» означает сделать что-то совершенно правильно. Таким образом, неграмотность среди взрослых является не только проблемой чтения, но и проблемой понимания культурно-обусловленных образных выражений. Изучая английские идиоматические выражения, учащиеся могут начать говорить и понимать по-английски, как носители языка.
Ключевые термины и понятия
Контекст — это ситуация, в которой что-то происходит.
Буквальный значение относится к обычному, повседневному, самому основному значению слова.
Не буквальное значение это когда слово означает что-то другое, чем его обычное, повседневное значение.
Образный язык — это когда вы используете слово или фразу, которые не имеют своего обычного, повседневного, буквального значения.
Идиома – это фраза или высказывание, значение которых сильно отличается от отдельных слов, составляющих фразу или высказывание.
Интерпретация является пояснением.
Разминка
Время: 3 минуты
Опубликовать любой два идиомы на доске: «пнуть ведро», «срезать углы», «ударить по простыням» и «плакать над пролитым молоком». Моделируйте чтение вслух, а затем разыгрывайте две идиомы. Используйте реквизит, если он есть.
Скажи: «Слова и фразы могут иметь буквальное или небуквальное значение. А буквальный Значение — это когда слово или фраза используются точно так, как они определены. А не буквальный значение — это когда значение слова или фразы приобретает особое значение».
Объясните буквальное и небуквальное значение два крылатые выражения.
Пример 1 : Когда кто-то говорит: «Вчера дедушка сдох. Я до сих пор в шоке». «Пнул в ведро» (небуквальное значение) означает, что кто-то умер (буквальное значение).
Пример 2 : Когда автор пишет: «Люси проработала на фабрике 14 часов. Она ударила по простыням, как только пришла домой», «ударила по простыням (сено)» (небуквальное значение) означает немедленно лечь спать (буквальное значение).
Пример 3 : Когда вы читаете: «Шеф-повар срезает углы (небуквальный смысл), когда готовит салат из морепродуктов. Он использует консервированный тунец вместо свежего. «Срезать углы» означает делать что-то самым простым или дешевым способом, пропуская что-то важное (буквальное значение).
Пример 4 : Джон был расстроен, потому что пропустил свой рейс, но я сказал ему, что бесполезно плакать над пролитым молоком. Плакать из-за пролитого молока означает расстраиваться из-за того, что уже произошло и ничего нельзя изменить.
Подчеркните, что хорошие читатели и носители английского языка должны быть в состоянии понять значение идиом, используя подсказки из того, что было сказано или написано до или после того, как идиома была произнесена или написана.
Введение
Время: 1 минута
Скажи: «Сегодня ты разберешься со значениями слов и идиом:
с помощью контекстных подсказок в предложениях
, рисуя идиомы без использования слов или букв
, давая письменные советы, используя идиомы
, создавая поздравительную открытку».
Презентация / Моделирование / Демонстрация
Время: 5 минут
Скажите: «Идиома — это высказывание, имеющее как прямое (точное), так и переносное (понятное) значение. Идиома — это тип образного языка, слово или фраза, не имеющая своего повседневного, точного значения».
Скажи: Давайте посмотрим короткое видео под названием «Исповедь идиомы». Речь идет о двух персонажах, которые забавным образом используют идиомы. Поднимайте руку каждый раз, когда слышите идиому, которую слышали раньше.
Включи видео «Исповедь идиомы».
Скажите: «Вы собираетесь изучать идиомы, которые мы используем каждый день».
Управляемая практика
Время: 11 минут
Скажи: «Идиома — это высказывание, имеющее как буквальное (точное), так и переносное (понятное) значение. Идиома – это вид образного языка, слово или словосочетание, не имеющее своего повседневного, точного значения. Идиомы меняются в зависимости от культуры, времени и ситуации».
Предложите учащимся рассказать об идиомах, которые они узнали в видео. Когда они слышали это раньше, кто это сказал и почему это было сказано?
Скажи: Когда кто-то говорит: «Присматривай за ребенком». Вы действительно не оторвете глаз и не поместите его на ребенка. Это просто означает, что вы должны следить за ребенком, чтобы он не причинил себе вреда.
Спросите: «Кто слышал выражение «подлить масла в огонь»?»
Повторите: «Подлить масла в огонь» означает сделать ситуацию еще хуже, чем она уже есть».
Скажите: «Доктор был измотан. Он круглосуточно работал в отделении неотложной помощи». Какая фраза является идиомой? Что это значит?
Повторите: «»Работать круглосуточно» означает работать все время или 24 часа подряд».
Скажите: «В английском языке более 4000 идиом. Иногда слова в идиомах являются подсказками о значении. Часто это не так, поэтому со временем вам приходится запоминать наиболее часто используемые идиомы».
Дайте каждому учащемуся копию Практика идиом рабочий лист.
Предложите учащимся работать самостоятельно или в парах.
Просмотрите ответы, проясняя любую путаницу. Задавайте вопросы, которые провоцируют более глубокое понимание, например:
Оценка
Время: 10 минут
(Low-Mid) Matching Game: вырежьте карточки соответствия идиом. Перемешайте и положите на ровную поверхность лицом вниз. Каждый игрок по очереди переворачивает по две карты. Если совпадение сделано, сохраните карты. Если совпадения нет, переверните карты обратно. Побеждает игрок, составивший наибольшее количество совпадений.
(дополнительно) Поздравительные открытки. В этом упражнении, ориентированном на продукт, инструктор объясняет, что идиомы часто представляют собой советы, передаваемые из поколения в поколение. Он/она публикует список идиом, упомянутых в уроке. Учащиеся выбирают свою любимую идиому и делают поздравительные открытки. Учащиеся пишут совет, используя идиому, и рисуют буквальное представление идиомы на карточке. Воспитатель раздает образцы поздравительных открыток. Он/она моделирует процесс изготовления карты, размещая буквальное визуальное представление на обложке и совет на внутренней странице.
Заявление
Время: 15-30 минут (Это занятие может быть продлено на другой учебный период или может использоваться в качестве домашнего задания.)
Новостная статья или обзор короткого рассказа: В этом упражнении по чтению учащиеся будут аннотировать текст. Преподаватель объясняет, что авторы часто используют идиомы, чтобы привлечь внимание читателя. Он/она представляет новостную статью, рекламу и/или рассказ. Он/она объясняет, что учащиеся будут искать в текстах идиомы. Затем класс обсудит буквальное и небуквальное значение идиом, цель автора для идиомы и успех / неудачу идиом в тексте. Затем учащиеся создадут свою собственную новостную статью, рекламу или короткий рассказ, используя идиомы.
Дополнительные ресурсы
Интернет-журнал TESEL: викторины по идиомам для самостоятельного изучения, http://a4esl.org/q/h/9807/km-animalidioms.html
Обучающие игры для детей, http://www.learninggamesforkids.com/vocabulary_games/idioms.html
Рабочие листы по чтению: образный язык, http://www.erreadingworksheets.com/figurative-language/figurative-language-worksheets/figurative-language-worksheet/
Заявления об авторстве
Я из кожи вон лезу ради тебя…! by Lisa Cyr под лицензией CC BY 2.0
The Cavalier, созданный Тони Альтером, находится под лицензией CC BY 2.0
.
Давайте сравним яблоки и апельсины от frankieleon под лицензией CC BY 2.0
его лай НАМНОГО хуже, чем его укус Эми МакГиббон Лэнг лицензировано под CC BY 2.0
Грустный пингвин от Bart M лицензируется на условиях открытой лицензии.
Признания идиомы, созданные Амандой Кох и Молли Хелмс из Колледжа искусств и дизайна Ринглинга, первоначально опубликованные на https://vimeo. com/63083013 под лицензией CC BY 3.0.
Дифференциация обучения
Этот урок дает много возможностей дифференцировать обучение. Включены: чтение для всей группы, упражнение, ориентированное на продукт, письменная часть, упражнение по текстовой аннотации и практика, которая включает прогнозирование, визуализацию, вопросы, уточнение и обобщение слов и фраз. Тем не менее, преподаватели могут также сделать следующее, чтобы поддержать учащихся:
предоставить возможность самостоятельного чтения (т.е. Amelia Bedelia серия книг),
использование диаграмм «Что я знаю, что я хочу знать и чему я научился» (KWL),
аннотировать тексты возрастающей сложности Итого,
включить Возможности физического реагирования (TPR),
использование онлайн-видео и обучающих игр
Буквенные уравнения – определение, решение, примеры
Буквенные уравнения — это уравнения, включающие буквы и алфавиты. Уравнения, состоящие из переменных, где каждая переменная буквально означает значение/количество, называются буквальными уравнениями. Некоторыми распространенными примерами буквальных уравнений являются формулы в геометрии, например, площадь квадрата определяется как A = s ² , где s обозначает длину стороны квадрата, а A обозначает его площадь.
В этой статье мы понимаем концепцию буквальных уравнений и способы их решения с помощью некоторых примеров и практических вопросов. Буквальное уравнение состоит из двух или более переменных, так что одна переменная может быть выражена через другие переменные.
1. Что такое буквальные уравнения?
2. Формула буквенных уравнений
3. Использование буквенных уравнений
4. Решение буквенных уравнений
5. Часто задаваемые вопросы о буквальных уравнениях
Что такое буквальные уравнения?
Иногда нам дают уравнения в виде формул геометрических фигур, например, периметр квадрата определяется как P = 4s, где P — периметр квадрата, а s — длина стороны квадрата. Имеются две переменные P и s, такие что P выражается через s. Это пример буквального уравнения. В буквальных уравнениях мы не можем получить точное числовое значение переменной.
Буквенные уравнения Определение
Буквенные уравнения определяются как уравнения, состоящие из двух или более переменных (букв или алфавитов), так что каждая переменная может быть выражена через другие переменные. При решении буквенных уравнений цель состоит в том, чтобы изолировать одну переменную и явно выразить решение через остальные переменные. Каждая переменная в буквальном уравнении означает количество.
Формула буквальных уравнений
Не существует единой фиксированной формулы для решения буквенных уравнений. Мы можем идентифицировать буквальное уравнение, если оно имеет более одной отдельной переменной. Буквенные уравнения могут быть линейными уравнениями, квадратными уравнениями, кубическими уравнениями и т. д. Буквенные уравнения могут быть решены путем явного выражения каждой переменной уравнения через другие переменные. Обратите внимание, что если одна и та же переменная появляется в уравнении в разных формах, уравнение может не быть буквальным уравнением. Давайте рассмотрим пример, чтобы понять это:
Например, : Уравнение x + x ² + 1 = 0 не является буквальным уравнением, поскольку оно содержит только одну переменную, то есть x, но в разных формах. Единственная переменная, которая появляется в этом уравнении, это x.
Использование буквенных уравнений
Буквенные уравнения обычно используются в формулах в математике и физике. Некоторые общие примеры буквальных уравнений:
Уравнение массы-энергии: E = mc ² . В этом буквальном уравнении есть 3 переменные, а именно E, m, c, и каждая переменная означает физическую величину.
Площадь круга: A = πr ² . В этом буквальном уравнении есть две переменные, а именно A и r, где A — площадь, а r — радиус.
Объем сферы: V = (4/3)πr ³ . В этом буквальном уравнении есть две переменные, а именно A и r, где V — объем, а r — радиус.
Алгебраическое уравнение: x + y = 1. В этом буквальном уравнении есть 2 переменные, а именно x и y.
Решение буквенных уравнений
Буквенные уравнения можно решить, выделив одну переменную и выразив ее через другие переменные. Иногда нам дают формулу для определения площади геометрической фигуры, и нам нужно вывести формулу для определения длины стороны фигуры. Шаги для решения буквенных уравнений:
Определите переменную, которую вы хотите иметь отдельно.
Считать все остальные переменные/буквы числами.
Сложение, вычитание или умножение на переменную.
Вы также можете делить на переменную, если она никогда не равна нулю.
Используйте все правила алгебры, которые мы используем для решения алгебраических уравнений.
Изолировать переменную на одной стороне уравнения и, следовательно, получить решение
Давайте рассмотрим несколько примеров и решим буквальные уравнения, чтобы лучше понять.
Пример 1: Формула для определения площади прямоугольника: A = lb, где A обозначает площадь, l обозначает длину, а b обозначает ширину прямоугольника. Нам нужно вывести формулу для определения длины прямоугольника. У нас есть,
A = lb. Нам нужно выделить l и выразить его через A и b. Разделите обе части уравнения на b (поскольку ширина прямоугольника никогда не может быть равна 0)
A/b = lb/b ⇒ l = A/b
Мы решили буквальное уравнение A = lb относительно l и получили формула для l будет l = A/b.
Рассмотрим еще один пример алгебраического буквального уравнения и решим его.
Пример 2: Решите буквальное уравнение 2x + 7y = 12 относительно x.
Мы хотим, чтобы переменная x была одна в одной части уравнения, а y — в другой. Добавьте минус 7y к обеим частям уравнения 2x + 7y = 12,
2x + 7y + (-7y) = 12 + (-7y)
2x = 12 — 7y, Разделите все члены буквального уравнения на коэффициент x, чтобы изолировать переменную, то есть разделите уравнение на 2
2x/2 = (12 — 7y)/2
x = (12 — 7y)/2 = 6 — 7y/2
Следовательно, решение буквального уравнения 2x + 7y = 12 есть x = 6 — 7y/2
Важные примечания к литеральным уравнениям
Буквенное уравнение — это уравнение, в котором переменные представляют известные значения.
Буквенные уравнения используются для получения таких формул, как расстояние, скорость, площадь, объем, сила, время, температура и т. д.
Чтобы решить буквальные уравнения, выделите переменную и выразите ее как комбинацию остальных переменных.
Связанные темы по литеральным уравнениям
Переменные, константы и выражения
Выражения переменных
Линейные уравнения с двумя переменными
Часто задаваемые вопросы о буквальных уравнениях
Что такое буквальные уравнения в математике?
Буквенные уравнения определяются как уравнения, состоящие из двух или более переменных (букв или алфавитов), так что каждая переменная может быть выражена через другие переменные.
Как решать буквальные уравнения?
Буквенные уравнения можно решить, выделив одну переменную и выразив ее через другие переменные.
Что является примером буквального уравнения?
Типичными примерами буквальных уравнений являются такие формулы, как E = mc ² , A = bh, C = 2πr и т. д.
Почему мы переставляем буквенные уравнения?
Буквенные уравнения перестраиваются таким образом, чтобы показать взаимосвязь между переменными, и часто помогают нам решать такие формулы, как площадь, скорость, объем и т. д. При переписывании или перестановке буквенных уравнений нам просто нужно использовать обратные операции, чтобы получить конкретное значение. переменная сама по себе.
Как выглядят буквальные уравнения?
Буквенные уравнения — это уравнения, включающие буквы и алфавиты. Они состоят из двух или более переменных.
В чем разница между линейными и буквальными уравнениями?
Линейные уравнения – это уравнения, имеющие переменные степени 1 и также могут иметь только одну переменную. С другой стороны, буквальные уравнения — это уравнения, которые имеют по крайней мере две переменные.
Как выглядит буквальное уравнение?
Литеральные уравнения — это уравнения с более чем одной переменной.
No related posts.